A Three-Parameter Hydrological Model for Monthly Runoff Simulation—A Case Study of Upper Hanjiang River Basin
Abstract
:1. Introduction
2. Methodology
2.1. SCS Runoff Model and Generalized Proportionality Hypothesis
2.2. Proportionality Hypothesis Application for Monthly Water Balance
2.3. Model Structure and Solution Method
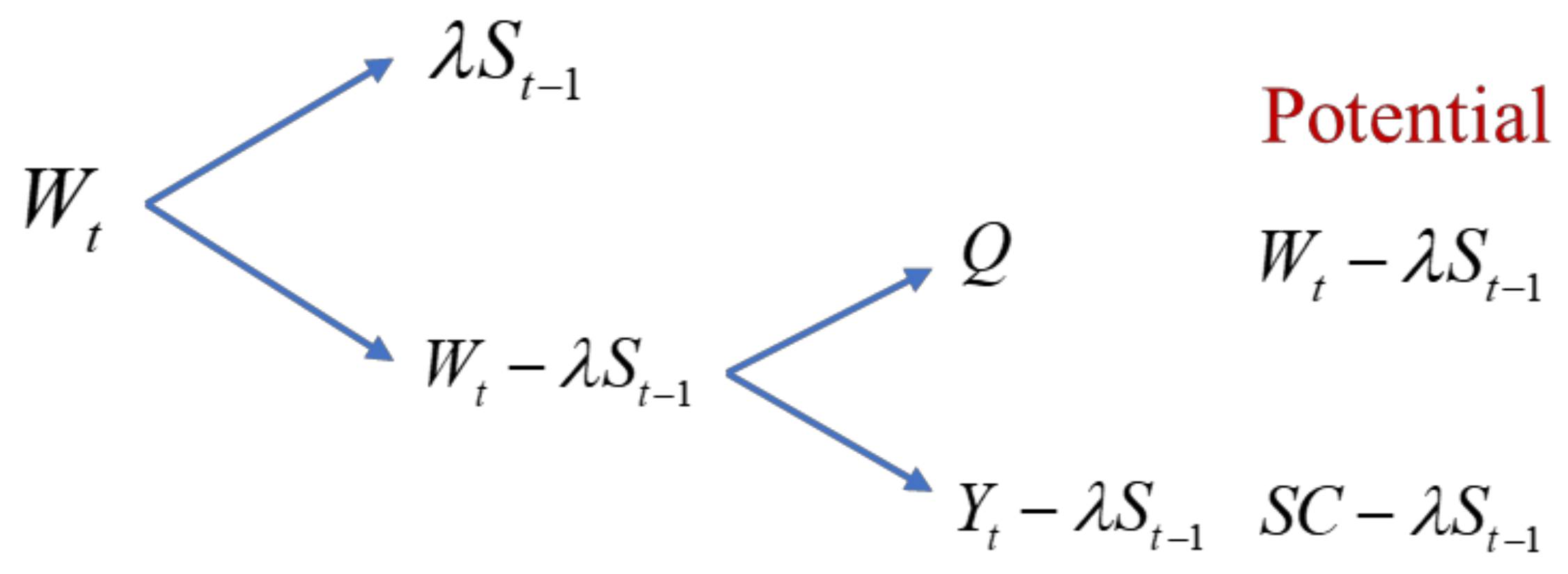
2.3.1. The Solution of Actual Evapotranspiration
2.3.2. The Solution of Soil Water Content and Runoff
2.4. Parameter Optimization
2.5. Model Evaluations
- (1)
- Nash-Sutcliffe Efficiency (NSE)
- (2)
- Kling–Gupta Efficiency (KGE)
3. Case Study
3.1. Study Area
3.2. Data Sources
4. Result and Discussion
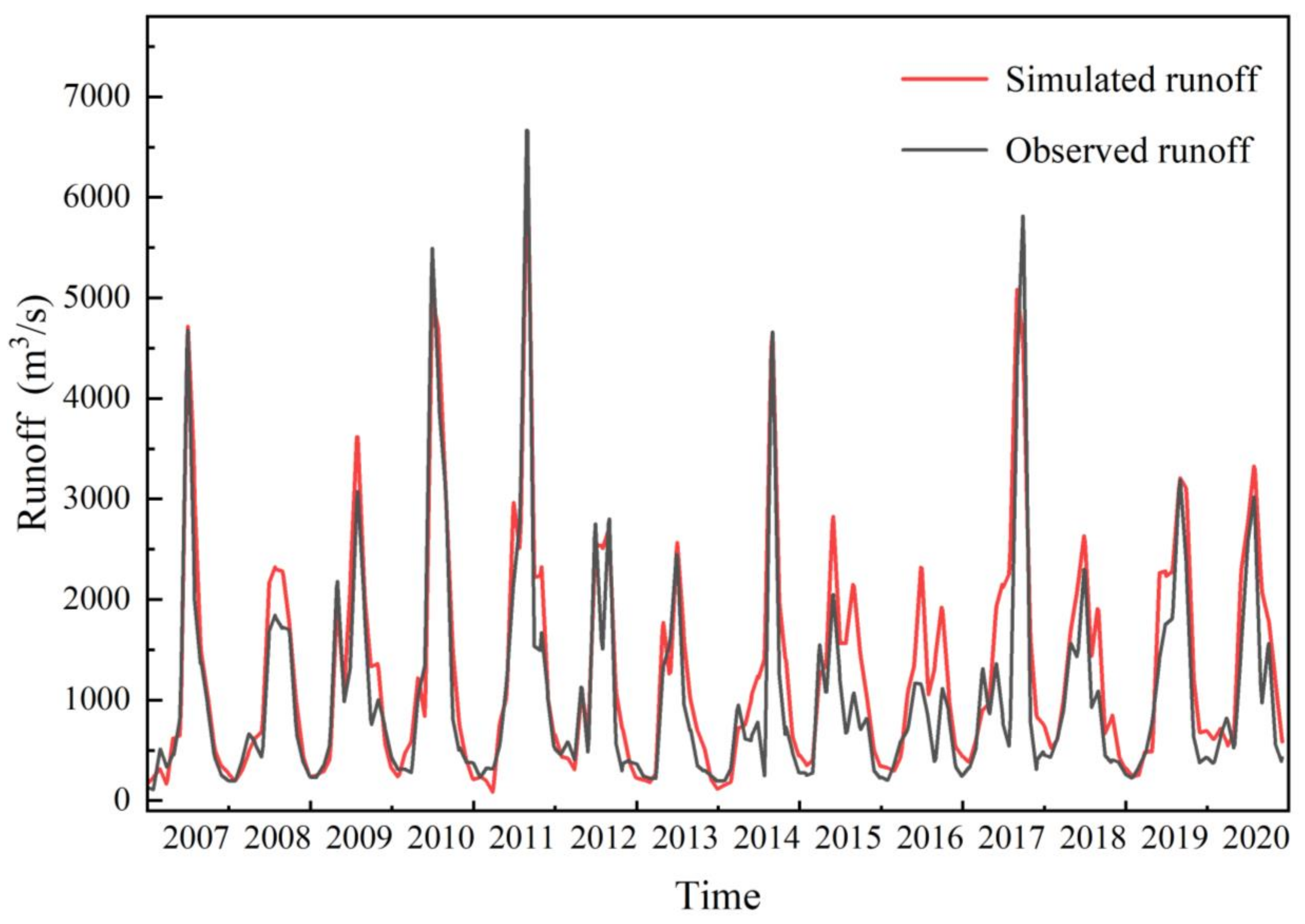
4.1. Model Performance and Parameter Result
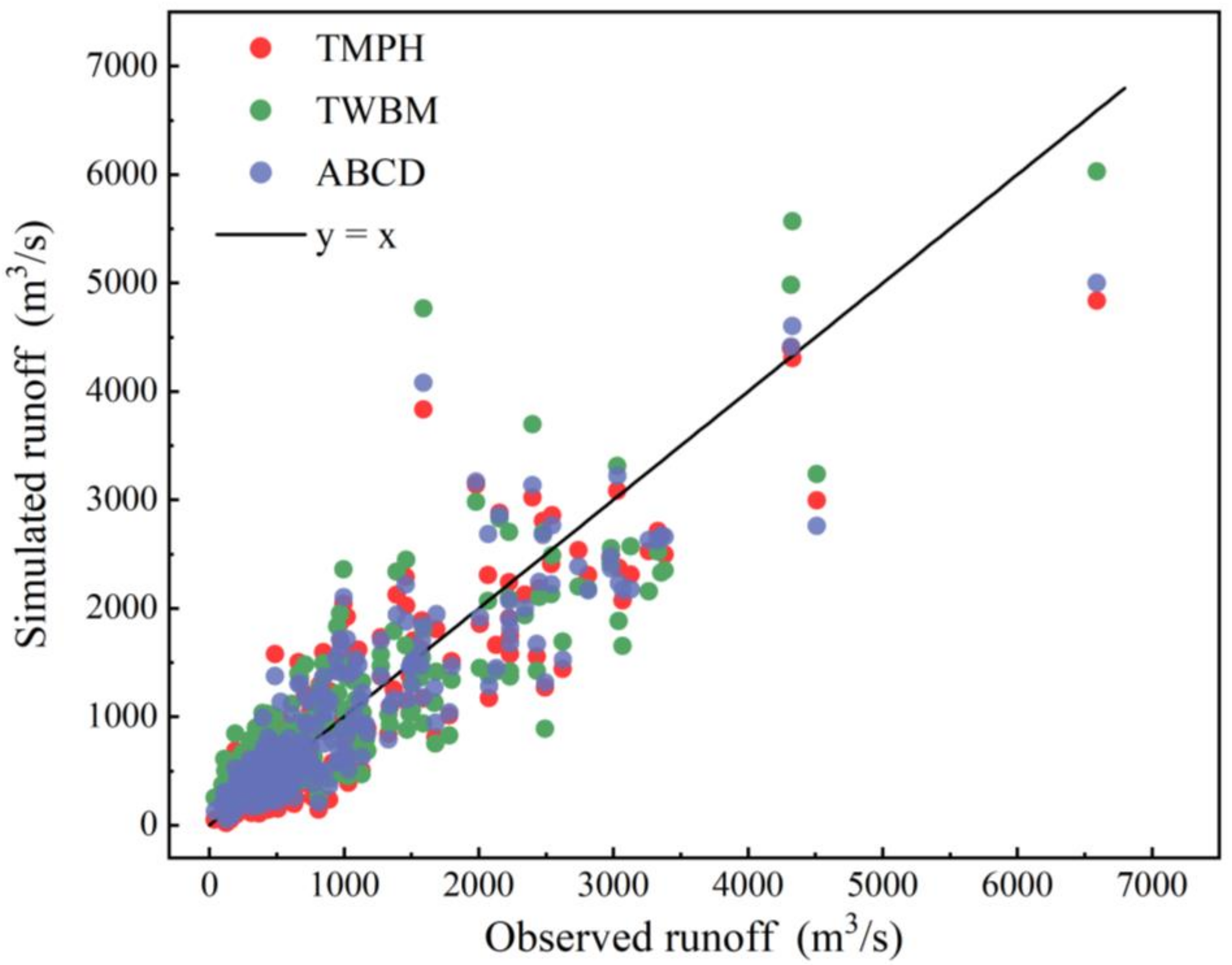
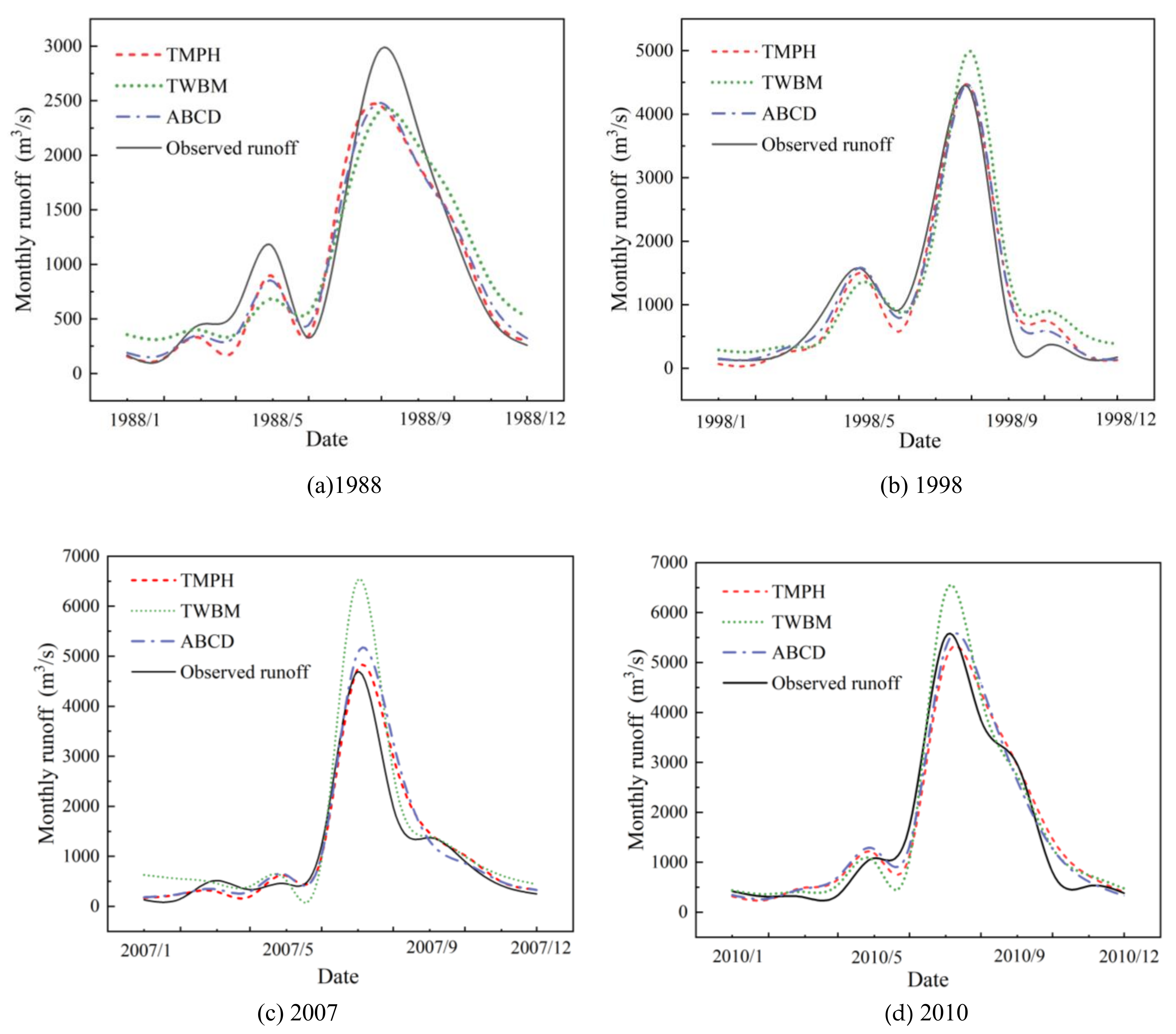
4.2. Comparison of Model Performance with the TWBM Model and the ABCD Model
4.3. Sensitivity Analysis of TMPH Model Parameters
5. Conclusions
- (1)
- The proposed TMPH model shows good performance in the monthly runoff simulation in UHRB, with a simple model structure and few parameters. Specifically, the values of NSE are 0.79 for the calibration period and 0.83 for the validation period, with the value of KGE are 0.86 for the calibration period and 0.78 for the validation period;
- (2)
- In UHRB, the proposed TMPH model have better performance than the TWBM model, especially in the case of higher runoff values. Specifically, the value of NSE increases from 0.72 to 0.79 for the calibration period, and from 0.72 to 0.83 for the validation period. Meanwhile, the value of KGE increases from 0.84 to 0.86 for the calibration period, and from 0.62 to 0.78 for the validation period;
- (3)
- In UHRB, the TMPH model shows a comparable result with the ABCD model in the calibration period, with NSE values of TMPH and ABCD of 0.79 and 0.80, respectively, the KGE values are both 0.86, respectively. While in the validation period, the TMPH model has improved slightly, with the value of NSE increasing from 0.81 to 0.83, while increasing the KGE from 0.75 to 0.78;
- (4)
- The sensitivity analysis of TMPH model parameters shows that the simulation result is most sensitive to parameter n, followed by parameter SC and parameter .
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Monthly Models
Appendix A.1. TWBM Model
Appendix A.2. ABCD Model
References
- Cheng, S.; Cheng, L.; Liu, P.; Zhang, L.; Xu, C.; Xiong, L.; Xia, J. Evaluation of baseflow modelling structure in monthly water balance models using 443 Australian catchments. J. Hydrol. 2020, 591, 125572. [Google Scholar] [CrossRef]
- Schär, C.; Vasilina, L.; Pertziger, F.; Dirren, S. Seasonal runoff forecasting using precipitation from meteorological data assimilation systems. J. Hydrometeorol. 2004, 5, 959–973. [Google Scholar] [CrossRef]
- Deng, C.; Wang, W. A two-stage partitioning monthly model and assessment of its performance on runoff modeling. J. Hydrol. 2021, 592, 125829. [Google Scholar] [CrossRef]
- Mohseni, O.; Stefan, H.G. A monthly streamflow model. Water Resour. Res. 1998, 34, 1287–1298. [Google Scholar] [CrossRef]
- Wang, G.; Xia, J.; Chen, J. Quantification of effects of climate variations and human activities on runoff by a monthly water balance model: A case study of the Chaobai River basin in northern China. Water Resour. Res. 2009, 45, W00A1. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Balay, J.W.; Liu, C. Regional regression models for estimating monthly streamflows. Sci. Total Environ. 2020, 706, 135729. [Google Scholar] [CrossRef] [PubMed]
- Ndzabandzaba, C.; Hughes, D.A. Regional water resources assessments using an uncertain modelling approach: The example of Swaziland. J. Hydrol. Reg. Stud. 2017, 10, 47–60. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Thornthwaite, C.W.; Mather, J.R. The Water Balance; Laboratory of Climatology, Drexel Institute of Technology: Centerton, NJ, USA, 1955; Volume 8, pp. 1–104. [Google Scholar]
- Thomas, H. Improved Methods for National Water Assessment: Final Report; U.S. Geological Survey: Reston, VA, USA, 1981; Volume 44.
- Boughton, W.C. An Australian water balance model for semiarid watersheds. J. Soil Water Conserv. 1995, 50, 454–457. [Google Scholar]
- Xiong, L.; Guo, S. A two-parameter monthly water balance model and its application. J. Hydrol. 1999, 216, 111–123. [Google Scholar] [CrossRef]
- Zhang, L.; Potter, N.; Hickel, K.; Zhang, Y.; Shao, Q. Water balance modeling over variable time scales based on the Budyko framework—Model development and testing. J. Hydrol. 2008, 360, 117–131. [Google Scholar] [CrossRef]
- Bai, P.; Liu, X.; Liang, K.; Liu, C. Comparison of performance of twelve monthly water balance models in different climatic catchments of China. J. Hydrol. 2015, 529, 1030–1040. [Google Scholar] [CrossRef]
- Jiang, T.; Chen, Y.Q.D.; Xu, C.Y.Y.; Chen, X.H.; Chen, X.; Singh, V.P. Comparison of hydrological impacts of climate change simulated by six hydrological models in the Dongjiang Basin, South China. J. Hydrol. 2007, 336, 316–333. [Google Scholar] [CrossRef]
- Vandewiele, G.L.; Ni Lar, W. Monthly water balance models for 55 basins in 10 countries. Hydrol. Sci. J. 1998, 43, 687–699. [Google Scholar] [CrossRef]
- Ye, W.; Bates, B.; Viney, N.; Sivapalan, M.; Jakeman, A. Performance of conceptual rainfall-runoff models in low-yielding ephemeral catchments. Water Resour. Res. 1997, 33, 153–166. [Google Scholar] [CrossRef]
- Al-Ghobari, H.; Dewidar, A.Z. Integrating GIS-Based MCDA Techniques and the SCS-CN Method for Identifying Potential Zones for Rainwater Harvesting in a Semi-Arid Area. Water 2021, 13, 704. [Google Scholar] [CrossRef]
- Amatya, D.M.; Walega, A.; Callahan, T.J.; Morrison, A.; Vulava, V.; Hitchcock, D.R.; Williams, T.M.; Epps, T. Storm event analysis of four forested catchments on the Atlantic coastal plain using a modified SCS-CN rainfall-runoff model. J. Hydrol. 2022, 608, 127772. [Google Scholar] [CrossRef]
- Kumar, A.; Kanga, S.; Taloor, A.K.; Singh, S.K.; Đurin, B. Surface runoff estimation of Sind river basin using integrated SCS-CN and GIS techniques. HydroResearch 2021, 4, 61–74. [Google Scholar] [CrossRef]
- Poncea, V.M.; Shetty, A.V. A conceptual model of catchment water balance: 1. Formulation and calibration. J. Hydrol. 1995, 173, 27–40. [Google Scholar] [CrossRef]
- Wang, D.B.; Tang, Y. A one-parameter Budyko model for water balance captures emergent behavior in darwinian hydrologic models. Geophys. Res. Lett. 2014, 41, 4569–4577. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.B.; Zhao, J.S.; Tang, Y.; Sivapalan, M. A thermodynamic interpretation of Budyko and L’vovich formulations of annual water balance: Proportionality Hypothesis and maximum entropy production. Water Resour. Res. 2015, 51, 3007–3016. [Google Scholar] [CrossRef]
- Zhao, J.S.; Wang, D.B.; Yang, H.B.; Sivapalan, M. Unifying catchment water balance models for different time scales through the maximum entropy production principle. Water Resour. Res. 2016, 52, 7503–7512. [Google Scholar] [CrossRef]
- Sivapalan, M.; Yaeger, M.A.; Harman, C.J.; Xu, X.; Troch, P.A. Functional model of water balance variability at the catchment scale: 1. Evidence of hydrologic similarity and space-time symmetry. Water Resour. Res. 2011, 47, W02522. [Google Scholar] [CrossRef]
- Chen, X.; Wang, D. Modeling seasonal surface runoff and base flow based on the generalized proportionality hypothesis. J. Hydrol. 2015, 527, 367–379. [Google Scholar] [CrossRef]
- Yang, H.; Yang, D.; LEI, Z.; LEI, H. Derivation and validation of watershed coupled water-energy balance equation at arbitrary time scale. J. Hydraul. Eng. 2008, 39, 610–617. [Google Scholar]
- Yang, H.; Yang, D.; Lei, Z.; Sun, F. New analytical derivation of the mean annual water-energy balance equation. Water Resour. Res. 2008, 44, W03410. [Google Scholar] [CrossRef]
- Xu, X.; Li, X.; He, C.; Tia, W.; Tian, J. Development of a simple Budyko-based framework for the simulation and attribution of ET variability in dry regions. J. Hydrol. 2022, 610, 127955. [Google Scholar] [CrossRef]
- Zhang, X.; Dong, Q.J.; Zhang, Q.; Yu, Y.G. A unified framework of water balance models for monthly, annual, and mean annual timescales. J. Hydrol. 2020, 589, 125186. [Google Scholar] [CrossRef]
- Xin, Z.H.; Li, Y.; Zhang, L.; Ding, W.; Ye, L.; Wu, J.; Zhang, C. Quantifying the relative contribution of climate and human impacts on seasonal streamflow. J. Hydrol. 2019, 574, 936–945. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V.K. Optimal use of the SCE-UA global optimization method for calibrating watershed models. J. Hydrol. 1994, 158, 265–284. [Google Scholar] [CrossRef]
- Zhang, S.; Shi, J. A Microwave Wetland Surface Emissivity Calibration Scheme Using SCE-UA Algorithm and AMSR-E Brightness Temperature Data. Procedia Environ. Sci. 2011, 10, 2731–2739. [Google Scholar] [CrossRef] [Green Version]
- Duan, Q.Y.; Gupta, V.K.; Sorooshian, S. Shuffled complex evolution approach for effective and efficient global minimization. J. Optim. Theory Appl. 1993, 76, 501–521. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. Asabe 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Li, Y.; Grimaldi, S.; Pauwels, V.R.N.; Walker, J.P. Hydrologic model calibration using remotely sensed soil moisture and discharge measurements: The impact on predictions at gauged and ungauged locations. J. Hydrol. 2018, 557, 897–909. [Google Scholar] [CrossRef]
- Xiong, L.H.; Yu, K.X.; Gottschalk, L. Estimation of the distribution of annual runoff from climatic variables using copulas. Water Resour. Res. 2014, 50, 7134–7152. [Google Scholar] [CrossRef]
- Xu, Y.N.; Fu, X.; Chu, X.F. Analyzing the Impacts of Climate Change on Hydro-Environmental Conflict-Resolution Management. Water Resour. Manag. 2019, 33, 1591–1607. [Google Scholar] [CrossRef]

| Parameters | Defintion | Ranges |
|---|---|---|
| Initial water loss ratio (-) | 0–1 | |
| SC | Water loss capacity of the basin (mm) | 0–2000 |
| n | Evapotranspiration parameter (-) | 0–2 |
| Model | Calibration Period | Validation Period | ||
|---|---|---|---|---|
| NSE | KGE | NSE | KGE | |
| TMPH | 0.79 | 0.86 | 0.83 | 0.78 |
| TWBM | 0.72 | 0.84 | 0.72 | 0.62 |
| ABCD | 0.80 | 0.86 | 0.81 | 0.75 |
| Parameters | Changes | Index Value | Percentage Change | ||
|---|---|---|---|---|---|
| NSE | KGE | NSE | KGE | ||
| +50% | 0.76 | 0.76 | −3.80% | −11.63% | |
| −50% | 0.77 | 0.88 | −2.53% | 2.33% | |
| SC | +50% | 0.74 | 0.69 | −6.33% | −19.77% |
| −50% | 0.64 | 0.71 | −18.99% | −17.44% | |
| n | +50% | 0.58 | 0.66 | −26.58% | −23.26% |
| −50% | −0.13 | 0.13 | −116.46% | −84.88% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, Y.; Yan, B.; Feng, B.; Zhang, J.; Tang, Y. A Three-Parameter Hydrological Model for Monthly Runoff Simulation—A Case Study of Upper Hanjiang River Basin. Water 2023, 15, 474. https://doi.org/10.3390/w15030474
Zou Y, Yan B, Feng B, Zhang J, Tang Y. A Three-Parameter Hydrological Model for Monthly Runoff Simulation—A Case Study of Upper Hanjiang River Basin. Water. 2023; 15(3):474. https://doi.org/10.3390/w15030474
Chicago/Turabian StyleZou, Yixuan, Baowei Yan, Baofei Feng, Jun Zhang, and Yiwei Tang. 2023. "A Three-Parameter Hydrological Model for Monthly Runoff Simulation—A Case Study of Upper Hanjiang River Basin" Water 15, no. 3: 474. https://doi.org/10.3390/w15030474









