1. Introduction
At present, with the rapid development of society and the economy, coal resources occupy an important position [
1]; however, at the same time, the existence of hidden dangers, such as mine floods and the occurrence of accidents, restrict and hinder the safe production of mines. These have led to major disasters occurring in China [
2,
3,
4]. After a water outburst, coal mines bear huge drainage costs [
5]. In addition, mine water inrushes will also lead to a shortage of water resources and underground water pollution, which brings great risks to the safe use of water resources [
6,
7,
8]. Mine inrushes will cause serious threats and losses to the economy and resource utilization [
9,
10,
11]. Once a mine water inrush occurs, only by quickly and accurately identifying the source of the water inrush can targeted governance be carried out [
5]. Seen from the actual situation of coal mine water disaster, although many new theories, methods, and technologies have been put forward in the prediction of coal mine water inrush, the serious and super large water inrush accidents have not been effectively curbed, which shows that the prediction of floor water inrush is far from the actual application.
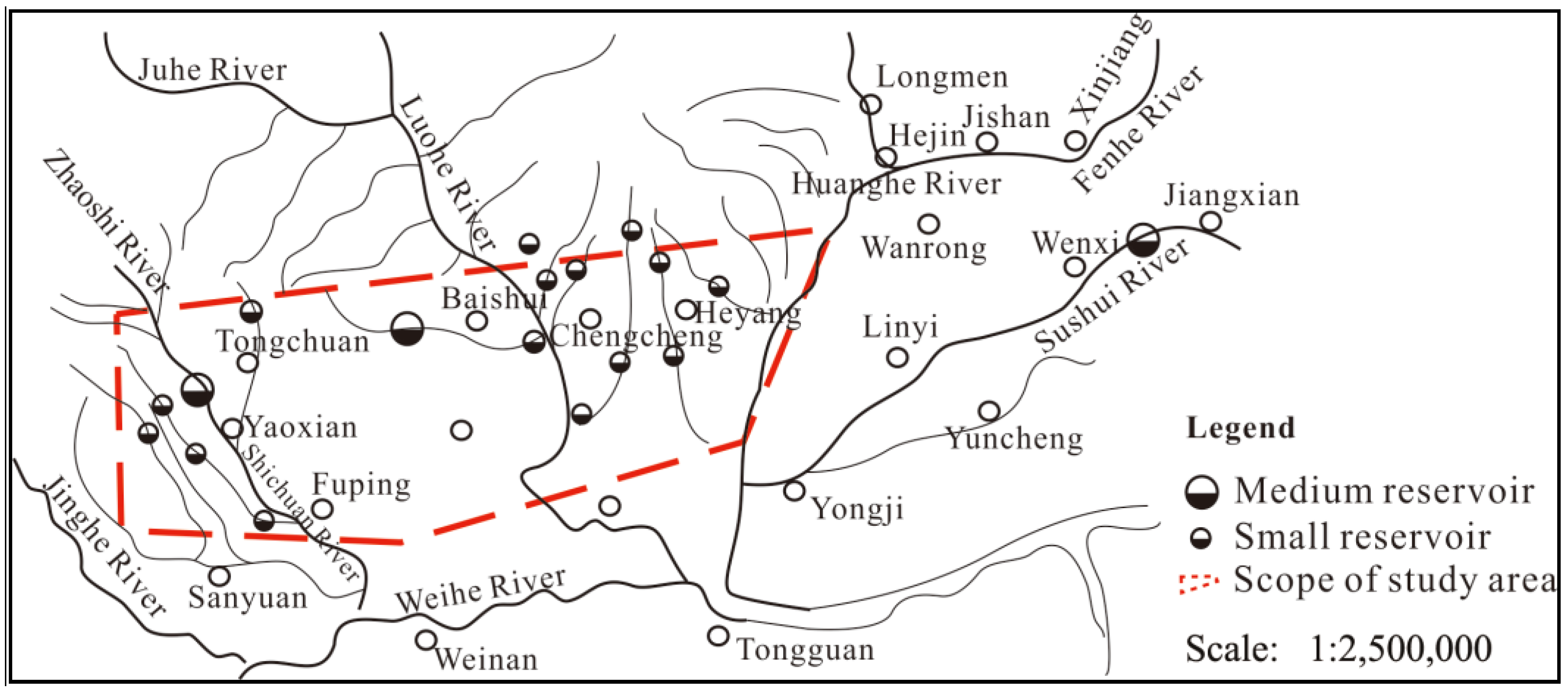
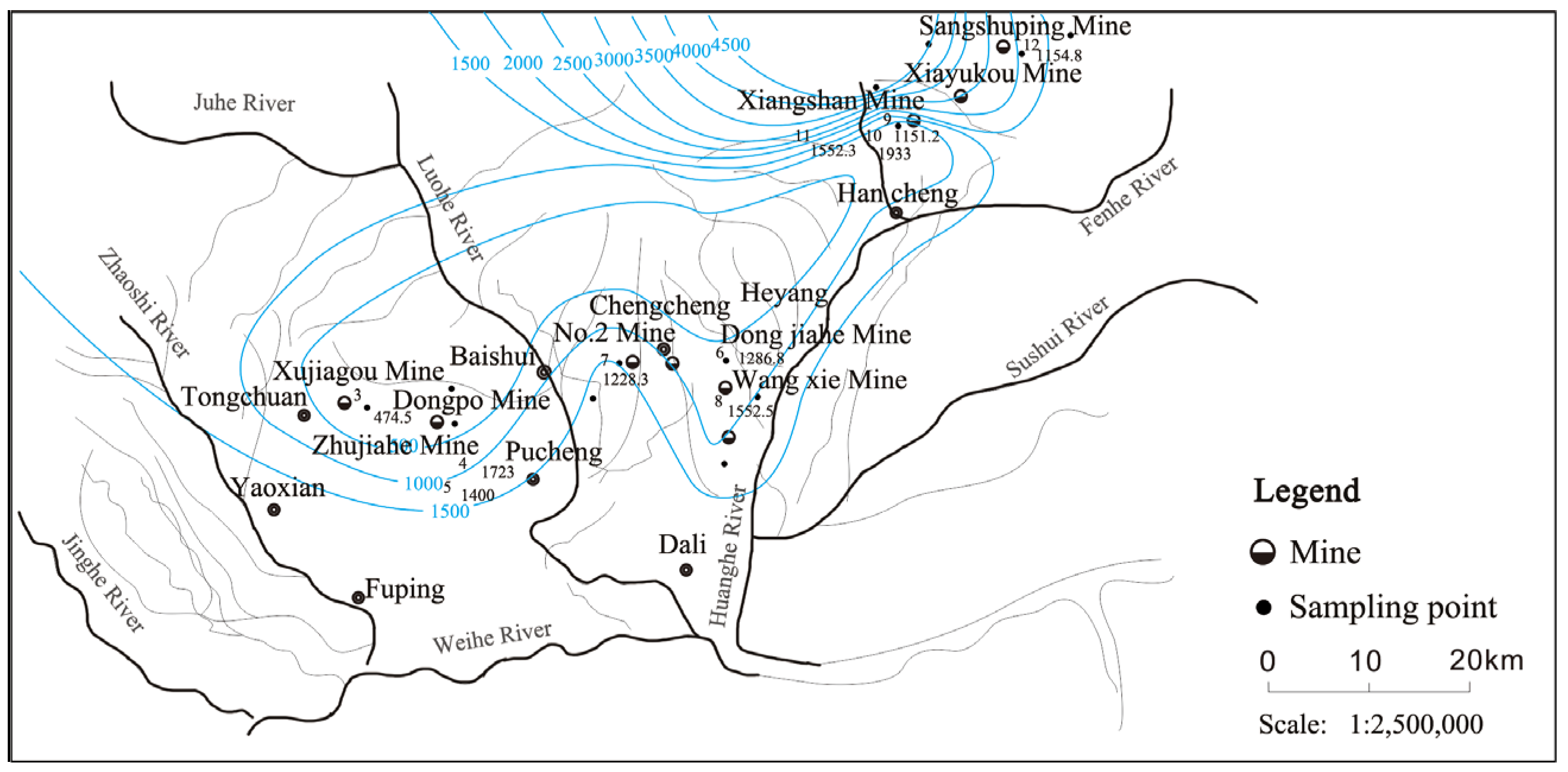
For the Weibei mining area, there are difficulties in exploring the source of sudden water inflows. The conventional hydrochemical characteristics of the Taiyuan limestone aquifer and Ordovician limestone aquifer are similar. The groundwater quality in the mining area changes due to the mixing, overflow, and recharge of multiple water sources. The hydrogeological conditions of limestone aquifers are complex, karst development is uneven, strong runoff zones occur, water richness varies greatly, and the hydraulic connection is changeable. Geochemical exploration can identify hydrogeological conditions to a certain extent, as well as guide production and prevent water disasters.
With the deepening of the mining level, mining intensity and scale have also increased, and the frequency of water inrush has also increased. Therefore, it is imperative to control mine outbursts [
5,
12]. In recent years, a large number of ideas and methods have emerged for the identification of outburst water sources, such as feature component discrimination [
13], the water chemical feature method [
12,
14,
15,
16], water temperature and water level discrimination [
17], and geophysical exploration [
17,
18]. Among them, the water chemical feature method is the most widely used in water source identification due to its advantages of economy, efficiency, and high accuracy [
5,
19,
20], and it can provide an important basis for mine water control. Judging from the change in water volume, there is generally a process from quantitative change to qualitative change from “wet gang → dripping water → water spraying → flowing water → water inrush”. Each aquifer in the mining area has different water chemistry characteristics [
21,
22]. Therefore, according to the characteristics of water chemical ion components, a mathematical statistical method can be used to build a water source discrimination model. Common water source discriminant models include gray correlation [
16,
23], the fuzzy comprehensive evaluation method [
17,
24], cluster analysis [
13,
15,
17,
25,
26], discriminant analysis [
2,
16,
18,
25,
27], and BP neural network discrimination [
16]. However, in recent decades, this research has been based on the mathematical statistical methods used to build water-discriminative models, ignoring the similarity between outbursts and the chemical control mechanism of each water-bearing layer [
5]. By studying the similarity between the water chemical control mechanism, it is possible to determine whether the water chemical properties of different water layers are similar and, to a certain extent, judge the hydraulic connection between different water layers. Knowing the changes in water connections in advance can prevent mine water inrushes [
16]. Even if mine water inrush is discovered, looking at the similarities in the water chemical mechanism, we can quickly obtain the source of water inrush for governance through a comparison between the water inrush. Therefore, the comparative analysis of hydrochemical types, identification of hydrochemical components, and comprehensive mathematical analysis of hydrochemical components can be used to supplement the detection of water inrush sources and allow for the early warning regarding water inrush.
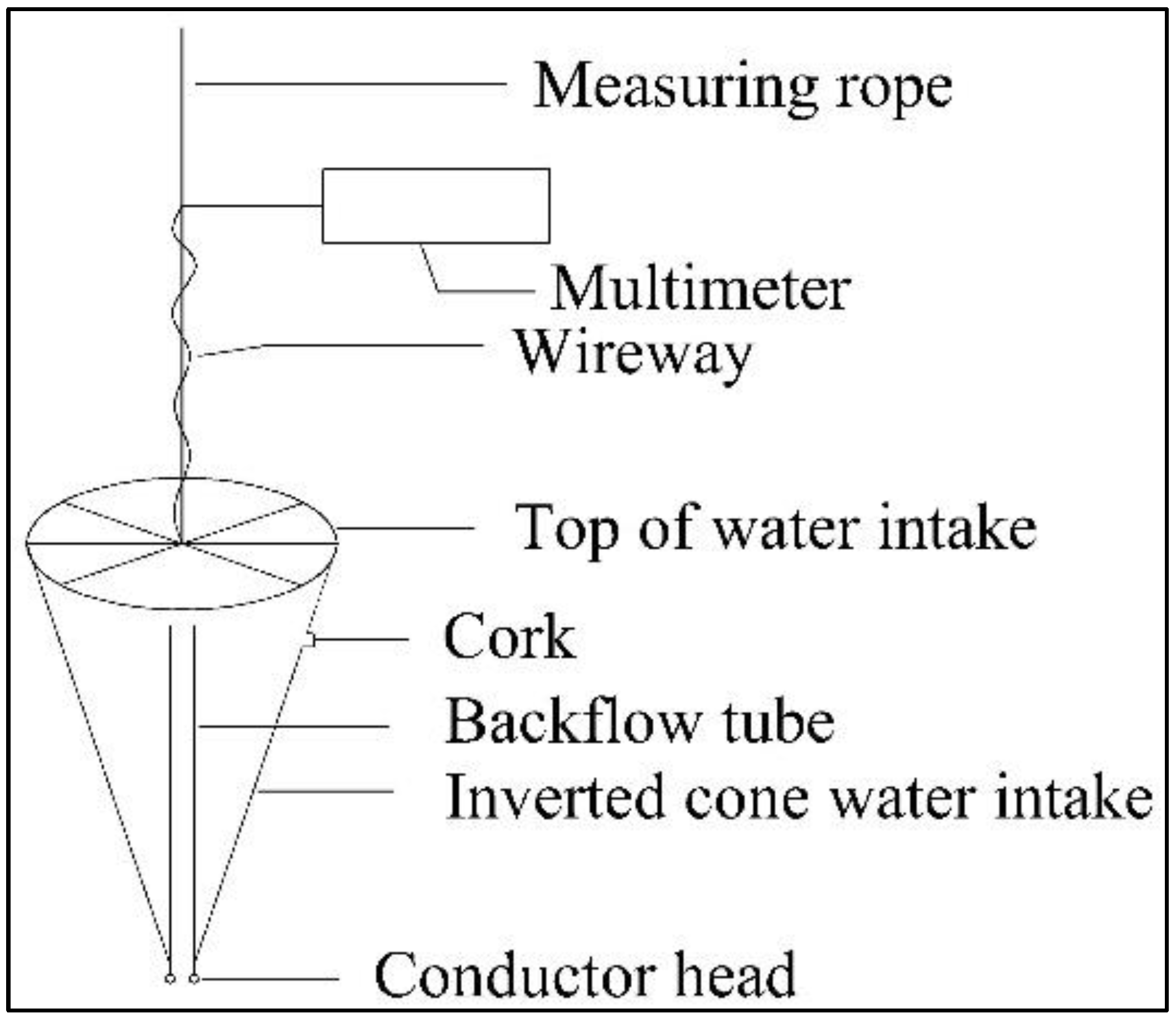
This paper takes the regional water outburst in Weibei coalfield, Shaanxi Province, as the research background. Based on the changes in water sample data from regular observation holes, downhole outbursts, water sample data from water inflow points, conventional hydrochemical test data, and ICP-MS data, the regional groundwater hydrogeological conditions, hydrogeochemical characteristics of the mining area, and establishment of hydrochemical characteristics files were obtained. The discriminant mode, considering the similarities between the water inrush and the chemical control mechanism of each aquifer, can be used to identify the source of water inrush in the Weibei coalfield area.
4. Discussion
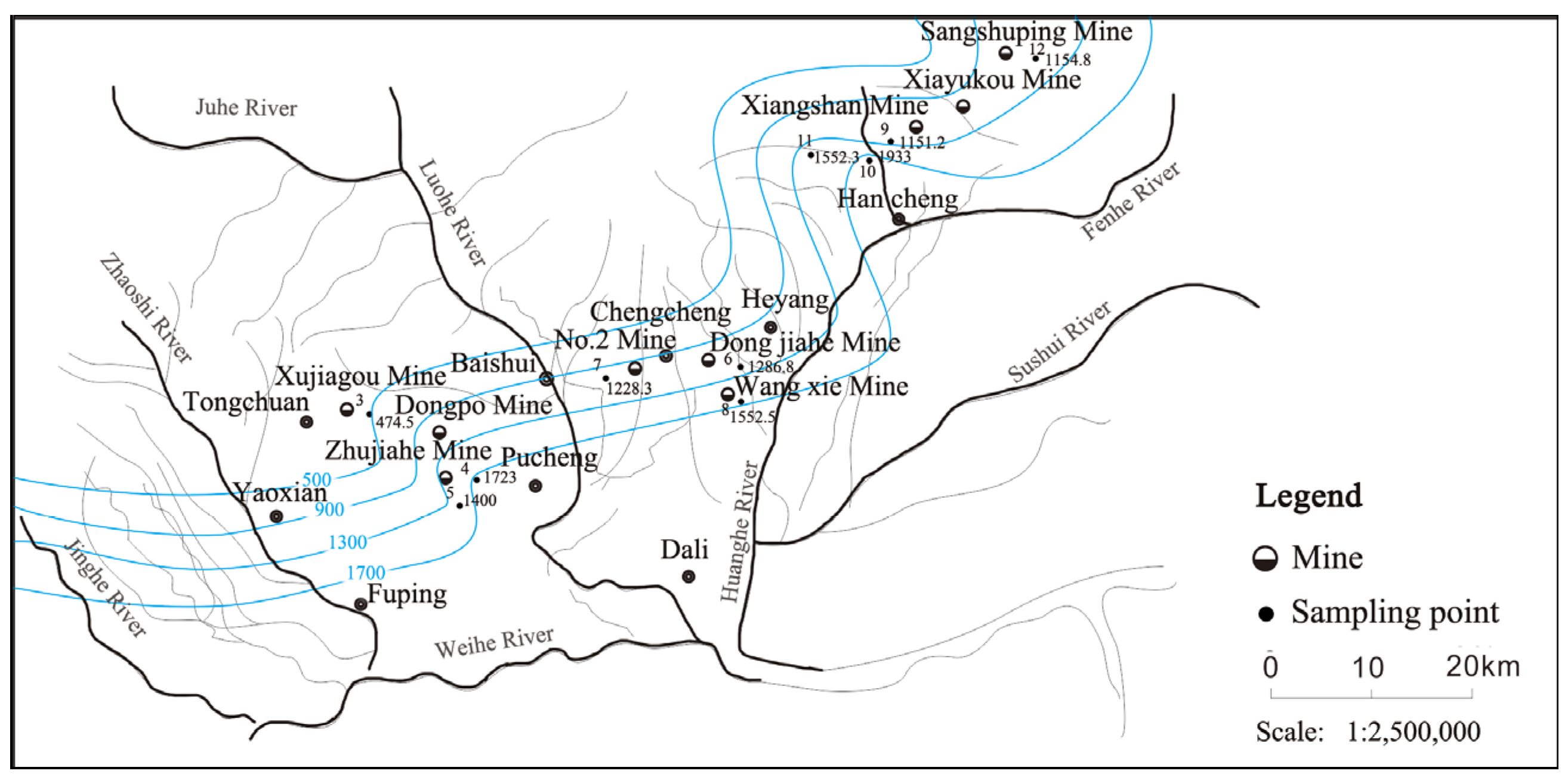
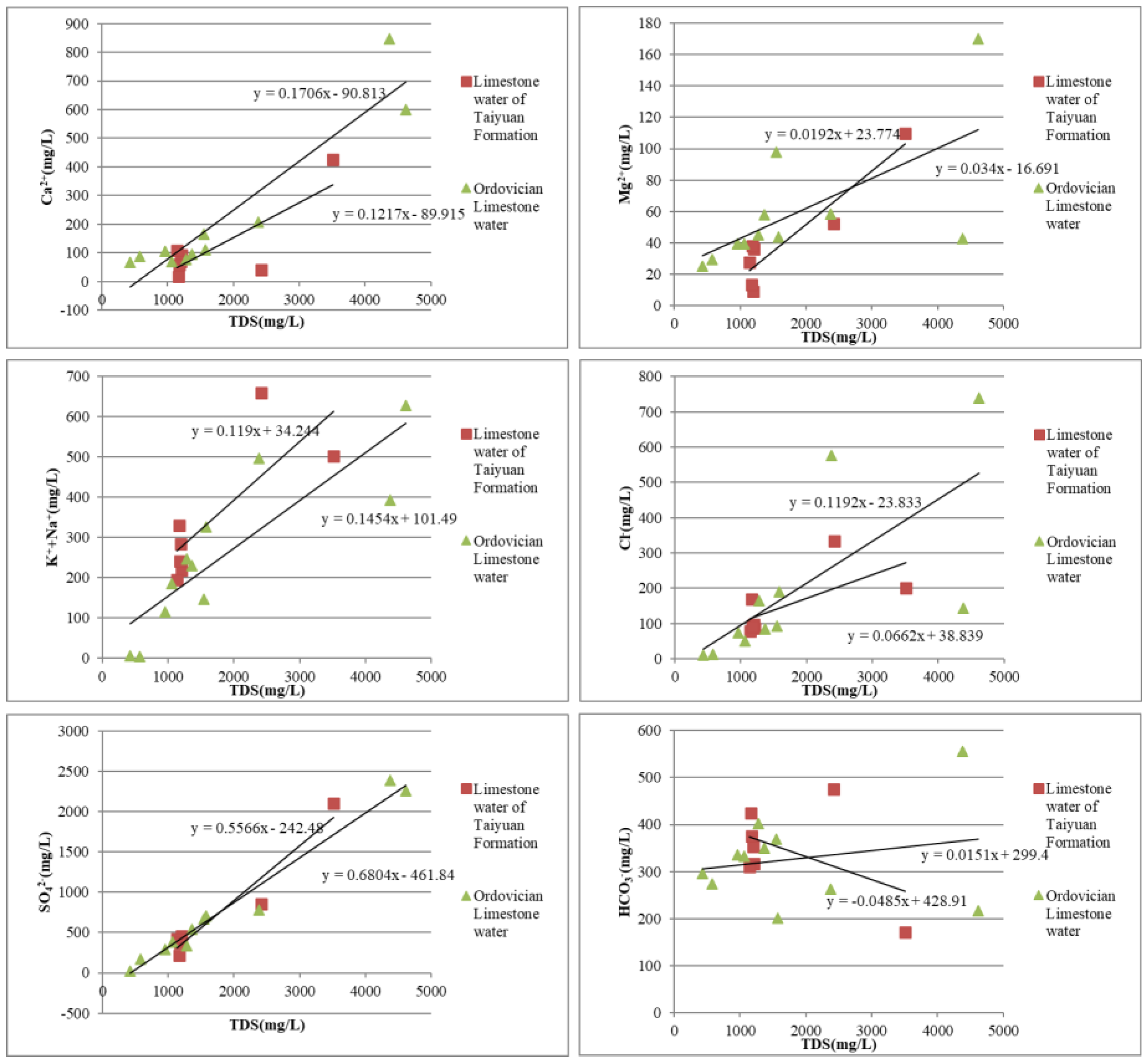
In the groundwater circulation system, the smaller the TDS, the more sufficient the water recharge and the shorter the groundwater retention time [
34]. This also leads to the relative weakening of hydrogeochemical effects such as karst filtration. In a groundwater circulation system, at a certain level, water quality is generally considered to migrate from a small TDS area to a large TDS area. The tighter the contour line, the more sufficient the filtration effect with the surrounding karst; the sparser the contour line, the weaker the filtration effect with the surrounding karst. Among them, limestone water of the Taiyuan formation and Ordovician limestone water in the Weibei mining area are the two major karst water inrush water sources, and the water-bearing medium is composed of carbonate minerals such as limestone, marl, and dolomite. The water quality of too-ash and ash water in the whole mining area varies greatly with the geographical distribution of the mining area. The groundwater anions and cations in the two aquifers show their own characteristics, which are distinct from the recharge area, the runoff area and the discharge area or the stagnation area. On the one hand, carbonate rocks in karst strata are easily dissolved by water and transported by hydrodynamics; The relationship shows that there is a good linear correlation between the conventional ions and the TDS in the ash water. Therefore, it is possible to study the hydrochemical characteristics of the karst water aquifer subsystem and the Orthodox ash aquifer subsystem as a single karst water system to analyze the relationship between the conventional ions of karst water and TDS, especially the relationship between Ca
2+ and TDS, which is helpful for understanding the karst water system. The water cycle is very important. In addition, most of the conventional ion content in the Weibei mining area increases with the increase of TDS, which shows the accuracy and reliability of using TDS as a comprehensive index to simulate the groundwater concentration gradient field to analyze its cycle characteristics [
35]. The karst water system of the Tongchuan-Pucheng-Heyang hydrogeological unit is closely related to the overlying shallow aquifer, surface water, and atmospheric precipitation. The dissolution of limestone and dolomite reaches saturation in the recharge area, and the karst groundwater in this area has poor solubility in the karst minerals in this area. In addition, the currently exploited Hancheng hydrogeological unit is the middle and deep detention area of the karst water system, with a relatively closed environment and poor exchange environment with surface water and atmospheric precipitation.
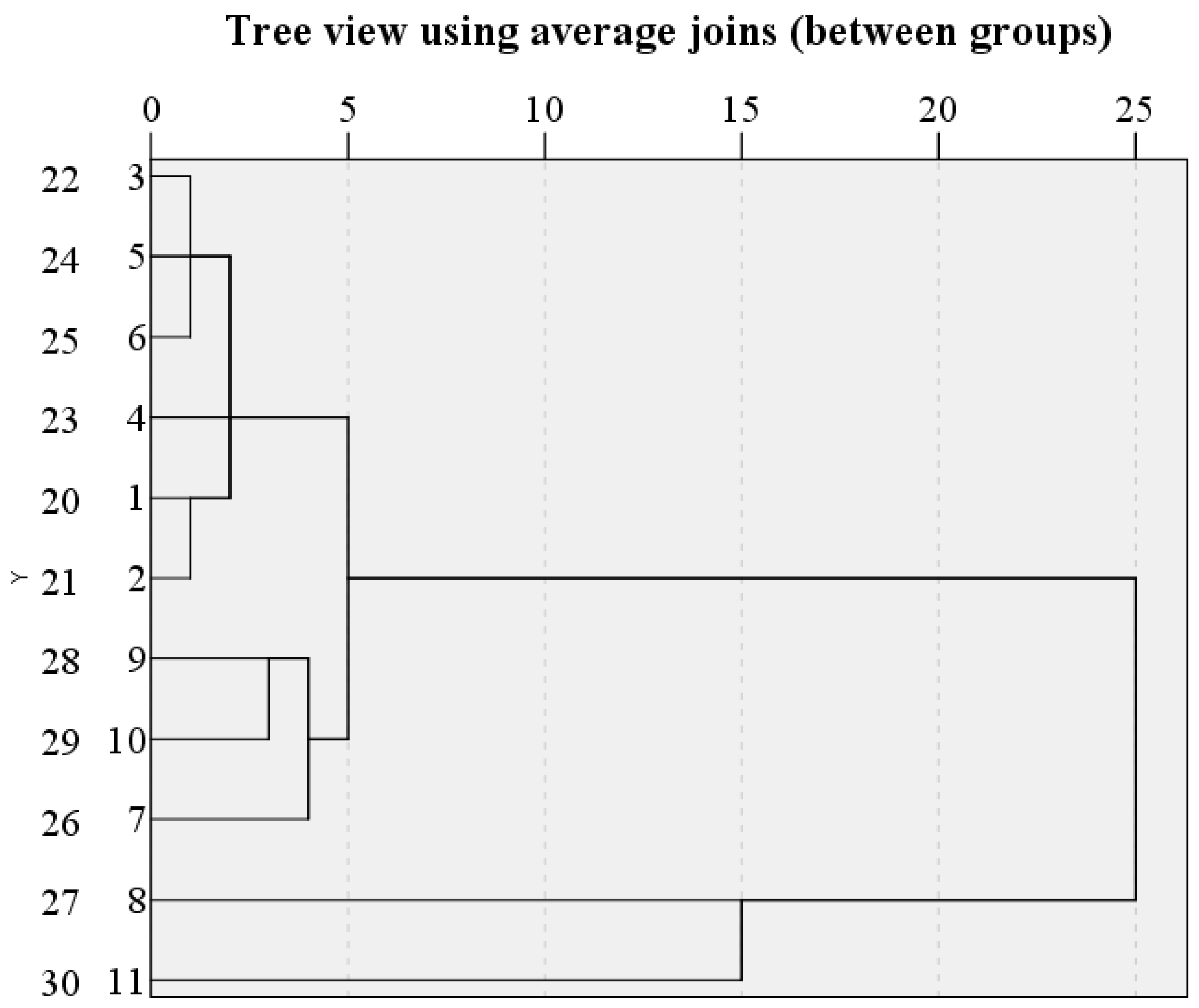
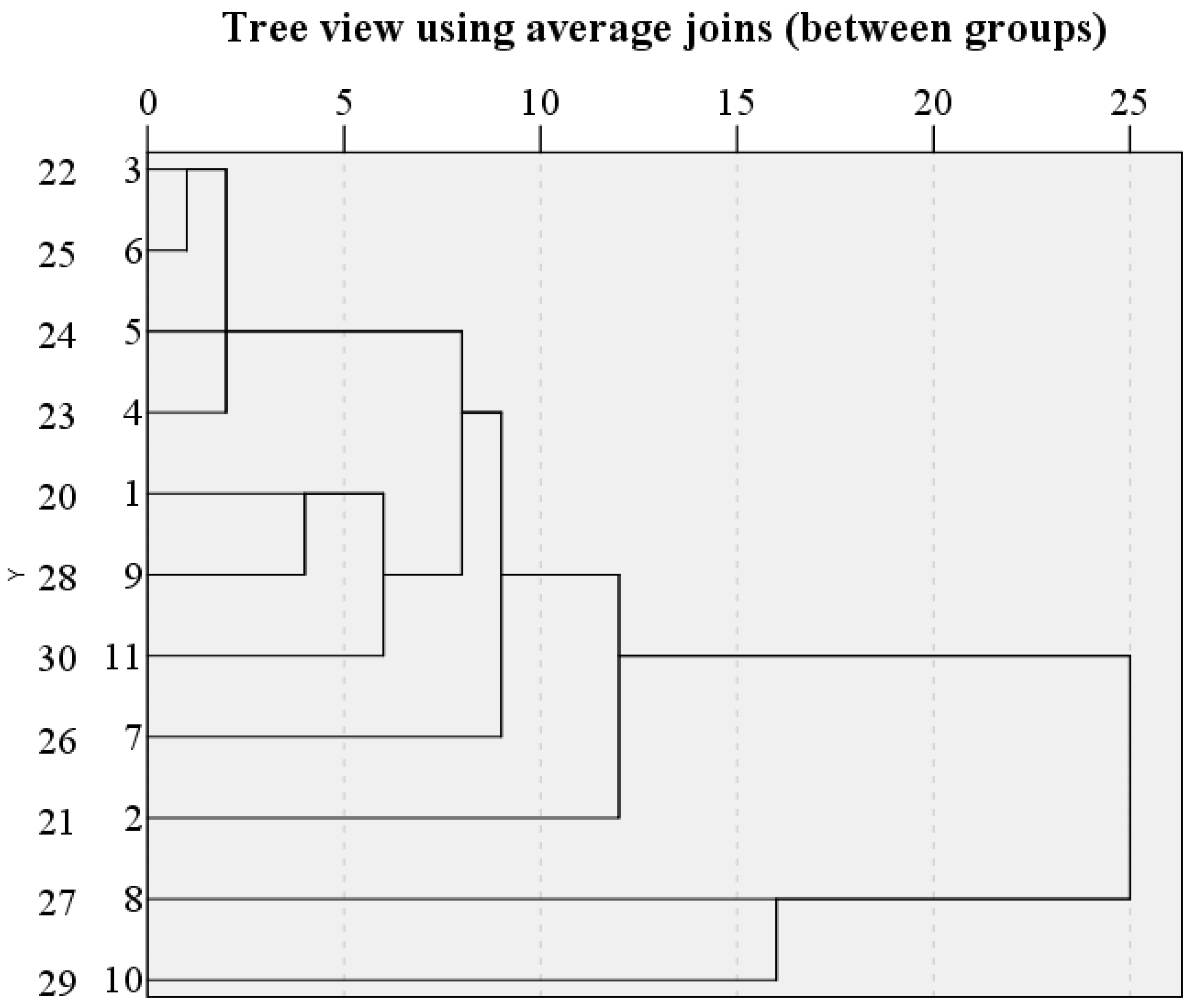
Twenty water samples were selected from the conventional hydrochemical test results using the cluster stepwise discriminant analysis method, and three hydrochemical discriminant models of the Permian sandstone fractures, the Carboniferous sandstone (limestone) fractures, and the Ordovician limestone aquifers in the Weibei coalfield were established using the ten indicators of K+ + Na+, Ca2+, Mg2+, NH4+, Cl−, SO42−, HCO3−, pH value, total hardness, and TDS, and total hardness. The model was found to be able to better distinguish the source of water inrush through the Mahalanobian distance test. Through F test, it is considered that the six selected variables K+ + Na+, Mg2+, NH4+, Cl−, SO42−, and pH have significant discrimination ability and good effect, and effectively identify the three main water-inrush aquifers in Weibei mining area.
According to the difference in the principal component discriminant analysis results, combined with the regional geological background and structural geological characteristics of the aquifer in the mining area, the hydrogeochemical principal component discrimination can be carried out for different types of groundwater [
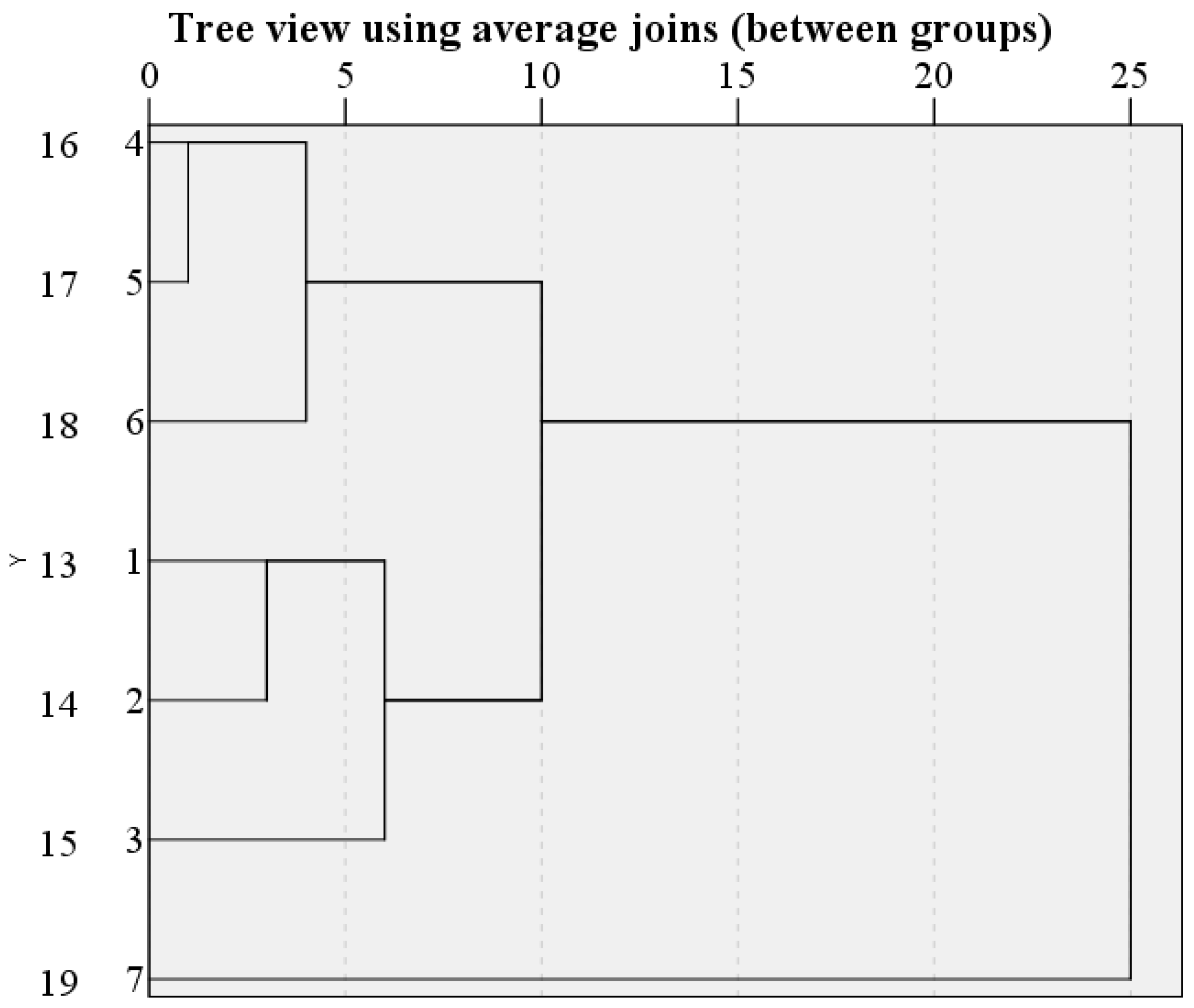
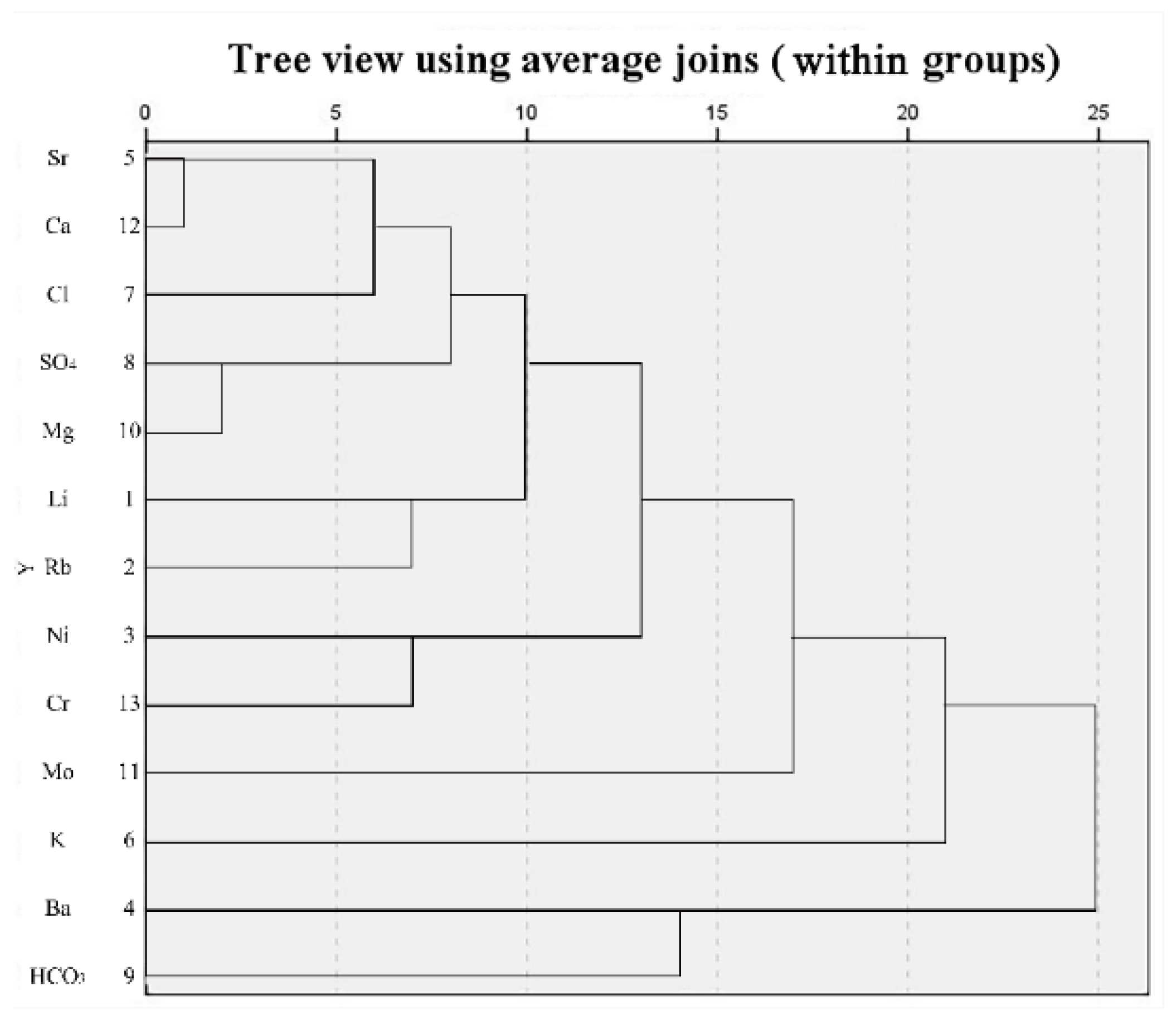
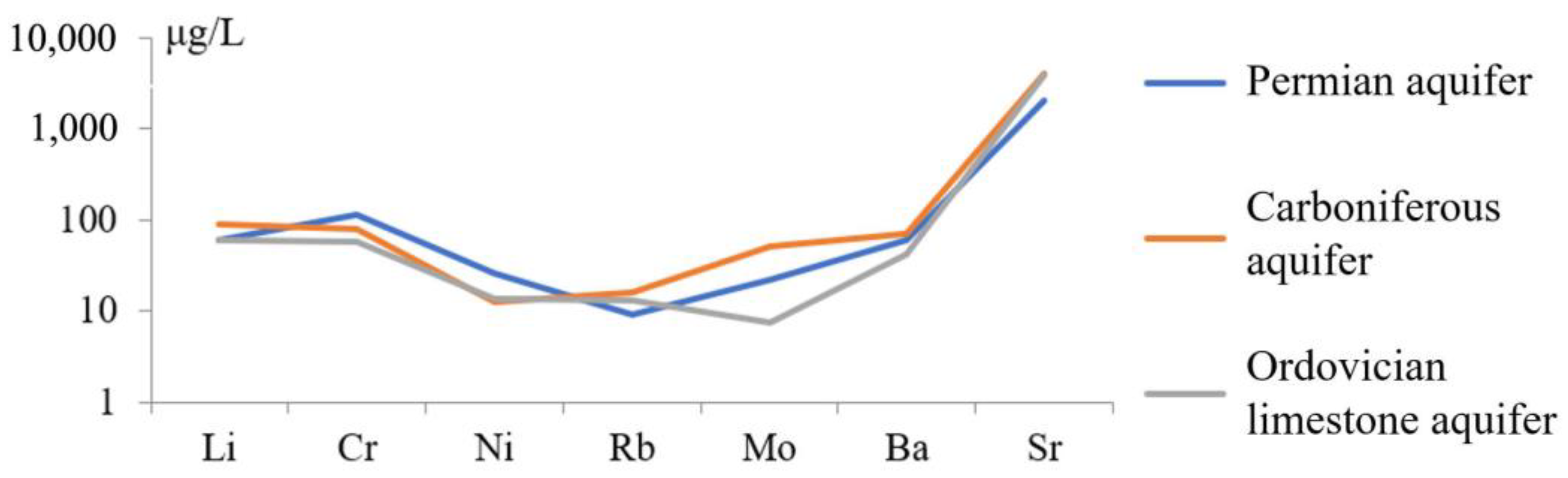
36]. This can better determine the trace element hydrogeochemical characteristics of the water inrush source in the mining area, accurately identify the water source, and serve the safe production of coal mines. Based on the principal component analysis and the cluster stepwise discriminant analysis method, twenty-four water samples and fourteen trace element indicators were selected from the conventional hydrochemical test results, and the principal component analysis discriminant model of trace elements for four main aquifers was established. On this basis, seven characteristic trace elements, Ni, Cr, Rb, Li, Sr, Mo, and Ba, are selected as the characteristic trace elements to identify the type of water inrush source and analyze the hydrogeochemical characteristics of the mining area. According to Bayes multi-class LDA model, the correct rate of discrimination with characteristic trace elements as explanatory variables is 89.3%, and the wrong rate is 10.07%. The correct rate of discrimination with conventional ions as explanatory variables was 64.3%, and the false rate was 35.7%. In order to improve the discrimination probability, the correct rate of Bayes multi-class linear discrimination of characteristic trace elements modified by conventional ions is 92.9%, and the discrimination effect is significantly improved.
5. Conclusions
Based on the regional hydrogeological conditions of the Weibei coalfield, the water inrush source in the mining area was selected as the research object, and the hydrogeochemical characteristics of trace elements were obtained. For the Quaternary loose aquifer, the Permian sandstone aquifer, the Carboniferous aquifer, and the Ordovician limestone aquifer, regular and trace water inrush source discrimination models were established for mathematical verification. Ten indicators were extracted from each water sample point to reflect the hydrogeological and chemical characteristics. The six indicators selected by the cluster stepwise discriminant analysis method through the Mahalanobis distance test have the significant discriminant ability and good effect and can better distinguish the water inrush sources. Through the principal component analysis and content characteristics analysis of trace elements, it is believed that the content-change trend of seven characteristic trace elements in the three aquifers is roughly the same; namely, Ni, Cr, Rb, Li, Sr, Mo, and Ba. However, with different aquifers, their migration characteristics and regular pattern in groundwater are different. A key comparison can be made between the modified trace element model and the conventional element model. The accuracy of the conventional element model was higher, with an accuracy rate of 92.9%. This lays a foundation for the systematic understanding of regional hydrogeological conditions in the Weibei coalfield and the establishment of a water inrush source discrimination model in the Weibei mining area. The research results can be further extended to all hydrogeological units in coal mining enterprises, and even to the whole country, with broad application prospects.