Comparison of Hydrological Platforms in Assessing Rainfall-Runoff Behavior in a Mediterranean Watershed of Northern Morocco
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of OLW Area
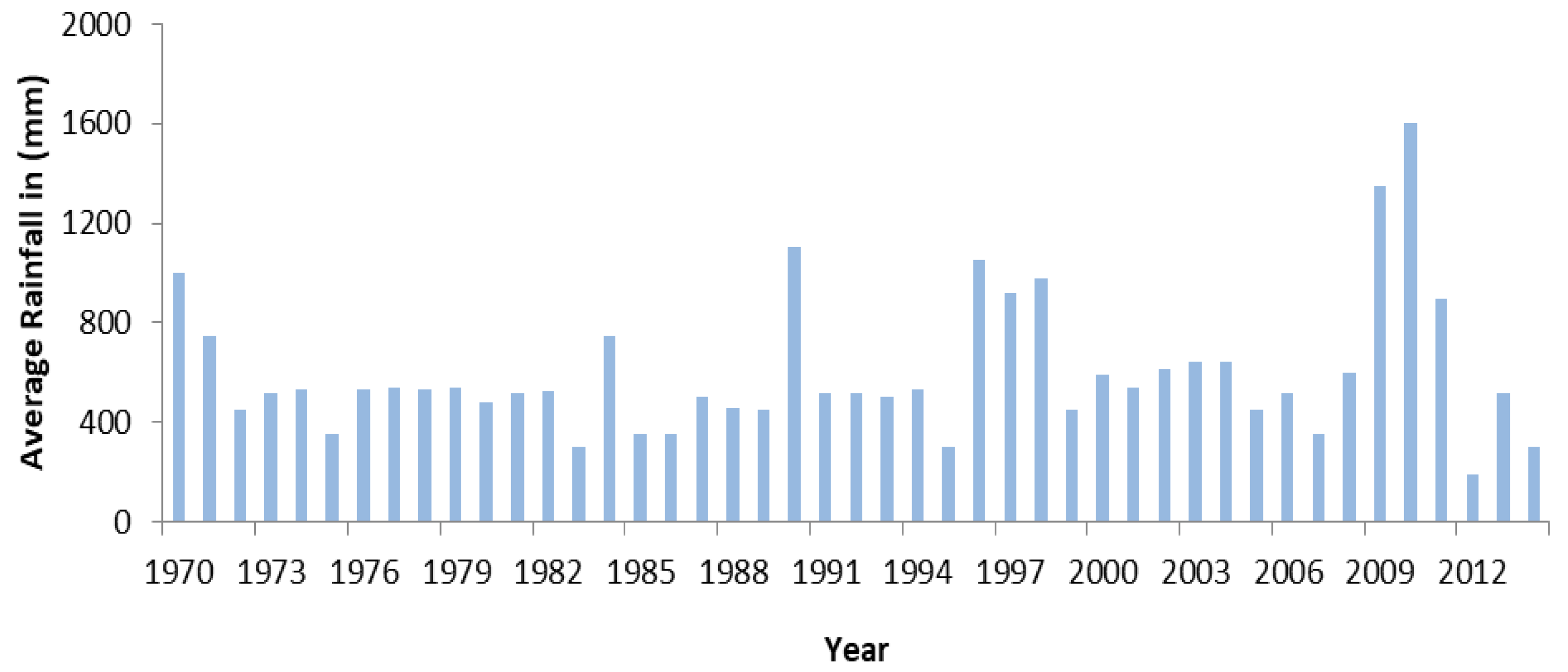
2.2. Data
2.3. Description of Selected Rainfall-Runoff Models
2.3.1. HEC-HMS
2.3.2. ATHYS
2.3.3. SWAT
2.4. Calibration and Validation Procedures and Performance Criteria
2.5. Performance Criteria
3. Results and Discussion
3.1. Optimized Values of Calibrated Parameters
3.2. Analysis of the Calibration and Validation Performances
3.3. Detailed Discussion on Models’ Performance
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hong, X.; Guo, S.; Chen, G.; Guo, N.; Jiang, C. A Modified Two-Parameter Monthly Water Balance Model for Runoff Simulation to Assess Hydrological Drought. Water 2022, 14, 3715. [Google Scholar] [CrossRef]
- Shigute, M.; Alamirew, T.; Abebe, A.; Ndehedehe, C.E.; Kassahun, H.T. Understanding Hydrological Processes under Land Use Land Cover Change in the Upper Genale River Basin, Ethiopia. Water 2022, 14, 3881. [Google Scholar] [CrossRef]
- Rueda, V.; Young, M.H.; Faust, K.; Rateb, A.; Leibowicz, B.D. System Dynamics Modeling in Local Water Management: Assessing Strategies for the City of Boerne, Texas. Water 2022, 14, 3682. [Google Scholar] [CrossRef]
- Mendez, M.; Calvo-Valverde, L.-A.; Imbach, P.; Maathuis, B.; Hein-Grigg, D.; Hidalgo-Madriz, J.-A.; Alvarado-Gamboa, L.-F. Hydrological Response of Tropical Catchments to Climate Change as Modeled by the GR2M Model: A Case Study in Costa Rica. Sustainability 2022, 14, 16938. [Google Scholar] [CrossRef]
- Rufino, P.R.; Gücker, B.; Faramarzi, M.; Boëchat, I.G.; Cardozo, F.D.S.; Santos, P.R.; Zanin, G.D.; Mataveli, G.; Pereira, G. Evaluation of the SWAT Model for the Simulation of Flow and Water Balance Based on Orbital Data in a Poorly Monitored Basin in the Brazilian Amazon. Geographies 2022, 3, 1–18. [Google Scholar] [CrossRef]
- Janicka, E.; Kanclerz, J. Assessing the Effects of Urbanization on Water Flow and Flood Events Using the HEC-HMS Model in the Wirynka River Catchment, Poland. Water 2022, 15, 86. [Google Scholar] [CrossRef]
- Rocha, J.; Duarte, A.; Fabres, S.; Quintela, A.; Serpa, D. Influence of DEM Resolution on the Hydrological Responses of a Terraced Catchment: An Exploratory Modelling Approach. Remote Sens. 2022, 15, 169. [Google Scholar] [CrossRef]
- Van, S.P.; Le, H.M.; Thanh, D.V.; Dang, T.D.; Loc, H.H.; Anh, D.T. Deep learning convolutional neural network in rainfall–runoff modelling. J. Hydroinforma. 2020, 22, 541–561. [Google Scholar] [CrossRef] [Green Version]
- Deb, P.; Kiem, A.S. Evaluation of rainfall–runoff model performance under non-stationary hydroclimatic conditions. Hydrol. Sci. J. 2020, 65, 1667–1684. [Google Scholar] [CrossRef]
- Dubovský, V.; Dlouhá, D.; Pospíšil, L. The Calibration of Evaporation Models against the Penman–Monteith Equation on Lake Most. Sustainability 2020, 13, 313. [Google Scholar] [CrossRef]
- Paniconi, C.; Putti, M. Physically based modeling in catchment hydrology at 50: Survey and outlook. Water Resour. Res. 2015, 51, 7090–7129. [Google Scholar] [CrossRef] [Green Version]
- Ouermi, K.S.; Paturel, J.-E.; Adounpke, J.; Lawin, A.E.; Goula, B.T.A.; Amoussou, E. Comparison of hydrological models for use in climate change studies: A test on 241 catchments in West and Central Africa. Comptes Rendus Geosci. 2019, 351, 477–486. [Google Scholar] [CrossRef]
- Archfield, S.A.; Clark, M.P.; Arheimer, B.; Hay, L.E.; McMillan, H.; Kiang, J.E.; Seibert, J.; Hakala-Assendelft, K.; Bock, A.; Wagener, T.; et al. Accelerating advances in continental domain hydrologic modeling. Water Resour. Res. 2015, 51, 10078–10091. [Google Scholar] [CrossRef] [Green Version]
- Xu, T.; Liang, F. Machine learning for hydrologic sciences: An introductory overview. WIREs Water 2021, 8, e1533. [Google Scholar] [CrossRef]
- KlemeŠ, V. Operational Testing of Hydrological Simulation Models. Hydrol. Sci. J. 1986, 31, 13–24. [Google Scholar] [CrossRef]
- Ewen, J.; Parkin, G. Validation of Catchment Models for Predicting Land-Use and Climate Change Impacts. 1. Method. J. Hydrol. 1996, 175, 583–594. [Google Scholar] [CrossRef]
- Wood, A.; Leung, L.R.; Sridhar, V.; Lettenmaier, D.P. Hydrologic Implications of Dynamical and Statistical Approaches to Downscaling Climate Model Outputs. Clim. Chang. 2004, 62, 189–216. [Google Scholar] [CrossRef]
- Fowler, H.J.; Blenkinsop, S.; Tebaldi, C. Linking Climate Change Modelling to Impacts Studies: Recent Advances in Downscaling Techniques for Hydrological Modelling. Int. J. Climatol. 2007, 27, 1547–1578. [Google Scholar] [CrossRef]
- Rosero, E.; Yang, Z.-L.; Wagener, T.; Gulden, L.E.; Yatheendradas, S.; Niu, G.-Y. Quantifying Parameter Sensitivity, Interaction, and Transferability in Hydrologically Enhanced Versions of the Noah Land Surface Model over Transition Zones during the Warm Season. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Merz, R.; Parajka, J.; Blöschl, G. Time Stability of Catchment Model Parameters: Implications for Climate Impact Analyses. Water Resour. Res. 2011, 47, 1–17. [Google Scholar] [CrossRef]
- Seiller, G.; Anctil, F.; Perrin, C. Multimodel Evaluation of Twenty Lumped Hydrological Models under Contrasted Climate Conditions. Hydrol. Earth Syst. Sci. 2012, 16, 1171–1189. [Google Scholar] [CrossRef] [Green Version]
- Gharari, S.; Hrachowitz, M.; Fenicia, F.; Savenije, H.H.G. An Approach to Identify Time Consistent Model Parameters: Sub-Period Calibration. Hydrol. Earth Syst. Sci. 2013, 17, 149–161. [Google Scholar] [CrossRef] [Green Version]
- Coron, L.; Andréassian, V.; Perrin, C.; Bourqui, M.; Hendrickx, F. On the Lack of Robustness of Hydrologic Models Regarding Water Balance Simulation: A Diagnostic Approach Applied to Three Models of Increasing Complexity on 20 Mountainous Catchments. Hydrol. Earth Syst. Sci. 2014, 18, 727–746. [Google Scholar] [CrossRef] [Green Version]
- Ewert, F.; Rötter, R.P.; Bindi, M.; Webber, H.; Trnka, M.; Kersebaum, K.C.; Olesen, J.E.; van Ittersum, M.K.; Janssen, S.; Rivington, M.; et al. Crop Modelling for Integrated Assessment of Risk to Food Production from Climate Change. Environ. Model. Softw. 2015, 72, 287–303. [Google Scholar] [CrossRef]
- Dakhlaoui, H.; Ruelland, D.; Tramblay, Y.; Bargaoui, Z. Evaluating the Robustness of Conceptual Rainfall-Runoff Models under Climate Variability in Northern Tunisia. J. Hydrol. 2017, 550, 201–217. [Google Scholar] [CrossRef]
- Wilby, R.L.; Dessai, S. Robust Adaptation to Climate Change. Weather 2010, 65, 180–185. [Google Scholar] [CrossRef] [Green Version]
- Tramblay, Y.; Ruelland, D.; Somot, S.; Bouaicha, R.; Servat, E. High-Resolution Med-CORDEX Regional Climate Model Simulations for Hydrological Impact Studies: A First Evaluation of the ALADIN-Climate Model in Morocco. Hydrol. Earth Syst. Sci. 2013, 17, 3721–3739. [Google Scholar] [CrossRef] [Green Version]
- Jaber, F.H.; Shukla, S. MIKE SHE: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1479–1489. [Google Scholar] [CrossRef]
- Bergström, S. The HBV model. Comput. Model. Watershed Hydrol. 1995, 443–476–476. [Google Scholar]
- Lindström, G.; Pers, C.; Rosberg, J.; Strömqvist, J.; Arheimer, B. Development and testing of the HYPE (Hydrological Predictions for the Environment) water quality model for different spatial scales. Hydrol. Res. 2010, 41, 295–319. [Google Scholar] [CrossRef]
- Markstrom, S.L.; Regan, R.S.; Hay, L.E.; Viger, R.J.; Webb, R.M.; Payn, R.A.; LaFontaine, J.H. PRMS-IV, the precipitation-runoff modeling system, version 4. US Geol. Surv. Tech. Methods 2015, 6, B7. [Google Scholar]
- Akoko, G.; Le, T.; Gomi, T.; Kato, T. A Review of SWAT Model Application in Africa. Water 2021, 13, 1313. [Google Scholar] [CrossRef]
- Halwatura, D.; Najim, M. Application of the HEC-HMS model for runoff simulation in a tropical catchment. Environ. Model. Softw. 2013, 46, 155–162. [Google Scholar] [CrossRef]
- Bouvier, C.; DelClaux, F. ATHYS: A hydrological environment for spatial modelling and coupling with GIS. Appl. GIS Hydrol. Water Resour. Manag. 1996, 235, 572–582. [Google Scholar]
- Yang, S.; Tan, M.L.; Song, Q.; He, J.; Yao, N.; Li, X.; Yang, X. Coupling SWAT and Bi-LSTM for improving daily-scale hydro-climatic simulation and climate change impact assessment in a tropical river basin. J. Environ. Manag. 2023, 330, 117244. [Google Scholar] [CrossRef] [PubMed]
- Aqnouy, M.; Stitou El Massari, J.E.; Bouadila, A.; Bouizrou, I.; Aoulad Mansour, M.R. Application of Hydrological Model “HEC HMS” In a Mediterranean Watershed (Oued Laou, Northern of Morocco). Int. J. Innov. Appl. Stud. 2018, 24, 1773–1781. [Google Scholar]
- Faouzi, E.; Arioua, A.; Hssaisoune, M.; Boudhar, A.; Elaloui, A.; Karaoui, I. Sensitivity analysis of CN using SCS-CN approach, rain gauges and TRMM satellite data assessment into HEC-HMS hydrological model in the upper basin of Oum Er Rbia, Morocco. Model. Earth Syst. Environ. 2022, 8, 4707–4729. [Google Scholar] [CrossRef]
- Aqnouy, M.; El Messari, J.E.S.; Ismail, H.; Bouadila, A.; Navarro, J.G.M.; Loubna, B.; Mansour, M.R.A. Assessment of the SWAT Model and the Parameters Affecting the Flow Simulation in the Watershed of Oued Laou (Northern Morocco). J. Ecol. Eng. 2019, 20, 104–113. [Google Scholar] [CrossRef]
- Ouallali, A.; Briak, H.; Aassoumi, H.; Beroho, M.; Bouhsane, N.; Moukhchane, M. Hydrological foretelling uncertainty evaluation of water balance components and sediments yield using a multi-variable optimization approach in an external Rif’s catchment. Morocco. Alex. Eng. J. 2020, 59, 775–789. [Google Scholar] [CrossRef]
- Aqnouy, M.; El Messari, J.E.S.; Bouadila, A.; Morabbi, A.; Benaabidate, L.; Al-Djazouli, M.O. Modeling of Continuous and Extreme Hydrological Processes Using Spatially Distributed Models Mercedes, Vicair and Vishyr in a Mediterranean Watershed. Ecol. Eng. Environ. Technol. 2021, 22, 9–23. [Google Scholar] [CrossRef]
- Bouizrou, I.; Chahinian, N.; Perrin, J.L.; Müller, R.; Rais, N. Network Representation in Hydrological Modelling on Urban Catchments in Data-Scarce Contexts: A Case Study on the Oued Fez Catchment (Morocco). J. Hydrol. Reg. Stud. 2021, 34. [Google Scholar] [CrossRef]
- Abdelmounim, B.; Benaabidate, L.; Bouizrou, I.; Aqnouy, M. Implementation of Distributed Hydrological Modeling in a Semi-Arid Mediterranean Catchment “Azzaba, Morocco”. J. Ecol. Eng. 2019, 20, 236–254. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model development 1. JAWRA J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- CARD. SWAT Literature Database for Peer-Reviewed Journal Articles. 2019. Available online: https://www.card.iastate.edu/swat_articles/ (accessed on 31 December 2018).
- Perrin, C.; Michel, C.; Andréassian, V. Does a Large Number of Parameters Enhance Model Performance? Comparative Assessment of Common Catchment Model Structures on 429 Catchments. J. Hydrol. 2001, 242, 275–301. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a Parsimonious Model for Streamflow Simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Bormann, H.; Breuer, L.; Gräff, T.; Huisman, J.A. Analysing the Effects of Soil Properties Changes Associated with Land Use Changes on the Simulated Water Balance: A Comparison of Three Hydrological Catchment Models for Scenario Analysis. Ecol. Model. 2007, 209, 29–40. [Google Scholar] [CrossRef]
- Gao, C.; Yao, M.T.; Wang, Y.J.; Zhai, J.Q.; Buda, S.; Fischer, T.; Zeng, X.F.; Wang, W.P. Hydrological Model Comparison and Assessment: Criteria from Catchment Scales and Temporal Resolution. Hydrol. Sci. J. 2016, 61, 1941–1951. [Google Scholar] [CrossRef] [Green Version]
- Koch, J.; Cornelissen, T.; Fang, Z.; Bogena, H.; Diekkrüger, B.; Kollet, S.; Stisen, S. Inter-Comparison of Three Distributed Hydrological Models with Respect to Seasonal Variability of Soil Moisture Patterns at a Small Forested Catchment. J. Hydrol. 2016, 533, 234–249. [Google Scholar] [CrossRef]
- Stitou Messari, J. Aplicación Del Método DRASTIC Para Evaluar La Vulnerabilidad a La Contaminación Del Acuífero de Oued Laou (Marruecos). Geogaceta 2006, 41, 191–194. [Google Scholar]
- Qadem, Z.; Obda, K.; Qadem, A.; Lasri, M.; Bouizrou, I. Contribution of the GIS in Terms of Knowledge of the Situation of the Water Resources of the Plain of Saïs Fez and Its Middle Atlasic Borders—Morocco: Aspects, Methods and Quantification of Water Resources. In Geospatial Technology; Springer: Cham, Switzerland, 2020; pp. 83–94. [Google Scholar]
- Amellah, O.; El Morabiti, K.; Al-Djazouli, M.O. Spatialization and assessment of flood hazard using 1D numerical simulation in the plain of Oued Laou (north Morocco). Arab. J. Geosci. 2020, 13, 635. [Google Scholar] [CrossRef]
- Serur, A.B. Modeling blue and green water resources availability at the basin and sub-basin level under changing climate in the Weyb River basin in Ethiopia. Sci. Afr. 2020, 7, e00299. [Google Scholar] [CrossRef]
- Guiamel, I.A.; Lee, H.S. Watershed Modelling of the Mindanao River Basin in the Philippines Using the SWAT for Water Resource Management. Civ. Eng. J. 2020, 6, 626–648. [Google Scholar] [CrossRef] [Green Version]
- Fels, A.E.A.E.; Alaa, N.; Bachnou, A. Modelling of flood propagation in a semi-arid environment case of the N’FIS basin—Moroccan Western high atlas. Sci. Afr. 2020, 7, e00306. [Google Scholar] [CrossRef]
- Bouizrou, I.; Aqnouy, M.; Bouadila, A. Spatio-temporal analysis of trends and variability in precipitation across Morocco: Comparative analysis of recent and old non-parametric methods. J. Afr. Earth Sci. 2022, 196, 104691. [Google Scholar] [CrossRef]
- Melsen, L.A.; Addor, N.; Mizukami, N.; Newman, A.J.; Torfs, P.J.J.F.; Clark, M.P.; Uijlenhoet, R.; Teuling, A.J. Mapping (Dis)Agreement in Hydrologic Projections. Hydrol. Earth Syst. Sci. 2018, 22, 1775–1791. [Google Scholar] [CrossRef]
- Paul, P.K.; Zhang, Y.; Ma, N.; Mishra, A.; Panigrahy, N.; Singh, R. Selecting hydrological models for developing countries: Perspective of global, continental, and country scale models over catchment scale models. J. Hydrol. 2021, 600, 126561. [Google Scholar] [CrossRef]
- Bouvier, C.; Fuentes, G.; Dominguez, R. MERCEDES: Un Modèle Hydrologique d’analyse et de Prévision de Crues En Milieu Hétérogène. Crues et inondations. 23emes journées de l’hydraulique. In Proceedings of the Congrès de la Société Hydrotechnique de France, Nîmes France, 14–16 September 1994; Volume 23, pp. 257–260. [Google Scholar]
- Feldman, A.D. Hydrologic Modeling System HEC-HMS, Technical Reference Manual; U.S. Army Corps of Engineers, Hydrologic Engineering Center, HEC: Davis, CA, USA, 2000.
- Abushandi, E.; Merkel, B. Modelling Rainfall Runoff Relations Using HEC-HMS and IHACRES for a Single Rain Event in an Arid Region of Jordan. Water Resour. Manag. 2013, 27, 2391–2409. [Google Scholar] [CrossRef]
- Lehbab-Boukezzi, Z.; Boukezzi, L.; Errih, M. Uncertainty analysis of HEC-HMS model using the GLUE method for flash flood forecasting of Mekerra watershed, Algeria. Arab. J. Geosci. 2016, 9, 751. [Google Scholar] [CrossRef]
- brahim-Bathis, K.; Ahmed, S.A. Rainfall-runoff modelling of Doddahalla watershed—An application of HEC-HMS and SCN-CN in ungauged agricultural watershed. Arab. J. Geosci. 2016, 9, 170. [Google Scholar] [CrossRef]
- Ramly, S.; Tahir, W. Application of HEC-GeoHMS and HEC-HMS as Rainfall–Runoff Model for Flood Simulation. In ISFRAM; Springer: Singapore, 2016; pp. 181–192. [Google Scholar] [CrossRef]
- Wijayarathne, D.B.; Coulibaly, P. Identification of hydrological models for operational flood forecasting in St. John’s, Newfoundland, Canada. J. Hydrol. Reg. Stud. 2020, 27, 100646. [Google Scholar] [CrossRef]
- Hamdan, A.; Almuktar, S.; Scholz, M. Rainfall-Runoff Modeling Using the HEC-HMS Model for the Al-Adhaim River Catchment, Northern Iraq. Hydrology 2021, 8, 58. [Google Scholar] [CrossRef]
- Aronica, G.; Candela, A. Derivation of flood frequency curves in poorly gauged Mediterranean catchments using a simple stochastic hydrological rainfall-runoff model. J. Hydrol. 2007, 347, 132–142. [Google Scholar] [CrossRef]
- Kastridis, A.; Stathis, D. Evaluation of Hydrological and Hydraulic Models Applied in Typical Mediterranean Ungauged Watersheds Using Post-Flash-Flood Measurements. Hydrology 2020, 7, 12. [Google Scholar] [CrossRef] [Green Version]
- Hong, Y.; Adler, R.F. Estimation of global SCS curve numbers using satellite remote sensing and geospatial data. Int. J. Remote Sens. 2008, 29, 471–477. [Google Scholar] [CrossRef]
- Tramblay, Y.; Bouaicha, R.; Brocca, L.; Dorigo, W.; Bouvier, C.; Camici, S.; Servat, E. Estimation of Antecedent Wetness Conditions for Flood Modelling in Northern Morocco. Hydrol. Earth Syst. Sci. 2012, 16, 4375–4386. [Google Scholar] [CrossRef] [Green Version]
- Brirhet, H.; Benaabidate, L. Comparison Of Two Hydrological Models (Lumped And Distributed) Over A Pilot Area Of The Issen Watershed In The Souss Basin, Morocco. Eur. Sci. J. ESJ 2016, 12, 10–19044. [Google Scholar] [CrossRef] [Green Version]
- Bouvier, C.; DelClaux, F. ATHYS: A hydrological environment for spatial modelling and coupling with GIS. In IAHS Publications-Series of Proceedings and Reports; International Association of Hydrological Sciences: Wallingford, UK, 1996; Volume 235, pp. 19–28. [Google Scholar]
- Bouadila, A.; Tzoraki, O.; Benaabidate, L. Hydrological modeling of three rivers under Mediterranean climate in Chile, Greece, and Morocco: Study of high flow trends by indicator calculation. Arab. J. Geosci. 2020, 13, 1057. [Google Scholar] [CrossRef]
- Bouvier, C.; Alcoba, M.; Cazenave, F.; Chahinian, N.; Coulibaly, G.; Crès, A.; Crespy, A.; Gosset, M.; Miller, J.; Bouvier, C.; et al. Des Inondations Dans une Agglomération Urbaine, Par Couplage d’un Modele Hydrologique et D’un Modèle de Transfert en Réseau; HAL Id: Hal-01926155. La Houille Blanche Revue Internationale de l’Eau, EDP Sciences, A paraître. hal-01926155; EDP Sciences: Les Ulis, France, 2015. [Google Scholar]
- Ning, J.; Gao, Z.; Lu, Q. Runoff Simulation Using a Modified SWAT Model with Spatially Continuous HRUs. Environ. Earth Sci. 2015, 74, 5895–5905. [Google Scholar] [CrossRef]
- Perez-Valdivia, C.; Cade-Menun, B.; McMartin, D.W. Hydrological Modeling of the Pipestone Creek Watershed Using the Soil Water Assessment Tool (SWAT): Assessing Impacts of Wetland Drainage on Hydrology. J. Hydrol. Reg. Stud. 2017, 14, 109–129. [Google Scholar] [CrossRef]
- Desta, H.; Lemma, B. SWAT Based Hydrological Assessment and Characterization of Lake Ziway Sub-Watersheds, Ethiopia. J. Hydrol. Reg. Stud. 2017, 13, 122–137. [Google Scholar] [CrossRef]
- Mengistu, A.G.; van Rensburg, L.D.; Woyessa, Y.E. Techniques for Calibration and Validation of SWAT Model in Data Scarce Arid and Semi-Arid Catchments in South Africa. J. Hydrol. Reg. Stud. 2019, 25, 100621. [Google Scholar] [CrossRef]
- Lv, Z.; Zuo, J.; Rodriguez, D. Predicting of Runoff Using an Optimized SWAT-ANN: A Case Study. J. Hydrol. Reg. Stud. 2020, 29, 100688. [Google Scholar] [CrossRef]
- Flügel, W.-A. Delineating hydrological response units by geographical information system analyses for regional hydrological modelling using PRMS/MMS in the drainage basin of the River Bröl, Germany. Hydrol. Process. 1995, 9, 423–436. [Google Scholar] [CrossRef]
- Arnold, N.; Sharp, M. Influence of glacier hydrology on the dynamics of a large Quaternary ice sheet. J. Quat. Sci. 1992, 7, 109–124. [Google Scholar] [CrossRef]
- Williams, J. HYMO flood routing. J. Hydrol. 1975, 26, 17–27. [Google Scholar] [CrossRef]
- Overton, D.E. Muskingum flood routing of upland streamflow. J. Hydrol. 1966, 4, 185–200. [Google Scholar] [CrossRef]
- Mtibaa, S.; Asano, S. Hydrological evaluation of radar and satellite gauge-merged precipitation datasets using the SWAT model: Case of the Terauchi catchment in Japan. J. Hydrol. Reg. Stud. 2022, 42, 101134. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Garba, H.; Chukwujama, I.A. Evaluating the Performance of a Hydrological Model on River Kaduna Discharge. J. Eng. Res. Appl. 2016, 6, 25–29. [Google Scholar]
- Wang, J.; Wang, X.; Khu, S.T. A Decomposition-based Multi-model and Multi-parameter Ensemble Forecast Framework for Monthly Streamflow Forecasting. J. Hydrol. 2023, 129083. [Google Scholar] [CrossRef]
- Herzel, S. C Onsistent C Alibration of Hjm M Odels to C Ap I Mplied V Olatilities. J. Hydrol. Eng. 2005, 25, 1093–1120. [Google Scholar] [CrossRef]
- Bisselink, B.; Zambrano-Bigiarini, M.; Burek, P.; de Roo, A. Assessing the role of uncertain precipitation estimates on the robustness of hydrological model parameters under highly variable climate conditions. J. Hydrol. Reg. Stud. 2016, 8, 112–129. [Google Scholar] [CrossRef]
- Cecinati, F.; Moreno-Ródenas, A.M.; Rico-Ramirez, M.A.; Veldhuis, M.-C.T.; Langeveld, J.G. Considering Rain Gauge Uncertainty Using Kriging for Uncertain Data. Atmosphere 2018, 9, 446. [Google Scholar] [CrossRef] [Green Version]
- Dulal, K.N.; Takeuchi, K.; Ishidaira, H. A Framework for the Analysis of Uncertainty in the Measurement of Precipitation Data: A Case Study for Nepal. Int. Comm. Agric. Eng. 2006, 8, 1–16. [Google Scholar]
- Shekar, N.C.S.; Vinay, D.C. Performance of HEC-HMS and SWAT to simulate streamflow in the sub-humid tropical Hemavathi catchment. J. Water Clim. Chang. 2021, 12, 3005–3017. [Google Scholar] [CrossRef]
- Aliye, M.A.; Aga, A.O.; Tadesse, T.; Yohannes, P. Evaluating the Performance of HEC-HMS and SWAT Hydrological Models in Simulating the Rainfall-Runoff Process for Data Scarce Region of Ethiopian Rift Valley Lake Basin. Open J. Mod. Hydrol. 2020, 10, 105–122. [Google Scholar] [CrossRef]
- Kedem, B.; Chiu, L.S.; Karni, Z. An Analysis of the Threshold Method for Measuring Area-Average Rainfall. J. Appl. Meteorol. 1990, 29, 3–20. [Google Scholar] [CrossRef]
- Zhao, L.; Xia, J.; Xu, C.-Y.; Wang, Z.; Sobkowiak, L.; Long, C. Evapotranspiration estimation methods in hydrological models. J. Geogr. Sci. 2013, 23, 359–369. [Google Scholar] [CrossRef]






| Model | Calibrated Parameters | Parameters Names | Values | Parameter Range |
|---|---|---|---|---|
| HEC-HMS | CN (dimensionless) | Curve number, moisture condition II | 75 | (69.8–93.0) |
| Lag (min) | Lag time | 4.5 | ||
| ATHYS | CN (dimensionless) | Curve number, moisture condition II | 73.57 | (69.8–93.0) |
| ds (1/day) | Drainage coefficient f(t) infiltration | 0.12 | - | |
| VO (m/s) | Flow velocity | 1.80 | - | |
| S (mm/mm) | Soil reservoir capacity (the potential maximum retention) | 91.25 | (0–+∞) | |
| SWAT | CN2 (dimensionless) | Curve number, moisture condition II | 74 | (69.8–93.0) |
| ESCO (dimensionless) | Soil evaporation compensation factor | 0.83 | (0.01–1) | |
| SOL_AWC (mm/mm) | Available soil moisture capacity, mm h −1 | 0.4 | (−0.6 to 0.6) | |
| ALPHA_BF (1/day) | Base flow recession constant, days | 0.43 | (0–0.048) | |
| CH_N2 (s/m1/3) | Manning’s “n” value for the main channel | 0.15 | (0.01–0.25) | |
| CH_k2 (mm/h) | Effective hydraulic conductivity in the channel alluvium | 58 | (0–150) |
| Model | RSR | PBIAS | ||
|---|---|---|---|---|
| Calibration | Validation | Calibration | Validation | |
| HEC-HMS | 0.53 | 0.51 | 15% | 14% |
| ATHYS | 0.51 | 0.53 | 14% | 16% |
| SWAT | 0.52 | 0.41 | 12% | 9% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aqnouy, M.; Ahmed, M.; Ayele, G.T.; Bouizrou, I.; Bouadila, A.; Stitou El Messari, J.E. Comparison of Hydrological Platforms in Assessing Rainfall-Runoff Behavior in a Mediterranean Watershed of Northern Morocco. Water 2023, 15, 447. https://doi.org/10.3390/w15030447
Aqnouy M, Ahmed M, Ayele GT, Bouizrou I, Bouadila A, Stitou El Messari JE. Comparison of Hydrological Platforms in Assessing Rainfall-Runoff Behavior in a Mediterranean Watershed of Northern Morocco. Water. 2023; 15(3):447. https://doi.org/10.3390/w15030447
Chicago/Turabian StyleAqnouy, Mourad, Mohamed Ahmed, Gebiaw T. Ayele, Ismail Bouizrou, Abdelmounim Bouadila, and Jamal Eddine Stitou El Messari. 2023. "Comparison of Hydrological Platforms in Assessing Rainfall-Runoff Behavior in a Mediterranean Watershed of Northern Morocco" Water 15, no. 3: 447. https://doi.org/10.3390/w15030447








