Flood Management with SUDS: A Simulation–Optimization Framework
Abstract
:1. Introduction
| Study | Algorithm | Independent Variables | Dependent Variables | Type of Solution | Type of Temporal Modelation | Study Case Area (ha) |
|---|---|---|---|---|---|---|
| [12] | Fixed iterative steps | Area | Loads | Sensitivity analysis | Design events | 1.25 |
| [22] | Genetic algorithms | Design | Costs | Unique design | Design events | 2137 |
| [17] | Genetic algorithms | Area | Multi-objective | Pareto front | Design events | 500 |
| [9] | Particle swarm | Design | Multi-objective | Pareto front | Design events | 870 |
| [24] | Fixed iterative steps | Design Area | Cost | Unique design | Design events | Hypothetical |
| [10] | Genetic algorithms | Design | Multi-objective | Pareto front | Design events | 77 |
| [25] | Genetic algorithms | Type Location Area | Runoff volume Cost | Unique design | Design events | 73,000 |
| [15] | Simulated annealing | Area Number of structures | Cost/benefit | Unique design | Design events | 140 |
| [26] | Genetic algorithms | Area | Cost/benefit | Optimal scenarios | Continuous | |
| [18] | Genetic algorithms | Design | Volume Cost Peak flow | Pareto front | Design events | 14.7 |
| [27] | Genetic algorithms | Area | Volume Cost | Design events | ||
| [20] | PICEA-g | Area | Volume Loads Costs | Pareto front | Design events | 60 |
| [19] | Particle swarm | Number of structures | Volume Loads Costs | Pareto front | Design events | 1800 |
| [16] | Simulated annealing | Design | Volume Loads Costs | Optimal scenarios | Continuous | 181.97 |
| [21] | Genetic algorithms | Area | Volume Costs | Pareto front | Continuous | 11 |
| [11] | Genetic algorithms Particle swarm | Location | Volume Costs | Pareto front | Design events | 1398 |
2. Case Study
3. Materials and Methods
3.1. Hydrodynamic Simulation and Flooding
3.2. Flooded Area and Depth Definition
3.3. SUDS Design and Costs Estimation
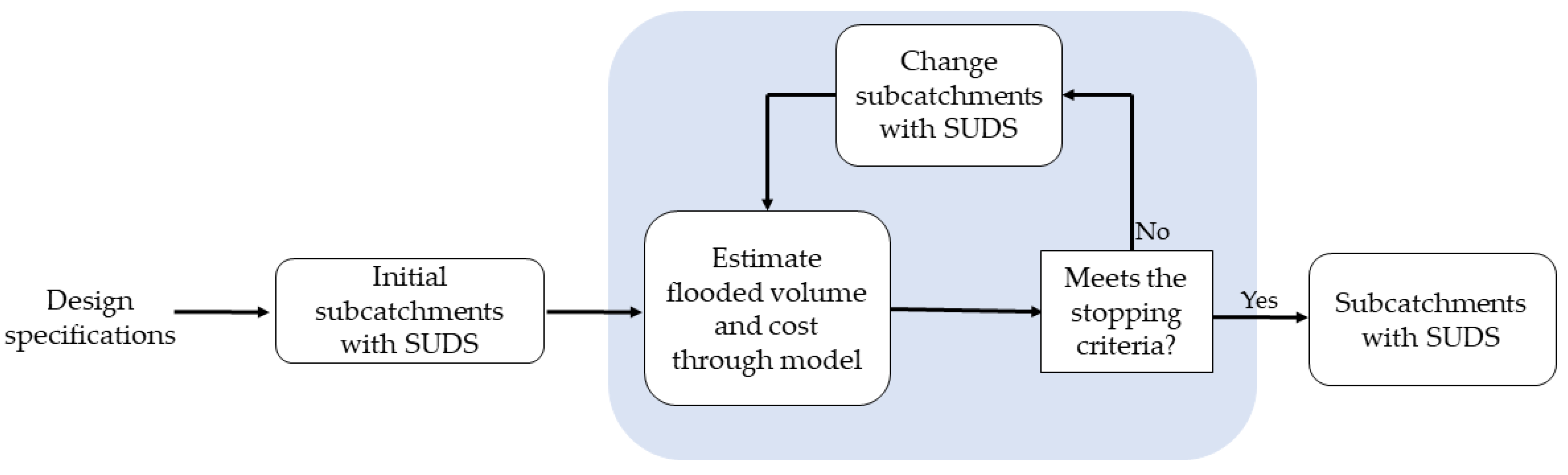
3.4. Optimization Algorithm and Modes Coupling
4. Results and Discussion
4.1. Reference Scenarios
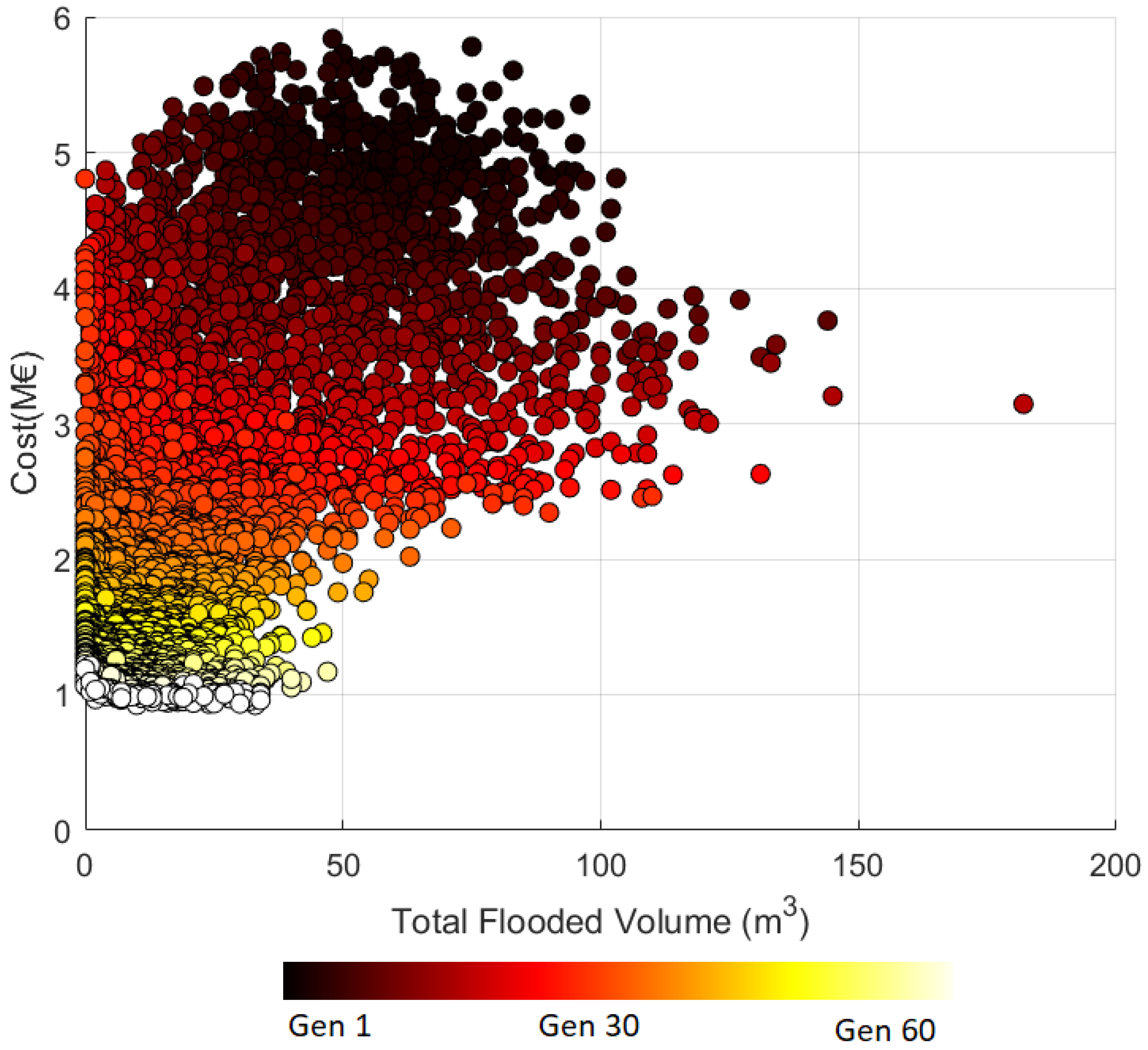
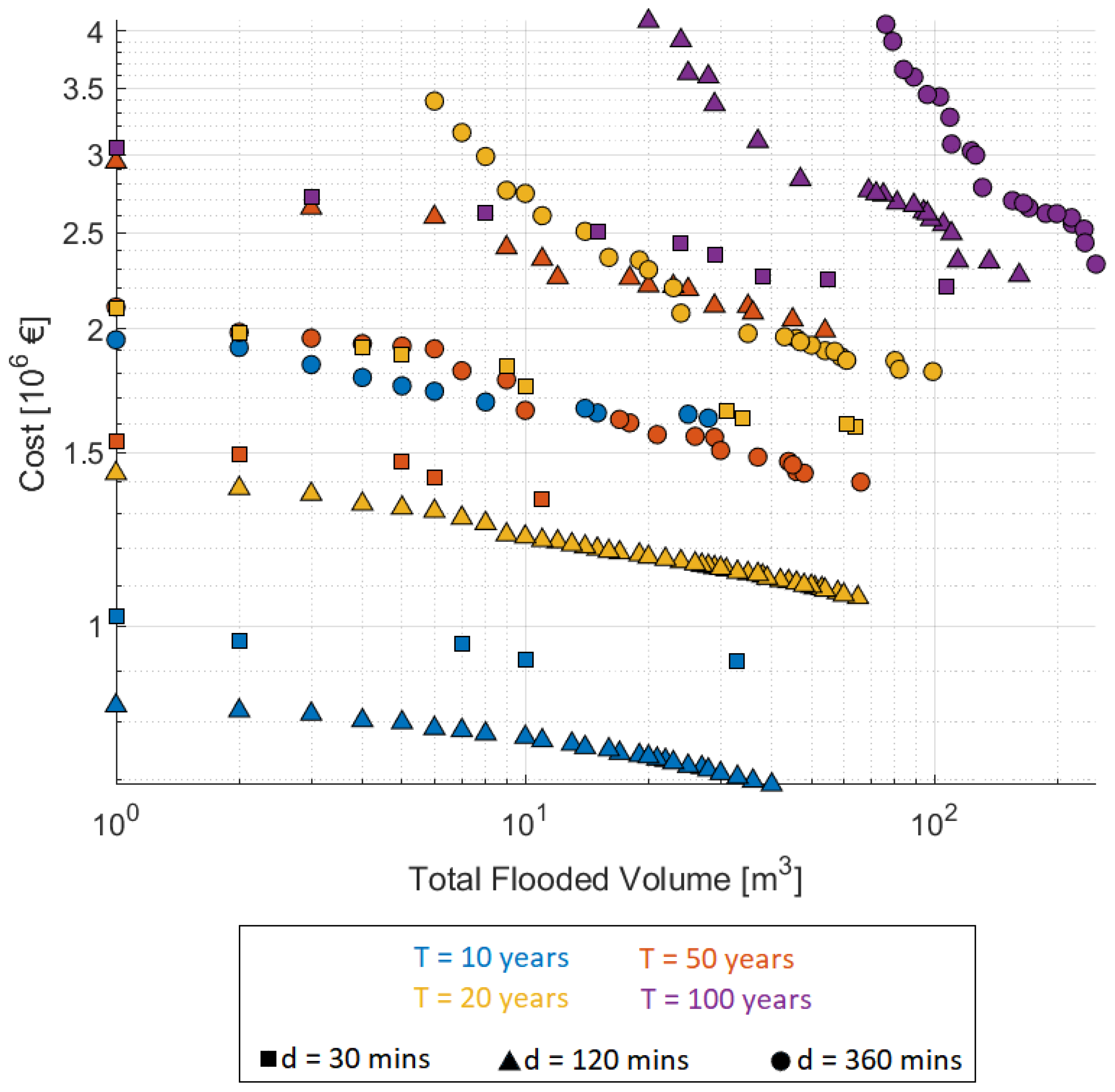
4.2. Pareto Front for SUDS Cost Efficiency
4.3. Typologies Selection and Distribution
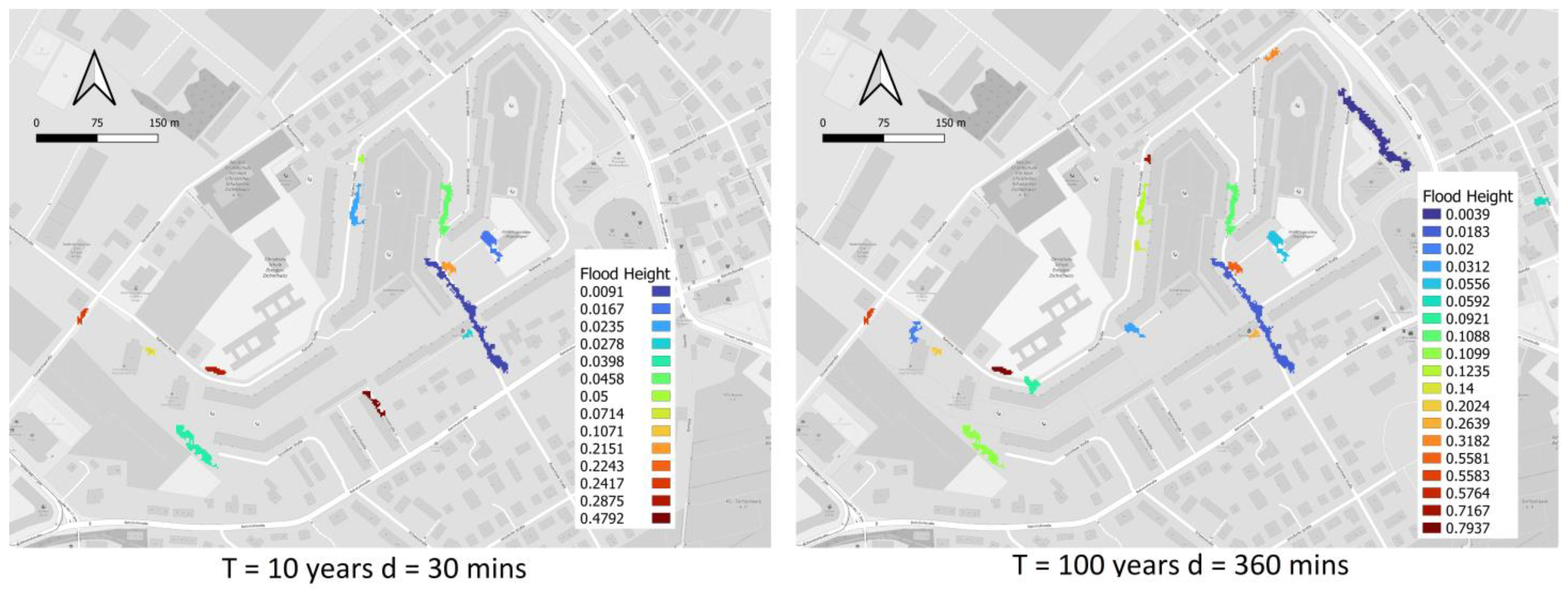
4.4. Flooded Area and Depth
4.5. Combined Frequencies Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arnone, E.; Pumo, D.; Francipane, A.; La Loggia, G.; Noto, L.V. The role of urban growth, climate change, and their interplay in altering runoff extremes. Hydrol. Process. 2018, 32, 1755–1770. [Google Scholar] [CrossRef]
- Zhou, Q. A Review of Sustainable Urban Drainage Systems Considering the Climate Change and Urbanization Impacts. Water 2014, 6, 976–992. [Google Scholar] [CrossRef] [Green Version]
- Ahiablame, L.; Shakya, R. Modeling flood reduction effects of low impact development at a watershed scale. J. Environ. Manag. 2016, 171, 81–91. [Google Scholar] [CrossRef]
- Muthanna, T.M.; Sivertsen, E.; Kliewer, D.; Jotta, L. Coupling Field Observations and Geographical Information System (GIS)-Based Analysis for Improved Sustainable Urban Drainage Systems (SUDS) Performance. Sustainability 2018, 10, 4683. [Google Scholar] [CrossRef] [Green Version]
- Ferrans, P.; Torres, M.N.; Temprano, J.; Sánchez, J.P.R. Sustainable Urban Drainage System (SUDS) modeling supporting decision-making: A systematic quantitative review. Sci. Total. Environ. 2021, 806, 150447. [Google Scholar] [CrossRef]
- Lerer, S.M.; Arnbjerg-Nielsen, K.; Mikkelsen, P.S. A Mapping of Tools for Informing Water Sensitive Urban Design Planning Decisions—Questions, Aspects and Context Sensitivity. Water 2015, 7, 993–1012. [Google Scholar] [CrossRef] [Green Version]
- Torres, M.N.; Sánchez, J.R.; Leitão, J.P.; de Oliveira Nascimento, N.; Granceri, M. Decision support tools for sustainable urban drainage systems: A systematic quantitative review. In Proceedings of the 9th International Conference on Planning and Technologies for Sustainable Management of Water in the City, Lyon, France, 28 June 2016. [Google Scholar]
- Zhang, K.; Chui, T.F.M.; Yang, Y. Simulating the hydrological performance of low impact development in shallow groundwater via a modified SWMM. J. Hydrol. 2018, 566, 313–331. [Google Scholar] [CrossRef]
- Yazdi, J.; Mohammadiun, S.; Sadiq, R.; Neyshabouri, S.S.; Gharahbagh, A.A. Assessment of different MOEAs for rehabilitation evaluation of Urban Stormwater Drainage Systems—Case study: Eastern catchment of Tehran. J. Hydro-Environ. Res. 2018, 21, 76–85. [Google Scholar] [CrossRef]
- Eckart, K.; McPhee, Z.; Bolisetti, T. Multiobjective optimization of low impact development stormwater controls. J. Hydrol. 2018, 562, 564–576. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, Q.; Lei, X.; Savić, D.A. Comparison of Multiobjective Optimization Methods Applied to Urban Drainage Adaptation Problems. J. Water Resour. Plan. Manag. 2018, 144, 4018070. [Google Scholar] [CrossRef]
- Baek, S.-S.; Choi, D.-H.; Jung, J.-W.; Lee, H.-J.; Lee, H.; Yoon, K.-S.; Cho, K.H. Optimizing low impact development (LID) for stormwater runoff treatment in urban area, Korea: Experimental and modeling approach. Water Res. 2016, 86, 122–131. [Google Scholar] [CrossRef]
- Yang, Y.; Chui, T.F.M. Optimizing surface and contributing areas of bioretention cells for stormwater runoff quality and quantity management. J. Environ. Manag. 2018, 206, 1090–1103. [Google Scholar] [CrossRef]
- Behroozi, A.; Niksokhan, M.H.; Nazariha, M. Developing a simulation-optimisation model for quantitative and qualitative control of urban run-off using best management practices. J. Flood Risk Manag. 2015, 11, S340–S351. [Google Scholar] [CrossRef]
- Huang, C.-L.; Hsu, N.-S.; Liu, H.-J.; Huang, Y.-H. Optimization of low impact development layout designs for megacity flood mitigation. J. Hydrol. 2018, 564, 542–558. [Google Scholar] [CrossRef]
- She, L.; Wei, M.; You, X.-Y. Multi-objective layout optimization for sponge city by annealing algorithm and its environmental benefits analysis. Sustain. Cities Soc. 2021, 66, 102706. [Google Scholar] [CrossRef]
- Bakhshipour, A.E.; Dittmer, U.; Haghighi, A.; Nowak, W. Toward Sustainable Urban Drainage Infrastructure Planning: A Combined Multiobjective Optimization and Multicriteria Decision-Making Platform. J. Water Resour. Plan. Manag. 2021, 147, 04021049. [Google Scholar] [CrossRef]
- Lopes, M.D.; da Silva, G.B.L. An efficient simulation-optimization approach based on genetic algorithms and hydrologic modeling to assist in identifying optimal low impact development designs. Landsc. Urban Plan. 2021, 216, 104251. [Google Scholar] [CrossRef]
- Rezaei, A.R.; Ismail, Z.; Niksokhan, M.H.; Dayarian, M.A.; Ramli, A.H.; Yusoff, S. Optimal implementation of low impact development for urban stormwater quantity and quality control using multi-objective optimization. Environ. Monit. Assess. 2021, 193, 241. [Google Scholar] [CrossRef]
- Men, H.; Lu, H.; Jiang, W.; Xu, D. Mathematical Optimization Method of Low-Impact Development Layout in the Sponge City. Math. Probl. Eng. 2020, 2020, 6734081. [Google Scholar] [CrossRef]
- Tavakol-Davani, H.E.; Tavakol-Davani, H.; Burian, S.J.; McPherson, B.J.; Barber, M.E. Green infrastructure optimization to achieve pre-development conditions of a semiarid urban catchment. Environ. Sci. Water Res. Technol. 2019, 5, 1157–1171. [Google Scholar] [CrossRef]
- Bahrami, M.; Bozorg-Haddad, O.; Loáiciga, H.A. Optimizing stormwater low-impact development strategies in an urban watershed considering sensitivity and uncertainty. Environ. Monit. Assess. 2019, 191, 14. [Google Scholar] [CrossRef] [PubMed]
- Li, J. A data-driven improved fuzzy logic control optimization-simulation tool for reducing flooding volume at downstream urban drainage systems. Sci. Total. Environ. 2020, 732, 138931. [Google Scholar] [CrossRef] [PubMed]
- Chui, T.F.M.; Liu, X.; Zhan, W. Assessing cost-effectiveness of specific LID practice designs in response to large storm events. J. Hydrol. 2015, 533, 353–364. [Google Scholar] [CrossRef]
- Ghodsi, S.H.; Zahmatkesh, Z.; Goharian, E.; Kerachian, R.; Zhu, Z. Optimal design of low impact development practices in response to climate change. J. Hydrol. 2019, 580, 124266. [Google Scholar] [CrossRef]
- Kumar, S.; Guntu, R.K.; Agarwal, A.; Villuri, V.G.K.; Pasupuleti, S.; Kaushal, D.R.; Gosian, A.K.; Bronstert, A. Multi-objective optimization for stormwater management by green-roofs and infiltration trenches to reduce urban flooding in central Delhi. J. Hydrol. 2022, 606, 127455. [Google Scholar] [CrossRef]
- Lu, W.; Qin, X. An Integrated Fuzzy Simulation-Optimization Model for Supporting Low Impact Development Design under Uncertainty. Water Resour. Manag. 2019, 33, 4351–4365. [Google Scholar] [CrossRef]
- JRC. The European Settlement Map 2017 Release; Methodology and Outputof the European Settlement Map (ESM2p5m); European Comission: Brussels, Belgium, 2017; 2p.
- Mindat.org. The Köppen Climate Classification. 2022. Available online: https://www.mindat.org/climate.php (accessed on 15 January 2023).
- DWD. Deutsche Wetter Dienst. 2022. Available online: https://www.dwd.de/DE/wetter/wetterundklima_vorort/sachsen/dresden/_node.html (accessed on 15 January 2023).
- Rossman, L. Storm Water Management Model Users Manual Version 5.1; US EPA Office of Research and Development; EPA: Washington, DC, USA, 2015.
- Warsta, L.; Niemi, T.J.; Taka, M.; Krebs, G.; Haahti, K.; Koivusalo, H.; Kokkonen, T. Development and application of an automated subcatchment generator for SWMM using open data. Urban Water J. 2017, 14, 954–963. [Google Scholar] [CrossRef]
- Criss, R.E.; Winston, W.E. Do Nash values have value? Discussion and alternate proposals. Hydrol. Process. 2008, 22, 2723–2725. [Google Scholar] [CrossRef]
- Kim, Y.; Chung, E.-S.; Won, K.; Gil, K. Robust Parameter Estimation Framework of a Rainfall-Runoff Model Using Pareto Optimum and Minimax Regret Approach. Water 2015, 7, 1246–1263. [Google Scholar] [CrossRef]
- DWA-A118; Abwasser und Abfall e.V. DWA Deutsche Vereinigung fur Wasserwirtschaft.Arbeitsblatt DWA-A 118 Hydraulische Bemessungund Nachweis Hydraulische Bemessung und Nachweis. Abwasser und Abfall e.V. DWA Deutsche Vereinigung fur Wasserwirtschaft: Hennef, Germany, 2006.
- Junghaenel, T.; Ertel, H.; Deutschländer, T. Bericht zur Revision der Koordinierten Starkregen Regionalisierung und -Auswertung des Deutschen Wetterdienstes in der Version; German Meteorological Service: Offenbach am Main, Germany, 2010.
- Chen, W.; Huang, G.; Zhang, H. Urban stormwater inundation simulation based on SWMM and diffusive overland-flow model. Water Sci. Technol. 2017, 76, 3392–3403. [Google Scholar] [CrossRef]
- Ferrans, P.; Temprano, J. Continuous Quantity and Quality Modeling for Assessing the Effect of SUDS: Application on a Conceptual Urban Drainage Basin. Environ. Process. 2022, 9, 58. [Google Scholar] [CrossRef]
- Torres, A.M. E2STORMED decision support tool guidelines. 2015. [Google Scholar]
- Matlab. 2022. Available online: https://es.mathworks.com/products/matlab.html (accessed on 15 January 2023).




| Event | Depth [mm] | Duration [h] | Return Period [Years] | NSE | PFE | VE |
|---|---|---|---|---|---|---|
| 1 | 5.8 | 220 | 0.16 | 0.72 | 0.07 | 0.02 |
| 2 | 6 | 255 | 0.16 | 0.87 | 0.23 | 0.28 |
| 3 | 5.3 | 240 | 0.13 | 0.77 | 0.30 | 0.30 |
| 4 | 10.6 | 235 | 0.50 | 0.95 | 0.03 | 0.07 |
| 5 | 5.9 | 150 | 0.17 | 0.95 | 0.30 | 0.04 |
| 6 | 9.5 | 245 | 0.39 | 0.55 | 0.24 | 0.20 |
| 7 | 11.8 | 365 | 0.62 | 0.87 | 0.25 | 0.17 |
| 8 | 9 | 305 | 0.35 | 0.78 | 0.28 | 0.22 |
| 9 | 5.4 | 220 | 0.14 | 0.49 | 0.08 | 0.48 |
| 10 | 6.9 | 335 | 0.21 | 0.78 | 0.33 | 0.03 |
| 11 | 7.5 | 195 | 0.25 | 0.87 | 0.29 | 0.05 |
| 12 | 9.9 | 380 | 0.42 | 0.74 | 0.00 | 0.12 |
| 13 | 5.1 | 205 | 0.13 | 0.69 | 0.60 | 0.08 |
| 14 | 22.1 | 670 | 3.15 | 0.84 | 0.36 | 0.24 |
| 15 | 5.7 | 70 | 0.17 | 0.70 | 0.26 | 0.09 |
| Variable | Units | GR | RG | IT | PP |
|---|---|---|---|---|---|
| Surface | |||||
| Berm Height | mm | 90.00 | 150.00 | 0.00 | 0.00 |
| Vegetation volume | mm | 0.10 | 0.00 | ||
| n Manning | mm | 0.09 | 0.11 | 0.24 | 0.03 |
| Slope | % | 1.00 | 1.00 | 1.00 | 1.00 |
| Soil | |||||
| Thickness | mm | 30.00 | 500.00 | 150.00 | |
| Porosity | % | 0.47 | 0.40 | 0.43 | |
| Field capacity | % | 0.24 | 0.17 | 0.10 | |
| Wilting point | % | 0.07 | 0.11 | 0.02 | |
| Conductivity | mm/h | 265.67 | 167.99 | 115.00 | |
| Conductivity slope | - | 10.00 | 21.09 | 10.00 | |
| Suction head | mm/h | 65.00 | 37.31 | 65.00 | |
| Storage | |||||
| Thickness | mm | 200.00 | 500.00 | 10.00 | |
| Void ratio | % | 0.58 | 0.75 | 0.54 | |
| Seepage rate | mm/h | 101.10 | 24.00 | 172.00 | |
| Drain | |||||
| Flow coefficient | - | 2.00 | 2.00 | ||
| Flow exponent | - | 0.50 | 0.50 | ||
| Offset | mm | 0.00 | 0.00 | ||
| Pavement | |||||
| Thickness | mm | 50.00 | |||
| Void ratio | % | 0.37 | |||
| Impervious surface fraction | % | 0.08 | |||
| Permeability | mm/h | 745.33 | |||
| Drainage Mat (Green Roofs) | |||||
| Thickness | mm | 10.00 | |||
| Void fraction | % | 0.47 | |||
| n Manning | mm | 0.07 | |||
| Typology | Capital Cost [€/m2] | Annual Maintenance Cost [%/m2-Year] |
|---|---|---|
| GR | 145 | 10 |
| RG | 50 | 5 |
| IT | 120 | 2.5 |
| PP | 60 | 0.1 |
| Land Use | Typology Assigned |
|---|---|
| Stone paver | Permeable pavement |
| Vegetation | Rain garden |
| Roof | Green roof |
| Street | Permeable pavement |
| Sand gravel | Infiltration trench |
| R. Period [Years] | Duration [Mins] | Flooded Volume [m3] | Flooded Area [m2] | Maximum Flooded Height [m] |
|---|---|---|---|---|
| 10 | 30 | 471 | 4172 | 0.48 |
| 10 | 120 | 526 | 4420 | 0.51 |
| 10 | 360 | 565 | 4020 | 0.54 |
| 20 | 30 | 612 | 4048 | 0.59 |
| 20 | 120 | 688 | 4212 | 0.64 |
| 20 | 360 | 724 | 4236 | 0.66 |
| 50 | 30 | 813 | 4236 | 0.76 |
| 50 | 120 | 937 | 4564 | 0.83 |
| 50 | 360 | 987 | 4480 | 0.66 |
| 100 | 30 | 978 | 4488 | 0.64 |
| 100 | 120 | 1182 | 4712 | 0.75 |
| 100 | 360 | 1250 | 6100 | 0.79 |
| R. Period [Years] | Duration [Mins] | Total Investment [106 €] | Cost Efficiency of Selected Configuration [% Volume Reduced/106 €] |
|---|---|---|---|
| 10 | 30 | 0.92 | 1.06 |
| 10 | 120 | 0.69 | 1.34 |
| 10 | 360 | 1.64 | 0.59 |
| 20 | 30 | 1.35 | 0.73 |
| 20 | 120 | 1.99 | 0.46 |
| 20 | 360 | 1.43 | 0.65 |
| 50 | 30 | 1.62 | 0.59 |
| 50 | 120 | 1.08 | 0.87 |
| 50 | 360 | 1.86 | 0.50 |
| 100 | 30 | 2.26 | 0.43 |
| 100 | 120 | 2.34 | 0.39 |
| 100 | 360 | 2.32 | 0.34 |
| R. Period [Years] | Duration [Mins] | Total Investment [106 €] | Reference Flooded Area [m2] | SUDS Flooded Area [m2] | Reduction Area Flooded [%] |
|---|---|---|---|---|---|
| 10 | 30 | 0.92 | 4172 | 4020 | 3.64 |
| 10 | 120 | 0.69 | 4420 | 4020 | 9.05 |
| 10 | 360 | 1.64 | 4020 | 4000 | 0.50 |
| 20 | 30 | 1.35 | 4048 | 4040 | 0.20 |
| 20 | 120 | 1.99 | 4212 | 3936 | 6.55 |
| 20 | 360 | 1.43 | 4236 | 3972 | 6.23 |
| 50 | 30 | 1.62 | 4236 | 3960 | 6.52 |
| 50 | 120 | 1.08 | 4564 | 4480 | 1.84 |
| 50 | 360 | 1.86 | 4480 | 2896 | 35.36 |
| 100 | 30 | 2.26 | 4488 | 3636 | 18.98 |
| 100 | 120 | 2.34 | 4712 | 3464 | 26.49 |
| 100 | 360 | 2.32 | 6100 | 3656 | 40.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferrans, P.; Reyes-Silva, J.D.; Krebs, P.; Temprano, J. Flood Management with SUDS: A Simulation–Optimization Framework. Water 2023, 15, 426. https://doi.org/10.3390/w15030426
Ferrans P, Reyes-Silva JD, Krebs P, Temprano J. Flood Management with SUDS: A Simulation–Optimization Framework. Water. 2023; 15(3):426. https://doi.org/10.3390/w15030426
Chicago/Turabian StyleFerrans, Pascual, Julian David Reyes-Silva, Peter Krebs, and Javier Temprano. 2023. "Flood Management with SUDS: A Simulation–Optimization Framework" Water 15, no. 3: 426. https://doi.org/10.3390/w15030426





