Pressure-Flow Scour under a Bridge Deck in Clear Water Conditions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Setup
2.2. Dimensional Analysis
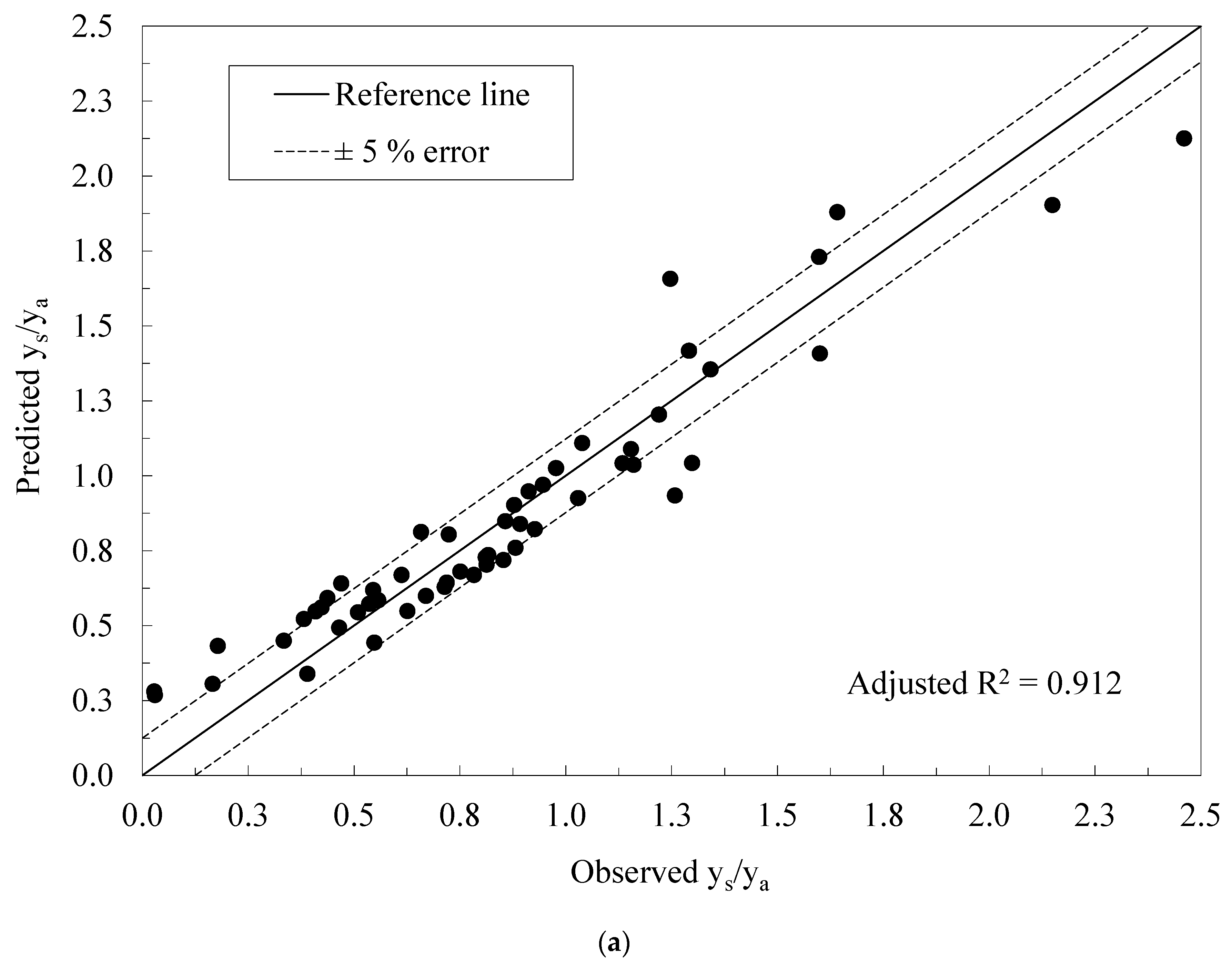
3. Results and Discussion
3.1. Free Surface and Pressure-Flow Scour
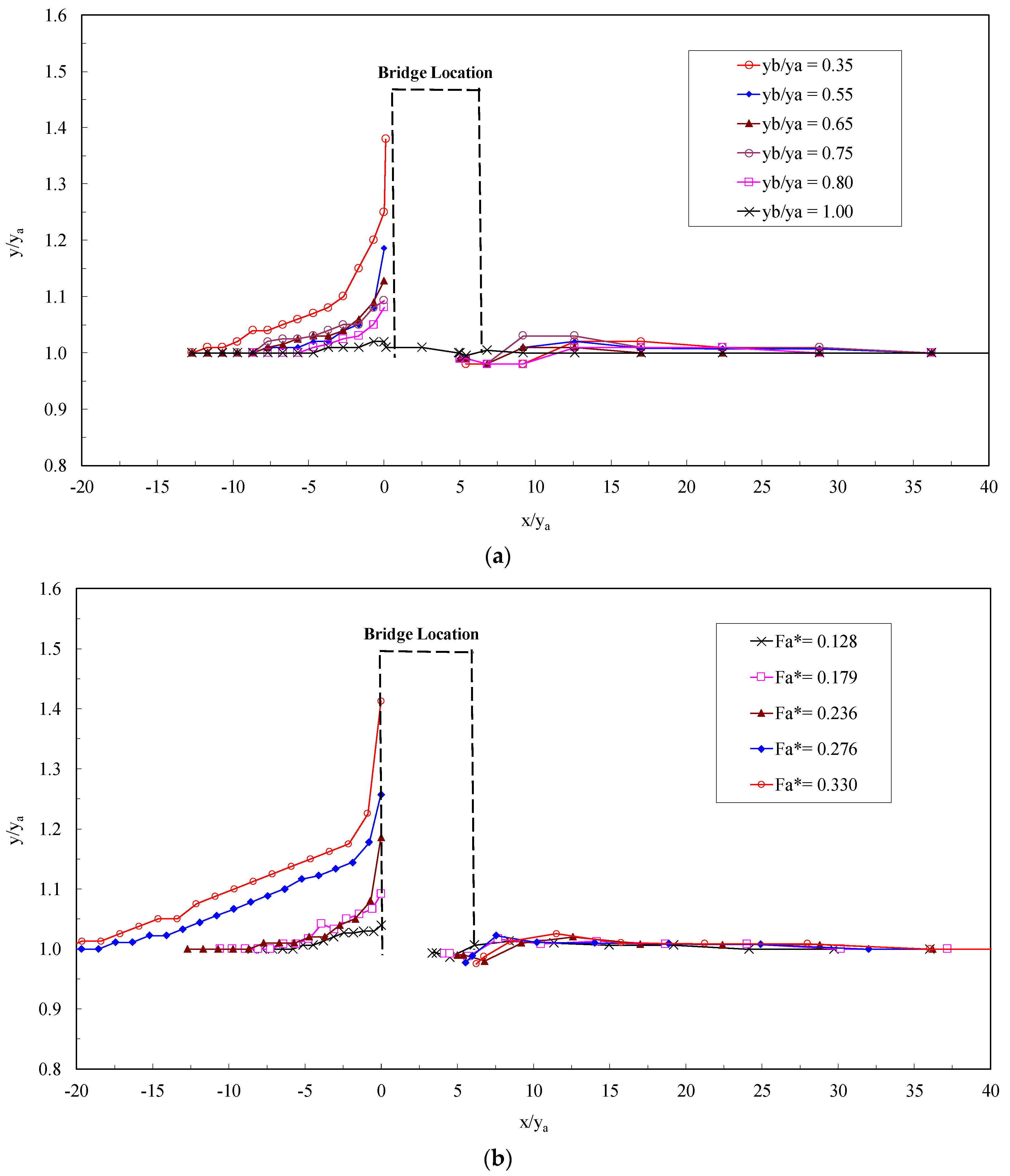
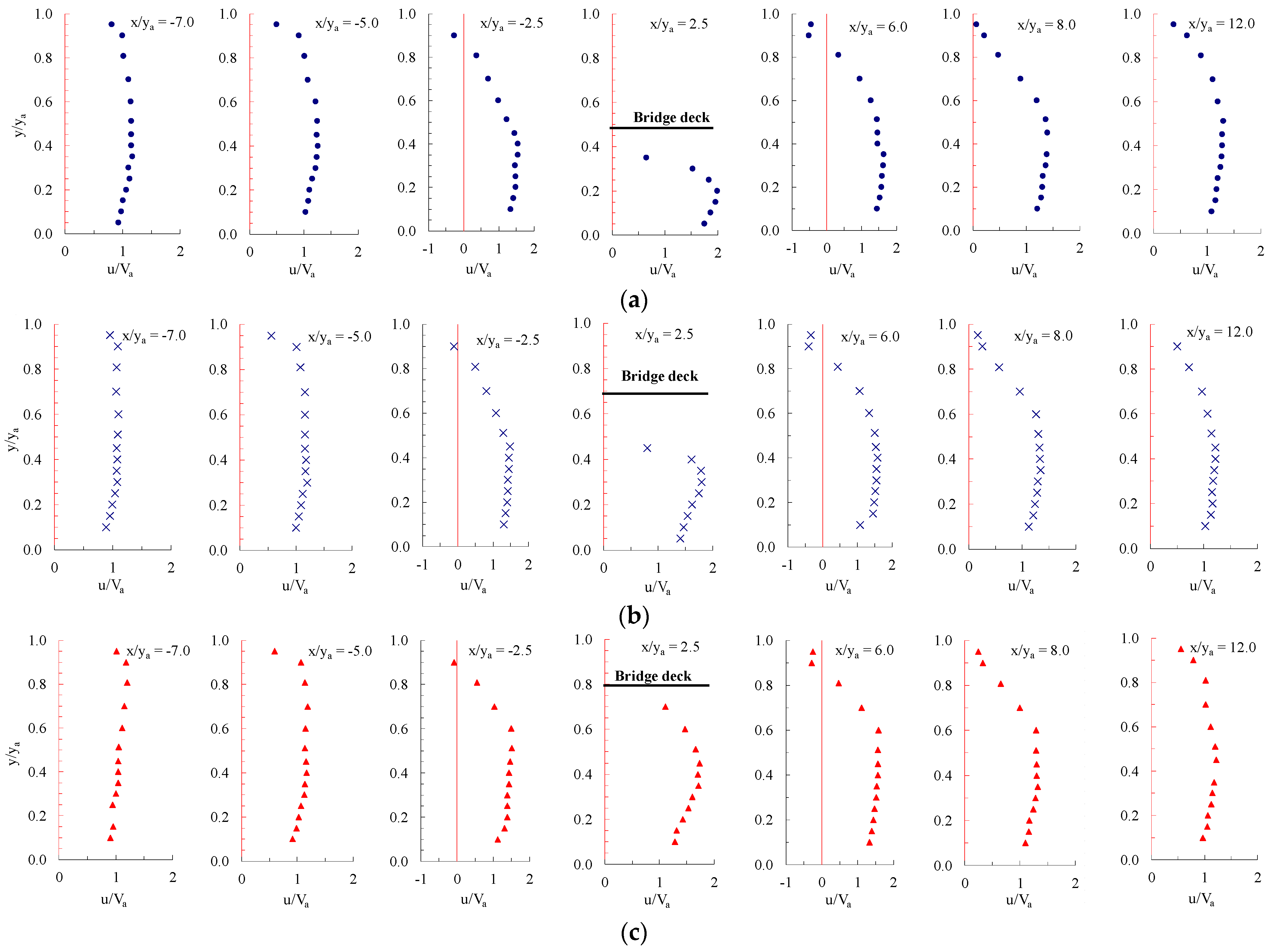
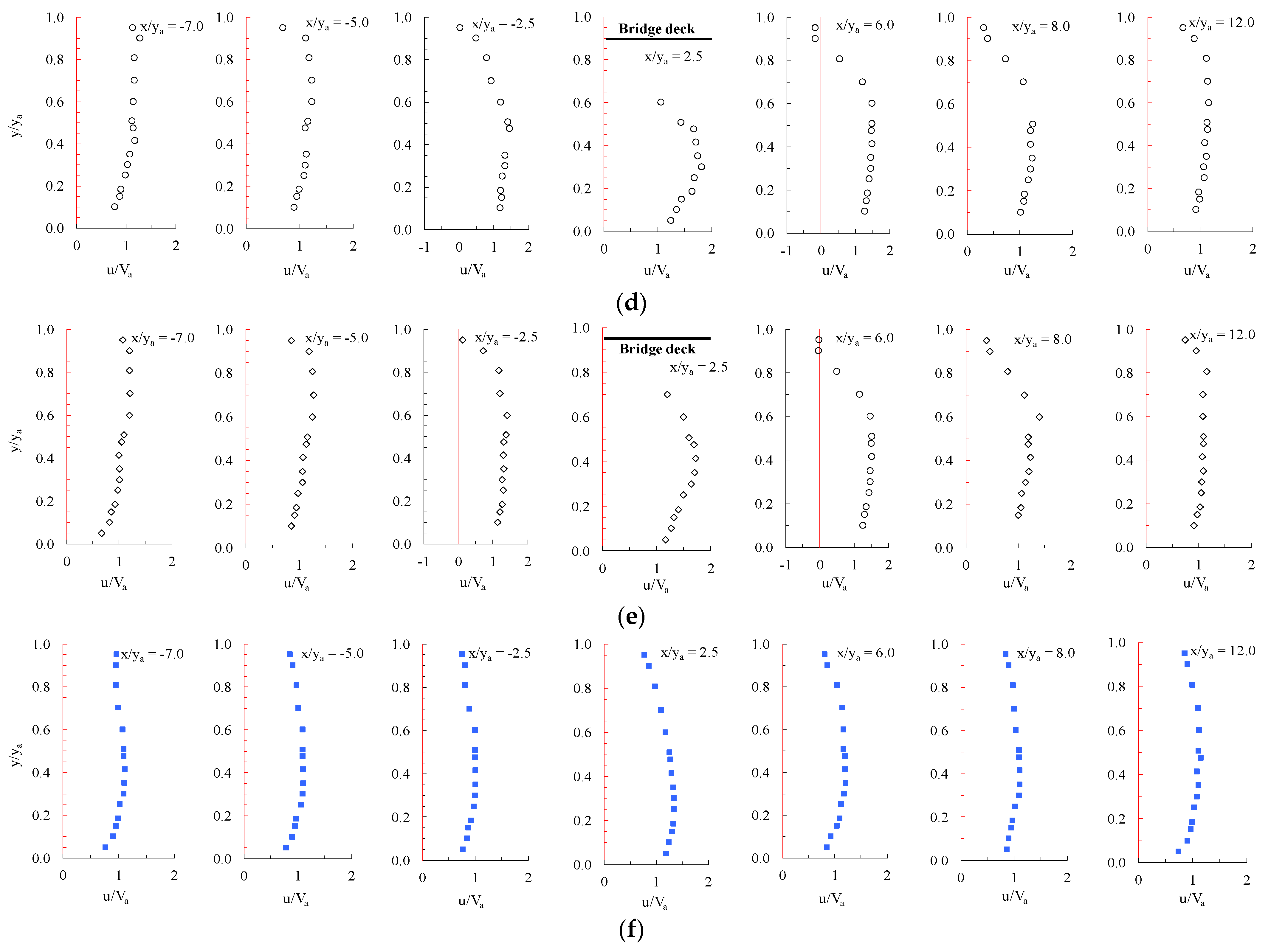
3.2. Water Surface Profile and Velocity Field
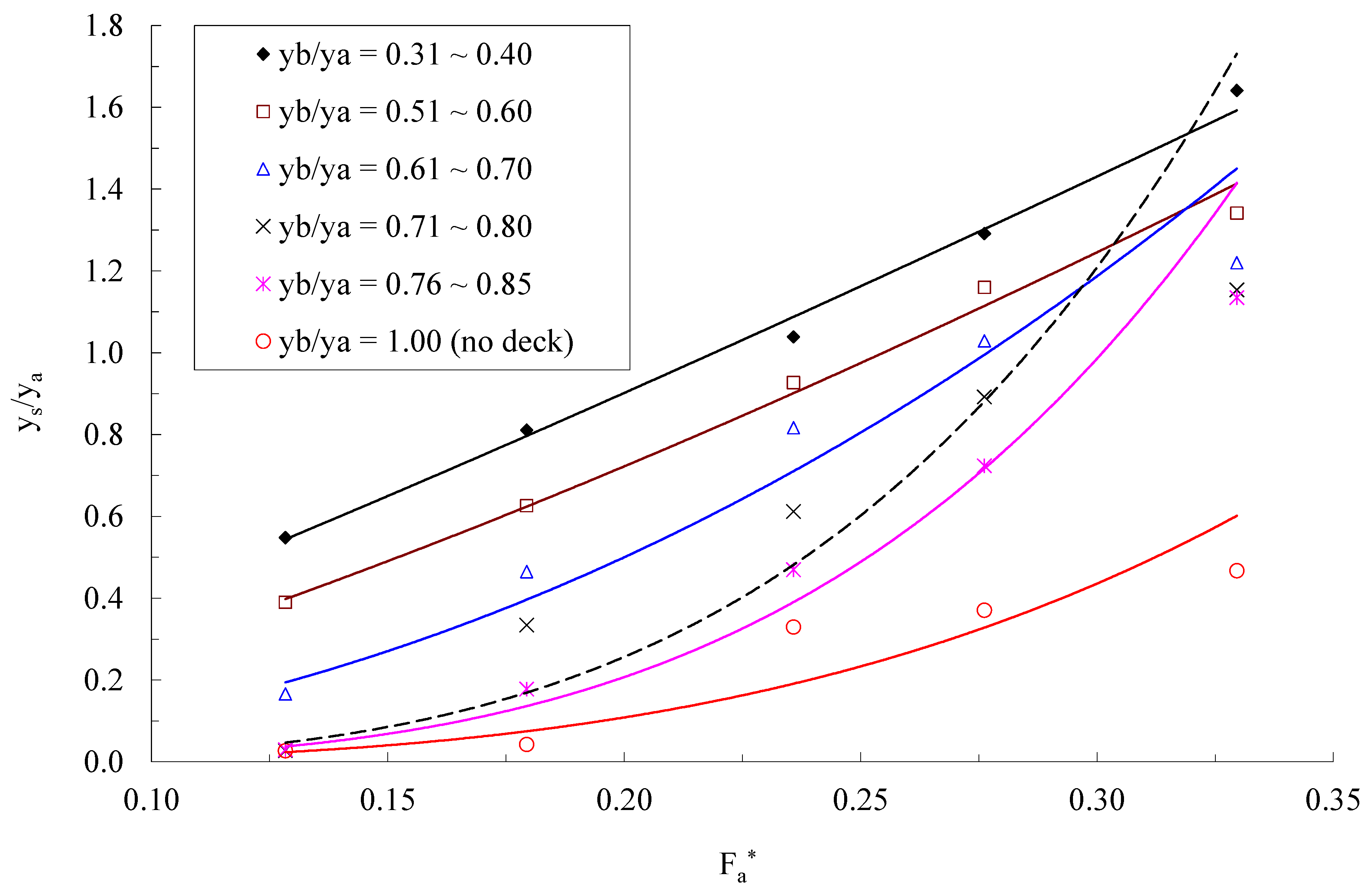
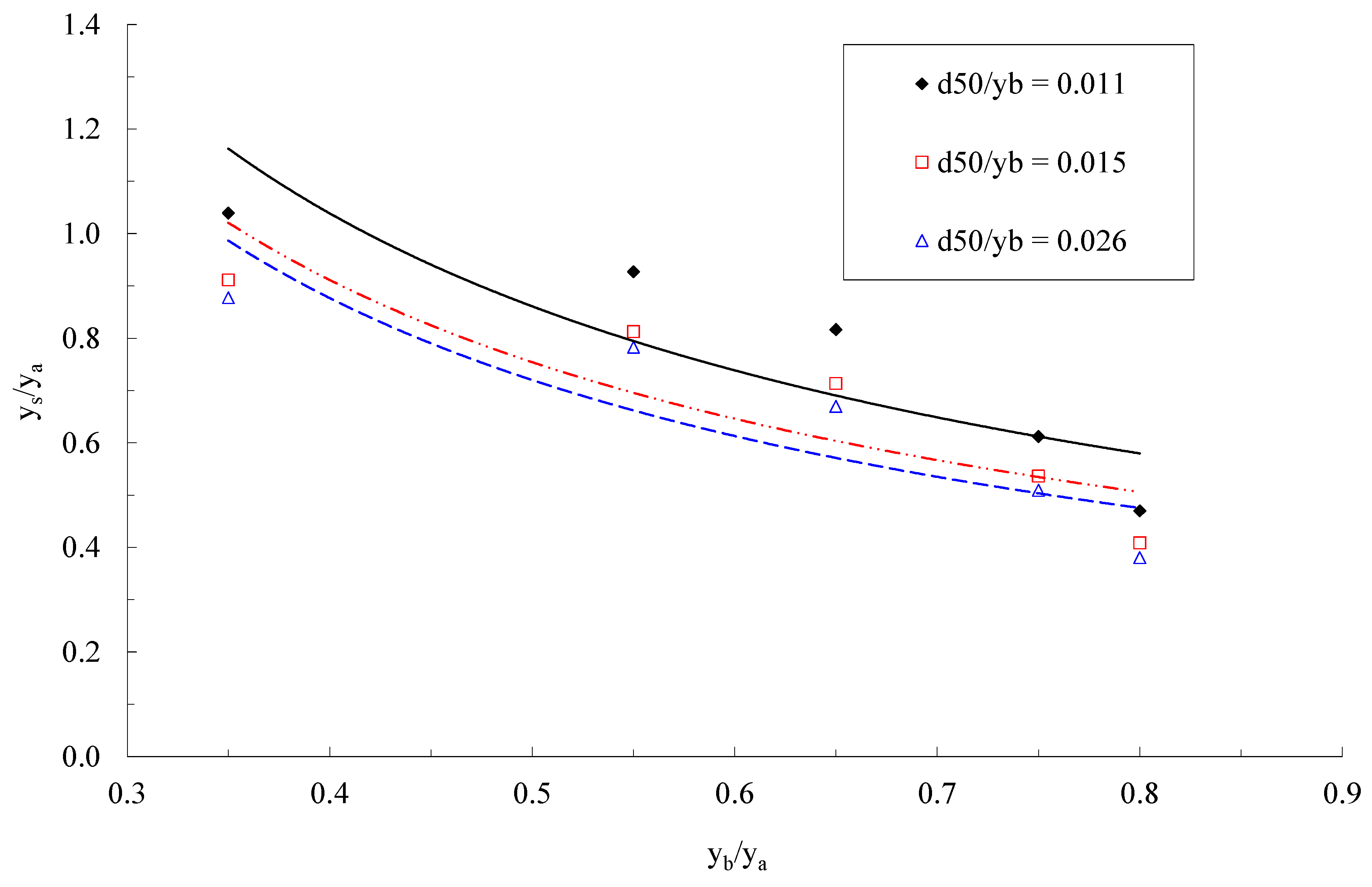
3.3. Pressure-Flow Scour Profile
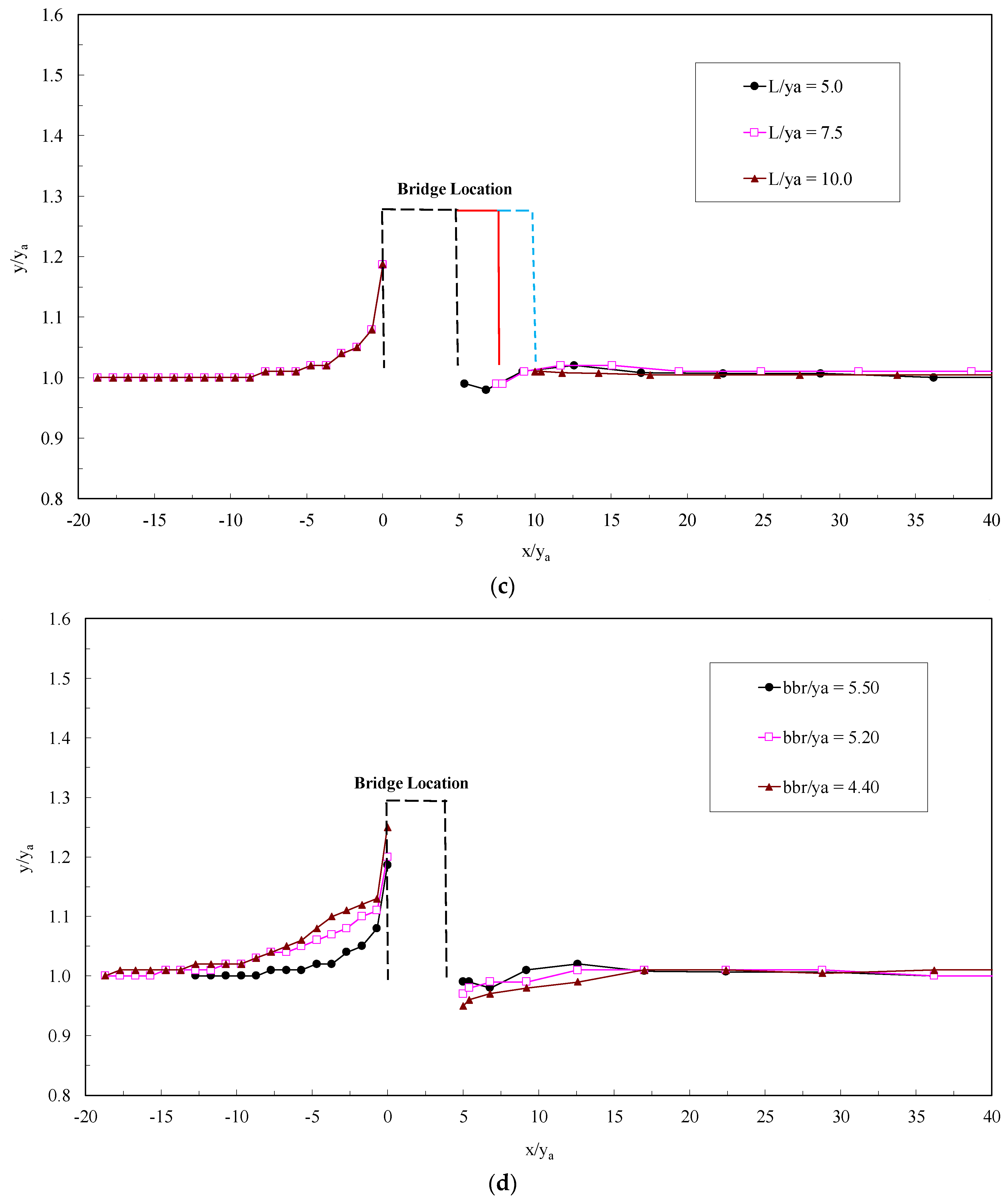
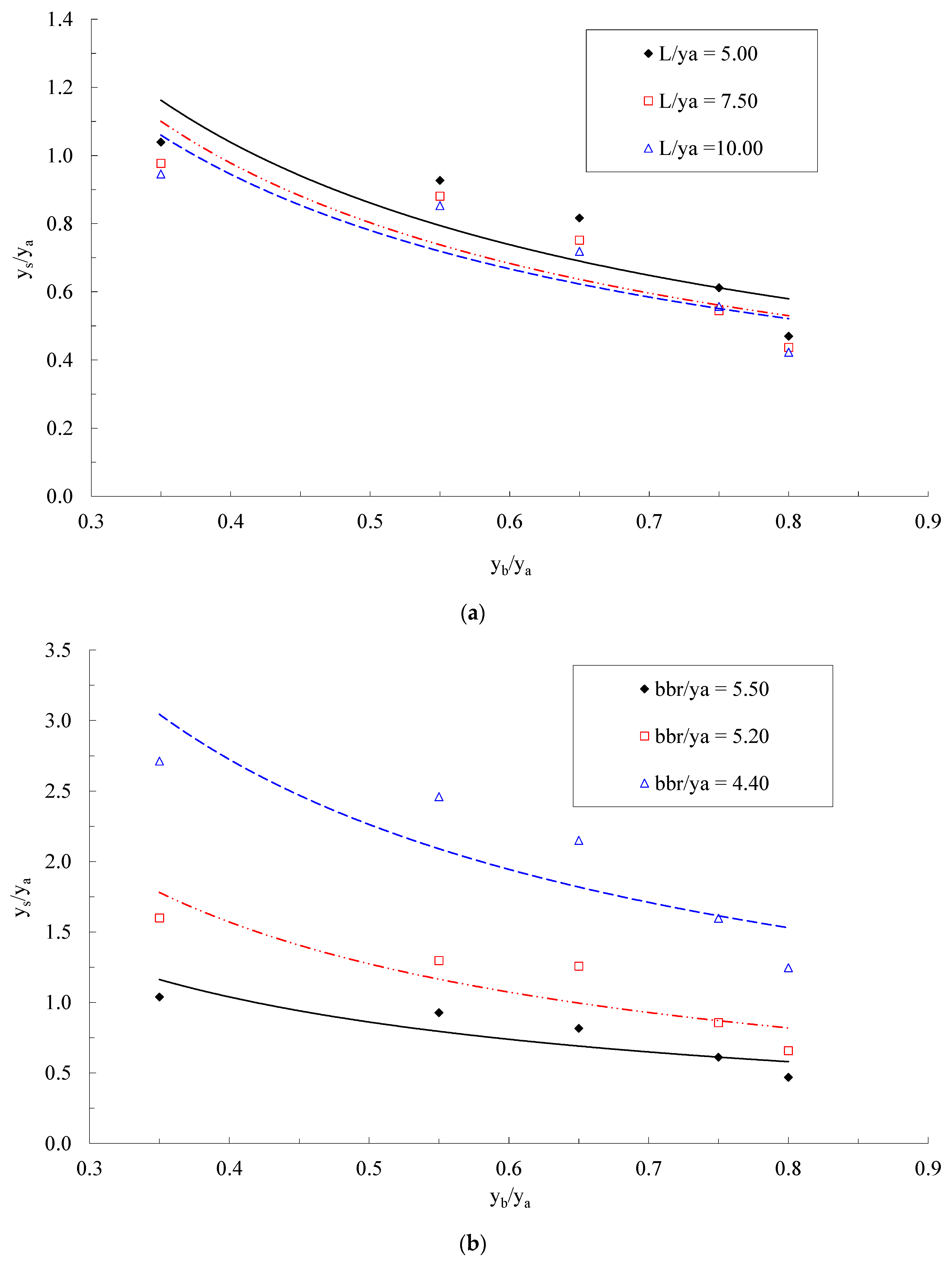
3.4. Effects of the Bridge Length and Width
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gaudio, R.; Tafarojnoruz, A.; Calomino, F. Combined flowaltering countermeasures against bridge pier scour. J. Hydraul. Res. 2012, 50, 35–43. [Google Scholar] [CrossRef]
- Arneson, L.A.; Zevenbergen, L.; Lagasse, P.; Clopper, P. Evaluating Scour at Bridges; Report No. FHWA-HIF-12-003; USDOT, National Highway Institute (US): Washington, DC, USA, 2012. [Google Scholar]
- Umbrell, E.R.; Young, G.; Stein, S.; Jones, J. Clearwater contraction scour under bridges in pressure flow. J. Hydraul. Eng. 1998, 124, 236–240. [Google Scholar] [CrossRef]
- Lyn, D.A. Pressure-flow scour: A reexamination of the HEC-18 equation. J. Hydraul. Eng. 2008, 134, 1015–1020. [Google Scholar] [CrossRef]
- Richardson, E.V.; Harrison, L.; Richardson, J.; Davis, S. Evaluating Scour at Bridges HEC 18: Hydraulic Engineering Circular, 2nd ed.; Federal Highway Administration: Washington, DC, USA, 1993; pp. 5–53. [Google Scholar]
- Carnacina, I.; Leonardi, N.; Pagliara, S. Characteristics of flow structure around cylindrical bridge piers in pressure-flow conditions. Water 2019, 11, 2240. [Google Scholar] [CrossRef] [Green Version]
- Majid, S.A.; Tripathi, S. Pressure-flow scour due to vertical contraction: A review. J. Hydraul. Eng. 2021, 147, 03121002. [Google Scholar] [CrossRef]
- Abed, L.M. Local Scour around Bridge Piers in Pressure Flow. Ph.D. Dissertation, Department of Civil Engineering, Colorado State University, Fort Collins, CO, USA, 1991; pp. 43–47, 61–63. [Google Scholar]
- Arneson, L.A.; Abt, S.R. Vertical contraction scour at bridges with water flowing under pressure conditions. Transp. Res. Rec. 1998, 1647, 10–17. [Google Scholar] [CrossRef]
- Arneson, L.A. The Effect of Pressure-Flow on Local Scour in Bridge Openings. Ph.D. Dissertation, Department of Civil Engineering, Colorado State University, Fort Collins, CO, USA, 1997. [Google Scholar]
- Guo, J.; Kerenyi, K.; Pagan-Ortiz, J. Bridge Pressure Flow Scour for Clear Water Conditions; Report No. FHWA-HRT-09-041; Turner-Fairbank Highway Research Center, FHWA: McLean, VA, USA, 2009; pp. 24–29. [Google Scholar]
- Lin, C.; Kao, M.J.; Hsieh, S.C.; Lo, L.F.; Raikar, R.V. On the flow structures under a partially inundated bridge deck. J. Mech. 2012, 28, 191–207. [Google Scholar] [CrossRef]
- Shan, H.; Bojanowski, C.; Xie, Z.; Suaznabar, O.; Lottes, S.; Shen, J.; Kerenyi, K. Submerged Flow Bridge Scour under Clear Water Conditions; Publication No. FHWA-HRT-12-034; Federal Highway Administration: Washington, DC, USA, 2012. [Google Scholar]
- Dankoo, A.; Yonesi, H.; Torabipoudeh, H.; Saneie, M. The effect of pressure flow conditions on bridge pier scour in compound open channels with vegetation. J. Hydraul. Iran. Hydraul. Assoc. 2022, 17, 89–103. [Google Scholar]
- Kocyigit, M.B.; Karakurt, O. Pressure flow and weir scour beneath a bridge deck. Can. J. Civ. Eng. 2019, 46, 534–543. [Google Scholar] [CrossRef]
- Melville, B.W. Scour at various hydraulic structures: Sluice gates, submerged bridges, low weirs. Aust. J. Water Resour. 2014, 18, 101–117. [Google Scholar] [CrossRef]
- Kumcu, S.Y. Steady and unsteady pressure scour under bridges at clear-water conditions. Can. J. Civ. Eng. 2016, 43, 334–342. [Google Scholar] [CrossRef]
- Dey, S.; Raikar, R.V.; Roy, A. Scour at submerged cylindrical obstacles under steady flow. J. Hydraul. Eng. 2008, 134, 105–109. [Google Scholar] [CrossRef]
- Raudkivi, A.J.; Ettema, R. Scour at cylindrical bridge piers in armored beds. J. Hydraul. Eng. 1985, 111, 713–731. [Google Scholar] [CrossRef]
- Helal, E. Experimental evaluation of changes in channel bed morphology due to a defective pressure flow pipe. J. Irrig. Drain. Eng. 2019, 145, 04019022. [Google Scholar] [CrossRef]
- Neill, C.R. Guide to Bridge Hydraulics; University of Toronto Press: Toronto, ON, Canada, 1973. [Google Scholar]
- Melville, B.W. The physics of local scour at bridge piers. In Proceedings of the 4th International Conference on Scour and Erosion (ICSE-4), Tokyo, Japan, 4–8 November 2008; Japanese Geotechnical Society: Tokyo, Japan, 2008; pp. 28–40. [Google Scholar]
- Guo, J.; Kerenyi, K.; Pagan-Ortiz, J.; Flora, K. Bridge pressure flow scour at clear water threshold condition. Trans. Tianjin Univ. 2009, 15, 79–94. [Google Scholar] [CrossRef]
- Henderson, F.M. Open Channel Flow; The Macmillan Company: New York, NY, USA, 1966; p. 93. [Google Scholar]
- Carnacina, I.; Pagliara, S.; Leonardi, N. Bridge pier scour under pressure flow conditions. River Res. Appl. 2019, 35, 844–854. [Google Scholar] [CrossRef]
- Picek, T.; Havlik, A.; Mattas, D.; Mares, K. Hydraulic calculation of bridges at high water stages. J. Hydraul. Res. 2007, 45, 400–406. [Google Scholar] [CrossRef]
- Hahn, E. Clear-Water Scour at Vertically or Laterally Contracted Bridge Sections. M.Sc. Dissertation, School of Civil Engineering, Purdue University, West Lafayette, IN, USA, 2005. [Google Scholar]
- Yoon, K.S.; Lee, S.; Hong, S. Time-averaged turbulent velocity flow field through the various bridge contractions during large flooding. Water 2019, 11, 143. [Google Scholar] [CrossRef] [Green Version]
- Hahn, E.M.; Lyn, D. Anomalous contraction scour? Vertical contraction case. J. Hydraul. Eng. 2010, 136, 137–141. [Google Scholar] [CrossRef]




| Model/ Equation | Remarks |
|---|---|
| Arneson and Abt [9] | Vc = critical velocity C = 1.52 |
| Umbrell et al. [3] | w = flow depth overtopping bridge C = 1.58 in critical velocity, Vc equation |
| Lyn [4] | |
| Guo et al. [11] | h = ya − yb = (hs + hg) Fi = inundation Froude number λ, m, β = constanta parameters |
| HEC-18 Equation [2] | Ku = 0.0077 (English units) Q = flow discharge (ft3/s) dm = diameter of the smallest non-transportable particle in the bed material (= 1.25.d50) hg = girder depth |
| Shan et al. [13] | Ku = constant = 6.17 m2/s |
| Melville [16] | |
| Kumcu [17] | |
| Kocyigit and Karakurt [15] | hg = girder depth = densimetric Froude number of the flow passing under the bridge deck |
| Parameter | Values |
|---|---|
| Approach flow depth, ya | 8, 9, 10, 12, and 15 cm |
| Girder dimension | 1.5 cm height and 0.8 cm width |
| Bridge length, L | 50, 75, and 100 cm |
| Bridge width, bbr | 55, 52, and 44 cm |
| Median diameter, d50 | 1.093, 1.469, and 2.575 mm |
| Geometric standard deviations, σg | 1.302, 1.198, and 1.274 |
| Test | ya (cm) | yb (c) | L (cm) | bbr (cm) | hs (cm) | Va (m/s) | d50 (mm) | σg (-) | Fa (-) | (-) | ys (cm) | Scour Number |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 15.0 | 6.00 | 50 | 55 | 7.50 | 0.200 | 1.093 | 1.302 | 0.165 | 0.128 | 8.22 | 0.948 |
| 2 | 15.0 | 9.00 | 50 | 55 | 4.50 | 0.200 | 1.093 | 1.302 | 0.165 | 0.128 | 5.86 | 0.990 |
| 3 | 15.0 | 10.50 | 50 | 55 | 3.0 | 0.200 | 1.093 | 1.302 | 0.165 | 0.128 | 2.49 | 0.866 |
| 4 | 15.0 | 12.00 | 50 | 55 | 1.5 | 0.200 | 1.093 | 1.302 | 0.165 | 0.128 | 0.42 | 0.828 |
| 5 | 15.0 | 12.75 | 50 | 55 | 0.8 | 0.200 | 1.093 | 1.302 | 0.165 | 0.128 | 0.45 | 0.880 |
| 6 | 12.0 | 4.50 | 50 | 55 | 6.0 | 0.250 | 1.093 | 1.302 | 0.230 | 0.179 | 9.73 | 1.186 |
| 7 | 12.0 | 6.90 | 50 | 55 | 3.6 | 0.250 | 1.093 | 1.302 | 0.230 | 0.179 | 7.51 | 1.201 |
| 8 | 12.0 | 8.10 | 50 | 55 | 2.4 | 0.250 | 1.093 | 1.302 | 0.230 | 0.179 | 5.58 | 1.140 |
| 9 | 12.0 | 9.30 | 50 | 55 | 1.2 | 0.250 | 1.093 | 1.302 | 0.230 | 0.179 | 4.01 | 1.109 |
| 10 | 12.0 | 9.90 | 50 | 55 | 0.6 | 0.250 | 1.093 | 1.302 | 0.230 | 0.179 | 2.14 | 1.003 |
| 11 | 10.0 | 3.50 | 50 | 55 | 5.0 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 10.39 | 1.389 |
| 12 | 10.0 | 5.50 | 50 | 55 | 3.0 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 9.27 | 1.477 |
| 13 | 10.0 | 6.50 | 50 | 55 | 2.0 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 8.17 | 1.467 |
| 14 | 10.0 | 7.50 | 50 | 55 | 1.0 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 6.120 | 1.362 |
| 15 | 10.0 | 8.00 | 50 | 55 | 0.5 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 4.69 | 1.270 |
| 16 | 9.00 | 3.00 | 50 | 55 | 4.5 | 0.333 | 1.093 | 1.302 | 0.355 | 0.276 | 11.62 | 1.624 |
| 17 | 9.00 | 4.80 | 50 | 55 | 2.7 | 0.333 | 1.093 | 1.302 | 0.355 | 0.276 | 10.44 | 1.693 |
| 18 | 9.00 | 5.70 | 50 | 55 | 1.8 | 0.333 | 1.093 | 1.302 | 0.355 | 0.276 | 9.26 | 1.662 |
| 19 | 9.00 | 6.60 | 50 | 55 | 0.9 | 0.333 | 1.093 | 1.302 | 0.355 | 0.276 | 8.03 | 1.625 |
| 20 | 9.00 | 7.05 | 50 | 55 | 0.5 | 0.333 | 1.093 | 1.302 | 0.355 | 0.276 | 6.51 | 1.507 |
| 21 | 8.00 | 2.50 | 50 | 55 | 4.0 | 0.375 | 1.093 | 1.302 | 0.423 | 0.330 | 13.13 | 1.954 |
| 22 | 8.00 | 4.10 | 50 | 55 | 2.4 | 0.375 | 1.093 | 1.302 | 0.423 | 0.330 | 10.73 | 1.854 |
| 23 | 8.00 | 4.90 | 50 | 55 | 1.6 | 0.375 | 1.093 | 1.302 | 0.423 | 0.330 | 9.76 | 1.832 |
| 24 | 8.00 | 5.70 | 50 | 55 | 0.8 | 0.375 | 1.093 | 1.302 | 0.423 | 0.330 | 9.23 | 1.866 |
| 25 | 8.00 | 6.10 | 50 | 55 | 0.4 | 0.375 | 1.093 | 1.302 | 0.423 | 0.330 | 9.08 | 1.897 |
| 26 | 10.0 | 3.50 | 50 | 55 | 5.0 | 0.300 | 1.469 | 1.198 | 0.303 | 0.236 | 9.12 | 1.262 |
| 27 | 10.0 | 5.50 | 50 | 55 | 3.0 | 0.300 | 1.469 | 1.198 | 0.303 | 0.236 | 8.13 | 1.363 |
| 28 | 10.0 | 6.50 | 50 | 55 | 2.0 | 0.300 | 1.469 | 1.198 | 0.303 | 0.236 | 7.14 | 1.364 |
| 29 | 10.0 | 7.50 | 50 | 55 | 1.0 | 0.300 | 1.469 | 1.198 | 0.303 | 0.236 | 5.36 | 1.286 |
| 30 | 10.0 | 8.00 | 50 | 55 | 0.5 | 0.300 | 1.469 | 1.198 | 0.303 | 0.236 | 4.09 | 1.209 |
| 31 | 10.0 | 3.50 | 50 | 55 | 5.0 | 0.300 | 2.575 | 1.274 | 0.303 | 0.236 | 8.78 | 1.228 |
| 32 | 10.0 | 5.50 | 50 | 55 | 3.0 | 0.300 | 2.575 | 1.274 | 0.303 | 0.236 | 7.83 | 1.333 |
| 33 | 10.0 | 6.50 | 50 | 55 | 2.0 | 0.300 | 2.575 | 1.274 | 0.303 | 0.236 | 6.69 | 1.320 |
| 34 | 10.0 | 7.50 | 50 | 55 | 1.0 | 0.300 | 2.575 | 1.274 | 0.303 | 0.236 | 5.09 | 1.259 |
| 35 | 10.0 | 8.00 | 50 | 55 | 0.5 | 0.300 | 2.575 | 1.274 | 0.303 | 0.236 | 3.81 | 1.181 |
| 36 | 10.0 | 3.50 | 75 | 55 | 5.0 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 9.77 | 1.327 |
| 37 | 10.0 | 5.50 | 75 | 55 | 3.0 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 8.81 | 1.431 |
| 38 | 10.0 | 6.50 | 75 | 55 | 2.0 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 7.51 | 1.401 |
| 39 | 10.0 | 7.50 | 75 | 55 | 1.0 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 5.45 | 1.295 |
| 40 | 10.0 | 8.00 | 75 | 55 | 0.5 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 4.37 | 1.237 |
| 41 | 10.0 | 3.50 | 100 | 55 | 5.0 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 9.46 | 1.296 |
| 42 | 10.0 | 5.50 | 100 | 55 | 3.0 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 8.53 | 1.403 |
| 43 | 10.0 | 6.50 | 100 | 55 | 2.0 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 7.19 | 1.369 |
| 44 | 10.0 | 7.50 | 100 | 55 | 1.0 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 5.57 | 1.307 |
| 45 | 10.0 | 8.00 | 100 | 55 | 0.5 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 4.23 | 1.223 |
| 46 | 10.0 | 3.50 | 50 | 52 | 5.0 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 16.00 | 1.950 |
| 47 | 10.0 | 5.50 | 50 | 52 | 3.0 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 12.98 | 1.848 |
| 48 | 10.0 | 6.50 | 50 | 52 | 2.0 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 12.58 | 1.908 |
| 49 | 10.0 | 7.50 | 50 | 52 | 1.0 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 8.57 | 1.607 |
| 50 | 10.0 | 8.00 | 50 | 52 | 0.5 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 6.58 | 1.458 |
| 51 | 10.0 | 3.50 | 50 | 44 | 5.0 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 27.12 | 3.062 |
| 52 | 10.0 | 5.50 | 50 | 44 | 3.0 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 24.60 | 3.010 |
| 53 | 10.0 | 6.50 | 50 | 44 | 2.0 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 21.49 | 2.799 |
| 54 | 10.0 | 7.50 | 50 | 44 | 1.0 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 15.98 | 2.348 |
| 55 | 10.0 | 8.00 | 50 | 44 | 0.5 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 12.47 | 2.047 |
| 56 | 15.0 | 15.00 | 50 | 55 | 0.0 | 0.200 | 1.093 | 1.302 | 0.165 | 0.128 | 0.41 | 1.028 |
| 57 | 12.0 | 12.00 | 50 | 55 | 0.0 | 0.250 | 1.093 | 1.302 | 0.230 | 0.179 | 0.51 | 1.043 |
| 58 | 10.0 | 10.00 | 50 | 55 | 0.0 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 3.30 | 1.330 |
| 59 | 9.00 | 9.00 | 50 | 55 | 0.0 | 0.333 | 1.093 | 1.302 | 0.355 | 0.276 | 3.34 | 1.371 |
| 60 | 8.00 | 8.00 | 50 | 55 | 0.0 | 0.375 | 1.093 | 1.302 | 0.423 | 0.330 | 3.74 | 1.467 |
| 62 | 10.0 | 10.00 | 50 | 55 | 0.0 | 0.300 | 1.469 | 1.198 | 0.303 | 0.236 | 1.81 | 1.861 |
| 63 | 10.0 | 10.00 | 50 | 55 | 0.0 | 0.300 | 2.575 | 1.274 | 0.303 | 0.236 | 0.73 | 1.181 |
| 64 | 10.0 | 10.00 | 75 | 55 | 0.0 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 3.14 | 1.073 |
| 65 | 10.0 | 10.00 | 100 | 55 | 0.0 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 3.00 | 1.314 |
| 66 | 10.0 | 10.00 | 50 | 52 | 0.0 | 0.300 | 1.093 | 1.302 | 0.303 | 0.236 | 4.62 | 1.300 |
| Model/ Statistical Characteristics | Average Error | Minimum Error | Maximum Error | Variance | RMSE |
|---|---|---|---|---|---|
| Arneson and Abt [9] | 0.522 | −0.241 | 2.477 | 0.157 | 0.650 |
| Umbrell et al. [3] | 0.463 | 0.028 | 2.135 | 0.045 | 0.509 |
| Lyn [4] | 0.402 | −0.017 | 2.112 | 0.047 | 0.455 |
| Guo et al. [11] | 0.357 | −0.225 | 0.980 | 0.120 | 0.494 |
| HEC-18 Equation [2] | 0.280 | −0.146 | 2.053 | 0.085 | 0.390 |
| Shan et al. [13] | 0.385 | −0.041 | 2.190 | 0.051 | 0.445 |
| Melville [16] | 0.544 | 0.001 | 2.488 | 0.088 | 0.618 |
| Kumcu [17] | -0.420 | −0.919 | 1.347 | 0.082 | 0.506 |
| Kocyigit and Karakurt [15] | 0.430 | 0.166 | 1.773 | 0.015 | 0.447 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelhaleem, F.S.; Mohamed, I.M.; Shaaban, I.G.; Ardakanian, A.; Fahmy, W.; Ibrahim, A. Pressure-Flow Scour under a Bridge Deck in Clear Water Conditions. Water 2023, 15, 404. https://doi.org/10.3390/w15030404
Abdelhaleem FS, Mohamed IM, Shaaban IG, Ardakanian A, Fahmy W, Ibrahim A. Pressure-Flow Scour under a Bridge Deck in Clear Water Conditions. Water. 2023; 15(3):404. https://doi.org/10.3390/w15030404
Chicago/Turabian StyleAbdelhaleem, Fahmy Salah, Ibrahim M. Mohamed, Ibrahim G. Shaaban, Atiyeh Ardakanian, Wael Fahmy, and Amir Ibrahim. 2023. "Pressure-Flow Scour under a Bridge Deck in Clear Water Conditions" Water 15, no. 3: 404. https://doi.org/10.3390/w15030404







