Evaluation of Local Scour along the Base of Longitudinal Training Walls
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Setup
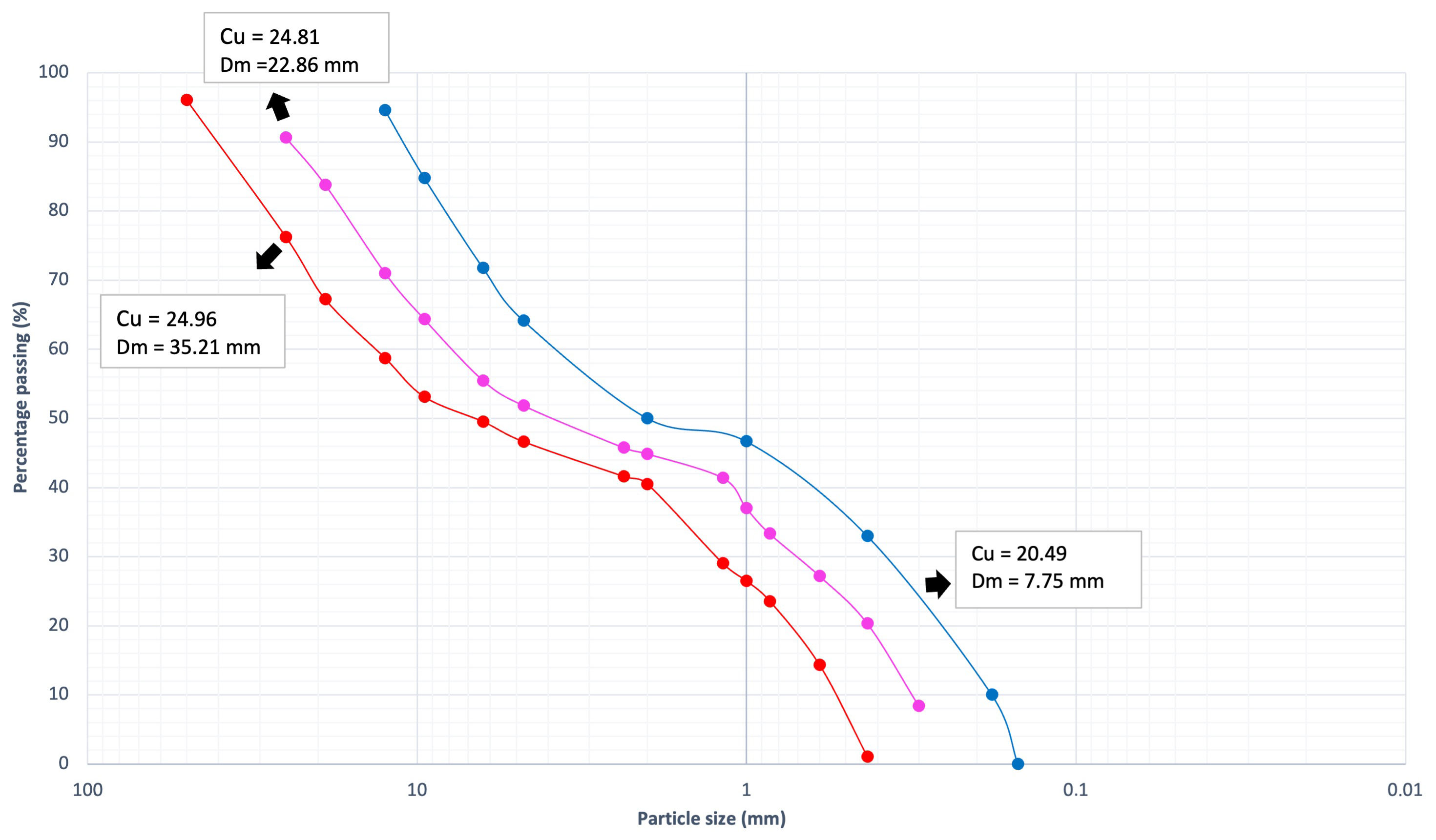
2.2. Riverbed Composition
2.3. Equations for Scour Depth Prediction
2.4. Statistical Validation
3. Results and Discussion
3.1. Riverbed Composition
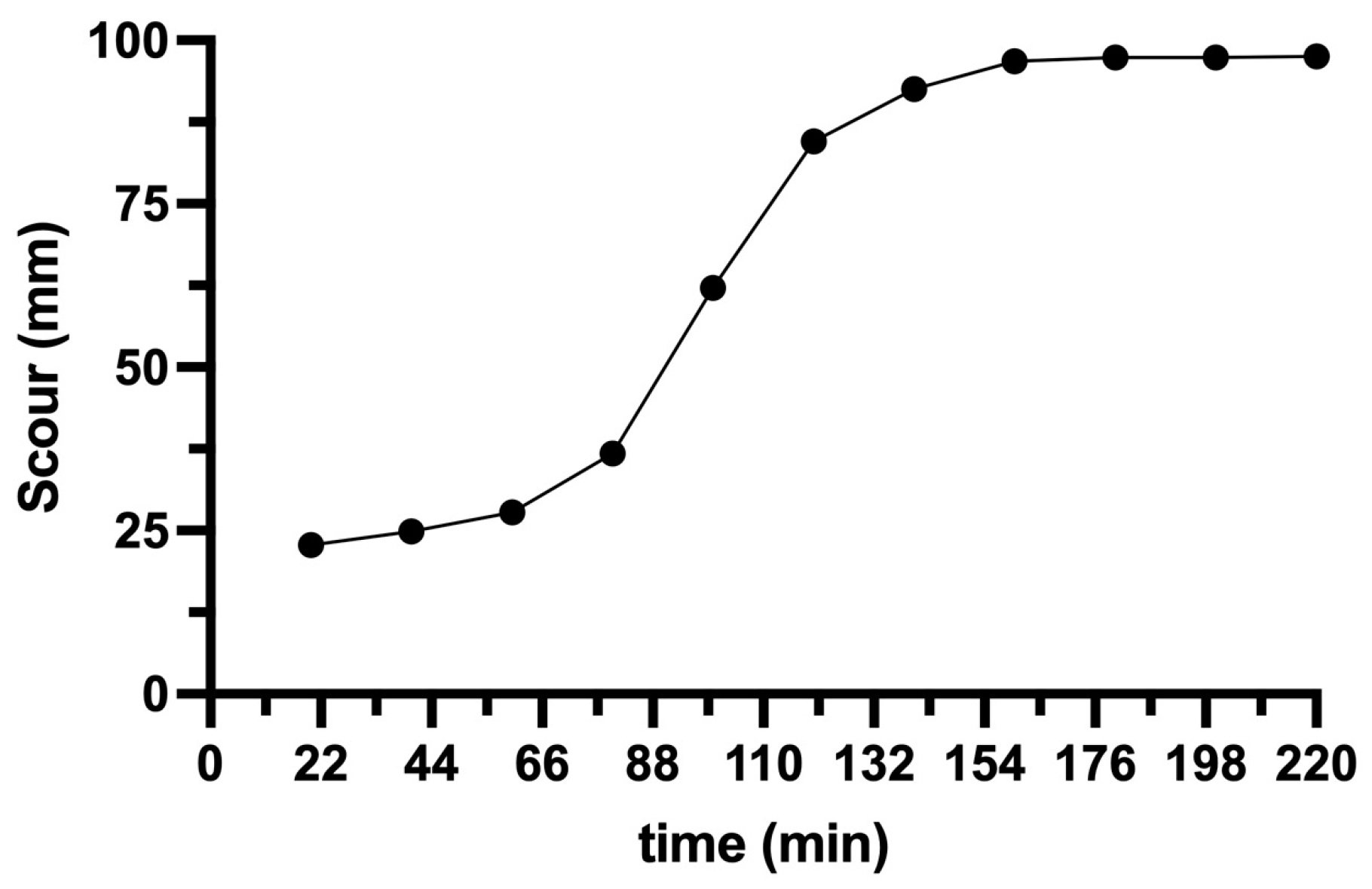
3.2. Experimental Results
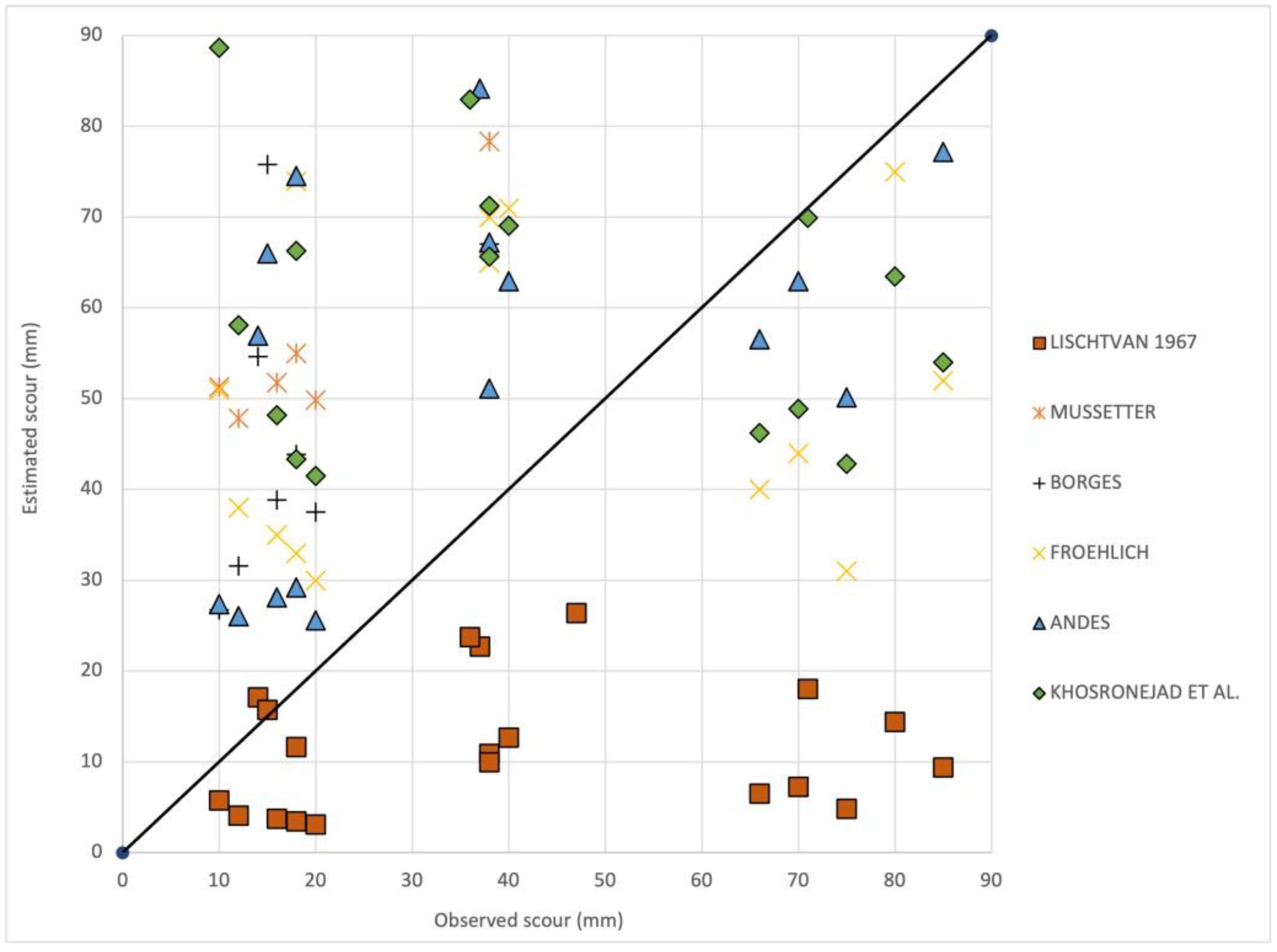
3.3. Analysis of Existing Equations Used to Predict Scour
3.4. Development of a New Mathematical Expression to Calculate Local Scour
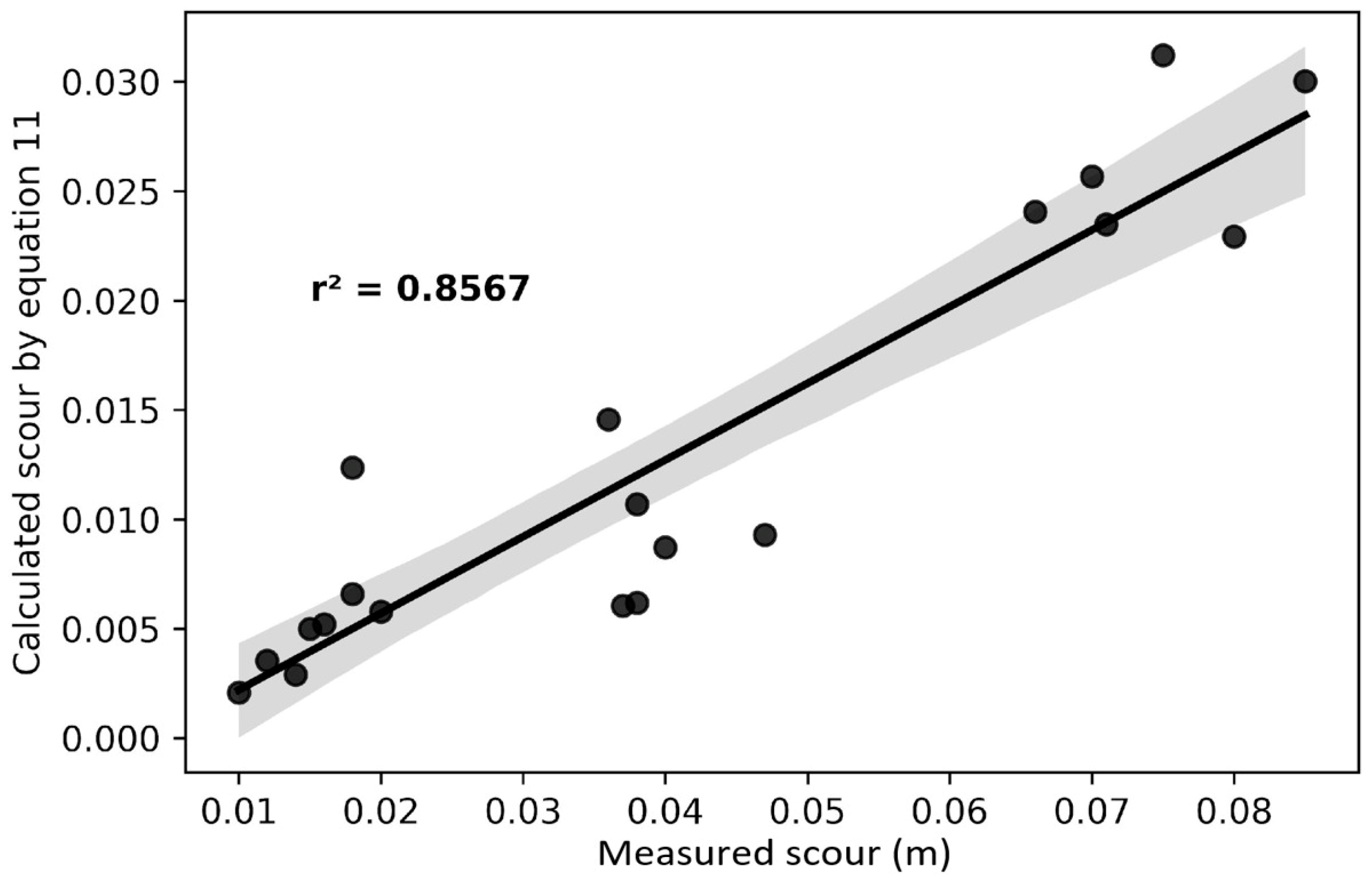
3.5. Validation of the New Mathematical Expression to Calculate the Local Scour
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Cohesive Soils | Non-Cohesive Soils | ||||
|---|---|---|---|---|---|
(mm) | (mm) | ||||
| 0.80 | 0.52 | 0.66 | 0.05 | 0.43 | 0.70 |
| 0.83 | 0.51 | 0.66 | 0.15 | 0.42 | 0.70 |
| 0.86 | 0.50 | 0.67 | 0.50 | 0.41 | 0.71 |
| 0.88 | 0.49 | 0.67 | 1.00 | 0.40 | 0.71 |
| 0.90 | 0.48 | 0.67 | 1.50 | 0.39 | 0.72 |
| 0.93 | 0.47 | 0.68 | 2.50 | 0.38 | 0.72 |
| 0.96 | 0.46 | 0.68 | 4.00 | 0.37 | 0.73 |
| 0.98 | 0.45 | 0.69 | 6.00 | 0.36 | 0.74 |
| 1.00 | 0.44 | 0.69 | 8.00 | 0.35 | 0.74 |
| 1.04 | 0.43 | 0.70 | 10.00 | 0.34 | 0.75 |
| 1.08 | 0.42 | 0.70 | 15.00 | 0.33 | 0.75 |
| 1.12 | 0.41 | 0.71 | 20.00 | 0.32 | 0.76 |
| 1.16 | 0.40 | 0.71 | 25.00 | 0.31 | 0.76 |
| 1.20 | 0.39 | 0.72 | 40.00 | 0.30 | 0.77 |
| 1.20 | 0.38 | 0.72 | 60.00 | 0.29 | 0.78 |
| 1.28 | 0.37 | 0.73 | 90.00 | 0.28 | 0.78 |
| 1.34 | 0.36 | 0.74 | 140.00 | 0.27 | 0.79 |
| 1.40 | 0.35 | 0.74 | 190.00 | 0.26 | 0.79 |
| 1.46 | 0.34 | 0.75 | 250.00 | 0.25 | 0.80 |
| 1.52 | 0.33 | 0.75 | 310.00 | 0.24 | 0.81 |
| 1.58 | 0.32 | 0.76 | 370.00 | 0.23 | 0.81 |
| 1.64 | 0.31 | 0.76 | 450.00 | 0.22 | 0.83 |
| 1.71 | 0.30 | 0.77 | 570.00 | 0.21 | 0.83 |
| 1.80 | 0.29 | 0.78 | 750.00 | 0.20 | 0.83 |
| 1.89 | 0.28 | 0.78 | 1000.00 | 0.19 | 0.84 |
| 2.00 | 0.27 | 0.79 | |||
References
- Czapiga, M.J.; Blom, A.; Viparelli, E. Efficacy of Longitudinal Training Walls to Mitigate Riverbed Erosion. Water Resour. Res. 2022, 58, e2022WR033072. [Google Scholar] [CrossRef]
- Yan, G.; Cheng, H.; Jiang, Z.; Teng, L.; Tang, M.; Shi, T.; Jiang, Y.; Yang, G.; Zhou, Q. Recognition of Fluvial Bank Erosion Along the Main Stream of the Yangtze River. Engineering 2022, 19, 50–61. [Google Scholar] [CrossRef]
- Sohrabi, M.; Keshavarzi, A.; Javan, M. Impact of Bed Sill Shapes on Scour Protection in River Bed and Banks. Int. J. River Basin Manag. 2019, 17, 277–287. [Google Scholar] [CrossRef]
- Shahriar, A.R.; Ortiz, A.C.; Montoya, B.M.; Gabr, M.A. Bridge Pier Scour: An Overview of Factors Affecting the Phenomenon and Comparative Evaluation of Selected Models. Transp. Geotech. 2021, 28, 100549. [Google Scholar] [CrossRef]
- Qi, H.; Yuan, T.; Zhao, F.; Chen, G.; Tian, W.; Li, J. Local Scour Reduction around Cylindrical Piers Using Permeable Collars in Clear Water. Water 2023, 15, 897. [Google Scholar] [CrossRef]
- Le, T.B.; Crosato, A.; Uijttewaal, W.S.J. Long-Term Morphological Developments of River Channels Separated by a Longitudinal Training Wall. Adv. Water Resour. 2018, 113, 73–85. [Google Scholar] [CrossRef]
- Toapaxi, J.; Galiano, L.; Castro, M.; Hidalgo, X.; Valencia, N. Análisis de La Socavación En Cauces Naturales. Rev. Politec. 2015, 35, 1–11. [Google Scholar]
- Kokusho, T.; Hara, T.; Hiraoka, R. Undrained Shear Strength of Granular Soils with Different Particle Gradations. J. Geotech. Geoenvironmental Eng. 2004, 130, 621–629. [Google Scholar] [CrossRef]
- Biron, P.M.; Robson, C.; Lapointe, M.F.; Gaskin, S.J. Three-Dimensional Flow Dynamics around Deflectors. River Res. Appl. 2005, 21, 961–975. [Google Scholar] [CrossRef]
- Istanbulluoglu, E.; Tarboton, D.G.; Pack, R.T.; Luce, C. A Sediment Transport Model for Incision of Gullies on Steep Topography. Water Resour. Res. 2003, 39, 4. [Google Scholar] [CrossRef]
- Attal, M.; Lavé, J. Pebble Abrasion during Fluvial Transport: Experimental Results and Implications for the Evolution of the Sediment Load along Rivers. J. Geophys. Res. 2009, 114, F04023. [Google Scholar] [CrossRef]
- Barbosa Gil, S. Metodología Para Calcular La Profundidad de Socavación General En Ríos de Montaña (Lecho de Gravas). Ph.D. Thesis, Universidad Nacional de Colombia, Bogota, Colombia, 2013. [Google Scholar]
- Cañas, R. Estudio de La Socavación Local En Pilas Circulares de Puentes En Lechos No Cohesivos Con Modelación Física En Laboratorio. Master’s Thesis, Escuela Colombiana de Ingenieria Julio Garavito, Bogota, Colombia, 2018. [Google Scholar]
- Khosronejad, A.; Diplas, P.; Angelidis, D.; Zhang, Z.; Heydari, N.; Sotiropoulos, F. Scour Depth Prediction at the Base of Longitudinal Walls: A Combined Experimental, Numerical, and Field Study. Environ. Fluid Mech. 2020, 20, 459–478. [Google Scholar] [CrossRef]
- Taha, N.; El-Feky, M.M.; El-Saiad, A.A.; Fathy, I. Numerical Investigation of Scour Characteristics Downstream of Blocked Culverts. Alex. Eng. J. 2020, 59, 3503–3513. [Google Scholar] [CrossRef]
- Johnson, P.A.; Clopper, P.E.; Zevenbergen, L.W.; Lagasse, P.F. Quantifying Uncertainty and Reliability in Bridge Scour Estimations. J. Hydraul. Eng. 2015, 141, 04015013. [Google Scholar] [CrossRef]
- Lacey, G. Stable channels in alluvium (includes appendices). Minutes Proc. Inst. Civ. Eng. 1930, 229, 259–292. [Google Scholar] [CrossRef]
- Blench, T. A new theory of turbulent flow in liquids of small viscosity. (in abstract form). J. Inst. Civ. Eng. 1939, 11, 611–612. [Google Scholar] [CrossRef]
- Lischtvan, L.; Lebediev, V. Gidrologia I Gidraulika v Mostovom Doroshnom, Straitielvie. In Hydrology and Hydraulics in Bridge and Road Building; Gidrometeoizdat: St. Petersburg, Russian, 1959. [Google Scholar]
- Laursen, E.M.; Toch, A. Bulletin no Scour around Bridge Piers and Abutments Iowa Institute of Hydraulic Research in Cooperation with Thl Iowa State Highway Commission and the Bureau of Public Roads; Iowa Highway Research Board: Ames, IA, USA, 1956. [Google Scholar]
- Straub, L.G. Report of Committee on Dynamics of Streams, 1937–1938. Trans. Am. Geophys. Union 1938, 19, 349. [Google Scholar] [CrossRef]
- Komura, S. Equilibrium Depth of Scour in Long Constrictions. J. Hydraul. Div. 1966, 92, 17–37. [Google Scholar] [CrossRef]
- Borges, M. Socavacion al Pie de Muros Longitudinales. Bachelor’s Thesis, Universidad de Merida, Merida, Mexico, 2008. [Google Scholar]
- Richardson, E.V.; Simons, D.B.; Julien, P.Y. Highways in the River Environment: Participant Notebook; Federal Highway Administration: Washington, DC, USA, 1990. [Google Scholar]
- Melville, B.W. Pier and Abutment Scour: Integrated Approach. J. Hydraul. Eng. 1997, 123, 125–136. [Google Scholar] [CrossRef]
- Froehlich, D.C. Local Scour at Bridge Abutments. In Proceedings of the 1989 National Conference on Hydraulic Engineering, ASCE, New Orleans, LA, USA, 14 August 1989; pp. 13–18. [Google Scholar]
- Melville, B.W. Local Scour at Bridge Abutments. J. Hydraul. Eng. 1992, 118, 615–631. [Google Scholar] [CrossRef]
- Mussetter, B.; Stoliker, D.; Foglesong, R.; Alsop, T.; Aguirre, F.; Stone, H.; Dodge, C.; Mortenson, J.; Carroll, R. Sediment and Erosion Design Guide Sscafca Sediment and Erosion Design Guide. 2008. Available online: https://sscafca.org/development/documents/sediment_design_guide/Sediment%20Design%20Guide%2012-30-08.pdf (accessed on 7 November 2023).
- Look, B.G. Handbook of Geotechnical Investigation and Design Tables; Taylor & Francis: Oxfordshire, UK, 2007; ISBN 9780429224379. [Google Scholar]
- Chachereau, Y.; Chanson, H. Free-Surface Fluctuations and Turbulence in Hydraulic Jumps. Exp. Therm. Fluid Sci. 2011, 35, 896–909. [Google Scholar] [CrossRef]
- Guzmán, R.; Bezada, M.; Rodríguez-Santalla, I. Granulometric Characterization of Sediments in the Anastomosed System of the Apure River Venezuela. J. S. Am. Earth Sci. 2021, 109, 103274. [Google Scholar] [CrossRef]
- Khan, U.A.; Valentino, R. Investigating the Granulometric Distribution of Fluvial Sediments through the Hybrid Technique: Case Study of the Baganza River (Italy). Water 2022, 14, 1511. [Google Scholar] [CrossRef]
- Pereira, L.M. Erosión Local En Estribos. Master’s Thesis, Universidad de los Andes, Merida, Mexico, 1995. [Google Scholar]
- Gonzalez, J.R.P.; Escobar-Vargas, J.; Vargas-Luna, A.; Castiblanco, S.; Trujillo, D.; Guatame, A.C.; Corzo, G.; Santos, G.; Perez, L.A. Hydroinformatic Tools and Their Potential in the Search for Missing Persons in Rivers. Forensic Sci. Int. 2022, 341, 111478. [Google Scholar] [CrossRef] [PubMed]
- Oliveto, G.; Hager, W.H. Temporal Evolution of Clear-Water Pier and Abutment Scour. J. Hydraul. Eng. 2002, 128, 811–820. [Google Scholar] [CrossRef]
- Di Pietro, P.; Mahajan, R.R. Erosion Control Solutions with Case Studies; Springer: Berlin/Heidelberg, Germany, 2022; pp. 71–94. [Google Scholar]
- Radice, A.; Davari, V. Roughening Elements as Abutment Scour Countermeasures. J. Hydraul. Eng. 2014, 140, 06014014. [Google Scholar] [CrossRef]
- Aguirre-Pe, J.; Olivero, M.L.; Moncada, A.T. Particle Densimetric Froude Number for Estimating Sediment Transport. J. Hydraul. Eng. 2003, 129, 428–437. [Google Scholar] [CrossRef]



| Slope (%) | Discharge (m3/s) | Maximum Scour Depth (mm) | ||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ||
| 0.5 | 0.008 | 10 | 10.6 | 3 | 5 | 4.4 | 7.8 | 8.2 | 8.8 | 2 | 2.4 | 6 |
| 0.017 | 2.5 | 6 | 8.2 | 0 | 5.5 | 5 | 10 | 10 | 2.7 | 2.1 | 5.6 | |
| 0.025 | 28 | 34.5 | 27.6 | 15.6 | 15 | 10 | 14.7 | 8.5 | 11.9 | 11.5 | 11.3 | |
| 0.03 | 28 | 40 | 36.1 | 26 | 19.5 | 12.5 | 14.8 | 15.5 | 15.2 | 16.9 | 14.4 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ||
| 2.5 | 0.008 | 29.7 | 28.2 | 21.9 | 26.9 | 17.9 | 12.9 | 16.9 | 17.7 | 18.2 | 10.8 | 12.3 |
| 0.017 | 56 | 57 | 56 | 38.9 | 37.6 | 23.9 | 24.1 | 27.1 | 19.2 | 18.9 | 23.2 | |
| 0.025 | 58.9 | 64 | 92 | 85 | 98 | 80 | 61.2 | 58.9 | 40 | 24.5 | 24.2 | |
| 0.03 | 62.1 | 97.5 | 83.5 | 80 | 83.9 | 68.7 | 74.5 | 27.8 | 24.9 | 22.8 | 29.8 | |
| MNE | MPF | MSE (mm2) | RMSE (mm) | Equation | Reference |
|---|---|---|---|---|---|
| 63.03 | 4.67 | 0.0015 | 0.0381 | Lischtvan-Lebediev | [19] |
| 219.54 | 2.78 | 0.0024 | 0.0485 | Froehlich | [26] |
| 170.53 | 2.11 | 0.0012 | 0.0353 | Pereira | [33] |
| 110.41 | 2.93 | 0.0053 | 0.0690 | Borges | [23] |
| 1816.46 | 3.20 | 0.0038 | 0.0619 | Mussetter | [28] |
| 201.93 | 3.06 | 0.0023 | 0.0483 | Khosronejad et al. | [14] |
| 68.72 | 3.60 | 0.0010 | 0.0321 | Proposed equation | This research |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cely Calixto, N.J.; Galvis Castaño, A.; Carrillo Soto, G.A. Evaluation of Local Scour along the Base of Longitudinal Training Walls. Water 2023, 15, 4001. https://doi.org/10.3390/w15224001
Cely Calixto NJ, Galvis Castaño A, Carrillo Soto GA. Evaluation of Local Scour along the Base of Longitudinal Training Walls. Water. 2023; 15(22):4001. https://doi.org/10.3390/w15224001
Chicago/Turabian StyleCely Calixto, Nelson Javier, Alberto Galvis Castaño, and Gustavo Adolfo Carrillo Soto. 2023. "Evaluation of Local Scour along the Base of Longitudinal Training Walls" Water 15, no. 22: 4001. https://doi.org/10.3390/w15224001





