Progressive Dam-Failure Assessment by Smooth Particle Hydrodynamics (SPH) Method

Abstract

The dam-break water flow is a complex fluid motion, showing strong nonlinearity and stochasticity. In order to better study the characteristics of the dam burst flood, the smooth particle hydrodynamics (SPH) method was chosen to establish a two-dimensional classical dam-burst model, and the flow velocity distribution graph was obtained by calculation and compared with the experimental results in the literature, and the fitting degree of the two was obtained to be 88.4%, which verifies the validity of the model. On this basis, according to the principle of dam failure, the two failure modes of equal-interval gradual failure and progressive gradual failure were simulated, and the water body characteristics such as water flow velocity, energy, pressure, etc., were analyzed based on the different working conditions of the two modes to obtain the characteristics of gradual dam-failure water flow under the two kinds of numerical models. The simulation results show that, compared with the instantaneous dam failure mode, (1) the flow rate of the dam-failure stream reaching the downstream slows down in the gradual dam-failure mode; (2) the depth development of the breach extends downward in layers and stages over time, and the overall duration of the breach is prolonged; (3) the destructive power of the dam-failure flood is weakened as the number of segments increases. The results of the study show that, compared with the instant dam-failure mode, the calculation results of the breach development considering the progressive gradual dam-failure mode are more in line with the theoretical solution and closer to the actual process of dam failure, which can provide ideas and references for advancing the numerical study of dam failure.

1. Introduction

The occurrence of dam failure events is accompanied by powerful destructive forces, which bring serious threats to the lives and properties of downstream residents. According to statistics, from the 1950s to the beginning of the 21st century, about 3500 dam-failure events occurred in China [1,2]. Therefore, it is of great significance to establish a reasonable dam-failure-prediction model to study the dam-failure problem.

For the study of the dam-failure model, Brufau P [3] chose the most dangerous instant dam-failure model to analyze, and the results obtained had a large deviation compared with the actual measurements; Shi Hongda [4] and others also believed that the accuracy of the failure data obtained by calculating with the instant dam-failure model is low, and the academic community put forward the idea that the direction of dam-failure research should be towards the gradual dam-failure model.

The study of the dam-failure problem can be divided into the methods of failure testing and numerical simulation. In the early days, in the absence of measured data on dam failure, failure tests became an effective way to understand the process of dam failure. In the 19th century, researchers conducted a series of experimental studies based on Ritter’s theoretical solution to dam-burst flooding; Hanson et al. [5] summarized the process of breach depth development in the breaching model into four stages by using seven sets of diffuse roof-breaching tests; Alonso E. E et al. [6] proposed a progressive damage model for the Aznalcollar dam failure event from the perspectives of experimental tests, failure conditions, and flood evolution, respectively, and simulated the landslide problem. The above research work found that under the influence of special topographic and geological conditions, the characterization of dam-failure floods involves complex physics, which makes direct analytical solutions very difficult. With the advancement of various numerical simulation methods, the research of numerical using computer technology has developed rapidly [7,8]. For different fluid problems, there are many ways to study their flow problem by numerical simulation, but the traditional mesh method is subject to the constraints of the continuity condition and the interference of the interface tracking problem as well as the influence of the mesh size and deformation on the computational accuracy, and there are inherent difficulties in solving the complex flow problems, such as the fragmentation, separation, and overturning of the fluids [9,10].

The smooth particle hydrodynamics (SPH) method is a purely Lagrangian meshless method with strong advantages for modeling free-surface stream flows and dynamic boundary problems [11]. The SPH method is widely used in various engineering fields such as hydraulic engineering, mechanical engineering, ocean engineering, mechanical engineering, aerospace engineering, and medical engineering [12,13,14,15,16]. Originally proposed by Lucy and Monaghan and utilized in the study of complex galactic object problem solving [17], the special points in these problems are similar to those in fluid dynamics and thus can be approximated by using the control of non-Newtonian fluids to solve such problems [18,19]. The SPH algorithm can directly recognize and process the free-form surfaces and kinematic boundaries [20], which is continuous in small areas, and shows its advantages in dealing with the large deformation and fragmentation of water flow, which is very suitable for the study of dam-break flooding problems.

Monaghan was first used to simulate the motion problem of fluids in 1994, pioneering the use of the SPH method for research in the area of dam-failure flow problems. Later, domestic and foreign researchers used the SPH method to conduct relevant studies on the dam-failure problem, making the application of the SPH method in fluid mechanics more extensive. Zhang [21] proved that both the SPH method and the lattice Boltzmann method (LBM) can simulate dam-failure problems, but the SPH method has a smoother and clearer free surface when simulating dam-failure problems. For example, Edmond [22] introduced the large eddy simulation (LES) method into the smooth particle hydrodynamics method for numerical simulation of offshore isolated waves, which simulated the offshore isolated wave model well; Zhu [23] explored the problem of underwater blasting based on the SPH method and concluded that the smaller the charging angle, the greater the offset angle of directional crack propagation in the charging direction in response to the influence of the charging angle on the bidirectional charging tension. Dalrymple [24] modeled the water fluctuation problem and investigated the fluid motion problems of breaking waves on the beach, green water over the deck, and wave–structure interaction in depth; Xiaoyang [25] proposed a modification of the kernel gradient in order to improve the computational accuracy and pressure distribution, and the results proved that the improved SPH method can accurately and stably handle three-dimensional free-surface flows with large deformations and debris and compute the pressure field; Boregowda [26] improved both SPH boundary integral formulas. A new particle consistent boundary integral formula with first-order derivatives was derived; Gong Kai [27] proposed an improved boundary condition processing method to calculate the boundary repulsive force by pressure interpolation when modeling a two-dimensional dam-failure problem, which compensates the defects of boundary particle calculation to some extent and has been well applied; Zhang Weijie [28] proposed a numerical model of coupled soil-water SPH based on regularization correction for the accuracy of SPH method in geotechnical engineering, which can better avoid the tension instability problem. Wang Zhichao [29] proposed a SPH stress correction algorithm for the stress instability problem and verified that the method effectively improves the simulation accuracy of the compressive stress instability effect as well as the free-surface flow through the dam-failure example. Theoretical analysis and numerical experiments show that the SPH with a particle consistent boundary integral formulation has a significant advantage in terms of accuracy.

All the previous research works based on the SPH method are based on transient dam-failure modeling, and gradual failure mode has not been taken as the subject of research. The main research and innovations of this paper are as follows: (1) The classical transient dam-failure model is established based on the SPH method, and the effectiveness of the procedure is verified by comparing and analyzing the experimental results with those of the literature [26]. (2) On the basis of verifying the validity of the program, a gradual dam-failure model is established based on transient dam failure, and the gradual dam failure is subdivided into two forms, namely equal-interval dam failure and progressive dam failure. (3) The characteristics of dam-breaking water flow under various working conditions are studied, and the influence of different breaching modes on the development of breaching is analyzed; at the same time, the results of breaching development calculations with the theoretical solutions are compared, and the influence of different dividing layers and breaching models on the results of dam breaking is explored.

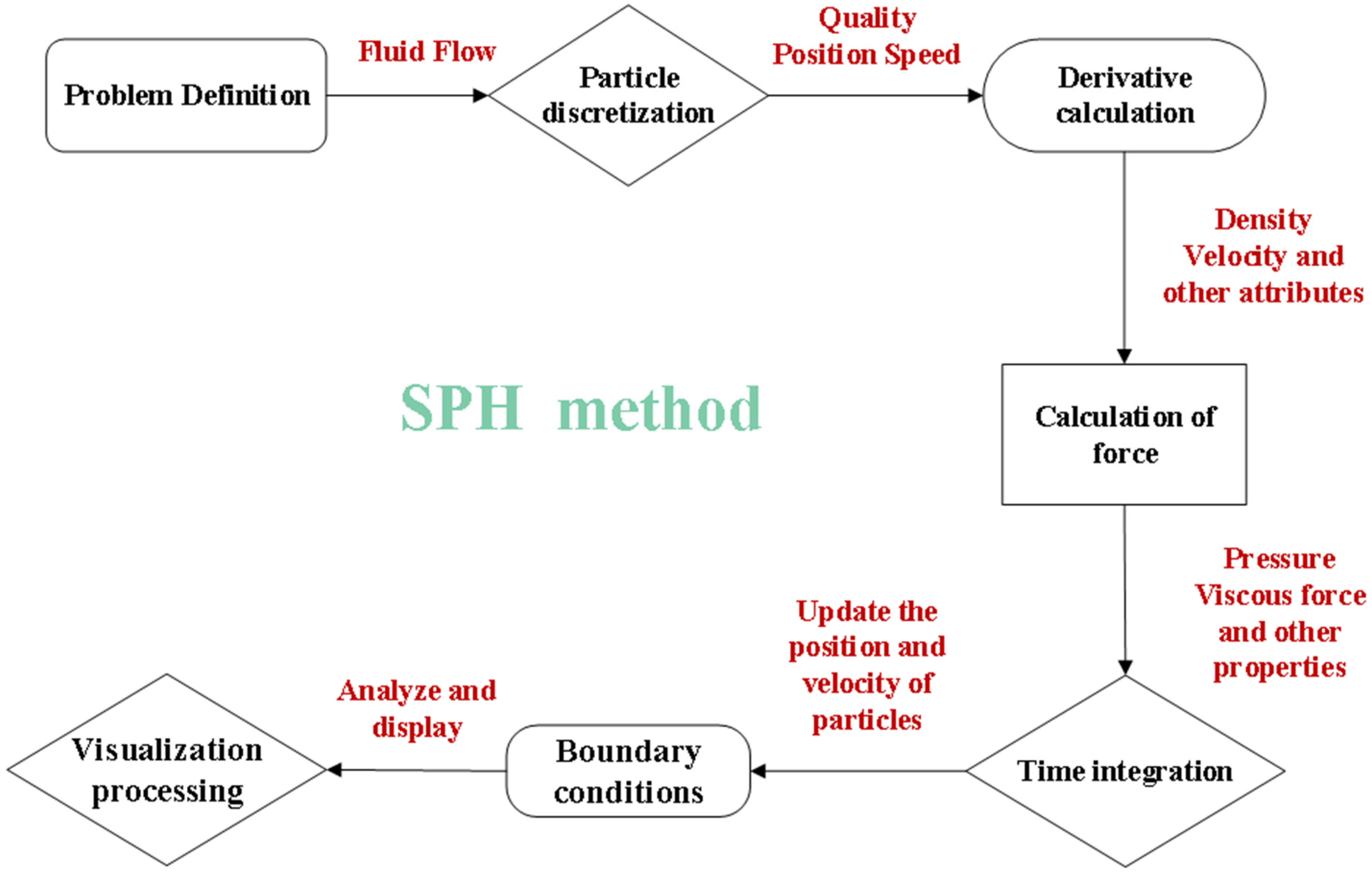
2. SPH Basic Theory

2.1. SPH Basic Ideas

The basic idea of the SPH method can be summarized as follows: (1) When the problem domain is a region composed of non-particles, the computational domain is represented by a set of interacting particles and there is no connection between them; (2) firstly, the problem in the computational domain is discretized by using the SPH kernel approximation method, and the analytical equations of the problem under the SPH kernel approximation are obtained; (3) is further approximated and solved by using particle approximation method, and this is achieved by superposition of corresponding covariates by similar particles inside the region; (4) the solution of the particle approximation occurs at all time steps, and the particles involved in the process are those in the current computational domain; (5) the equations of the ordinary differential equations (ODEs) under the SPH are obtained by the discretization and approximation of the partial differential equations (PDEs) in the research problem; (6) the equations of the ODEs in step 5 are solved by applying the display integral method to obtain the properties of the particle field variables in the region. The technical roadmap of the SPH method is shown in Figure 1.

The above steps sequentially embody the properties of meshless, kernel approximation, tight-branching, adaptive, and pure Lagrangian-method kernel stepwise-integration method properties, which cumulatively comprise the basic properties of the SPH method.

2.2. SPH Basic Equation

The SPH basic equations involve the processes of kernel approximation and particle approximation. Constructive equations are performed for the SPH method to obtain the standard form of the kernel function:

$$f(x)={\displaystyle {\int }_{\mathsf{\Omega }}f}\left(x^{\prime }\right)W\left(x-x^{\prime },h\right)d{x}^{\prime }$$

(1)

where x is the coordinate position vector, $f(x)$ is a function of the coordinate position vector x, W is the smooth kernel function, $\mathsf{\Omega }$ is the volume integral containing the coordinate position, and h is the smooth length.

Based on the basic idea of SPH, the use of particle approximation is another key step to realize it, and the kernel approximation is considered to be used to sum the integrals of all the particles in the range of the support domain. Its expression is as follows:

$$f\left(x_i\right)={\displaystyle \sum _{j=1}^n\frac{m_i}{{\rho }_i}}f\left(x_j\right)W_{ij}$$

(2)

where $m_i$ is the mass of particle i, ${\rho }_i$ is the density of particle i, $f\left(x_j\right)$ represents some physical property of particle j, n is the total number of particles in the supported domain at particle j, and $W_{ij}=W\left(x_i-x_j,h\right)$.

2.3. SPH Method for Solving the N-S Equation

2.3.1. Navier–Stokes Equations

The fluid control equations under the Lagrangian can be written as a series of differential equations.

Continuity equation:

$$\frac{\mathrm{d}\rho }{\mathrm{d}t}=-\rho \frac{\partial v^{\beta }}{\partial x^{\beta }}$$

(3)

Momentum equation:

$$\frac{\mathrm{d}{v}^a}{ \mathrm{d}t}=\frac{1}{\rho }\frac{\partial {\sigma }^{\alpha }}{\partial x^{\beta }}$$

(4)

Energy equations:

$$\frac{\mathrm{d}e}{ \mathrm{d}t}=\frac{{\sigma }^{a\beta }}{\rho }\frac{\partial v^{\alpha }}{\partial x^{\beta }}$$

(5)

where $\rho$ is the particle density; $v$ is the velocity tensor; $\sigma$ is the tensor of the total stress; e is the total stress tensor.

2.3.2. Density Particle Approximation Method for Solving the N-S Equation

The application of this method for any particle in a generalized fluid the density is expressed as given below:

$${\rho }_i={\displaystyle \sum _{j=1}^N{m}_j}{W}_{ij}$$

(6)

An SPH approximation to the velocity divergence yields an approximate expression for the density equation:

$$\frac{\mathrm{d}{\rho }_i}{ \mathrm{d}t}={\rho }_i{\displaystyle \sum _{j=1}^N\frac{m_j}{{\rho }_j}}{v}_{ij}^{\beta }\cdot \frac{\partial W_{ij}}{\partial x_i^{\beta }}$$

(7)

where $v_{ij}^{\beta }=\left(v_i^{\beta }-v_j^{\beta }\right)$.

2.4. Smooth Kernel Function Construction

The most widely used smoothing function is the cubic spline function.

$$W(R,h)={\alpha }_d\times \left\{\begin{array}{ll}\frac{2}{3}-R^2+\frac{1}{2}{R}^3,\hfill & 0⩽R<1;\hfill \\ \frac{1}{6}{(2-R)}^3,\hfill & 1⩽R<2;\hfill \\ 0,\hfill & R⩾2 .\hfill \end{array}\right.$$

(8)

where there are ${\alpha }_d=\frac{1}{h}$, $\frac{15}{7\pi h^2}$, and $\frac{3}{2\pi h^3}$ in one, two, and three dimensions, respectively.

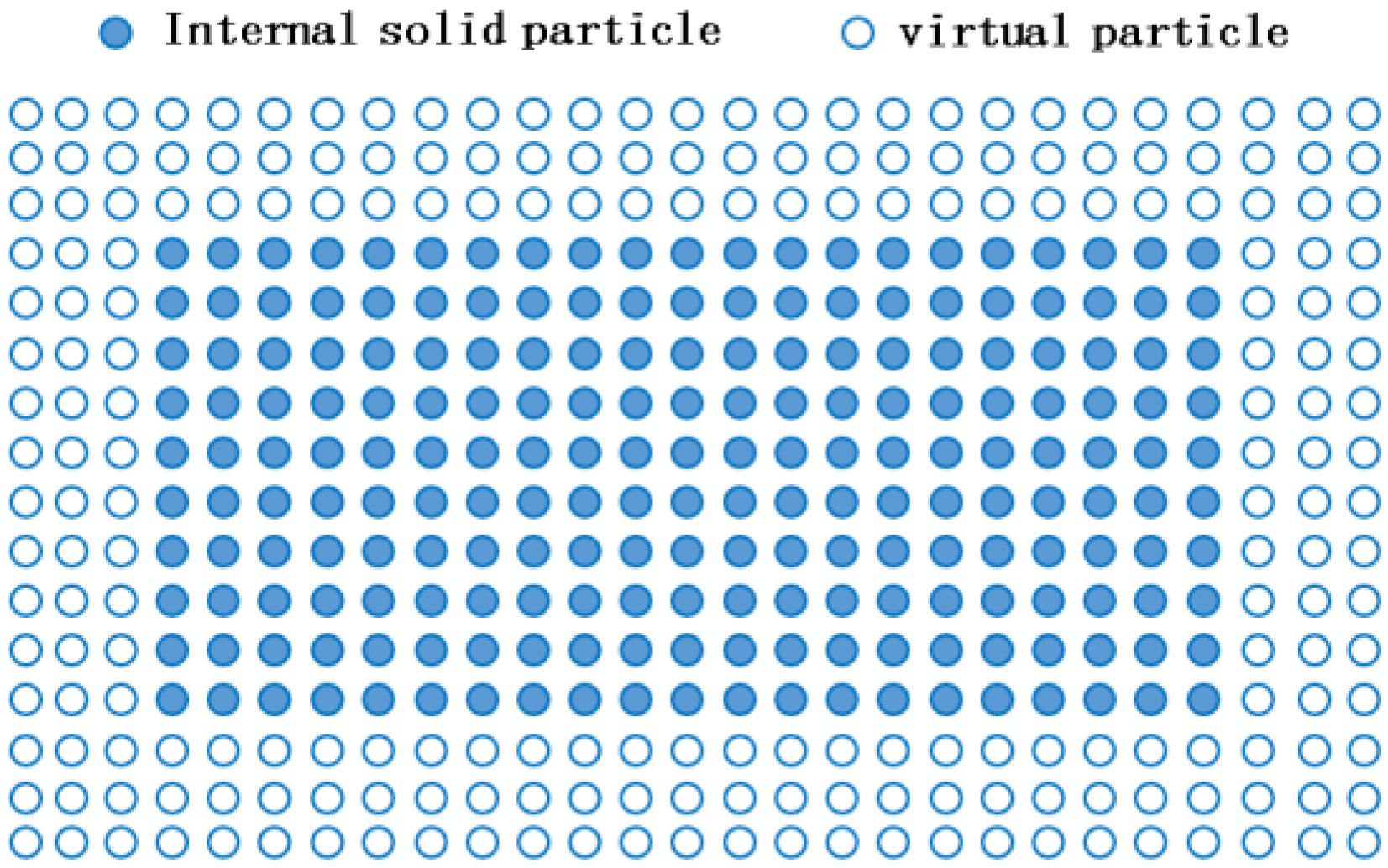
2.5. Other Key Technologies

Boundary processing: Since the SPH method is a pure Lagrangian meshless method, its pure particle nature can easily satisfy the free boundary conditions, but for the particles that are at and very close to the boundary, these particles are truncated at the endpoint positions when the integration calculation is carried out, so it cannot be applied to the whole region.

In the simulation of a fluid problem, both the dynamic boundary conditions and the dynamic boundary conditions will actually be present. In the study, the SPH method can be unified for the real problem to consider, i.e., the dynamic boundary conditions, which contains the boundary repulsion method and mirror virtual particle method, etc., and also can be used for the solid boundary problems with dynamic boundary conditions and for the free boundary problems with dynamic boundary conditions. In general, if one considers the need in the solid boundary processing to pay attention to the defective problem of the particle integral approximation near the boundary, as shown in Figure 1, in this paper, we use the mirror virtual particle method in the literature [20] for the solid-wall boundary processing, and the solid-wall boundary adopts a three-layer virtual particle arrangement, which makes the integral defective problem able to be alleviated.

Time integral: Courant–Friedrichs–Levy (CFL) conditions were selected:

$$\Delta t=\min \left(\frac{h_i}{c}\right)$$

(9)

Then, the expression for the time step is as follows:

$$\Delta t_{\mathrm{cv}}=\min \left(\frac{h_i}{c_i+0.6\left({\alpha }_{\mathsf{\Pi }}{c}_i+{\beta }_{\mathsf{\Pi }}\max \left({\varphi }_{ij}\right)\right)}\right)$$

(10)

$$\Delta t_{\mathrm{f}}=\min {\left(\frac{h_i}{f_i}\right)}^{\frac{1}{2}}$$

(11)

where f is the magnitude of the force acting per unit mass (i.e., acceleration). Combined with Equations (10) and (11), this gives the following:

$$\Delta t=\min \left({\lambda }_1\Delta t_{\mathrm{cv}},{\lambda }_2\Delta t_{\mathrm{f}}\right)$$

(12)

where λ₁ is taken as 0.4, and λ₂ is taken as 0.25.

Particle arrangement: Using a layered layout, given a fixed number of particles in each water body, and laying particles layer by layer, the advantage of the layout is that the diversity of the water body arrangement, not limited to the conventional rectangular water body, can be arranged according to the actual needs of the arrangement and in the solid particles outside the boundary of the arrangement of multiple virtual particles, as shown in Figure 2.

3. Calculus Analysis

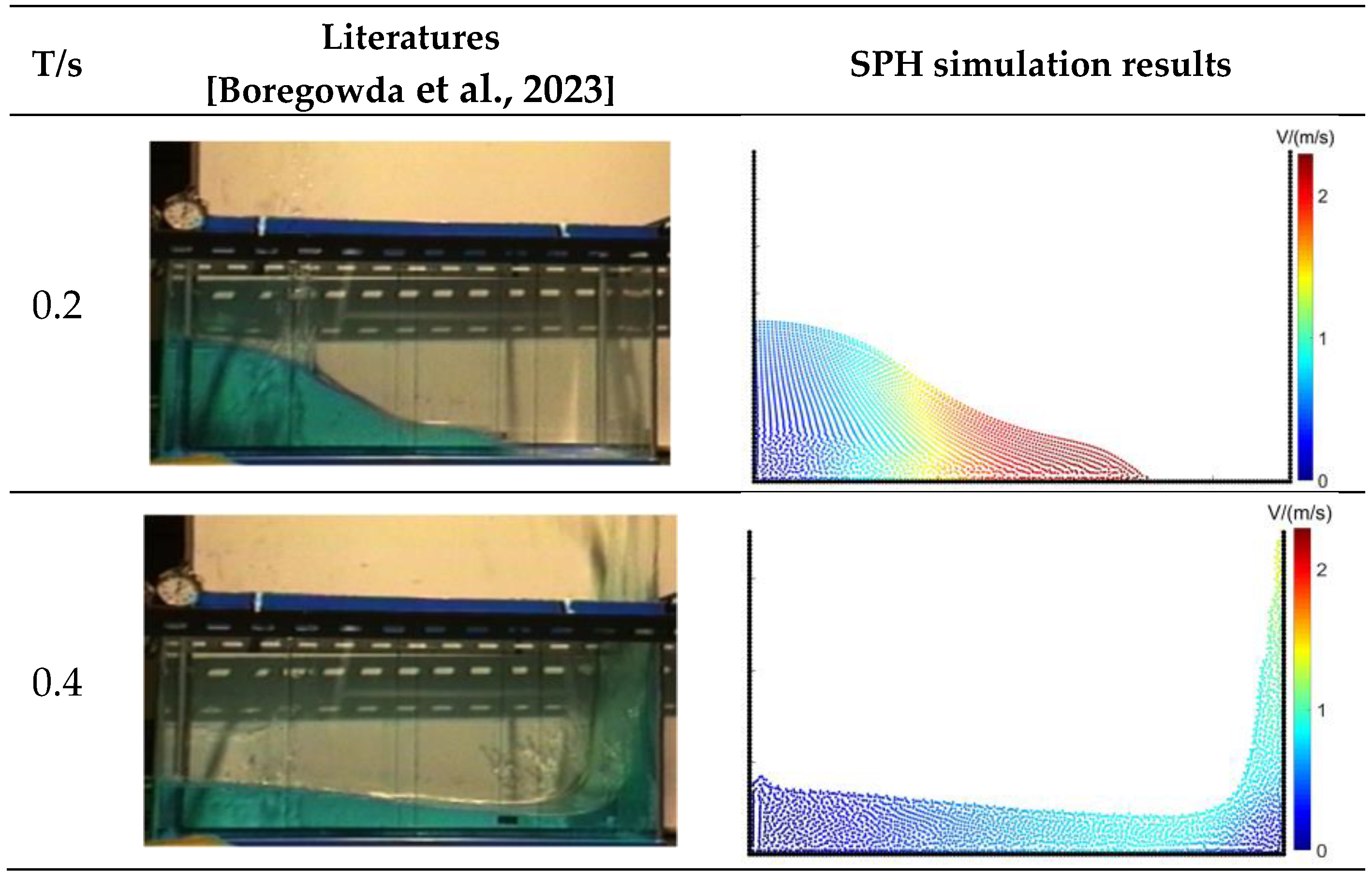
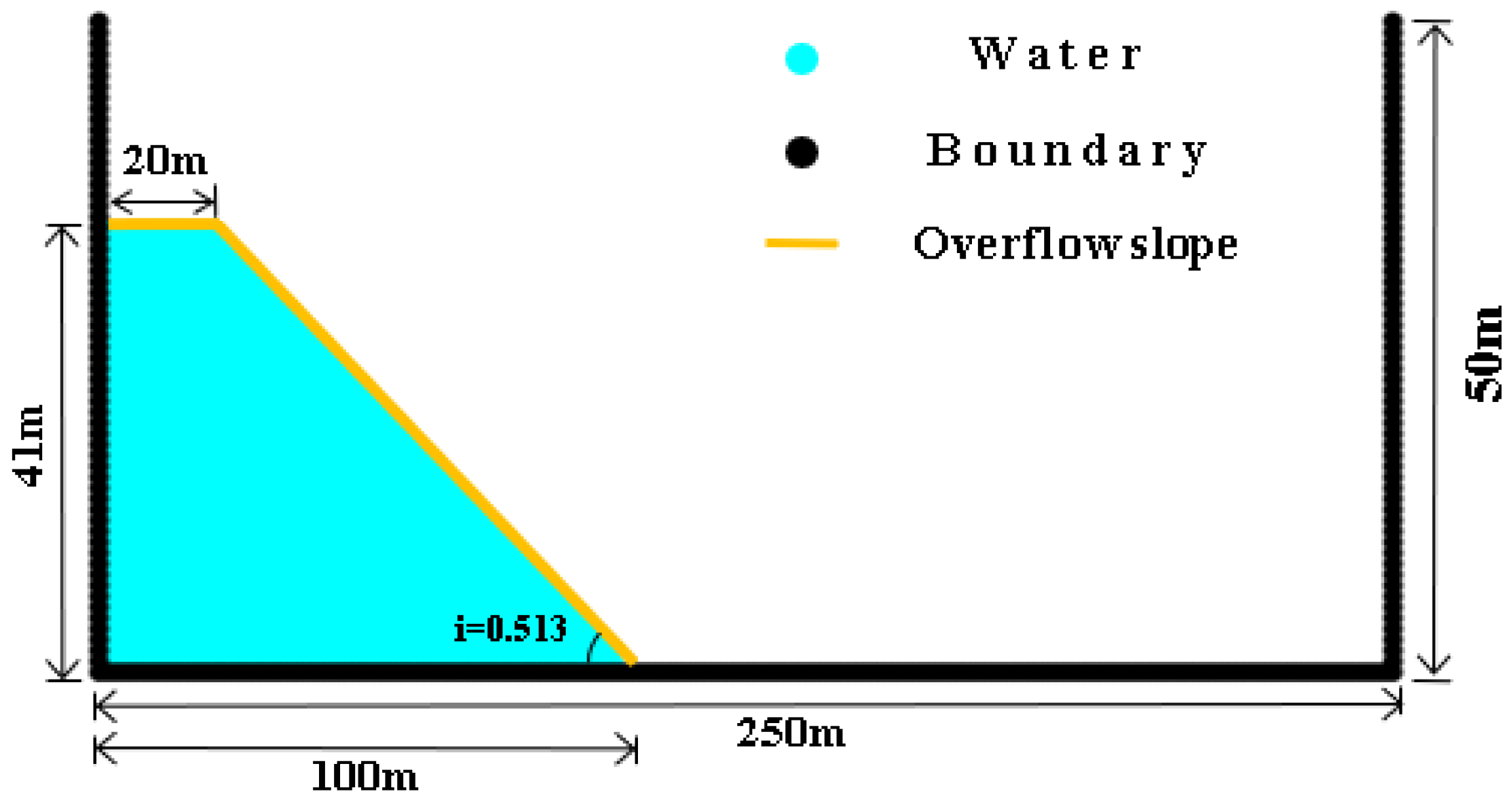
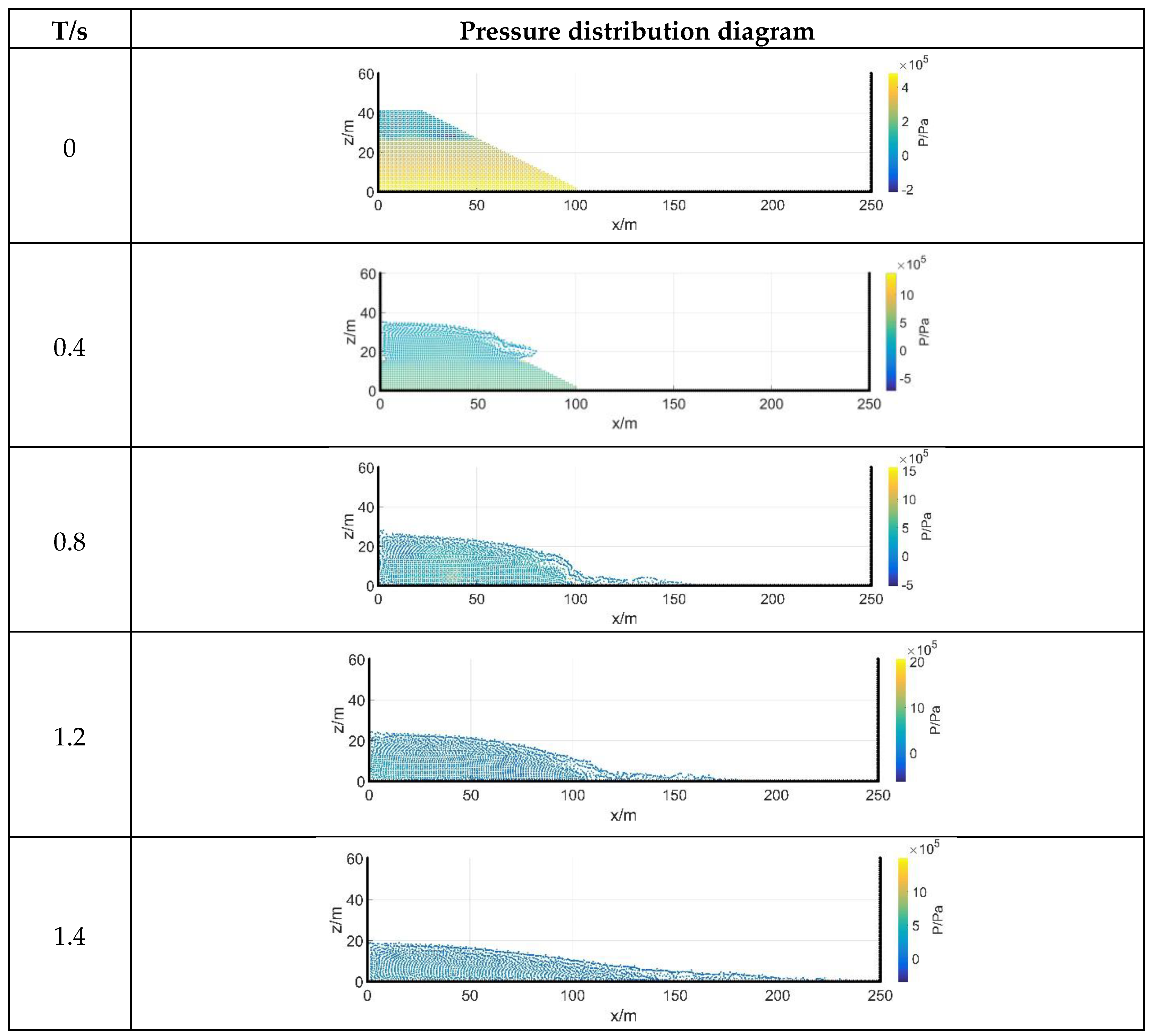
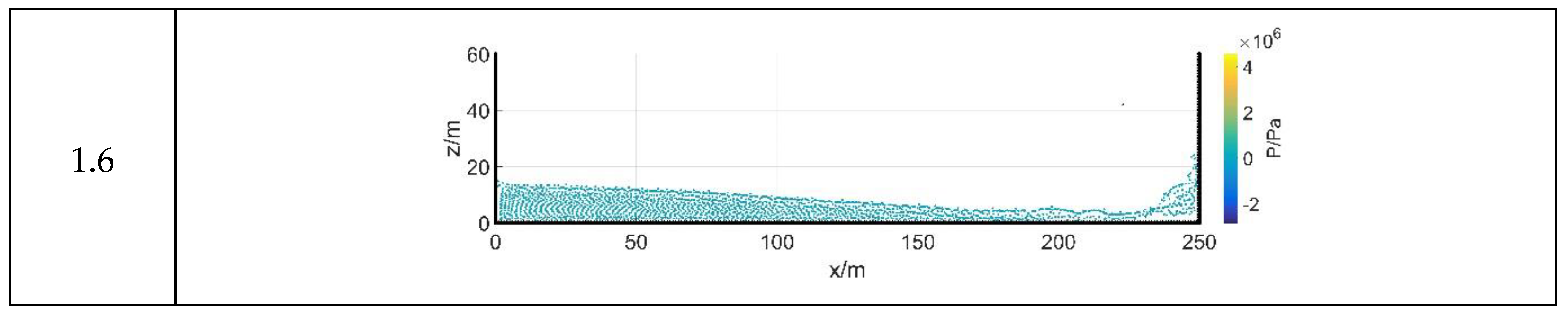
3.1. Transient Dam-Failure Arithmetic Simulation

For some rigid dams, such as concrete gravity dams, arch dams, buttress dams, etc., in the event of failure, the failure mode is often instantaneous. The instantaneous failure time is very short, and the dam is destroyed in a few seconds, which is very harmful. The working conditions are set up to compare the simulation of instantaneous failure with the literature [30] to verify the reliability of this model.

Figure 3 shows the transient dam-failure model arrangement; the size arrangement is the same as in the literature [26]. Model arrangement was as follows: In a unit-width rectangular water tank, a rectangular water body was arranged on the left side of the water tank, and a vertical gate was placed on the right side of the water body; the dimensions of the water tank are 0.584 m × 0.35 m, the width of the rectangular water body is 0.146 m, and the height is 0.293 m. The right boundary constraints were canceled at the moment 0 by instantaneous lifting of the gate to simulate the transient breach mode, and the specific computational parameters are shown in

Table 1. Parametric conditions for simulating the dam-failure process.

Serial Number	Calculation Condition	Parameter Condition
1	Total number of particles	2812
2	Boundary particle spacing	0.0026
3	SPH particle spacing	0.0038
4	Fluid density/(kg/m3)	1000
5	Kernel function type	Cubic spline function
6	Density approximation methods	Approximation of the continuity equation
7	Time step	0.0001 s
8	Smooth length	1.25 particle spacing
9	Coefficient of viscosity	1.2
10	Time	1.0

.

After the simulation and visualization of the results, the comparison graph shown in Figure 4 was obtained.

As can be seen from Figure 4, the overall movement of the dam-burst water body process is as follows: In the T = 0.2 s moment, the overall flow pattern is streamlined, the distribution of water particles uniformly has an overall forward movement, the front of the water body velocity is larger, and the velocity direction is shown as pointing diagonally downward. In the T = 0.4 s moment, the front end of the water flow reaches the right side of the wall, and in the constraints of the right wall, it cannot continue to move forward and appears close to the right wall’s upward movement; the water movement of this moment in time during the conversion of kinetic energy into potential energy manifested in the overall speed is small. At the moment of 0.6 s, the water particles reach the highest position of the right side wall, the kinetic energy and energy of the particles are converted into gravitational acceleration, and then, these particles move downward under the action of gravitational acceleration to hit the lower water particles; during 0.8–1.0 s, water falling, the process of liquid splashing, and surface tearing and breaking phenomena occur, and part of the region cyclotrons, among other phenomena. In the 1.0 s moment, the overall movement of the body of water is back to the left side of the wall, and by the limitation of the side of the wall, the particles appear to converge and merge, and finally, the particles cyclotron backward to the right side of the round-trip movement. During the whole process in 1 s time, it can be seen from the analysis of the flow pattern that the simulation results of the SPH method corresponding to each moment are basically consistent with the model experiments, and the SPH method demonstrates good linear fluid characteristics. The results show that the SPH method portrays the fluid in more detail and has good simulation results.

For the presentation of the simulation results of the dam-break water flow, one of the evaluation methods is carried out by comparing the fluid free liquid surface height curve in order to further explore the difference between the SPH numerical simulation and the experimental results, based on the following method: The three moments of T = 0.2 s, T = 0.4 s, and T = 0.8 s are selected to obtain the free liquid surface height curves of the two and compare them, as shown in Figure 5:

In order to quantify the difference between the experimental results and the simulation results of the SPH method, the position coordinates of the extracted points of the free liquid level height curve are labeled as N₁ for the experimental data points and N₂ for the numerical simulation data points by the free liquid level similarity equation:

$$\epsilon =\left(1-\frac{\left|{\displaystyle \sum _{i=1}^{N_1}{y}_{1i}}-{\displaystyle \sum _{i=1}^{N_2}{y}_{2i}}\right|}{{\displaystyle \sum _{i=1}^{N_1}{y}_{1i}}}\right)\times 100\%$$

(13)

where y_1i the experimental data vertical coordinate value, and y_2i is the simulation result vertical coordinate value.

After calculating the similarity between the two, the average value of the average similarity is 88.4%, and the data show that the simulation results of this model are in good agreement with the experiments, indicating that the numerical model of SPH can be well simulated to show the characteristics of the dam-break water flow. The calculation results are shown in

Table 2. Similarity between simulation results and experimental data.

Time	T = 0.2 s	T = 0.4 s	T = 0.8 s	Average
Similarity	92.1%	90.7%	82.3%	88.4%

.

Previous research work based on the SPH method did not consider the study of the progressive dam-failure model problem. Shi Hongda [4] and others also believed that the accuracy of the failure data obtained by using the transient dam-failure model for calculation is low and proposed that the future direction of dam-failure research should be toward the development of the progressive dam-failure model. In this paper, on the basis of the classical dam-failure model combined with the SPH method to establish a gradual dam-failure model and according to the method of gradual dam-failure, the model is further divided into two kinds, i.e., gradual dam failure and progressive gradual dam failure in equal intervals, in order to prepare for further study of the dam-failure problem in the future.

3.2. Example Simulation of Gradual Collapse

In previous studies, researchers have mostly based their work on rectangular breaching water bodies established by classical dam-collapse models, and for the study of gradual breaching dams, it is considered that non-rigid body dams (e.g., earth dams, rockfill dams, and other types of dams) tend to have a sloping slope downstream of the dam face.

(1)

The model has some improvements in the way the points are laid out, which can optimize the model to some extent for the traditional SPH dam-failure model;

(2)

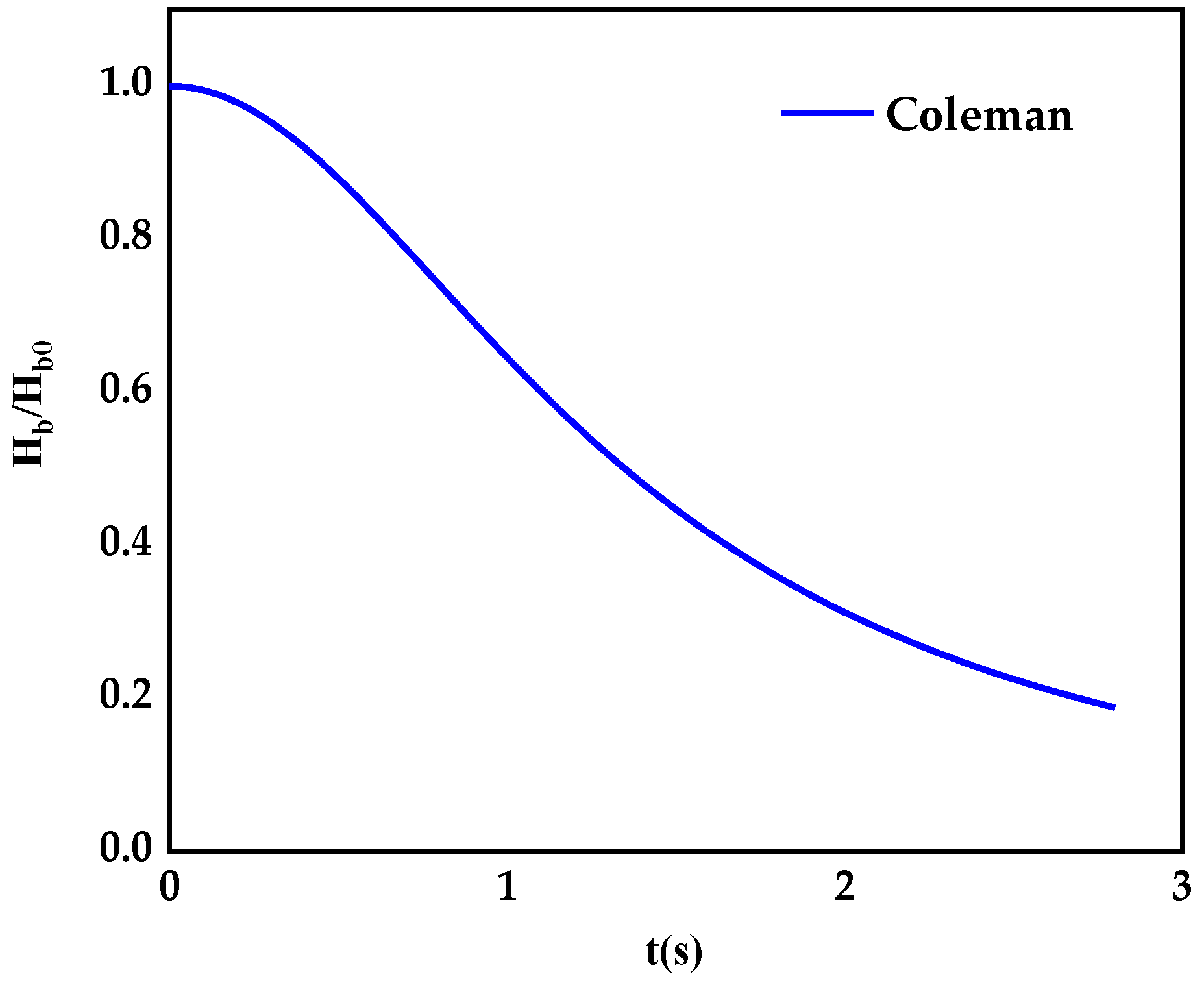
The model facilitates the development of later studies, and the calculation of the height of the initial dam height versus the height of the moment of failure over time can be analyzed in comparison with Coleman’s theoretical solutions in the literature.

S.E. Coleman [31] and others have argued that during the development of a dam failure, the elevation of the bottom of the breach, H_b, is a function of time t with a dimensionless expression:

$$H_b^{}/H_{b0}={\left(2.30g{t}^2/H_{b0}+1\right)}^{-1}$$

(14)

where H_b is the elevation of the bottom of the breach; H_b0 is the initial elevation of the dam; g is the acceleration of gravity. Equation (14) is mostly used in sea defense projects with an infinite water level in front of the dam. As shown in Figure 6, when the water level in front of the dam is constant, the trend of the elevation of the dam at the bottom can decrease indefinitely to approach 0. Due to the characteristics of the dam itself, it cannot eventually breach a height of 0 [32].

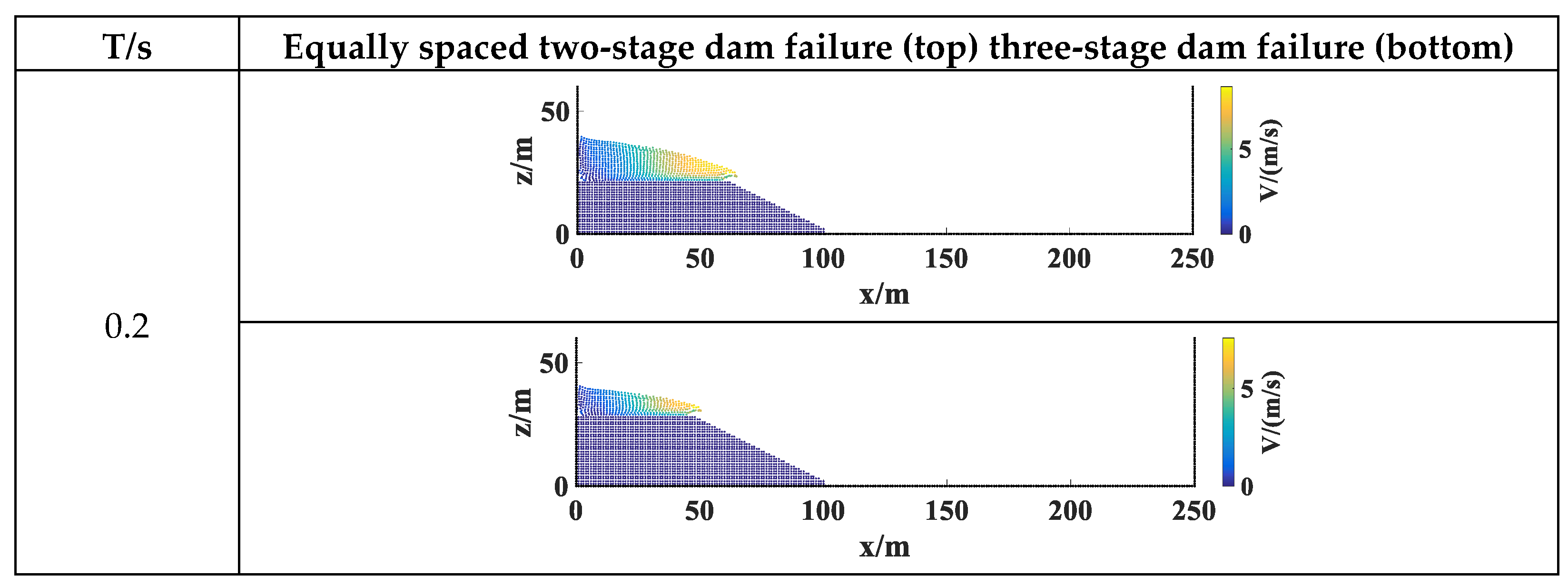
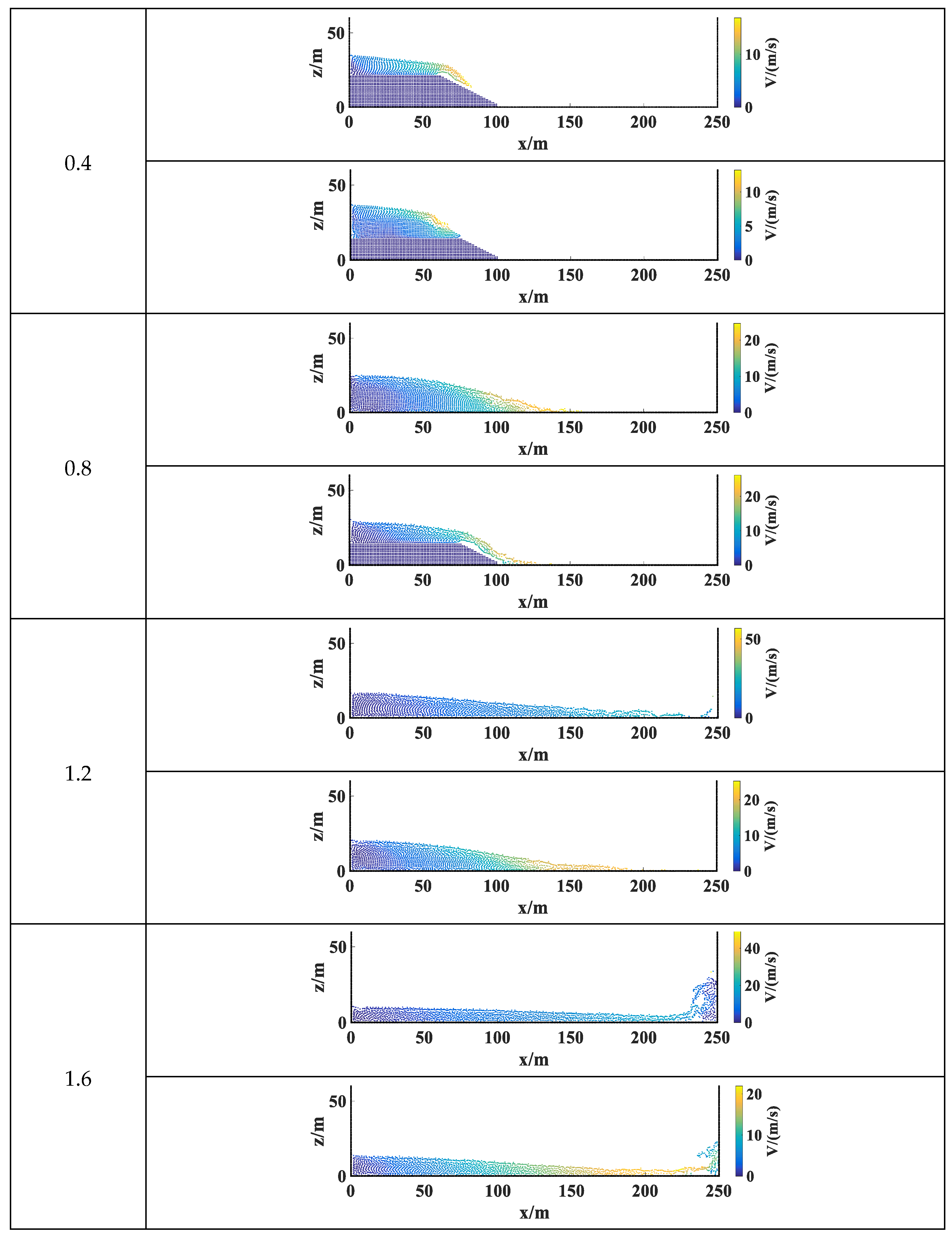
3.2.1. Equally Spaced Collapse Simulation

The next step was to simulate the working conditions of two-section collapse and three-section collapse under equal-interval-type division and compare the two. The specific working condition dimensions are shown in Figure 7. Inside the 250 m × 55 m single-width rectangular tank, the trapezoidal water body was arranged with an upper bottom length of 20 m, a lower bottom length of 100 m, a height of 41 m, and a slope of i = 0.513. The downstream boundary of the dam was generalized to a trapezoidal water body for the convenience of water body arrangement and computation, and the trapezoidal water body constraints were similarly lifted in segments at the moment 0 to simulate the motion of the dam-break water flow.

The initial parameter condition settings are shown in

Table 3. Initial parameter condition settings for SPH method dam-failure simulation.

Serial Number	Calculation Condition	Parameter Condition
1	Total number of particles	2911
2	Boundary particle spacing/m	1
3	SPH particle spacing/m	1
4	Kernel function type	Cubic spline function
5	Density approximation methods	Approximation of the continuity equation
6	Time step	0.0001 s
7	Smooth length h	1.25 particle spacing
8	Fluid density/(kg/m3)	1000
9	Coefficient of viscosity	1.2
10	Time/s	2.0

. The calculation uses 2911 particles, of which 2540 particles are in the water body and 371 particles in the side wall. The kernel function uses the cubic spline function, and the density-update algorithm is used for the density calculation, which is used to achieve the purpose of sectional routing by controlling the speed of particles in the corresponding area. Next, we simulate the two-section breach, three-section breach, four-section breach, and five-section breach conditions, respectively, due to the limited space, to show the flow pattern of the two-section and three-section dam-breaking water flow as a regular pattern (the picture time point is selected according to the typical flow section), as shown in Figure 8 (the left is the two-section breach, and the right is the three-section breach).

As can be seen from Figure 7, when the time t is from 0 to 0.25 s, the three-stage routing water flow pattern and two-stage routing is basically the same. After 0.25 s, the difference begins to appear and gradually manifests itself as the three-stage routing speed being slower than the two-stage, and the gap between the two routing development speeds gradually increases after 0.8 s. In the two-stage collapse, the upper water body completely collapses in about 0.65 s and falls to the bottom of the box. The depth of the collapse is 25 m; after 0.65 s, the lower water body begins to collapse and gradually fuses with the upper water body, with the collapse finally stabilizing at 10 m and moving to the right. In contrast, the three-stage routing has a routing depth of 14 m at 0.25 s, which is about one-third of the total depth, and at 0.25 to 0.8 s, the second layer of the water body begins to rout and intersect with the first layer, and the final depth of the routing stabilizes at about 28 m; at 1 s, the third layer of the water body begins to rout and push the water body forward. In terms of the overall time analysis, the two-stage routing speed is about 1.4 times that of the three-stage speed.

3.2.2. Progressive Collapse Simulation

In actual engineering, the dam-failure process has a certain incremental nature and is not transient for dam failure, so the simulation of incremental dam failure is carried out on the basis of exploring the equal-interval dam failure. Progressive dam failure simulates a different depth of failure each time as opposed to equal-interval failure, where the depth of failure increases in each time interval to simulate a real dam failure as closely as possible. Therefore, the condition is simulated with the same dimensions as above, with two, three, four, and five layers of incremental height of the water body, as shown in Figure 9. The two-stage dam breaching adopts the arrangement of 15 m in the first layer and 26 m in the second layer; the three-stage dam breaching adopts the arrangement of 7 m in the first layer, 14 m in the second layer, and 20 m in the third layer; the four-stage dam breaching adopts the arrangement of 5 m, 8 m, 12 m, and 16 m; and the five-stage dam breaching adopts the arrangement of 2 m, 4 m, 9 m, 11 m, and 15 m. The effect of controlling the breaching depth is achieved by changing the number of controlled particles and the time interval and compared and analyzed with the above working conditions.

For space reasons, Figure 10 only shows the water flow velocity and flow distribution of the two-stage and three-stage progressive routing mode in 1.6 s. From the analysis of Figure 9, it can be seen that at the moment of T = 0.2 s, the uppermost layer of the water body begins to flow, and the velocity distribution of the water particles is in the range of 5 m/s; at the moment of T = 0.4 s, the second layer of the water body begins to appear to be routed but does not form a water flow, and its flow velocity is in the range of 10 m/s. In the T = 0.6 s moment, in the two-stage and three-stage, the first two layers of the water body are basically collapsed, and in the two-stage collapse, most of the water body is basically collapsed, the front end of the water body converges into a “strand” downstream movement, and the flow velocity is distributed in the range of 20 m/s; in the moment of T = 0.8 s, in the three-stage, the third section of the body of water appears to be collapsed, and the front-end water flow reaches the lower wall. at the lower side wall. After that, the water body starts to move to the right side and starts to fold back when it reaches the right side wall. Compared with the previous section, the progressive routing model and other interval routing model are basically the same in terms of flow pattern and flow velocity distribution.

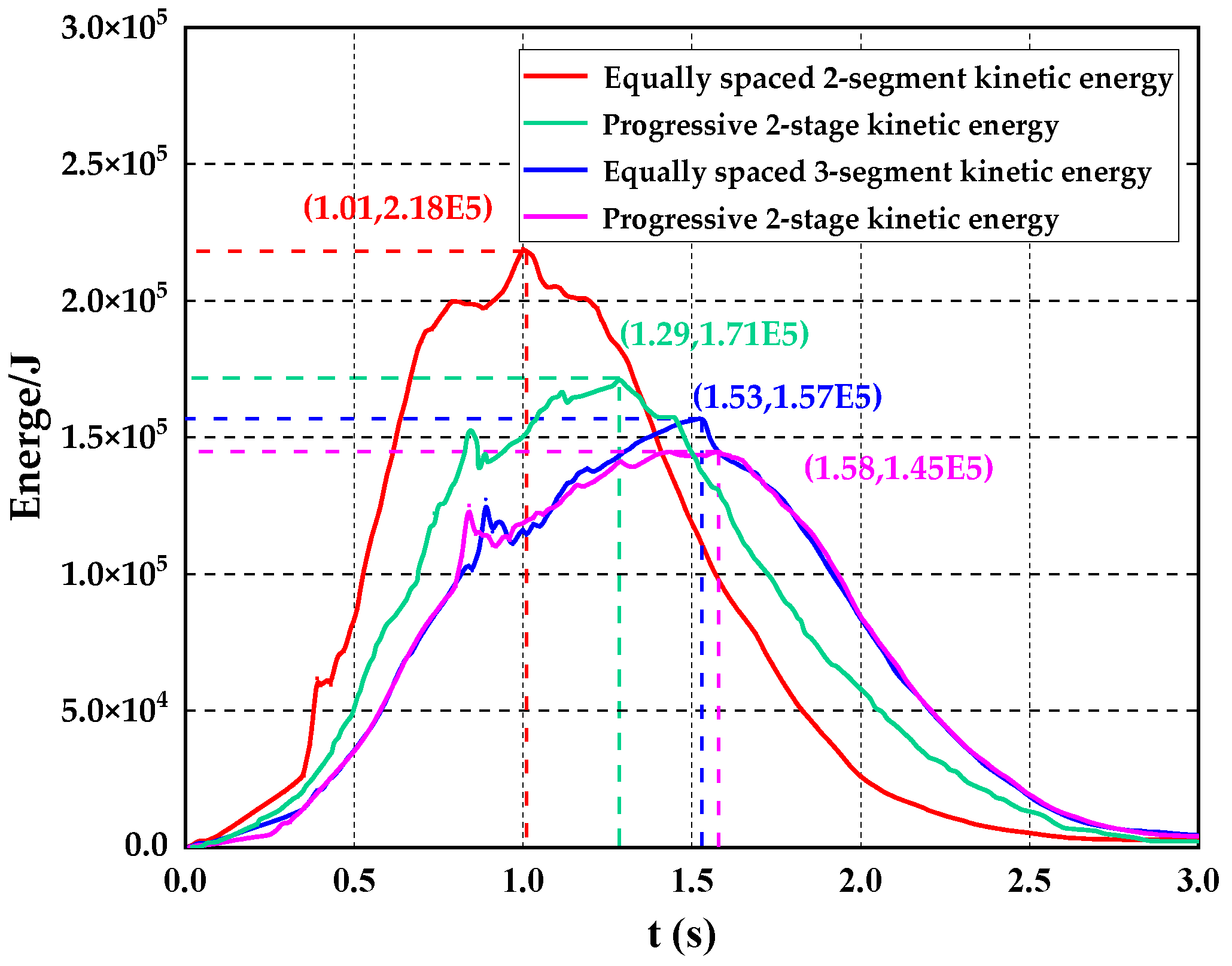
3.2.3. Analysis of Results

On the basis of comparing the dam breaches under the above multiple modes and plotting the dam elevation (breach development) versus time curves, Figure 11 is given.

From Figure 10 combined with Equation (13), it can be seen that with the increase in time, the height of the dam body becomes bigger and bigger, and the overall development trend of the dam body elevation is the same in many kinds of breaching modes. By quantitatively calculating the elevation change curve of the equidistant breaching and progressive breaching and comparing with Coleman’s theoretical calculation results, from the overall point of view, the more segments that are divided into the two modes of the gradual breaching and equidistant breaching in a certain range, the closer the calculation results are to the Coleman’s theoretical solution. The greater the number of segments for the two modes of progressive dam failure and equal-interval dam failure within a certain range, the closer the calculation results are to the Coleman [31] theory. At the same time, comparing the progressive dam failure with the equal-interval progressive dam failure, the progressive dam body elevation change curve is more consistent with the theoretical solution, which is more in line with the general law of development. As shown in

Table 4. Comparison of similarity between simulation results and Coleman’s [31] theoretical solution Table.

Gradual Dam-Failure Condition	2 Paragraph	3 Paragraph	4 Paragraph	5 Paragraph
Equidistant dam failure	72.2%	85.9%	92%	95.4%
Progressive dam failure	79.1%	95.2%	96.9%	97.1%

.

The variation of energy with time for multiple routing modes is shown in Figure 12, as well as the total kinetic energy peaks at the moment of T = 1.0 s with the size of 2180 KJ for the two-stage equal-interval routing mode. The total kinetic energy peaks at the moment T = 1.53 s, with a magnitude of 1570 KJ for the equally spaced three-stage collapse mode. For the progressive two-stage collapse mode, the total kinetic energy peaks at the moment T = 1.29 s, with a magnitude of 1710 KJ. The total kinetic energy peaks at the moment T = 1.58 s, with a magnitude of 1450 KJ, for the progressive three-stage collapse mode. Overall, the total kinetic energy of the dam-breaking flow shows a trend of increasing and then decreasing, and the total kinetic energy changes in the decreasing stage with a consistent trend. In the case of gradual dam failure at equal intervals, the maximum total kinetic energy decreases as the number of segments increases, and the arrival of the maximum total kinetic energy is delayed. Similarly, progressive dam failures show such a trend compared to equally spaced progressive dam failures. The results show that the destructive force of the dam-bursting flow decreases with the increase in the number of segments, and the moment in which the maximum total kinetic energy appears is shifted back. For the same number of dam-failure segments, the kinetic energy decreases the most, and the maximum destructive force of the dam-failure flow comes the furthest back in the progressive failure mode.

The results show that the destructive force of the dam-breaking flood decreases as the number of segments increases, and the moment of maximum total kinetic energy emergence is shifted back. By contrast, the incremental breaching pattern has the most weakened kinetic energy, and the maximum destructive force of the dam-breaking flood comes at a later time.

In order to further show the mechanism of the dam-breaching process, several typical moments under the three-stage progressive breaching mode were selected to obtain the pressure distribution graph with time, as shown in Figure 13.

Progressive three-stage dam-failure water flow pressure distribution is shown in Figure 12; the overall pressure of the water body in the segmental failure conforms to the hydrostatic pressure, which is because the lower dam body is less disturbed when the upper dam breaks, presenting hydrostatic pressure characteristics, which is in line with the actual project. When, in the initial moment of t = 0 s, the dam body pressure is in line with the hydrostatic pressure characteristics, and when the dam failure flood begins to flow downstream, the pressure distribution begins to change, presenting a local negative pressure zone. From further analysis, it can be seen that with the overall depth of the dam failure, the flood becomes smaller, and the water body pressure is also gradually reduced by the initial value of the maximum value of 4.1 MPa down to 1 MPa.

4. Conclusions

For the gradual dam-failure problem, the SPH numerical simulation algorithm was used to study and simulate the two-dimensional dam-failure water flow process under various working conditions. Firstly, we simulated and calculated the flow pattern under the classical dam-failure model and compared the calculation results with the similar experimental data in the literature, which are in good agreement with each other. On this basis, we simulated gradual dam failure based on a variety of different working conditions; analyzed the flow pattern, velocity vector, energy, and pressure cloud diagrams of the water under various working conditions; and compared the development curve of the failure over time as obtained from the calculations with the theoretical solution proposed by S.E. Coleman [31]. The following conclusions and outlook were obtained:

4.1. Conclusions

• The simulation of dam-failure flow using the smooth particle hydrodynamics (SPH) method, including the simulation of the classical dam-failure mode and the simulation of the step-by-step dam-failure mode, as well as the further division of the two modes of study of the equal-spaced and progressive modes were investigated to explore the failure modes in line with the dam-failure flow;
• Compared to instantaneous dam failure, the calculation results of the breach development considering the progressive gradual dam-failure model are more consistent with the theoretical solution and closer to the actual dam-failure process;
• Under multiple progressive dam-failure modes, as the number of segments increases, the degree of agreement between the calculated results of the breach development and the theoretical solution increases, and progressive dam failure has a higher degree of agreement than equal-interval dam failure, while the total kinetic energy of the breaching flood decreases with the increase in the number of segments of the progressive dam failure.

4.2. Outlook

This paper can provide some guidance for the working conditions of two dam-failure modes, i.e., gradual dam failure, intermediate-interval dam failure, and progressive dam failure, but the design of various working conditions in this paper has some errors, and the reasonableness, comprehensiveness, and accuracy of the various working condition setups need to be further researched.