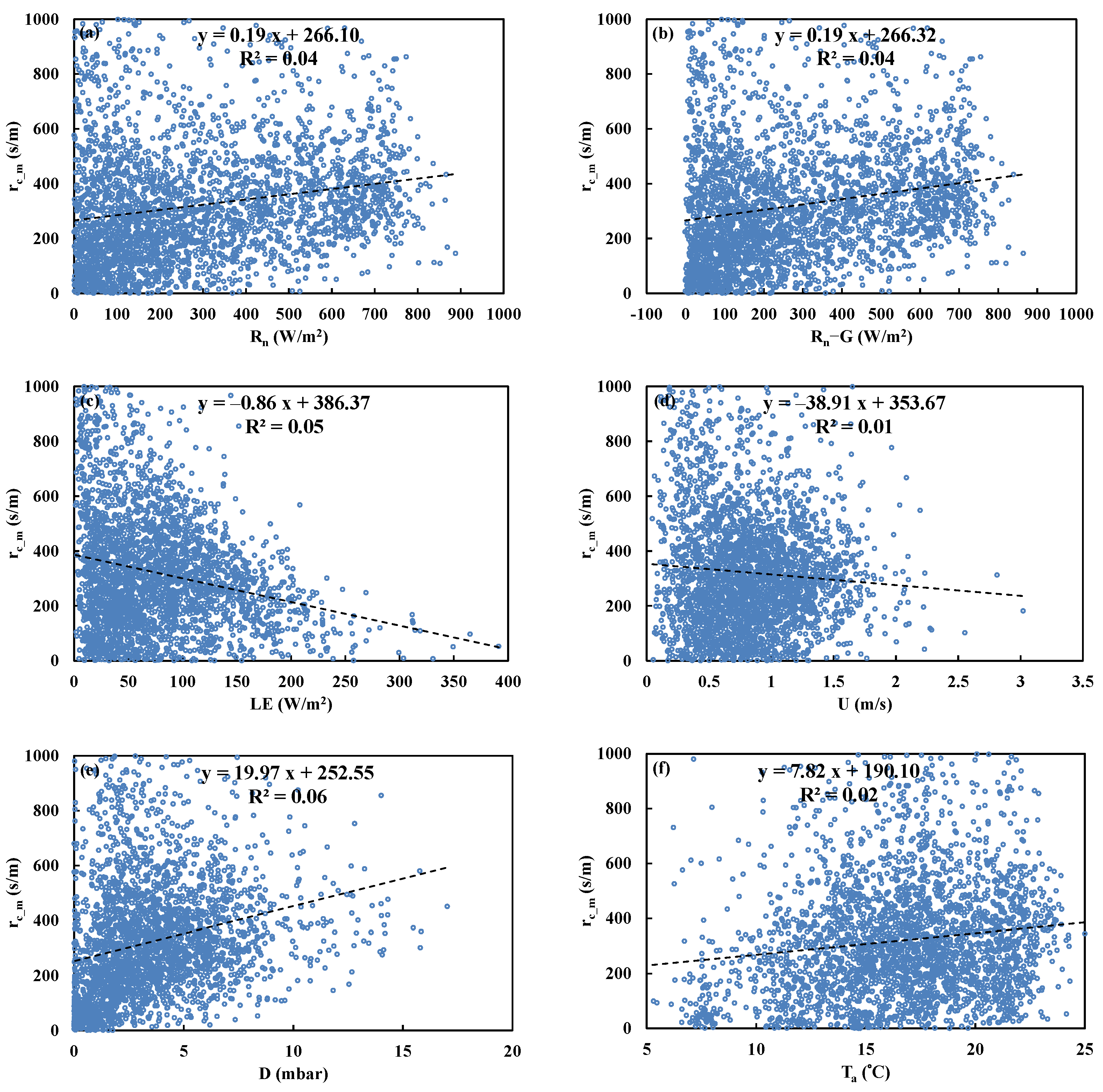
Figure 1.
Diurnal variations in canopy resistance (rc) and latent heat flux (LE) above (a) Dripsey grassland, (b) Chi-Lan forest, and (c) Sitou forest.
Figure 1.
Diurnal variations in canopy resistance (rc) and latent heat flux (LE) above (a) Dripsey grassland, (b) Chi-Lan forest, and (c) Sitou forest.
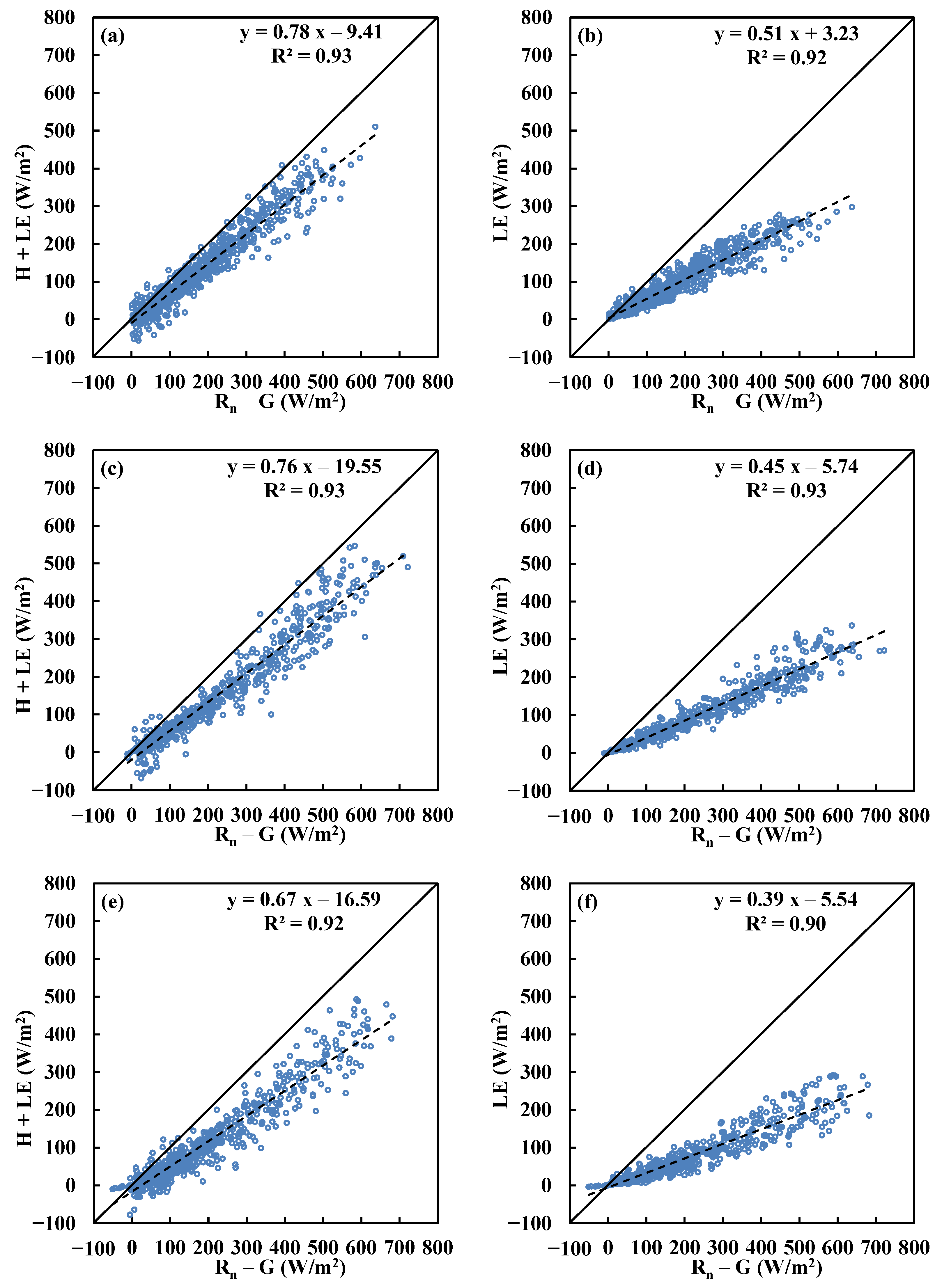
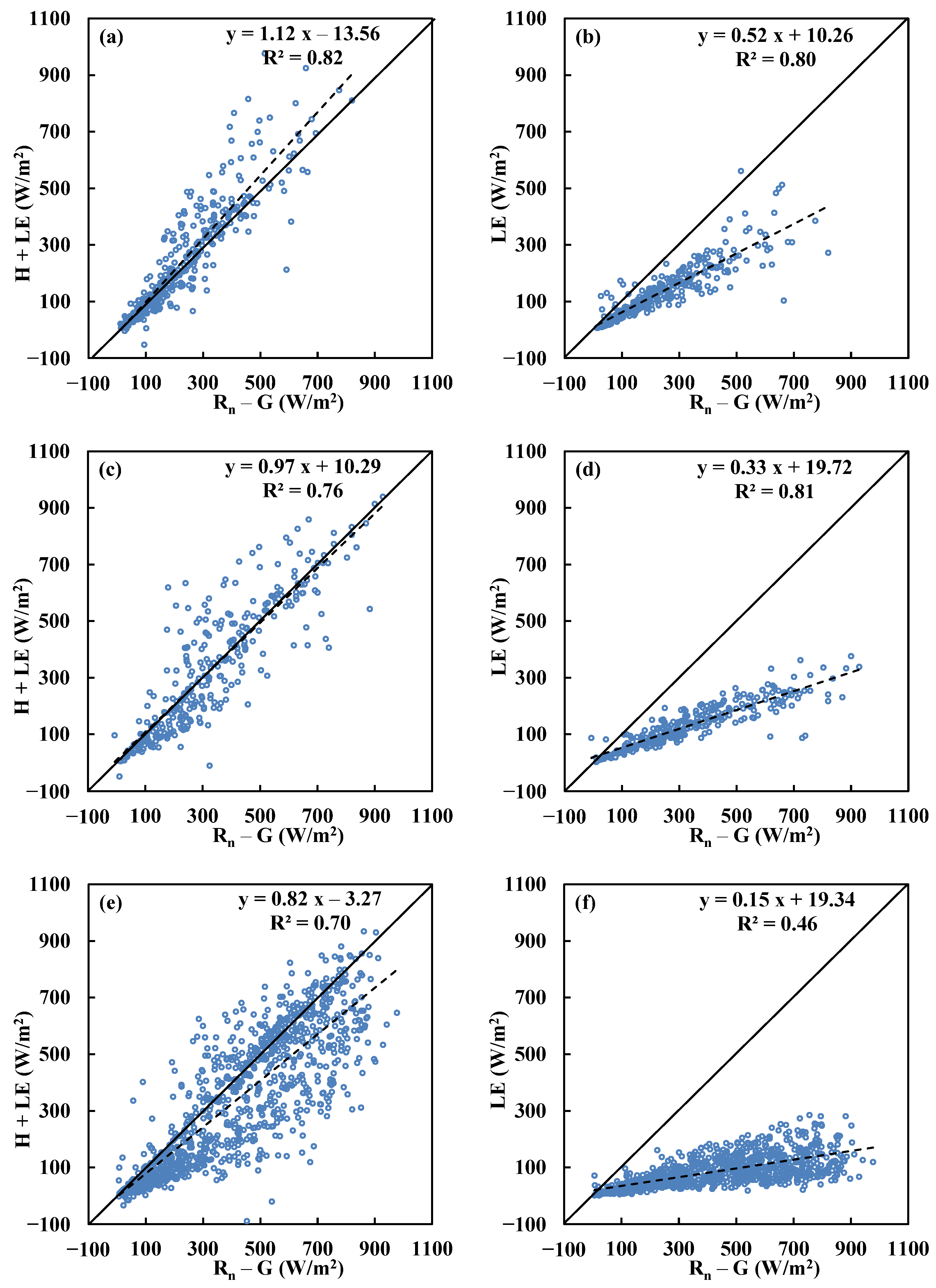
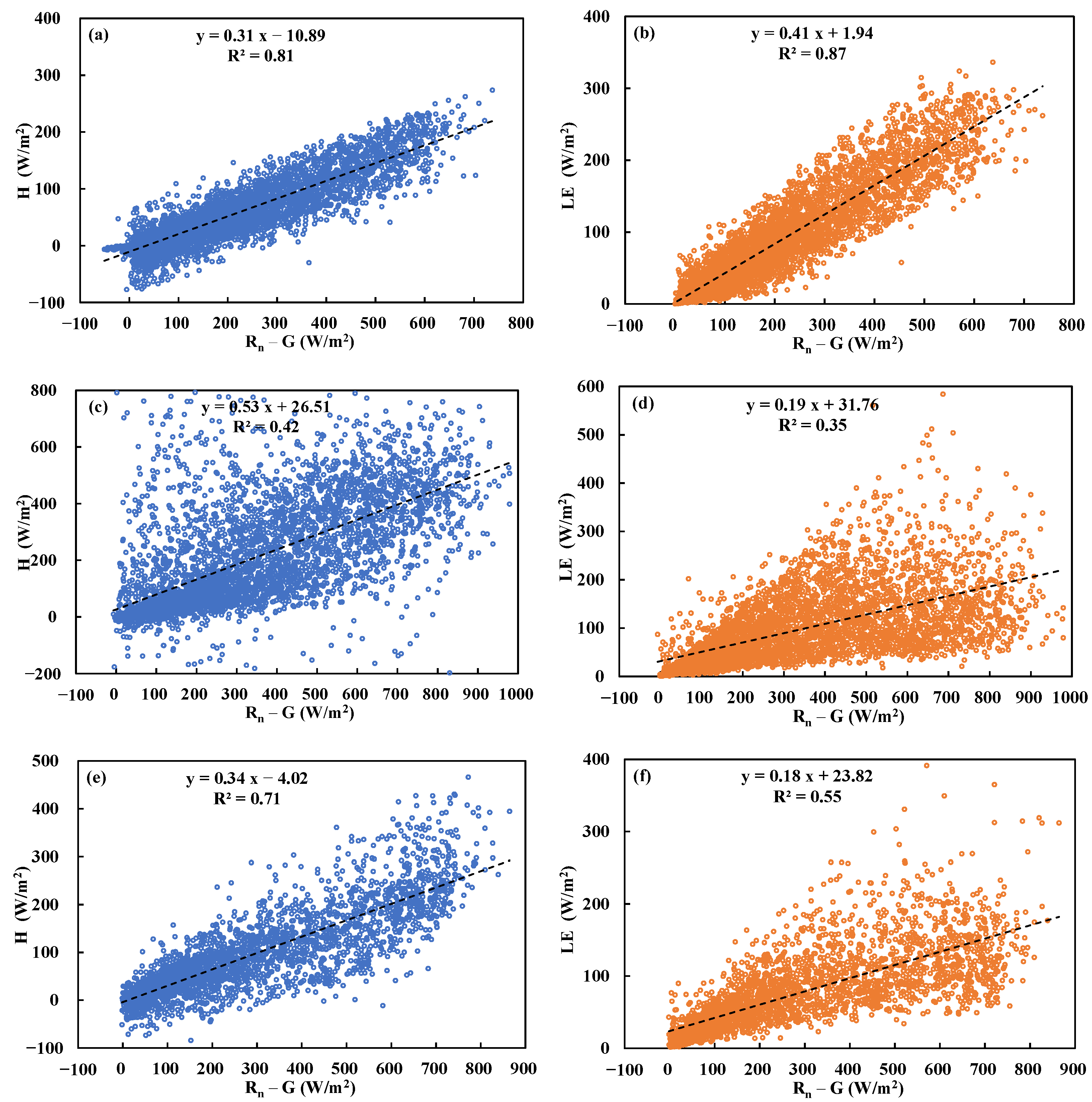
Figure 2.
Scatter plots of sensible heat (H) and latent heat (LE) fluxes as a function of Rn−G above the Dripsey grassland (a,b), Chi-Lan forest (c,d), and Sitou forest (e,f).
Figure 2.
Scatter plots of sensible heat (H) and latent heat (LE) fluxes as a function of Rn−G above the Dripsey grassland (a,b), Chi-Lan forest (c,d), and Sitou forest (e,f).
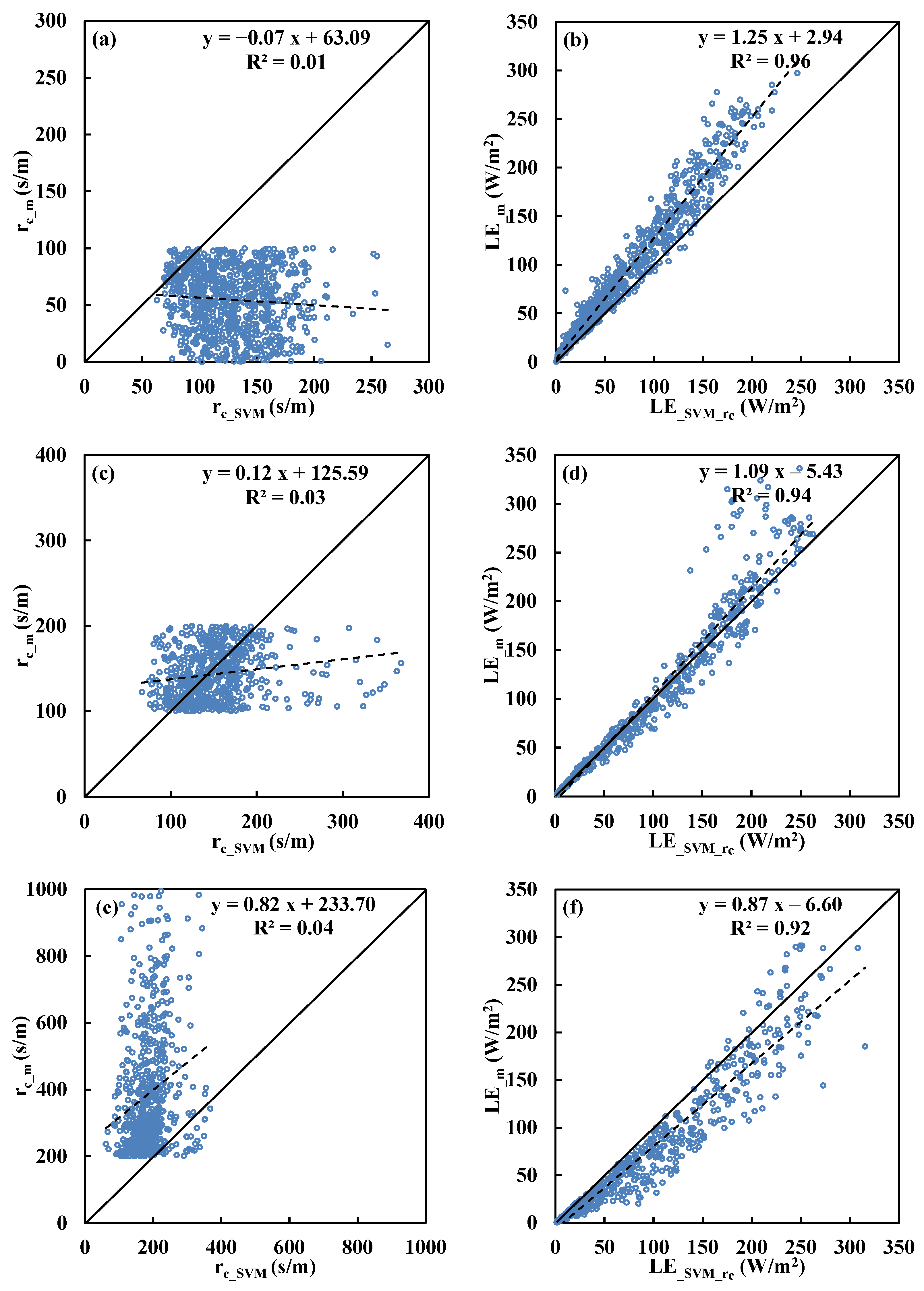
Figure 3.
Comparisons between measured canopy resistance (rc_m) and estimations by (a) SVM (rc_SVM) model and (b) Todorovic’s analytical solution (rc_TOD) above Dripsey grassland.
Figure 3.
Comparisons between measured canopy resistance (rc_m) and estimations by (a) SVM (rc_SVM) model and (b) Todorovic’s analytical solution (rc_TOD) above Dripsey grassland.
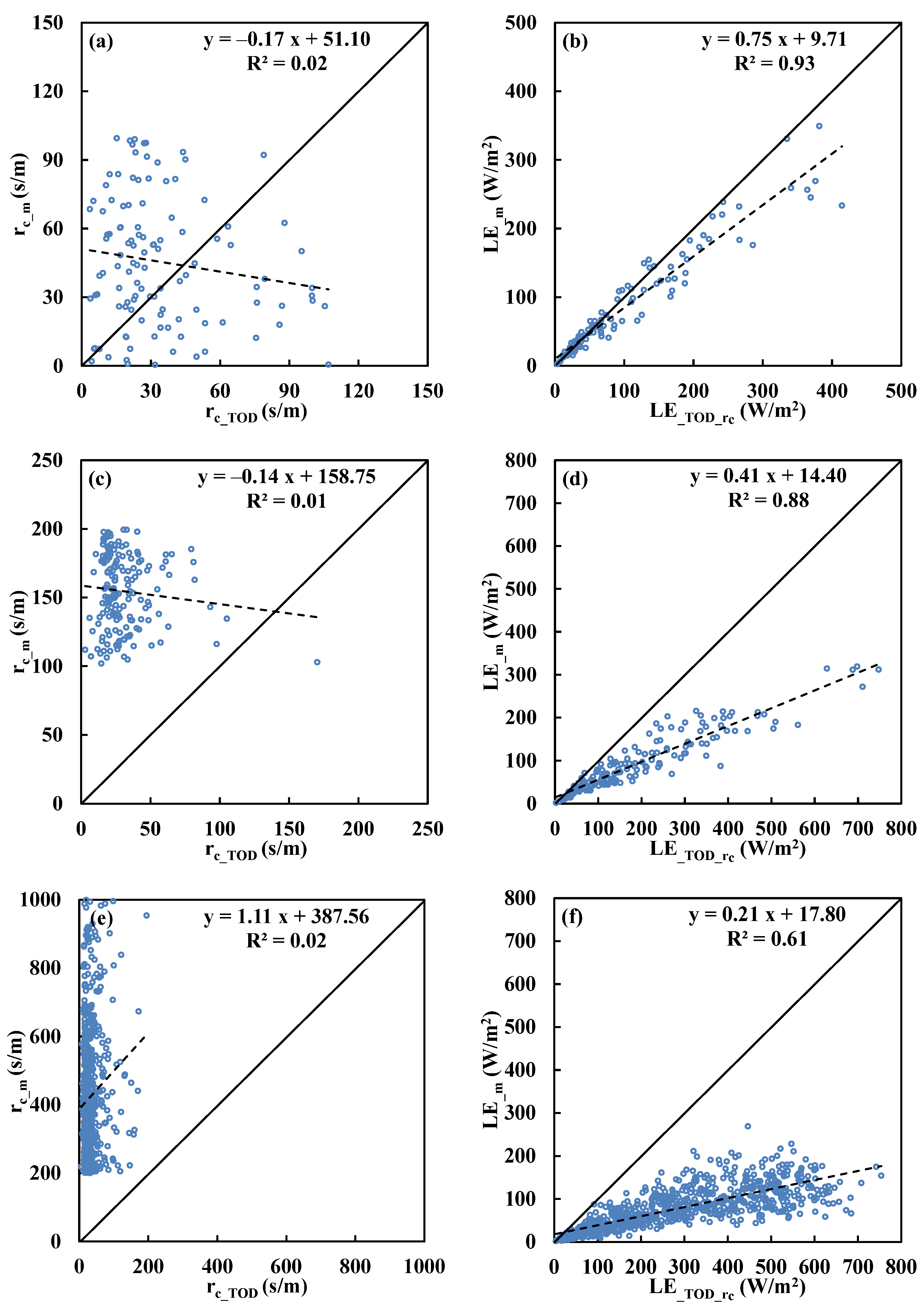
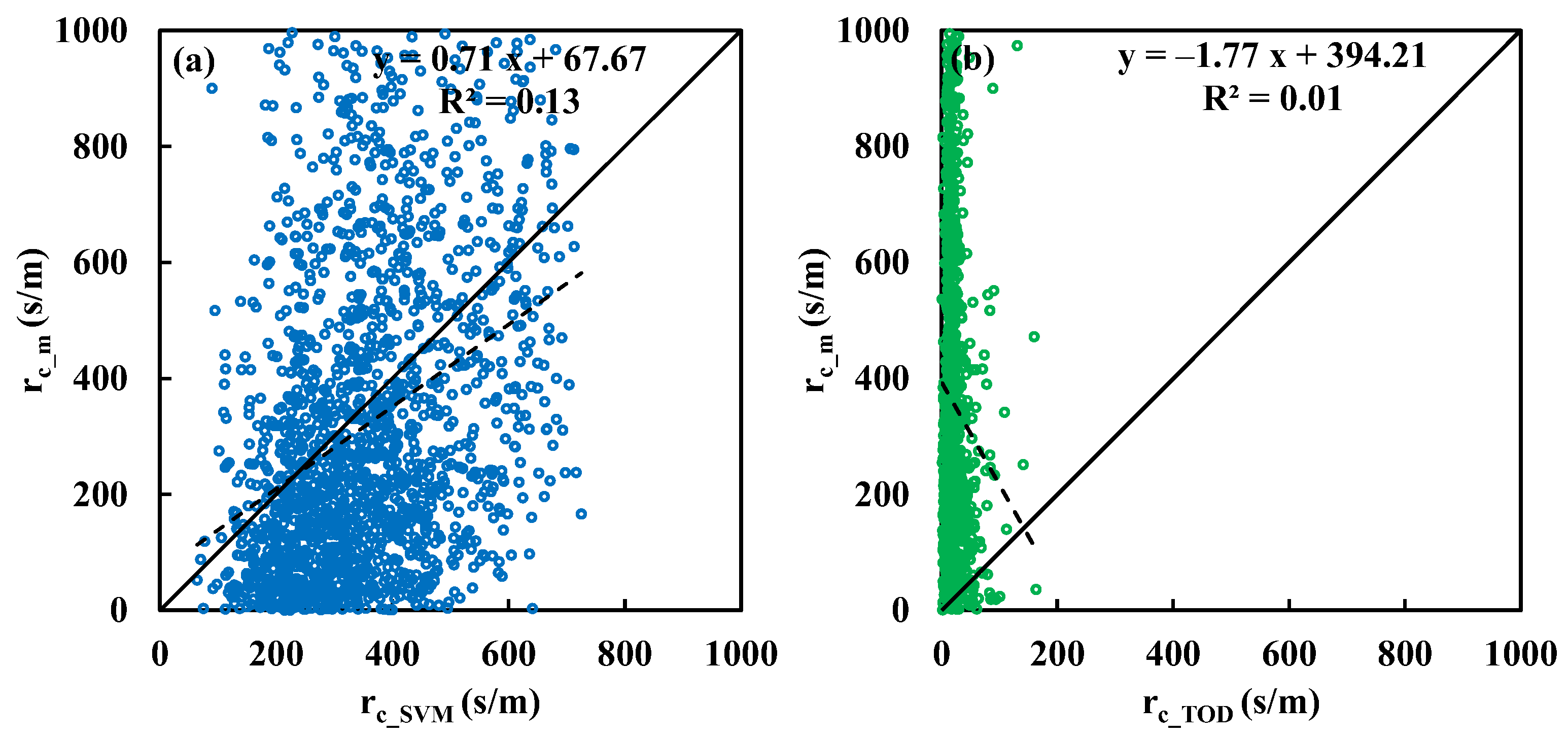
Figure 4.
Comparisons between measured canopy resistance (rc_m) and estimations by (a) SVM (rc_SVM) model and (b) Todorovic’s analytical solution (rc_TOD) above Chi-Lan forest.
Figure 4.
Comparisons between measured canopy resistance (rc_m) and estimations by (a) SVM (rc_SVM) model and (b) Todorovic’s analytical solution (rc_TOD) above Chi-Lan forest.
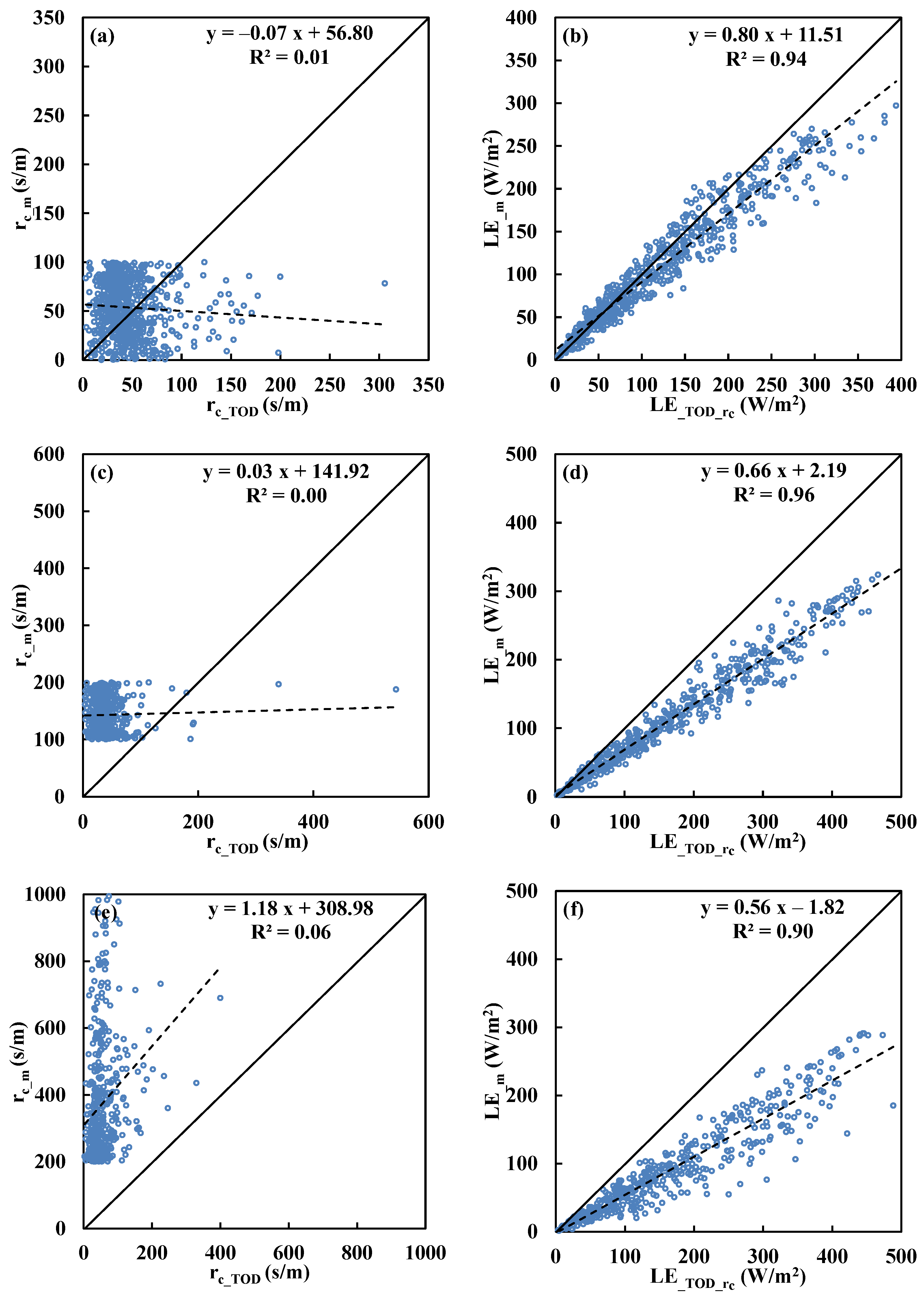
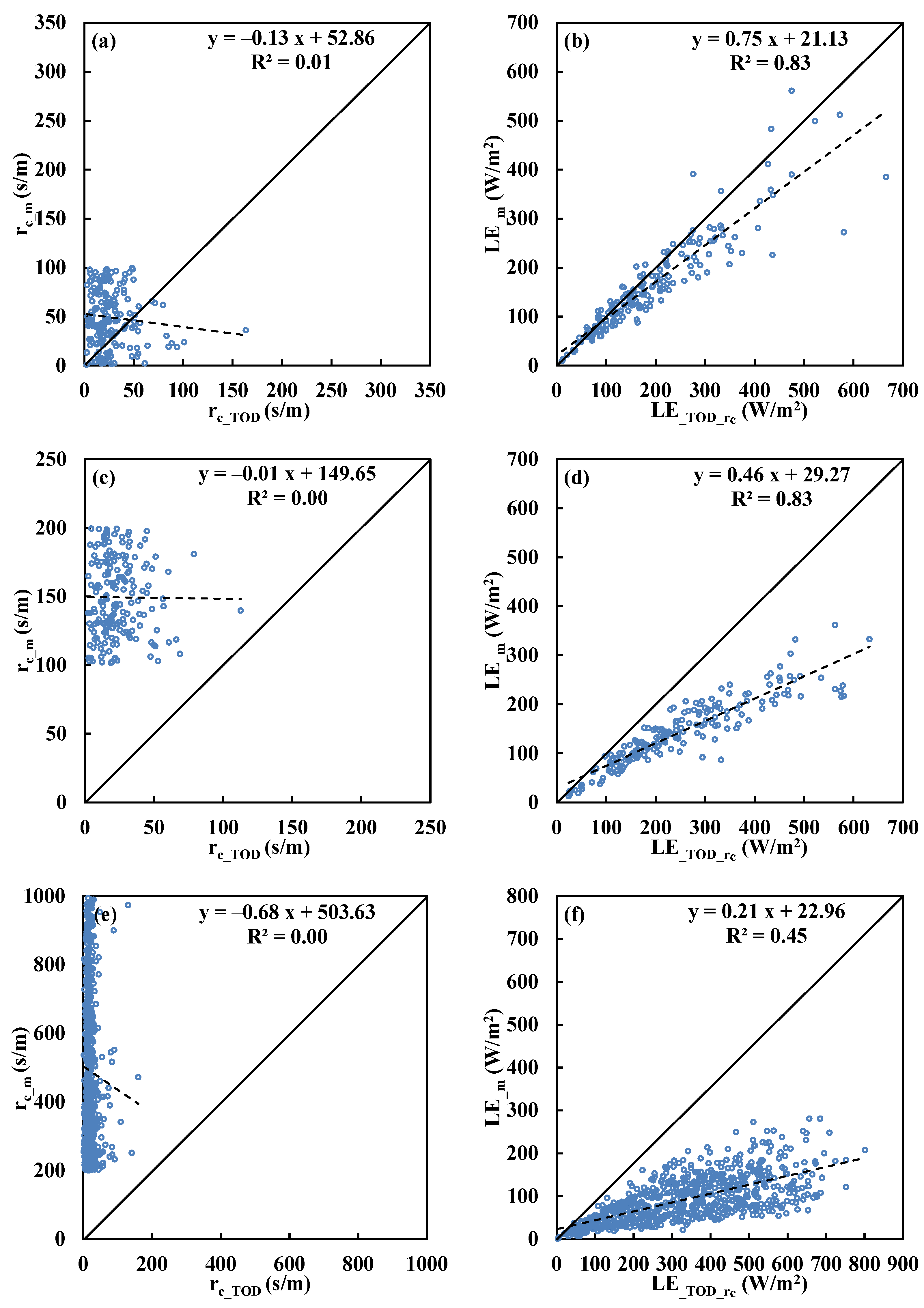
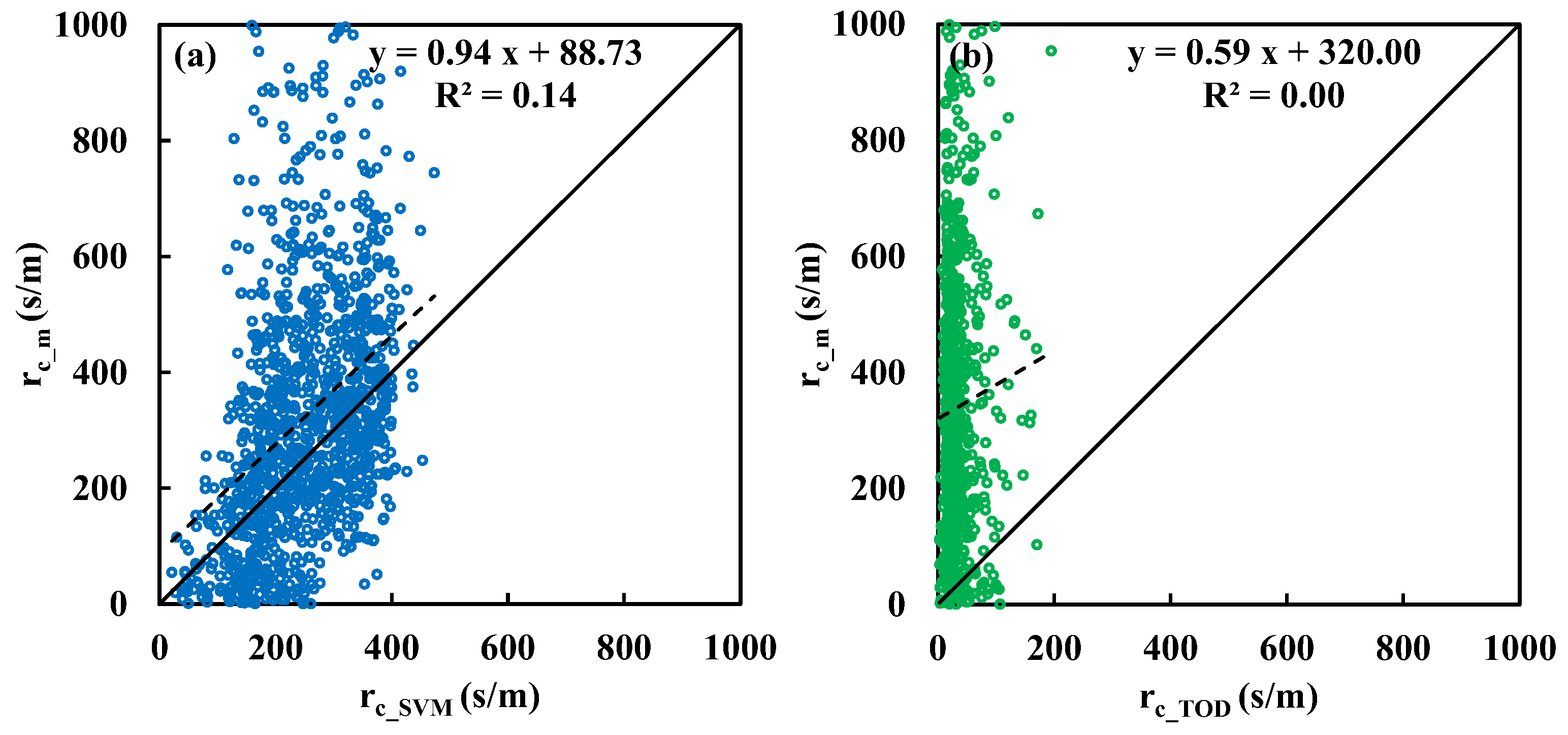
Figure 5.
Comparisons between measured canopy resistance (rc_m) and estimations by (a) SVM (rc_SVM) model and (b) Todorovic’s analytical solution (rc_TOD) above Sitou forest.
Figure 5.
Comparisons between measured canopy resistance (rc_m) and estimations by (a) SVM (rc_SVM) model and (b) Todorovic’s analytical solution (rc_TOD) above Sitou forest.
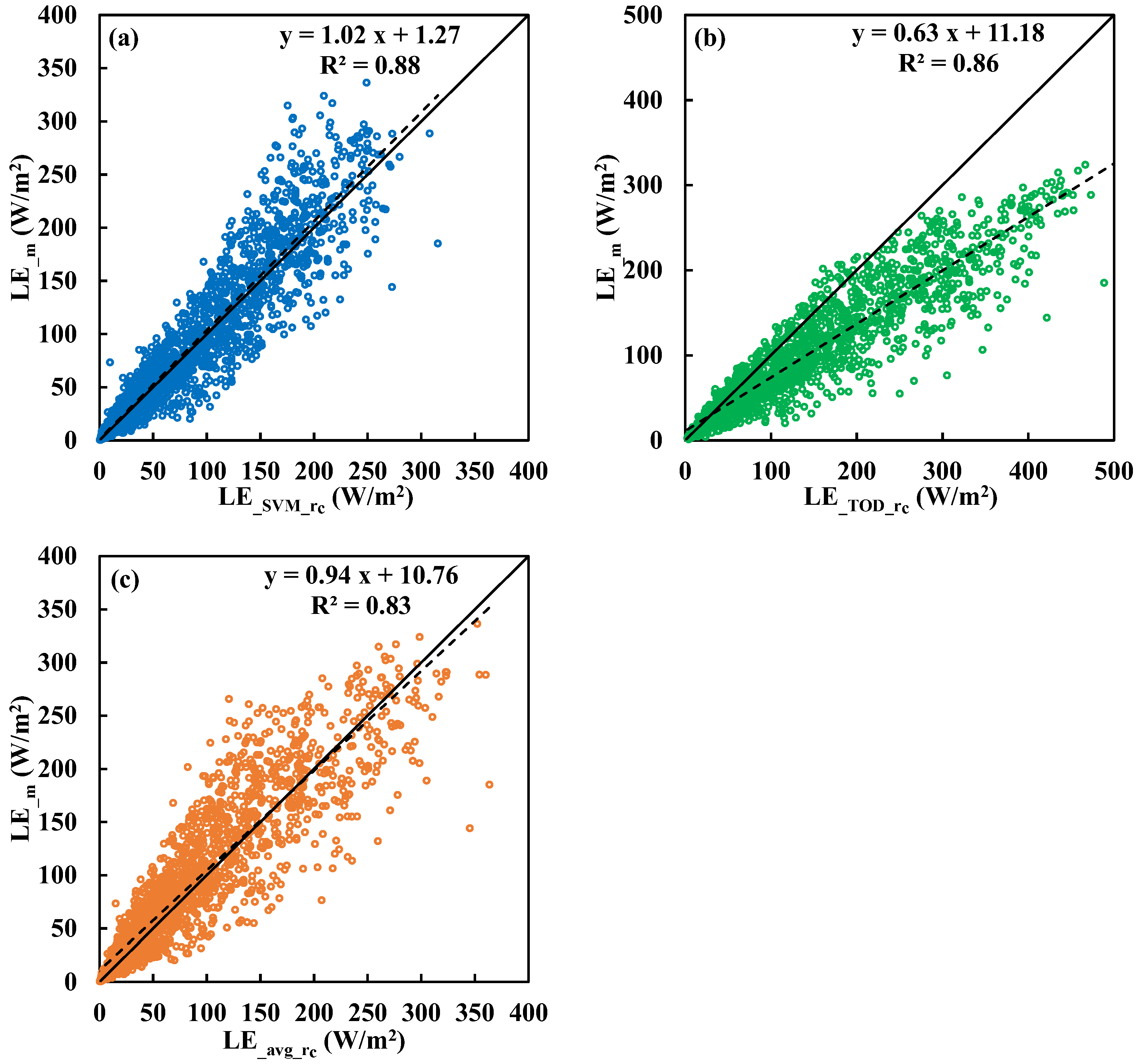
Figure 6.
Comparisons between measured latent heat flux (LE_m) and estimations by (a) SVM (LE_SVM_rc) model, (b) Todorovic’s analytical solution (LE_TOD_rc), and (c) constant rc (LE_avg_rc) above the Dripsey grassland.
Figure 6.
Comparisons between measured latent heat flux (LE_m) and estimations by (a) SVM (LE_SVM_rc) model, (b) Todorovic’s analytical solution (LE_TOD_rc), and (c) constant rc (LE_avg_rc) above the Dripsey grassland.
Figure 7.
Comparisons between measured latent heat flux (LE_m) and estimations by (a) SVM (LE_SVM_rc) model, (b) Todorovic’s analytical solution (LE_TOD_rc), and (c) constant rc (LE_avg_rc) above Chi-Lan forest.
Figure 7.
Comparisons between measured latent heat flux (LE_m) and estimations by (a) SVM (LE_SVM_rc) model, (b) Todorovic’s analytical solution (LE_TOD_rc), and (c) constant rc (LE_avg_rc) above Chi-Lan forest.
Figure 8.
Comparisons between measured latent heat flux (LE_m) and estimations by (a) SVM (LE_SVM_rc) model, (b) Todorovic’s analytical solution (LE_TOD_rc), and (c) constant rc (LE_avg_rc) above Sitou forest.
Figure 8.
Comparisons between measured latent heat flux (LE_m) and estimations by (a) SVM (LE_SVM_rc) model, (b) Todorovic’s analytical solution (LE_TOD_rc), and (c) constant rc (LE_avg_rc) above Sitou forest.
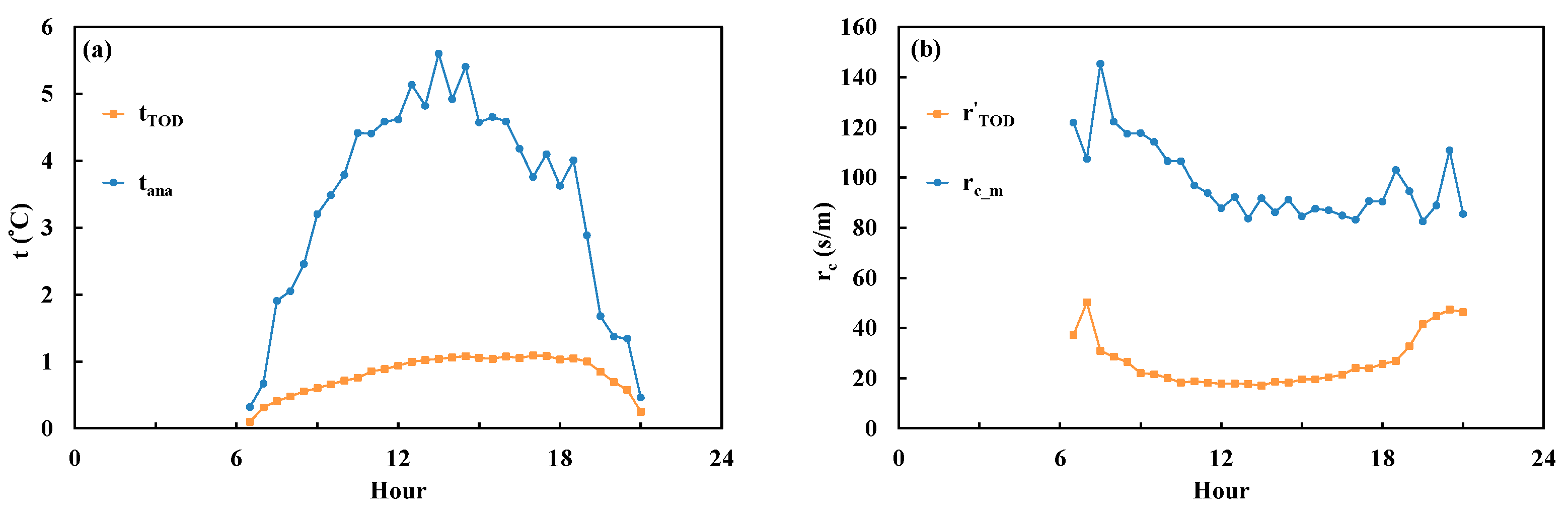
Figure 9.
Comparisons between (a) canopy temperature increase calculated by Todorovic’s expression (tTOD, Equation (6)) and the analytical solution (tana, Equation (16)); (b) pseudo resistance (r’TOD, calculated by Equation (17)) and measured canopy resistance (rc_m, calculated by Equation (3)) above Dripsey grassland.
Figure 9.
Comparisons between (a) canopy temperature increase calculated by Todorovic’s expression (tTOD, Equation (6)) and the analytical solution (tana, Equation (16)); (b) pseudo resistance (r’TOD, calculated by Equation (17)) and measured canopy resistance (rc_m, calculated by Equation (3)) above Dripsey grassland.
Figure 10.
Comparisons between (a) canopy temperature increase calculated by Todorovic’s expression (tTOD, Equation (6)) and the analytical solution (tana, Equation (16)); (b) pseudo resistance (r’TOD, calculated by Equation (17)) and measured canopy resistance (rc_m, calculated by Equation (3)) above Chi-Lan forest.
Figure 10.
Comparisons between (a) canopy temperature increase calculated by Todorovic’s expression (tTOD, Equation (6)) and the analytical solution (tana, Equation (16)); (b) pseudo resistance (r’TOD, calculated by Equation (17)) and measured canopy resistance (rc_m, calculated by Equation (3)) above Chi-Lan forest.
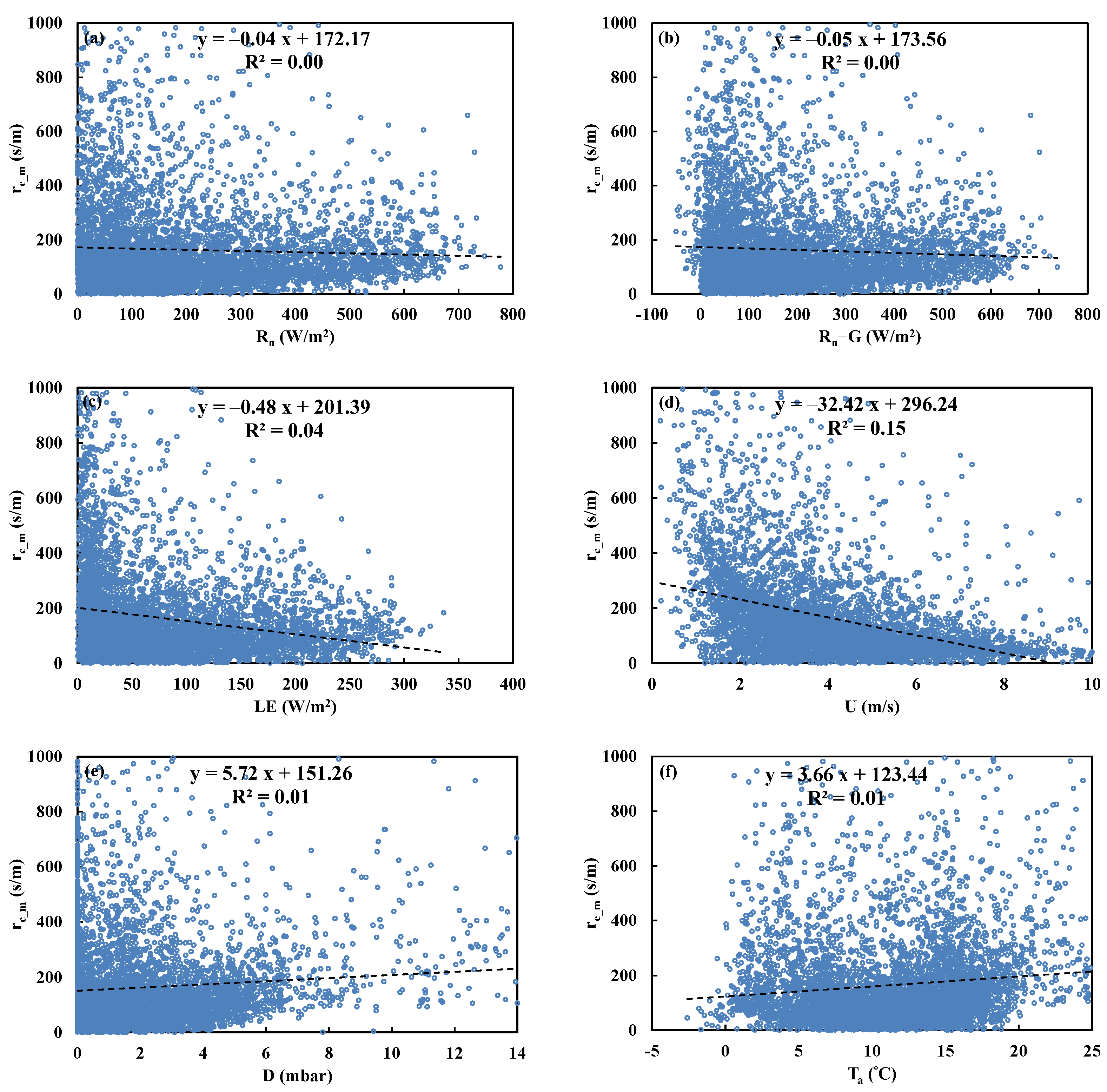
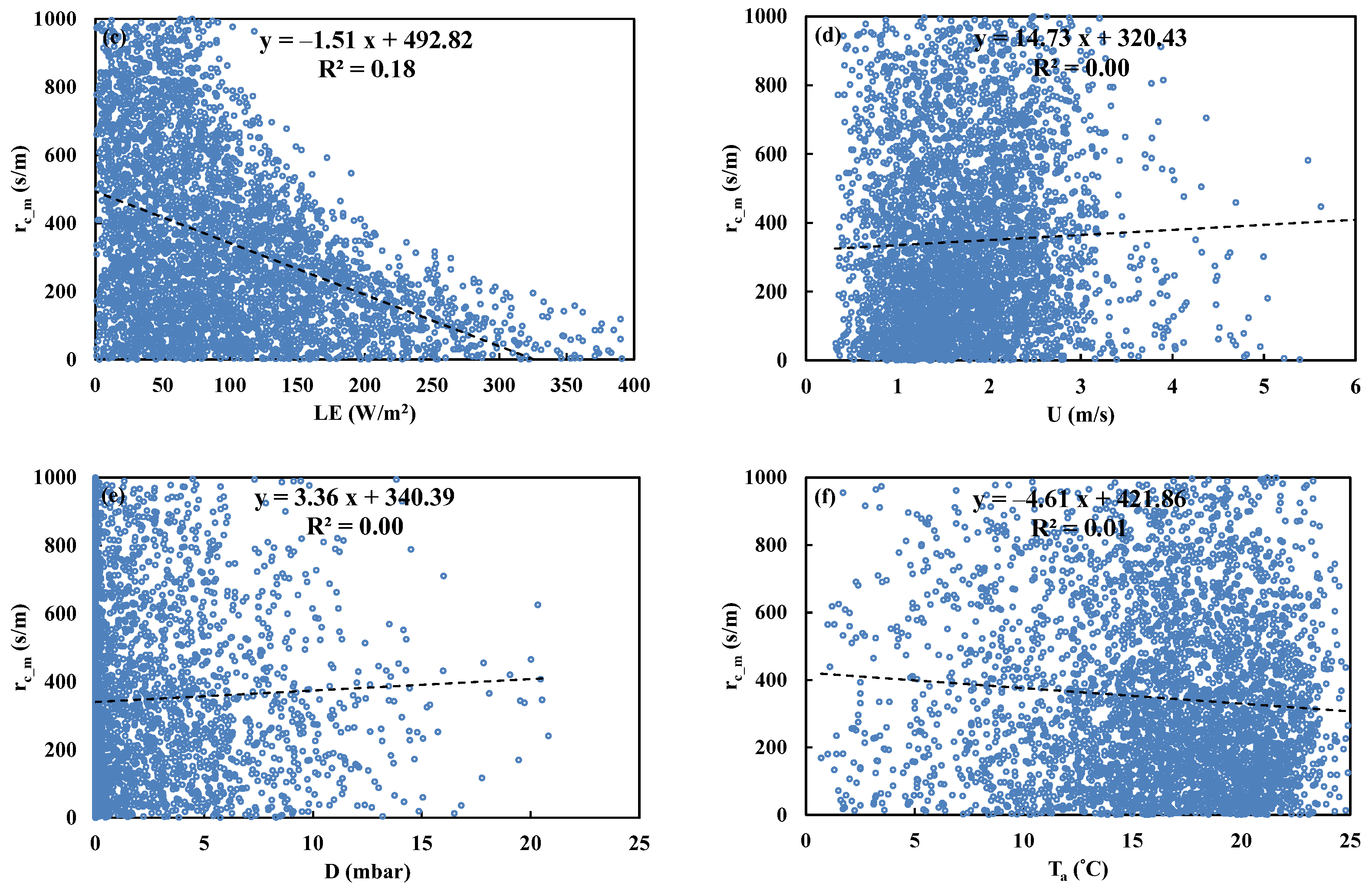
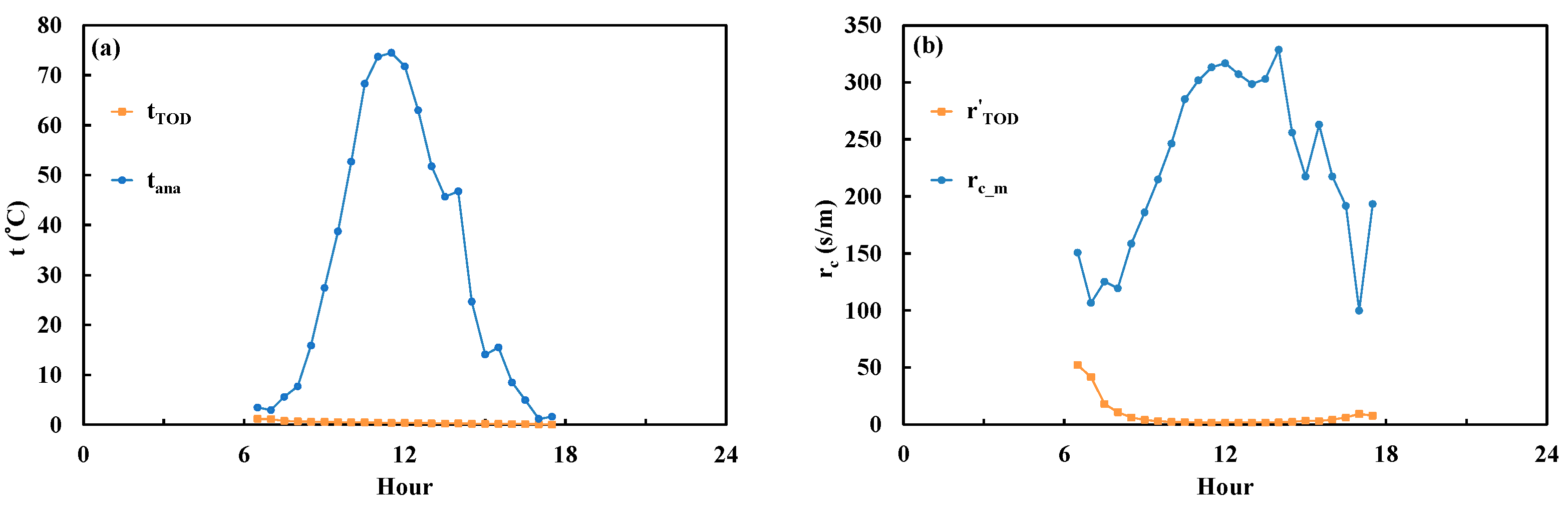
Figure 11.
Comparisons between (a) canopy temperature increase calculated by Todorovic’s expression (tTOD, Equation (6)) and the analytical solution (tana, Equation (16)); (b) pseudo resistance (r’TOD, calculated by Equation (17)) and measured canopy resistance (rc_m, calculated by Equation (3)) above Sitou forest.
Figure 11.
Comparisons between (a) canopy temperature increase calculated by Todorovic’s expression (tTOD, Equation (6)) and the analytical solution (tana, Equation (16)); (b) pseudo resistance (r’TOD, calculated by Equation (17)) and measured canopy resistance (rc_m, calculated by Equation (3)) above Sitou forest.
Table 1.
Summary of site features and instrumental heights.
Table 1.
Summary of site features and instrumental heights.
| Site | Dripsey Grassland | Chi-Lan Forest | Sitou Forest |
|---|
| Data period | 1 January 2013–31 December 2013 | 1 May 2005–30 April 2007 | 2 May 2009–31 July 2010 |
| Altitude (m) | 200 | 1650 | 1252 |
| Location | 51°59′ N, 8°46′ W | 24°35′ N, 121°30′ E | 23°39′ N, 120°47′ E |
| Annual rainfall (mm) | 1222.7 | 4000 | 2635 |
| Mean temperature (°C) | 9.6 | 13 | 16.6 |
| Mean humidity (%) | 86 | 91 | 89 |
| Canopy height (m) | 0.3 | 10.3 | 26 |
| Average Canopy resistance (s m−1) | 163.36 | 346.21 | 321.17 |
| Measurement height (m) | | | |
| Eddy-covariance system | 5 | 24 | 28 |
| Air temperature and humidity sensor | 2.5 | 23.6 | 27.5 |
| Net radiometer | 4 | 22.5 | 27.5 |
| Soil heat flux plate | −0.1 | −0.1 | −0.05 |
| Soil temperature sensor | −0.015, −0.05, −0.075 | −0.05 | −0.05 |
Table 2.
List of input factors used in the support vector machine model.
Table 2.
List of input factors used in the support vector machine model.
| Input Factors | Abbreviation | Definition |
|---|
| Time factor | JD | Julián day plus decimal time (converts 24 h in a day to a continuous value from 0 to 1) |
| Meteorological factors | Qn | available energy (W/m2) (=Rn–G) |
| | Ta | air temperature (°C) |
| | U | wind speed (m/s) |
| | D | vapor pressure deficit (hPa) |
Table 3.
Summary of linear regression between measured and model estimated canopy resistance (rc) and latent heat flux (LE) above Dripsey grassland. rc_SVM and rc_TOD denote the rc estimated by SVM and Todorovic’s method, respectively; LE_SVM_rc, LE_TOD_rc, and LE_avg_rc denote the estimated LE where the rc is from SVM, Todorovic’s method, and the average, respectively. RMSE: root mean square error.
Table 3.
Summary of linear regression between measured and model estimated canopy resistance (rc) and latent heat flux (LE) above Dripsey grassland. rc_SVM and rc_TOD denote the rc estimated by SVM and Todorovic’s method, respectively; LE_SVM_rc, LE_TOD_rc, and LE_avg_rc denote the estimated LE where the rc is from SVM, Todorovic’s method, and the average, respectively. RMSE: root mean square error.
| rc Model | Slope | Intercept | RMSE (s/m) | R2 | LE Model | Slope | Intercept | RMSE (W/m2) | R2 |
|---|
| rc_SVM | 1.72 | –79.19 | 165.49 | 0.22 | LE_SVM_rc | 1.02 | 1.27 | 25.87 | 0.88 |
| rc_TOD | 0.85 | 132.93 | 210.14 | 0.03 | LE_TOD_rc | 0.63 | 11.18 | 63.78 | 0.86 |
| Average rc = 163.36 (s/m) | LE_avg_rc | 0.94 | 10.76 | 30.71 | 0.83 |
Table 4.
Summary of linear regression between measured and model estimated canopy resistance (rc) and latent heat flux (LE) above Chi-Lan forest. rc_SVM and rc_TOD denote the rc estimated by SVM and Todorovic’s method, respectively; LE_SVM_rc, LE_TOD_rc, and LE_avg_rc denote the estimated LE where the rc is from SVM, Todorovic’s method, and the average, respectively. RMSE: root mean square error.
Table 4.
Summary of linear regression between measured and model estimated canopy resistance (rc) and latent heat flux (LE) above Chi-Lan forest. rc_SVM and rc_TOD denote the rc estimated by SVM and Todorovic’s method, respectively; LE_SVM_rc, LE_TOD_rc, and LE_avg_rc denote the estimated LE where the rc is from SVM, Todorovic’s method, and the average, respectively. RMSE: root mean square error.
| rc Model | Slope | Intercept | RMSE (s/m) | R2 | LE Model | Slope | Intercept | RMSE (W/m2) | R2 |
|---|
| rc_SVM | 0.71 | 67.67 | 248.32 | 0.13 | LE_SVM_rc | 1.03 | 19.90 | 57.39 | 0.46 |
| rc_TOD | –1.77 | 394.21 | 424.58 | 0.01 | LE_TOD_rc | 0.20 | 55.96 | 233.61 | 0.21 |
| Average rc = 346.21 (s/m) | LE_avg_rc | 0.91 | 28.10 | 59.13 | 0.41 |
Table 5.
Summary of linear regression between measured and model estimated canopy resistance (rc) and latent heat flux (LE) above Sitou forest. rc_SVM and rc_TOD denote the rc estimated by SVM and Todorovic’s method, respectively; LE_SVM_rc, LE_TOD_rc, and LE_avg_rc denote the estimated LE where the rc is from SVM, Todorovic’s method, and the average, respectively. RMSE: root mean square error.
Table 5.
Summary of linear regression between measured and model estimated canopy resistance (rc) and latent heat flux (LE) above Sitou forest. rc_SVM and rc_TOD denote the rc estimated by SVM and Todorovic’s method, respectively; LE_SVM_rc, LE_TOD_rc, and LE_avg_rc denote the estimated LE where the rc is from SVM, Todorovic’s method, and the average, respectively. RMSE: root mean square error.
| rc Model | Slope | Intercept | RMSE (s/m) | R2 | LE Model | Slope | Intercept | RMSE (W/m2) | R2 |
|---|
| rc_SVM | 0.94 | 88.73 | 150.19 | 0.14 | LE_SVM_rc | 1.07 | –5.51 | 33.74 | 0.64 |
| rc_TOD | 0.59 | 320.00 | 373.14 | 0.00 | LE_TOD_rc | 0.22 | 25.92 | 218.53 | 0.50 |
| Average rc = 321.17 (s/m) | LE_avg_rc | 0.86 | 16.54 | 37.33 | 0.58 |
Table 6.
Summary of linear regression between measured and model estimated canopy resistance (rc) and latent heat flux (LE) above Dripsey grassland for three different ranges (0–100, 100–200, and >200) of measured canopy resistance (rc_m). rc_SVM and rc_TOD denote the rc estimated by SVM and Todorovic’s method, respectively; LE_SVM_rc and LE_TOD_rc the estimated LE where the rc is from SVM and Todorovic’s method, respectively. RMSE: root mean square error; Int.: intercept.
Table 6.
Summary of linear regression between measured and model estimated canopy resistance (rc) and latent heat flux (LE) above Dripsey grassland for three different ranges (0–100, 100–200, and >200) of measured canopy resistance (rc_m). rc_SVM and rc_TOD denote the rc estimated by SVM and Todorovic’s method, respectively; LE_SVM_rc and LE_TOD_rc the estimated LE where the rc is from SVM and Todorovic’s method, respectively. RMSE: root mean square error; Int.: intercept.
| rc Range | High: rc_m = 0–100 (s/m) | Medium: rc_m = 100–200 (s/m) | Low: rc_m > 200 (s/m) |
|---|
| rc model | slope | Int. | RMSE | R2 | slope | Int. | RMSE | R2 | slope | Int. | RMSE | R2 |
| rc_SVM | –0.07 | 63.09 | 85.04 | 0.01 | 0.12 | 125.59 | 49.34 | 0.03 | 0.82 | 233.70 | 276.83 | 0.04 |
| rc_TOD | –0.07 | 56.80 | 42.52 | 0.01 | 0.03 | 141.92 | 111.27 | 0.00 | 1.18 | 308.98 | 369.12 | 0.06 |
| LE model | slope | Int. | RMSE | R2 | slope | Int. | RMSE | R2 | slope | Int. | RMSE | R2 |
| LE_SVM_rc | 1.25 | 2.94 | 27.25 | 0.96 | 1.09 | –5.43 | 21.59 | 0.94 | 0.87 | –6.60 | 27.66 | 0.92 |
| LE_TOD_ rc | 0.80 | 11.51 | 26.32 | 0.94 | 0.66 | 2.19 | 70.32 | 0.96 | 0.56 | –1.82 | 89.15 | 0.90 |
Table 7.
Summary of linear regression between measured and model estimated canopy resistance (rc) and latent heat flux (LE) above Chi-Lan forest for three different ranges (0–100, 100–200, and >200) of measured canopy resistance (rc_m). rc_SVM and rc_TOD denote the rc estimated by SVM and Todorovic’s method, respectively; LE_SVM_rc and LE_TOD_rc the estimated LE where the rc is from SVM and Todorovic’s method, respectively. RMSE: root mean square error; Int.: intercept.
Table 7.
Summary of linear regression between measured and model estimated canopy resistance (rc) and latent heat flux (LE) above Chi-Lan forest for three different ranges (0–100, 100–200, and >200) of measured canopy resistance (rc_m). rc_SVM and rc_TOD denote the rc estimated by SVM and Todorovic’s method, respectively; LE_SVM_rc and LE_TOD_rc the estimated LE where the rc is from SVM and Todorovic’s method, respectively. RMSE: root mean square error; Int.: intercept.
| rc Range | High: rc_m = 0–100 (s/m) | Medium: rc_m = 100–200 (s/m) | Low: rc_m > 200 (s/m) |
|---|
| rc model | slope | Int. | RMSE | R2 | slope | Int. | RMSE | R2 | slope | Int. | RMSE | R2 |
| rc_SVM | 0.03 | 38.65 | 261.90 | 0.01 | 0.03 | 141.47 | 205.17 | 0.01 | 0.36 | 342.02 | 255.00 | 0.05 |
| rc_TOD | –0.13 | 52.86 | 43.00 | 0.01 | –0.01 | 149.65 | 129.81 | 0.00 | –0.68 | 503.63 | 520.41 | 0.00 |
| LE model | slope | Int. | RMSE | R2 | slope | Int. | RMSE | R2 | slope | Int. | RMSE | R2 |
| LE_SVM_rc | 1.79 | 17.37 | 91.26 | 0.64 | 1.38 | 12.25 | 60.79 | 0.76 | 0.92 | 3.43 | 32.87 | 0.65 |
| LE_TOD_ rc | 0.75 | 21.13 | 55.48 | 0.83 | 0.46 | 29.27 | 132.06 | 0.83 | 0.21 | 22.96 | 279.33 | 0.45 |
Table 8.
Summary of linear regression between measured and model estimated canopy resistance (rc) and latent heat flux (LE) above Sitou forest for three different ranges (0–100, 100–200, and >200) of measured canopy resistance (rc_m). rc_SVM and rc_TOD denote the rc estimated by SVM and Todorovic’s method, respectively; LE_SVM_rc and LE_TOD_rc the estimated LE where the rc is from SVM and Todorovic’s method, respectively. RMSE: root mean square error; Int. intercept.
Table 8.
Summary of linear regression between measured and model estimated canopy resistance (rc) and latent heat flux (LE) above Sitou forest for three different ranges (0–100, 100–200, and >200) of measured canopy resistance (rc_m). rc_SVM and rc_TOD denote the rc estimated by SVM and Todorovic’s method, respectively; LE_SVM_rc and LE_TOD_rc the estimated LE where the rc is from SVM and Todorovic’s method, respectively. RMSE: root mean square error; Int. intercept.
| rc Range | High: rc_m = 0–100 (s/m) | Medium: rc_m = 100–200 (s/m) | Low: rc_m > 200 (s/m) |
|---|
| rc model | slope | Int. | RMSE | R2 | slope | Int. | RMSE | R2 | slope | Int. | RMSE | R2 |
| rc_SVM | 0.05 | 36.69 | 135.27 | 0.02 | 0.03 | 148.35 | 104.97 | 0.01 | 0.18 | 370.46 | 241.76 | 0.01 |
| rc_TOD | –0.17 | 51.10 | 41.65 | 0.02 | –0.14 | 158.75 | 128.79 | 0.01 | 1.11 | 387.56 | 431.50 | 0.02 |
| LE model | slope | Int. | RMSE | R2 | slope | Int. | RMSE | R2 | slope | Int. | RMSE | R2 |
| LE_SVM_rc | 1.87 | –10.39 | 50.62 | 0.89 | 1.75 | –28.25 | 42.43 | 0.88 | 1.05 | –15.70 | 26.15 | 0.77 |
| LE_TOD_ rc | 0.75 | 9.71 | 35.35 | 0.93 | 0.41 | 14.40 | 133.31 | 0.88 | 0.21 | 17.80 | 247.17 | 0.61 |