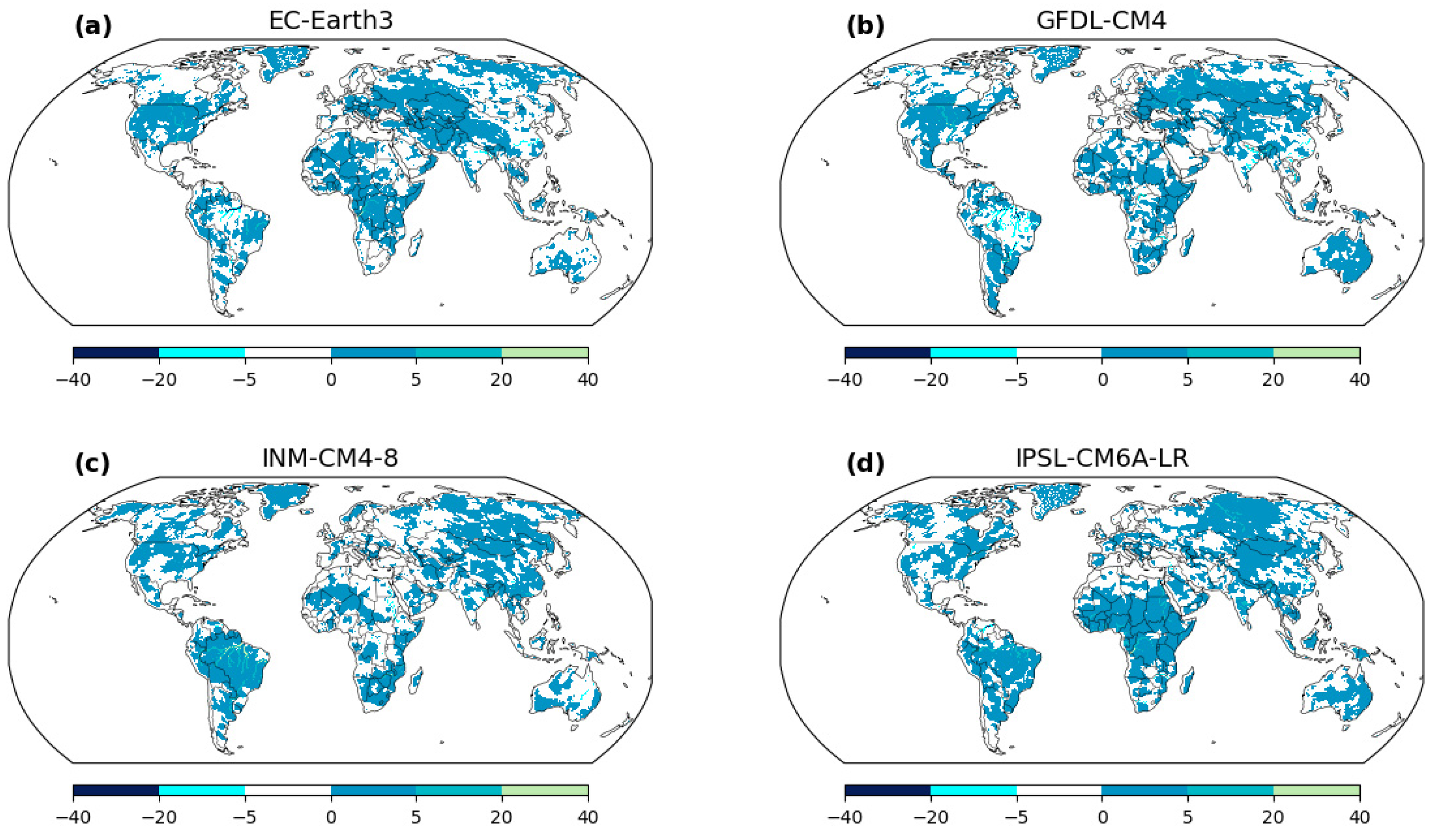
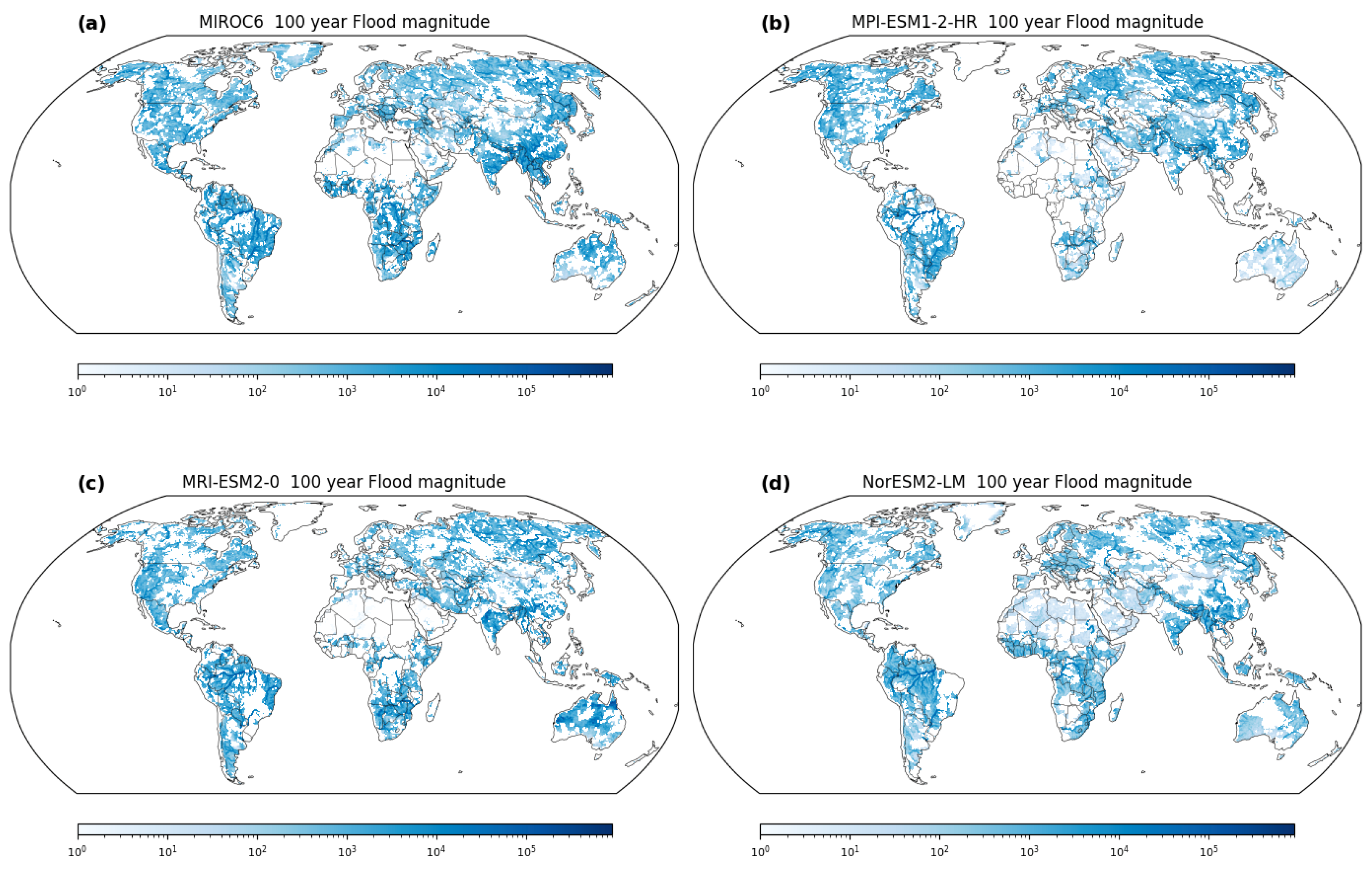
1. Introduction
Floods are among the most common natural devastating hazards with significant social and economic impacts worldwide [
1]. In the period between 1998 and 2017 alone, floods affected more than two billion people worldwide with approximately 11% fatalities (142,088 deaths) and a 23% economic loss (USD
$656 billion) [
2]. In recent years, we have observed that climate change has intensified the water cycle in many areas, changing rainfall characteristics and increasing flood frequency and magnitudes. The total of 176 flooding disasters in 2022 is slightly higher than the average from 2002 to 2021 (168), resulting in more than 2800 deaths and 3.3 billion dollars in economic losses [
3]. Future floods will likely be prone to greater magnitudes and occurrences due to climate change.
To minimize flood risks, accurate flood frequency analysis is essential, as it provides a basis for different flood risk measurements. The traditional approach to flood risk assessment relies on the assumption of stationarity, treating floods as independent and identically distributed over time. However, emerging evidence suggests that the characteristics of floods (e.g., frequency and magnitude) are subject to nonstationary changes due to shifts in climate patterns [
4,
5], land cover modifications [
6,
7], and both [
8]. As a result, there is widespread questioning regarding the validity of assuming time-invariant probability distributions (i.e., stationary methods) to estimate flood risks [
9,
10]. There is a need for new methods to better represent time-varying probability distributions and to assess the evolution of flood characteristics [
11,
12].
Nonstationary methods are proposed to estimate changes in the characteristics of flood extremes, including magnitudes, frequencies, durations, and intensities [
13,
14]. These approaches have the advantage of modeling changes in extreme event distributions based on explanatory variables such as time, climate variability, and land cover [
15,
16]. Many distributions (such as the Gumbel or Generalized Extreme Value distributions), are applied to annual/seasonal series of maximum discharge to estimate extreme floods [
17]. In contrast, the Generalized Additive Models for Location, Scale, and Shape (GAMLSS) framework has gained prominence [
18]. With GAMLSS, a wide range of distributions can be fitted to the response variable and distribution parameters can be modeled as smooth functions of time or other relevant covariates, resulting in a flexible and comprehensive analysis of nonstationary flood behaviors. It has become increasingly popular to use GAMLSS models as an alternative way to explain changes in design floods and flood magnitudes in relation to explanatory variables such as time, urbanization, and reservoir indices [
19,
20].
Application of nonstationary methods is used in both research and environmental management authorities, for instance in the design of engineering structures (such as dams, flood embankments, and bridges) [
21]. Using the probability distribution function, the frequency and magnitudes of different flood extremes can be linked. The T-year (e.g., 100-year) is usually regarded as the return period (or frequency), the value of the T-year flood (e.g., 100-year flood) is regarded as the return level (or magnitude). These flood extremes with given return periods can be estimated and used for setting safety standards and avoiding potential economic losses [
22]. However, despite these advancements, a comprehensive empirical assessment of nonstationarity in diverse flood extremes and its geographical variability across climate regions remains a notable research gap [
23,
24].
Furthermore, the availability of large ensembles of General Circulation Models (GCMs) offers new opportunities to simulate discharge and assess the nonstationary changes in flood magnitudes on a global scale [
25,
26]. These ensemble simulations provide valuable insights into future climate projections, allowing for the evaluation of flood risks under different climate scenarios. By integrating GCM-simulated discharge data with nonstationary methods, researchers can better understand the potential impacts of climate change on flood magnitudes and improve flood risk management strategies.
In the current study, our primary objective is to advance the field of nonstationary flood analysis by leveraging a substantial ensemble of GCMs and applying the GAMLSS framework to investigate global shifts in flood magnitudes. Our focus centers on generating a reference map that delineates the spatial suitability of stationary and nonstationary methods for extreme flood estimation. This reference map provides a comprehensive foundation for accurately estimating extreme flood events, accounting for the intricate interplay between geological characteristics, hydrological dynamics, and climatic variability. Additionally, we apply this reference map in estimating the 100-year flood magnitude to exemplify its practical utility. By scrutinizing the spatial distribution of suitable flood frequency analysis methodologies, we seek to enhance understanding of the nuances in hydrological behavior and provide a valuable tool for effective flood risk management and adaptation strategies.
In summary, our study aims to bridge the gap between climatic variability, hydrological dynamics, and flood estimation methodologies. The generated reference map serves as a powerful guide for methodological selection, harnessing the complexities of hydrological behavior to enhance the accuracy and reliability of extreme flood estimation. Amid the era of heightened climate uncertainty, the integration of adaptive methodologies and robust modeling practices remains paramount for effective flood risk assessment and management.
2. Materials and Methods
To simulate global river discharges and analyze flood extremes, we employed the Catchment-based Macro-scale Floodplain Model (CaMa-Flood) [
27]. This model is designed to simulate the behavior of river systems on a continental scale by discretizing global river networks into unit catchments. The key advantage of CaMa-Flood is its computational efficiency, enabling efficient flow computations and accurate flood diagnosis. In the CaMa-Flood model, the calculation of river flow and floodplain inundation occurs simultaneously within each unit catchment. By utilizing subgrid topographic parameters, water volume, water level, and flood extent can be determined. The model incorporates local inertial equations to accurately replicate backwater effects, which are crucial for precise simulations of inundated areas. Moreover, the adoption of bifurcated channels in CaMa-Flood enhances the accuracy of river flow simulations [
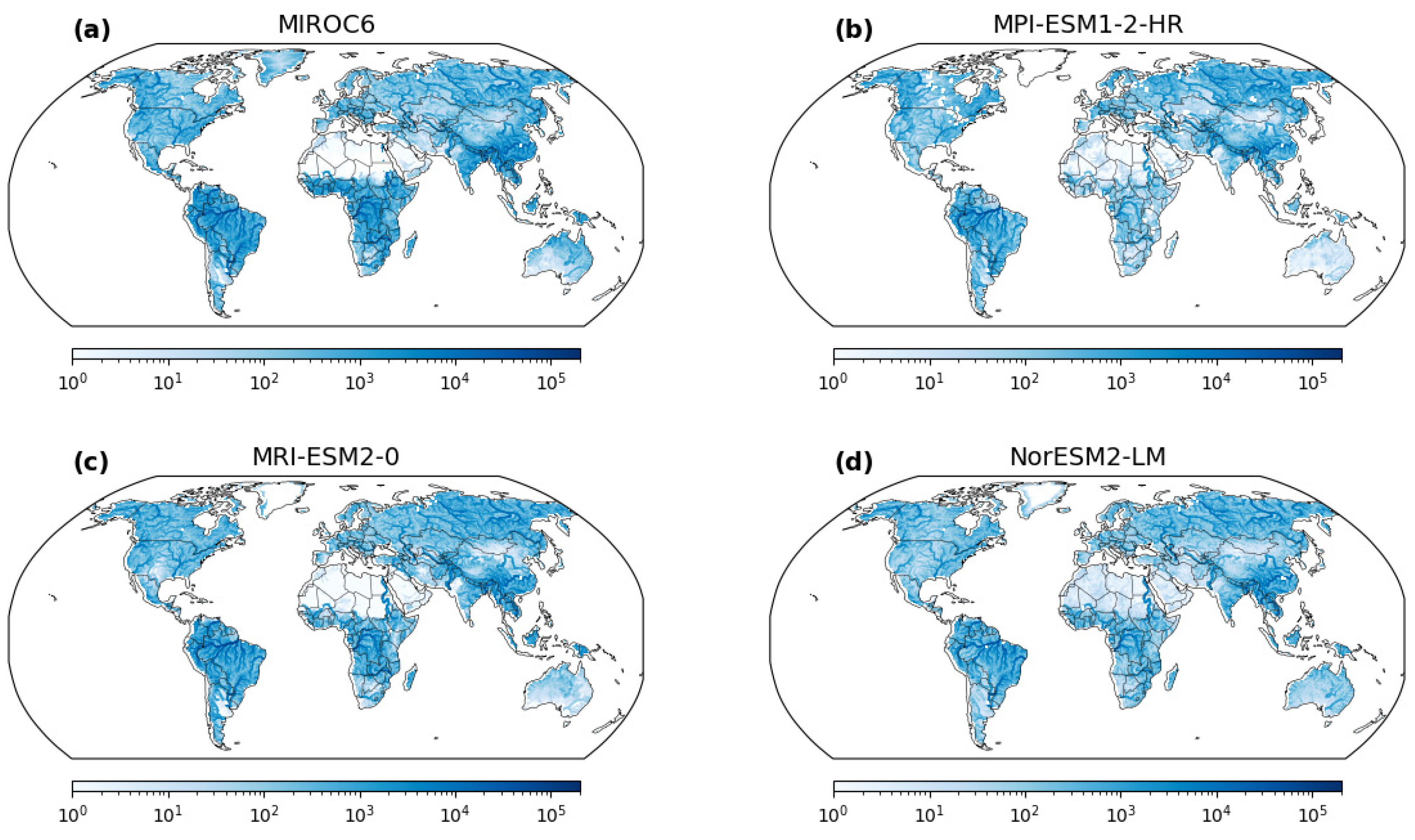
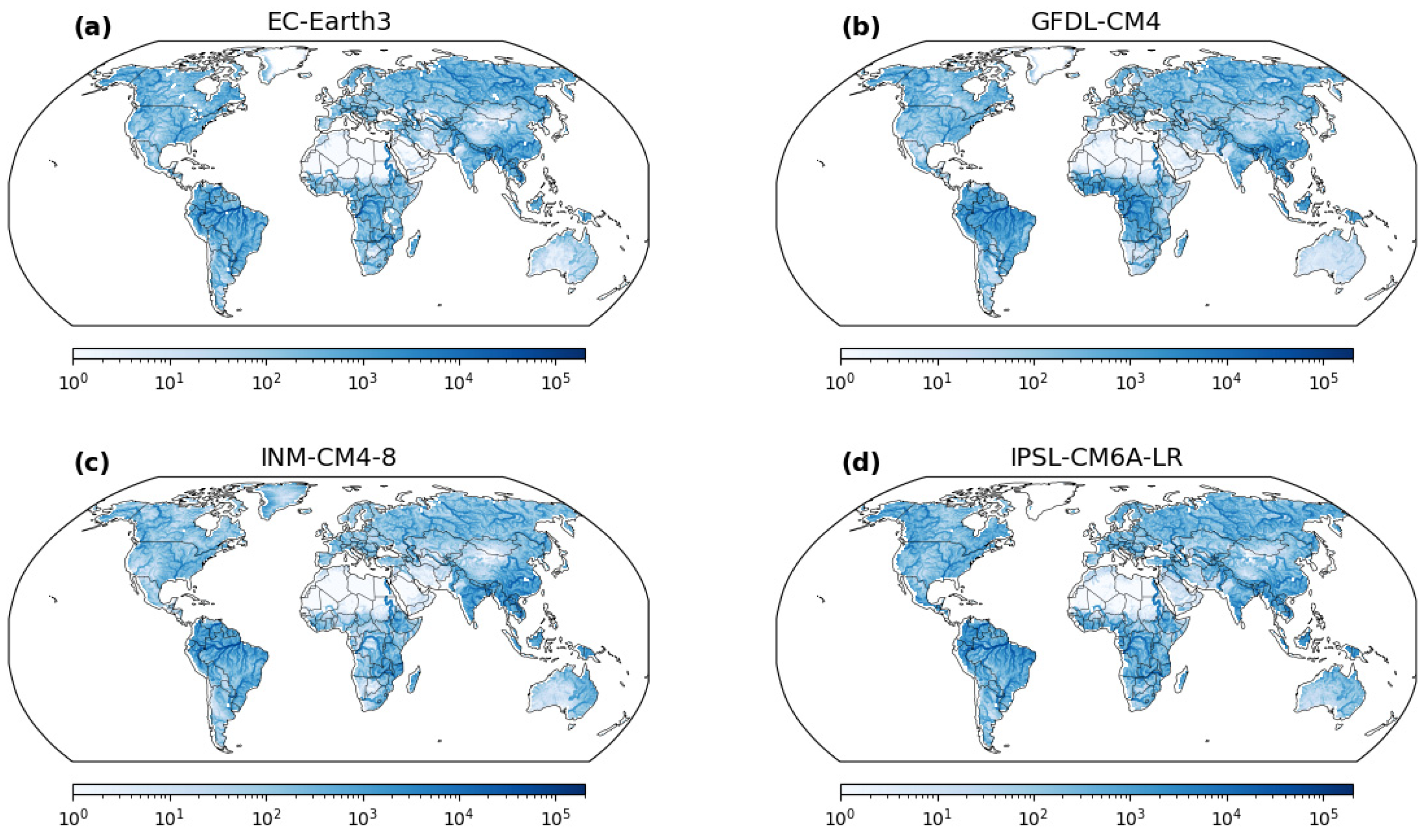
28]. To drive the CaMa-Flood model, we utilized runoff data obtained from General Circulation Models (GCMs) for the historical period from 1980 to 2014. Specifically, runoff data from nine GCMs, namely MIROC6, IPSL-CM6A-LR, GFDL-CM4, NorESM2-MM, ACCESS-CM2, INM-CM5-0, MPI-ESM1-2-HR, MRI-ESM2-0, and EC-Earth3, were analyzed in this study. Prior to inputting into the CaMa-Flood model, the GCM runoff data were converted from their original spatial resolution to 30 arcmin using bilinear interpolation. Consequently, the output of the CaMa-Flood model provided us with daily discharge data on a grid of 900 × 1440 cells (0.25°). Subsequently, data processing techniques were applied to extract the annual maximum discharge values for each grid cell.
To estimate extreme flood events under nonstationary scenarios, we employed the Generalized Additive Models for Location, Scale, and Shape (GAMLSS). The GAMLSS model is a widely used univariate distribution regression model that combines the Generalized Linear Model (GLM) and the Generalized Additive Model (GAM) approaches. In the GAMLSS framework, all the parameters of the assumed distribution for the response variable can be represented as additive functions of the explanatory variables. This modeling approach is particularly suitable when analyzing factors such as tails, variances, quantiles, skewness, and kurtosis, rather than solely focusing on the mean or location of the distribution. This is the formula of the GAMLSS model in vector form:
With the Generalized linear additive equation:
Based on the assumption that PDF types for hydrological sequences remain constant, such as Lognormal PDFs, the GAMLSS model has been extensively applied to study the relationship between covariates and PDF variability under climate change scenarios [
29,
30,
31,
32]. In our specific study, we applied the GAMLSS model to estimate flood return periods and magnitudes by utilizing three different distributions: Lognormal, Gamma, and Weibull. These distributions were chosen as they are commonly used to describe hydrological variables and capture the characteristics of extreme events.
The probability distribution function of Lognormal:
The probability distribution function of Gamma:
The probability distribution function of Weibull:
To conduct flood frequency analysis in this study, we utilized the GAMLSS package Version 5.4-12 in R, a statistical software environment. The analysis focused on exploring nonstationarity, considering time as the only covariate and location and scale parameters as covariate functions. Notably, the GAMLSS model employed linear covariate functions exclusively. In total, there were four combinations of covariate functions considered in the study (
Table 1). The first combination involved constant mean (μ) and constant scale (σ), representing a stationary model. The second combination featured a constant mean and time-varying scale, reflecting a nonstationary model. The third combination incorporated time-varying mean and constant scale, also representing a nonstationary model. Finally, the fourth combination involved time-varying mean and time-varying scale, representing another nonstationary model. Considering the inclusion of three distribution types (Lognormal, Gamma, and Weibull) and the aforementioned covariate function combinations, a total of nine combinations were evaluated within the GAMLSS model. The purpose of assessing these combinations was to select the most optimal distribution using the Bayesian Information Criterion (BIC). The BIC serves as a criterion for model selection, aiming to improve estimation accuracy. For the calculation of the 100-year flood, a nonstationary method with the lowest BIC value was consistently employed. This approach ensured that the most appropriate combination of distribution type and covariate functions was selected, enhancing the accuracy of estimating the extreme flood event with a long return period.
4. Discussion
4.1. GCMs Unveiling Spatial Suitability: Reference Map for Methodological Selection
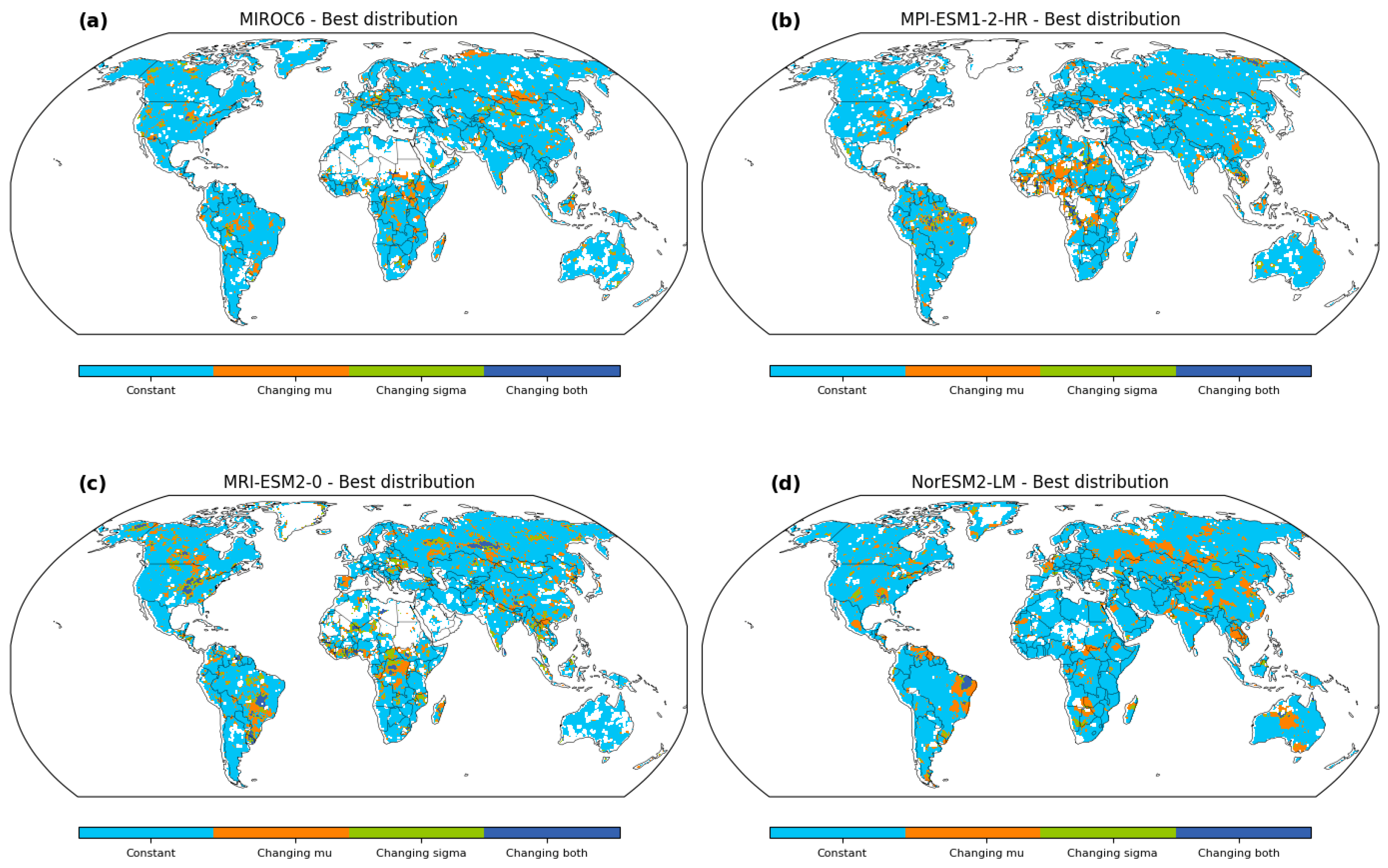
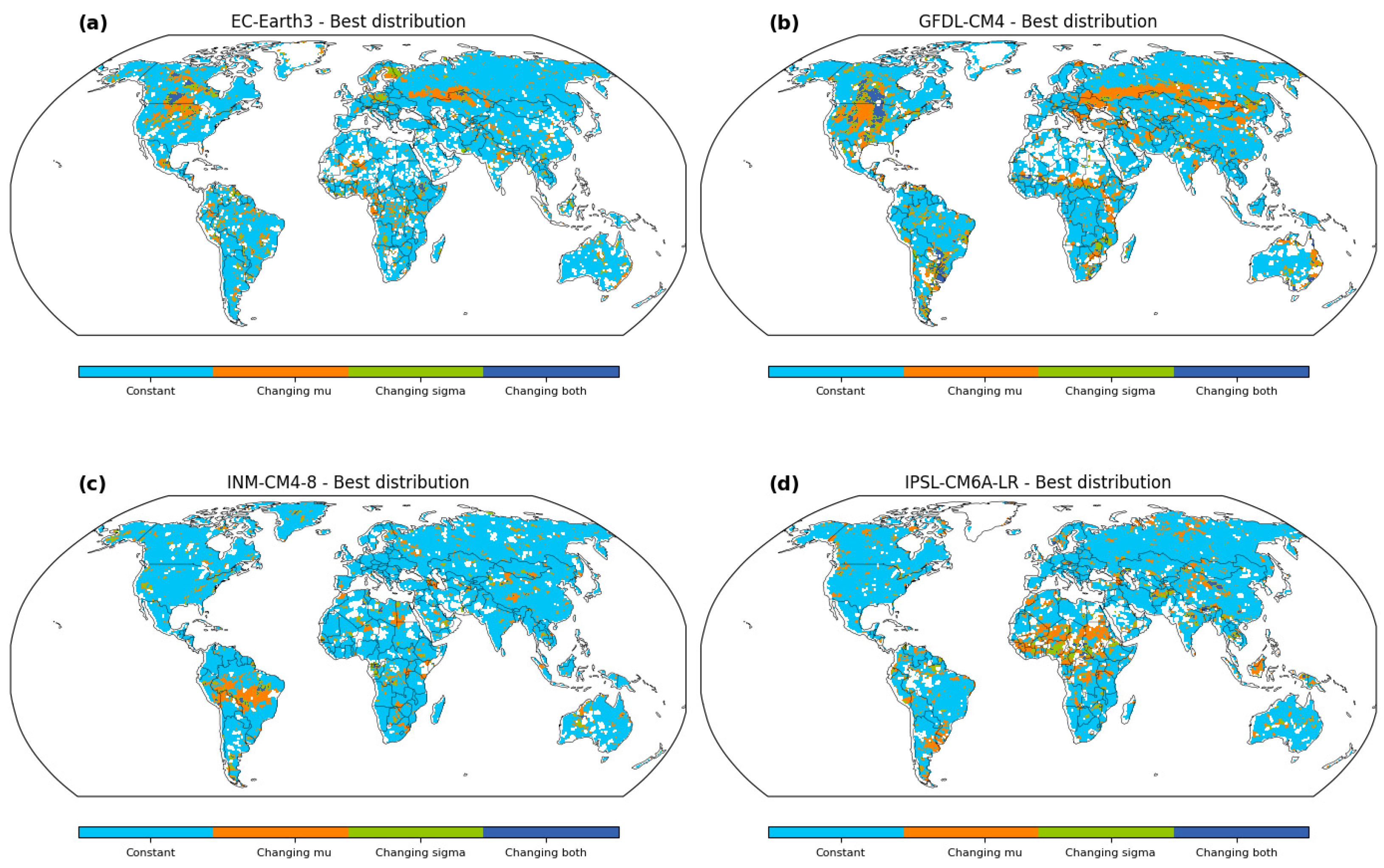
Our study introduces a pioneering approach to enhance flood risk assessment by constructing a reference map that delineates the spatial suitability of stationary and nonstationary methods. This map, as depicted in
Figure 6, encapsulates a wealth of information critical to flood estimation, making it an invaluable tool for policymakers, hydrologists, and decision makers. The delineation of regions where stationary methods prevail and areas where nonstationary approaches are imperative lays the foundation for a more refined and contextually appropriate flood analysis. The map’s spatial patterns are deeply rooted in the intricate interplay between geological characteristics, hydrological dynamics, and climatic variability. The regions favoring nonstationary methods, exemplified by changing mean (μ) or changing scale (σ) scenarios, underscore the underlying shifts in hydrological behavior [
33]. In contrast, the prevalence of stationary methods in more stable hydrological regimes reflects their adequacy for capturing long-term trends. This nuanced approach recognizes the inherent complexity of hydrological systems and provides a comprehensive basis for methodological selection.
The map provides valuable insights into the spatial distribution of suitable flood frequency analysis methodologies across the study area. Most regions are characterized by the constant distribution, representing the stationary method, where both the mean (μ) and scale (σ) parameters remain constant over time and space. This consistency indicates areas where the flood magnitudes exhibit relatively stable behavior, unaffected by significant temporal or spatial variations. In contrast, certain locations stand out with the changing μ distribution, which implies that the mean flood magnitude exhibits temporal variations. These regions experience dynamic hydrological conditions, and the flood events’ mean intensity varies over different time periods. These areas demand nonstationary approaches to account for these temporal fluctuations and obtain accurate flood estimations. Similarly, other areas exhibit the changing σ distribution, indicating spatial variations in flood variability while maintaining a constant mean flood magnitude. These regions may face altered flood characteristics due to factors such as land use changes, urbanization, or climate-induced alterations in precipitation patterns. Such changes in flood variability necessitate the application of nonstationary methods for precise flood estimations. Distinct GCM-output runoff datasets also lead to disparities in the estimated flood frequency. Certain regions are more compatible with changing μ in one GCM, while others exhibit changing σ in another GCM. This highlights the significance of understanding the nuances introduced by each GCM and its impact on flood frequency analysis. The identification of geological differences and GCM disparities in the best distribution is crucial for tailored flood risk management strategies. By accounting for spatial variations and considering the influence of different GCMs, decision makers and researchers can adopt suitable modeling approaches for each region, leading to more accurate estimations and improved flood risk preparedness.
4.2. Implications of Nonstationarity on Extreme Flood Estimation
The implications of our study transcend theoretical musings, manifesting tangibly in the realm of practical flood risk management [
34,
35,
36].
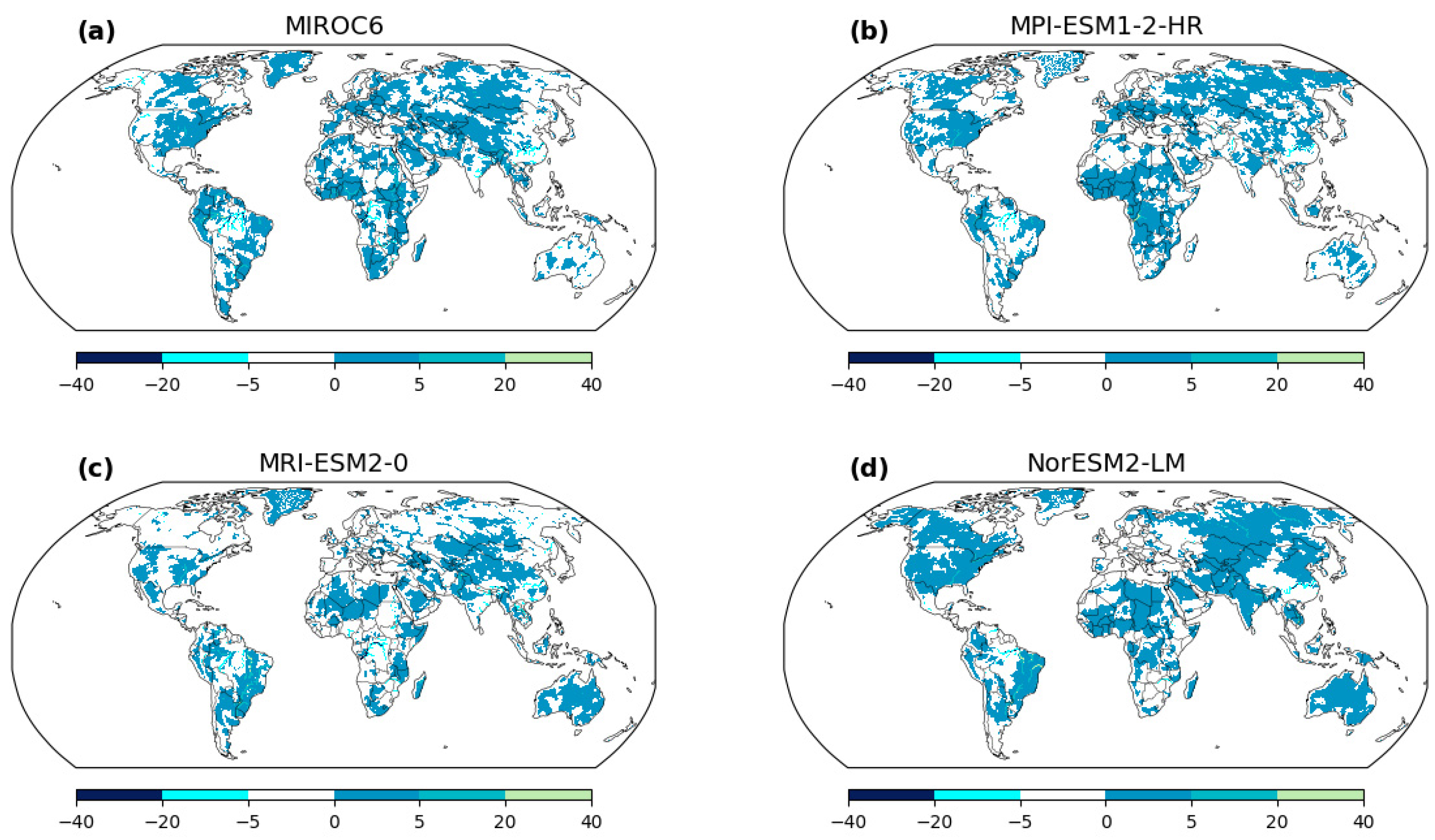
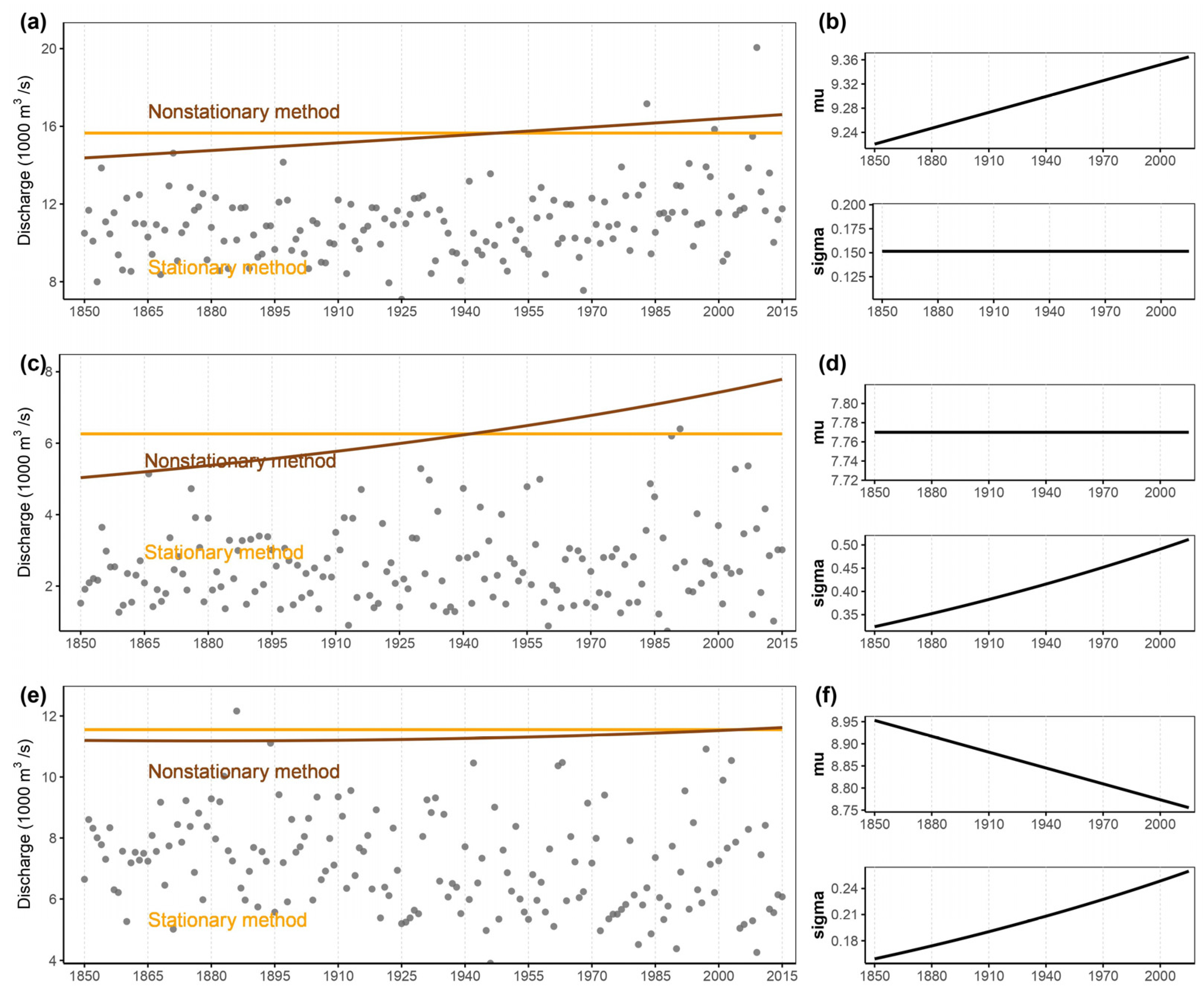
Figure 8 illuminates the stark divergence between stationary and nonstationary approaches, serving as a visual allegory for the consequential differences in extreme flood estimation. The scenarios of changing mean (μ) and changing scale (σ) underscore the intrinsic dynamism within hydrological systems, where flood magnitudes are not static entities but evolve over time. This realization underscores a paradigm shift in our understanding of extreme events, emphasizing the role of nonstationary methodologies as torchbearers of accurate estimation. A poignant message emanates from
Figure 8—the potential underestimation of extreme flood magnitudes by stationary methods. The inherent assumption of stationarity, rooted in historical data and temporal constancy, falls short in capturing the inherent variability introduced by changing climatic conditions. Such underestimations have profound implications for risk assessment and preparedness. The consequences of underestimating extreme flood magnitudes could be dire, resulting in inadequately designed infrastructure, ineffective floodplain management, and compromised disaster response strategies. Nonstationary methodologies emerge as the guiding light, providing a nuanced and comprehensive lens through which extreme flood events can be understood. By accounting for temporal and spatial variability, these approaches offer a realistic portrayal of the evolving hydrological landscape. This resonates deeply in the realm of policy formulation, where accurate estimations underpin effective decision making. Resilient infrastructure, adaptive land use planning, and robust emergency response mechanisms can only be realized by embracing the dynamic nature of hydrological systems—a realization underscored by the implications of nonstationary methodologies.
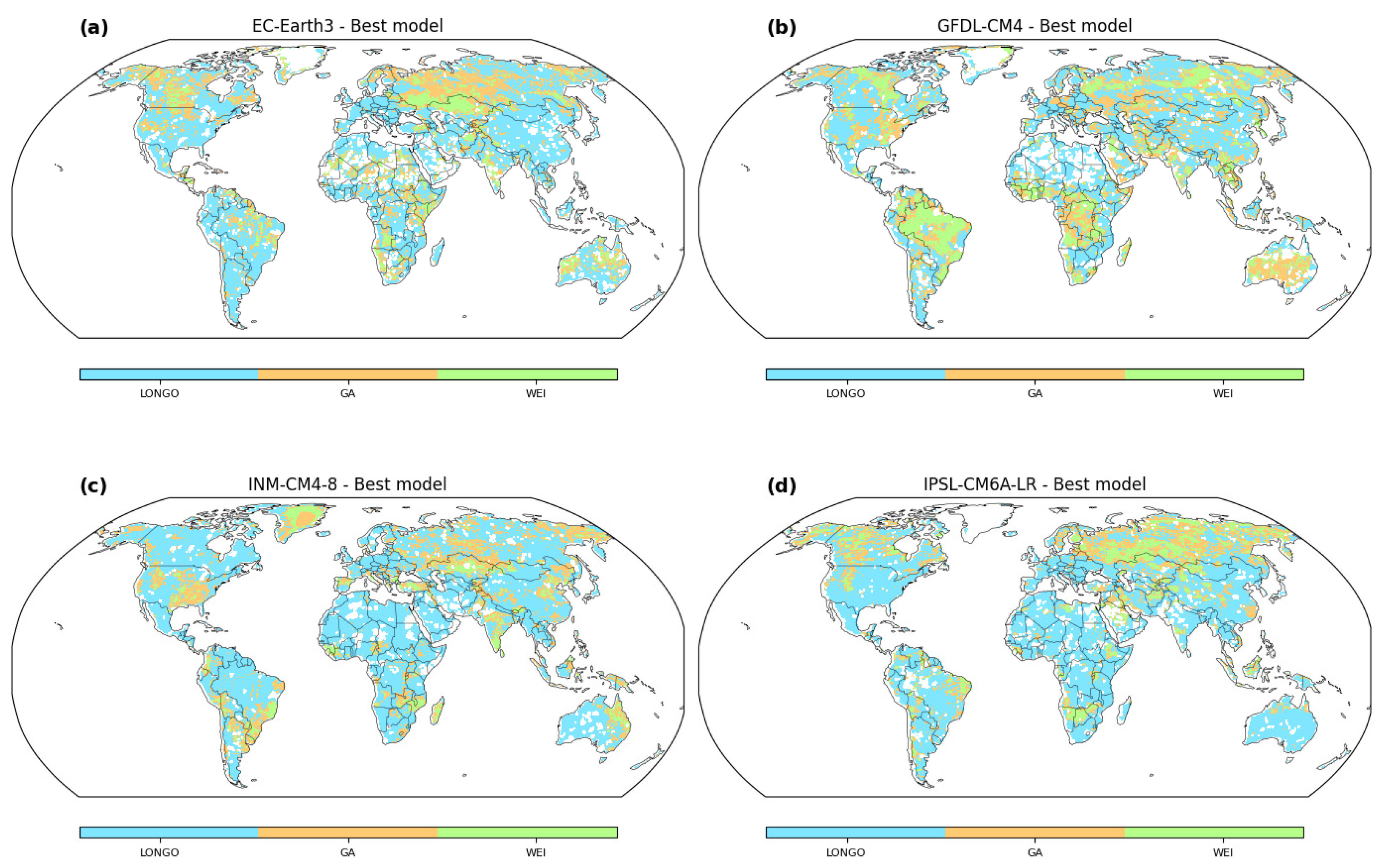
4.3. Navigating Uncertainty: GCMs and Model Selection
Our exploration of GCMs introduces a layer of uncertainty into the tapestry of flood estimation. The intricate interplay between GCMs and distribution models, highlighted by the disparities in model preferences across regions (
Figure 5), is a microcosm of the challenges inherent in climate and hydrological research. This uncertainty magnifies the importance of meticulous GCM evaluation, calibration, and validation. Accurate flood predictions hinge upon a nuanced understanding of the strengths and limitations of each GCM, illuminating a path towards robust modeling practices. The fusion of GCM characteristics with distribution model selection elucidates the multifaceted nature of climate–hydrology interactions. It beckons us to acknowledge the complexity of the climate system and its cascading influence on hydrological behavior. The impact transcends the realm of flood estimation, permeating diverse disciplines that rely on accurate climate projections. From agricultural planning to urban design, from water resource management to biodiversity conservation, the fidelity of climate models reverberates across societal and ecological domains. In navigating this sea of uncertainty, the onus lies upon researchers and stakeholders to collaboratively unravel the intricacies of GCMs. Rigorous scrutiny, ensemble modeling, and validation against real-world observations can chip away at the veil of uncertainty, enhancing the reliability of flood predictions. Beyond the immediate scope of hydrological research, this endeavor underscores the interconnectedness of disciplines under the umbrella of climate science.
4.4. Limitation and Future Research
While our research marks a significant step in improving flood risk assessment by introducing a reference map for methodological selection, several limitations warrant consideration. The use of Generalized Additive Models for Location, Scale, and Shape (GAMLSS) presents certain constraints, and future investigations could explore alternative statistical methods or hybrids for enhanced model selection. Additionally, the reference map’s resolution may not capture localized variations in hydrological behavior, suggesting a need for higher-resolution mapping. The choice of a 0.25-degree spatial resolution in our reference map was influenced by the availability of Global Climate Model (GCM) outputs. While this resolution serves the purpose of large-domain flood-related decision making, it is important to acknowledge that it may result in some underestimation of peak flow at smaller scales. Future research endeavors could explore the feasibility of employing higher resolutions, such as 0.01 degrees, for more localized studies, which could provide a more fine-grained representation of hydrological conditions. Looking ahead, the reference map offers a versatile platform for various lines of inquiry. Researchers can leverage this map to estimate extreme flood characteristics, encompassing flood magnitudes and inundation extents. Validation, a critical step, involves comparing model-derived estimates with historical flood events, field observations, or remote sensing data to ensure the reliability of our methodology. Furthermore, future research can delve into exploring the disparities between nonstationary and stationary methods for estimating extreme floods. This investigation can shed light on the contrasting performance of these methodologies and the implications for flood risk assessment. Additionally, there is ample scope for conducting flood analyses under climate change scenarios, utilizing the reference map as a foundation for understanding how evolving climatic conditions may impact future flood events. In summary, while the 0.25-degree spatial resolution was chosen due to GCM data constraints and the requirements of large-scale flood-related decision making, the potential exists for future research to employ higher resolutions for localized investigations. The reference map serves as a valuable resource for estimating and validating extreme flood events, exploring methodological disparities, and considering the influence of climate change on future flood scenarios.
5. Conclusions
Our study makes significant strides in advancing flood risk assessment by introducing a reference map that guides the selection of suitable methodologies for extreme flood estimation. The map encapsulates the spatial intricacies of hydrological behavior, unveiling the spatial divide between stationary and nonstationary methods. This novel approach, rooted in robust hydrological modeling and GCM data, provides a comprehensive framework for accurately estimating extreme flood events. As climate change intensifies, the need for adaptive and contextually tailored methodologies becomes ever more apparent. Our findings emphasize the inadequacy of static approaches and illuminate the potential of nonstationary methods to provide a more comprehensive understanding of evolving hydrological dynamics. The implications for flood risk management are profound, with direct relevance to infrastructure design, policy formulation, and disaster preparedness. In conclusion, our study bridges the gap between climatic variability, hydrological dynamics, and flood estimation methodologies. The reference map serves as a powerful tool to guide methodological selection, harnessing the intricate nuances of hydrological behavior to enhance the accuracy and reliability of extreme flood estimation. As we navigate an era of heightened climate uncertainty, the integration of adaptive methodologies and robust modeling practices remains paramount for effective flood risk assessment and management.