Investigating Soil Pore Network Connectivity in Varied Vegetation Types Using X-ray Tomography
Abstract
:1. Introduction
2. Materials and Methods
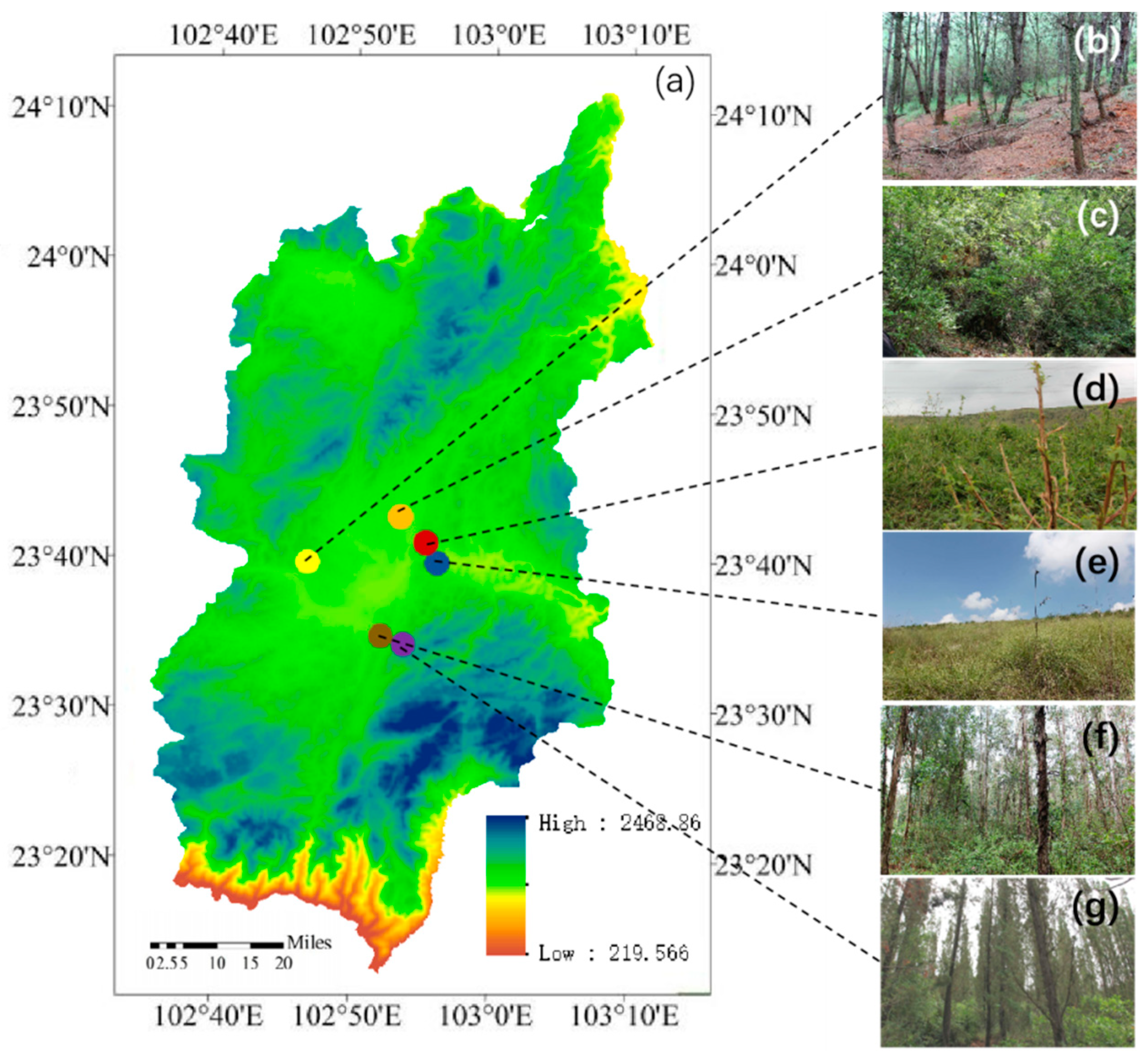
2.1. Study Site
2.2. Sample Plot Setting
2.2.1. Vegetation Survey
2.2.2. Soil Survey
2.3. Soil Column Collection and X-ray CT Scanning
2.4. Quantitative Description of 3D Soil Macropores
2.5. Water Penetration Simulation Test
3. Results
3.1. Spatial Structure Characteristics of Soil Pores
3.2. Quantitative Characteristics of Soil Pores
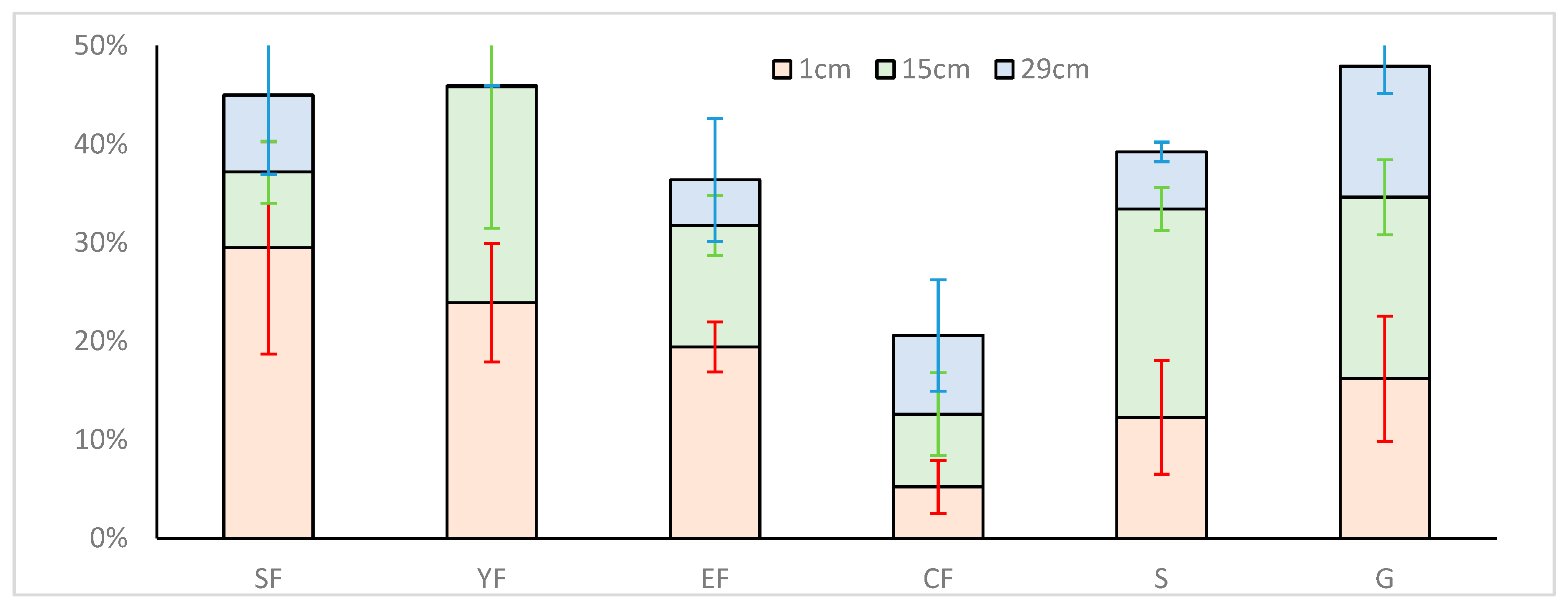
3.2.1. Volume and Quantity Proportion
3.2.2. Diameter and Surface
3.2.3. Curvature and Twist
3.2.4. Vertical Connectivity
3.3. Effect of Soil Porosity on Water Transport
3.4. Structural Equation Model (SEM) Analysis
4. Discussion
4.1. Soil Pore Morphology
4.2. Vertical Connectivity of Soil Pores
4.3. Contribution of Soil Pore Vertical Connectivity to Water Transport
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, H.; Li, D.J.; Xiao, K.C.; Wang, K. Soil microbial processes and resource limitation in karst and non-karst forests. Funct. Ecol. 2018, 32, 1400–1409. [Google Scholar] [CrossRef]
- Chen, H.; Hu, K.; Nie, Y. Analysis of soil water movement inside a footslope and a depression in a karst catchment, Southwest China. Sci. Rep. 2017, 7, 2544. [Google Scholar] [CrossRef] [PubMed]
- Kan, X.; Cheng, J.; Hou, F. Response of Preferential Soil Flow to Different Infiltration Rates and Vegetation Types in the Karst Region of Southwest China. Water 2020, 12, 1778. [Google Scholar] [CrossRef]
- Katharina, S.; Andrew, D.; Nico, E.; Kai, U. Depth-differentiated, multivariate control of biopore number under different land-use practices. Geoderma 2022, 418, 115852. [Google Scholar]
- Wand, S.; Li, R.; Sun, C. How Types of carbonate assemblages constrain the distribution of karst rocky desertification in Guizhou Province, P.R. China: Phenomena and mechanism. Land Degrad. Dev. 2004, 15, 123–131. [Google Scholar]
- Palmer, A. Origin and morphology of limestone caves. GSA Bull. 1991, 103, 1–21. [Google Scholar] [CrossRef]
- Karsanina, M.V.; Gerke, K.M.; Skvortsova, E.B.; Mallants, D. Universal spatial correlation functions for describing and reconstructing soil microstructure. PLoS ONE 2015, 10, e0126515. [Google Scholar] [CrossRef]
- Hallett, P.D.; Feeney, D.S.; Bengough, A.G.; Rillig, M.C.; Scrimgeour, C.M.; Young, I.M. Disentangling the impact of AM fungi versus roots on soil structure and water transport. Plant Soil 2009, 314, 183–196. [Google Scholar] [CrossRef]
- Zhang, Z.B.; Zhou, H.; Zhao, Q.G.; Peng, X. Characteristics of cracks in two paddy soils and their impacts on preferential flow. Geoderma 2014, 228, 114–121. [Google Scholar] [CrossRef]
- Köhne, J.M.; Köhne, S.; Šimůnek, J. A review of model applications for structured soils: a) Water flow and tracer transport. J. Contam. Hydrol. 2009, 104, 4–35. [Google Scholar] [CrossRef]
- Köhne, J.M.; Schlüter, S.; Vogel, H.J. Predicting solute transport in structured soil using pore network models. Vadose Zone J. 2011, 10, 1082–1096. [Google Scholar] [CrossRef]
- Batany, S.; Peyneau, P.E.; Lassabatère, L.; Béchet, B.; Faure, P.; Dangla, P. Interplay between Molecular Diffusion and Advection during Solute Transport in Macroporous Media. Vadose Zone J. 2019, 18, 1–15. [Google Scholar] [CrossRef]
- Jarvis, N. A review of non-equilibrium water flow and solute transport in soil macropores: Principles, controlling factors and consequences for water quality. Eur. J. Soil Sci. 2007, 58, 523–546. [Google Scholar] [CrossRef]
- Wang, C.; Wang, R.; Huo, Z.; Xie, E.; Dahlke, H.E. Colloid transport through soil and other porous media under transient flow conditions—A review. Wiley Interdiscip. Rev. Water 2020, 7, e1439. [Google Scholar] [CrossRef]
- Sander, T.; Gerke, H.H. Preferential flow patterns in paddy fields using a dye tracer. Vadose Zone J. 2007, 6, 105–115. [Google Scholar] [CrossRef]
- Jarvis, N.; Koestel, J.; Larsbo, M. Understanding preferential flow in the vadose zone: Recent advances and future prospects. Vadose Zone J. 2016, 15, 1–11. [Google Scholar] [CrossRef]
- Kaufmann, G. Modelling karst aquifer evolution in fractured, porous rocks. J. Hydrol. 2016, 543, 796–807. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, M.; Guo, X. Effects of topographic factors on runoff and soil loss in Southwest China. Catena 2018, 160, 394–402. [Google Scholar] [CrossRef]
- Guo, L.; Liu, Y.; Wu, G.L.; Huang, Z.; Cui, Z.; Cheng, Z.; Zhang, R.-Q.; Tian, F.-P.; He, H. Preferential water flow: Influence of alfalfa (Medicago sativa L.) decayed root channels on soil water infiltration. J. Hydrol. 2019, 578, 124019. [Google Scholar] [CrossRef]
- Meng, C.; Niu, J.Z.; Li, X.; Luo, Z.; Du, X.; Du, J.; Lin, X.; Yu, X. Quantifying soil macropore networks in different forest communities using industrial computed tomography in a mountainous area of North China. J. Soils Sediments 2017, 17, 2357–2370. [Google Scholar] [CrossRef]
- Meng, C.; Niu, J.; Yin, Z.; Luo, Z.; Lin, X.; Jia, J. Characteristics of rock fragments in different forest stony soil and its relationship with macropore characteristics in mountain area, northern China. J. Mt. Sci. 2018, 15, 519–531. [Google Scholar] [CrossRef]
- Perret, J.; Prasher, S.O.; Kantzas, A.; Langford, C. Three-dimensional quantification of macropore networks in undisturbed soil cores. Soil Sci. Soc. Am. J. 1999, 63, 1530–1543. [Google Scholar] [CrossRef]
- Noguchi, S.; Tsuboyama, Y.; Sidle, R.C.; Hosoda, I. Morphological characteristics of macropores and the distribution of preferential flow pathways in a forested slope segment. Soil Sci. Soc. Am. J. 1999, 63, 1413–1423. [Google Scholar] [CrossRef]
- Pierret, A.; Capowiez, Y.; Belzunces, L.; Moran, C.J. 3D reconstruction and quantification of macropores using X-ray computed tomography and image analysis. Geoderma 2002, 106, 247–271. [Google Scholar] [CrossRef]
- Mooney, S.J.; Korošak, D. Using complex networks to model two- and three-dimensional soil porous architecture. Soil Sci. Soc. Am. J. 2009, 73, 1094–1100. [Google Scholar] [CrossRef]
- Luo, L.; Lin, H.; Schmidt, J. Quantitative relationships between soil macropore characteristics and preferential flow and transport. Soil Sci. Soc. Am. J. 2010, 74, 1929–1937. [Google Scholar] [CrossRef]
- Nieber, J.L.; Sidle, R.C. How do disconnected macropores in sloping soils facilitate preferential flow? Hydrol. Process 2010, 24, 1582–1594. [Google Scholar] [CrossRef]
- Katuwal, S.; Norgaard, T.; Moldrup, P.; Lamandé, M.; Wildenschild, D.; de Jonge, L.W. Linking air and water transport in intact soils to macropore characteristics inferred from X-ray computed tomography. Geoderma 2015, 237, 9–20. [Google Scholar] [CrossRef]
- Hyväluoma, J.; Thapaliya, M.; Alaraudanjoki, J.; Sirén, T. Using microtomography, image analysis and flow simulations to characterize soil surface seals. Comput. Geosci. 2012, 48, 93–101. [Google Scholar] [CrossRef]
- Scheibe, T.D.; Perkins, W.A.; Richmond, M.C.; McKinley, M.I.; Romero-Gomez, P.D.J.; Oostrom, M.; Wietsma, T.W.; Serkowski, J.A.; Zachara, J.M. Pore-scale and multiscale numerical simulation of flow and transport in a laboratory-scale column. Water Resour. Res. 2015, 51, 1023–1035. [Google Scholar] [CrossRef]
- Francesco, A.; Petrucci, G.; Matzl, M.; Schneebeli, M.; De Michele, C. Early formation of preferential flow in a homogeneous snowpack observed by micro-CT. Water Resour. Res. 2017, 53, 3713–3729. [Google Scholar]
- Larsbo, M.; Koestel, J.; Jarvis, N. Relations between macropore network characteristics and the degree of preferential solute transport. Hydrol. Earth Syst. Sci. Discuss. 2014, 18, 5255–5269. [Google Scholar] [CrossRef]
- Jarvis, N.; Larsbo, M.; Koestel, J. Connectivity and percolation of structural pore networks in a cultivated silt loam soil quantified by X-ray tomography. Geoderma 2017, 287, 71–79. [Google Scholar] [CrossRef]
- Bottinelli, N.; Zhou, H.; Boivin, P.; Zhang, Z.; Jouquet, P.; Hartmann, C.; Peng, X. Macropores generated during shrinkage in two paddy soils using X-ray micro-computed tomography. Geoderma 2016, 265, 78–86. [Google Scholar] [CrossRef]
- Chen, X. Study on characteristics of preferential flow on four land use tupes in Simian Mountain of Chongqing. Beijing For. Univ. 2005, 19, 887–899. [Google Scholar]
- Kan, X.; Cheng, J.; Hu, X.; Zhu, F.; Li, M. Effects of Grass and Forests and the Infiltration Amount on Preferential Flow in Karst Regions of China. Water 2019, 11, 1634. [Google Scholar] [CrossRef]
- Angel, A.A.; Ingrid, P.; Raul, M.; Vesper, D.J.; Meeker, J.D.; Alshawabkeh, A.N. Estimating preferential flow in Karstic aquifers using statistical mixed Models. Ground Water 2014, 52, 584–596. [Google Scholar]
- Green, R.T.; Bertetti, F.T.; Miller, M.S. Focused groundwater flow in a carbonate aquifer in a semi-arid environment. J. Hydrol. 2014, 517, 284–297. [Google Scholar] [CrossRef]
- Yang, J.L.; Zhang, G.L. Water infiltration in urban soils and its effects on the quantity and quality of runoff. J. Soils Sediments 2011, 11, 751–761. [Google Scholar] [CrossRef]
- Dusek, J.; Vogel, T. Modeling subsurface hillslope runoff dominated by preferential flow: One- vs. two-dimensional approximation. Vadose Zone J. 2014, 13, 1–13. [Google Scholar] [CrossRef]
- Chen, X.; Cheng, J.; Zhang, H. Application of landscape pattern analysis to quantitatively evaluate the spatial structure characteristics of preferential flow paths in farmland. Appl. Eng. Agric. 2016, 32, 203–215. [Google Scholar]
- Kung, K.J.S. Preferential flow in a sandy vadose zone: 1. Field observation. Geoderma 1990, 46, 51–58. [Google Scholar] [CrossRef]
- McDonnell, J.J. A rationale for old water discharge through macropores in a steep, humid catchment. Water Resour. Res. 1990, 26, 2821–2832. [Google Scholar] [CrossRef]
- Peng, T.; Wang, S.J. Effects of land use, land cover and rainfall regimes on the surface runoff and soil loss on karst slopes in southwest China. Catena 2012, 90, 53–62. [Google Scholar] [CrossRef]
- Guo, L.; Lin, H. Addressing two bottlenecks to advance the understanding of preferential flow in soils. Adv. Agron. 2018, 147, 61–117. [Google Scholar]
- Collon, P.; Bernasconi, D.; Vuilleumier, C.; Renard, P. Statistical metrics for the characterization of karst network geometry and topology. Geomorphology 2017, 283, 122–142. [Google Scholar] [CrossRef]
- Lai, X.; Zhu, Q.; Michael, J.; Liao, K. Soil rock fragments: Unquantified players in terrestrial carbon and nitrogen cycles. Geoderma 2022, 406, 115530. [Google Scholar] [CrossRef]
- Kadyampakeni, D.M.; Nkedi-Kizza, P.; Leiva, J.A.; Muwamba, A.; Fletcher, E.; Morgan, K.T. Ammonium and nitrate transport during saturated and unsaturated water flow through sandy soils. J. Plant Nutr. Soil Sci. 2018, 181, 198–210. [Google Scholar] [CrossRef]
- Fishkis, O.; Noell, U.; Diehl, L.; Jaquemotte, J.; Lamparter, A.; Stange, C.; Burke, V.; Koeniger, P.; Stadler, S. Multitracer irrigation experiment for assessing the relevance of preferential flow for non-sorbing solute transport in agricultural soils. Geoderma 2019, 371, 114386. [Google Scholar] [CrossRef]




| Site | Arbor | Shrub | Herb | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Latin Name of Plant | Canopy Density | Relative Density | Latin Name of Plant | Coverage | Relative Density | Latin Name of Plant | Coverage | Relative Density | |
| SF | Quercus baronii Skan | 0.16 | 0.15 | Campylotropis polyantha | 0.06 | 0.24 | Asparagus cochinchinensis (Lour.) Merr | 0.06 | 0.18 |
| Rhamnus leptophylla Schneid. | 0.14 | 0.15 | Osteomeles anthyllidifolia Lindl. | 0.08 | 0.29 | Arundinella setosa | 0.03 | 0.09 | |
| Pittosporum brevicalyx (Oliv.) Gagnep. | 0.19 | 0.23 | Pistacia weinmannifolia J. Poisson ex Franch. | 0.03 | 0.12 | Themeda triandra Forsk. Var. Japonica (Willd.) Makino | 0.09 | 0.27 | |
| Pistacia chinensis Bunge | 0.03 | 0.08 | Carissa spinarum | 0.09 | 0.35 | Dioscorea arachidna Prain et Burkill | 0.05 | 0.14 | |
| Crataegus cuneata | 0.17 | 0.31 | Pistacia chinensis Bunge | 0.03 | 0.09 | ||||
| Albizia bracteata Dunn | 0.06 | 0.08 | Arundinella anomala. | 0.06 | 0.18 | ||||
| Heteropogon Pers. | 0.02 | 0.05 | |||||||
| YF | Pinus yunnanensis Franch. | 0.72 | 1 | Myrsine africana Linn. | 0.08 | 0.45 | Arundinella setosa Trin. | 0.05 | 0.50 |
| Dodonaea viscosa (L.) Jacq. | 0.06 | 0.36 | Capillipedium assimile (Steud) A. Camus | 0.02 | 0.17 | ||||
| Smilax China L. | 0.03 | 0.18 | Heteropogon Pers. | 0.03 | 0.33 | ||||
| EF | Eucalyptus maideni F. V. Muell. | 0.8 | 1 | Dodonaea viscosa L. | 0.11 | 0.39 | Rubia cordifolia L. | 0.06 | 0.50 |
| Myrsine africana Linn. | 0.06 | 0.22 | Asparagus cochinchinensis (Lour.) Merr | 0.03 | 0.25 | ||||
| Carissa spinarum | 0.11 | 0.39 | Arundinella setosa | 0.03 | 0.25 | ||||
| CF | Platycladus orientalis(L.)Francoptmxjjkmsc | 0.65 | 1 | Passiflora wilsonii | 0.08 | 0.26 | Dioscorea arachidna Prain et Burkill | 0.05 | 0.25 |
| Phyllanthus emblica Linn. | 0.06 | 0.21 | Pistacia chinensis Bunge | 0.03 | 0.17 | ||||
| Carissa spinarum | 0.16 | 0.53 | Themeda triandra Forsk. Var. Japonica (Willd.) Makino | 0.05 | 0.25 | ||||
| Dioscorea arachidna Prain et Burkill | 0.06 | 0.33 | |||||||
| S | Dodonaea viscosa L. | 0.85 | 1 | Bidens pilosa L. | 0.17 | 0.44 | |||
| Asparagus cochinchinensis(Lour.) Merr | 0.06 | 0.16 | |||||||
| Arundinella setosa | 0.11 | 0.28 | |||||||
| Themeda triandra Forsk. Var. Japonica (Willd.) Makino | 0.03 | 0.08 | |||||||
| Dioscorea arachidna Prain et Burkill | 0.02 | 0.04 | |||||||
| G | - | - | - | - | - | - | Themeda triandra Forsk. var. japonica (Willd.) Makino | 1 | 1 |
| Forest Type | Soil Depth (cm) | Altitude (m.a.s.l.) | Latitude (N) | Longitude (E) | Slope (°) | Soil Bulk Density (g·cm−3) | Sand Content (%) | Silt Particles Content (%) | Clay Content (%) | Organic Carbon Content (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| SF | 0–10 | 1370 | 23°43′53″–23°43′57″ | 102°54′52″–102°54′57″ | 7.00 ± 1.00 | 1.20 ± 0.21 | 1.23 ± 0.61 | 20.57 ± 3.85 | 77.34 ± 3.32 | 3.01 ± 1.02 |
| 10–20 | 1.23 ± 0.19 | 0.72 ± 0.27 | 21.84 ± 5.79 | 77.44 ± 6.29 | 1.59 ± 1.10 | |||||
| 20–30 | 1.18 ± 0.22 | 0.53 ± 0.38 | 22.17 ± 5.12 | 77.30 ± 5.77 | 1.34 ± 0.57 | |||||
| YF | 0–10 | 1530 | 23°40′10″–23°40′15″ | 102°46′41″–102°46′46″ | 1.50 ± 0.50 | 1.13 ± 0.08 | 67.56 ± 18.34 | 31.04 ± 8.97 | 1.40 ± 1.15 | 2.05 ± 0.98 |
| 10–20 | 1.19 ± 0.11 | 31.21 ± 17.57 | 35.79 ± 9.93 | 33.11 ± 18.36 | 2.32 ± 0.85 | |||||
| 20–30 | 1.15 ± 0.06 | 19.19 ± 11.32 | 39.18 ± 13.21 | 41.63 ± 21.41 | 2.31 ± 0.33 | |||||
| EF | 0–10 | 1370 | 23°37′20″–23°37′24″ | 102°54′13″–102°54′25″ | 3.50 ± 0.50 | 1.17 ± 0.13 | 2.82 ± 0.32 | 26.86 ± 7.06 | 70.32 ± 9.27 | 2.35 ± 1.11 |
| 10–20 | 1.10 ± 0.08 | 2.53 ± 0.33 | 29.75 ± 6.58 | 67.72 ± 9.33 | 3.54 ± 1.04 | |||||
| 20–30 | 1.11 ± 0.15 | 2.47 ± 0.41 | 42.93 ± 9.41 | 54.60 ± 18.16 | 3.31 ± 1.15 | |||||
| CF | 0–10 | 1370 | 23°37′13″–23°37′20″ | 102°53′48″–102°53′56″ | 1.50 ± 0.50 | 1.07 ± 0.14 | 9.86 ± 5.77 | 26.54 ± 13.24 | 63.60 ± 10.02 | 0.31 ± 0.17 |
| 10–20 | 1.10 ± 0.11 | 6.89 ± 5.01 | 24.11 ± 7.78 | 69.00 ± 11.34 | 0.98 ± 0.34 | |||||
| 20–30 | 1.12 ± 0.16 | 0.37 ± 0.12 | 14.48 ± 7.35 | 85.15 ± 15.77 | 0.60 ± 0.26 | |||||
| S | 0–10 | 1510 | 23°40′10″–23°40′15″ | 102°56′37″–102°56′44″ | 2.00 ± 0.50 | 1.14 ± 0.10 | 3.29 ± 1.23 | 61.77 ± 31.52 | 34.94 ± 18.07 | 1.45 ± 0.89 |
| 10–20 | 1.19 ± 0.27 | 2.45 ± 1.11 | 78.13 ± 34.68 | 28.16 ± 17.75 | 0.49 ± 0.15 | |||||
| 20–30 | 1.20 ± 0.15 | 1.90 ± 1.13 | 84.86 ± 30.07 | 13.24 ± 11.29 | 0.35 ± 0.11 | |||||
| G | 0–10 | 1510 | 23°41′40″–23°41′45″ | 102°56′42″–102°56′52″ | 10.00 ± 0.50 | 1.25 ± 0.33 | 1.63 ± 1.12 | 35.69 ± 17.56 | 62.68 ± 24.33 | 3.15 ± 1.59 |
| 10–20 | 1.25 ± 0.12 | 1.77 ± 1.24 | 42.86 ± 19.85 | 55.37 ± 21.06 | 0.86 ± 0.63 | |||||
| 20–30 | 1.11 ± 0.21 | 2.94 ± 1.33 | 74.39 ± 13.49 | 22.67 ± 17.09 | 3.01 ± 0.99 |
| Site | Average Diameter/mm | Total Volume of Macropores/(104 mm3) | Total Surface Area of Macropores/(104 mm2) |
|---|---|---|---|
| SF-1 | 1.26 ± 0.03 | 20.97 ± 1.31 | 11.65 ± 2.79 |
| SF-2 | 1.18 ± 0.01 | 25.16 ± 2.18 | 17.76 ± 3.61 |
| SF-3 | 1.24 ± 0.01 | 33.26 ± 1.28 | 20.43 ± 2.24 |
| YF-1 | 1.17 ± 0.04 | 16.65 ± 1.09 | 11.34 ± 1.17 |
| YF-2 | 1.23 ± 0.02 | 14.69 ± 0.29 | 6.33 ± 0.73 |
| YF-3 | 1.21 ± 0.01 | 17.29 ± 0.31 | 6.55 ± 1.04 |
| EF-1 | 1.15 ± 0.03 | 51.65 ± 1.41 | 37.55 ± 2.79 |
| EF-2 | 1.23 ± 0.01 | 40.05 ± 1.37 | 20.38 ± 1.95 |
| EF-3 | 1.25 ± 0.01 | 18.46 ± 0.24 | 10.99 ± 1.10 |
| CF-1 | 1.27 ± 0.01 | 15.41 ± 0.34 | 9.03 ± 2.11 |
| CF-2 | 1.19 ± 0.01 | 16.42 ± 0.21 | 14.06 ± 1.55 |
| CF-3 | 1.20 ± 0.01 | 24.17 ± 0.17 | 18.34 ± 1.08 |
| S-1 | 1.20 ± 0.01 | 16.28 ± 0.79 | 13.71 ± 2.32 |
| S-2 | 1.14 ± 0.05 | 12.68 ± 1.47 | 5.90 ± 1.93 |
| S-3 | 1.21 ± 0.01 | 21.04 ± 2.89 | 8.82 ± 3.03 |
| G-1 | 1.19 ± 0.01 | 32.14 ± 2.07 | 24.37 ± 2.36 |
| G-2 | 1.23 ± 0.01 | 29.46 ± 0.79 | 20.36 ± 1.99 |
| G-3 | 1.23 ± 0.03 | 33.75 ± 1.02 | 25.46 ± 2.01 |
| Site | Pore Tortuosity/(°) | Pore Cumulative Distortion/(°) | Site | Pore Tortuosity/(°) | Pore Cumulative Distortion/(°) |
|---|---|---|---|---|---|
| SF-1 | 0.55 ± 0.15 | 149.15 ± 23.78 | CF-1 | 0.48 ± 0.12 | 183.91 ± 28.11 |
| SF-2 | 0.53 ± 0.49 | 156.30 ± 44.30 | CF-2 | 0.62 ± 0.07 | 158.31 ± 22.43 |
| SF-3 | 0.86 ± 0.39 | 100.41 ± 17.04 | CF-3 | 0.55 ± 0.14 | 129.60 ± 33.01 |
| YF-1 | 0.53 ± 0.06 | 169.85 ± 13.99 | S-1 | 0.53 ± 0.15 | 138.53 ± 15.80 |
| YF-2 | 0.45 ± 0.08 | 188.61 ± 10.23 | S-2 | 0.53 ± 0.03 | 174.64 ± 51.33 |
| YF-3 | 0.52 ± 0.11 | 174.74 ± 21.02 | S-3 | 0.51 ± 0.11 | 131.29 ± 40.00 |
| EF-1 | 0.56 ± 0.04 | 138.54 ± 37.49 | G-1 | 0.59 ± 0.35 | 135.39 ± 69.74 |
| EF-2 | 0.47 ± 0.01 | 131.36 ± 45.51 | G-2 | 0.55 ± 0.24 | 150.88 ± 44.32 |
| EF-3 | 0.51 ± 0.05 | 145.49 ± 39.09 | G-3 | 0.58 ± 0.31 | 129.30 ± 56.88 |
| Site | Initial Moisture Conductivity (μs/cm) | Add Water after Saturation * | Add 25 ms/cm NaCl Solution 2000 mL | Add Water after Saturation | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Total Time (min) | Average Water Transport Velocity (mL/min) | Average Change Rate of Conductivity (μs.cm−1/min) | Total Time (min) | Average Water Transport Velocity (mL/min) | Average Change Rate of Conductivity (μs.cm−1/min) | Total Time (min) | Average Water Transport Velocity (mL/min) | Average Change Rate of Conductivity (μs.cm−1/min) | ||
| SF | 303.83 ± 59.20 | 217.00 ± 292.04 | 107.98 ± 66.67 | 311.17 ± 39.93 | 371.00 ± 501.34 | 85.06 ± 45.63 | 18,412.65 ± 417.50 | 1078.00 ± 1316.64 | 30.42 ± 10.84 | 1970.17 ± 33.49 |
| YF | 337.60 ± 4.13 | 229.00 ± 157.19 | 64.18 ± 69.18 | 314.49 ± 15.83 | 253.67 ± 171.64 | 57.89 ± 49.59 | 17,385.36 ± 1116.32 | 1912.00 ± 1277.56 | 34.64 ± 6.68 | 1813.72 ± 108.81 |
| EF | 333.87 ± 44.37 | 465.67 ± 463.18 | 61.76 ± 71.74 | 339.58 ± 44.58 | 617.67 ± 638.03 | 57.49 ± 49.32 | 13,928.80 ± 7386.19 | 1915.00 ± 1277.56 | 28.70 ± 13.37 | 2715.49 ± 1650.25 |
| CF | 334.50 ± 54.71 | 640.00 ± 269.81 | 12.43 ± 5.26 | 313.34 ± 61.38 | 883.33 ± 436.07 | 20.93 ± 1.90 | 11,785.06 ± 6264.83 | 2890.00 ± 63.77 | 17.59 ± 4.69 | 304.54 ± 1781.76 |
| S | 343.67 ± 57.81 | 299.00 ± 215.47 | 61.69 ± 62.60 | 315.30 ± 61.10 | 432.67 ± 357.27 | 52.14 ± 41.62 | 16,145.22 ± 4137.98 | 1813.33 ± 1183.51 | 26.66 ± 7.47 | 1739.98 ± 212.75 |
| G | 322.67 ± 36.00 | 114.00 ± 138.61 | 107.19 ± 64.65 | 327.08 ± 37.39 | 132.67 ± 160.75 | 82.55 ± 42.06 | 17,700.44 ± 1516.12 | 1041.67 ± 1229.20 | 33.62 ± 2.87 | 1850.61 ± 202.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kan, X.; Zheng, W.; Cheng, J.; Zhangzhong, L.; Li, J.; Liu, B.; Zhang, X. Investigating Soil Pore Network Connectivity in Varied Vegetation Types Using X-ray Tomography. Water 2023, 15, 3823. https://doi.org/10.3390/w15213823
Kan X, Zheng W, Cheng J, Zhangzhong L, Li J, Liu B, Zhang X. Investigating Soil Pore Network Connectivity in Varied Vegetation Types Using X-ray Tomography. Water. 2023; 15(21):3823. https://doi.org/10.3390/w15213823
Chicago/Turabian StyleKan, Xiaoqing, Wengang Zheng, Jinhua Cheng, Lili Zhangzhong, Jing Li, Binchang Liu, and Xin Zhang. 2023. "Investigating Soil Pore Network Connectivity in Varied Vegetation Types Using X-ray Tomography" Water 15, no. 21: 3823. https://doi.org/10.3390/w15213823
APA StyleKan, X., Zheng, W., Cheng, J., Zhangzhong, L., Li, J., Liu, B., & Zhang, X. (2023). Investigating Soil Pore Network Connectivity in Varied Vegetation Types Using X-ray Tomography. Water, 15(21), 3823. https://doi.org/10.3390/w15213823






