Ungauged Basin Flood Prediction Using Long Short-Term Memory and Unstructured Social Media Data
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Data
2.2.1. Observation Data
2.2.2. Flow Rate from the Hec-1 Model
2.2.3. Social Media Data
3. Methodology
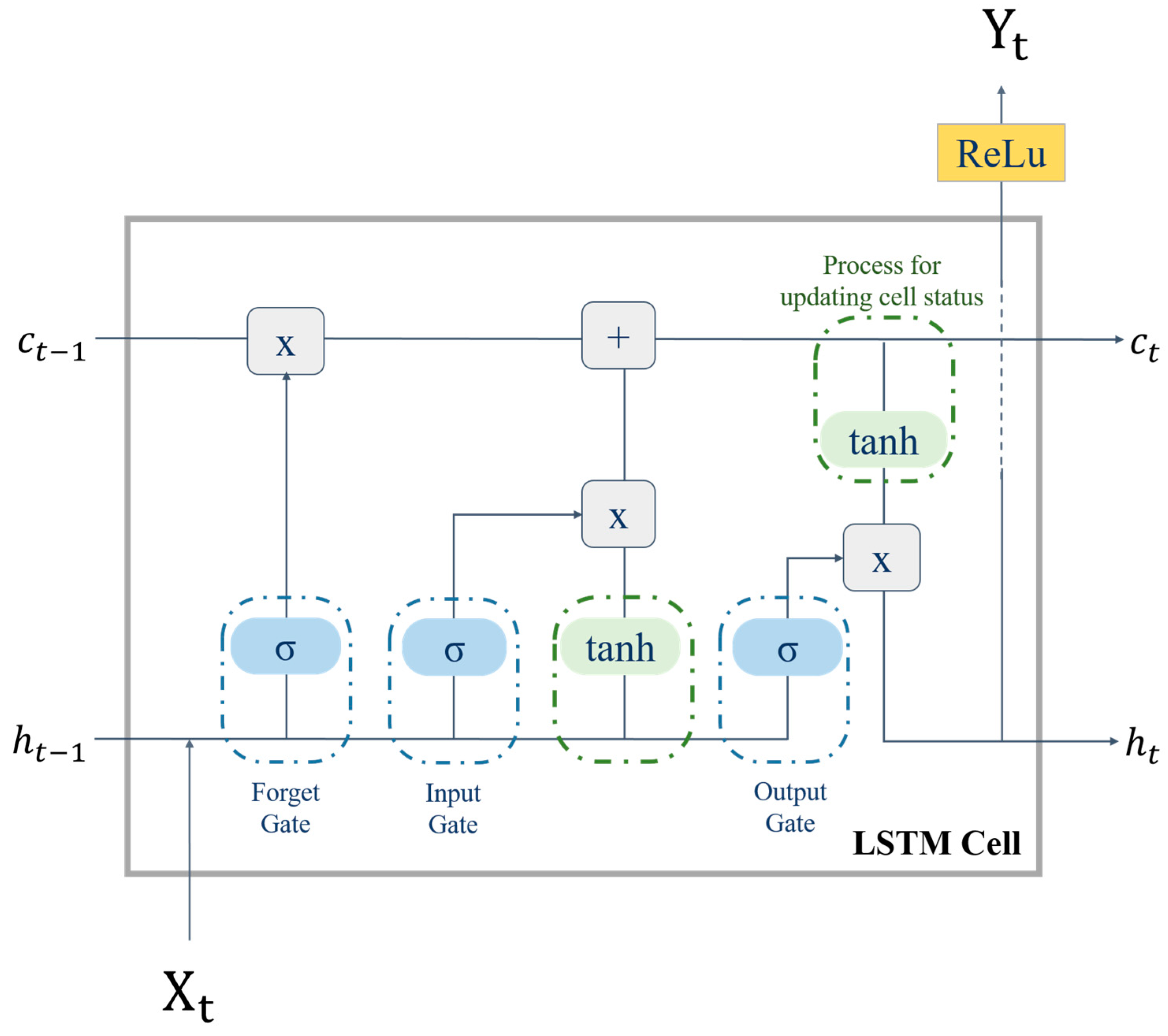
3.1. Long Short-Term Memory Network
3.2. Training Data Settings and Predictive Accuracy Assessment Method
3.2.1. Training Data Settings
3.2.2. Predictive Accuracy Assessment Method
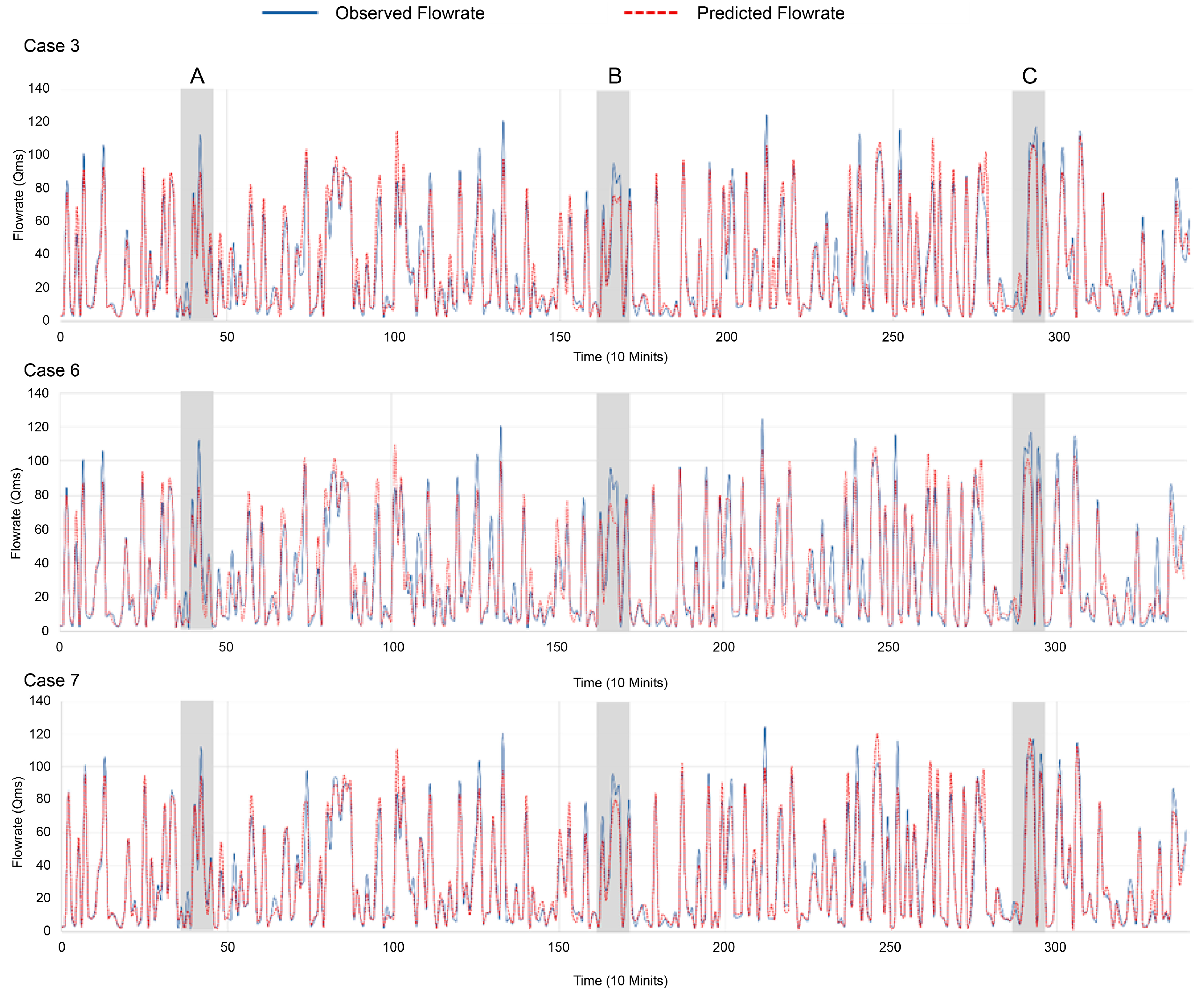
4. Experiment Results
5. Discussion
6. Conclusions
- (1)
- In general, the model’s prediction accuracy improved when social media data were used as an input factor along with other factors.
- (2)
- The study found that combinations of social media and modeling data yielded better accuracy for 1 h predictions, whereas combinations of rainfall and modeling data provided more accuracy in the 30 min, 2 h, and 3 h predictions.
- (3)
- Notably, cases that included all data as input factors demonstrated the highest accuracy, achieving an NSE of 82 and r of 0.91 in the 2 h predictions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- World Meteorological Organization. State of the Global Climate; WMO: Geneva, Switzerland, 2022. [Google Scholar]
- Shkolnik, I.; Pavlova, T.; Efimov, S.; Zhuravlev, S. Future changes in peak river flows across northern Eurasia as inferred from an ensemble of regional climate projections under the IPCC RCP8. 5 scenario. Clim. Dyn. 2018, 50, 215–230. [Google Scholar] [CrossRef]
- Zhou, Q.; Leng, G.; Su, J.; Ren, Y. Comparison of urbanization and climate change impacts on urban flood volumes: Importance of urban planning and drainage adaptation. Sci. Total Environ. 2019, 658, 24–33. [Google Scholar] [CrossRef] [PubMed]
- Dhunny, A.Z.; Seebocus, R.H.; Allam, Z.; Chuttur, M.Y.; Eltahan, M.; Mehta, H. Flood prediction using artificial neural networks: Empirical evidence from Mauritius as a case study. Knowl. Eng. Data Sci. 2020, 3, 1–10. [Google Scholar] [CrossRef]
- Duncan, A.; Chen, A.S.; Keedwell, E.; Djordjevic, S.; Savic, D. Urban flood prediction in real-time from weather radar and rainfall data using artificial neural networks. In Proceedings of the Weather Radar and Hydrology: IAHS Red Book Proceedings, Exeter, UK, 18–21 April 2011. [Google Scholar]
- Lee, J.; Hwang, S. Water level prediction of small and medium-sized rivers using artificial neural networks. J. Korean Soc. Hazard Mitig. 2022, 22, 61–68. [Google Scholar] [CrossRef]
- Rezaeianzadeh, M.; Tabari, H.; Arabi Yazdi, A.; Isik, S.; Kalin, L. Flood flow forecasting using ANN, ANFIS and regression models. Neural Comput. Appl. 2014, 25, 25–37. [Google Scholar] [CrossRef]
- Samantaray, S.; Agnihotri, A.; Sahoo, A. Flood Replication Using ANN Model Concerning with Various Catchment Characteristics: Narmada River Basin. J. Inst. Eng. (India) A 2023, 104, 381–396. [Google Scholar] [CrossRef]
- Shrestha, R.R.; Theobald, S.; Nestmann, F. Simulation of flood flow in a river system using artificial neural networks. Hydrol. Earth Syst. Sci. 2005, 9, 313–321. [Google Scholar] [CrossRef]
- Tawfik, A.M. River flood routing using artificial neural networks. Ain Shams Eng. J. 2023, 14, 101904. [Google Scholar] [CrossRef]
- Tsakiri, K.; Marsellos, A.; Kapetanakis, S. Artificial neural network and multiple linear regression for flood prediction in Mohawk River, New York. Water 2018, 10, 1158. [Google Scholar] [CrossRef]
- Mirzaei, S.; Vafakhah, M.; Pradhan, B.; Alavi, S.J. Flood susceptibility assessment using extreme gradient boosting (EGB), Iran. Earth Sci. Inform. 2021, 14, 51–67. [Google Scholar] [CrossRef]
- Ilhan, A. Forecasting of river water flow rate with machine learning. Neural Comput. Appl. 2022, 34, 20341–20363. [Google Scholar] [CrossRef]
- Le, X.H.; Nguyen, D.H.; Jung, S.; Yeon, M.; Lee, G. Comparison of deep learning techniques for river streamflow forecasting. IEEE Access 2021, 9, 71805–71820. [Google Scholar] [CrossRef]
- Dehghani, A.; Moazam, H.M.Z.H.; Mortazavizadeh, F.; Ranjbar, V.; Mirzaei, M.; Mortezavi, S.; Ng, J.L.; Dehghani, A. Comparative evaluation of LSTM, CNN, and ConvLSTM for hourly short-term streamflow forecasting using deep learning approaches. Ecol. Inform. 2023, 75, 102119. [Google Scholar] [CrossRef]
- Atashi, V.; Kardan, R.; Gorji, H.T.; Lim, Y.H. Comparative Study of Deep Learning LSTM and 1D-CNN Models for Real-time Flood Prediction in Red River of the North, USA. In Proceedings of the 2023 IEEE International Conference on Electro Information Technology (eIT), Romeoville, IL, USA, 18–20 May 2023; pp. 22–28. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, Y.; Zhang, L.; Wang, Z. Regionalization of hydrological modeling for predicting streamflow in ungauged catchments: A comprehensive review. WIREs Water 2021, 8, e1487. [Google Scholar] [CrossRef]
- Kastridis, A.; Kirkenidis, C.; Sapountzis, M. An integrated approach of flash flood analysis in ungauged Mediterranean watersheds using post-flood surveys and unmanned aerial vehicles. Hydrol. Process. 2020, 34, 4920–4939. [Google Scholar] [CrossRef]
- Liu, L. Unravelling and improving the potential of global discharge reanalysis dataset in streamflow estimation in ungauged basins. J. Clean. Prod. 2023, 419, 138282. [Google Scholar] [CrossRef]
- Xiao, Q.; Zhou, L.; Xiang, X.; Liu, L.; Liu, X.; Li, X.; Ao, T. Integration of Hydrological Model and Time Series Model for Improving the Runoff Simulation: A Case Study on BTOP Model in Zhou River Basin, China. Appl. Sci. 2022, 12, 6883. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, L.; Qin, F.; Zhou, L.; Zhang, X.; Chen, T.; Li, X.; Ao, T. Application of the regression-augmented regionalization approach for BTOP model in ungauged basins. Water 2021, 13, 2294. [Google Scholar] [CrossRef]
- Kheimi, M.; Almadani, M.; Zounemat-Kermani, M. Stochastic (S [ARIMA]), shallow (NARnet, NAR-GMDH, OS-ELM), and deep learning (LSTM, Stacked-LSTM, CNN-GRU) models, application to river flow forecasting. Acta Geophys. 2023, 1–15, 82. [Google Scholar] [CrossRef]
- Fohringer, J.; Dransch, D.; Kreibich, H.; Schröter, K.J. Social media as an information source for rapid flood inundation mapping. Nat. Hazards Earth Syst. Sci. 2015, 15, 2725–2738. [Google Scholar] [CrossRef]
- Herfort, B.; De Albuquerque, J.P.; Schelhorn, S.J.; Zipf, A.B. Exploring the geographical relations between social media and flood phenomena to improve situational awareness. In Connecting a Digital Europe through Location and Place; Huerta, J., Schade, S., Granell, C., Eds.; Springer: Castellon, Spain, 2014; pp. 55–71. [Google Scholar] [CrossRef]
- Lee, J.; Hwang, S.J. A study on the application of social network service data for monitoring flood damage. J. Korean Soc. Hazard Mitig. 2019, 19, 77–85. [Google Scholar] [CrossRef]
- Murthy, D.; Longwell, S.A.D. Twitter and disasters: The uses of Twitter during the 2010 Pakistan floods. Inf. Commun. Soc. 2013, 16, 837–855. [Google Scholar] [CrossRef]
- Spielhofer, T.; Greenlaw, R.; Markham, D.; Hahne, A. Data mining Twitter during the UK floods: Investigating the potential use of social media in emergency management. In Proceedings of the 2016 3rd International Conference on Information and Communication Technologies for Disaster Management (ICT-DM), Vienna, Austria, 13–15 December 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Kanth, A.K.; Chitra, P.; Sowmya, G.G. Deep learning-based assessment of flood severity using social media streams. Stoch. Environ. Res. Risk Assess. 2022, 36, 473–493. [Google Scholar] [CrossRef]
- Songchon, C.; Wright, G.; Beevers, L. The use of crowdsourced social media data to improve flood forecasting. J. Hydrol. 2023, 622, 129703. [Google Scholar] [CrossRef]
- Jungnangcheon Area (Seoul Metropolitan Government) River Basic Plan; Ministry of Land, Transport and Maritime Affairs: Sejong, Republic of Korea, 2012.
- Jungnangcheon Area (Gyeonggi-Dogovernment) River Basic Plan; Ministry of Land, Transport and Maritime Affairs: Sejong, Republic of Korea, 2012.
- Corps of Engineers Washington DC. Flood-Runoff Analysis; US Army Corps of Engineers: Washington, DC, USA, 1994.
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef]
- Xiang, Z.; Yan, J.; Demir, I. A rainfall-runoff model with LSTM-based sequence-to-sequence learning. Water Resour. Res. 2020, 56, e2019WR025326. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Chen, R.; Ju, M.; Chu, C.; Jing, W.; Wang, Y. Identification and quantification of physicochemical parameters influencing chlorophyll-a concentrations through combined principal component analysis and factor analysis: A case study of the Yuqiao Reservoir in China. Sustainability 2018, 10, 936. [Google Scholar] [CrossRef]
- Abas, S.; Addou, M. Geospatial Forecasting and Social Media Exploration Based on Sentiment Analysis: Application to Flood Forecasting. Geospat. Intell. Appl. Future Trends 2022, 19–29. [Google Scholar]
- Brown, J.M.; Yelland, M.J.; Pullen, T.; Silva, E.; Martin, A.; Gold, I.; Whittle, L.; Wisse, P. Novel use of social media to assess and improve coastal flood forecasts and hazard alerts. Sci. Rep. 2021, 11, 13727. [Google Scholar] [CrossRef] [PubMed]
- Eilander, D.; Trambauer, P.; Wagemaker, J.; Van Loenen, A. Harvesting social media for generation of near real-time flood maps. Procedia Eng. 2016, 154, 176–183. [Google Scholar] [CrossRef]
- Li, Y.; Osei, F.B.; Hu, T.; Stein, A. Urban flood susceptibility mapping based on social media data in Chengdu city, China. Sustain. Cities Soc. 2023, 88, 104307. [Google Scholar] [CrossRef]
- Yang, T.; Xie, J.; Li, G.; Zhang, L.; Mou, N.; Wang, H.; Zhang, X.; Wang, X. Extracting disaster-related location information through social media to assist remote sensing for disaster analysis: The case of the flood disaster in the Yangtze River Basin in China in 2020. Remote Sens. 2022, 14, 1199. [Google Scholar] [CrossRef]
- Chaudhary, P.; D’Aronco, S.; Moy de Vitry, M.; Leitão, J.P.; Wegner, J.D. Flood-water level estimation from social media images. ISPRS Ann. Photogram. Remote Sens. Spat. Inf. Sci. 2019, 4, 5–12. [Google Scholar] [CrossRef]
- Rosser, J.F.; Leibovici, D.G.; Jackson, M.J. Rapid flood inundation mapping using social media, remote sensing and topographic data. Nat. Hazards 2017, 87, 103–120. [Google Scholar] [CrossRef]
- Smith, L.; Liang, Q.; James, P.; Lin, W. Assessing the utility of social media as a data source for flood risk management using a real-time modelling framework. J. Flood Risk Manag. 2017, 10, 370–380. [Google Scholar] [CrossRef]
- Asif, A.; Khatoon, S.; Hasan, M.M.; Alshamari, M.A.; Abdou, S.; Elsayed, K.M.; Rashwan, M. Automatic analysis of social media images to identify disaster type and infer appropriate emergency response. J. Big Data 2021, 8, 83. [Google Scholar] [CrossRef]
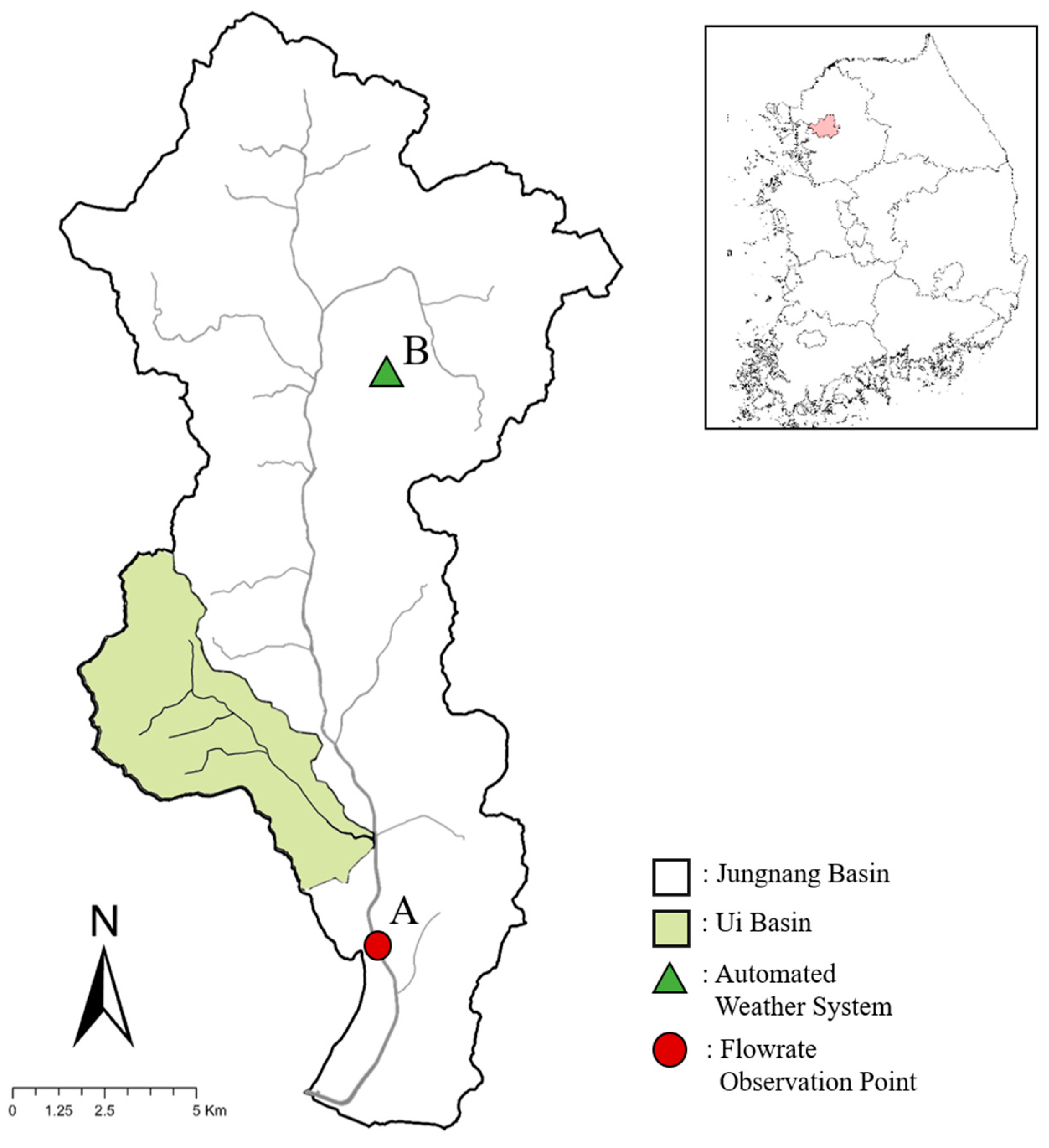


| Data | Unit (Total Data Count) | Usage | Location | Source |
|---|---|---|---|---|
| Precipitation | 10 min (2448) | Input Variable | Upstream of Jungnang Basin (B) | Korea Meteorological Administration |
| Flow rate | Output Variable | Downstream of Jungnang Basin (A) | Han River Flood Control Office |
| Routing Method | Parameters | Formula |
|---|---|---|
| CLARK watershed routing method | Travel Time (TC) | Kraven (II) [30] |
| Storage Constant (R) | Sabol formula [32] | |
| Muskingum hydrologic channel flood routing method | Retention Constant (K) | Passage time of the peak flood from the HEC-RAS unsteady flow model |
| Variable | Description |
|---|---|
| Keyword | Configuring disaster types with keywords |
| Region | Extracting local information where the event occurred |
| Time | Enabled a specified search of the time when the event occurred and extracted the time when the social media post was created |
| Title | Extracted to determine if the content contained in the body of the social media post was relevant to local information or crisis events |
| Article | |
| Web address | Prevented data from being stored when data from the same address was extracted to avoid duplicate data |
| Meteorological data | Extracted for comparative analysis with weather-related disasters |
| Dataset Case No. | Training Periods | Testing Periods | Input Data Composition | ||
|---|---|---|---|---|---|
| Precipitation | Flow Rate (Model) | Social Media | |||
| 1 | 22–24 April 2018 16–18 May 2018 26–28 June 2018 1–3 July 2018 26–28 August 2018 | 3–5 September 2018 6–8 October 2018 | ○ | ||
| 2 | ○ | ||||
| 3 | ○ | ○ | |||
| 4 | ○ | ||||
| 5 | ○ | ○ | |||
| 6 | ○ | ○ | |||
| 7 | ○ | ○ | ○ | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Hwang, S. Ungauged Basin Flood Prediction Using Long Short-Term Memory and Unstructured Social Media Data. Water 2023, 15, 3818. https://doi.org/10.3390/w15213818
Lee J, Hwang S. Ungauged Basin Flood Prediction Using Long Short-Term Memory and Unstructured Social Media Data. Water. 2023; 15(21):3818. https://doi.org/10.3390/w15213818
Chicago/Turabian StyleLee, Jeongha, and Seokhwan Hwang. 2023. "Ungauged Basin Flood Prediction Using Long Short-Term Memory and Unstructured Social Media Data" Water 15, no. 21: 3818. https://doi.org/10.3390/w15213818
APA StyleLee, J., & Hwang, S. (2023). Ungauged Basin Flood Prediction Using Long Short-Term Memory and Unstructured Social Media Data. Water, 15(21), 3818. https://doi.org/10.3390/w15213818





