Utilizing the Sobol’ Sensitivity Analysis Method to Address the Multi-Objective Operation Model of Reservoirs
Abstract
:1. Introduction
2. Materials and Methods
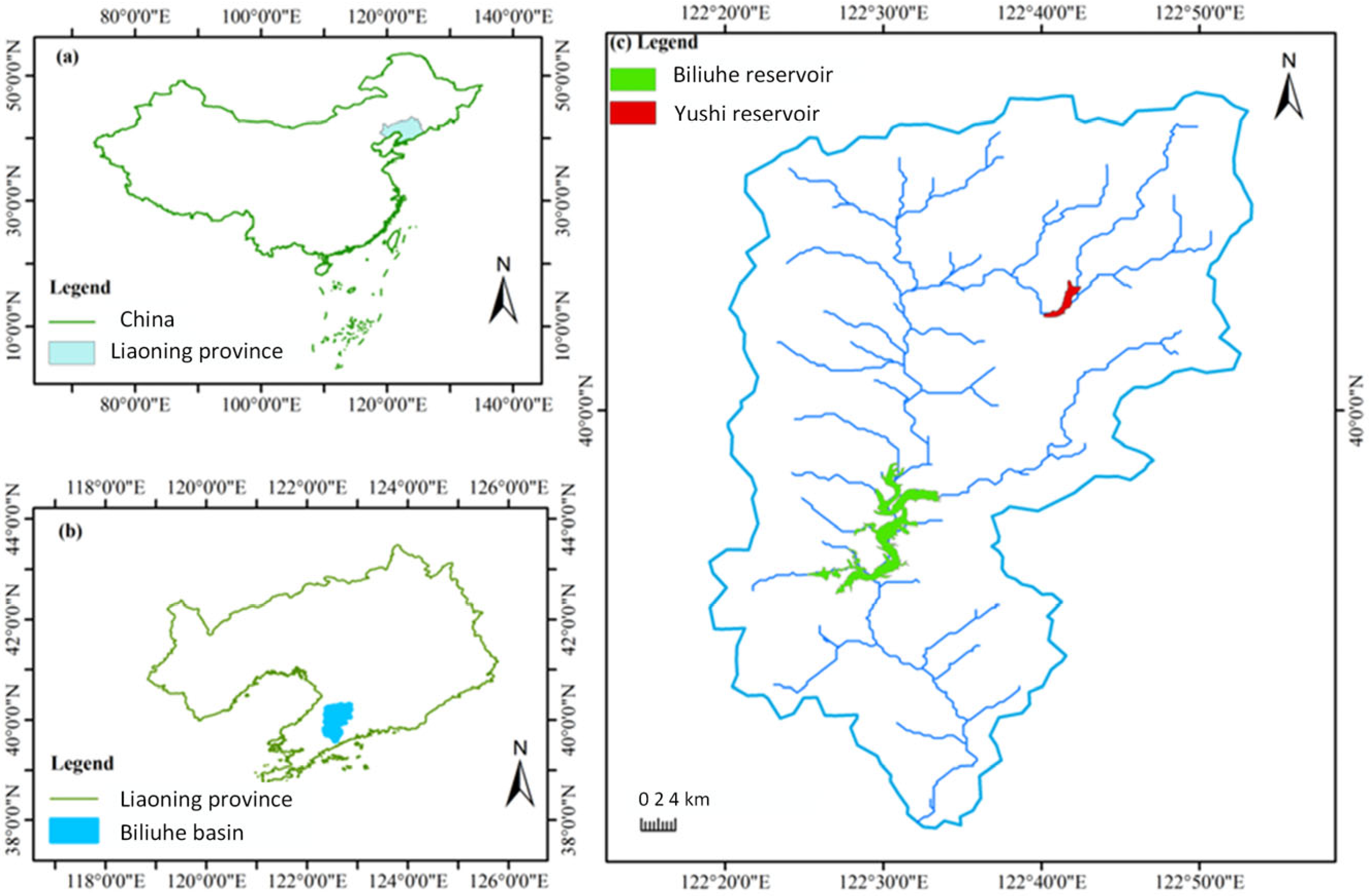
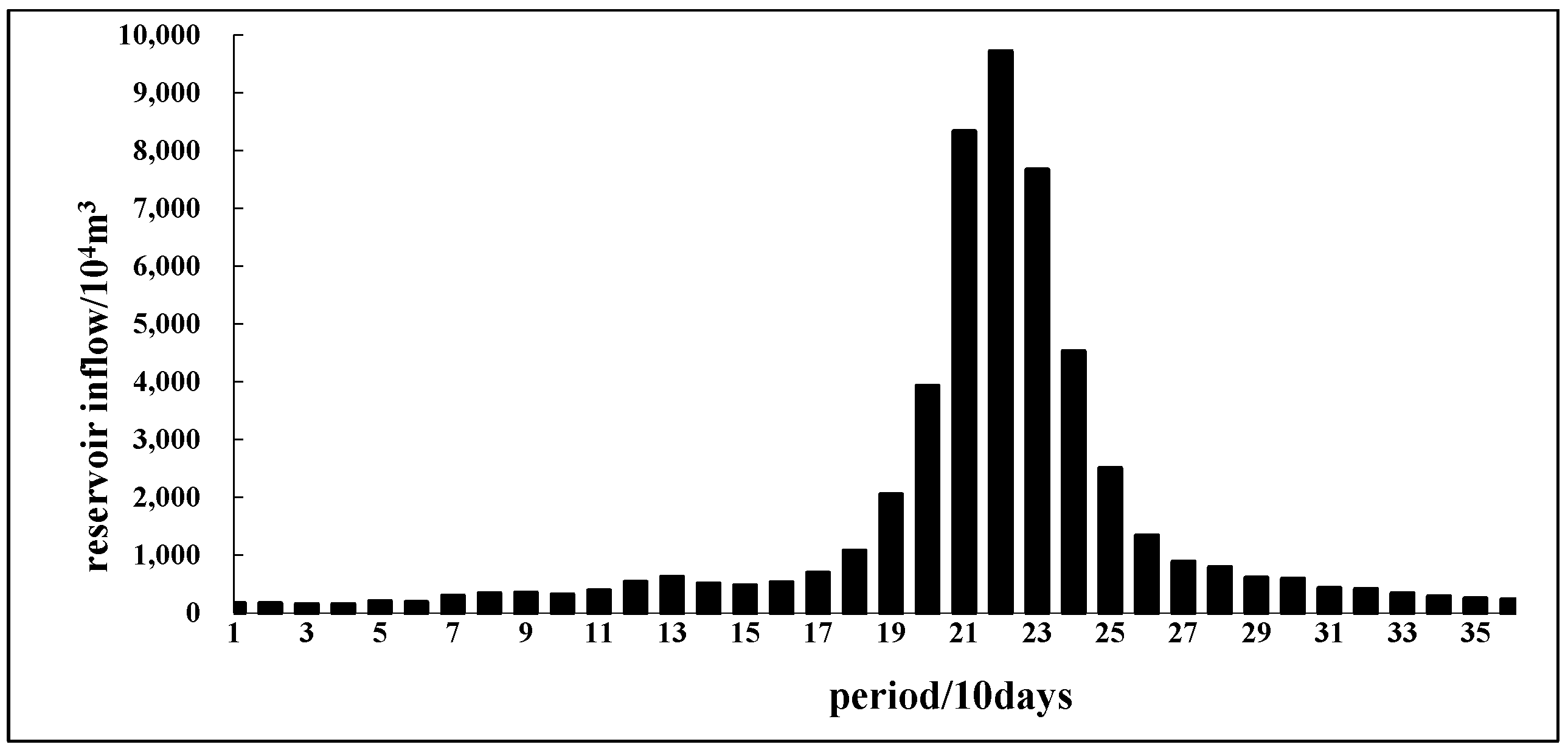
2.1. Study Area
2.2. Sobol’ Method
- Each dimension in the uncertainty space is split into N intervals with an equal length, and equally spaced levels corresponding to [0, 1/N), [1/N, 2/N), …, [1–1/N, 1] for each variable;
- A random point in the range is generated in any one interval of each variable. Then, they are combined into multivariate samples that preserve the space-filling property of the marginal distribution [38].
- All of the samples produced by LHS form a N × k matrix (xi,j), where N represents the number of samples and k denotes the number of variables, and xi,j is the value of the jth variable in the ith sample.
2.3. Ecological Scheduling Method
2.4. Scenarios Design
2.4.1. The Objective Functions
- I&D and agricultural objectives: To reflect the situations of I&D and agricultural water supply, the I&D water shortage index (ISI) and agricultural water shortage index (ASI) are used as objective functions. The shortage index (SI) is the indicator to measure the damage degree of water shortage to different users. Therefore, smaller SI values equate to better efficiency for I&D and agricultural water supply. The objective function is as follow:
- where N is the total number of years; T denotes the time periods in a year; and are the water demand and water supply for the ith users (I&D or agriculture) during the jth time period, respectively; and k is an index to reflect the socio-economic impact of water shortage, which in this paper k is 2. Because I&D (or agricultural) the water supply is nonnegative, and it cannot be bigger than the water demand, the possible range of SI is from 0 to 100.
- Water diversion objective: In addition to the ecological objective, as mentioned in Section 2.2 (Formula (7)), the water diversion objective is also considered in this paper. To minimize the long-distance water division cost, the least amount of water should be diverted from the Dahuofang reservoir. The objective function is as follows:
- where D is the annual amount of diverted water; m and n are the number of years and the time periods in one year, respectively; and denotes the amount of diverted water in the ith year for the jth time period. The actual water supply capacity of this project is 288 million m3/year after deducting the water leakage loss, so the value interval for water diversion objective D is (0, 288 million m3/year).
- Constraints:
2.4.2. The Implementation of Sobol’ Method
- Parameters of the model: In the water diversion and water supply combined operation model, the parameters are the water levels on different dispatching lines during the operation time periods. In this paper, the total number of parameters is 160 (agricultural limit line 16, I&D limit line 36, ecological limit line 36, upper water diversion line 36, and lower water diversion line 36).
- Range of parameter values: For the parameters of each dispatching line at different periods, the water level values range from the normal water level (the flood-limit water level in the flood season) to the dead water level.
- Sampling method: The LHS technique is used to compute the Sobol’ sensitivity indices. All of the parameters obey the uniform distribution. A set of 2000 LH samples is used per parameter and a total number of model simulations are required to compute the Sobol’ indices.
- Sensitivity calculation: The sampled parameters are placed into the reservoir multi-objective operation model to obtain the objective function values for different sampling sequences. Then, the variance-based analysis method is applied to analyze the influence of single and multiple water levels on other objectives at different time periods.
- All of the water level parameters will be optimized by 500,000 calculations, which is the full search scenario;
- Firstly, the sensitivity parameters are optimized by 5000 calculations to obtain the feasible solutions, then these solutions are subsequently taken as the initial solutions for the global optimization problem of all parameters, and (500,000–5000) calculations are run to search for the final feasible solutions, which is the pre-conditioned full search scenario.
2.5. The Evaluation Indicators
- Generational distance: Generational distance was proposed by Van Veldhuizen and Lamont in 1998 [42]. This indicator is used to measure the gap between the solutions obtained by the algorithm and the real Pareto frontier solutions. It is defined as follows:
- where n is the number of the optimal solutions, di is the minimum Euclidean distance between the target space and theoretical Pareto front for the ith individual. The smaller the value for the generation distance, the closer the solutions obtained are to the real Pareto frontier solutions. When all of the solutions obtained by the algorithm are exactly the real Pareto frontier solutions, GD = 0.
- Additive indicator: The additive indicator [43] evaluates the minimum distance for which the current solutions can completely dominate the reference solutions. It is defined as follows:
- where Q is the non-inferior solution sets, and is the approaching degree of the non-inferior solution sets and the Pareto front. The smaller the value of the additive indicator, the closer the current solutions are to the reference solutions.
- Hypervolume indicator: The hypervolume indicator [44] is used to evaluate the target space of the dominated solutions. It not only shows the distance between the current solutions and the optimal solutions, but also the distribution of the current solutions in the target space. It is defined as follows:
- where |S| represents the number of non-dominant solution sets and vi represents the hypervolume formed by the reference point and the ith solution. The bigger the value of the hypervolume indicator, the greater the improvement in the current solutions and the farther away they are from the worst solution.
3. Results and Discussion
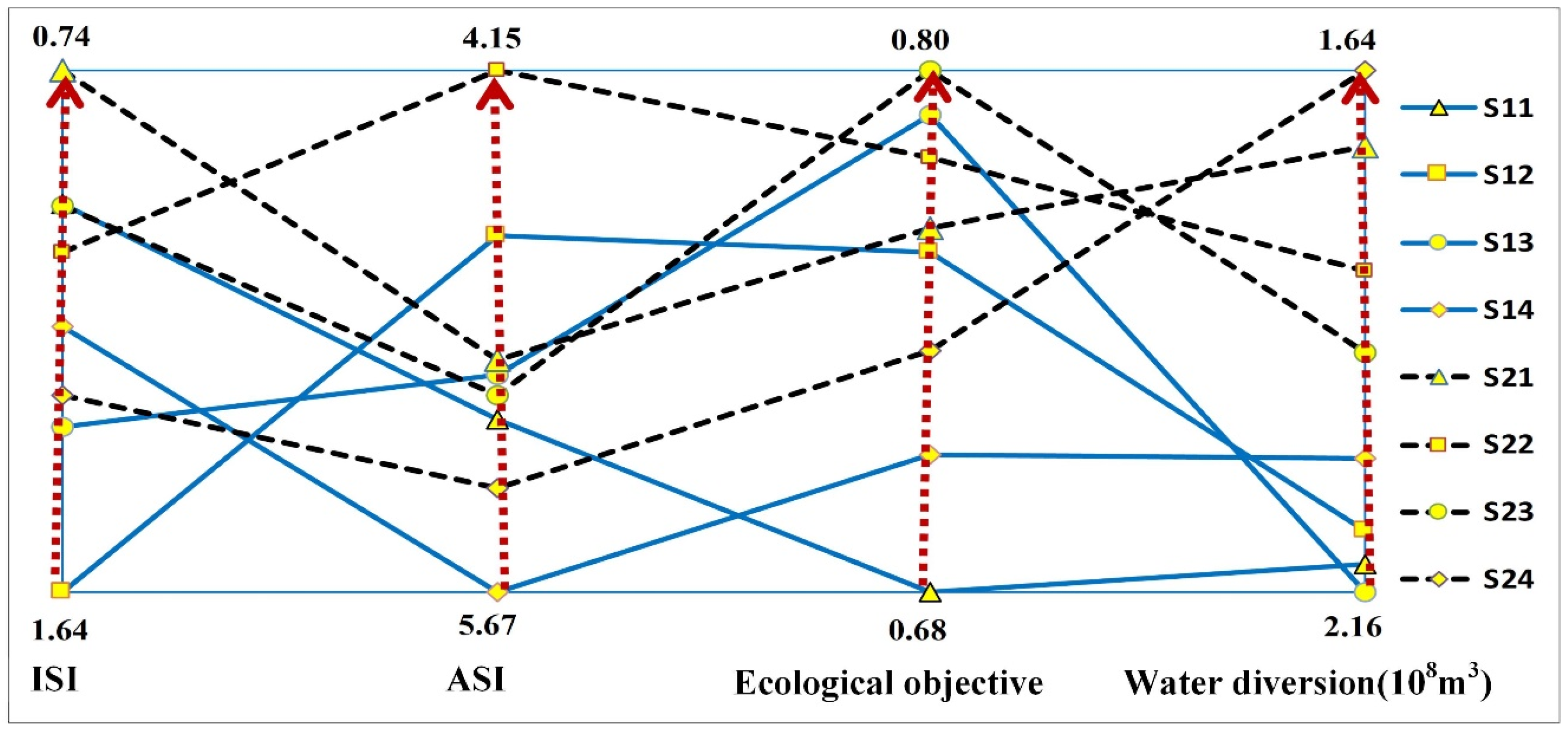
3.1. The Sensitive Parameters
3.2. The Evaluation Indicators
3.3. The Feasible Solutions Analysis
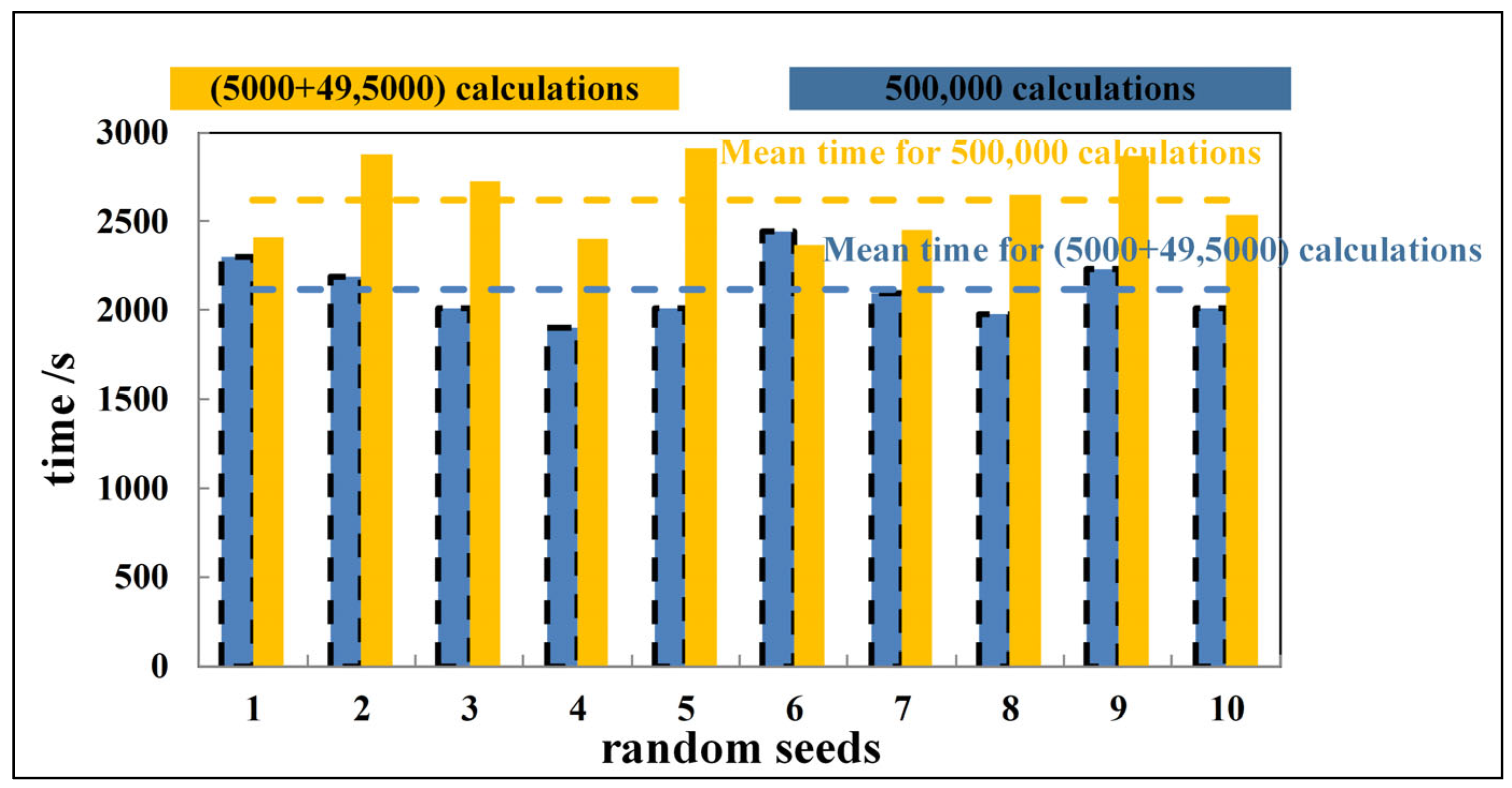
3.4. The Processing Speed Analysis
3.5. The Implication for Reservoirs Management
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yu, Y.; Zhou, T.; Zhao, R.; Zhang, J.; Min, X. Bi-Level Hybrid Game Model for Optimal Operation of Multi-Function Reservoir Considering Integrated Water Resource Management. Environ. Sci. Pollut. Res. 2022. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Ji, X.; Tang, J.; Li, H. A Fuzzy Cooperative Game Theoretic Approach for Multinational Water Resource Spatiotemporal Allocation. Eur. J. Oper. Res. 2020, 282, 1025–1037. [Google Scholar] [CrossRef]
- Bai, T.; Sun, X.-G.; Wei, J.; Wu, L. Hydrological Response and Ecological Flow Optimization in Water Diversion Area of Inter-Basin Water Diversion Project. Water Resour. Manag. 2022, 36, 5839–5865. [Google Scholar] [CrossRef]
- Bai, T.; Li, L.; Mu, P.; Pan, B.; Liu, J. Impact of Climate Change on Water Transfer Scale of Inter-Basin Water Diversion Project. Water Resour. Manag. 2023, 37, 2505–2525. [Google Scholar] [CrossRef]
- Fang, R.; Popole, Z. Multi-Objective Optimized Scheduling Model for Hydropower Reservoir Based on Improved Particle Swarm Optimization Algorithm. Environ. Sci. Pollut. Res. 2020, 27, 12842–12850. [Google Scholar] [CrossRef]
- Cui, B.-L.; Chang, X.-L.; Shi, W.-Y. Abrupt Changes of Runoff and Sediment Load in the Lower Reaches of the Yellow River, China. Water Resour. 2014, 41, 252–260. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, P.; Wang, C.; Wang, X. Optimal Reservoir Operation Using Multi-Objective Evolutionary Algorithms for Potential Estuarine Eutrophication Control. J. Environ. Manag. 2018, 223, 758–770. [Google Scholar] [CrossRef]
- Wang, Y.; Lei, X.; Wen, X.; Fang, G.; Tan, Q.; Tian, Y.; Wang, C.; Wang, H. Effects of Damming and Climatic Change on the Eco-Hydrological System: A Case Study in the Yalong River, Southwest China. Ecol. Indic. 2019, 105, 663–674. [Google Scholar] [CrossRef]
- Castelletti, A.; Pianosi, F.; Soncini-Sessa, R. Water Reservoir Control under Economic, Social and Environmental Constraints. Automatica 2008, 44, 1595–1607. [Google Scholar] [CrossRef]
- Higgins, A.J.; Bryan, B.A.; Overton, I.C.; Holland, K.; Lester, R.E.; King, D.; Nolan, M.; Connor, J.D. Integrated Modelling of Cost-Effective Siting and Operation of Flow-Control Infrastructure for River Ecosystem Conservation: Integrated Modelling of Flow Control Infrastructure. Water Resour. Res. 2011, 47, W05519. [Google Scholar] [CrossRef]
- Mao, J.; Zhang, P.; Dai, L.; Dai, H.; Hu, T. Optimal Operation of a Multi-Reservoir System for Environmental Water Demand of a River-Connected Lake. Hydrol. Res. 2016, 47, 206–224. [Google Scholar] [CrossRef]
- Adams, L.E.; Lund, J.R.; Moyle, P.B.; Quiñones, R.M.; Herman, J.D.; O’Rear, T.A. Environmental Hedging: A Theory and Method for Reconciling Reservoir Operations for Downstream Ecology and Water Supply. Water Resour. Res. 2017, 53, 7816–7831. [Google Scholar] [CrossRef]
- Feng, Z.; Niu, W.; Cheng, C. Optimization of Hydropower Reservoirs Operation Balancing Generation Benefit and Ecological Requirement with Parallel Multi-Objective Genetic Algorithm. Energy 2018, 153, 706–718. [Google Scholar] [CrossRef]
- Niu, W.; Feng, Z.; Cheng, C.; Wu, X. A Parallel Multi-Objective Particle Swarm Optimization for Cascade Hydropower Reservoir Operation in Southwest China. Appl. Soft Comput. 2018, 70, 562–575. [Google Scholar] [CrossRef]
- Li, Y.; Kinzelbach, W. Resolving Conflicts between Irrigation Agriculture and Ecohydrology Using Many-Objective Robust Decision Making. J. Water Resour. Plan. Manag. 2020, 146, 05020014. [Google Scholar] [CrossRef]
- Dong, Z.; Ni, X.; Chen, M.; Yao, H.; Jia, W.; Zhong, J.; Ren, L. Time-Varying Decision-Making Method for Multi-Objective Regulation of Water Resources. Water Resour. Manag. 2021, 35, 3411–3430. [Google Scholar] [CrossRef]
- Feng, Z.; Liu, S.; Niu, W.; Li, S.; Wu, H.; Wang, J. Ecological Operation of Cascade Hydropower Reservoirs by Elite-Guide Gravitational Search Algorithm with Lévy Flight Local Search and Mutation. J. Hydrol. 2020, 581, 124425. [Google Scholar] [CrossRef]
- Zhang, C.; Ding, W.; Li, Y.; Meng, F.; Fu, G. Cost-Benefit Framework for Optimal Design of Water Transfer Systems. J. Water Resour. Plan. Manag. 2019, 145, 04019007. [Google Scholar] [CrossRef]
- Feng, Z.; Niu, W.; Zhang, R.; Wang, S.; Cheng, C. Operation Rule Derivation of Hydropower Reservoir by K-Means Clustering Method and Extreme Learning Machine Based on Particle Swarm Optimization. J. Hydrol. 2019, 576, 229–238. [Google Scholar] [CrossRef]
- Jiang, Z.; Ji, C.; Qin, H.; Feng, Z. Multi-Stage Progressive Optimality Algorithm and Its Application in Energy Storage Operation Chart Optimization of Cascade Reservoirs. Energy 2018, 148, 309–323. [Google Scholar] [CrossRef]
- Wang, S.; Cao, Y.; Huang, T.; Wen, S. Passivity and Passification of Memristive Neural Networks with Leakage Term and Time-Varying Delays. Appl. Math. Comput. 2019, 361, 294–310. [Google Scholar] [CrossRef]
- SeethaRam, K.V. Three Level Rule Curve for Optimum Operation of a Multipurpose Reservoir Using Genetic Algorithms. Water Resour. Manag. 2021, 35, 353–368. [Google Scholar] [CrossRef]
- Chen, H.; Wang, W.; Chen, X.; Qiu, L. Multi-Objective Reservoir Operation Using Particle Swarm Optimization with Adaptive Random Inertia Weights. Water Sci. Eng. 2020, 13, 136–144. [Google Scholar] [CrossRef]
- Diao, Y.; Ma, H.; Wang, H.; Wang, J.; Li, S.; Li, X.; Pan, J.; Qiu, Q. Optimal Flood-Control Operation of Cascade Reservoirs Using an Improved Particle Swarm Optimization Algorithm. Water 2022, 14, 1239. [Google Scholar] [CrossRef]
- Ma, Y.; Zhong, P.; Xu, B.; Zhu, F.; Lu, Q.; Wang, H. Spark-Based Parallel Dynamic Programming and Particle Swarm Optimization via Cloud Computing for a Large-Scale Reservoir System. J. Hydrol. 2021, 598, 126444. [Google Scholar] [CrossRef]
- Niu, W.; Feng, Z.; Liu, S.; Chen, Y.; Xu, Y.; Zhang, J. Multiple Hydropower Reservoirs Operation by Hyperbolic Grey Wolf Optimizer Based on Elitism Selection and Adaptive Mutation. Water Resour. Manag. 2021, 35, 573–591. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, C.; Fu, G.; Li, Y.; Ding, W. Bi-Level Optimization for Determining Operating Strategies for Inter-Basin Water Transfer-Supply Reservoirs. Water Resour Manag. 2017, 31, 4415–4432. [Google Scholar] [CrossRef]
- Ming, B.; Liu, P.; Bai, T.; Tang, R.; Feng, M. Improving Optimization Efficiency for Reservoir Operation Using a Search Space Reduction Method. Water Resour. Manag. 2017, 31, 1173–1190. [Google Scholar] [CrossRef]
- Hart, J.L.; Bessac, J.; Constantinescu, E.M. Global Sensitivity Analysis for Statistical Model Parameters. SIAM/ASA J. Uncertain. Quantif. 2019, 7, 67–92. [Google Scholar] [CrossRef]
- Sobol, I.M. Sensitivity Estimates for Nonlinear Mathematical Models. In Mathematical Modelling and Computational Experiments; Association for Computing Machinery: New York, NY, USA, 1993; pp. 112–118. [Google Scholar]
- Tang, Y.; Reed, P.; Van Werkhoven, K.; Wagener, T. Advancing the Identification and Evaluation of Distributed Rainfall-Runoff Models Using Global Sensitivity Analysis: Distributed Model Sensitivity Analysis. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Fu, G.; Kapelan, Z.; Reed, P. Reducing the Complexity of Multiobjective Water Distribution System Optimization through Global Sensitivity Analysis. J. Water Resour. Plan. Manag. 2012, 138, 196–207. [Google Scholar] [CrossRef]
- Zhang, C.; Chu, J.; Fu, G. Sobol’s Sensitivity Analysis for a Distributed Hydrological Model of Yichun River Basin, China. J. Hydrol. 2013, 480, 58–68. [Google Scholar] [CrossRef]
- Han, J.; Wang, L.; Ma, F.; Ge, Z.; Wang, D.; Li, X. Sensitivity Analysis of Geometric Error for a Novel Slide Grinder Based on Improved Sobol Method and Its Application. Int. J. Adv. Manuf. Technol. 2022, 121, 6661–6684. [Google Scholar] [CrossRef]
- Feng, Z.; Niu, W.; Jiang, Z.; Qin, H.; Song, Z. Monthly Operation Optimization of Cascade Hydropower Reservoirs with Dynamic Programming and Latin Hypercube Sampling for Dimensionality Reduction. Water Resour. Manag. 2020, 34, 2029–2041. [Google Scholar] [CrossRef]
- Niu, W.; Feng, Z.; Chen, Y.; Zhang, H.; Cheng, C. Annual Streamflow Time Series Prediction Using Extreme Learning Machine Based on Gravitational Search Algorithm and Variational Mode Decomposition. J. Hydrol. Eng. 2020, 25, 04020008. [Google Scholar] [CrossRef]
- Scherholz, M.L.; Forder, J.; Androulakis, I.P. A Framework for 2-Stage Global Sensitivity Analysis of GastroPlusTM Compartmental Models. J. Pharmacokinet. Pharmacodyn. 2018, 45, 309–327. [Google Scholar] [CrossRef]
- Hajihassanpour, M.; Kesserwani, G.; Pettersson, P.; Bellos, V. Sampling-Based Methods for Uncertainty Propagation in Flood Modeling Under Multiple Uncertain Inputs: Finding Out the Most Efficient Choice. Water Resour. Res. 2023, 59, e2022WR034011. [Google Scholar] [CrossRef]
- Richter, B.D.; Baumgartner, J.V.; Powell, J.; Braun, D.P. A Method for Assessing Hydrologic Alteration within Ecosystems. Conserv. Biol. 1996, 10, 1163–1174. [Google Scholar] [CrossRef]
- Shiau, J.-T.; Wu, F.-C. A Histogram Matching Approach for Assessment of Flow Regime Alteration: Application to Environmental Flow Optimization. River Res. Appl. 2008, 24, 914–928. [Google Scholar] [CrossRef]
- Lu, X.; Wang, X.; Ban, X.; Singh, V.P. Considering Ecological Flow in Multi-Objective Operation of Cascade Reservoir Systems under Climate Variability with Different Hydrological Periods. J. Environ. Manag. 2022, 309, 114690. [Google Scholar] [CrossRef]
- Van Veldhuizen, D.A.; Lamont, G.B. Multiobjective Evolutionary Algorithm Test Suites. In Proceedings of the 1999 ACM Symposium on Applied Computing, San Antonio, TX, USA, 28 February–2 March 1999; Association for Computing Machinery: New York, NY, USA, 1999; pp. 351–357. [Google Scholar]
- Zitzler, E.; Thiele, L. Multiobjective Optimization Using Evolutionary Algorithms—A Comparative Case Study. In Proceedings of the 5th International Conference on Parallel Problem Solving from Nature, Amsterdam, The Netherlands, 27–30 September 1998; Springer: Berlin/Heidelberg, Germany, 1998; pp. 292–304. [Google Scholar]
- Zitzler, E.; Thiele, L.; Laumanns, M.; Fonseca, C.M.; Da Fonseca, V.G. Performance Assessment of Multiobjective Optimizers: An Analysis and Review. IEEE Trans. Evol. Computat. 2003, 7, 117–132. [Google Scholar] [CrossRef]
- Wang, H.; Jing, G.; Chi, Z.; Hui, C. Identifying the key water levels in reservoir operation on ecological objectives. Water Sci. Technol. Water Supply 2014, 14, 1160–1167. [Google Scholar] [CrossRef]
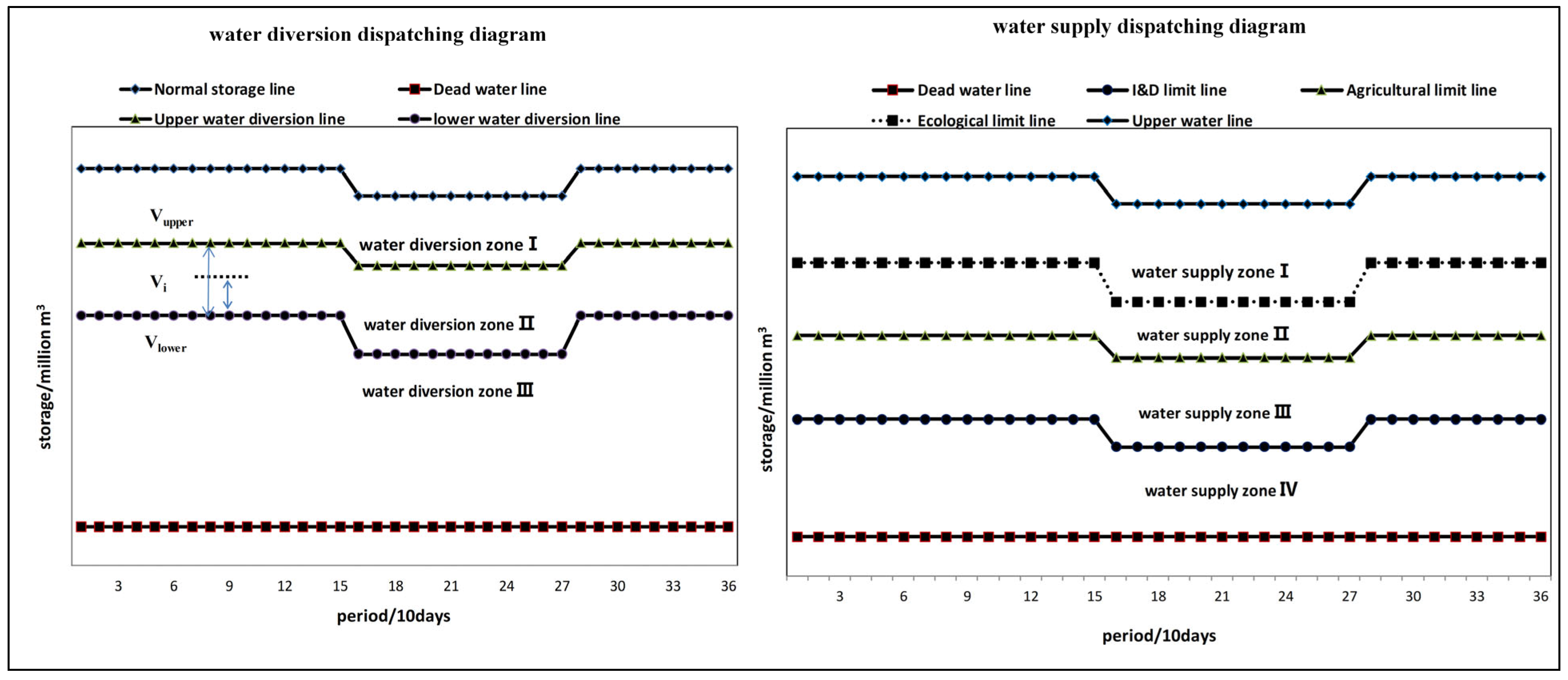



| Combined Dispatching Diagrams | Dispatching Zones | Dispatching Rules |
|---|---|---|
| water diversion dispatching diagram | water diversion zone I | no water diversion |
| water diversion zone II | water diversion on a prorate | |
| water diversion zone III | water diversion based on the capacity of pipeline | |
| water supply dispatching diagram | water supply zone I | normal water supply for I&D, agriculture, and ecosystem |
| water supply zone II | normal water supply for I&D and agriculture, limited water supply for ecosystem | |
| water supply zone III | normal water supply for I&D, limited water supply for agriculture and ecosystem | |
| water supply zone IV | limited water supply for I&D, agriculture, and ecosystem | |
| limiting factors | I&D is 0.9, agriculture is 0.7, ecosystem is 0.5 | |
| dispatching time period | 10-days | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhao, Y.; Fu, W. Utilizing the Sobol’ Sensitivity Analysis Method to Address the Multi-Objective Operation Model of Reservoirs. Water 2023, 15, 3795. https://doi.org/10.3390/w15213795
Wang H, Zhao Y, Fu W. Utilizing the Sobol’ Sensitivity Analysis Method to Address the Multi-Objective Operation Model of Reservoirs. Water. 2023; 15(21):3795. https://doi.org/10.3390/w15213795
Chicago/Turabian StyleWang, Haixia, Ying Zhao, and Wenyuan Fu. 2023. "Utilizing the Sobol’ Sensitivity Analysis Method to Address the Multi-Objective Operation Model of Reservoirs" Water 15, no. 21: 3795. https://doi.org/10.3390/w15213795






