Research on the Prediction Model of Loess Collapsibility in Xinyuan County, Ili River Valley Area

Abstract

Collapsibility is a unique engineering geological property of loess. Choosing appropriate parameters to build the prediction model of loess collapsibility is an essential step toward solving the loess collapsibility problem. A case study was performed for the loess in Xinyuan County of the Yili River Basin, China. A large amount of data was collected from preliminary geotechnical tests in this region. Mathematical statistics were applied to analyse the correlations between the loess collapsibility and soil parameters. Multiple linear regression and neural network theories were adopted to build this region’s prediction model of loess collapsibility. The results showed that microscopically, the soils in this region were predominantly flocculated structures. The soil particles were flaky and in bracket contact, and the pores were round or irregularly shaped. Regarding the material composition, the soils were primarily composed of quartz and albite, with a low hematite content. In the study area, the correlation coefficients between the collapsibility coefficient of the loess vs. the density, dry density, saturation, porosity ratio, and porosity varied between 0.628 and 0.857, indicating a strong or very strong correlation. In terms of predicting loess collapsibility, the effectiveness of neural networks based on RBF (radial basis function) and multiple linear regression models was contrasted. The latter was discovered to be more appropriate, dependable, and accurate, with an accuracy percentage of 94.42%. Simultaneously, the model’s assessment index is 0.014 for the root mean squared error (RMSE), 0.962 for the correlation coefficient (CC), 0.919 for the Nash–Sutcliffe efficiency coefficient (NSE), and −1.494 percent for the percent bias (PBIAS). It works well for estimating whether local loess may collapse. Therefore, the RBF neural network model built in the present study has adequate precision and meets the engineering requirements. Our research sheds new light on loess collapsibility assessment in this region.

1. Introduction

Collapsible loess refers to soil that undergoes significant additional deformation due to the structural failure of the soil following water immersion under the self-weight stress of the overlying soil layer or under the combined action of self-weight stress and additional stress. It is a type of special soil [1]. At this stage, many geotechnical test data have been accumulated during extensive engineering practices in the Ili River Valley area; however, the technicians have not effectively used and mined these data. Therefore, it is necessary to establish a prediction model that can quickly evaluate the loess collapsibility in the Ili River Valley area based on the correlation analysis between the collapsibility coefficient of the loess in Xinyuan County and the soil property indices.

Through the use of mathematical statistics, scholars globally have conducted extensive research on the correlation between loess collapsibility and soil properties. Shu et al. [2] established a binary regression relationship between the initial moisture content, the initial void ratio, and the collapsibility coefficient through the multivariate statistical analysis method by increasing and decreasing the loess moisture content in the experiments. Su [3] carried out many double-line indoor loess collapsibility tests and established the regression equation between the collapsibility coefficient and various soil property indicators with the help of mathematical statistics. Li [4] analysed the degree of correlation between the basic physical property indicators of loess-like soil in southern Hebei, and the collapsibility coefficient and initial pressure of collapse through qualitative and partial correlation analysis, and ranked these. Zhu [5] used mathematical statistics to analyse the correlation between the loess collapsibility coefficient and each soil property indicator and used factor analysis theory to analyse the loess physical property indicators. The author eliminated the impact of collinearity on the fitting and conducted an evaluation on the non-self-weight and self-weight collapsible sites. Zhang used mathematical statistics to analyse relevant loess physical indicators. Lv [6] used mathematical statistics to analyse the correlation between loess collapsibility and moisture content and studied the correlation between the collapsibility coefficient and various physical property indicators. Garakani [7] et al. studied the correlation between loess collapsibility and moisture content under isotropic and shear loads.

Establishing a prediction model for loess collapsibility is an effective means to solve the collapsibility problem. Liu [8], Shao [9], Wang [10], Xing [11], and Wang [12] et al. used univariate linear regression, multiple linear regression, or non-linear regression methods to conduct regression analysis on the relationship between the collapsibility coefficient and a single soil property indicator or multiple soil property indicators and established regression equations. Li [13], Jing [14], Gao [15], and Han [16] et al. used data mining techniques, fuzzy information technology, and neural networks to predict the loess collapsibility coefficient. The soil property indicators considered by researchers when establishing the prediction model were also more diverse. In addition, Ren [17] et al. proposed a discrete binomial coefficient combination prediction model for loess collapsibility based on a variety of data mining methods and achieved acceptable prediction accuracy. Zhou [18] established a matrix calculation equation for the collapsibility coefficient through multiple quadratic non-linear regression using MATLAB and achieved acceptable prediction accuracy. Zheng et al. [19] analysed the correlation between moisture content and the mechanical properties of loess through microscopic means. Sun [20] analysed the correlation between moisture content and loess collapsibility when identifying the main causes of collapse diseases of masonry structures in loess areas. Wong et al. [21] evaluated the impact of sedimentary moisture content on the collapse potential of a remoulded sample of natural loess through microscopic means. Reznik [22] proposed an analytical expression to describe the relationship between the mechanical properties of collapsible soil and the void ratio and moisture content of the soil. Parichehr [23] proposed an artificial neural network prediction model that links compaction characteristics, permeability, and soil shear strength with soil property indicators.

Due to its special geological conditions and topographic and geomorphic characteristics, the loess in the Ili River Valley area is distinct from that in other regions of China [24]. However, at present, the evaluation of loess collapsibility in China has mainly focused on the loess in northeast, central, and east China, and few scholars have evaluated the loess collapsibility in Xinjiang. Therefore, this paper collected various physical, hydraulic, and mechanical parameters of loess in Xinyuan County and analysed the correlation of various soil property indicators of collapsible loess by means of mathematical statistics based on observed engineering cases. In addition, a prediction model for loess collapsibility in this area was established using multiple linear regression theory and the neural network method. Finally, the rationality, effectiveness, and accuracy of the established prediction model were verified through observed engineering in the area. By analysing the correlation of various soil property indicators of collapsible loess in the Ili River Valley area and establishing the prediction model, geological bases can be provided for the survey, design, and construction of engineering projects in the area.

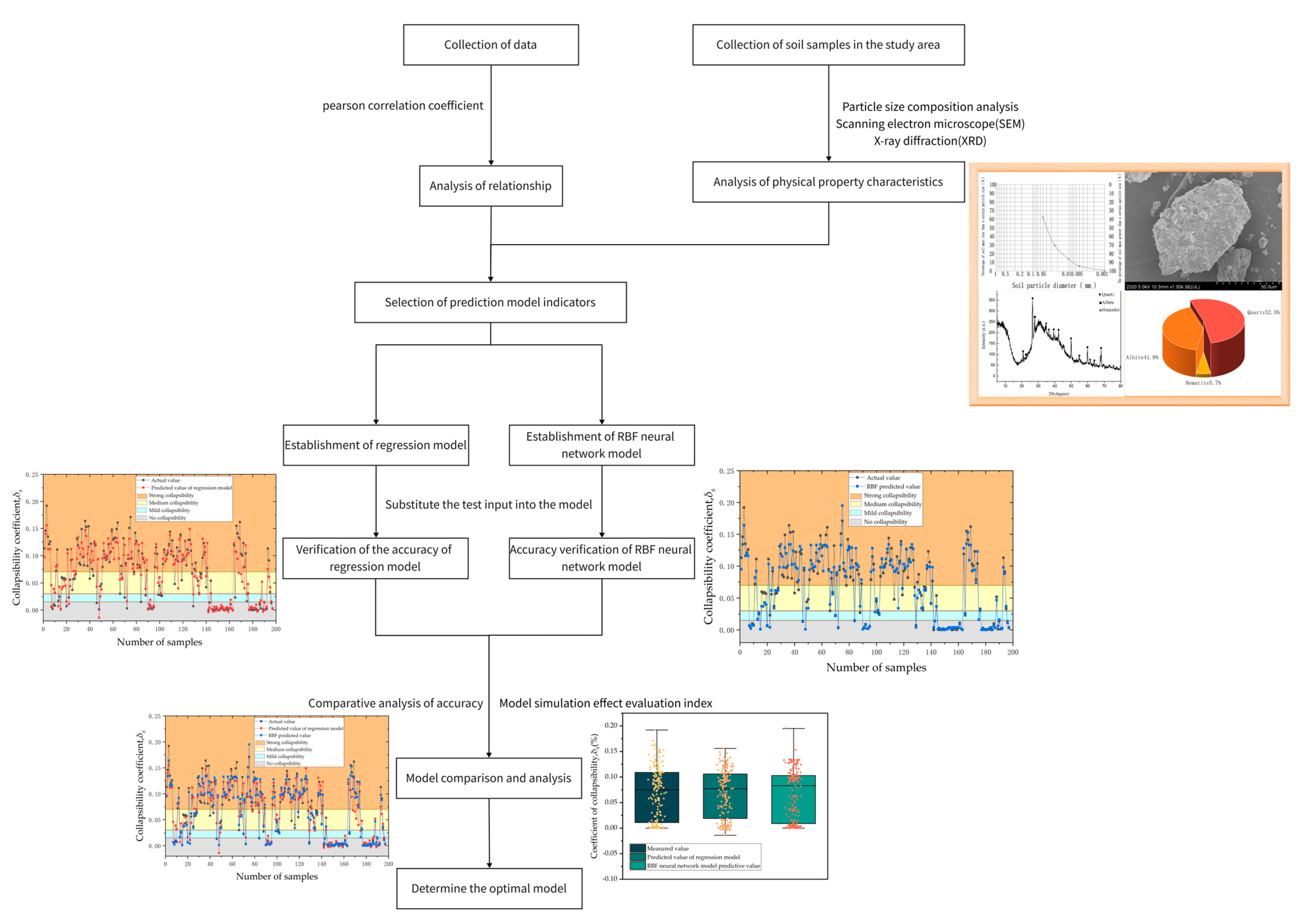
2. Materials and Methods

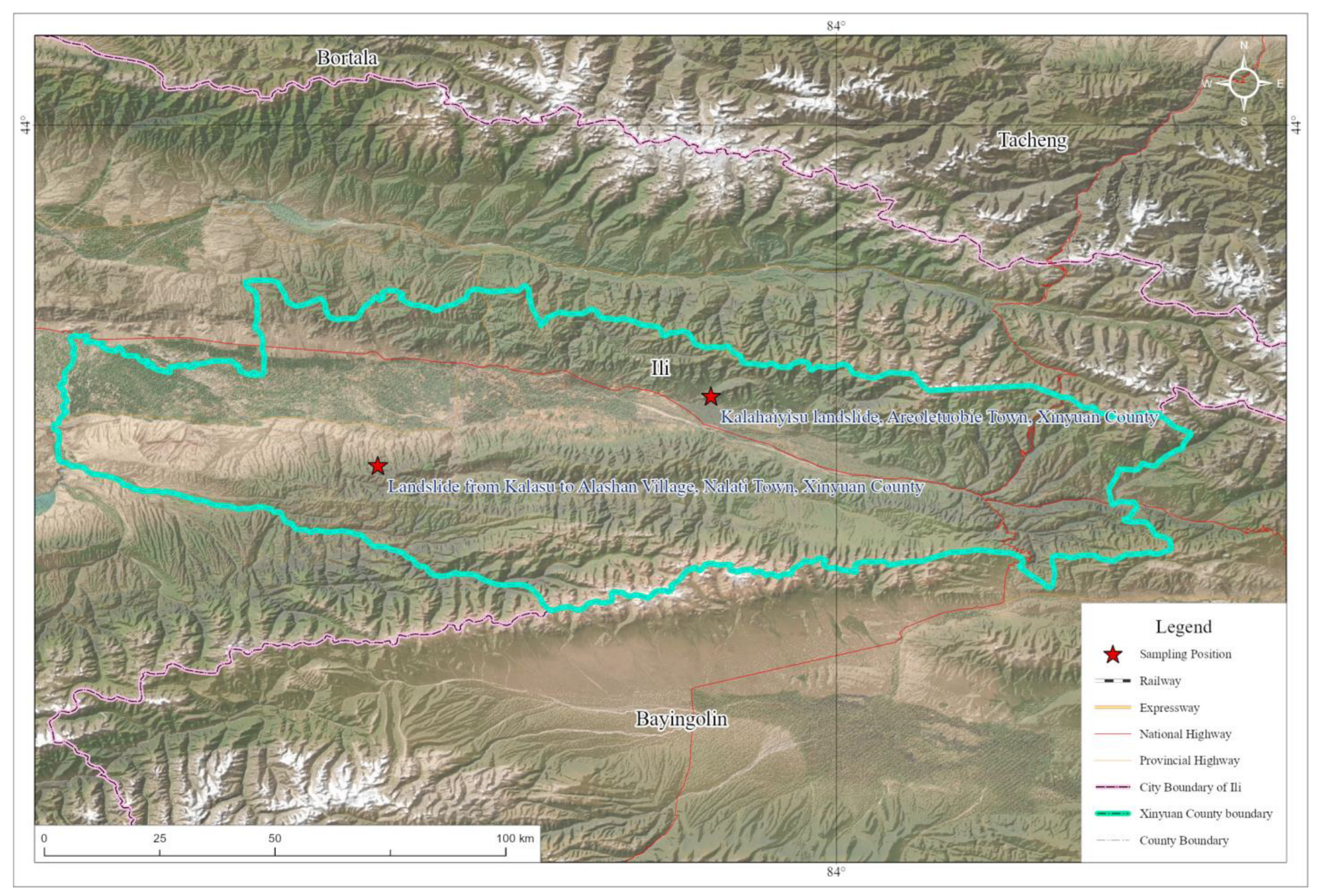
2.1. Data Sources

This study compiled the results of 197 groups of loess strata in Xinyuan County’s Yili Valley that underwent geotechnical testing. The geotechnical test data are primarily derived from the special exploration project of the landslide geological environment from Kalasu to Alashan Village, Nalati Town, Xinyuan County, Xinjiang, the special exploration project of the landslide disaster in Kalahaiyisu, Areoletuobie Town, Xinyuan County, Xinjiang, and the findings of previous studies in this region. Figure 1 depicts the research area’s location. The research flow chart for this work is shown in Figure 2.

In the probabilistic statistical analysis of the physical and mechanical parameters of collapsible loess in Xinyuan County, characteristic statistics, such as mean value, standard deviation, and coefficient of variation, can be obtained. These characteristic statistics can characterize the spatial randomness of geotechnical physical and mechanical parameters. The statistical information of geotechnical test data of loess stratum in the study area is shown in

Table 1. Soil properties analysis of collapsible loess in the study area.

	Mean Value	Standard Deviation	Coefficient of Variation	Maximum Value	Minimum Value
Sampling depth, h	11.93	13.44	1.13	74.8	0.60
Moisture content, ω (%)	12.73	5.32	0.42	26.97	3.39
Density, ρ (g/cm3)	1.58	0.23	0.14	2.13	1.232
Dry density, ρd (g/cm3)	1.4	0.17	0.12	1.90	1.06
Porosity ratio, e	0.95	0.23	0.24	1.53	0.42
Saturation, Sr (%)	39.96	23.33	0.58	110.05	8.31
Porosity, n (%)	47.88	6.3	0.13	60.51	29.51
Liquid limit, ωL (%)	26.59	1.46	0.06	31.6	24.00
Plastic limit, ωp (%)	17.65	1.43	0.08	22.6	14.80
Plasticity index, Ip	8.94	0.72	0.08	9.96	6.10
Liquidity index, IL	−0.54	0.57	−1.05	1.11	−1.54

.

2.2. Test Method

Firstly, indoor geotechnical tests were conducted on the collapsible loess in the study area. The testing of physical and mechanical parameters was conducted in accordance with the “Standard for Soil Test Methods” (2019, China) [25]. Afterwards, the micro-structure and material composition of collapsible loess in the study area were tested at the Physical and Chemical Testing Centre of Xinjiang University. The SU8000 series field emission scanning electron microscope and D8 Advance series X-ray powder diffractometer were utilised.

2.3. Physical Properties

• Particle size composition analysis

The soil samples obtained from the Kalasu–Alashan Village landslide in Nalati Town, Xinyuan County, were tested for particle analysis, and their particle grading curves were plotted, as shown in Figure 3.

According to “Soil Properties and Soil Mechanics (Fifth Edition) [26]”, when the cumulative curve of the soil concaves upward, the slope is gentle, the non-uniformity coefficient (Cu) is greater than 5, and the curvature coefficient Cs = 1–3; this indicates that the particle size grading of the soil is good. From Figure 3, the Cu and Cs of the loess in the study area are 6.12 and 1.47, respectively, indicating a good particle size grading.

2.

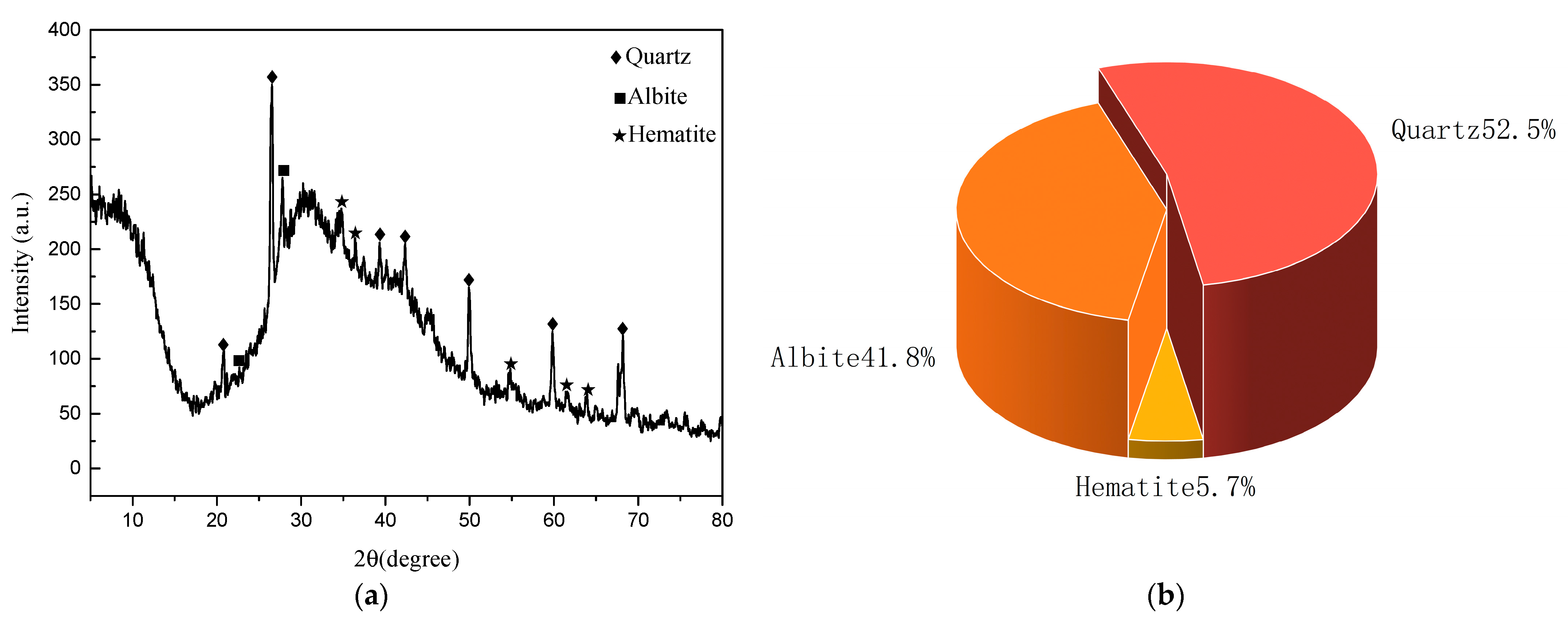
Micro-structure analysis

With a field emission scanning electron microscope of the SU8000 series, the pore size and contact relationship of the loess particles in Xinyuan County were studied. Figure 4a to Figure 4d display the loess observation data obtained using a scanning electron microscope in Xinyuan County.

Figure 4 shows that the loess exhibits a flocculent structure, mainly in the form of support contact. Mineral particles often appear in thin flakes. Thin minerals form a stacked structure and are arranged in a relatively scattered manner. Mineral particles and loess particles are interconnected in a support–inlay contact manner. The pore structure is often porous or irregular.

3.

Material composition analysis

As seen in Figure 5a, the primary mineral components of collapsible loess in the research area were examined by X-ray diffraction. As can be seen, quartz, albite, and hematite make up the majority of the collapsible loess’ mineral composition in the study area. Other important minerals are SiO₂, Na (ALSi₃O₈), Fe₂O₃, and others. Figure 5b was produced using a quantitative analysis of the XRD test data. As can be shown, the loess samples in the study area have a Na (ALSi₃O₈) content of 52.5%, a SiO₂ content of 41.8%, and a Fe₂O₃ content of 5.7%.

3. Correlation Analysis between Soil Properties and Loess Collapsibility

3.1. Correlation Analysis Data

In this study, the collapsibility coefficient and soil index of the loess were correlated using the Pearson correlation analysis method and SPSS 26 software.

Table 2. Correlation analysis between the collapsibility coefficient and each soil property parameter in the study area.

Correlation Index	Regression Equation	Saliency Score	Correlation Coefficient	Correlation
δs − ρ	δs = −0.194ρ + 0.375	0.000	−0.857	extremely strong
δs − Sr	δs = −0.002Sr + 0.138	0.000	−0.800	extremely strong
δs − n	δs = 0.006n − 0.233	0.000	0.768	strong
δs − ρd	δs = −0.233ρd + 0.395	0.000	−0.768	strong
δs − e	δs = 0.172e − 0.095	0.000	0.757	strong
δs − ω	δs = −0.006ω + 0.145	0.000	−0.628	strong
δs − IL	δs = −0.054IL + 0.039	0.000	−0.595	medium
δs − h	δs = −0.001h + 0.086	0.000	−0.385	weak
δs − IP	δs = 0.015Ip − 0.066	0.003	0.211	weak
δs − ωP	δs = −0.005ωp + 0.161	0.039	−0.147	extremely weak
δs − Es	δs = 8.134E − 4Es + 0.059	0.197	0.092	no
δs − a	δs = 0.017a + 0.063	0.305	0.073	no
δs − ωL	δs = −0.001ωL + 0.106	0.571	−0.041	no

δ_s is the collapsibility coefficients, ρ is the density, Sr is the saturation, n is the porosity, ρ_d is the dry density, e is the porosity ratio, ω is the moisture content, I_L is the liquidity index, h is the sampling depth, I_P is the plasticity index, ω_P is the Plastic limit, E_s is the compression modulus, a is the compressibility coefficient, ω_L is the liquid limit.

displays the details of the analysis.

According to conventional wisdom, a correlation coefficient |r| between 0.8 and 1.0 indicates an extremely strong correlation; 0.6 to 0.8 indicates a strong correlation; 0.4 to 0.6 indicates a moderate correlation; 0.2 to 0.4 indicates a weak correlation; and 0 to 0. 2 indicates either no correlation or an extremely weak correlation. Table 2’s correlation analysis findings show that. As can be seen, there is a strong, moderate, medium, weak, and no link between the collapsibility and soil indexes in the research area [27,28,29]. The following is a strong specific analysis and strong correlation:

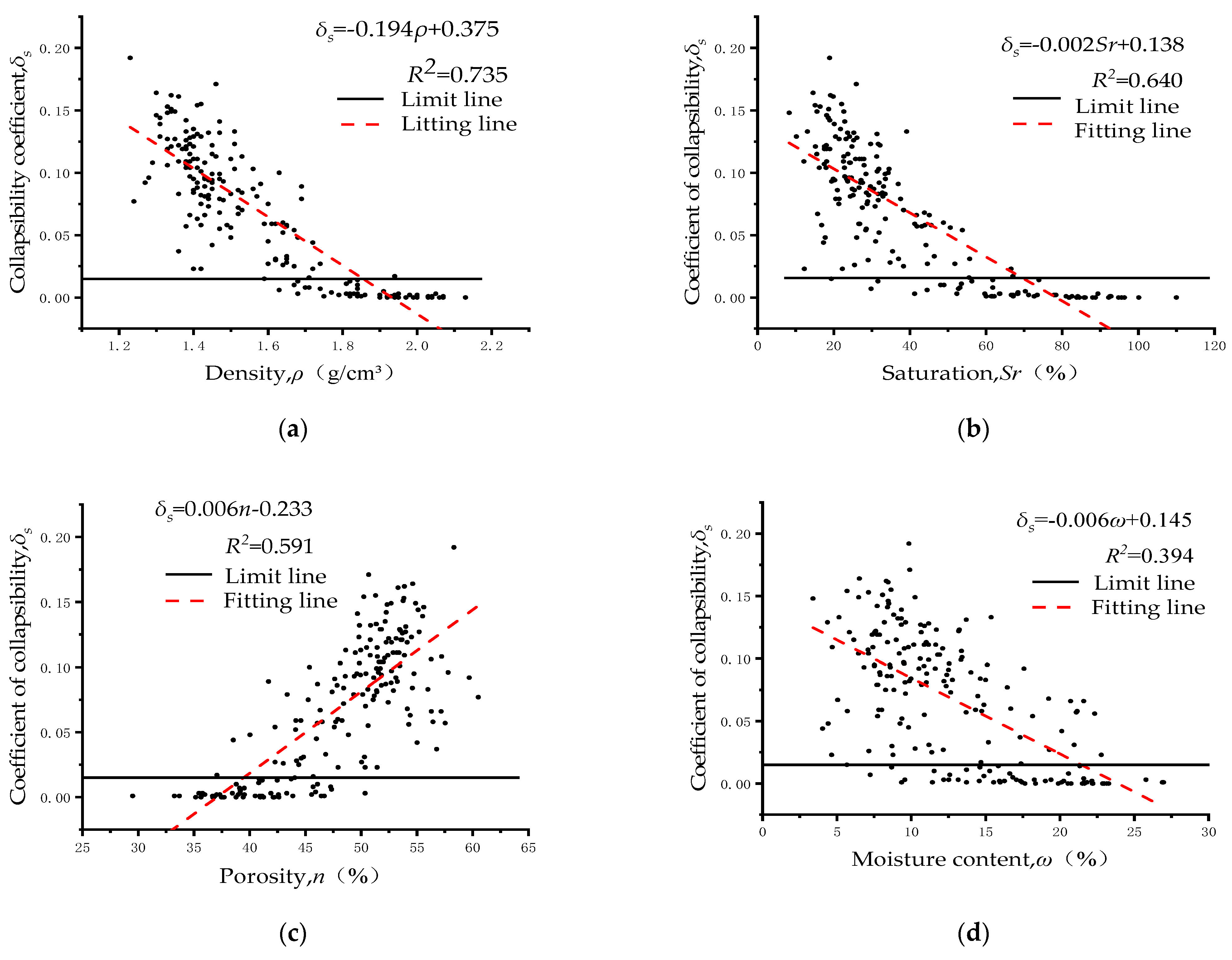
• Between 0.800 and 0.857, or a substantial association, is shown by the Pearson correlation coefficient between the collapsibility coefficients δ_s, density ρ, and saturation Sr. The density ρ, saturation Sr, and collapsibility coefficients δ_s all have an extremely strong negative connection. Figure 6a through Figure 6b display the scatter plots. The scatter plots of the sample points in the figures show that they are ordered in a systematic way, with a high correlation trend and great significance.
• Between 0.628 and 0.768, or a strong association, is indicated by the Pearson correlation coefficient between the collapsibility coefficient δ_s, porosity n, dry density ρ_d, void ratio e, and moisture content ω. The collapsibility coefficient δ_s and porosity n and void ratio e have a strong positive correlation, whereas the collapsibility coefficient δ_s and dry density ρd and moisture content ω have a strong negative correlation. Figure 6c through Figure 6f display the scatter plots. The scatter plots of the sample points in the figures can be seen to be organized and to have a high correlation trend and great significance.

3.2. Correlation Analysis between Collapsibility Index and Single Physical Index

Six characteristics of loess density, saturation Sr, porosity n, dry density ρd, void ratio e, and moisture content in the study area were chosen to discuss their correlation with the collapsibility coefficient based on the findings of the correlation analysis of the loess in the area.

Because of the destruction of the soil structure caused by immersion and the overlying pressure when the loess is in a high−porosity and low−density state, a significant portion of the soil pores are filled with soil particles. This is why density, dry density, the void ratio, and porosity are strongly correlated with the loess collapsibility coefficient. Reduced soil pores, higher compactness, decreased volume, and a significant collapsible deformation are all produced. Loess’s collapsibility coefficient and its moisture content and saturation are highly correlated. This is due to the fact that as the moisture content rises, the loess’s structural strength will vary substantially. High friction, high shear strength, and strong bonding forces between soil particles are present when the natural moisture content in the soil is low. Natural loess hence typically has a strong structural strength at a low moisture content, easily creates an overhead loose structure, and is easily capable of producing substantial collapsible deformation when subjected to external loads and water intrusion. Large amounts of water in loess cause an increase in pore water pressure and a drop in effective normal stress. Additionally, when the amount of free water increases and the water film thickens, there will be less friction between soil particles, which will result in a fall in molecular gravity. It lacks the overhead structure required to create strong collapsibility, has poor structural strength, and gradually forms a rather thick structure under its own weight. Loess has a weak collapsibility in conditions of high natural moisture content and saturation [30,31].

3.3. Selection of Prediction Model Indicators

According to the correlation analysis between the loess collapsibility coefficient and the loess property indicators in the study area, the correlation degrees of the six parameters, density ρ, dry density ρ_d, void ratio e, degree of saturation S_r, porosity n, and moisture content ω, of loess in the study area were extremely strong and strong. There was a computational relationship between density ρ and dry density ρ_d, as well as between porosity n and the void ratio e, and their physical meaning was similar. In addition, in the prediction model, they lead to a strong collinearity relationship, affecting the significance and effectiveness of the prediction model. Therefore, this paper selected four parameters, density ρ, degree of saturation S_r, porosity n, and moisture content ω, as the discriminative indicators of the prediction model.

4. Construction of the Prediction Model of Loess Collapsibility

4.1. Multiple Linear Regression Model

With the help of prior research findings and 197 sets of geotechnical test data from typical projects in Xinyuan County, Xinjiang, the regression model for this study was created. Using SPSS 26 software, it was then tested to see how well the chosen index parameters fit the study area.

Table 3. Constant statistics.

Model	R	R2	$\overline{{\mathit{R}}^{\mathbf{2}}}$	The Error of the Standard Estimate (S)
1	0.903	0.816	0.812	0.02233

displays the test results.

Table 3 shows that the regression model for predicting the loess collapsibility in the study area had a multiple correlation coefficient of R = 0.903, the square of which was R² = 0.816. The square of the modified correlation coefficient was R² = 0.812, and the error of the standard estimate was S = 0.02233. When 0.8 < R < 1, this indicates that the fitting degree of the prediction regression model is extremely high [28].

Based on the fitting degree of the regression model and the test results of significance in

Table 4. Variance analysis.

Model	Parameter	Non−Normalized Coefficients		Normal Coefficient	t	Sig
		B	Standard Error
1	(Constant)	−0.672	0.904		−0.743	0.458
	Moisture content, ω (%)	−0.013	0.003	−1.379	4.330	0.00
	Density, ρ (g/cm3)	0.116	0.334	0.513	0.349	0.728
	Degree of saturation, Sr (%)	0.002	0.001	1.063	3.217	0.002
	Porosity, n (%)	0.013	0.009	1.614	1.444	0.150

, a prediction regression model for loess collapsibility in the region was established, as shown in Equation (1):

$${\delta }_s=-0.672-0.013\omega +0.116\rho +0.002Sr+0.013n$$

(1)

where ω is the moisture content, ρ is the density, Sr is the saturation, and n is the porosity.

Table 3 shows that the Sig values of the model constant, density ρ, and porosity n were greater than 0.05, so further optimization was needed for this model.

This paper used the stepwise regression method to further optimize the established multiple linear regression model. After optimization and parameter selection, a prediction regression model for loess collapsibility in the region was established, as shown in Equation (2):

$${\delta }_s=0.633-0.364\rho -0.009\omega +0.003Sr$$

(2)

where ω is the moisture content, ρ is the density, Sr is the saturation.

To further confirm the prediction regression model’s accuracy in the study area, 197 sets of geotechnical test data from previous research findings and a collection of typical projects in Xinyuan County were substituted into the model using the loess collapsibility criteria found in the “Engineering Geological Handbook [32]”. Figure 7 displays the specific verification results.

As shown in Figure 7, the verification of the multiple linear regression model can yield the following results. Among the 197 sets of sample data, 157 sets predicted by the multiple linear regression model had the same degree of collapsibility as the actual value, while 40 sets had predicted degree of collapsibility that differed from the actual value. The effectiveness of the multiple linear regression model was 79.70%.

4.2. Neural Network−Based Prediction Model

The MLP (multi−layer perceptron) and RBF (radial basis function) are the two fundamental components of the neural network prediction model creation process. The RBF (radial basis function) method stands out among the rest due to its self−adaptive structure determination and output value independence from beginning weights. In prediction and classification, the activation function is employed as the mean square error function, and the RBF network has faster training times than the MLP. As a result, the RBF (radial basis function) method was mostly used in this research to develop the prediction model of the loess collapsibility in the studied area. RBF neural networks are capable of accurately approximating any continuous function. The input of an RBF neural network is mapped non−linearly to the hidden layer, while the hidden layer is mapped linearly to the output. The local minimum problem is avoided, and the learning speed is increased with this structure [33].

In this work, the prediction model of loess collapsibility in the investigated area was established using the RBF neural network. In Xinyuan County, the model’s partition setting designates 62.9% of the sample data as the training set, 26.4% as the test set, and 10.7% as the persistence set.

Table 5. Data value processing summary.

Data Message	Number of Samples N (Group)	Percentage
Train	124	62.9%
Test	52	26.4%
Reservation	21	10.7%
Valid	197	100%
Excluded	0
Grand total	197

displays a summary of how the model data values were processed. The assigned data were then fed into the neural network model as the model’s input layer. The buried layer space was directly transferred to the input data. The final model was obtained by mapping the vector from the low dimension to the high latitude using the linear weighted sum of the hidden layer space [34,35].

The prediction model was substituted into the 197 sets of geotechnical parameters obtained from the typical projects in Xinyuan County, and the predicted value of collapsibility was obtained. This further verifies the accuracy of the RBF neural network prediction model of loess collapsibility in the study area. To assess the accuracy and validity of the prediction model, the predicted and actual collapsibility degrees were compared. Figure 8 displays the particular outcomes of the verification.

Figure 8 shows that among the 197 sets of geotechnical test data collected from typical projects in Xinyuan County, 186 sets of RBF neural network models have the same degree of collapsibility with the actual value, and 11 sets of RBF neural network models have different degrees of collapsibility with the actual value. The effectiveness of the RBF neural network prediction model reached 94.42%. Therefore, the established RBF neural network prediction model can effectively predict the grade of loess collapsibility in the study area.

4.3. Model Simulation Effect Evaluation Index

The following four performance indicators were extensively employed to qualitatively assess the performance of the generated models in order to further assess the established regression model and neural network model: The following expressions were used to express the root mean squared error (RMSE), correlation coefficient (CC), Nash–Sutcliffe efficiency coefficient (NSE), and percent bias (PBIAS) [36,37,38,39]:

$$RMSE=\sqrt{\frac{{\displaystyle {\sum }_{i=1}^n{({\delta }_{sim}-{\delta }_{obs})}^2}}{n}}$$

(3)

$$CC=\frac{{\displaystyle {\sum }_{i=1}^n({\delta }_{obs}-{\overline{\delta }}_{\mathit{obs}})({\delta }_{sim}-{\overline{\delta }}_{\mathrm{sim}})}}{\sqrt{{\displaystyle {\sum }_{i=1}^n{({\delta }_{obs}-{\overline{\delta }}_{\mathit{obs}})}^2{\displaystyle {\sum }_{i=1}^n{\left({\delta }_{sim}-{\overline{\delta }}_{\mathrm{sim}}\right)}^2}}}}$$

(4)

$$NSE=1-\frac{{\displaystyle {\sum }_{i=1}^n{({\delta }_{obs}-{\delta }_{sim})}^2}}{{\displaystyle {\sum }_{i=1}^n{({\delta }_{sim}-{\overline{\delta }}_{obs})}^2}}$$

(5)

$$PBIAS(\%)=\frac{{\displaystyle {\sum }_{i=1}^n({\delta }_{sim}-{\delta }_{obs})}}{{\displaystyle {\sum }_{i=1}^n{\delta }_{\mathit{obs}}}}\times 100$$

(6)

where n is the number of measured values; δ_obs represents the measured collapsibility coefficient; δ_sim represents the collapsible coefficient δ_obs simulated by the prediction model; ${\overline{\delta }}_{\mathit{obs}}$ and ${\overline{\delta }}_{\mathit{sim}}$ represent the average value of the measured collapsible coefficient and the collapsible coefficient simulated by the prediction model.

Table 6. Simulation effect evaluation indicators.

Name	Definition	Value Ranges	Optimal Value
Root Mean Squared Error (RMSE)	Measure the deviation between the predicted value and the true value	[0, +∞]	0
Correlation Coefficient (CC)	Evaluate the simulated value and the measured value	[−1, 1]	1 or −1
Nash–Sutcliffe Efficiency Coefficient (NSE)	The prediction accuracy of the quantitative simulation model	[0, 1]	1
Percent Bias (PBIAS)	Evaluate the simulated value and the measured value	[−∞, +∞]	0

is the evaluation index of the model simulation effect.

Regression and neural network model performance indicators were computed in order to assess the model.

Table 7. Model’s assessment index.

Forecasting Model	Evaluating Indicator
	RMSE	CC	NSE	PBIAS (%)
Regression model	0.022	0.903	0.773	−0.007
RBF neural network model	0.014	0.962	0.919	−1.494

presents the evaluation outcomes.

The evaluation index of the model indicates that both the RBF neural network model and the regression model are effective and that their evaluation indices are near the ideal value. The regression model is not as good as the RBF neural network model in terms of prediction accuracy or the degree of fitting between the measured and simulated values. This is seen with the higher RMSE, CC, and NSE values of the RBF neural network model. The percentage variation between the expected and actual values of the RBF neural network model is somewhat more than that of the regression model, and the PBIAS value of the regression model is superior to that of the RBF neural network model. It is evident from a thorough investigation that the RBF neural network model outperforms the regression model by a wide margin.

5. Discussion

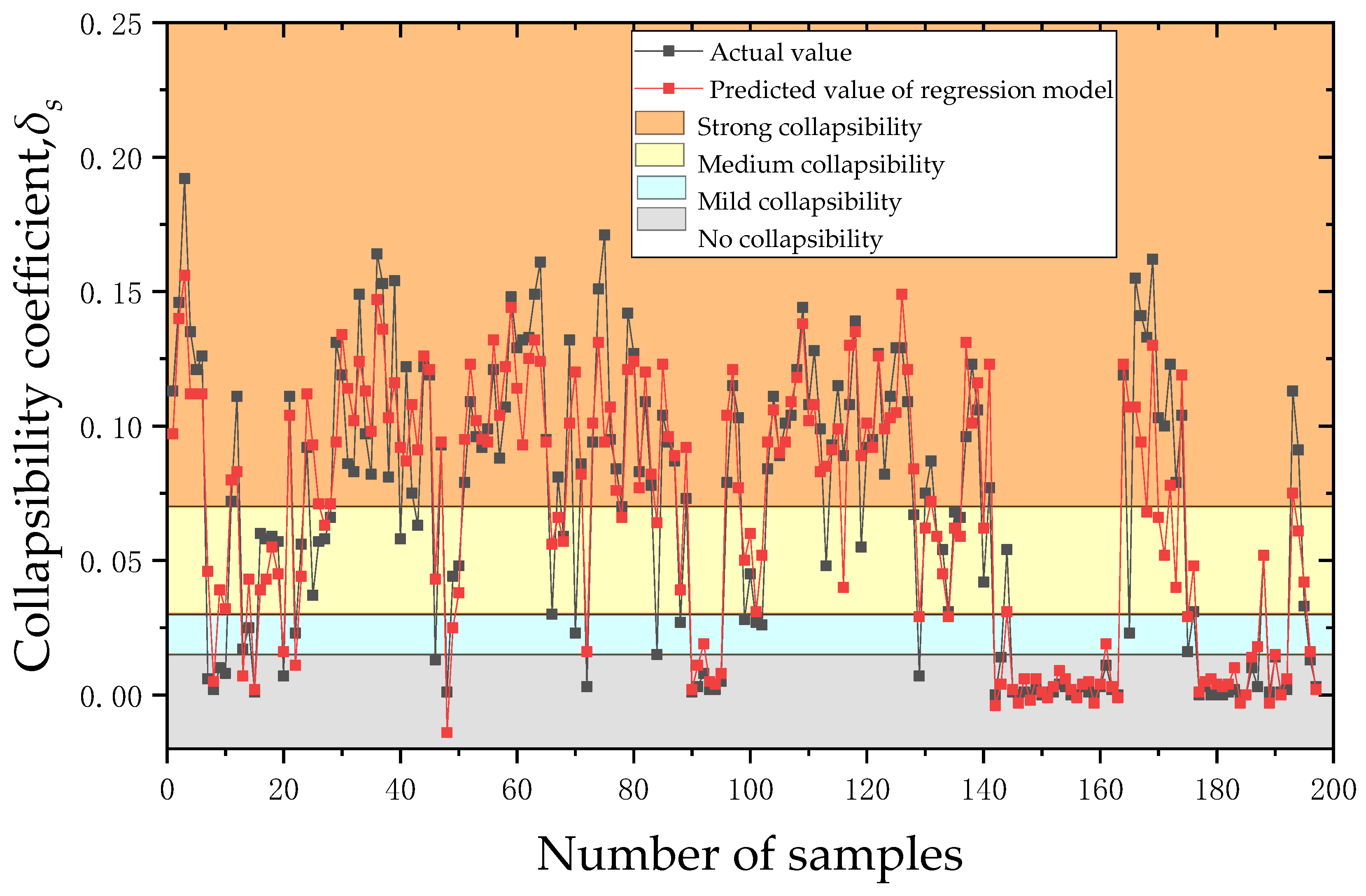
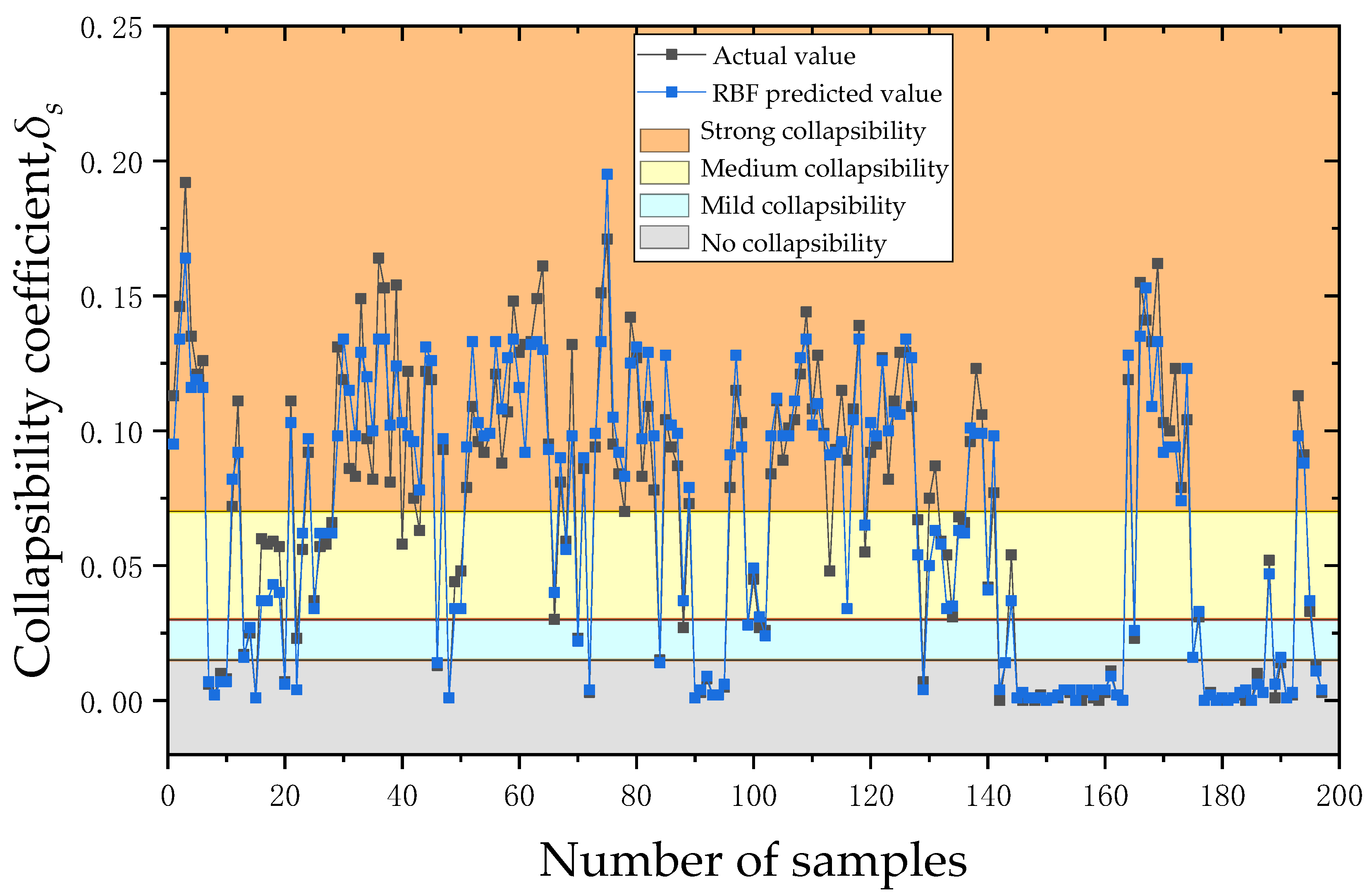
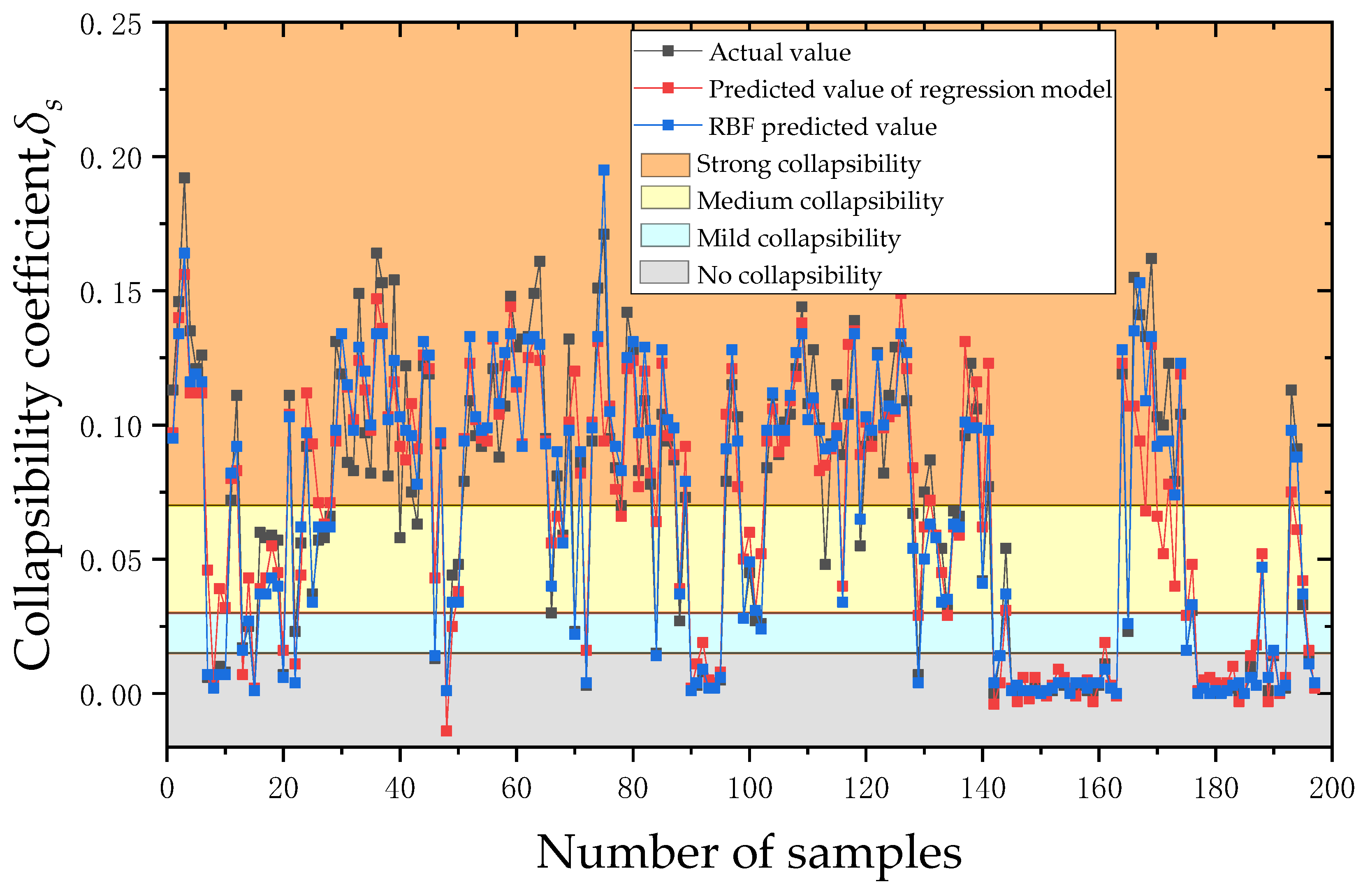
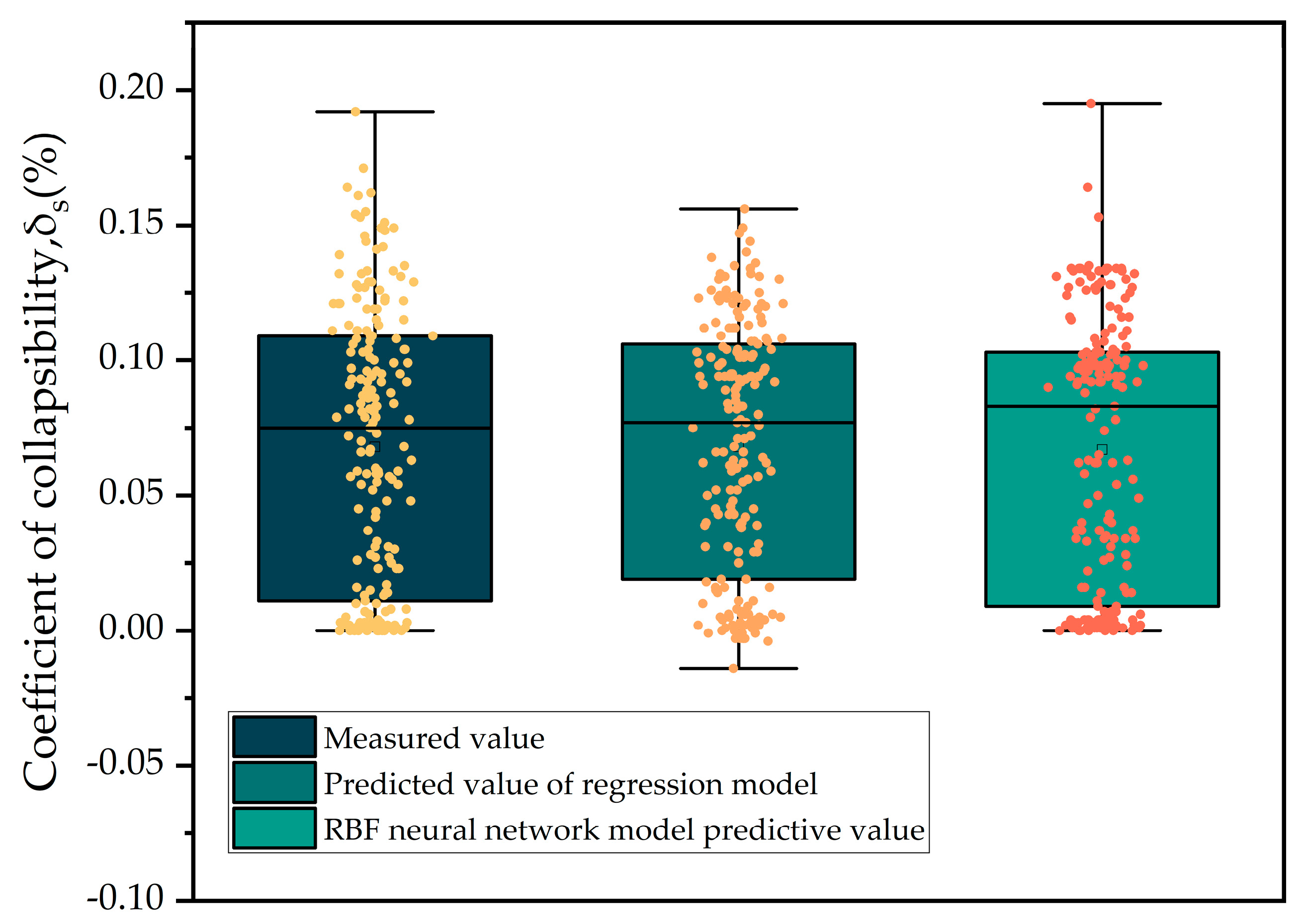
5.1. Comprehensive Comparative Analysis of the Models

The two loess collapsibility prediction models were thoroughly compared and analyzed in order to further verify the adaptability and accuracy of the established multiple linear regression model and RBF neural network model in Xinyuan County. The best prediction model suitable for the study area was then chosen. Figure 9 displays the comparison outcomes between the regression model and RBF neural network model for the research area’s prediction of loess collapsibility.

Figure 9 shows that the actual collapsibility coefficient in the study area ranged from 0 to 0.162 with a mean value of 0.068. The predicted value of the regression model ranged from −0.003 to 0.156 with a mean value of 0.068. The predicted value of the RBF neural network ranged from 0 to 0.195 with a mean value of 0.067. In addition, according to the evaluation criteria for loess collapsibility, 157 out of 197 sets of sample data in the study area predicted by the multiple linear regression model had the same degree of collapsibility as the actual value. For the remaining 40 sets of sample data, the predicted degree of collapsibility was different from the actual value. Thus, the prediction effectiveness was 79.70%. There were 186 groups of sample data predicted by the RBF neural network model to have the same degree of collapsibility as the actual value, and 11 groups of data predicted to have different degrees of collapsibility from the actual value. The effectiveness of the RBF neural network prediction model reached 94.42%.

The RBF neural network model and the regression model were assessed based on the model assessment indicator. The regression model’s values were as follows: The correlation coefficient (CC) was 0.903, the Nash–Sackliff efficiency coefficient (NSE) was 0.773, the percentage of deviation (PBIAS) was −0.007%, and the root mean square error (RMSE) was 0.022. The RBF neural network model has the following values: The correlation coefficient (CC) was 0.962, the Nash–Sutcliffe efficiency coefficient (NSE) was 0.919, the percentage of deviation (PBIAS) was −1.494%, and the root mean square error (RMSE) was 0.014.

The box diagram in Figure 10 shows the predicted value of the RBF neural network model, the predicted value of the regression model, and the measured value of the loess collapsibility coefficient. The box plot illustrates how well the upper and lower lines of the measured value and the predicted value of the RBF neural network model correspond and how the overall data distribution trend is similar to the measured value data distribution trend. Overall, the RBF neural network model’s projected value box plot score is greater than the regression model’s, and the surface RBF neural network model is more effective than the regression model [40].

After a comprehensive comparison, the RBF neural network prediction model was more suitable for the prediction of loess collapsibility in this area.

5.2. The Advantages and Limitations of RBF Neural Network Model

In an effort to offer a quick method for the analysis and evaluation of Loess collapsibility in the study area, the RBF neural network prediction model has been shown through thorough comparative analysis to have higher reliability and accuracy than the regression model. Additionally, the model’s validity and accuracy were further verified through a variety of evaluation indicators. The fast learning curve, arbitrary precision of arbitrary continuous function approximation, internal force of multi−dimensional nonlinear mapping, and an easy to understand learning algorithm are some of the benefits of the RBF neural network model. It can also predict and assess the collapsibility of loess with speed. However, there are still several issues with this study.

The establishment of an RBF neural network model requires a large amount of data. When the amount of data is too small, there may be overfitting, which will lead to the accuracy of the prediction model in the use process. At the same time, the model is very sensitive to the abnormal use of data. When the data used has a large discrete type, it may lead to the instability of the training results of the model.

6. Conclusions

This paper collected many physical, hydraulic, and mechanical parameters of collapsible loess in Xinyuan County, Ili River Valley, and analysed the correlations of soil parameters of collapsible loess with the collapsibility coefficient via mathematical statistics. In addition, the optimal parameters were selected as the determination indicators for the prediction model. Finally, the collapsibility prediction model of loess in Xinyuan County, Ili River Valley, was established with multiple linear regression theory and the neural network method. The following main conclusions were drawn:

• The engineering geological conditions and the physical properties of the loess in the study area were analyzed. The single−layer soil of the Quaternary loess in the research area is mostly collapsible and self−weight collapsible, with poor engineering geological conditions. The loess particle structure in this area is mainly cylindrical, flat, and irregular. The main contact between particles is support contact, supplemented by inlay contact, forming many inter−particle pores and some large pores. The loess in the study area is mainly composed of quartz and albite, with less hematite.
• The correlation between the loess collapsibility coefficient and soil property indicators in the study area was analyzed. The correlation analysis results showed that the loess collapsibility coefficient δ_s in the study area was extremely strongly correlated with the density ρ and the degree of saturation Sr; strongly correlated with the porosity n, dry density ρd, void ratio e, and moisture content ω; moderately correlated with the liquidity index I_L; weakly correlated with the sampling depth h and plasticity index Ip; extremely weakly correlated with the plastic limit ωp; and not correlated with the compression modulus Es, compression coefficient a, and liquid limit ω_L. Finally, four parameters, the density ρ, degree of saturation Sr, porosity n, and moisture content ω, were selected as determination indicators for the prediction model.
• In the studied region, a prediction model for loess collapsibility was developed. According to the prediction model’s results, the likelihood that a given event will occur is predicted with a 76.70% accuracy for multiple linear regression and a 94.42% accuracy for RBF neural network prediction. Simultaneously, the RBF neural network prediction model’s evaluation index clearly outperforms the regression prediction model’s. As a result, the thorough comparison analysis demonstrates that the RBF neural network prediction model outperforms the regression prediction model in terms of accuracy and dependability.
• The collapsibility of loess is the primary subject of this investigation. Subsequent research can take into account the relationship between additional soil indicators, such as the relationship between soil physical parameters and the compression coefficient, and develop a prediction model. At the same time, how to further deal with the results of this study, so that one can carry out rapid evaluation in engineering construction, is a direction of future research.