1. Introduction
Collapsible loess refers to soil that undergoes significant additional deformation due to the structural failure of the soil following water immersion under the self-weight stress of the overlying soil layer or under the combined action of self-weight stress and additional stress. It is a type of special soil [
1]. At this stage, many geotechnical test data have been accumulated during extensive engineering practices in the Ili River Valley area; however, the technicians have not effectively used and mined these data. Therefore, it is necessary to establish a prediction model that can quickly evaluate the loess collapsibility in the Ili River Valley area based on the correlation analysis between the collapsibility coefficient of the loess in Xinyuan County and the soil property indices.
Through the use of mathematical statistics, scholars globally have conducted extensive research on the correlation between loess collapsibility and soil properties. Shu et al. [
2] established a binary regression relationship between the initial moisture content, the initial void ratio, and the collapsibility coefficient through the multivariate statistical analysis method by increasing and decreasing the loess moisture content in the experiments. Su [
3] carried out many double-line indoor loess collapsibility tests and established the regression equation between the collapsibility coefficient and various soil property indicators with the help of mathematical statistics. Li [
4] analysed the degree of correlation between the basic physical property indicators of loess-like soil in southern Hebei, and the collapsibility coefficient and initial pressure of collapse through qualitative and partial correlation analysis, and ranked these. Zhu [
5] used mathematical statistics to analyse the correlation between the loess collapsibility coefficient and each soil property indicator and used factor analysis theory to analyse the loess physical property indicators. The author eliminated the impact of collinearity on the fitting and conducted an evaluation on the non-self-weight and self-weight collapsible sites. Zhang used mathematical statistics to analyse relevant loess physical indicators. Lv [
6] used mathematical statistics to analyse the correlation between loess collapsibility and moisture content and studied the correlation between the collapsibility coefficient and various physical property indicators. Garakani [
7] et al. studied the correlation between loess collapsibility and moisture content under isotropic and shear loads.
Establishing a prediction model for loess collapsibility is an effective means to solve the collapsibility problem. Liu [
8], Shao [
9], Wang [
10], Xing [
11], and Wang [
12] et al. used univariate linear regression, multiple linear regression, or non-linear regression methods to conduct regression analysis on the relationship between the collapsibility coefficient and a single soil property indicator or multiple soil property indicators and established regression equations. Li [
13], Jing [
14], Gao [
15], and Han [
16] et al. used data mining techniques, fuzzy information technology, and neural networks to predict the loess collapsibility coefficient. The soil property indicators considered by researchers when establishing the prediction model were also more diverse. In addition, Ren [
17] et al. proposed a discrete binomial coefficient combination prediction model for loess collapsibility based on a variety of data mining methods and achieved acceptable prediction accuracy. Zhou [
18] established a matrix calculation equation for the collapsibility coefficient through multiple quadratic non-linear regression using MATLAB and achieved acceptable prediction accuracy. Zheng et al. [
19] analysed the correlation between moisture content and the mechanical properties of loess through microscopic means. Sun [
20] analysed the correlation between moisture content and loess collapsibility when identifying the main causes of collapse diseases of masonry structures in loess areas. Wong et al. [
21] evaluated the impact of sedimentary moisture content on the collapse potential of a remoulded sample of natural loess through microscopic means. Reznik [
22] proposed an analytical expression to describe the relationship between the mechanical properties of collapsible soil and the void ratio and moisture content of the soil. Parichehr [
23] proposed an artificial neural network prediction model that links compaction characteristics, permeability, and soil shear strength with soil property indicators.
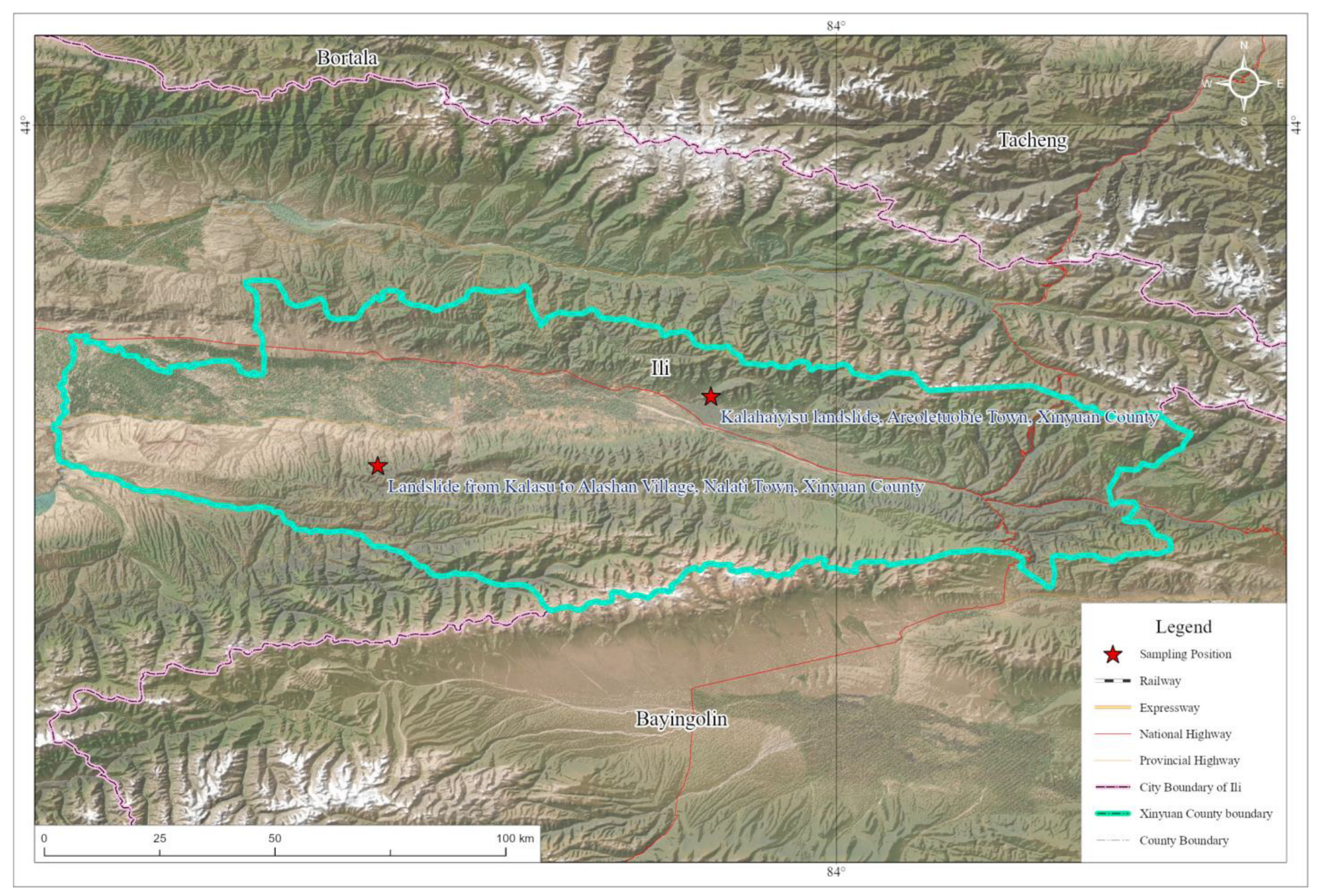
Due to its special geological conditions and topographic and geomorphic characteristics, the loess in the Ili River Valley area is distinct from that in other regions of China [
24]. However, at present, the evaluation of loess collapsibility in China has mainly focused on the loess in northeast, central, and east China, and few scholars have evaluated the loess collapsibility in Xinjiang. Therefore, this paper collected various physical, hydraulic, and mechanical parameters of loess in Xinyuan County and analysed the correlation of various soil property indicators of collapsible loess by means of mathematical statistics based on observed engineering cases. In addition, a prediction model for loess collapsibility in this area was established using multiple linear regression theory and the neural network method. Finally, the rationality, effectiveness, and accuracy of the established prediction model were verified through observed engineering in the area. By analysing the correlation of various soil property indicators of collapsible loess in the Ili River Valley area and establishing the prediction model, geological bases can be provided for the survey, design, and construction of engineering projects in the area.
3. Correlation Analysis between Soil Properties and Loess Collapsibility
3.1. Correlation Analysis Data
In this study, the collapsibility coefficient and soil index of the loess were correlated using the Pearson correlation analysis method and SPSS 26 software.
Table 2 displays the details of the analysis.
According to conventional wisdom, a correlation coefficient |r| between 0.8 and 1.0 indicates an extremely strong correlation; 0.6 to 0.8 indicates a strong correlation; 0.4 to 0.6 indicates a moderate correlation; 0.2 to 0.4 indicates a weak correlation; and 0 to 0. 2 indicates either no correlation or an extremely weak correlation.
Table 2’s correlation analysis findings show that. As can be seen, there is a strong, moderate, medium, weak, and no link between the collapsibility and soil indexes in the research area [
27,
28,
29]. The following is a strong specific analysis and strong correlation:
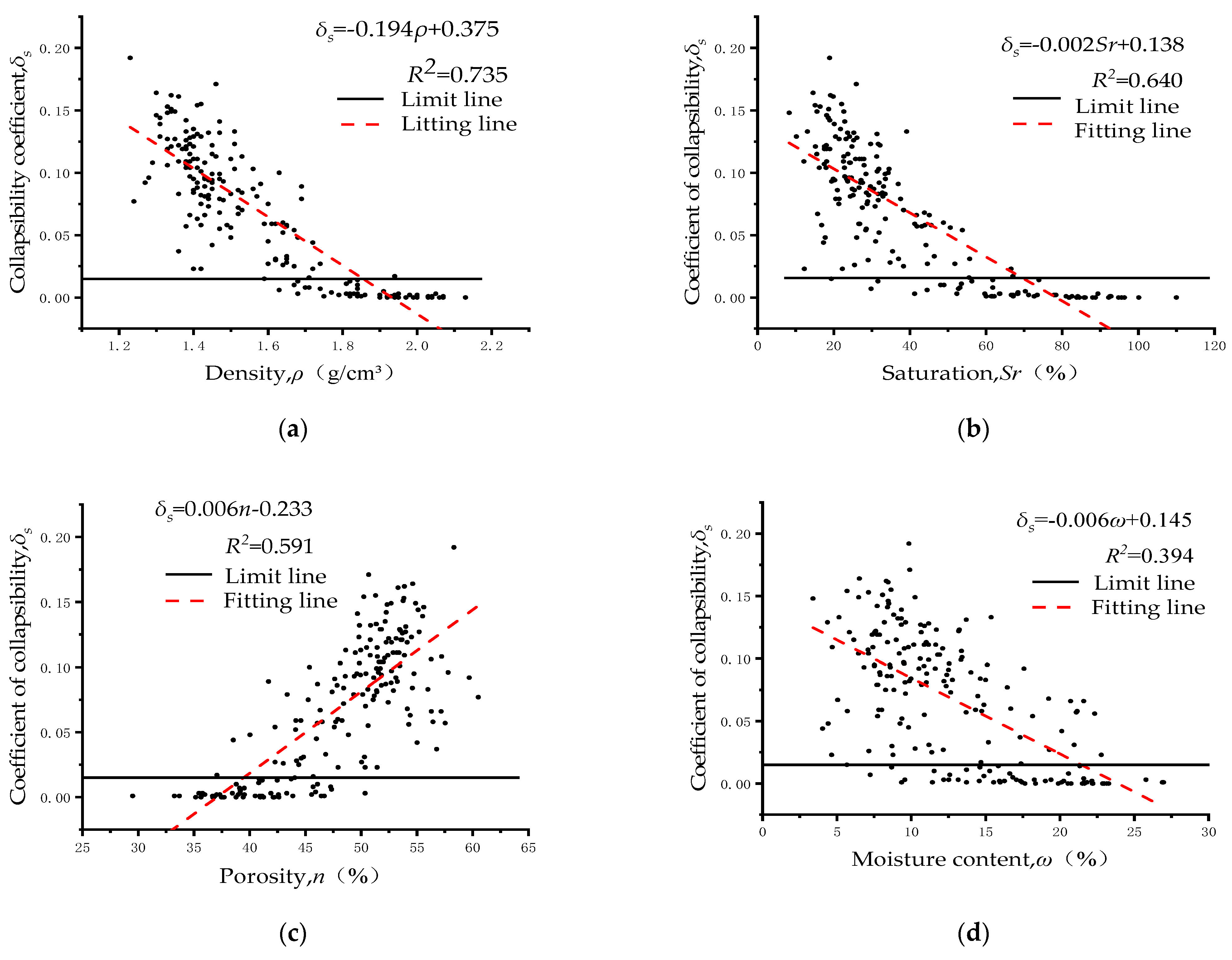
Between 0.800 and 0.857, or a substantial association, is shown by the Pearson correlation coefficient between the collapsibility coefficients
δs, density
ρ, and saturation
Sr. The density
ρ, saturation
Sr, and collapsibility coefficients
δs all have an extremely strong negative connection.
Figure 6a through
Figure 6b display the scatter plots. The scatter plots of the sample points in the figures show that they are ordered in a systematic way, with a high correlation trend and great significance.
Between 0.628 and 0.768, or a strong association, is indicated by the Pearson correlation coefficient between the collapsibility coefficient
δs, porosity
n, dry density
ρd, void ratio
e, and moisture content
ω. The collapsibility coefficient
δs and porosity
n and void ratio
e have a strong positive correlation, whereas the collapsibility coefficient
δs and dry density ρd and moisture content ω have a strong negative correlation.
Figure 6c through
Figure 6f display the scatter plots. The scatter plots of the sample points in the figures can be seen to be organized and to have a high correlation trend and great significance.
3.2. Correlation Analysis between Collapsibility Index and Single Physical Index
Six characteristics of loess density, saturation Sr, porosity n, dry density ρd, void ratio e, and moisture content in the study area were chosen to discuss their correlation with the collapsibility coefficient based on the findings of the correlation analysis of the loess in the area.
Because of the destruction of the soil structure caused by immersion and the overlying pressure when the loess is in a high−porosity and low−density state, a significant portion of the soil pores are filled with soil particles. This is why density, dry density, the void ratio, and porosity are strongly correlated with the loess collapsibility coefficient. Reduced soil pores, higher compactness, decreased volume, and a significant collapsible deformation are all produced. Loess’s collapsibility coefficient and its moisture content and saturation are highly correlated. This is due to the fact that as the moisture content rises, the loess’s structural strength will vary substantially. High friction, high shear strength, and strong bonding forces between soil particles are present when the natural moisture content in the soil is low. Natural loess hence typically has a strong structural strength at a low moisture content, easily creates an overhead loose structure, and is easily capable of producing substantial collapsible deformation when subjected to external loads and water intrusion. Large amounts of water in loess cause an increase in pore water pressure and a drop in effective normal stress. Additionally, when the amount of free water increases and the water film thickens, there will be less friction between soil particles, which will result in a fall in molecular gravity. It lacks the overhead structure required to create strong collapsibility, has poor structural strength, and gradually forms a rather thick structure under its own weight. Loess has a weak collapsibility in conditions of high natural moisture content and saturation [
30,
31].
3.3. Selection of Prediction Model Indicators
According to the correlation analysis between the loess collapsibility coefficient and the loess property indicators in the study area, the correlation degrees of the six parameters, density ρ, dry density ρd, void ratio e, degree of saturation Sr, porosity n, and moisture content ω, of loess in the study area were extremely strong and strong. There was a computational relationship between density ρ and dry density ρd, as well as between porosity n and the void ratio e, and their physical meaning was similar. In addition, in the prediction model, they lead to a strong collinearity relationship, affecting the significance and effectiveness of the prediction model. Therefore, this paper selected four parameters, density ρ, degree of saturation Sr, porosity n, and moisture content ω, as the discriminative indicators of the prediction model.
5. Discussion
5.1. Comprehensive Comparative Analysis of the Models
The two loess collapsibility prediction models were thoroughly compared and analyzed in order to further verify the adaptability and accuracy of the established multiple linear regression model and
RBF neural network model in Xinyuan County. The best prediction model suitable for the study area was then chosen.
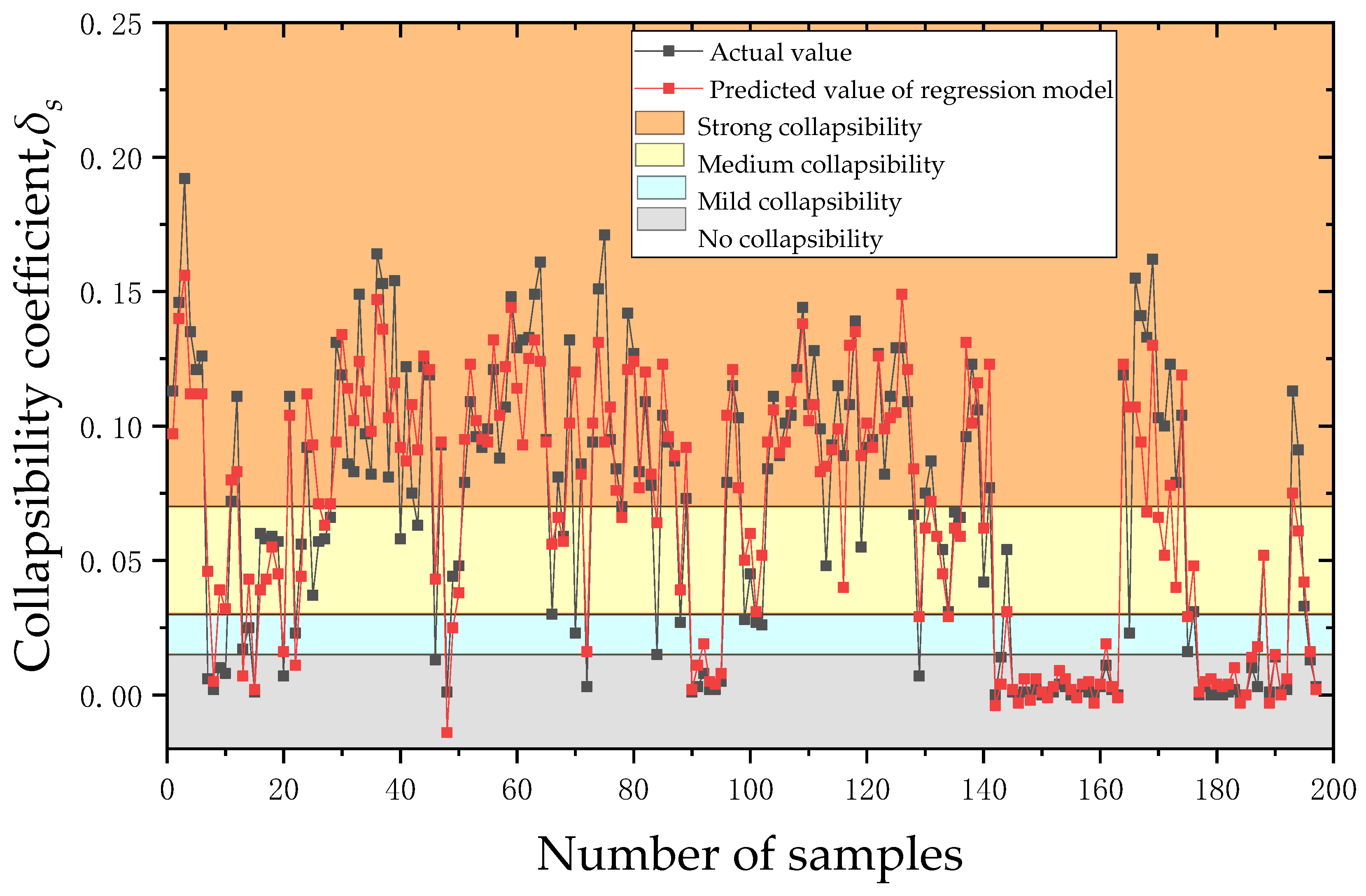
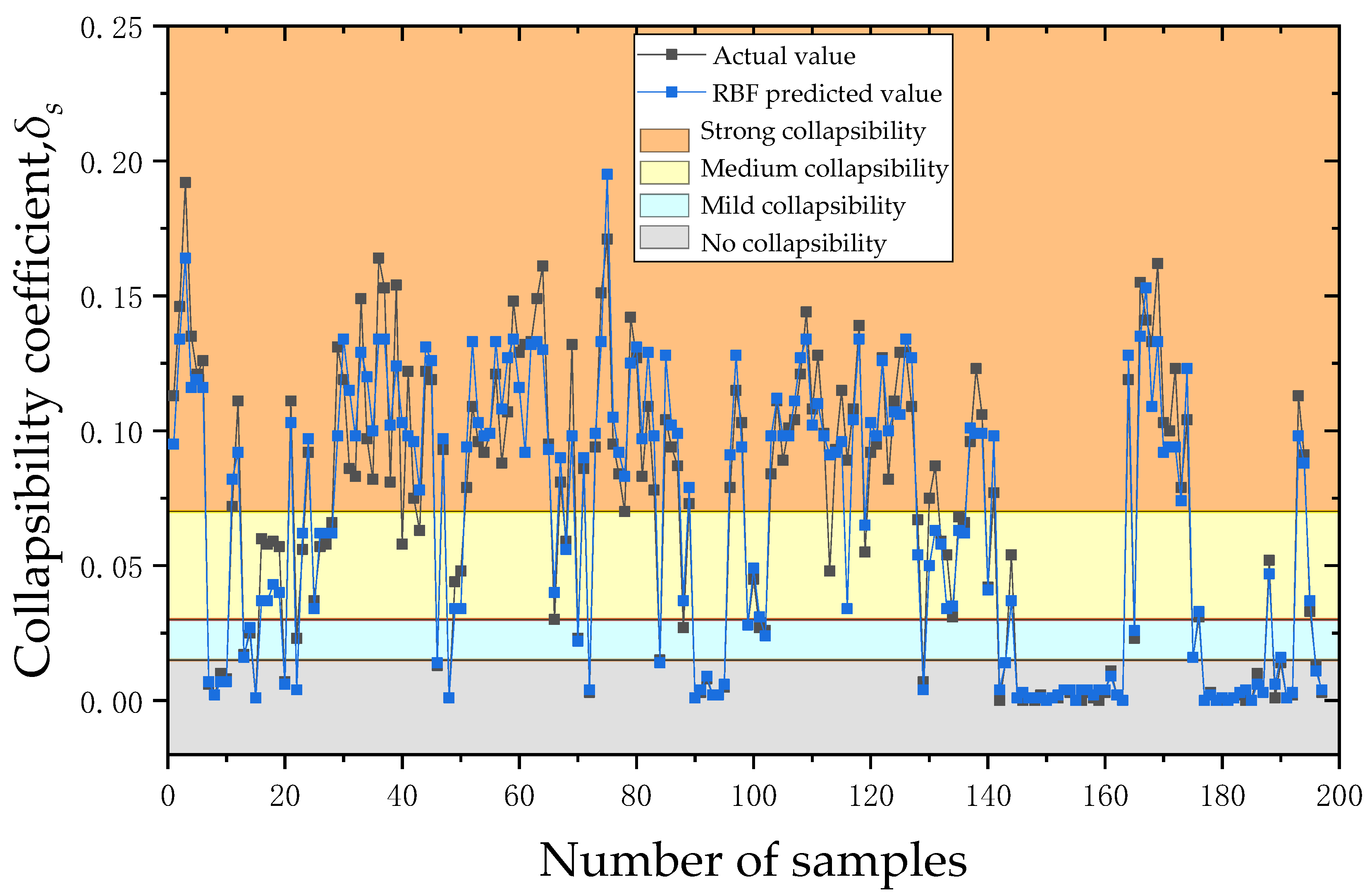
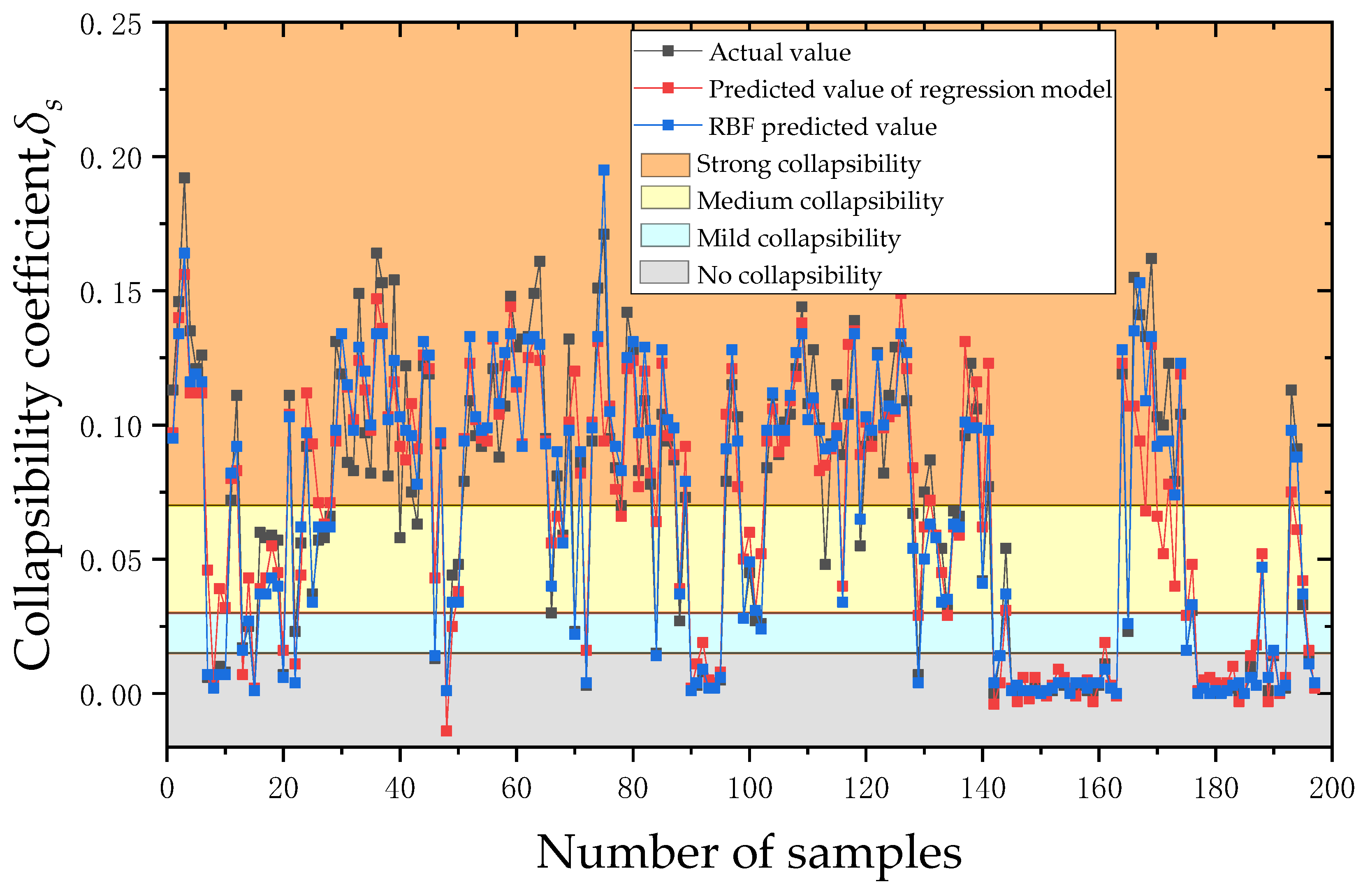
Figure 9 displays the comparison outcomes between the regression model and RBF neural network model for the research area’s prediction of loess collapsibility.
Figure 9 shows that the actual collapsibility coefficient in the study area ranged from 0 to 0.162 with a mean value of 0.068. The predicted value of the regression model ranged from −0.003 to 0.156 with a mean value of 0.068. The predicted value of the
RBF neural network ranged from 0 to 0.195 with a mean value of 0.067. In addition, according to the evaluation criteria for loess collapsibility, 157 out of 197 sets of sample data in the study area predicted by the multiple linear regression model had the same degree of collapsibility as the actual value. For the remaining 40 sets of sample data, the predicted degree of collapsibility was different from the actual value. Thus, the prediction effectiveness was 79.70%. There were 186 groups of sample data predicted by the
RBF neural network model to have the same degree of collapsibility as the actual value, and 11 groups of data predicted to have different degrees of collapsibility from the actual value. The effectiveness of the
RBF neural network prediction model reached 94.42%.
The RBF neural network model and the regression model were assessed based on the model assessment indicator. The regression model’s values were as follows: The correlation coefficient (CC) was 0.903, the Nash–Sackliff efficiency coefficient (NSE) was 0.773, the percentage of deviation (PBIAS) was −0.007%, and the root mean square error (RMSE) was 0.022. The RBF neural network model has the following values: The correlation coefficient (CC) was 0.962, the Nash–Sutcliffe efficiency coefficient (NSE) was 0.919, the percentage of deviation (PBIAS) was −1.494%, and the root mean square error (RMSE) was 0.014.
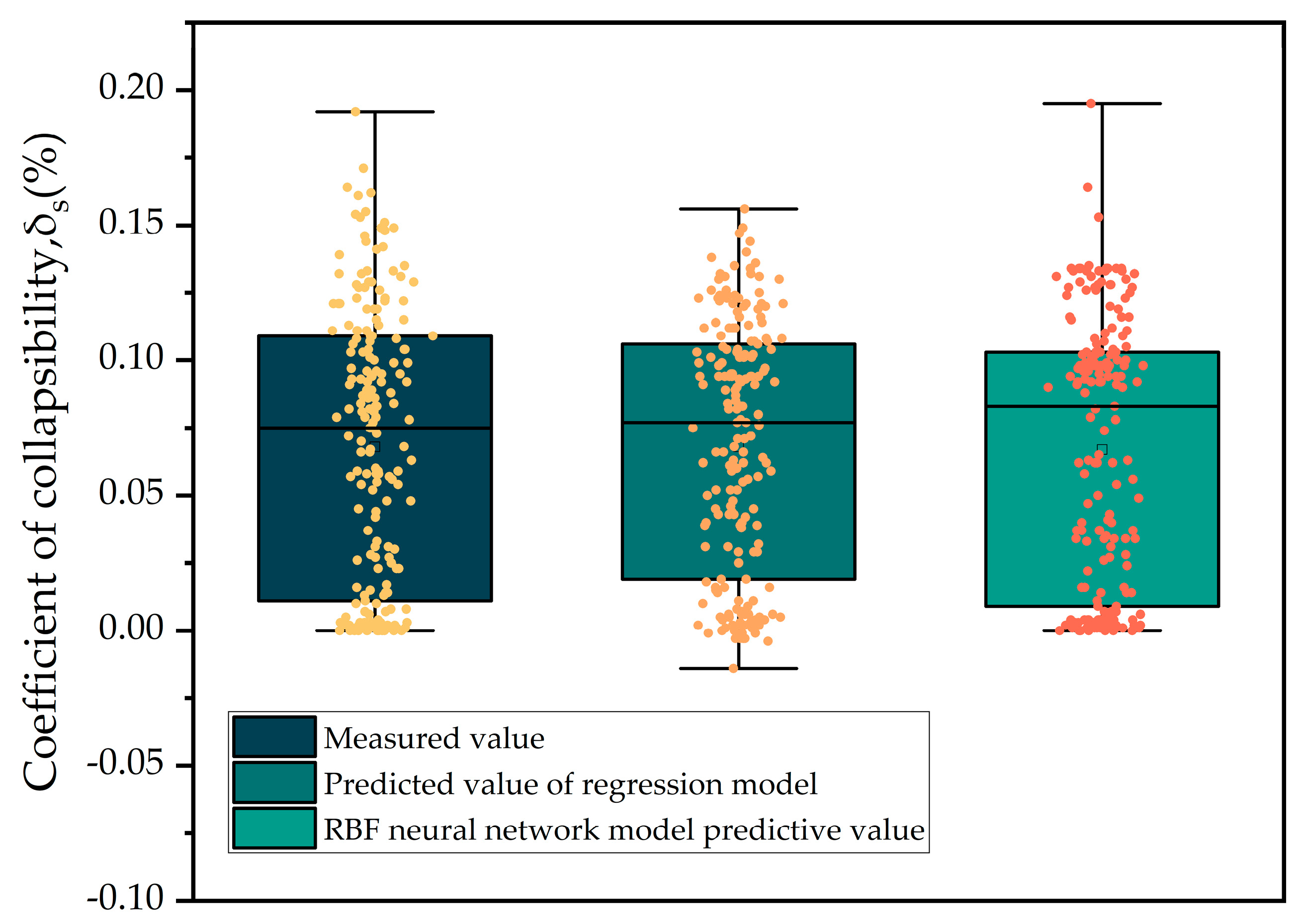
The box diagram in
Figure 10 shows the predicted value of the
RBF neural network model, the predicted value of the regression model, and the measured value of the loess collapsibility coefficient. The box plot illustrates how well the upper and lower lines of the measured value and the predicted value of the
RBF neural network model correspond and how the overall data distribution trend is similar to the measured value data distribution trend. Overall, the
RBF neural network model’s projected value box plot score is greater than the regression model’s, and the surface
RBF neural network model is more effective than the regression model [
40].
After a comprehensive comparison, the RBF neural network prediction model was more suitable for the prediction of loess collapsibility in this area.
5.2. The Advantages and Limitations of RBF Neural Network Model
In an effort to offer a quick method for the analysis and evaluation of Loess collapsibility in the study area, the RBF neural network prediction model has been shown through thorough comparative analysis to have higher reliability and accuracy than the regression model. Additionally, the model’s validity and accuracy were further verified through a variety of evaluation indicators. The fast learning curve, arbitrary precision of arbitrary continuous function approximation, internal force of multi−dimensional nonlinear mapping, and an easy to understand learning algorithm are some of the benefits of the RBF neural network model. It can also predict and assess the collapsibility of loess with speed. However, there are still several issues with this study.
The establishment of an RBF neural network model requires a large amount of data. When the amount of data is too small, there may be overfitting, which will lead to the accuracy of the prediction model in the use process. At the same time, the model is very sensitive to the abnormal use of data. When the data used has a large discrete type, it may lead to the instability of the training results of the model.
6. Conclusions
This paper collected many physical, hydraulic, and mechanical parameters of collapsible loess in Xinyuan County, Ili River Valley, and analysed the correlations of soil parameters of collapsible loess with the collapsibility coefficient via mathematical statistics. In addition, the optimal parameters were selected as the determination indicators for the prediction model. Finally, the collapsibility prediction model of loess in Xinyuan County, Ili River Valley, was established with multiple linear regression theory and the neural network method. The following main conclusions were drawn:
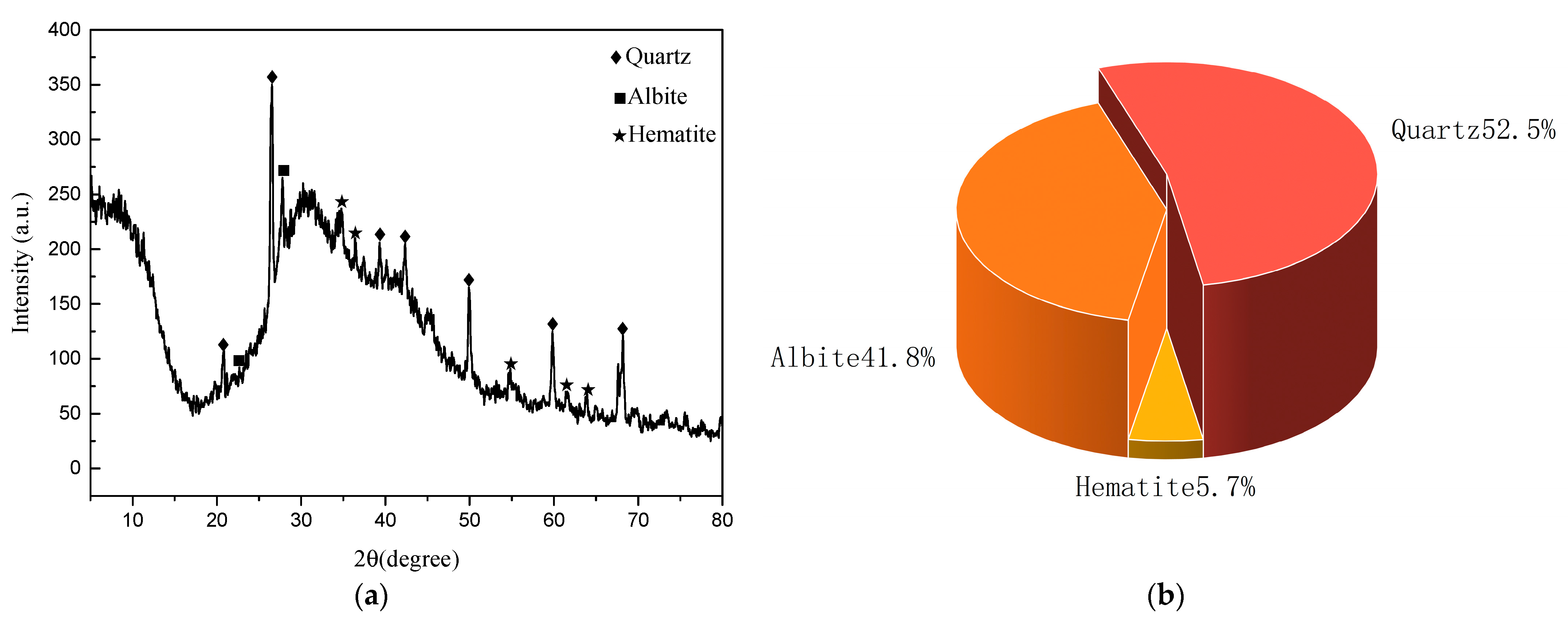
The engineering geological conditions and the physical properties of the loess in the study area were analyzed. The single−layer soil of the Quaternary loess in the research area is mostly collapsible and self−weight collapsible, with poor engineering geological conditions. The loess particle structure in this area is mainly cylindrical, flat, and irregular. The main contact between particles is support contact, supplemented by inlay contact, forming many inter−particle pores and some large pores. The loess in the study area is mainly composed of quartz and albite, with less hematite.
The correlation between the loess collapsibility coefficient and soil property indicators in the study area was analyzed. The correlation analysis results showed that the loess collapsibility coefficient δs in the study area was extremely strongly correlated with the density ρ and the degree of saturation Sr; strongly correlated with the porosity n, dry density ρd, void ratio e, and moisture content ω; moderately correlated with the liquidity index IL; weakly correlated with the sampling depth h and plasticity index Ip; extremely weakly correlated with the plastic limit ωp; and not correlated with the compression modulus Es, compression coefficient a, and liquid limit ωL. Finally, four parameters, the density ρ, degree of saturation Sr, porosity n, and moisture content ω, were selected as determination indicators for the prediction model.
In the studied region, a prediction model for loess collapsibility was developed. According to the prediction model’s results, the likelihood that a given event will occur is predicted with a 76.70% accuracy for multiple linear regression and a 94.42% accuracy for RBF neural network prediction. Simultaneously, the RBF neural network prediction model’s evaluation index clearly outperforms the regression prediction model’s. As a result, the thorough comparison analysis demonstrates that the RBF neural network prediction model outperforms the regression prediction model in terms of accuracy and dependability.
The collapsibility of loess is the primary subject of this investigation. Subsequent research can take into account the relationship between additional soil indicators, such as the relationship between soil physical parameters and the compression coefficient, and develop a prediction model. At the same time, how to further deal with the results of this study, so that one can carry out rapid evaluation in engineering construction, is a direction of future research.