Study on Unsteady Flow Characteristics of Cooling Water Pump for Nuclear Power Plant Equipment under Low Flow Rate Conditions
Abstract
:1. Introduction
2. Experimental System and Model Pump
2.1. Experimental System
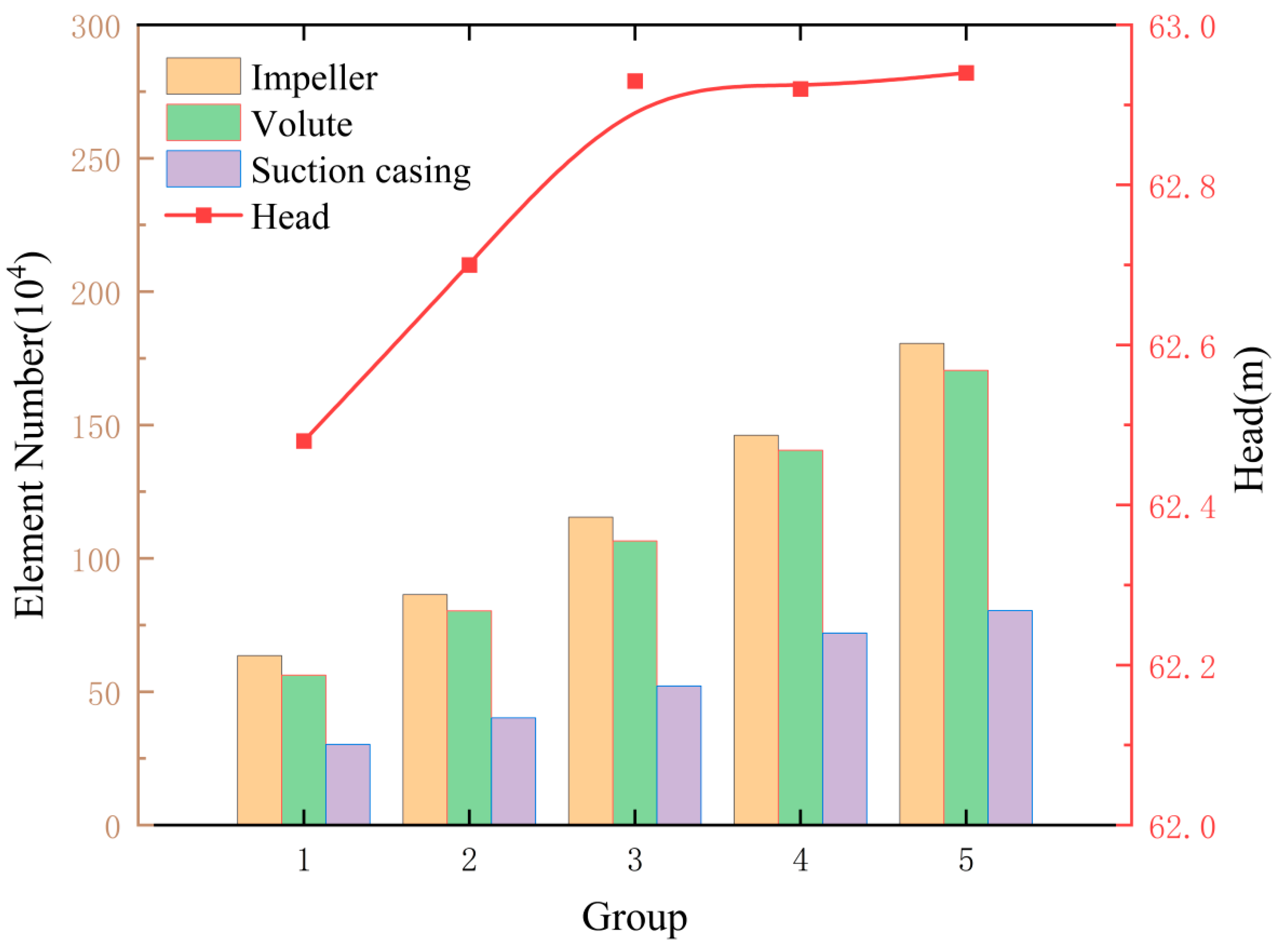
2.2. Mesh Generation
2.3. Governing Equation and Turbulence Model
2.4. Boundary Conditions
3. Results and Discussions
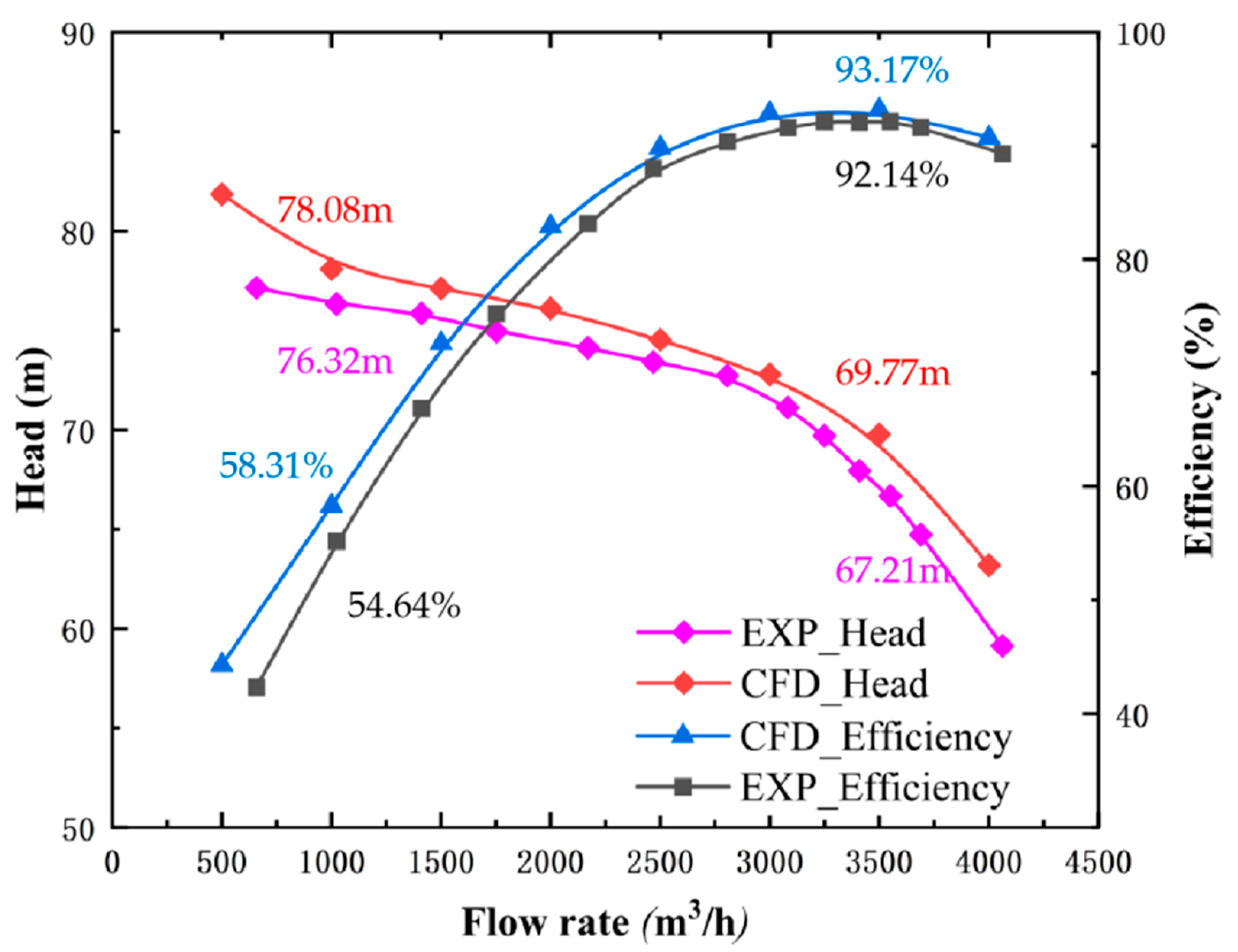
3.1. Pump Performance Analysis
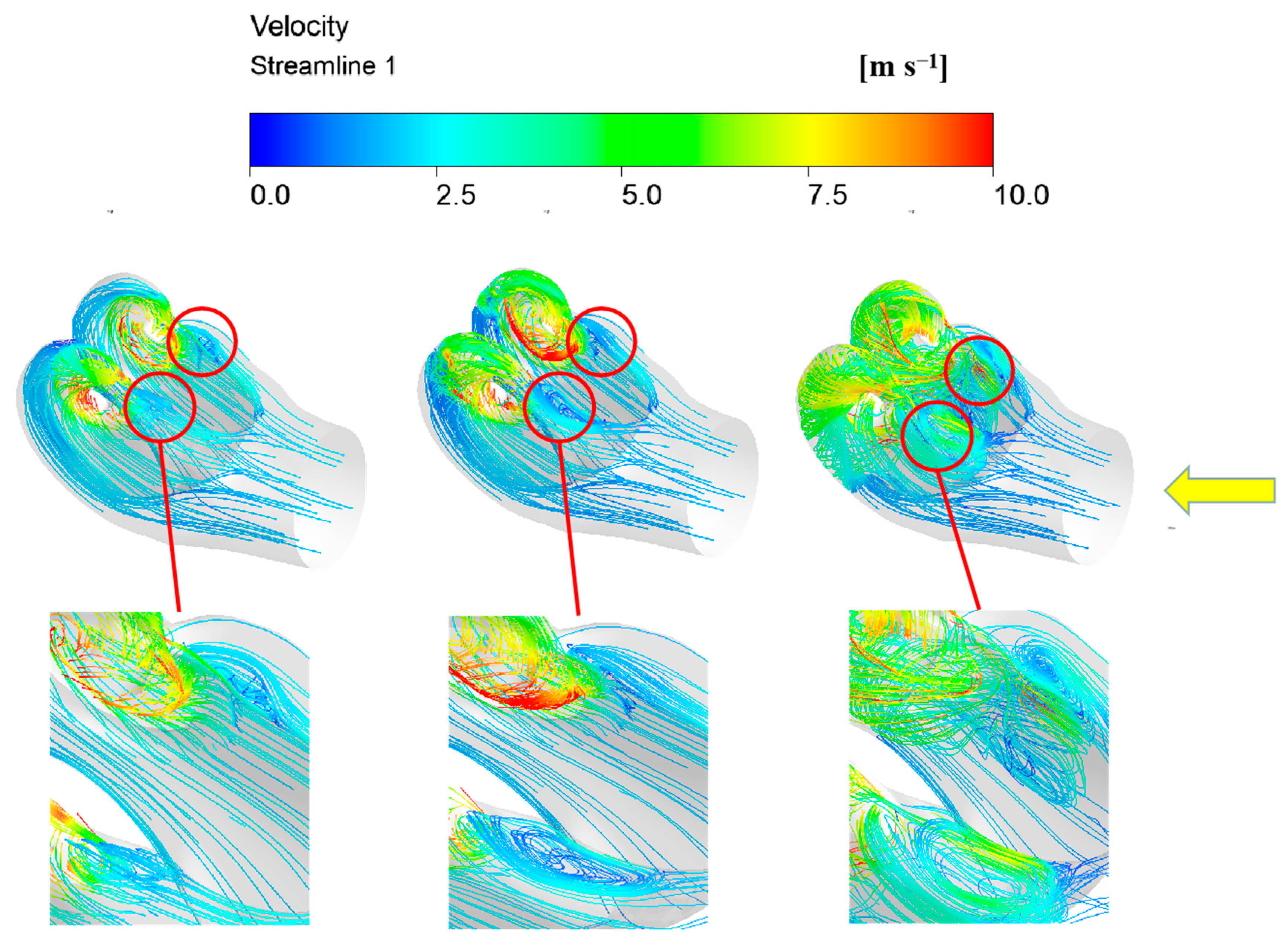
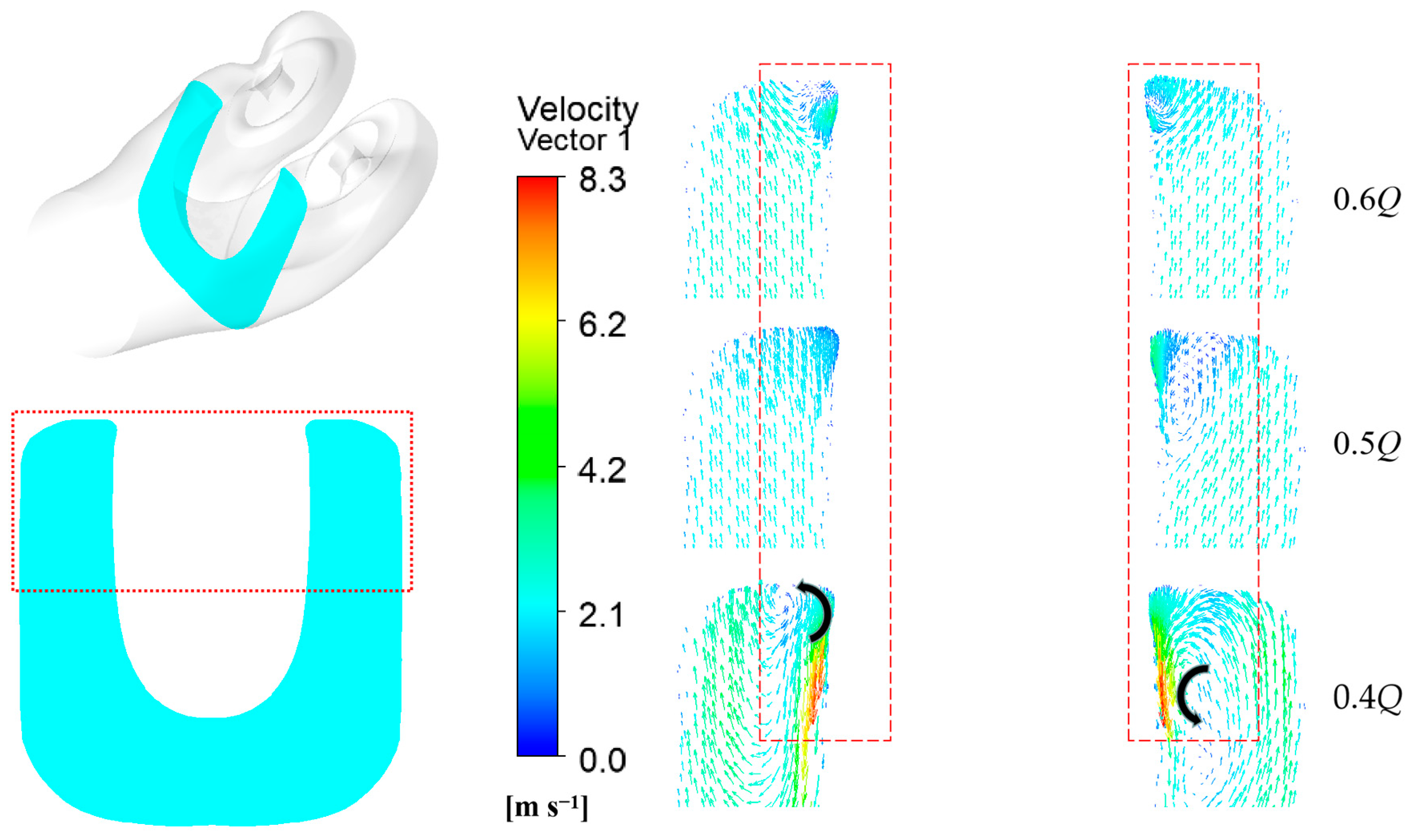
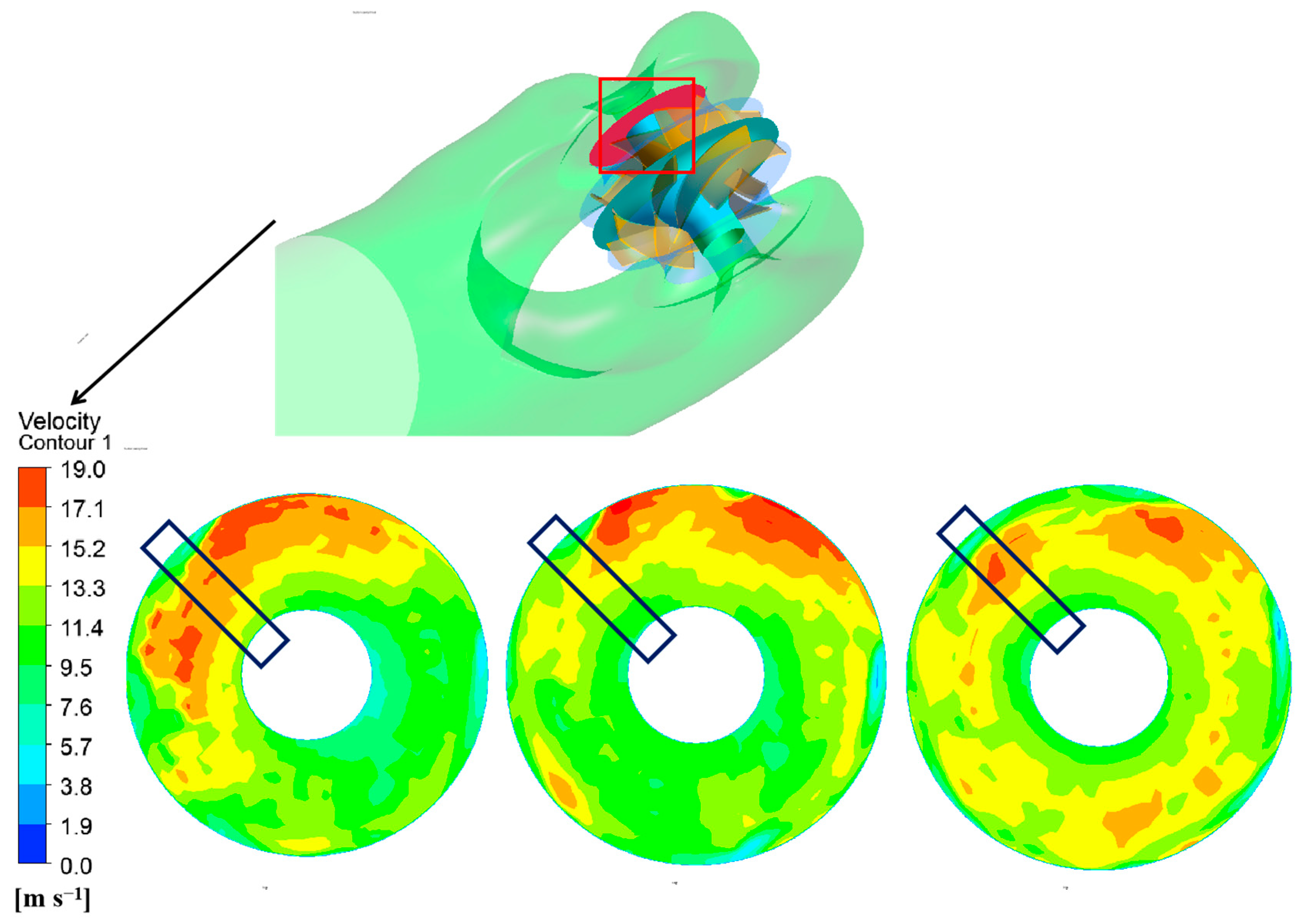
3.2. Analysis of Internal Flow in Suction Casing
3.3. Analysis of Velocity Shape in the Impeller
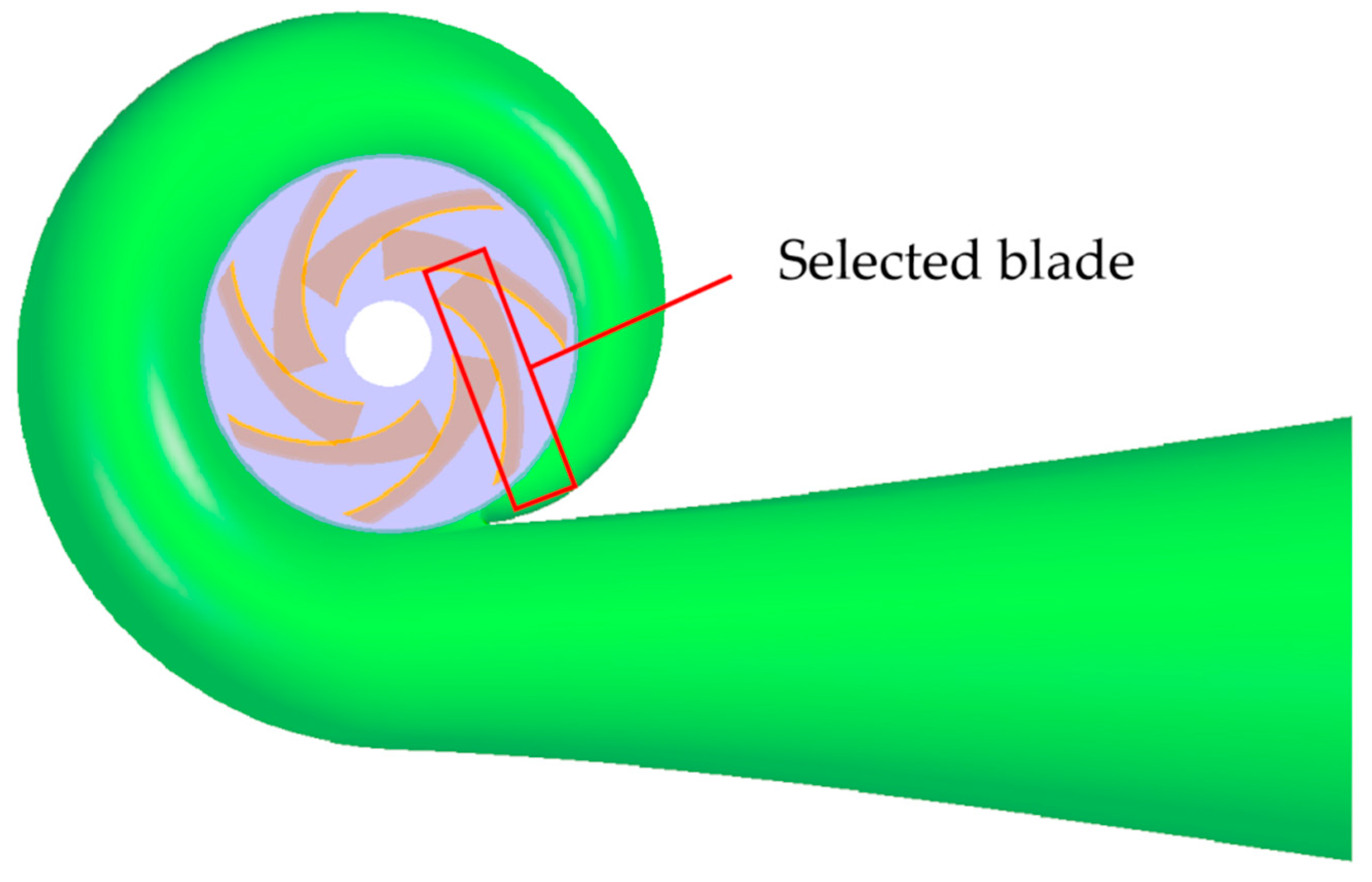
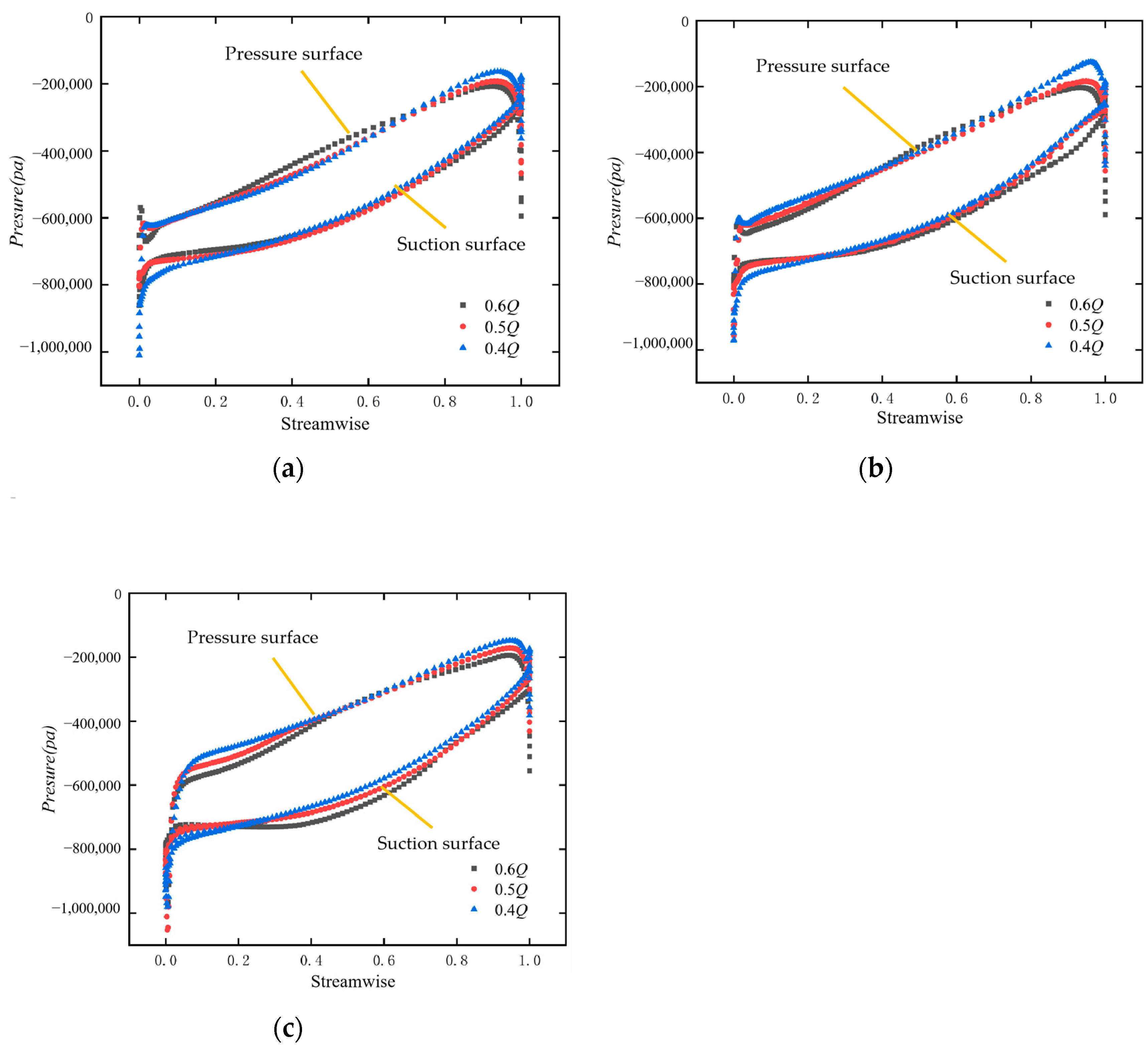
3.4. Blade Load Analysis
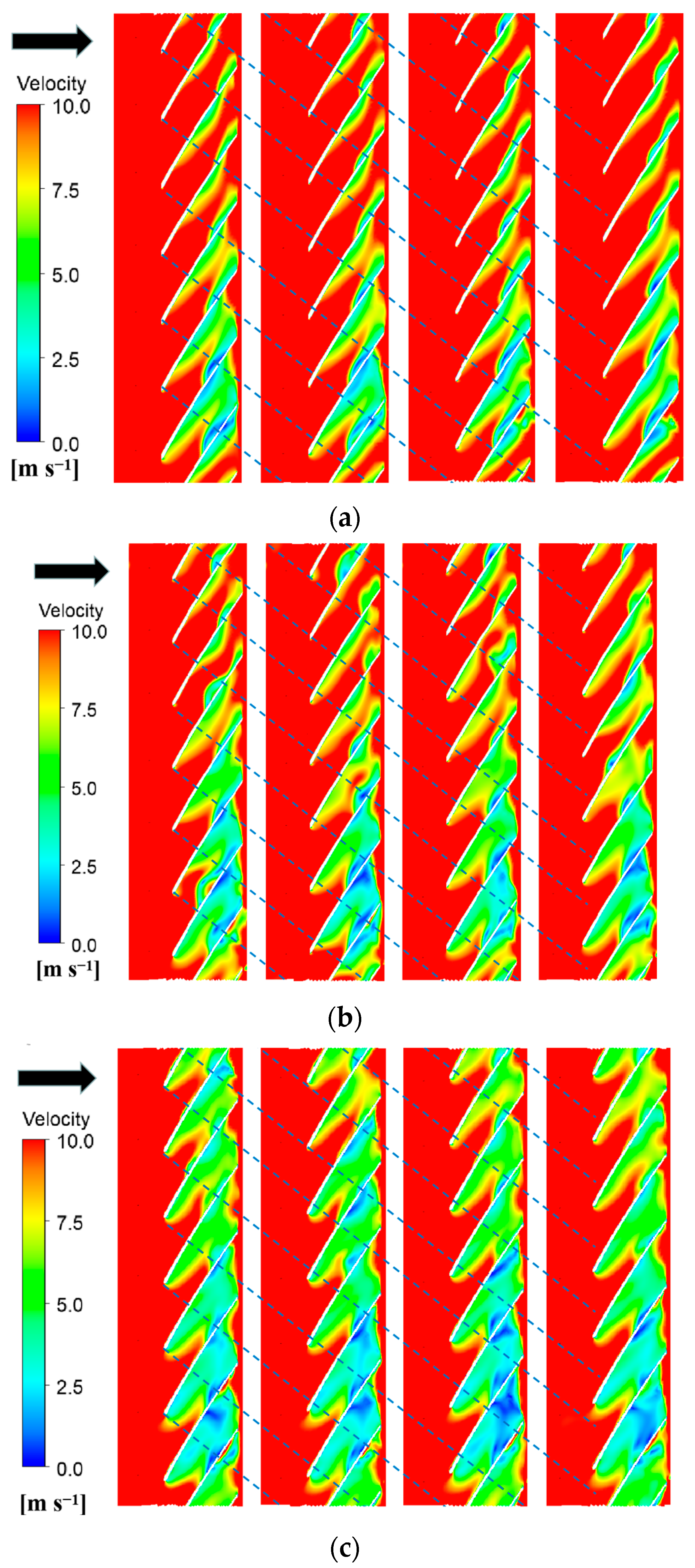
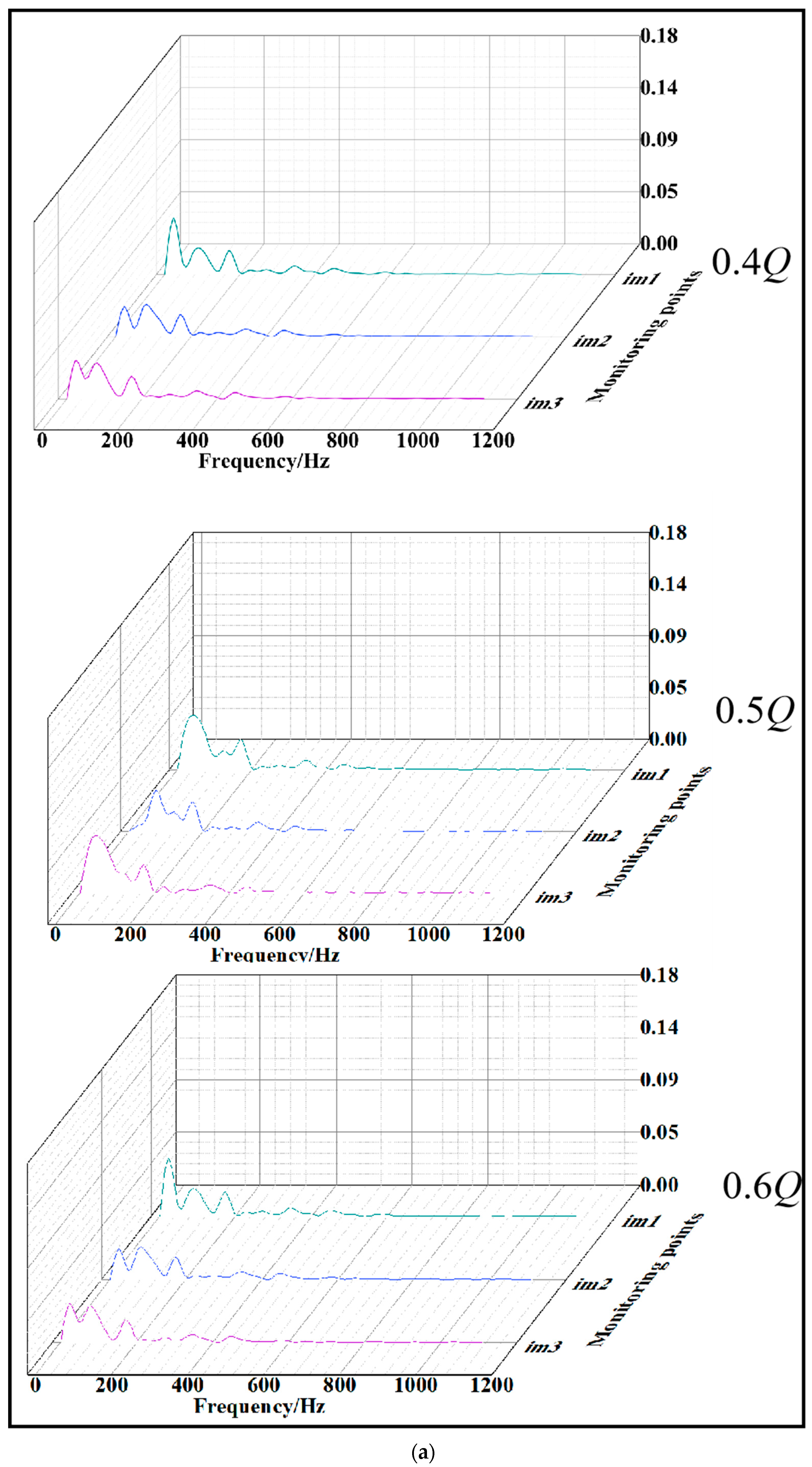
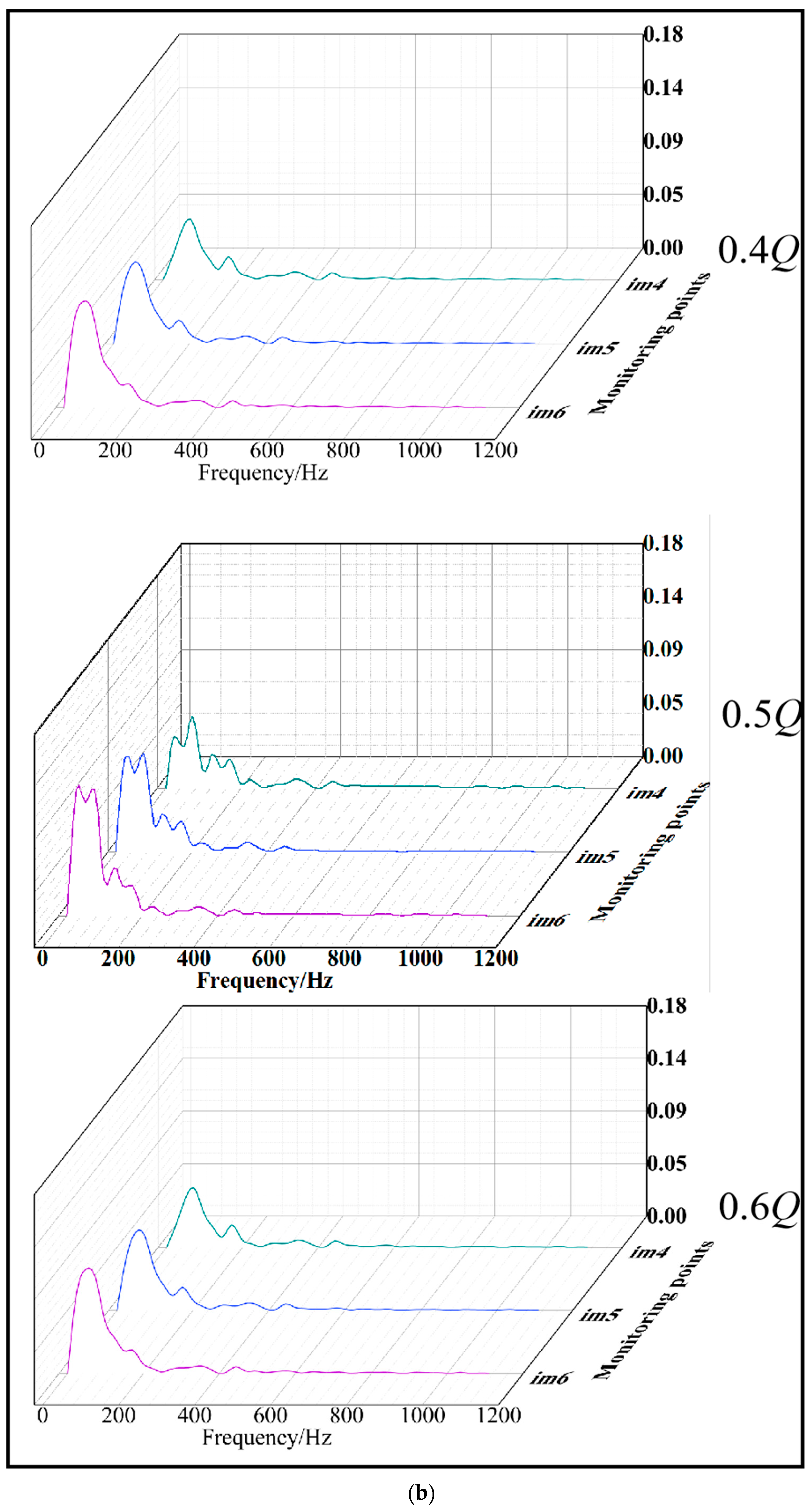
3.5. Research on Unsteady Flow in Impeller
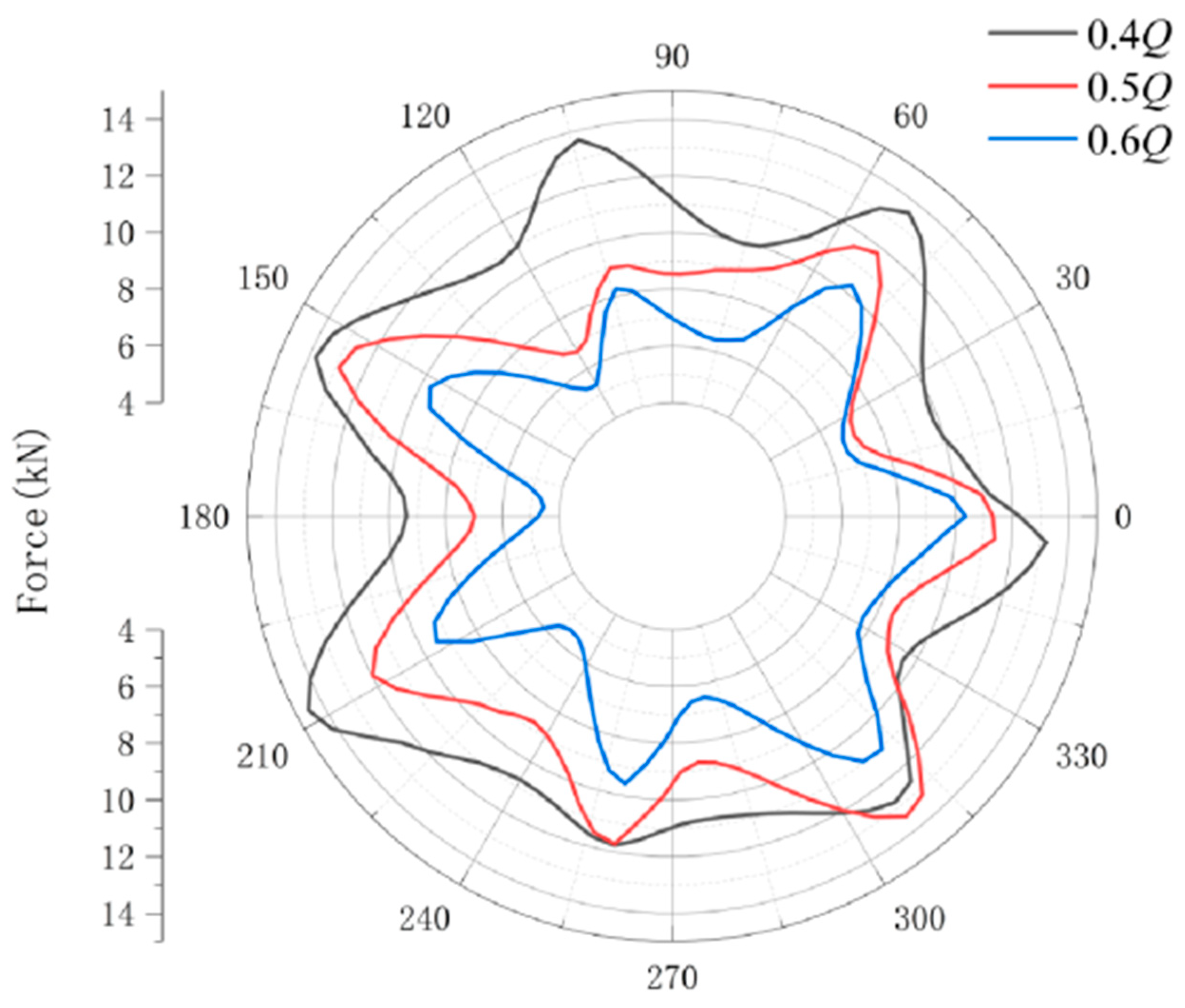
3.6. Research on Impeller Pressure Pulsation and Internal Radial Force
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jin, F.; Yao, Z.; Li, D.; Xiao, R.; Wang, F.; He, C. Experimental Investigation of Transient Characteristics of a Double Suction Centrifugal Pump System during Starting Period. Energies 2019, 12, 4135. [Google Scholar] [CrossRef]
- Botero, F.; Hasmatuchi, V.; Roth, S.; Farhat, M. Non-intrusive detection of rotating stall in pump-turbines. Mech. Syst. Signal Process 2014, 48, 162–173. [Google Scholar] [CrossRef]
- Lu, J.; Yuan, S.; Luo, Y.; Yuan, J.; Zhou, B.; Sun, H. Numerical and experimental investigation on the development of cavitation in a centrifugal pump. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2014, 230, 171–182. [Google Scholar] [CrossRef]
- Li, D.; Qin, Y.; Zuo, Z.; Wang, H.; Liu, S.; Wei, X. Numerical simulation on pump transient characteristic in a model pump turbine. J. Fluid Eng. 2019, 141, 111101. [Google Scholar] [CrossRef]
- Feng, J.; Ge, Z.; Yang, H.; Zhu, G.; Li, C.; Luo, X. Rotating stall characteristics in the vaned diffuser of a centrifugal pump. Ocean Eng. 2021, 229, 108955. [Google Scholar] [CrossRef]
- Cui, B.L.; Zhang, Y.B.; Huang, Y.K. Analysis of the pressure pulsation and vibration in a low-specific-speed centrifugal pump. J. Fluid Eng. 2020, 143, 021201. [Google Scholar] [CrossRef]
- Li, W.; Ji, L.; Li, E.; Shi, W.; Agarwal, R.; Zhou, L. Numerical investigation of energy loss mechanism of mixedflow pump under stall condition. Renew. Energy 2021, 167, 740–760. [Google Scholar] [CrossRef]
- Zhang, W.; Zhu, B.; Yu, Z.; Yang, C. Numerical study of pressure fluctuation in the whole flow passage of a low specific speed mixed-flow pump. Adv. Mech. Eng. 2017, 9, 1–11. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, Z.; Xia, C.; Liu, Z. Experimental investigation of pressure fluctuation, vibration, and noise in a multistage pump. Shock. Vib. 2018, 2018, 2784079. [Google Scholar] [CrossRef]
- Pedersen, N.; Larsen, P.S.; Jacobsen, C.B. Flow in a Centrifugal Pump Impeller at Design and Off-Design Conditions: Particle Image Velocimetry (PIV) and Laser Doppler Velocimetry (LDV) Measurements. J. Fluids Eng. 2003, 125, 61–72. [Google Scholar] [CrossRef]
- Byskov, R.K.; Jacobsen, C.B.; Pedersen, N. Flow in a Centrifugal Pump Impeller at Design and Off-Design Conditions: Large Eddy Simulations. J. Fluids Eng. 2003, 125, 73–83. [Google Scholar] [CrossRef]
- Zhao, X.; Xiao, Y.; Wang, Z.; Luo, Y.; Cao, L. Unsteady Flow and Pressure Pulsation Characteristics Analysis of Rotating Stall in Centrifugal Pumps Under Off-Design Conditions. J. Fluids Eng. 2017, 140, 021105. [Google Scholar] [CrossRef]
- Jia, X.-Q.; Zhu, Z.-C.; Yu, X.-L.; Zhang, Y.-L. Internal unsteady flow characteristics of centrifugal pump based on entropy generation rate and vibration energy. Proc. Inst. Mech. Eng. 2018, 233, 456–473. [Google Scholar] [CrossRef]
- Ni, D.; Zhang, N.; Gao, B.; Li, Z.; Yang, M. Dynamic measurements on unsteady pressure pulsations and flow distributions in a nuclear reactor coolant pump. Energy 2020, 198, 117305. [Google Scholar] [CrossRef]
- Zheng, L.L.; Chen, X.P.; Zhang, W.; Zhu, Z.C.; Cheng, C. Investigation on characteristics of pressure fluctuation in a cen-trifugal pump with clearance flow. J. Mech. Sci. Technol. 2020, 34, 3657–3666. [Google Scholar] [CrossRef]
- Gao, B.; Zhang, N.; Li, Z.; Ni, D.; Yang, M. Influence of the Blade Trailing Edge Profile on the Performance and Unsteady Pressure Pulsations in a Low Specific Speed Centrifugal Pump. J. Fluids Eng. 2016, 138, 051106. [Google Scholar] [CrossRef]
- Wang, Z.; Qian, Z.; Lu, J.; Wu, P. Effects of flow rate and rotational speed on pressure fluctuations in a double-suction cen-trifugal pump. Energy 2018, 170, 212–227. [Google Scholar] [CrossRef]
- Huang, P.; Xiao, Y.; Zhang, J.; Cai, H.; Song, H. The Influence of Flow Rates on Pressure Fluctuation in the Pump Mode of Pump-Turbine with Splitter Blades. Appl. Sci. 2020, 10, 6752. [Google Scholar] [CrossRef]
- Lucius, A.; Brenner, G. Numerical simulation and evaluation ofvelocity fluctuations during rotating stall of a centrifugal pump. J. Fluids Eng. Trans. ASME 2011, 133, 081102. [Google Scholar] [CrossRef]
- Zhang, N.; Yang, M.; Gao, B.; Li, Z.; Ni, D. Unsteady pressure pulsation and rotating stall characteristics in a centrifugal pump with slope volute. Adv. Mech. Eng. 2014, 6, 710791. [Google Scholar] [CrossRef]
- Zhou, P.; Wang, F.; Mou, J. Investigation of rotating stall characteristics in a centrifugal pump impeller at low flow rates. Eng. Comput. 2017, 34, 1849–1873. [Google Scholar] [CrossRef]
- Gao, B.; Guo, P.; Zhang, N.; Li, Z.; Yang, M. Unsteady pressure pulsation measurements and analysis of a low specific speed centrifugal pump. J. Fluids Eng. Trans. ASME 2017, 139, 071101. [Google Scholar] [CrossRef]
- Gyarmathy, G.; Inderbitzen, A.; Staubli, T. Visualization of rotating stall in a full size water model of a single-stage centrifugal compressor. Houille Blanche 2001, 87, 40–45. [Google Scholar] [CrossRef]
- Maeda, H.; Jittani, Y. Unstable head-flow characteristic generation mechanism of a low specific speed mixed flow pump. J. Therm. Sci. 2006, 15, 115–120. [Google Scholar]
- Berten, S. Hydrodynamics of High Specific Power Pumps for Off-Design Operating Conditions. Ph.D. Thesis, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 2010. [Google Scholar] [CrossRef]
- Pacot, O. Large Scale Computation of the Rotating Stall in a Pump-Turbine using an Overset Finite Element Large Eddy Simulation Numerical Code PAR. 6183. Ph.D. Thesis, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 2014. [Google Scholar] [CrossRef]
- Fu, D.-C.; Wang, F.-J.; Zhou, P.-J.; Xiao, R.-F.; Yao, Z.-F. Impact of impeller stagger angles on pressure fluctuation for a double-suction centrifugal pump. Chin. J. Mech. Eng. 2018, 31, 10. [Google Scholar] [CrossRef]
- Cheng, W.; Song, W.; Wan, L. Analysis of pressure fluctuation characteristic in the volute tongue of centrifugal pump. Water Power 2018, 44, 59–61. [Google Scholar]
- Cao, R.; Si, Q.; Sheng, G.; Lin, G. Influence of the oblique trimmed impeller on pressure fluctuations in centrifugal pump at low flow rate. In Proceedings of the International Conference on Mechanical Design, ICMD 2017 The19th Annual Conference on Mechanical Design, Beijing, China, 13–15 October 2017; pp. 239–251. [Google Scholar]









| Specific speed | ns | 162 |
| Design flow rate | Qopt | 3400 m3/h |
| Rotating speed | n | 1480 r/min |
| Diameter of impeller inlet | D1 | 324 mm |
| Diameter of impeller outlet | D2 | 496 mm |
| Number of impeller blades | Z | 7 |
| Correlation Parameter | Prototype Pump | Model Pump | |||
|---|---|---|---|---|---|
| Scale | |||||
| 0.583 | 0.567 | 0.55 | 0.5 | ||
| Inlet pipe diameter D (mm) | 600 | 350 | 340 | 330 | 300 |
| Nominal diameter D2 (mm) | 486 | 283.5 | 275.4 | 267.3 | 243 |
| Flow rate Q (m3/h) | 3400 | 675 | 618 | 565 | 425 |
| Head H (m) | 65 | 22.12 | 20.87 | 19.65 | 16.25 |
| Circumferential velocity u (m/s) | 38.7 | 22.6 | 22.0 | 21.3 | 19.4 |
| Reynolds number Re × 106 | 20.12 | 6.85 | 6.46 | 6.08 | 5.03 |
| Compliance with criteria (Yes/No) | Yes | Yes | Yes | No | No |
| Component | Minimum Value | Maximum Value | Average Value |
|---|---|---|---|
| Impeller | 21.44 | 1375.81 | 690.50 |
| Volute | 24.67 | 5342.50 | 2954.30 |
| Suction casing | 17.74 | 5043.21 | 2621.40 |
| Governing equation | Reynolds-averaged Navier-Stokes (RANS) |
| Discretization | finite volume method (FVM) |
| Advection scheme | high-resolution, second-order approximation |
| Root mean square (RMS) residuals | below 1.0 × 10−4 |
| Turbulence mode | k-ω-based shear stress transport (SST) standard |
| Wall function | automatic with smooth and non-slip conditions |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Q.; Yang, D.; Zhang, J.; Zhu, R.; Shi, W. Study on Unsteady Flow Characteristics of Cooling Water Pump for Nuclear Power Plant Equipment under Low Flow Rate Conditions. Water 2023, 15, 3780. https://doi.org/10.3390/w15213780
Fu Q, Yang D, Zhang J, Zhu R, Shi W. Study on Unsteady Flow Characteristics of Cooling Water Pump for Nuclear Power Plant Equipment under Low Flow Rate Conditions. Water. 2023; 15(21):3780. https://doi.org/10.3390/w15213780
Chicago/Turabian StyleFu, Qiang, Dawei Yang, Jilai Zhang, Rongsheng Zhu, and Wenhao Shi. 2023. "Study on Unsteady Flow Characteristics of Cooling Water Pump for Nuclear Power Plant Equipment under Low Flow Rate Conditions" Water 15, no. 21: 3780. https://doi.org/10.3390/w15213780
APA StyleFu, Q., Yang, D., Zhang, J., Zhu, R., & Shi, W. (2023). Study on Unsteady Flow Characteristics of Cooling Water Pump for Nuclear Power Plant Equipment under Low Flow Rate Conditions. Water, 15(21), 3780. https://doi.org/10.3390/w15213780





