Clustering Daily Extreme Precipitation Patterns in China
Abstract
:1. Introduction
2. Materials and Methods
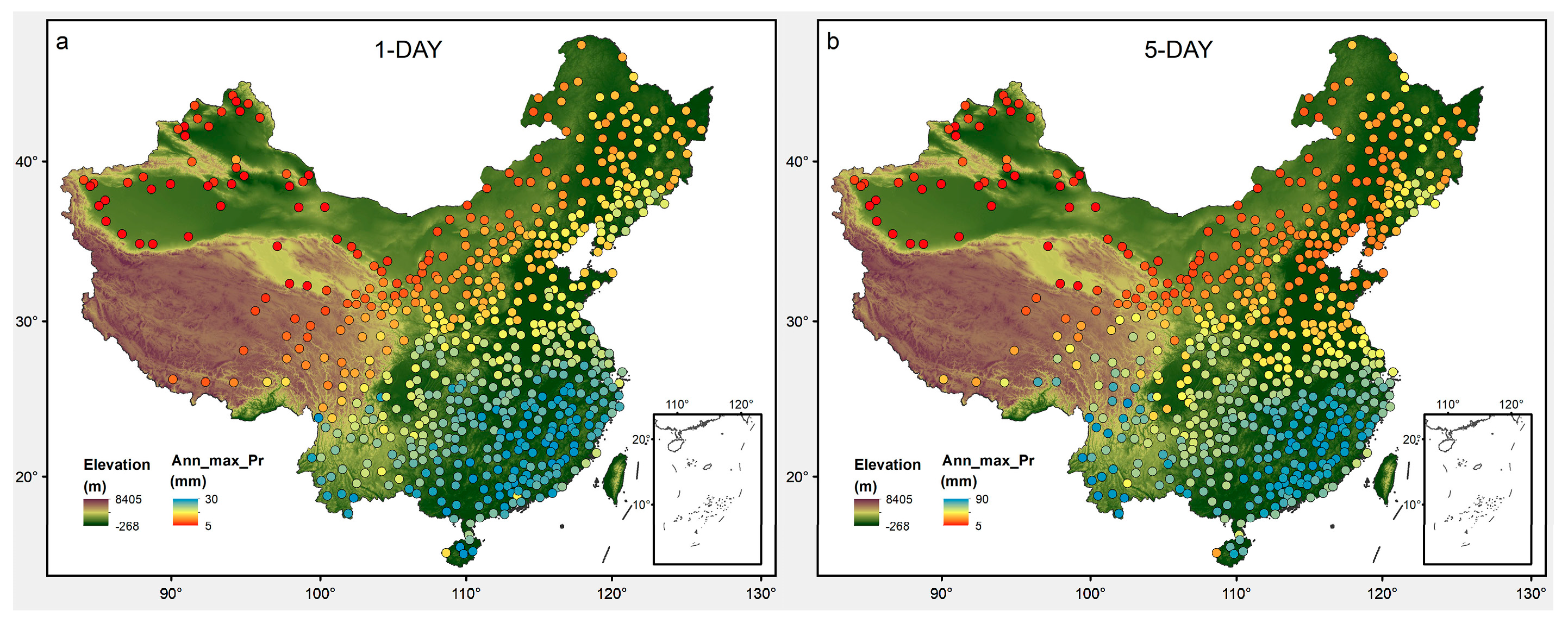
2.1. Rain Gauge Data
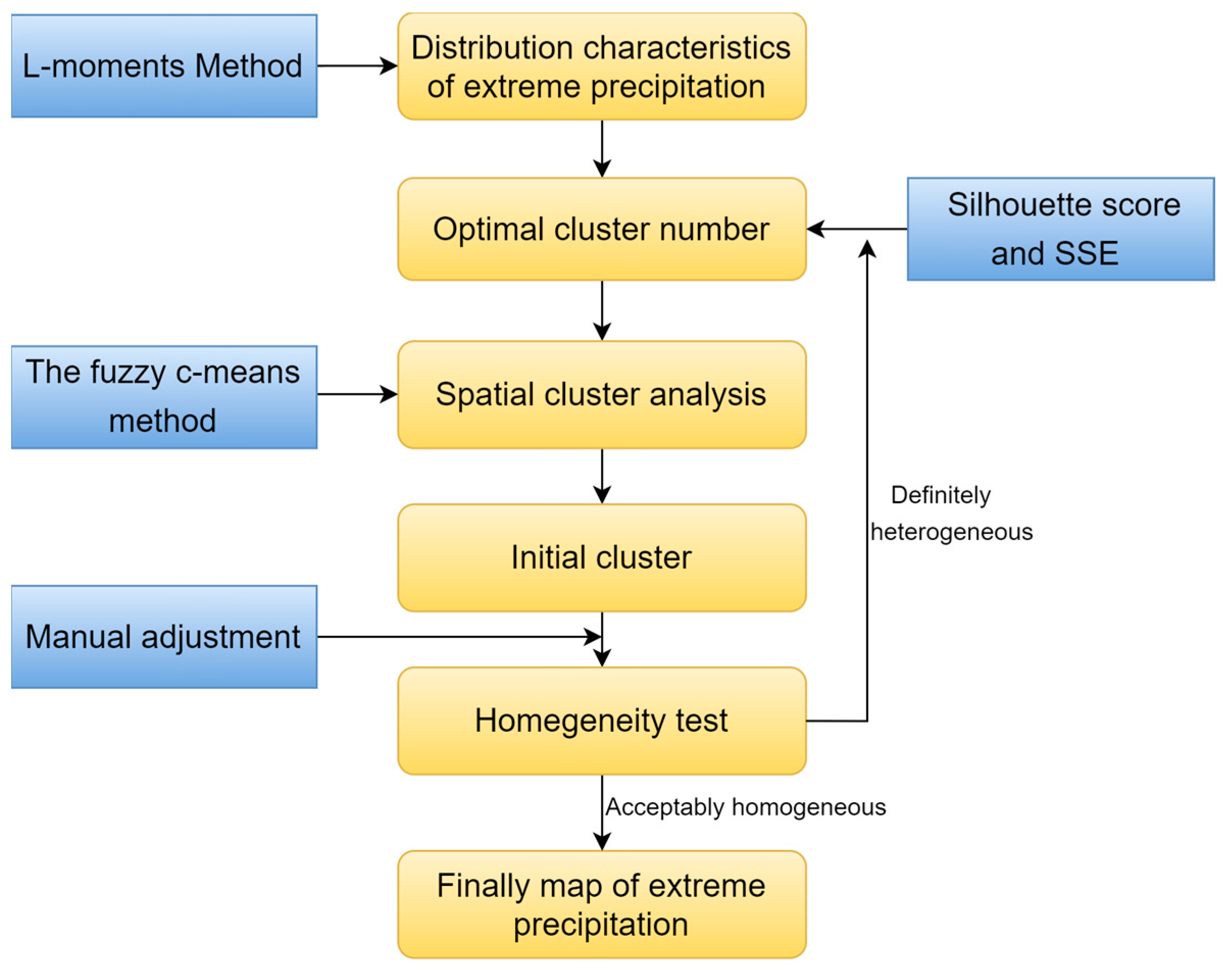
2.2. Methods
2.2.1. L–Moments Method and Data Preprocessing
2.2.2. Fuzzy C–Means (FCM) Cluster Analysis
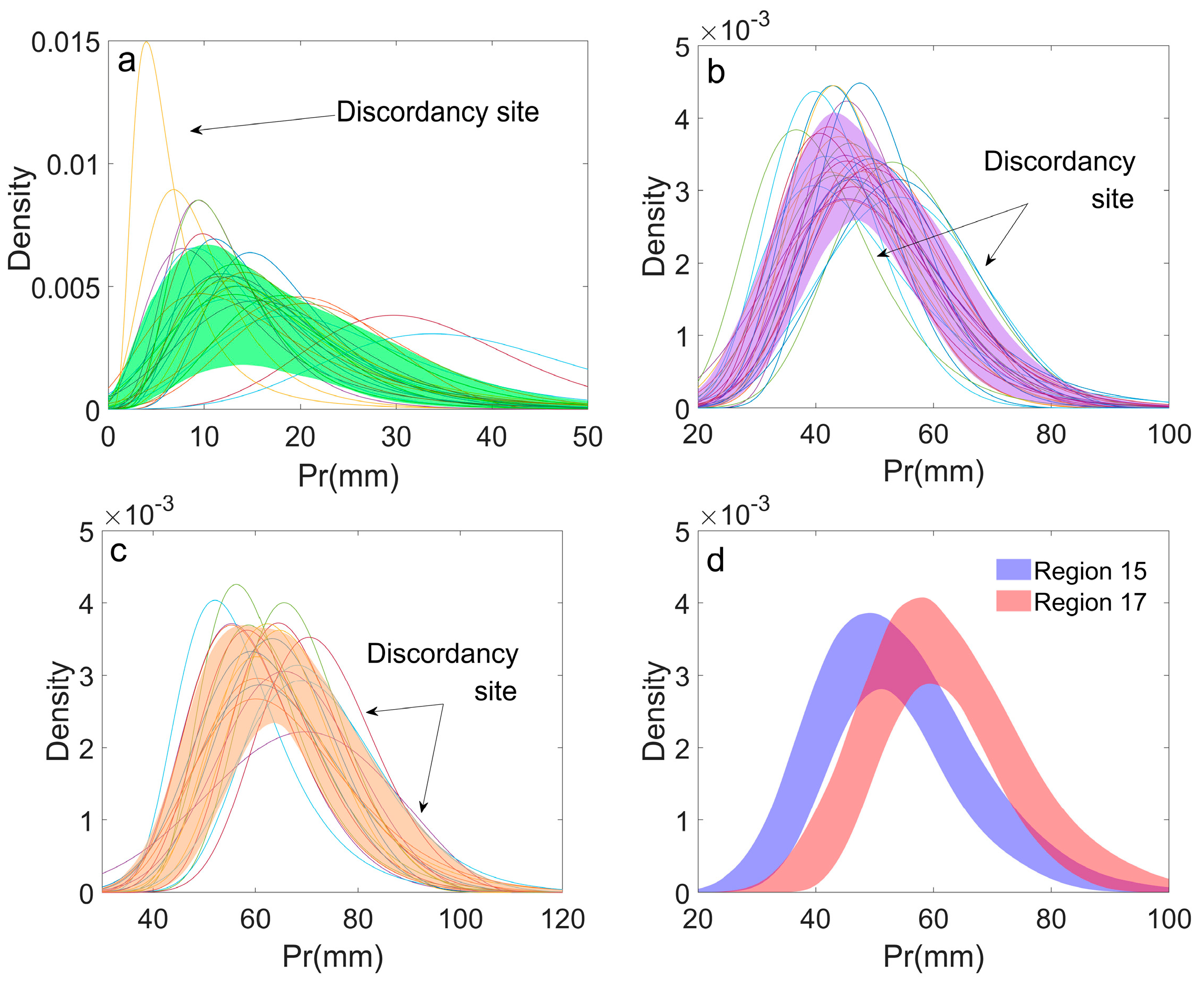
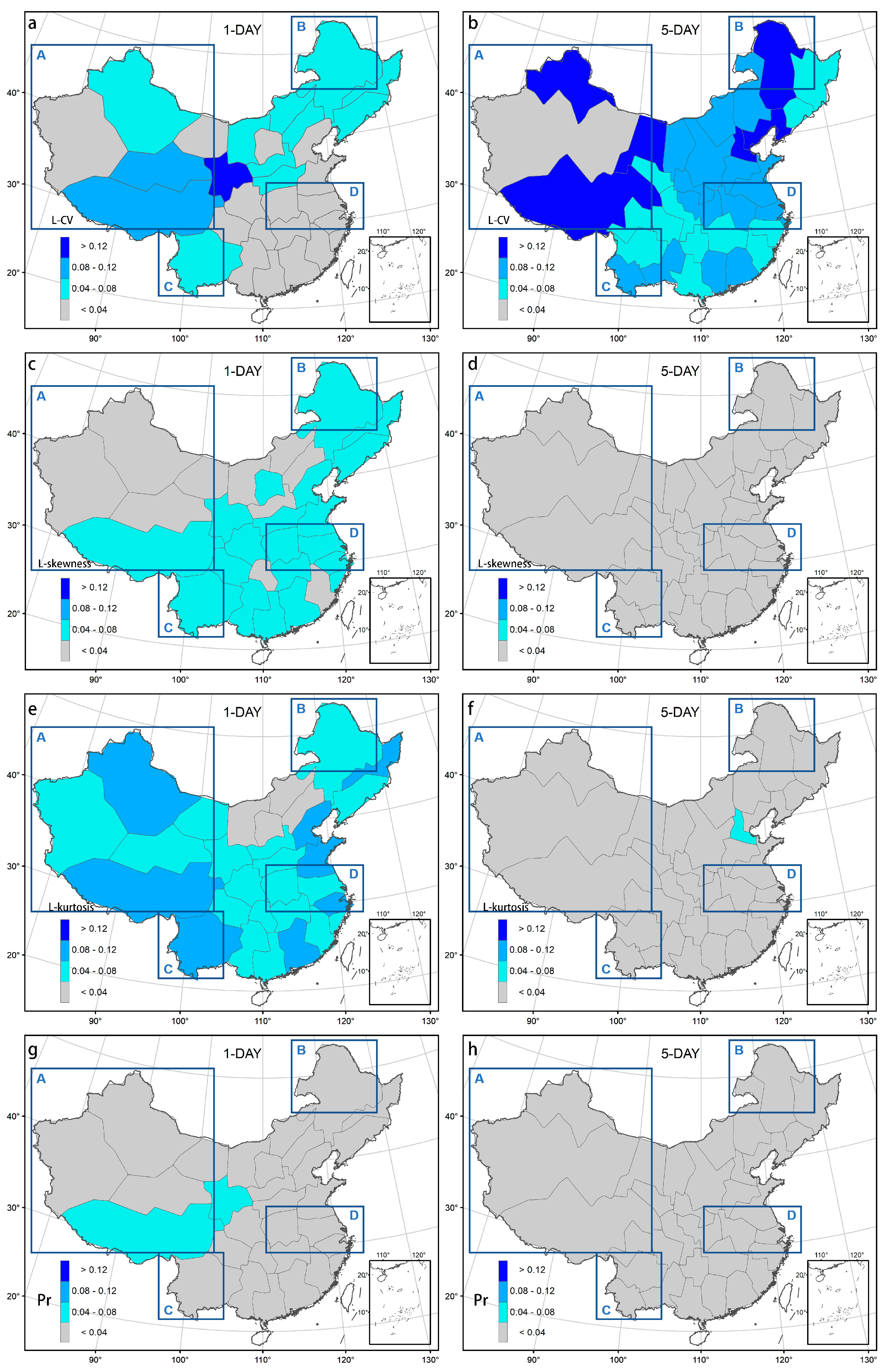
2.2.3. Homogeneity Test
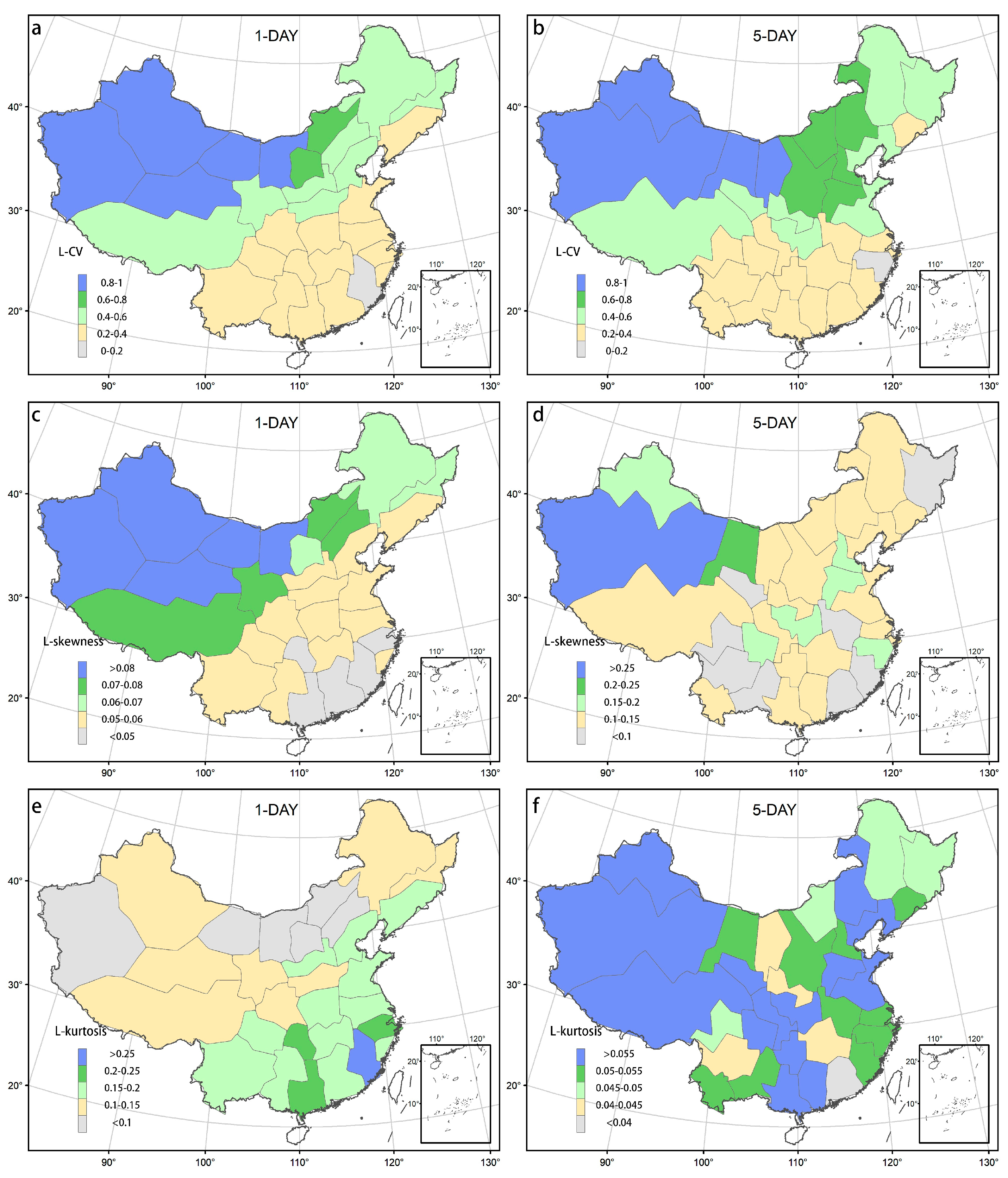
3. Results
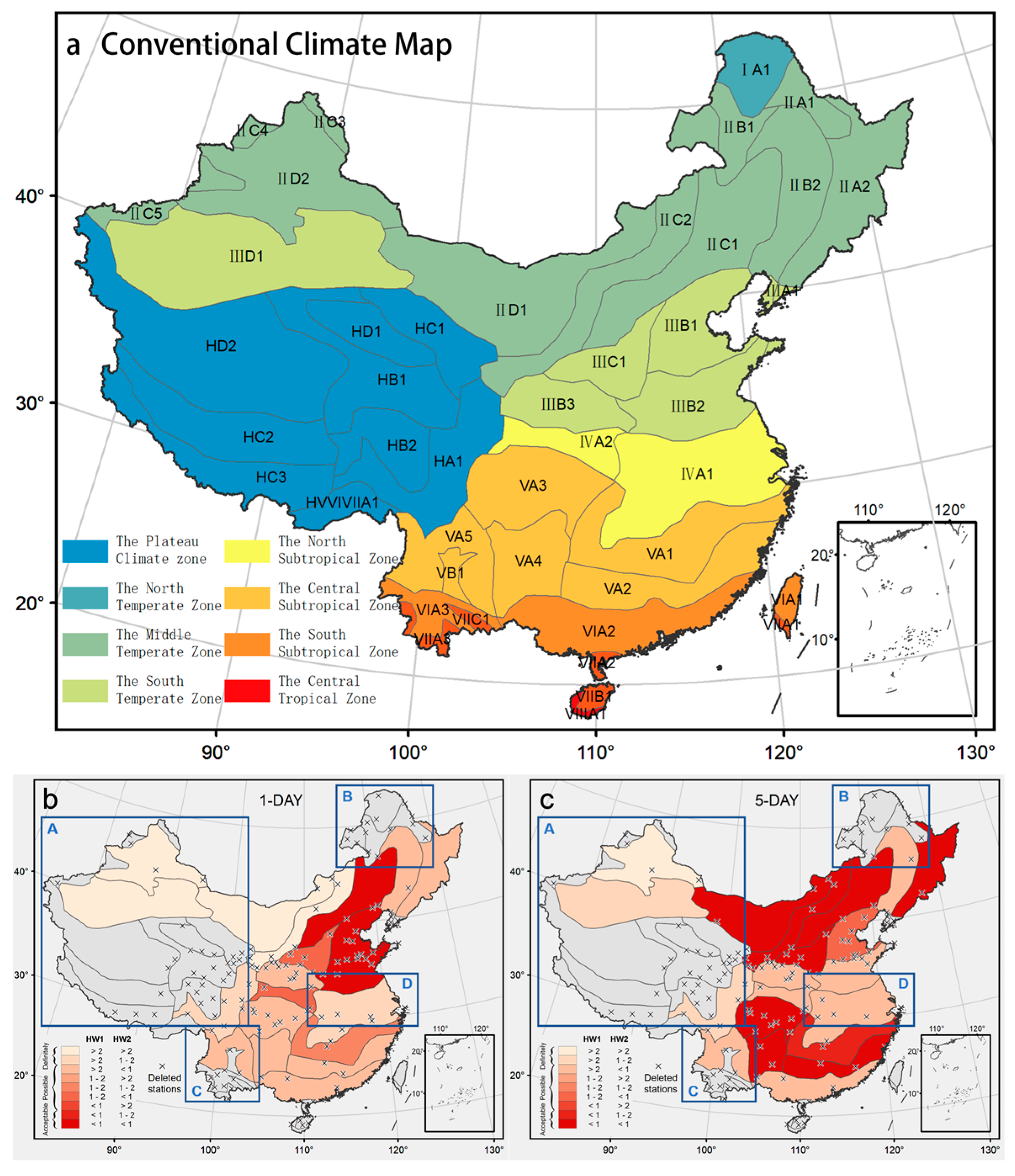
3.1. Conventional Climate Regions of China
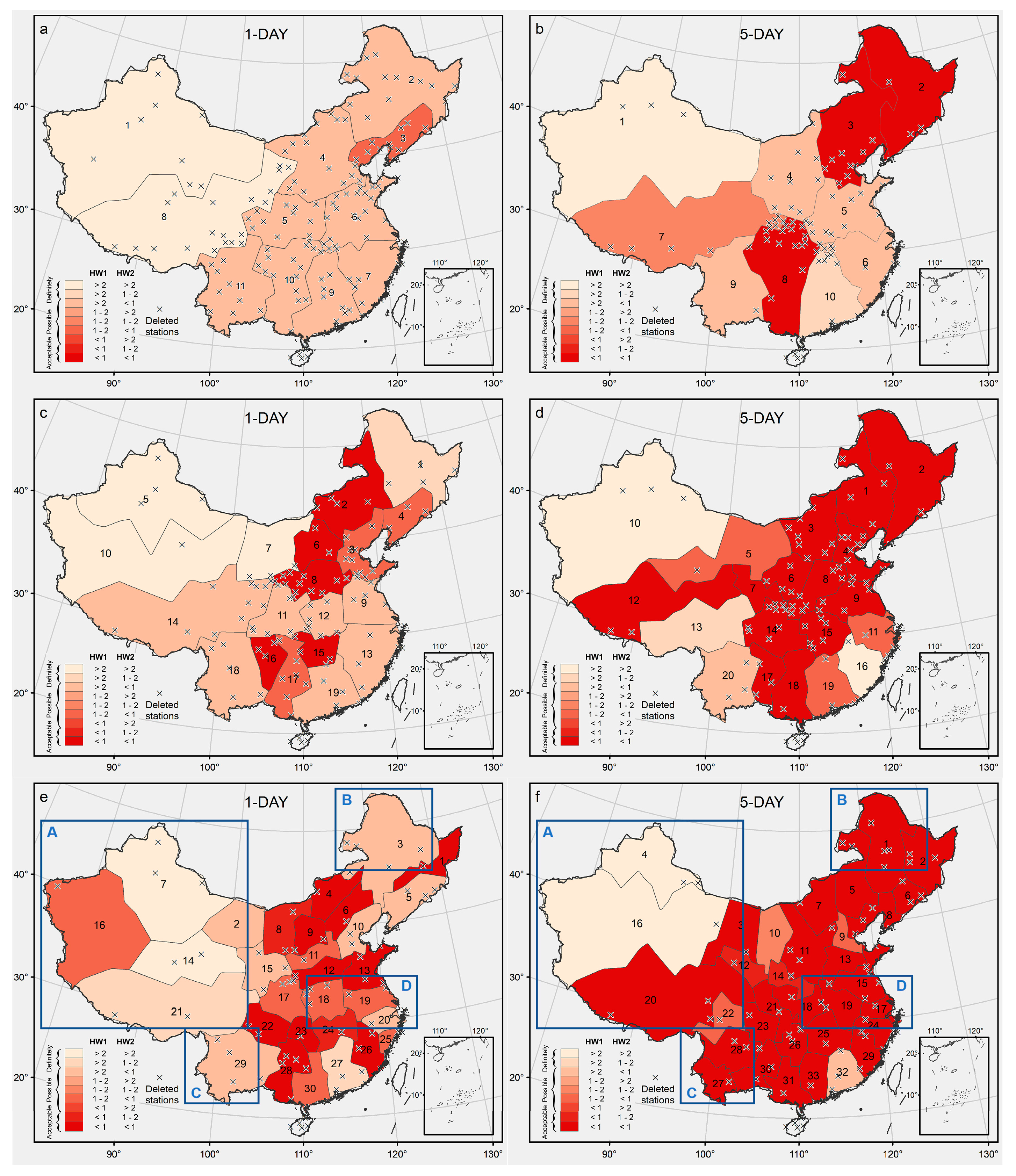
3.2. Clustering Based on Extreme Precipitation Characteristics
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abbas, A.; Waseem, M.; Ullah, W.; Zhao, C.; Zhu, J. Spatiotemporal analysis of meteorological and hydrological droughts and their propagations. Water 2021, 13, 2237. [Google Scholar] [CrossRef]
- Dottori, F.; Szewczyk, W.; Ciscar, J.C.; Zhao, F.; Alfieri, L.; Hirabayashi, Y.; Bianchi, A.; Mongelli, I.; Frieler, K.; Betts, R.A.; et al. Increased human and economic losses from river flooding with anthropogenic warming. Nat. Clim. Chang. 2018, 8, 781–786. [Google Scholar] [CrossRef]
- Elahi, E.; Khalid, Z.; Tauni, M.Z.; Zhang, H.; Lirong, X. Extreme weather events risk to crop-production and the adaptation of innovative management strategies to mitigate the risk: A retrospective survey of rural Punjab, Pakistan. Technovation 2022, 117, 102255. [Google Scholar] [CrossRef]
- Elahi, E.; Khalid, Z.; Zhang, Z. Understanding farmers’ intention and willingness to install renewable energy technology: A solution to reduce the environmental emissions of agriculture. Appl. Energy 2022, 309, 118459. [Google Scholar] [CrossRef]
- Jenifer, M.A.; Jha, M.K. Assessment of precipitation trends and its implications in the semi-arid region of Southern India. Environ. Chall. 2021, 5, 100269. [Google Scholar] [CrossRef]
- Jongman, B. Effective adaptation to rising flood risk COMMENT. Nat. Commun. 2018, 9, 1986. [Google Scholar] [CrossRef]
- Waseem, M.; Khurshid, T.; Abbas, A.; Ahmad, I.; Javed, Z. Impact of meteorological drought on agriculture production at different scales in Punjab, Pakistan. J. Water Clim. Chang. 2022, 13, 113–124. [Google Scholar] [CrossRef]
- Cavanaugh, N.R.; Gershunov, A.; Panorska, A.K.; Kozubowski, T.J. The probability distribution of intense daily precipitation. Geophys. Res. Lett. 2015, 42, 1560–1567. [Google Scholar] [CrossRef]
- Gentilucci, M.; Barbieri, M.; Pambianchi, G. Reliability of the IMERG product through reference rain gauges in Central Italy. Atmos. Res. 2022, 278, 106340. [Google Scholar] [CrossRef]
- Huang, H.; Cui, H.; Ge, Q. Assessment of potential risks induced by increasing extreme precipitation under climate change. Nat. Hazards 2021, 108, 2059–2079. [Google Scholar] [CrossRef]
- Huang, H.; Cui, H.; Ge, Q. Will a nonstationary change in extreme precipitation affect dam security in China? J. Hydrol. 2021, 603, 126859. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Montanari, A. Global and Regional Increase of Precipitation Extremes Under Global Warming. Water Resour. Res. 2019, 55, 4901–4914. [Google Scholar] [CrossRef]
- Trenberth, K.E. Changes in precipitation with climate change. Clim. Res. 2011, 47, 123–138. [Google Scholar] [CrossRef]
- Huang, J.P.; Ran, J.J.; Ji, M.X. Preliminary analysis of the flood disaster over the arid and semi-arid regions in China. Acta Meteorol. Sin. 2014, 72, 1096–1107. [Google Scholar]
- Zheng, W.W.; Yang, Y.D.; Man, Z.M. Multiple movement characteristics of the Meiyu rain belt in East Asia: Reconstructing historical data on the southern margin from 1861 to 2017. Clim. Chang. 2021, 165, 20. [Google Scholar]
- Abdi, A.; Hassanzadeh, Y.; Ouarda, T.B. Regional frequency analysis using Growing Neural Gas network. J. Hydrol. 2017, 550, 92–102. [Google Scholar] [CrossRef]
- Wang, Z.L.; Zeng, Z.Y.; Lai, C.G.; Lin, W.X.; Wu, X.S.; Chen, X.H. A regional frequency analysis of precipitation extremes in Mainland China with fuzzy c-means and L-moments approaches. Int. J. Climatol. 2017, 37, 429–444. [Google Scholar] [CrossRef]
- Yang, T.; Shao, Q.X.; Hao, Z.C.; Chen, X.; Zhang, Z.X.; Xu, C.Y.; Sun, L.M. Regional frequency analysis and spatio-temporal pattern characterization of rainfall extremes in the Pearl River Basin, China. J. Hydrol. 2010, 380, 386–405. [Google Scholar] [CrossRef]
- Darwish, M.M.; Tye, M.R.; Prein, A.F.; Fowler, H.J.; Blenkinsop, S.; Dale, M.; Faulkner, D. New hourly extreme precipitation regions and regional annual probability estimates for the UK. Int. J. Climatol. 2021, 41, 582–600. [Google Scholar] [CrossRef]
- Liu, J.; Doan, C.D.; Liong, S.-Y.; Sanders, R.; Dao, A.T.; Fewtrell, T. Regional frequency analysis of extreme rainfall events in Jakarta. Nat. Hazards 2015, 75, 1075–1104. [Google Scholar] [CrossRef]
- Zakaria, Z.A.; Shabri, A.; Ahmad, U.N. Regional Frequency Analysis of Extreme Rainfalls in the West Coast of Peninsular Malaysia using Partial L-Moments. Water Resour. Manag. 2012, 26, 4417–4433. [Google Scholar] [CrossRef]
- Rajsekhar, D.; Mishra, A.K.; Singh, V.P. Regionalization of Drought Characteristics Using an Entropy Approach. J. Hydrol. Eng. 2013, 18, 870–887. [Google Scholar] [CrossRef]
- Zhuang, W.Y.; Ding, W. Long-lead prediction of extreme precipitation cluster via a spatiotemporal convolutional neural network. In Proceedings of the 6th International Workshop on Climate Informatics (CI 2016), San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Zhang, B.K.; Zhu, G.K. The Climate Regionalization in China; China Science Publishing: Beijing, China, 1959; pp. 1–297. [Google Scholar]
- Amini, S.; Straus, D.M. Control of Storminess over the Pacific and North America by Circulation Regimes: The role of large-scale dynamics in weather extremes. Clim. Dyn. 2019, 52, 4749–4770. [Google Scholar] [CrossRef]
- Horton, D.E.; Johnson, N.C.; Singh, D.; Swain, D.L.; Rajaratnam, B.; Diffenbaugh, N.S. Contribution of changes in atmospheric circulation patterns to extreme temperature trends. Nature 2015, 522, 465–469. [Google Scholar] [CrossRef]
- Zhang, Q.; Qi, T.Y.; Singh, V.P.; Chen, Y.D.; Xiao, M.Z. Regional Frequency Analysis of Droughts in China: A Multivariate Perspective. Water Resour. Manag. 2015, 29, 1767–1787. [Google Scholar] [CrossRef]
- Chen, Y.D.; Zhang, Q.; Xiao, M.Z.; Singh, V.P.; Leung, Y.; Jiang, L.G. Precipitation extremes in the Yangtze River Basin, China: Regional frequency and spatial-temporal patterns. Theor. Appl. Climatol. 2014, 116, 447–461. [Google Scholar] [CrossRef]
- Hosking, J.R.M. L-Moments: Analysis and Estimation of Distributions Using Linear Combinations of Order Statistics. J. R. Stat. Soc. Ser. B 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Fowler, H.J.; Kilsby, C.G. A regional frequency analysis of United Kingdom extreme rainfall from 1961 to 2000. Int. J. Clim. 2003, 23, 1313–1334. [Google Scholar] [CrossRef]
- Gaál, L.; Kyselý, J.; Szolgay, J. Region-of-influence approach to a frequency analysis of heavy precipitation in Slovakia. Hydrol. Earth Syst. Sci. 2008, 12, 825–839. [Google Scholar] [CrossRef]
- Dunn, J.C. A fuzzy relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters. J. Cybern. 1973, 3, 32–57. [Google Scholar] [CrossRef]
- Askari, S. Fuzzy C-Means clustering algorithm for data with unequal cluster sizes and contaminated with noise and outliers: Review and development. Expert Syst. Appl. 2021, 165, 113856. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R. Regional frequency analysis: An approach based on L-moments. J. Am. Stat. Assoc. 1997, 93, 1233. [Google Scholar]
- Norbiato, D.; Borga, M.; Sangati, M.; Zanon, F. Regional frequency analysis of extreme precipitation in the eastern Italian Alps and the August 29, 2003 flash flood. J. Hydrol. 2007, 345, 149–166. [Google Scholar] [CrossRef]
- Du, H.B.; Alexander, L.V.; Donat, M.G.; Lippmann, T.; Srivastava, A.; Salinger, J.; Kruger, A.; Choi, G.; He, H.S.; Fujibe, F.; et al. Precipitation From Persistent Extremes is Increasing in Most Regions and Globally. Geophys. Res. Lett. 2019, 46, 6041–6049. [Google Scholar] [CrossRef]
- Dwyer, J.G.; O’Gorman, P.A. Changing duration and spatial extent of midlatitude precipitation extremes across different climates. Geophys. Res. Lett. 2017, 44, 5863–5871. [Google Scholar] [CrossRef]


| Clustering Input Information | Relative Weight | |
|---|---|---|
| Averaged annual maximum daily precipitation | 1 | |
| Dispersion Degree | L–CV | 0.33 |
| Asymmetry | L–skewness | 0.33 |
| Steepness | L–kurtosis | 0.33 |
| Geographic Information | Elevation | 0.5 |
| Longitude | 1 | |
| Latitude | 1 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Cui, H.; Singh, V.P. Clustering Daily Extreme Precipitation Patterns in China. Water 2023, 15, 3651. https://doi.org/10.3390/w15203651
Huang H, Cui H, Singh VP. Clustering Daily Extreme Precipitation Patterns in China. Water. 2023; 15(20):3651. https://doi.org/10.3390/w15203651
Chicago/Turabian StyleHuang, Hefei, Huijuan Cui, and Vijay P. Singh. 2023. "Clustering Daily Extreme Precipitation Patterns in China" Water 15, no. 20: 3651. https://doi.org/10.3390/w15203651
APA StyleHuang, H., Cui, H., & Singh, V. P. (2023). Clustering Daily Extreme Precipitation Patterns in China. Water, 15(20), 3651. https://doi.org/10.3390/w15203651







