Improving Forecasting Accuracy of Multi-Scale Groundwater Level Fluctuations Using a Heterogeneous Ensemble of Machine Learning Algorithms
Abstract
:1. Introduction
- Performance evaluation of the seven ML-based individual models to forecast multi-step ahead GWL fluctuations.
- Development of a heterogeneous ensemble of the GWL forecast models using the BMA approach and comparison of the performance of the ensemble with that of the standalone forecast models.
2. Materials and Methods
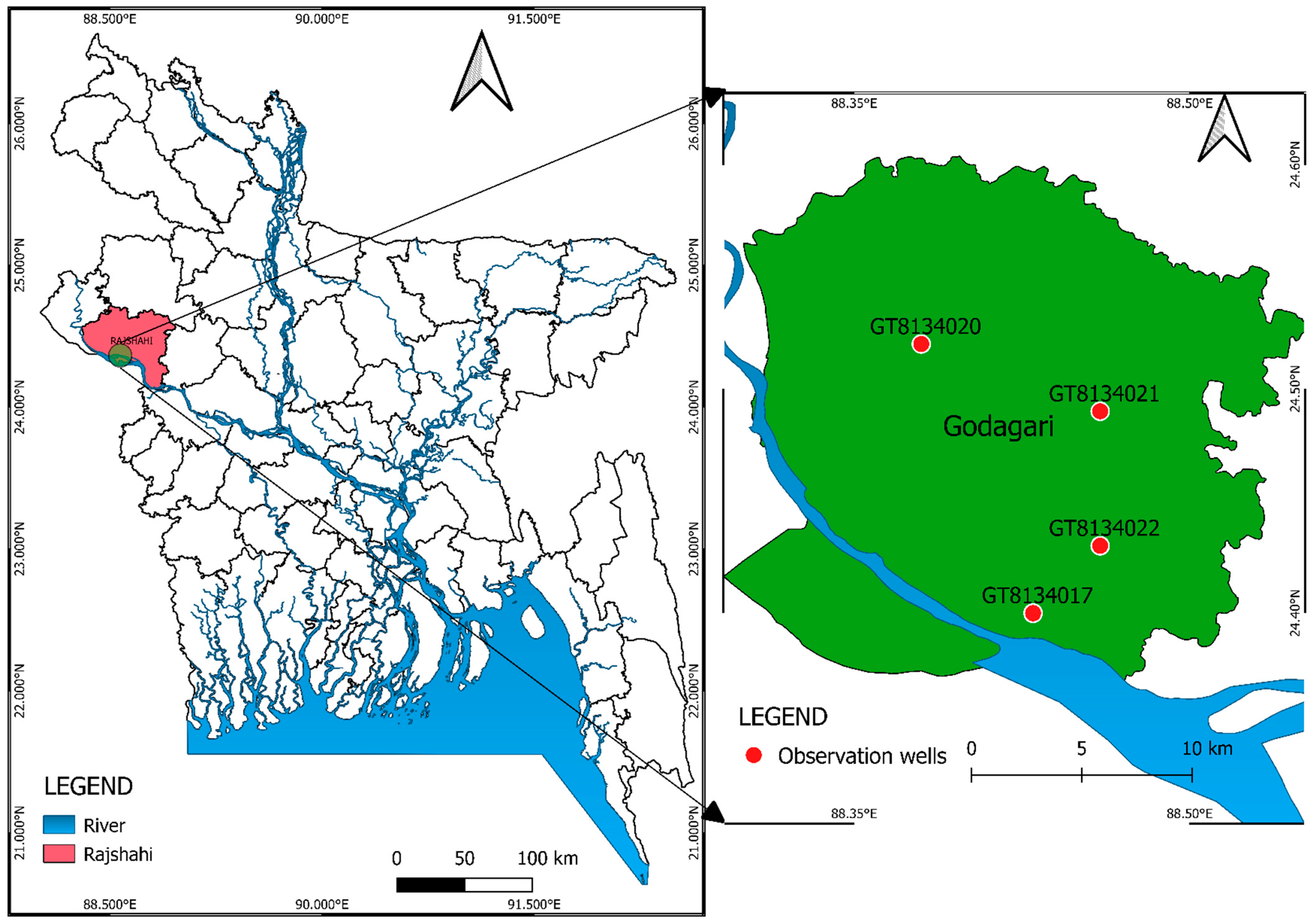
2.1. Study Area and the Data
2.2. Machine Learning-Based Models
2.2.1. Adaptive Neuro-Fuzzy Inference System (ANFIS)
2.2.2. Bagged and Boosted RF
2.2.3. Gaussian Process Regression (GPR)
2.2.4. Bidirectional Long Short-Term Memory (Bi-LSTM) Network
- A sequence input layer, which matched the number of input variables or features.
- A Bi-LSTM layer, whose units corresponded to the number of hidden units.
- A fully connected layer, tailored to the number of output variables or response variables.
- Finally, a regression layer.
2.2.5. Multivariate Adaptive Regression Spline (MARS)
2.2.6. Support Vector Regression (SVR)
2.3. Modeling Techniques
2.3.1. Data Preprocessing
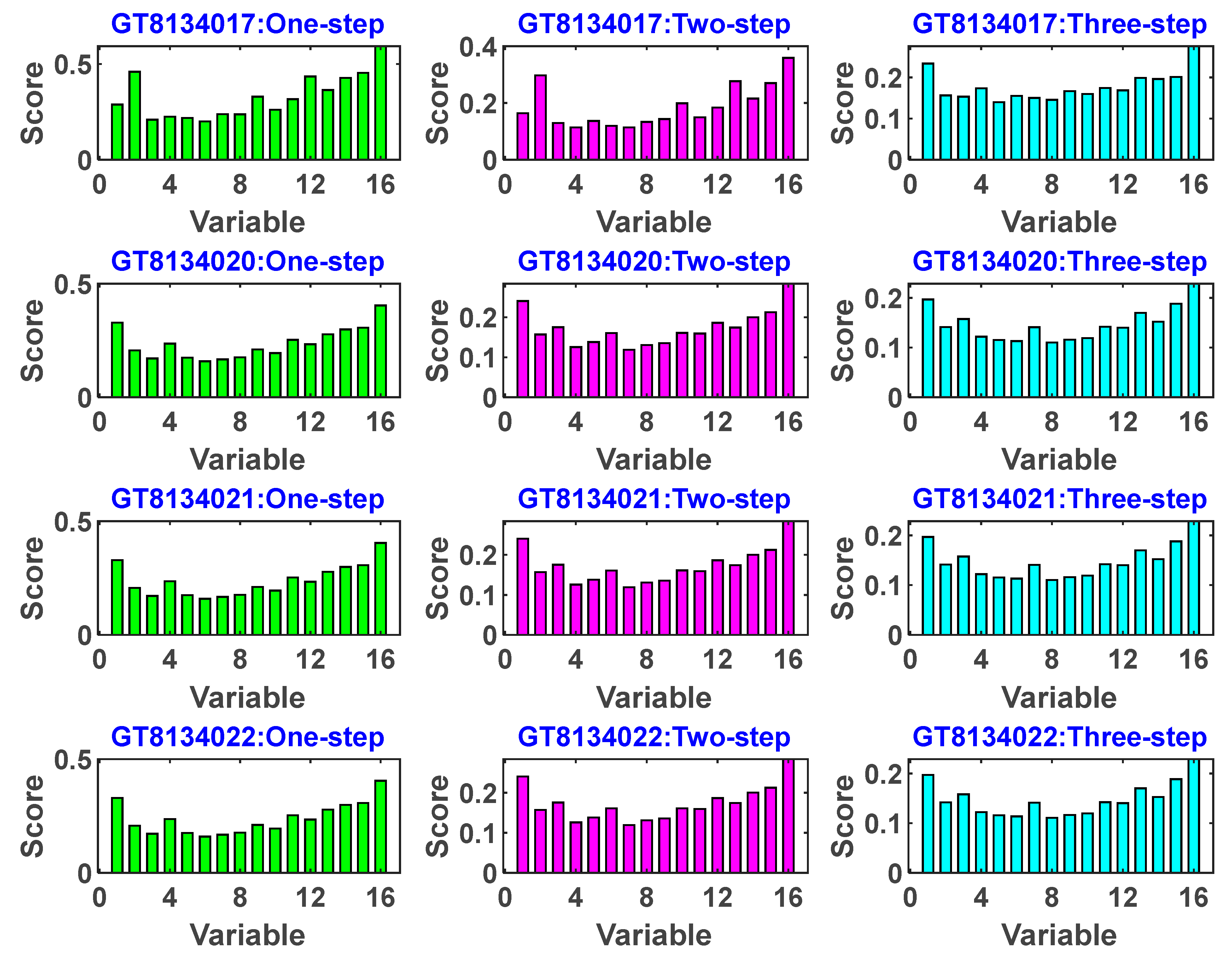
2.3.2. Selection of Input Variables
2.3.3. Standardization of Data
2.3.4. Development of Individual Models
2.3.5. Development of Ensemble Models
2.4. Model Performance Evaluation
2.5. Variable Importance
3. Results and Discussion
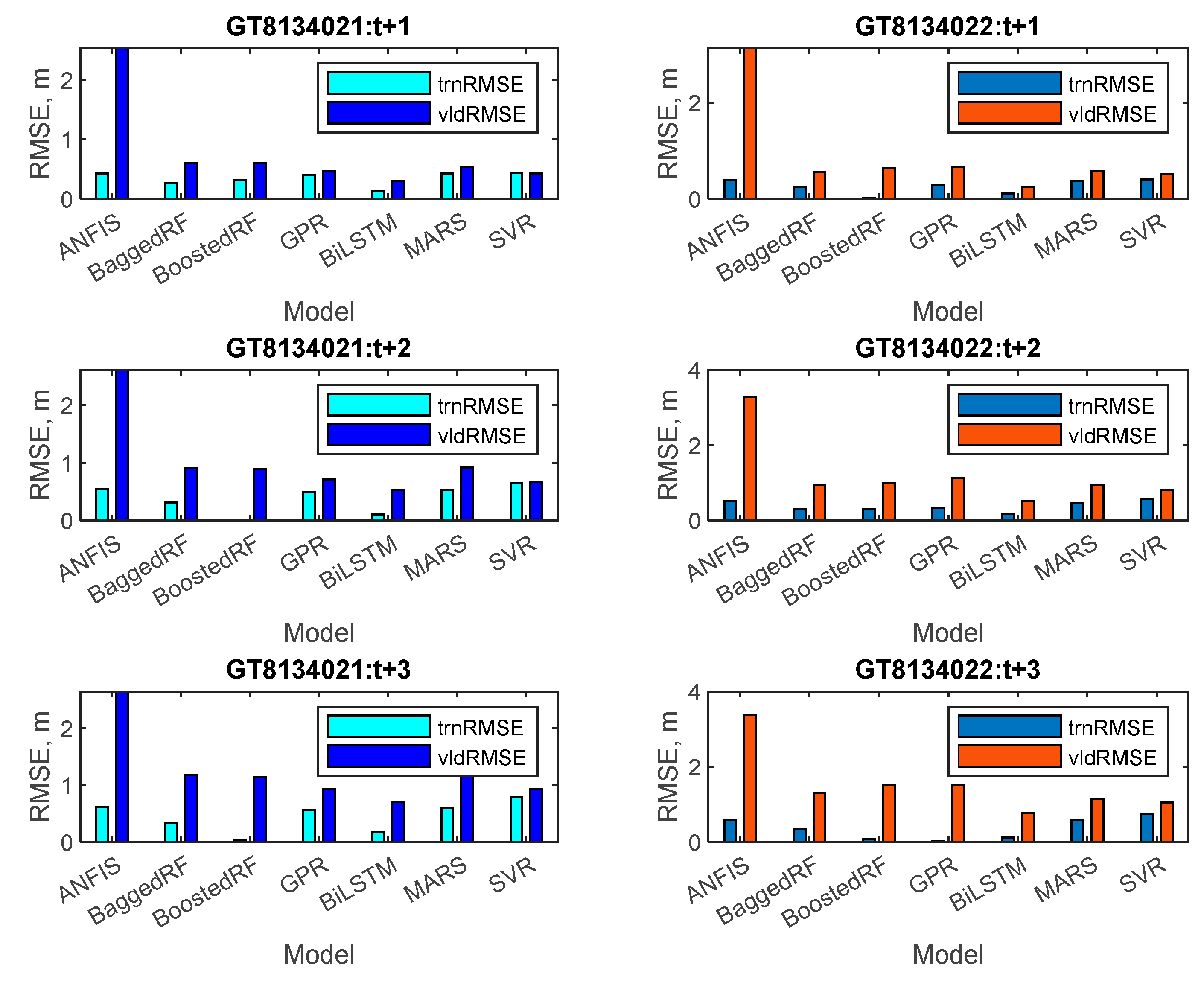
3.1. Performance of the Individual Forecasting Models during Training and Validation
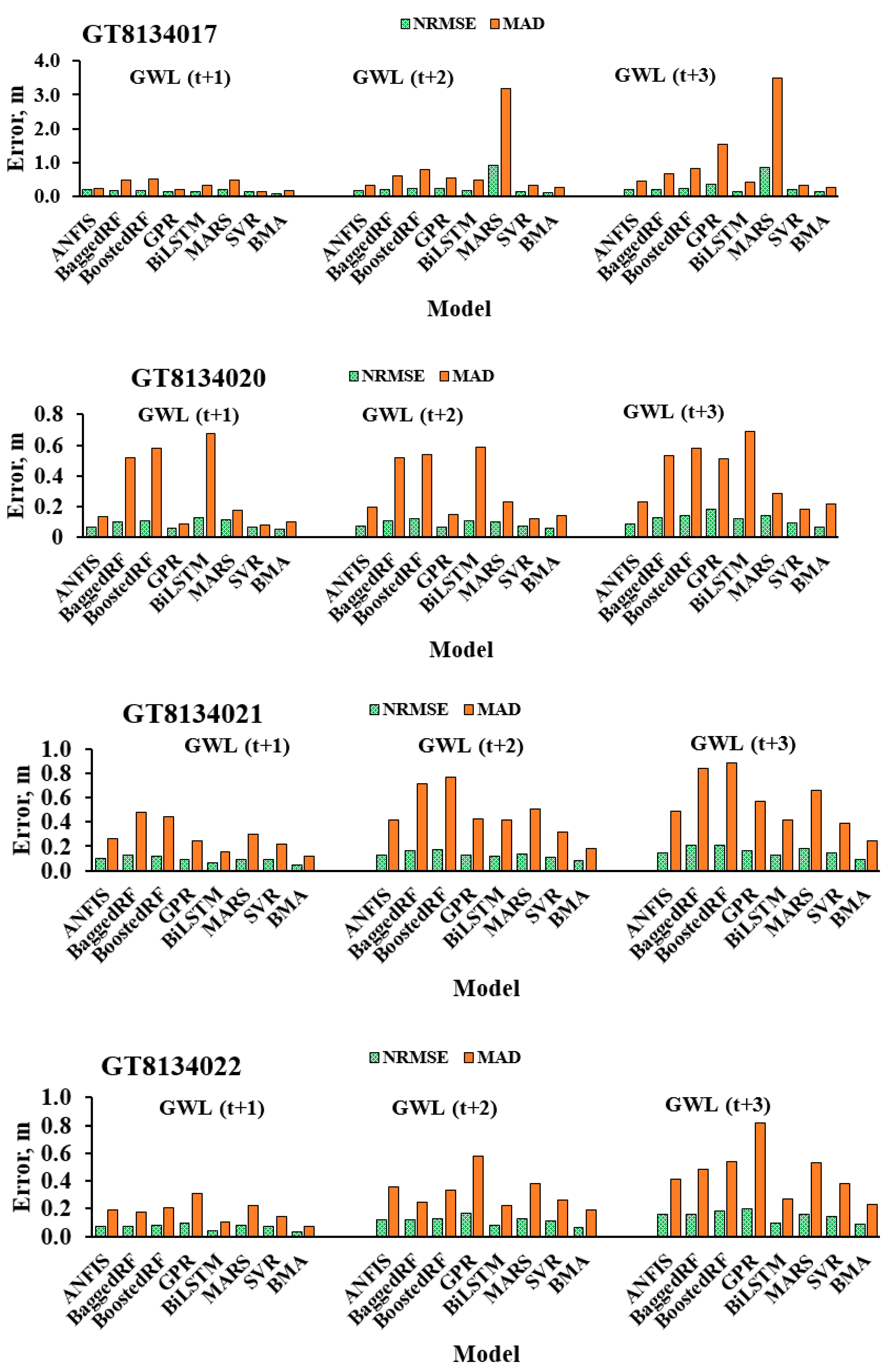
3.2. Performance of the Standalone and Ensemble Models on the Independent Test Dataset
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hasan, M.R.; Mostafa, M.; Rahman, N.; Islam, S.; Islam, M. Groundwater Depletion and Its Sustainable Management in Barind Tract of Bangladesh. Res. J. Environ. Sci. 2018, 12, 247–255. [Google Scholar] [CrossRef]
- Monir, M.; Sarker, S.; Sarkar, S.K.; Mohd, A.; Mallick, J.; Islam, A.R.M.T. Spatiotemporal Depletion of Groundwater Level in a Drought-Prone Rangpur District, Northern Region of Bangladesh. 21 June 2022; PREPRINT (Version 1). [Google Scholar] [CrossRef]
- Murphy, J.; Sexton, D.; Barnett, D.; Jones, G.; Webb, M.; Collins, M.; Stainforth, D. Quantification of Modelling Uncertainties in a Large Ensemble of Climate Change Simulations. Nature 2004, 430, 768–772. [Google Scholar] [CrossRef] [PubMed]
- Ewen, J.; O’Donnell, G.; Burton, A.; O’Connell, E. Errors and Uncertainty in Physically-Basedrainfall-Runoff Modeling of Catchment Change Effects. J. Hydrol. 2006, 330, 641–650. [Google Scholar] [CrossRef]
- Vu, M.; Jardani, A.A.; Massei, N.; Fournier, M. Reconstruction of Missing Groundwater Level Data by Using Long Short-Term Memory (LSTM) Deep Neural Network. J. Hydrol. 2020, 597, 125776. [Google Scholar] [CrossRef]
- Pham, Q.; Kumar, M.; Di Nunno, F.; Elbeltagi, A.; Granata, F.; Islam, A.R.M.T.; Talukdar, S.; Nguyen, X.; Najah, A.-M.; Tran Anh, D. Groundwater Level Prediction Using Machine Learning Algorithms in a Drought-Prone Area. Neural Comput. Appl. 2022, 34, 10751–10773. [Google Scholar] [CrossRef]
- Jeong, J.; Park, E. Comparative Applications of Data-Driven Models Representing Water Table Fluctuations. J. Hydrol. 2019, 572, 261–273. [Google Scholar] [CrossRef]
- Sun, J.; Hu, L.; Li, D.; Sun, K.; Yang, Z. Data-Driven Models for Accurate Groundwater Level Prediction and Their Practical Significance in Groundwater Management. J. Hydrol. 2022, 608, 127630. [Google Scholar] [CrossRef]
- Zanotti, C.; Rotiroti, M.; Sterlacchini, S.; Cappellini, G.; Fumagalli, L.; Stefania, G.A.; Nannucci, M.S.; Leoni, B.; Bonomi, T. Choosing between Linear and Nonlinear Models and Avoiding Overfitting for Short and Long Term Groundwater Level Forecasting in a Linear System. J. Hydrol. 2019, 578, 124015. [Google Scholar] [CrossRef]
- Vadiati, M.; Yami, Z.; Eskandari, E.; Nakhaei, M.; Kisi, O. Application of Artificial Intelligence Models for Prediction of Groundwater Level Fluctuations: Case Study (Tehran-Karaj Alluvial Aquifer). Environ. Monit. Assess. 2022, 194, 619. [Google Scholar] [CrossRef]
- Jafari, M.M.; Ojaghlou, H.; Zare, M.; Schumann, G.J. Application of a Novel Hybrid Wavelet-ANFIS/Fuzzy c-Means Clustering Model to Predict Groundwater Fluctuations. Atmosphere 2021, 12, 9. [Google Scholar] [CrossRef]
- Che Nordin, N.F.; Mohd, N.S.; Koting, S.; Ismail, Z.; Sherif, M.; El-Shafie, A. Groundwater Quality Forecasting Modelling Using Artificial Intelligence: A Review. Groundw. Sustain. Dev. 2021, 14, 100643. [Google Scholar] [CrossRef]
- Kombo, O.; Santhi, K.; Sheikh, Y.; Bovim, A.; Jayavel, K. Long-Term Groundwater Level Prediction Model Based on Hybrid KNN-RF Technique. Hydrology 2020, 7, 59. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, Y.-P.; Yang, Z.; Wang, G.; Zhu, Q. Integration of a Parsimonious Hydrological Model with Recurrent Neural Networks for Improved Streamflow Forecasting. Water 2018, 10, 1655. [Google Scholar] [CrossRef]
- Ebrahimy, H.; Feizizadeh, B.; Salmani, S.; Azadi, H. A Comparative Study of Land Subsidence Susceptibility Mapping of Tasuj Plane, Iran, Using Boosted Regression Tree, Random Forest and Classification and Regression Tree Methods. Environ. Earth Sci. 2020, 79, 223. [Google Scholar] [CrossRef]
- Arabameri, A.; Yamani, M.; Pradhan, B.; Melesse, A.; Shirani, K.; Tien Bui, D. Novel Ensembles of COPRAS Multi-Criteria Decision-Making with Logistic Regression, Boosted Regression Tree, and Random Forest for Spatial Prediction of Gully Erosion Susceptibility. Sci. Total Environ. 2019, 688, 903–916. [Google Scholar] [CrossRef]
- Band, S.S.; Heggy, E.; Bateni, S.; Karami, H.; Rabiee, M.; Samadianfard, S.; Chau, K.; Mosavi, A. Groundwater Level Prediction in Arid Areas Using Wavelet Analysis and Gaussian Process Regression. Eng. Appl. Comput. Fluid Mech. 2021, 15, 1147–1158. [Google Scholar] [CrossRef]
- Gong, Z.; Zhang, H. Research on GPR Image Recognition Based on Deep Learning. MATEC Web Conf. 2020, 309, 3027. [Google Scholar] [CrossRef]
- Cheng, X.; Tang, H.; Wu, Z.; Liang, D.; Xie, Y. BILSTM-Based Deep Neural Network for Rock-Mass Classification Prediction Using Depth-Sequence MWD Data: A Case Study of a Tunnel in Yunnan, China. Appl. Sci. 2023, 13, 6050. [Google Scholar] [CrossRef]
- Peng, Y.; Han, Q.; Su, F.; He, X.; Feng, X. Meteorological Satellite Operation Prediction Using a BiLSTM Deep Learning Model. Secur. Commun. Netw. 2021, 2021, 9916461. [Google Scholar] [CrossRef]
- Tien Bui, D.; Hoang, N.-D.; Samui, P. Spatial Pattern Analysis and Prediction of Forest Fire Using New Machine Learning Approach of Multivariate Adaptive Regression Splines and Differential Flower Pollination Optimization: A Case Study at Lao Cai Province (Viet Nam). J. Environ. Manag. 2019, 237, 476–487. [Google Scholar] [CrossRef]
- Fung, K.F.; Huang, Y.F.; Koo, C.H.; Mirzaei, M. Improved SVR Machine Learning Models for Agricultural Drought Prediction at Downstream of Langat River Basin, Malaysia. J. Water Clim. Chang. 2019, 11, 1383–1398. [Google Scholar] [CrossRef]
- Servos, N.; Liu, X.; Teucke, M.; Freitag, M. Travel Time Prediction in a Multimodal Freight Transport Relation Using Machine Learning Algorithms. Logistics 2020, 4, 1. [Google Scholar] [CrossRef]
- Roy, D.K.; Datta, B. Saltwater Intrusion Prediction in Coastal Aquifers Utilizing a Weighted-Average Heterogeneous Ensemble of Prediction Models Based on Dempster-Shafer Theory of Evidence. Hydrol. Sci. J. 2020, 65, 1555–1567. [Google Scholar] [CrossRef]
- Tang, J.; Fan, B.; Xiao, L.; Tian, S.; Zhang, F.; Zhang, L.; Weitz, D. A New Ensemble Machine-Learning Framework for Searching Sweet Spots in Shale Reservoirs. SPE J. 2021, 26, 482–497. [Google Scholar] [CrossRef]
- Cao, Y.; Geddes, T.A.; Yang, J.Y.H.; Yang, P. Ensemble Deep Learning in Bioinformatics. Nat. Mach. Intell. 2020, 2, 500–508. [Google Scholar] [CrossRef]
- Liu, H.; Yu, C.; Wu, H.; Duan, Z.; Yan, G. A New Hybrid Ensemble Deep Reinforcement Learning Model for Wind Speed Short Term Forecasting. Energy 2020, 202, 117794. [Google Scholar] [CrossRef]
- Zhou, T.; Wen, X.; Feng, Q.; Yu, H.; Xi, H. Bayesian Model Averaging Ensemble Approach for Multi-Time-Ahead Groundwater Level Prediction: Combining the GRACE, GLEAM, and GLDAS Data in Arid Areas. Remote Sens. 2022, 15, 188. [Google Scholar] [CrossRef]
- Roy, D.K.; Biswas, S.K.; Mattar, M.A.; El-Shafei, A.A.; Murad, K.F.I.; Saha, K.K.; Datta, B.; Dewidar, A.Z. Groundwater Level Prediction Using a Multiple Objective Genetic Algorithm-Grey Relational Analysis Based Weighted Ensemble of ANFIS Models. Water 2021, 13, 3130. [Google Scholar] [CrossRef]
- Afan, H.A.; Ibrahem, A.O.A.; Essam, Y.; Ahmed, A.N.; Huang, Y.F.; Kisi, O.; Sherif, M.; Sefelnasr, A.; Chau, K.-W.; El-Shafie, A. Modeling the Fluctuations of Groundwater Level by Employing Ensemble Deep Learning Techniques. Eng. Appl. Comput. Fluid Mech. 2021, 15, 1420–1439. [Google Scholar] [CrossRef]
- Tao, H.; Hameed, M.M.; Marhoon, H.A.; Zounemat-Kermani, M.; Heddam, S.; Kim, S.; Sulaiman, S.O.; Tan, M.L.; Sa’adi, Z.; Mehr, A.D.; et al. Groundwater Level Prediction Using Machine Learning Models: A Comprehensive Review. Neurocomputing 2022, 489, 271–308. [Google Scholar] [CrossRef]
- Gong, Y.; Wang, Z.; Xu, G.; Zhang, Z. A Comparative Study of Groundwater Level Forecasting Using Data-Driven Models Based on Ensemble Empirical Mode Decomposition. Water 2018, 10, 730. [Google Scholar] [CrossRef]
- Seifi, A.; Ehteram, M.; Soroush, F.; Torabi Haghighi, A. Multi-Model Ensemble Prediction of Pan Evaporation Based on the Copula Bayesian Model Averaging Approach. Eng. Appl. Artif. Intell. 2022, 114, 105124. [Google Scholar] [CrossRef]
- Hossain, M.; Haque, M.; Keramat, M.; Wang, X. Groundwater Resource Evaluation of Nawabganj and Godagari Thana of Greater Rajshahi District. J. Bangladesh Acad. Sci. 1996, 20, 191–196. [Google Scholar]
- Zahid, A.; Hossain, A. Bangladesh Water Development Board: A Bank of Hydrological Data Essential for Planning and Design in Water Sector. In Proceedings of the International Conference on Advances in Civil Engineering 2014, Istanbul, Turkey, 21–25 October 2014; Chittagong University of Engineering and Technology: Chattogram, Bangladesh, 2014. [Google Scholar]
- Rahman, A.T.M.S.; Hosono, T.; Quilty, J.M.; Das, J.; Basak, A. Multiscale Groundwater Level Forecasting: Coupling New Machine Learning Approaches with Wavelet Transforms. Adv. Water Resour. 2020, 141, 103595. [Google Scholar] [CrossRef]
- Jang, J.-S.R.; Sun, C.T.; Mizutani, E. Neuro-Fuzzy and Soft Computing: A Computational Approach to Learning and Machine Intelligence. IEEE Trans. Autom. Control. 1997, 42, 1482–1484. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Bishop, C. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Rasmussen, C.E. Gaussian Processes in Machine Learning BT—Advanced Lectures on Machine Learning: ML Summer Schools 2003, Canberra, Australia, February 2–14, 2003, Tübingen, Germany, August 4–16, 2003, Revised Lectures; Bousquet, O., von Luxburg, U., Rätsch, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 63–71. ISBN 978-3-540-28650-9. [Google Scholar]
- Friedman, J.H. Multivariate Adaptive Regression Splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Roy, D.K.; Datta, B. Multivariate Adaptive Regression Spline Ensembles for Management of Multilayered Coastal Aquifers. J. Hydrol. Eng. 2017, 22, 4017031. [Google Scholar] [CrossRef]
- Chen, C.-C.; Wu, J.-K.; Lin, H.-W.; Pai, T.-P.; Fu, T.-F.; Wu, C.-L.; Tully, T.; Chiang, A.-S. Visualizing Long-Term Memory Formation in Two Neurons of the Drosophila Brain. Science 2012, 335, 678–685. [Google Scholar] [CrossRef]
- Vapnik, V.N.; Golowich, S.E.; Smola, A. Support Vector Method for Function Approximation, Regression Estimation and Signal Processing. Adv. Neural Inf. Process. Syst. 1996, 9. [Google Scholar]
- Yin, Z.; Feng, Q.; Yang, L.; Deo, R.C.; Wen, X.; Si, J.; Xiao, S. Future Projection with an Extreme-Learning Machine and Support Vector Regression of Reference Evapotranspiration in a Mountainous Inland Watershed in North-West China. Water 2017, 9, 880. [Google Scholar] [CrossRef]
- Barzegar, R.; Ghasri, M.; Qi, Z.; Quilty, J.; Adamowski, J. Using Bootstrap ELM and LSSVM Models to Estimate River Ice Thickness in the Mackenzie River Basin in the Northwest Territories, Canada. J. Hydrol. 2019, 577, 123903. [Google Scholar] [CrossRef]
- Galelli, S.; Humphrey, G.B.; Maier, H.R.; Castelletti, A.; Dandy, G.C.; Gibbs, M.S. An Evaluation Framework for Input Variable Selection Algorithms for Environmental Data-Driven Models. Environ. Model. Softw. 2014, 62, 33–51. [Google Scholar] [CrossRef]
- Quilty, J.; Adamowski, J.; Khalil, B.; Rathinasamy, M. Bootstrap Rank-Ordered Conditional Mutual Information (BroCMI): A Nonlinear Input Variable Selection Method for Water Resources Modeling. Water Resour. Res. 2016, 52, 2299–2326. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Jaafar, O.; Deo, R.C.; Kisi, O.; Adamowski, J.; Quilty, J.; El-Shafie, A. Stream-Flow Forecasting Using Extreme Learning Machines: A Case Study in a Semi-Arid Region in Iraq. J. Hydrol. 2016, 542, 603–614. [Google Scholar] [CrossRef]
- Hadi, S.J.; Abba, S.I.; Sammen, S.S.; Salih, S.Q.; Al-Ansari, N.; Yaseen, Z.M. Non-Linear Input Variable Selection Approach Integrated with Non-Tuned Data Intelligence Model for Streamflow Pattern Simulation. IEEE Access 2019, 7, 141533–141548. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Taormina, R.; Galelli, S.; Karakaya, G.; Ahipasaoglu, S.D. An Information Theoretic Approach to Select Alternate Subsets of Predictors for Data-Driven Hydrological Models. J. Hydrol. 2016, 542, 18–34. [Google Scholar] [CrossRef]
- Peng, H.; Long, F.; Ding, C. Feature Selection Based on Mutual Information Criteria of Max-Dependency, Max-Relevance, and Min-Redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef]
- Berrendero, J.R.; Cuevas, A.; Torrecilla, J.L. The MRMR Variable Selection Method: A Comparative Study for Functional Data. J. Stat. Comput. Simul. 2016, 86, 891–907. [Google Scholar] [CrossRef]
- Shah, M.; Javed, M.; Alqahtani, A.; Aldrees, A. Environmental Assessment Based Surface Water Quality Prediction Using Hyper-Parameter Optimized Machine Learning Models Based on Consistent Big Data. Process Saf. Environ. Prot. 2021, 151, 324–340. [Google Scholar] [CrossRef]
- Sahoo, M.; Das, T.; Kumari, K.; Dhar, A. Space–Time Forecasting of Groundwater Level Using a Hybrid Soft Computing Model. Hydrol. Sci. J. 2017, 62, 561–574. [Google Scholar] [CrossRef]
- Wang, W.; Gelder, P.; Vrijling, J.; Ma, J. Forecasting Daily Streamflow Using Hybrid ANN Models. J. Hydrol. 2006, 324, 383–399. [Google Scholar] [CrossRef]
- Probst, P.; Wright, M.N.; Boulesteix, A.-L. Hyperparameters and Tuning Strategies for Random Forest. WIREs Data Min. Knowl. Discov. 2019, 9, e1301. [Google Scholar] [CrossRef]
- Zhang, F.; Deb, C.; Lee, S.E.; Yang, J.; Shah, K.W. Time Series Forecasting for Building Energy Consumption Using Weighted Support Vector Regression with Differential Evolution Optimization Technique. Energy Build. 2016, 126, 94–103. [Google Scholar] [CrossRef]
- Goel, T.; Haftka, R.T.; Shyy, W.; Queipo, N.V. Ensemble of Surrogates. Struct. Multidiscip. Optim. 2007, 33, 199–216. [Google Scholar] [CrossRef]
- Hoeting, J.A.; Madigan, D.; Raftery, A.E.; Volinsky, C.T. Bayesian Model Averaging: A Tutorial (with Comments by M. Clyde, David Draper and E. I. George, and a Rejoinder by the Authors. Stat. Sci. 1999, 14, 382–417. [Google Scholar] [CrossRef]
- Duan, Q.; Ajami, N.K.; Gao, X.; Sorooshian, S. Multi-Model Ensemble Hydrologic Prediction Using Bayesian Model Averaging. Adv. Water Resour. 2007, 30, 1371–1386. [Google Scholar] [CrossRef]
- Qu, B.; Zhang, X.; Pappenberger, F.; Zhang, T.; Fang, Y. Multi-Model Grand Ensemble Hydrologic Forecasting in the Fu River Basin Using Bayesian Model Averaging. Water 2017, 9, 74. [Google Scholar] [CrossRef]
- Kirch, W. (Ed.) Pearson’s Correlation Coefficient. In Encyclopedia of Public Health; Springer: Dordrecht, The Netherlands, 2008; pp. 1090–1091. ISBN 978-1-4020-5614-7. [Google Scholar]
- LeGates, D.R.; McCabe, G.J., Jr. Evaluating the Use of “Goodness-of-Fit” Measures in Hydrologic and Hydroclimatic Model Validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another Look at Measures of Forecast Accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Pham-Gia, T.; Hung, T.L. The Mean and Median Absolute Deviations. Math. Comput. Model. 2001, 34, 921–936. [Google Scholar] [CrossRef]
- Willmott, C.J. On the Validation of Models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Pledger, S. Unified Maximum Likelihood Estimates for Closed Capture–Recapture Models Using Mixtures. Biometrics 2000, 56, 434–442. [Google Scholar] [CrossRef]
- Rahman, A.T.M.S.; Hosono, T.; Kisi, O.; Dennis, B.; Imon, A.H.M.R. A Minimalistic Approach for Evapotranspiration Estimation Using the Prophet Model. Hydrol. Sci. J. 2020, 65, 1994–2006. [Google Scholar] [CrossRef]
- Darbandsari, P.; Coulibaly, P. Inter-Comparison of Different Bayesian Model Averaging Modifications in Streamflow Simulation. Water 2019, 11, 1707. [Google Scholar] [CrossRef]




| Observation Well | Mean | STD | Skewness | Kurtosis |
|---|---|---|---|---|
| GT8134017 | 6.796 | 2.797 | −0.172 | −0.446 |
| GT8134020 | 7.735 | 2.683 | −0.043 | −0.596 |
| GT8134021 | 6.612 | 2.555 | −0.457 | −0.535 |
| GT8134022 | 6.534 | 2.274 | −0.218 | −0.557 |
| Model | Parameters |
|---|---|
| ANFIS | Number of clusters: GT8134017-GWL (t + 1) = 6, GT3330001-GWL (t + 2) = 3, GT3330001-GWL (t + 3) = 3 GT8134020-GWL (t + 1) = 3, GT3330002-GWL (t + 2) = 2, GT3330002-GWL (t + 3) = 4 GT8134021-GWL (t + 1) = 6, GT3330020-GWL (t + 2) = 3, GT3330020-GWL (t + 3) = 5 GT813402-GWL (t + 1) = 5, GT3330020-GWL (t + 2) = 4, GT3330020-GWL (t + 3) = 3 Initial FIS: Fuzzy partition matrix exponent = 2 Maximum number of iterations = 500 Minimum improvement = 1 × 10−5 ANFIS: Maximum number of epochs: 500 Error goal = 0 Initial step size = 0.01 Step size decrease rate = 0.9 Step size increase rate = 1.1 |
| Bagged RF | Number of variables to sample = all Predictor selection = interaction-curvature Method = bag Number of learning cycles = 200 Learn rate = 1 |
| Boosted RF | Method = LSBoost Minimum number of parents = 10 Minimum number of leafs = 5 Maximum splits = 12 Number of learning cycles = 57 Learn rate = 0.1929 |
| GPR | Basis function = Linear Kernel function = Rational Quadratic Fit method = Exact, predict method = Exact Beta = 0, Sigma = 0.4081 Optimizer = quasinewton |
| MARS | Number of Basis functions at the forward pass = 100 Number of Basis functions at the backward pass = 50 Minimum number of observations between the knots = 3 No penalty is added to the variables to give equal priority to all input variables |
| Bi-LSTM | Gradient decay factor = 0.9, Epsilon = 1 × 10−8, Initial learn rate = 0.01 Learn rate drop factor = 0.1, Learn rate drop period = 10, Gradient threshold = 1 L2 regularization = 1 × 10−4, Gradient threshold method = l2norm, Maximum number of epochs = 1000, Mini batch size = 150 |
| SVR | Kernel function = linear, Box constraint = 25.4335, Epsilon = 0.1021 Delta gradient tolerance = 0, Gap tolerance = 1 × 10−3, Kernel scale = 7.4663 Solver = SMO, Bias = 6.7549, Iteration limit = 1,000,000 |
| Model | GWL (t + 1) | GWL (t + 2) | GWL (t + 3) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | NS | MBE | RMSE | MAE | NS | MBE | RMSE | MAE | NS | MBE | |
| GT8134017 | ||||||||||||
| ANFIS | 1.85 | 0.93 | 0.40 | −0.25 | 1.57 | 0.95 | 0.57 | −0.29 | 1.82 | 1.16 | 0.43 | −0.44 |
| BaggedRF | 1.59 | 1.01 | 0.56 | −0.86 | 1.83 | 1.33 | 0.41 | −1.17 | 2.03 | 1.56 | 0.28 | −1.41 |
| BoostedRF | 1.67 | 1.12 | 0.51 | −0.92 | 2.20 | 1.63 | 0.16 | −1.48 | 2.09 | 1.59 | 0.24 | −1.40 |
| GPR | 1.29 | 0.67 | 0.71 | −0.16 | 2.16 | 1.48 | 0.18 | −1.14 | 3.43 | 2.60 | −1.04 | −2.42 |
| BiLSTM | 1.38 | 0.80 | 0.67 | −0.67 | 1.49 | 0.98 | 0.61 | −0.68 | 1.47 | 0.98 | 0.63 | −0.59 |
| MARS | 1.95 | 1.10 | 0.33 | −0.67 | 8.65 | 5.40 | −12.06 | −5.23 | 8.13 | 5.49 | −10.46 | −5.22 |
| SVR | 1.42 | 0.70 | 0.64 | −0.17 | 1.46 | 0.88 | 0.63 | −0.33 | 1.85 | 1.31 | 0.40 | −0.80 |
| BMA | 0.87 | 0.50 | 0.87 | 0.00 | 1.13 | 0.68 | 0.78 | 0.00 | 1.23 | 0.77 | 0.74 | 0.00 |
| GT8134020 | ||||||||||||
| ANFIS | 0.76 | 0.45 | 0.52 | −0.10 | 0.80 | 0.51 | 0.47 | −0.15 | 0.98 | 0.67 | 0.20 | −0.17 |
| BaggedRF | 1.17 | 0.89 | −0.15 | −0.84 | 1.25 | 1.00 | −0.31 | −0.96 | 1.42 | 1.19 | −0.70 | −1.16 |
| BoostedRF | 1.25 | 0.96 | −0.30 | −0.94 | 1.39 | 1.15 | −0.61 | −1.13 | 1.63 | 1.40 | −1.23 | −1.39 |
| GPR | 0.67 | 0.41 | 0.63 | −0.21 | 0.77 | 0.54 | 0.50 | −0.36 | 2.08 | 1.86 | −2.62 | −1.86 |
| BiLSTM | 1.46 | 1.16 | −0.77 | −0.98 | 1.21 | 0.90 | −0.23 | −0.83 | 1.40 | 1.08 | −0.64 | −1.00 |
| MARS | 1.32 | 0.68 | −0.46 | −0.01 | 1.12 | 0.67 | −0.05 | −0.17 | 1.61 | 0.92 | −1.16 | 0.06 |
| SVR | 0.71 | 0.41 | 0.58 | −0.18 | 0.84 | 0.58 | 0.41 | −0.39 | 1.07 | 0.81 | 0.04 | −0.63 |
| BMA | 0.59 | 0.33 | 0.71 | 0.00 | 0.64 | 0.38 | 0.66 | 0.00 | 0.71 | 0.47 | 0.58 | 0.00 |
| GT8134021 | ||||||||||||
| ANFIS | 0.85 | 0.60 | 0.79 | −0.35 | 1.15 | 0.88 | 0.62 | −0.65 | 1.30 | 0.97 | 0.52 | −0.59 |
| BaggedRF | 1.10 | 0.80 | 0.66 | −0.69 | 1.47 | 1.15 | 0.38 | −1.03 | 1.85 | 1.51 | 0.02 | −1.39 |
| BoostedRF | 1.07 | 0.79 | 0.68 | −0.65 | 1.53 | 1.19 | 0.33 | −1.05 | 1.83 | 1.47 | 0.05 | −1.31 |
| GPR | 0.78 | 0.54 | 0.83 | −0.29 | 1.11 | 0.85 | 0.65 | −0.66 | 1.42 | 1.13 | 0.43 | −0.96 |
| BiLSTM | 0.58 | 0.40 | 0.91 | −0.23 | 1.02 | 0.75 | 0.70 | −0.29 | 1.08 | 0.84 | 0.67 | −0.31 |
| MARS | 0.83 | 0.60 | 0.80 | −0.31 | 1.22 | 0.96 | 0.58 | −0.39 | 1.64 | 1.26 | 0.24 | −0.60 |
| SVR | 0.78 | 0.51 | 0.82 | −0.12 | 0.98 | 0.73 | 0.73 | −0.46 | 1.28 | 1.02 | 0.54 | −0.82 |
| BMA | 0.44 | 0.27 | 0.95 | 0.00 | 0.75 | 0.50 | 0.84 | 0.00 | 0.83 | 0.61 | 0.81 | 0.00 |
| GT8134022 | ||||||||||||
| ANFIS | 0.63 | 0.45 | 0.92 | −0.23 | 1.02 | 0.73 | 0.81 | −0.42 | 1.35 | 1.07 | 0.66 | −0.61 |
| BaggedRF | 0.63 | 0.44 | 0.93 | −0.20 | 1.01 | 0.72 | 0.81 | −0.44 | 1.39 | 1.08 | 0.65 | −0.83 |
| BoostedRF | 0.70 | 0.48 | 0.91 | −0.26 | 1.07 | 0.78 | 0.79 | −0.55 | 1.57 | 1.19 | 0.55 | −0.95 |
| GPR | 0.82 | 0.63 | 0.87 | −0.49 | 1.41 | 1.15 | 0.63 | −1.00 | 1.70 | 1.37 | 0.47 | −1.20 |
| BiLSTM | 0.34 | 0.22 | 0.98 | −0.17 | 0.70 | 0.53 | 0.91 | −0.34 | 0.82 | 0.64 | 0.88 | −0.23 |
| MARS | 0.69 | 0.49 | 0.91 | −0.14 | 1.10 | 0.79 | 0.78 | −0.28 | 1.40 | 1.08 | 0.64 | −0.53 |
| SVR | 0.62 | 0.45 | 0.93 | −0.23 | 0.99 | 0.80 | 0.82 | −0.52 | 1.26 | 1.02 | 0.71 | −0.66 |
| BMA | 0.28 | 0.18 | 0.98 | 0.00 | 0.55 | 0.38 | 0.94 | 0.00 | 0.77 | 0.56 | 0.89 | 0.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roy, D.K.; Munmun, T.H.; Paul, C.R.; Haque, M.P.; Al-Ansari, N.; Mattar, M.A. Improving Forecasting Accuracy of Multi-Scale Groundwater Level Fluctuations Using a Heterogeneous Ensemble of Machine Learning Algorithms. Water 2023, 15, 3624. https://doi.org/10.3390/w15203624
Roy DK, Munmun TH, Paul CR, Haque MP, Al-Ansari N, Mattar MA. Improving Forecasting Accuracy of Multi-Scale Groundwater Level Fluctuations Using a Heterogeneous Ensemble of Machine Learning Algorithms. Water. 2023; 15(20):3624. https://doi.org/10.3390/w15203624
Chicago/Turabian StyleRoy, Dilip Kumar, Tasnia Hossain Munmun, Chitra Rani Paul, Mohamed Panjarul Haque, Nadhir Al-Ansari, and Mohamed A. Mattar. 2023. "Improving Forecasting Accuracy of Multi-Scale Groundwater Level Fluctuations Using a Heterogeneous Ensemble of Machine Learning Algorithms" Water 15, no. 20: 3624. https://doi.org/10.3390/w15203624
APA StyleRoy, D. K., Munmun, T. H., Paul, C. R., Haque, M. P., Al-Ansari, N., & Mattar, M. A. (2023). Improving Forecasting Accuracy of Multi-Scale Groundwater Level Fluctuations Using a Heterogeneous Ensemble of Machine Learning Algorithms. Water, 15(20), 3624. https://doi.org/10.3390/w15203624







