Advancing Sustainable Wastewater Treatment Using Enhanced Membrane Oil Flux and Separation Efficiency through Experimental-Based Chemometric Learning
Abstract
:1. Introduction
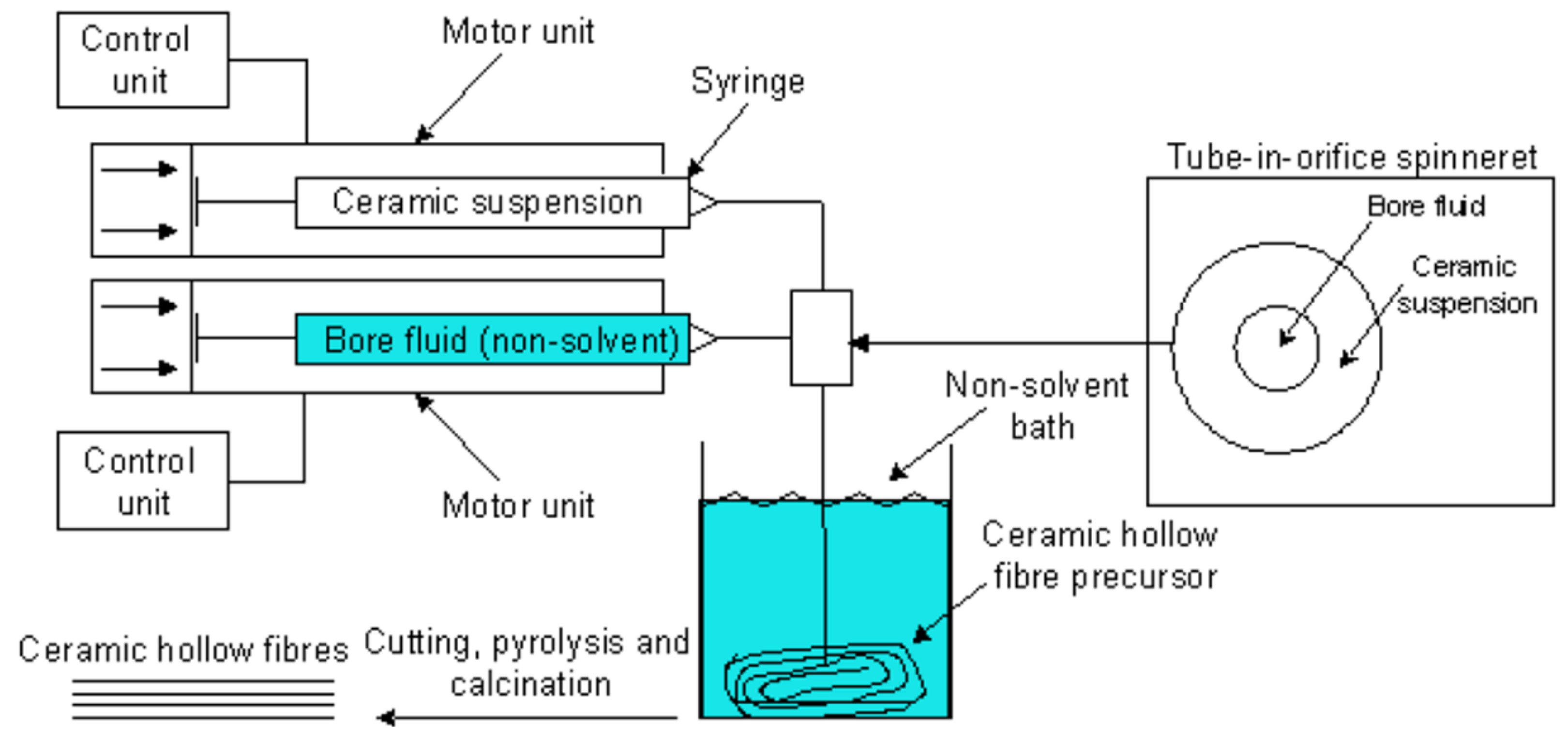
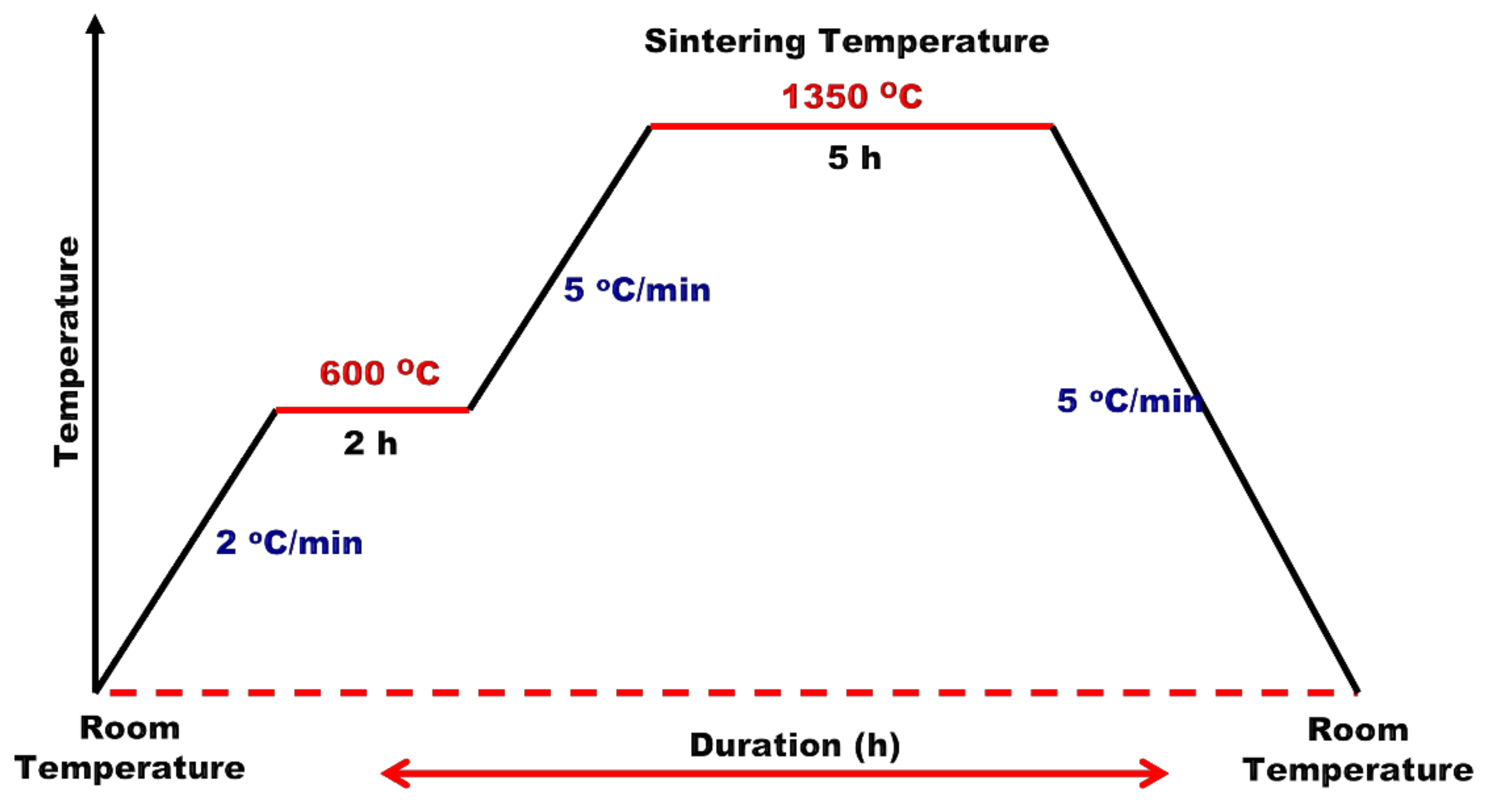
2. Experimental Methodology
3. Proposed AI Models
3.1. Support Vector Regression
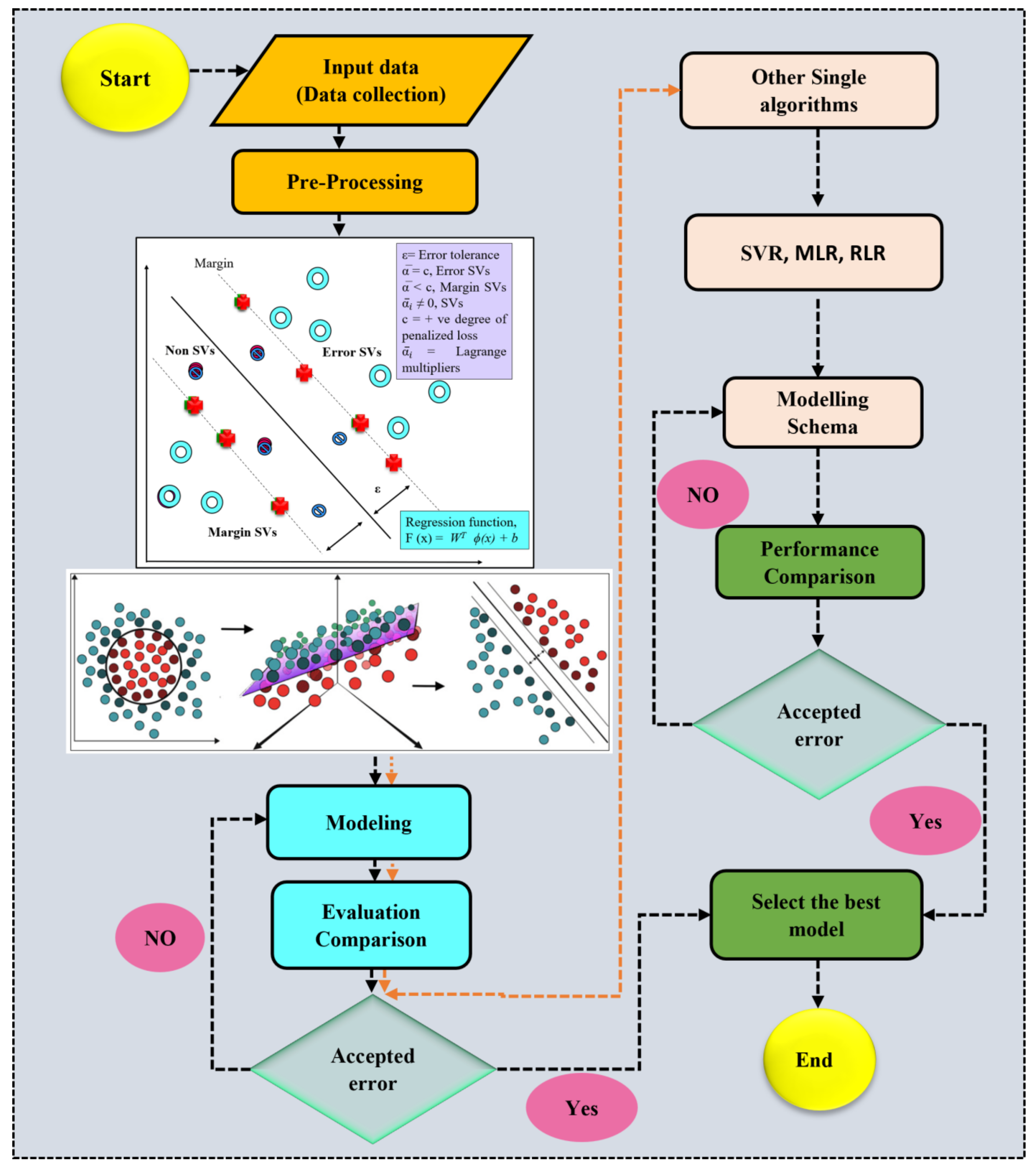
3.2. Robust Linear Regression (RLR)
3.3. Multilinear Regression Analysis (MLR)
3.4. Evaluation Criteria
- I.
- Coefficient of Determinacy
- II.
- Correlation Coefficient
- III.
- Mean Square Error
- IV.
- Root Mean Square Error
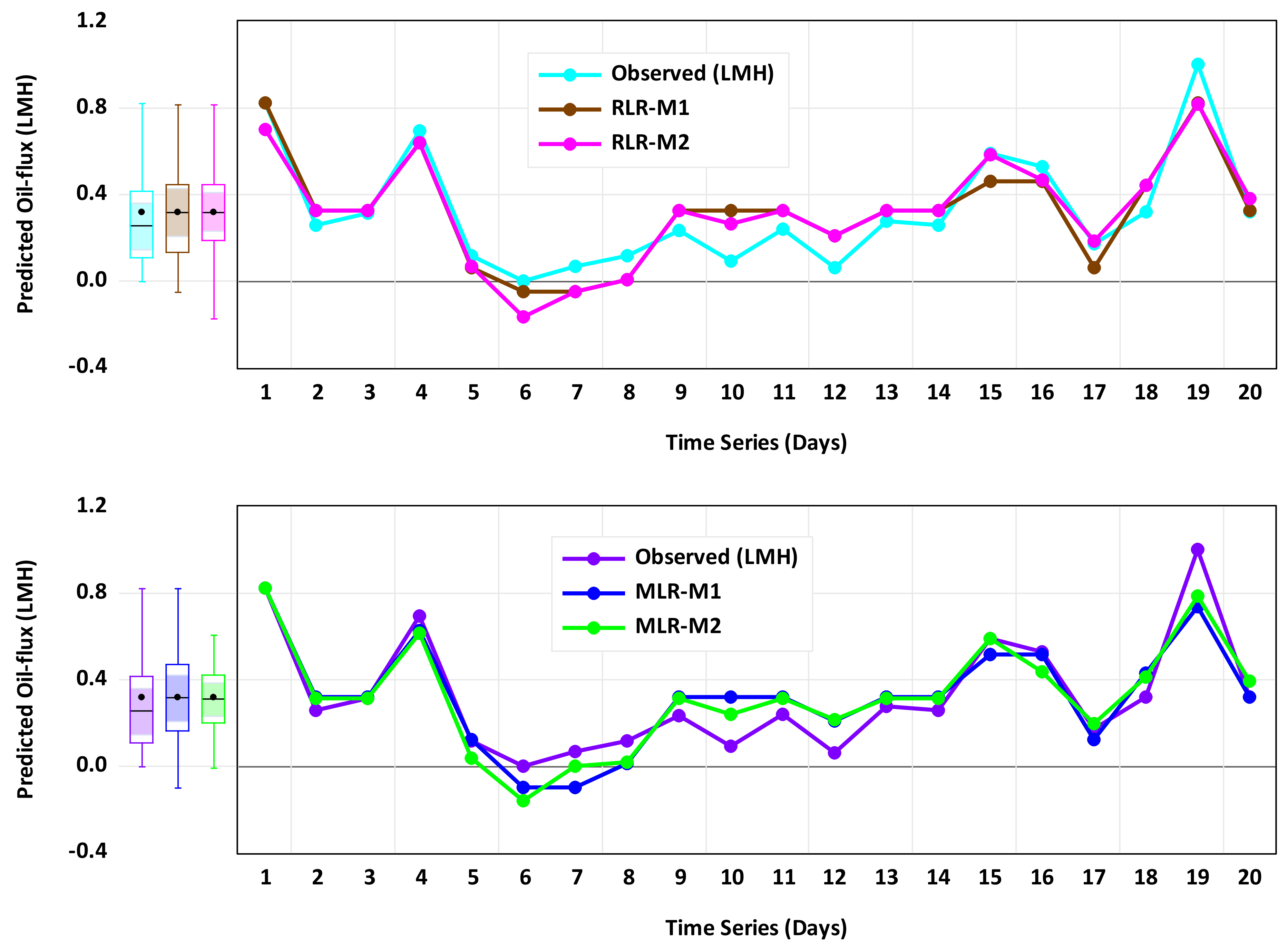
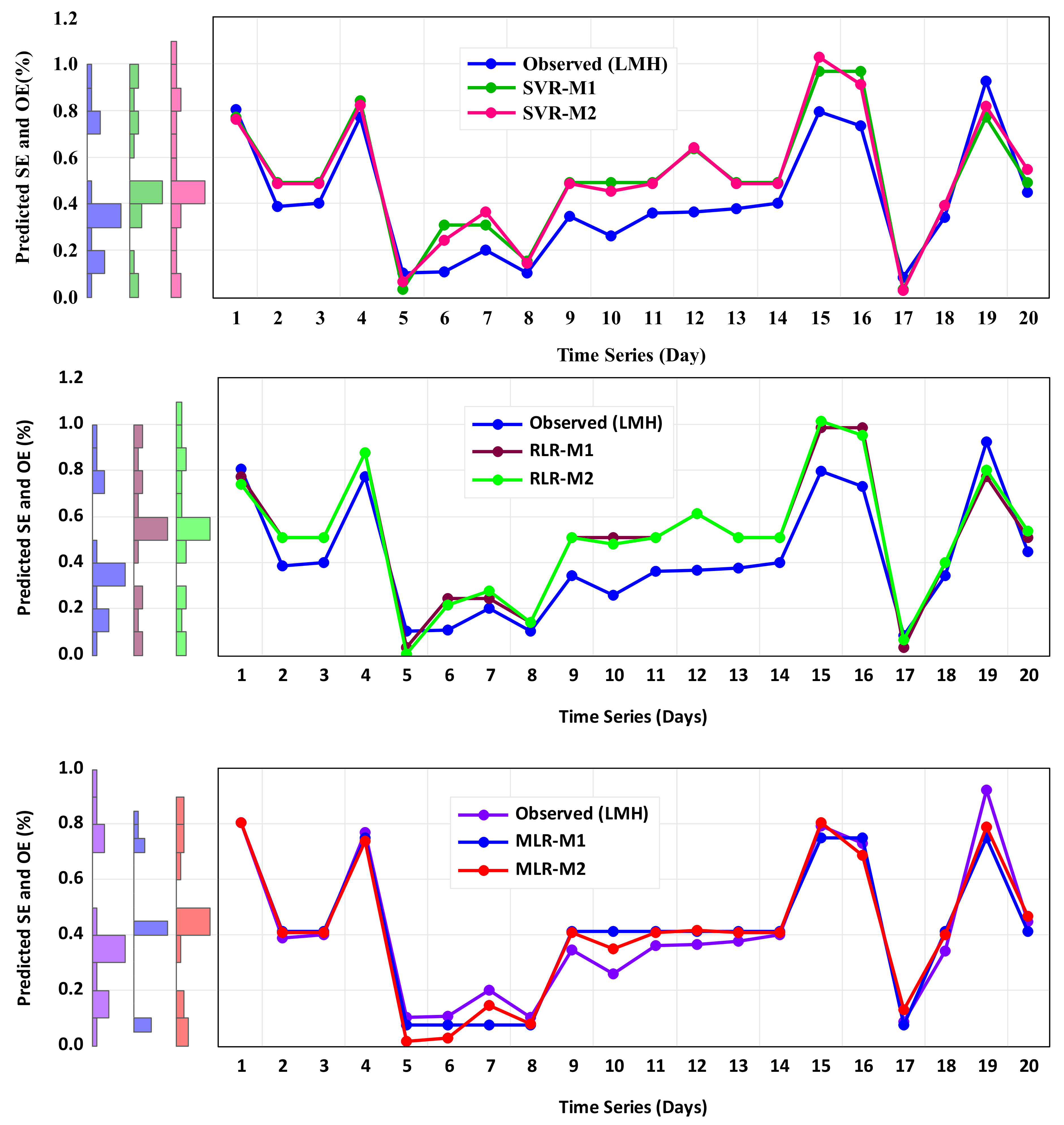
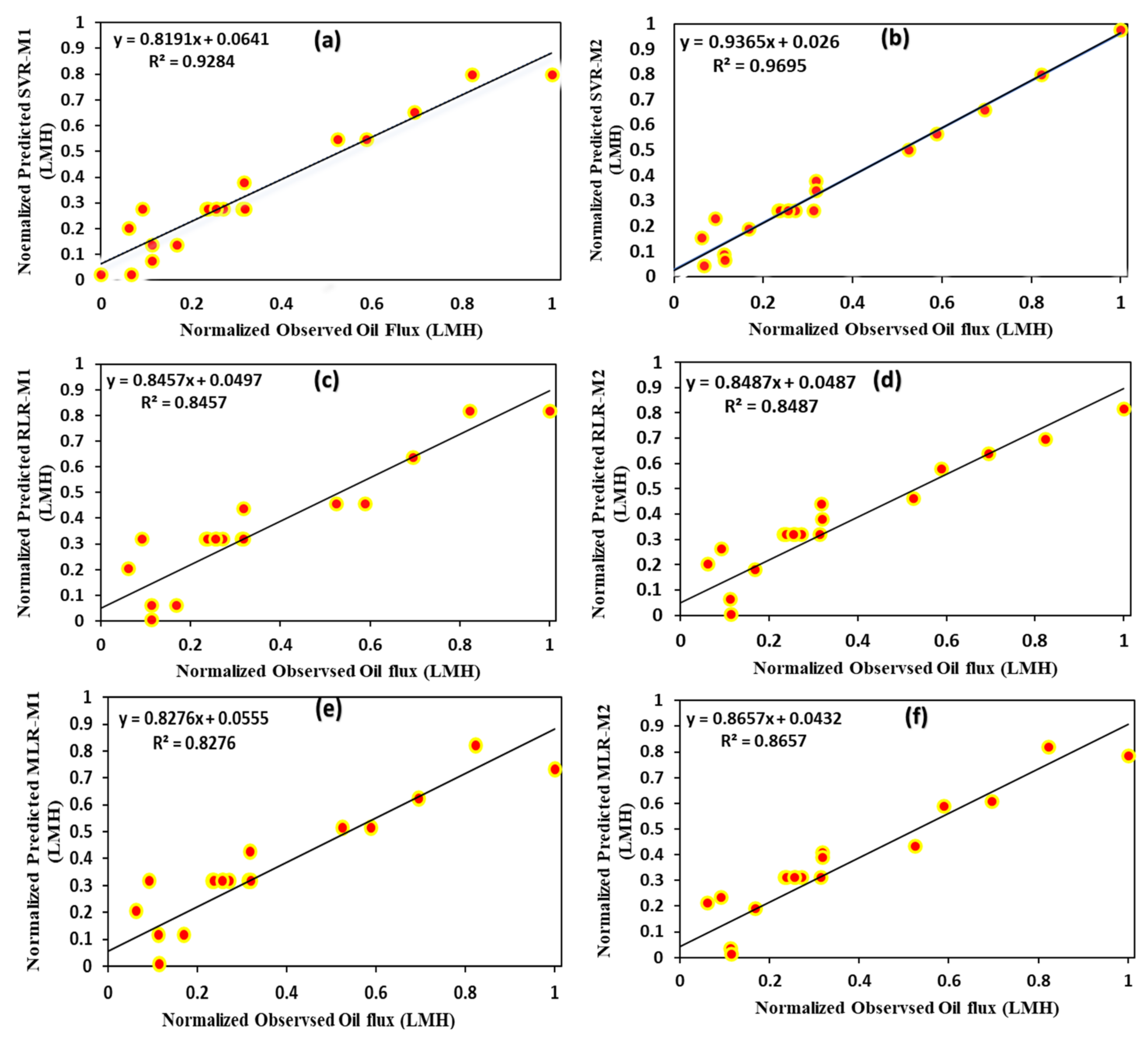
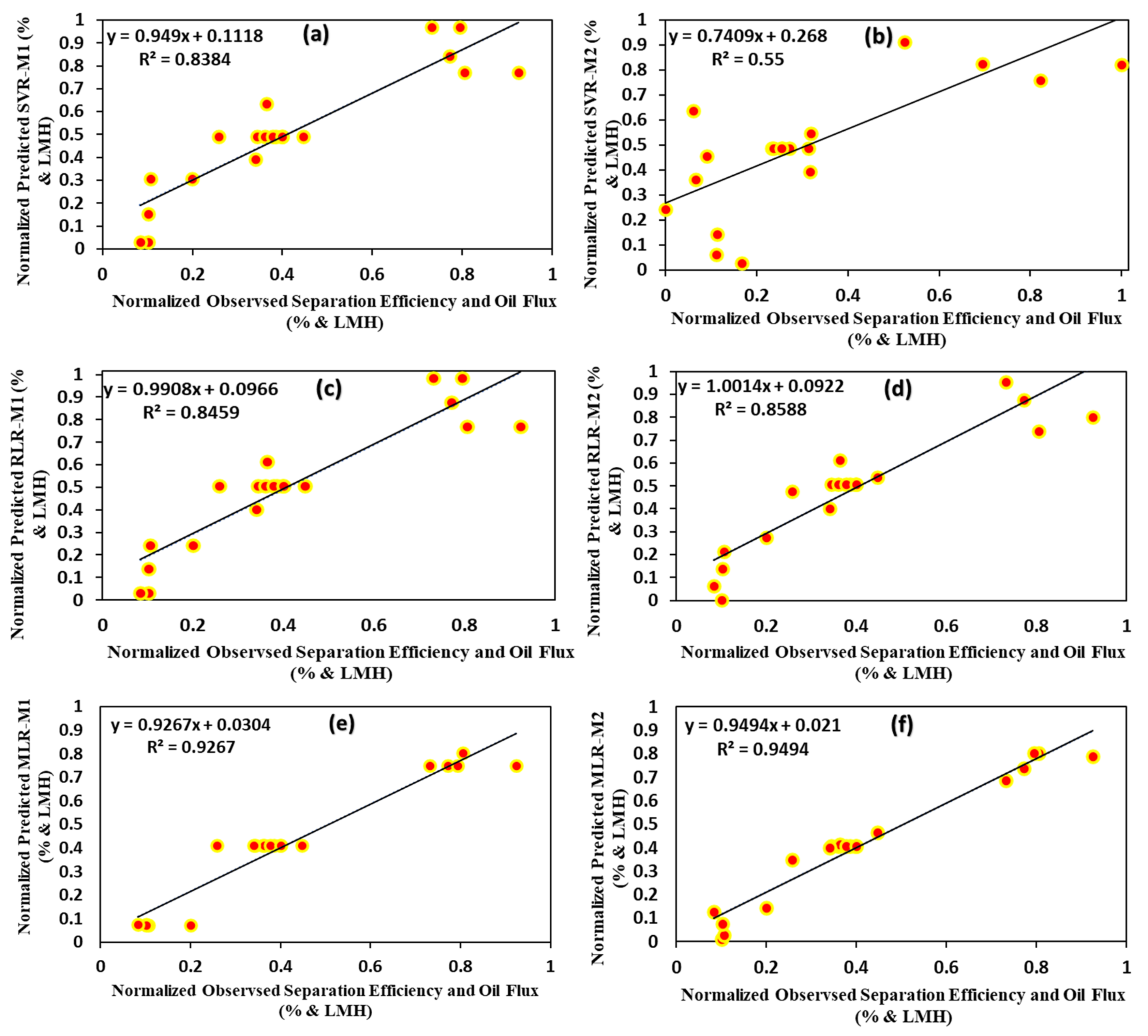
4. Results of AI-Based Models
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gupta, R.K.; Dunderdale, G.J.; England, M.W.; Hozumi, A. Oil/water separation techniques: A review of recent progresses and future directions. J. Mater. Chem. A 2017, 5, 16025–16058. [Google Scholar] [CrossRef]
- Sabir, S. Approach of cost-effective adsorbents for oil removal from oily water. Crit. Rev. Environ. Sci. Technol. 2015, 45, 1916–1945. [Google Scholar] [CrossRef]
- Yu, L.; Han, M.; He, F. A review of treating oily wastewater. Arab. J. Chem. 2017, 10, S1913–S1922. [Google Scholar] [CrossRef]
- Zhang, H.; Bukosky, S.C.; Ristenpart, W.D. Low-Voltage Electrical Demulsification of Oily Wastewater. Ind. Eng. Chem. Res. 2018, 57, 8341–8347. [Google Scholar] [CrossRef]
- Li, Y. Pretreatment of Oilfield Produced Water Using Ionic Liquids for Dissolved Air. Ph.D. Thesis, Faculty of Graduate Studies and Research, University of Regina, Regina, SK, Canada, 2017. [Google Scholar]
- Labhasetwar, P.K.; Yadav, A. Membrane Based Point-of-Use Drinking Water Treatment Systems; IWA Publishing: London, UK, 2023; ISBN 9781789062724. [Google Scholar]
- Usman, J.; Othman, M.H.D.; Ismail, A.F.; Rahman, M.A.; Jaafar, J.; Raji, Y.O.; El Badawy, T.H.; Gbadamosi, A.O.; Kurniawan, T.A. Impact of organosilanes modified superhydrophobic-superoleophilic kaolin ceramic membrane on efficiency of oil recovery from produced water. J. Chem. Technol. Biotechnol. 2020, 95, 3300–3315. [Google Scholar] [CrossRef]
- Usman, J.; Hafiz, M.; Othman, D.; Fauzi, A.; Rahman, M.A.; Jaafar, J.; Olabode, Y.; Gbadamosi, A.O.; Hassan, T.; Badawy, E. An overview of superhydrophobic ceramic membrane surface modification for oil-water separation. J. Mater. Res. Technol. 2021, 12, 643–667. [Google Scholar] [CrossRef]
- Liu, J.; Li, P.; Chen, L.; Feng, Y.; He, W.; Lv, X. Modified superhydrophilic and underwater superoleophobic PVDF membrane with ultralow oil-adhesion for highly efficient oil/water emulsion separation. Mater. Lett. 2016, 185, 169–172. [Google Scholar] [CrossRef]
- Wu, H.; Shi, J.; Ning, X.; Long, Y.-Z.; Zheng, J. The High Flux of Superhydrophilic-Superhydrophobic Janus Membrane of cPVA-PVDF/PMMA/GO by Layer-by-Layer Electrospinning for High Efficiency Oil-Water Separation. Polymers 2022, 14, 621. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Yu, Y.; Zhou, J.; Song, L.; Hu, X.; Larbot, A. FAS grafted superhydrophobic ceramic membrane. Appl. Surf. Sci. 2009, 255, 9092–9099. [Google Scholar] [CrossRef]
- Ibrahim, M.; Salami, B.A.; Amer Algaifi, H.; Kalimur Rahman, M.; Nasir, M.; Ewebajo, A.O. Assessment of acid resistance of natural pozzolan-based alkali-activated concrete: Experimental and optimization modelling. Constr. Build. Mater. 2021, 304, 124657. [Google Scholar] [CrossRef]
- Algaifi, H.A.; Khan, M.I.; Shahidan, S.; Fares, G.; Abbas, Y.M.; Huseien, G.F.; Salami, B.A.; Alabduljabbar, H. Strength and acid resistance of ceramic-based self-compacting alkali-activated concrete: Optimizing and predicting assessment. Materials 2021, 14, 6208. [Google Scholar] [CrossRef]
- Usman, A.G.; IŞIK, S.; Abba, S.I. Qualitative prediction of Thymoquinone in the high-performance liquid chromatography optimization method development using artificial intelligence models coupled with ensemble machine learning. Sep. Sci. Plus 2022, 5, 579–587. [Google Scholar] [CrossRef]
- Zobel, C.W.; Cook, D.F. Evaluation of neural network variable influence measures for process control. Eng. Appl. Artif. Intell. 2011, 24, 803–812. [Google Scholar] [CrossRef]
- Okpalaeke, K.E.; Ibrahim, T.H.; Latinwo, L.M.; Betiku, E. Mathematical Modeling and Optimization Studies by Artificial Neural Network, Genetic Algorithm and Response Surface Methodology: A Case of Ferric Sulfate–Catalyzed Esterification of Neem (Azadirachta indica) Seed Oil. Front. Energy Res. 2020, 8, 614621. [Google Scholar] [CrossRef]
- Betiku, E.; Ajala, S.O. Modeling and optimization of Thevetia peruviana (yellow oleander) oil biodiesel synthesis via Musa paradisiacal (plantain) peels as heterogeneous base catalyst: A case of artificial neural network vs. response surface methodology. Ind. Crops Prod. 2014, 53, 314–322. [Google Scholar] [CrossRef]
- Khatti, T.; Naderi-Manesh, H.; Kalantar, S.M. Application of ANN and RSM techniques for modeling electrospinning process of polycaprolactone. Neural Comput. Appl. 2019, 31, 239–248. [Google Scholar] [CrossRef]
- Pham, Q.B.; Sammen, S.S.; Abba, S.I.; Mohammadi, B.; Shahid, S.; Abdulkadir, R.A. A new hybrid model based on relevance vector machine with flower pollination algorithm for phycocyanin pigment concentration estimation. Environ. Sci. Pollut. Res. 2021, 28, 32564–32579. [Google Scholar] [CrossRef] [PubMed]
- Sarve, A.; Sonawane, S.S.; Varma, M.N. Ultrasound assisted biodiesel production from sesame (Sesamum indicum L.) oil using barium hydroxide as a heterogeneous catalyst: Comparative assessment of prediction abilities between response surface methodology (RSM) and artificial neural network (ANN). Ultrason. Sonochem. 2015, 26, 218–228. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Lv, E.; Du, L.; Lu, J.; Ding, J. Statistical modeling/optimization and process intensification of microwave-assisted acidified oil esterification. Energy Convers. Manag. 2016, 122, 411–418. [Google Scholar] [CrossRef]
- Usman, A.G.; IŞik, S.; Abba, S.I.; MerİÇlİ, F. Artificial intelligence-based models for the qualitative and quantitative prediction of a phytochemical compound using HPLC method. Turk. J. Chem. 2020, 44, 1339–1351. [Google Scholar] [CrossRef] [PubMed]
- Nandi, B.K.; Moparthi, A.; Uppaluri, R.; Purkait, M.K. Treatment of oily wastewater using low cost ceramic membrane: Comparative assessment of pore blocking and artificial neural network models. Chem. Eng. Res. Des. 2010, 88, 881–892. [Google Scholar] [CrossRef]
- Chen, P.-C.; Xu, Z.-K. Mineral-Coated Polymer Membranes with Superhydrophilicity and Underwater Superoleophobicity for Effective Oil/Water Separation. Sci. Rep. 2013, 3, 2776. [Google Scholar] [CrossRef]
- Rahimzadeh, A.; Ashtiani, F.Z.; Okhovat, A. Application of adaptive neuro-fuzzy inference system as a reliable approach for prediction of oily wastewater microfiltration permeate volume. J. Environ. Chem. Eng. 2016, 4, 576–584. [Google Scholar] [CrossRef]
- Ma, W.; Samal, S.K.; Liu, Z.; Xiong, R.; De Smedt, S.C.; Bhushan, B.; Zhang, Q.; Huang, C. Dual pH- and ammonia-vapor-responsive electrospun nanofibrous membranes for oil-water separations. J. Memb. Sci. 2017, 537, 128–139. [Google Scholar] [CrossRef]
- Zhu, Y.; Xie, W.; Zhang, F.; Xing, T.; Jin, J. Superhydrophilic In-Situ-Cross-Linked Zwitterionic Polyelectrolyte/PVDF-Blend Membrane for Highly Efficient Oil/Water Emulsion Separation. ACS Appl. Mater. Interfaces 2017, 9, 9603–9613. [Google Scholar] [CrossRef] [PubMed]
- Kang, H.; Cheng, Z.; Lai, H.; Ma, H.; Liu, Y.; Mai, X.; Wang, Y.; Shao, Q.; Xiang, L.; Guo, X.; et al. Superlyophobic anti-corrosive and self-cleaning titania robust mesh membrane with enhanced oil/water separation. Sep. Purif. Technol. 2018, 201, 193–204. [Google Scholar] [CrossRef]
- Ismail, N.H.; Salleh, W.N.W.; Ismail, A.F.; Hasbullah, H.; Yusof, N.; Aziz, F.; Jaafar, J. Hydrophilic polymer-based membrane for oily wastewater treatment: A review. Sep. Purif. Technol. 2020, 233, 116007. [Google Scholar] [CrossRef]
- Usman, J.; Salami, B.A.; Gbadamosi, A.; Adamu, H.; GarbaUsman, A.; Benaafi, M.; Abba, S.I.; Dzarfan Othman, M.H.; Aljundi, I.H. Intelligent optimization for modelling superhydrophobic ceramic membrane oil flux and oil-water separation efficiency: Evidence from wastewater treatment and experimental laboratory. Chemosphere 2023, 331, 138726. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Mu, P.; Li, J.; Wang, Q. Inverse desert beetle-like ZIF-8/PAN composite nanofibrous membrane for highly efficient separation of oil-in-water emulsions. J. Mater. Chem. A 2021, 9, 4167–4175. [Google Scholar] [CrossRef]
- Stöber, W.; Fink, A.; Bohn, E. Controlled Growth of Monodisperse Silica Spheres in the Micron Size Range. J. Colloid Interface Sci. 1968, 69, 62–69. [Google Scholar] [CrossRef]
- Alhaji, U.; Chinemezu, E.; Isah, S. Bioresource Technology Reports Machine learning models for biomass energy content prediction: A correlation-based optimal feature selection approach. Bioresour. Technol. Rep. 2022, 19, 101167. [Google Scholar] [CrossRef]
- Alhaji, U.; Chinemezu, E.; Nwachukwu, J.; Isah, S. Prediction of energy content of biomass based on hybrid machine learning ensemble algorithm. Energy Nexus 2022, 8, 100157. [Google Scholar] [CrossRef]
- Baig, N.; Usman, J.; Abba, S.I.; Benaafi, M.; Aljundi, I.H. Fractionation of dyes/salts using loose nanofiltration membranes: Insight from machine learning prediction. J. Clean. Prod. 2023, 418, 138193. [Google Scholar] [CrossRef]
- Abdullahi, H.U.; Usman, A.G.; Abba, S.I.; Abdullahi, H.U. Modelling the Absorbance of a Bioactive Compound in HPLC Method using Artificial Neural Network and Multilinear Regression Methods. Dutse J. Pure Appl. Sci. 2020, 6, 362–371. [Google Scholar]
- Usman, A.G.; Işik, S.; Abba, S.I. A Novel Multi-model Data-Driven Ensemble Technique for the Prediction of Retention Factor in HPLC Method Development. Chromatographia 2020, 83, 933–945. [Google Scholar] [CrossRef]
- Benaafi, M.; Tawabini, B.; Abba, S.I.; Humphrey, J.D.; Al-Areeq, A.M.; Alhulaibi, S.A.; Usman, A.G.; Aljundi, I.H. Integrated Hydrogeological, Hydrochemical, and Isotopic Assessment of Seawater Intrusion into Coastal Aquifers in Al-Qatif Area, Eastern Saudi Arabia. Molecules 2022, 27, 6841. [Google Scholar] [CrossRef] [PubMed]
- Abba, S.I.; Pham, Q.B.; Usman, A.G.; Linh, N.T.T.; Aliyu, D.S.; Nguyen, Q.; Bach, Q.V. Emerging evolutionary algorithm integrated with kernel principal component analysis for modeling the performance of a water treatment plant. J. Water Process Eng. 2020, 33, 101081. [Google Scholar] [CrossRef]
- Abubakar, A.; Jibril, M.M.; Almeida, C.F.M.; Gemignani, M.; Yahya, M.N.; Abba, S.I. A Novel Hybrid Optimization Approach for Fault Detection in Photovoltaic Arrays and Inverters Using AI and Statistical Learning Techniques: A Focus on Sustainable Environment. Processes 2023, 11, 2549. [Google Scholar] [CrossRef]
- Adamu, M.; Haruna, S.I.; Malami, S.I.; Ibrahim, M.N.; Abba, S.I.; Ibrahim, Y.E. Prediction of compressive strength of concrete incorporated with jujube seed as partial replacement of coarse aggregate: A feasibility of Hammerstein–Wiener model versus support vector machine. Model. Earth Syst. Environ. 2021, 8, 3435–3445. [Google Scholar] [CrossRef]
- Malami, S.I.; Anwar, F.H.; Abdulrahman, S.; Haruna, S.I.; Ali, S.I.A.; Abba, S.I. Implementation of hybrid neuro-fuzzy and self-turning predictive model for the prediction of concrete carbonation depth: A soft computing technique. Results Eng. 2021, 10, 100228. [Google Scholar] [CrossRef]
- Nourani, V.; Elkiran, G.; Abba, S.I. Wastewater treatment plant performance analysis using artificial intelligence—An ensemble approach. Water Sci. Technol. 2018, 78, 2064–2076. [Google Scholar] [CrossRef]
- Tahsin, A.; Abdullahi, J.; Rotimi, A.; Anwar, F.H.; Malami, S.I.; Abba, S.I. Multi-state comparison of machine learning techniques in modelling reference evapotranspiration: A case study of Northeastern Nigeria. In Proceedings of the 2021 1st International Conference on Multidisciplinary Engineering and Applied Science (ICMEAS), Abuja, Nigeria, 15–16 July 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Kemper, T.; Sommer, S. Estimate of heavy metal contamination in soils after a mining accident using reflectance spectroscopy. Environ. Sci. Technol. 2002, 36, 2742–2747. [Google Scholar] [CrossRef] [PubMed]
- Wiangkham, A.; Ariyarit, A.; Aengchuan, P. Prediction of the influence of loading rate and sugarcane leaves concentration on fracture toughness of sugarcane leaves and epoxy composite using artificial intelligence. Theor. Appl. Fract. Mech. 2022, 117, 103188. [Google Scholar] [CrossRef]
- Doulati Ardejanii, F.; Rooki, R.; Jodieri Shokri, B.; Eslam Kish, T.; Aryafar, A.; Tourani, P. Prediction of Rare Earth Elements in Neutral Alkaline Mine Drainage from Razi Coal Mine, Golestan Province, Northeast Iran, Using General Regression Neural Network. J. Environ. Eng. 2013, 139, 896–907. [Google Scholar] [CrossRef]
- Pham, Q.B.; Abba, S.I.; Usman, A.G.; Thi, N.; Linh, T. Potential of Hybrid Data-Intelligence Algorithms for Multi-Station Modelling of Rainfall. Water Resour. Manag. 2019, 33, 5067–5087. [Google Scholar] [CrossRef]
- Abba, S.I.; Linh, N.T.T.; Abdullahi, J.; Ali, S.I.A.; Pham, Q.B.; Abdulkadir, R.A.; Costache, R.; Nam, V.T.; Anh, D.T. Hybrid machine learning ensemble techniques for modeling dissolved oxygen concentration. IEEE Access 2020, 8, 157218–157237. [Google Scholar] [CrossRef]
- Asnake Metekia, W.; Garba Usman, A.; Hatice Ulusoy, B.; Isah Abba, S.; Chirkena Bali, K. Artificial intelligence-based approaches for modeling the effects of spirulina growth mediums on total phenolic compounds. Saudi J. Biol. Sci. 2022, 29, 1111–1117. [Google Scholar] [CrossRef] [PubMed]
- Elkiran, G.; Nourani, V.; Abba, S.I.; Abdullahi, J. Artificial intelligence-based approaches for multi-station modelling of dissolve oxygen in river. Glob. J. Environ. Sci. Manag. 2018, 4, 439–450. [Google Scholar] [CrossRef]
- Manzar, M.S.; Benaafi, M.; Costache, R.; Alagha, O.; Mu’azu, N.D.; Zubair, M.; Abdullahi, J.; Abba, S.I. New generation neurocomputing learning coupled with a hybrid neuro-fuzzy model for quantifying water quality index variable: A case study from Saudi Arabia. Ecol. Inform. 2022, 70, 101696. [Google Scholar] [CrossRef]
- Usman, A.G.; Işik, S.; Abba, S.I.; Meriçli, F. Chemometrics-based models hyphenated with ensemble machine learning for retention time simulation of isoquercitrin in Coriander sativum L. using high-performance liquid chromatography. J. Sep. Sci. 2021, 44, 843–849. [Google Scholar] [CrossRef]
- Abba, S.I.; Hadi, S.J.; Abdullahi, J. River water modelling prediction using multi-linear regression, artificial neural network, and adaptive neuro-fuzzy inference system techniques. Procedia Comput. Sci. 2017, 120, 75–82. [Google Scholar] [CrossRef]
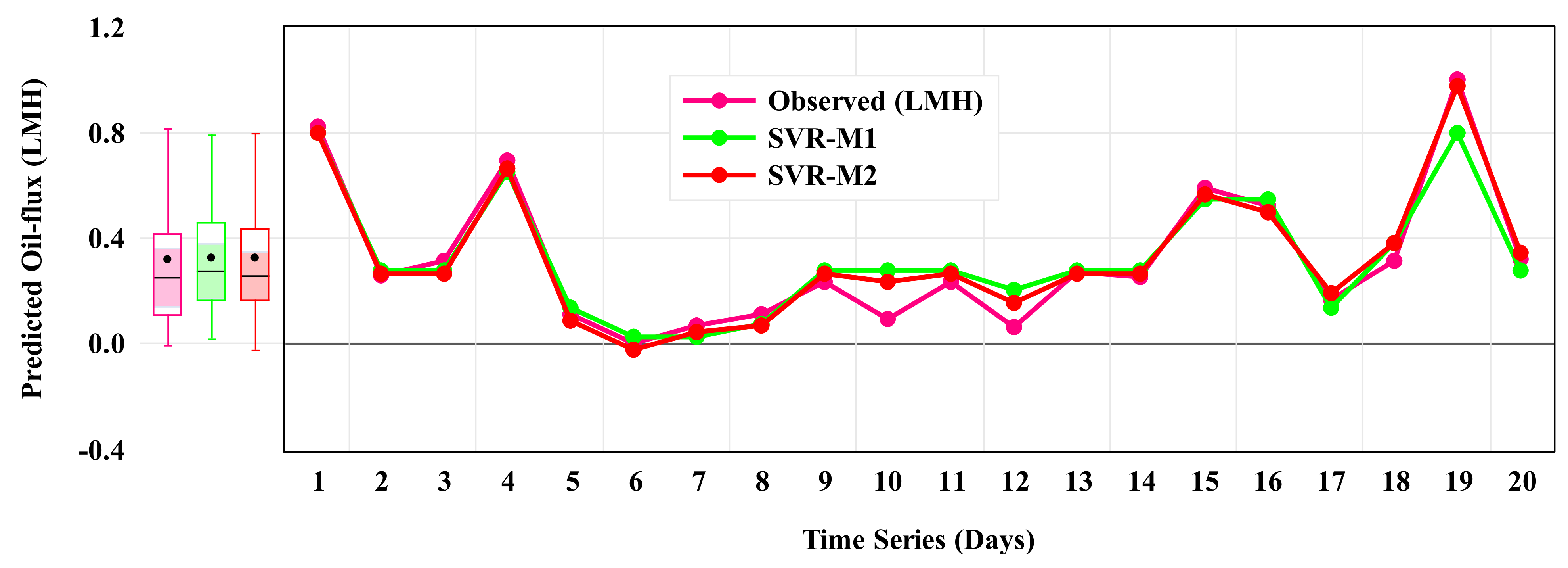




| Model | Training Phase (Oil Flux) | |||
|---|---|---|---|---|
| R2 | MSE | RMSE | R | |
| SVR-M1 | 0.9055 | 0.0049 | 0.0699 | 0.9516 |
| SVR-M2 | 0.9477 | 0.0027 | 0.052 | 0.9735 |
| RLR-M1 | 0.8151 | 0.0096 | 0.0978 | 0.9029 |
| RLR-M2 | 0.7889 | 0.0109 | 0.1045 | 0.8882 |
| MLR-M1 | 0.7936 | 0.0107 | 0.1033 | 0.8908 |
| MLR-M2 | 0.8369 | 0.0084 | 0.0919 | 0.9148 |
| Training Phase (S.E) | ||||
| R2 | MSE | RMSE | R | |
| SVR-M1 | 0.9781 | 0.002 | 0.0444 | 0.989 |
| SVR-M2 | 0.9891 | 0.001 | 0.0313 | 0.9946 |
| RLR-M1 | 0.9752 | 0.0022 | 0.0474 | 0.9875 |
| RLR-M2 | 0.9777 | 0.002 | 0.0449 | 0.9888 |
| MLR-M1 | 0.976 | 0.0022 | 0.0466 | 0.9879 |
| MLR-M2 | 0.9808 | 0.0017 | 0.0416 | 0.9904 |
| Training Phase (Oil Flux + S.E) | ||||
| R2 | MSE | RMSE | R | |
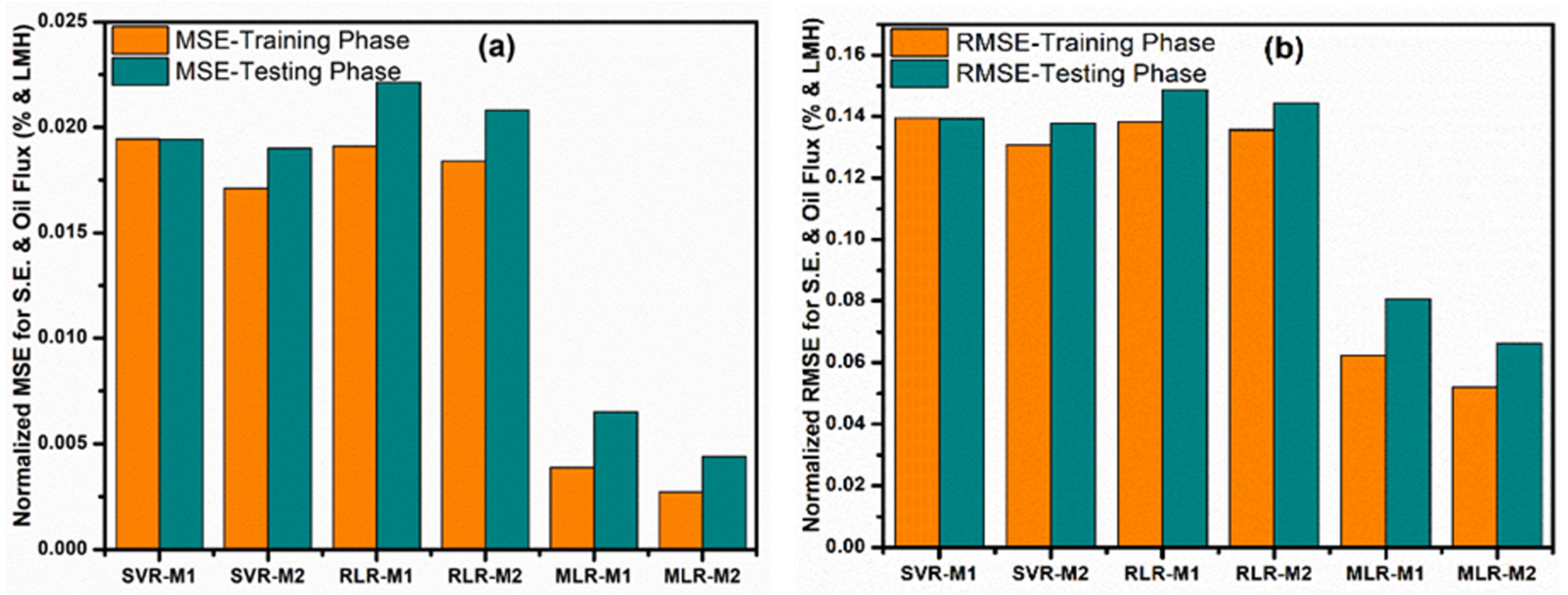
| SVR-M1 | 0.6398 | 0.0194 | 0.1394 | 0.7999 |
| SVR-M2 | 0.6831 | 0.0171 | 0.1308 | 0.8265 |
| RLR-M1 | 0.6459 | 0.0191 | 0.1382 | 0.8037 |
| RLR-M2 | 0.6591 | 0.0184 | 0.1356 | 0.8119 |
| MLR-M1 | 0.928 | 0.0039 | 0.0623 | 0.9633 |
| MLR-M2 | 0.9496 | 0.0027 | 0.0521 | 0.9745 |
| Model | Testing Phase (Oil Flux) | |||
|---|---|---|---|---|
| R2 | MSE | RMSE | R | |
| SVR-M1 | 0.8859 | 0.0083 | 0.0908 | 0.9412 |
| SVR-M2 | 0.9847 | 0.0011 | 0.0333 | 0.9923 |
| RLR-M1 | 0.8943 | 0.0018 | 0.0427 | 0.9457 |
| RLR-M2 | 0.8683 | 0.0095 | 0.0976 | 0.9318 |
| MLR-M1 | 0.7931 | 0.015 | 0.1223 | 0.8906 |
| MLR-M2 | 0.8427 | 0.0114 | 0.1067 | 0.918 |
| Testing Phase (S.E) | ||||
| R2 | MSE | RMSE | R | |
| SVR-M1 | 0.9807 | 0.0028 | 0.0526 | 0.9903 |
| SVR-M2 | 0.9945 | 0.0008 | 0.0282 | 0.9972 |
| RLR-M1 | 0.9823 | 0.0025 | 0.0505 | 0.9911 |
| RLR-M2 | 0.9892 | 0.0016 | 0.0394 | 0.9946 |
| MLR-M1 | 0.9815 | 0.0027 | 0.0516 | 0.9907 |
| MLR-M2 | 0.9885 | 0.0016 | 0.0406 | 0.9942 |
| Testing Phase (Oil Flux + SE) | ||||
| R2 | MSE | RMSE | R | |
| SVR-M1 | 0.7809 | 0.0194 | 0.1394 | 0.8837 |
| SVR-M2 | 0.7856 | 0.019 | 0.1378 | 0.8864 |
| RLR-M1 | 0.7504 | 0.0221 | 0.1487 | 0.8663 |
| RLR-M2 | 0.7653 | 0.0208 | 0.1442 | 0.8748 |
| MLR-M1 | 0.9266 | 0.0065 | 0.0807 | 0.9626 |
| MLR-M2 | 0.9504 | 0.0044 | 0.0663 | 0.9749 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Usman, J.; Abba, S.I.; Muhammed, I.; Abdulazeez, I.; Lawal, D.U.; Yogarathinam, L.T.; Bafaqeer, A.; Baig, N.; Aljundi, I.H. Advancing Sustainable Wastewater Treatment Using Enhanced Membrane Oil Flux and Separation Efficiency through Experimental-Based Chemometric Learning. Water 2023, 15, 3611. https://doi.org/10.3390/w15203611
Usman J, Abba SI, Muhammed I, Abdulazeez I, Lawal DU, Yogarathinam LT, Bafaqeer A, Baig N, Aljundi IH. Advancing Sustainable Wastewater Treatment Using Enhanced Membrane Oil Flux and Separation Efficiency through Experimental-Based Chemometric Learning. Water. 2023; 15(20):3611. https://doi.org/10.3390/w15203611
Chicago/Turabian StyleUsman, Jamilu, Sani I. Abba, Ibrahim Muhammed, Ismail Abdulazeez, Dahiru U. Lawal, Lukka Thuyavan Yogarathinam, Abdullah Bafaqeer, Nadeem Baig, and Isam H. Aljundi. 2023. "Advancing Sustainable Wastewater Treatment Using Enhanced Membrane Oil Flux and Separation Efficiency through Experimental-Based Chemometric Learning" Water 15, no. 20: 3611. https://doi.org/10.3390/w15203611







