A Machine Learning Framework for Enhancing Short-Term Water Demand Forecasting Using Attention-BiLSTM Networks Integrated with XGBoost Residual Correction
Abstract
:1. Introduction
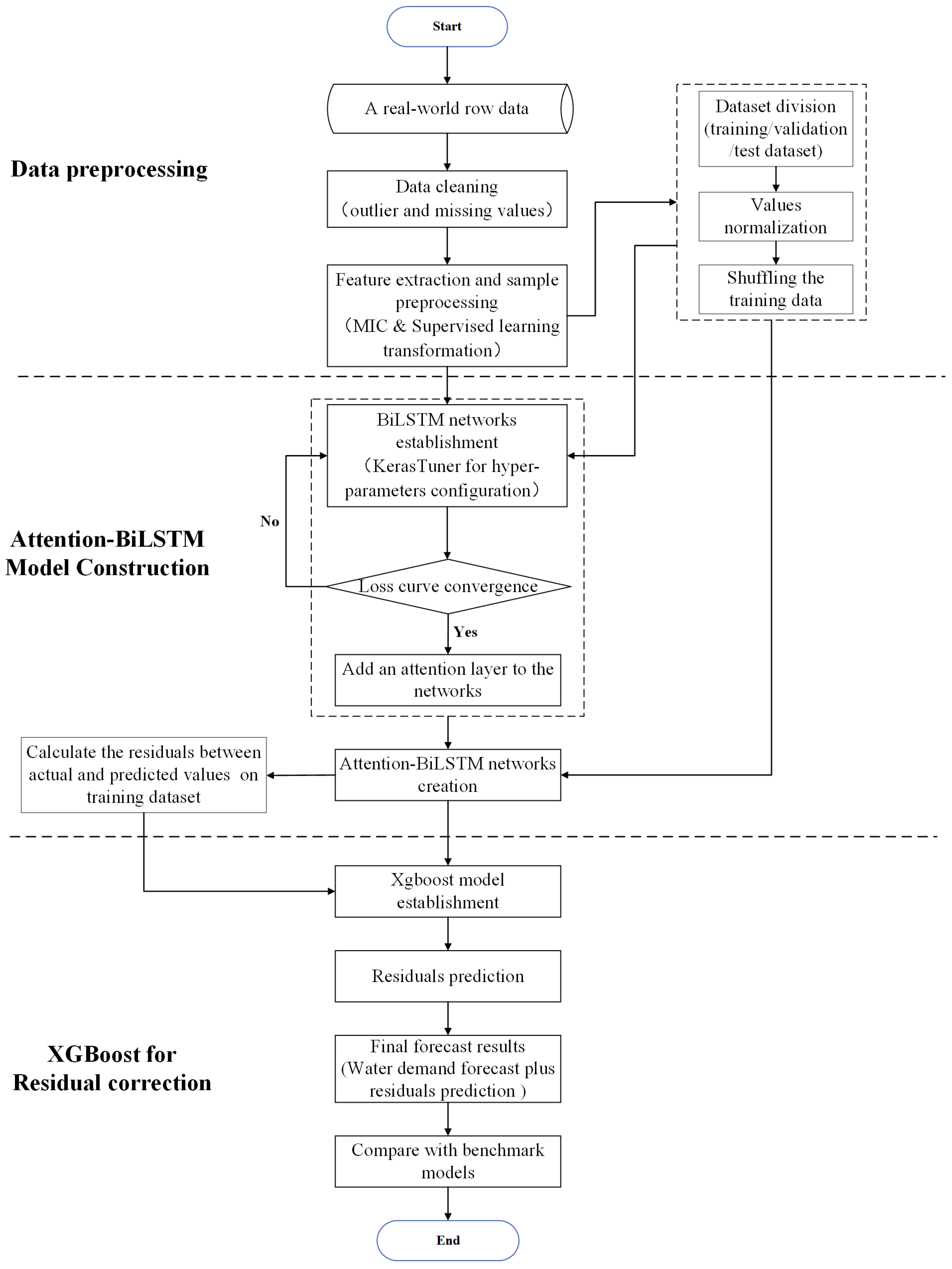
2. Methodology
2.1. Maximal Information Coefficient Method
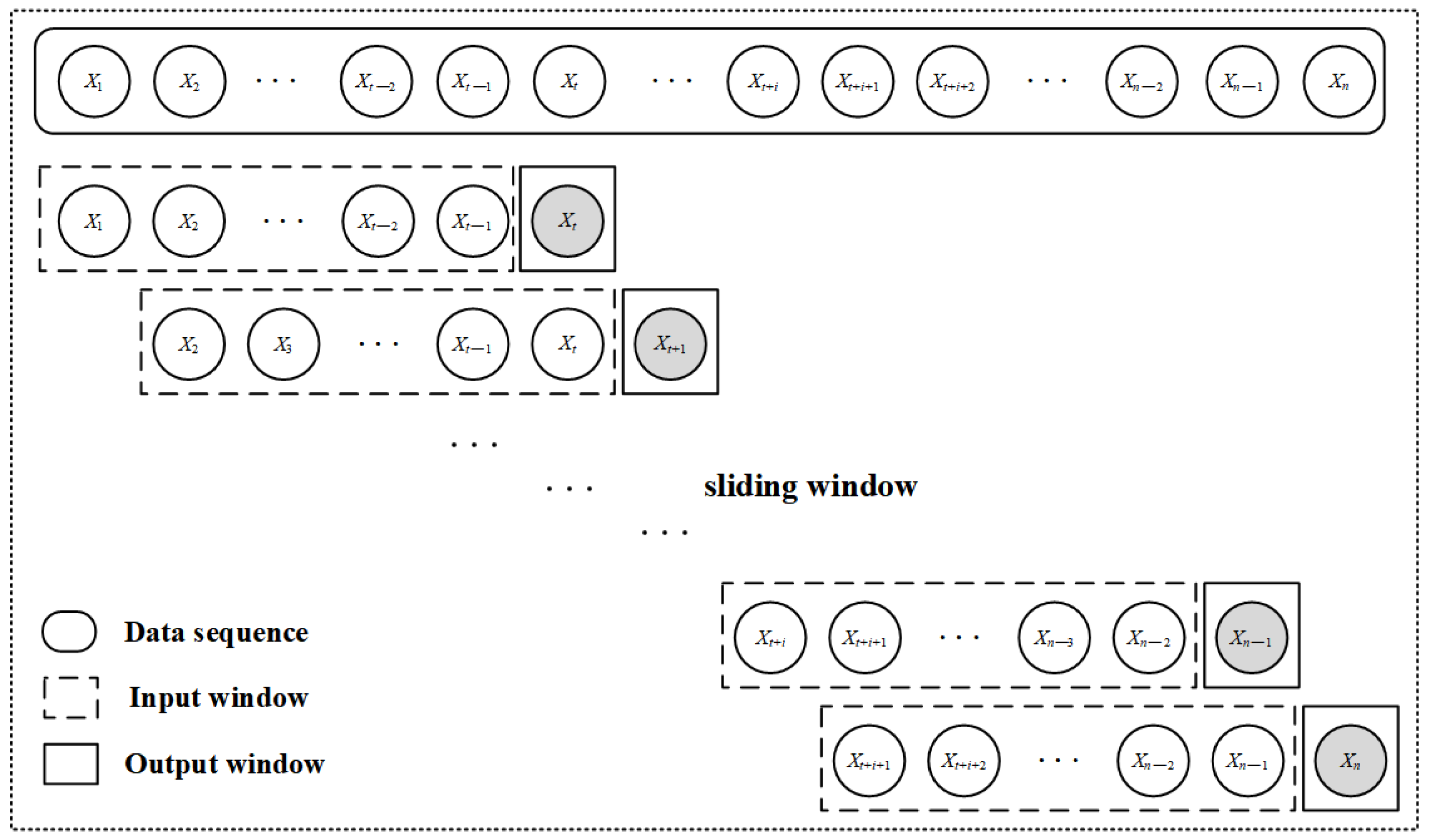
2.2. Feature Extraction and Sample Processing
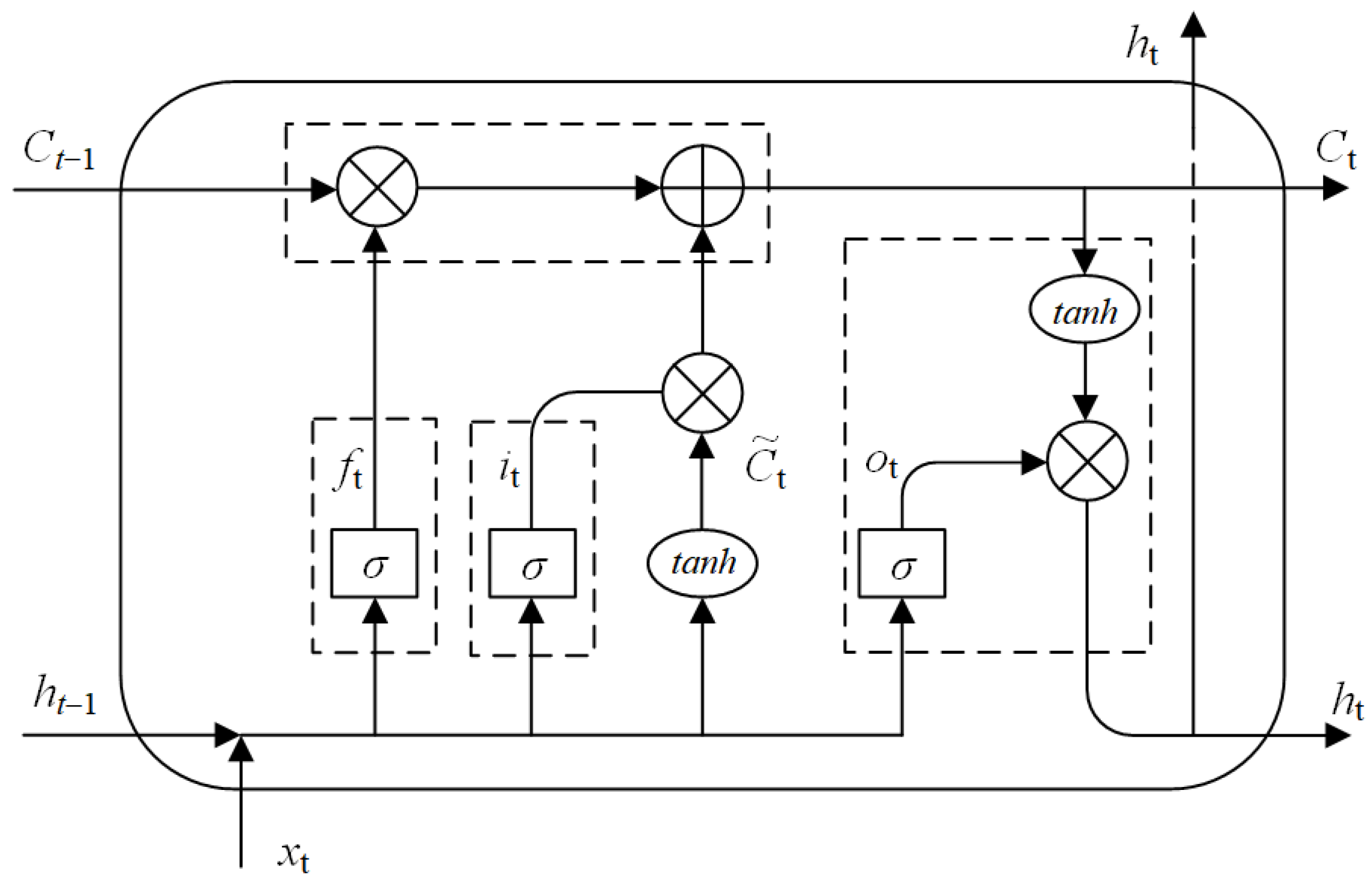
2.3. Bi-Directional Long Short Memory Network
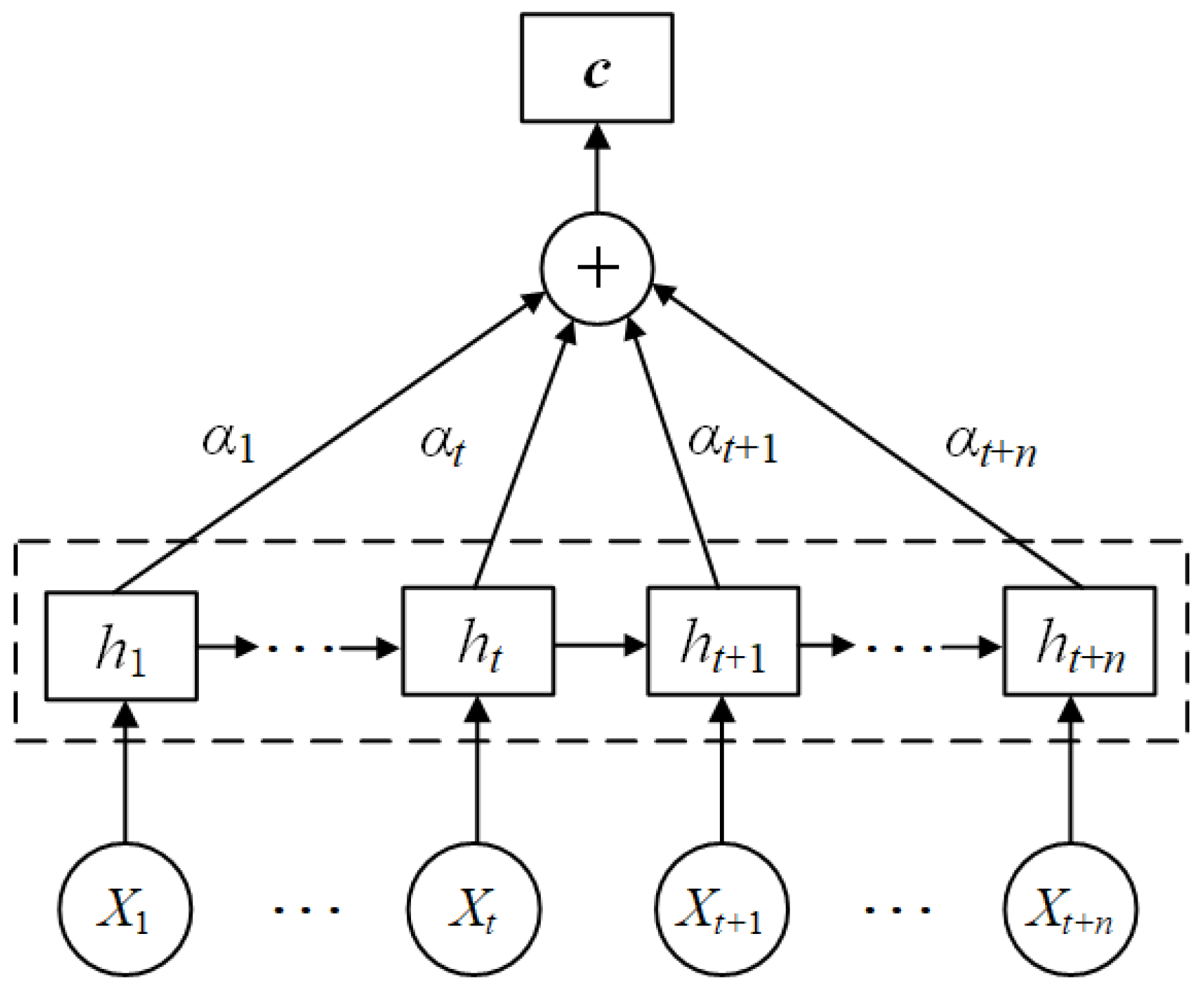
2.4. Attention Mechanism
2.5. XGBoost Algorithm
2.6. Performance Metrics of Forecast Models
3. Case Study
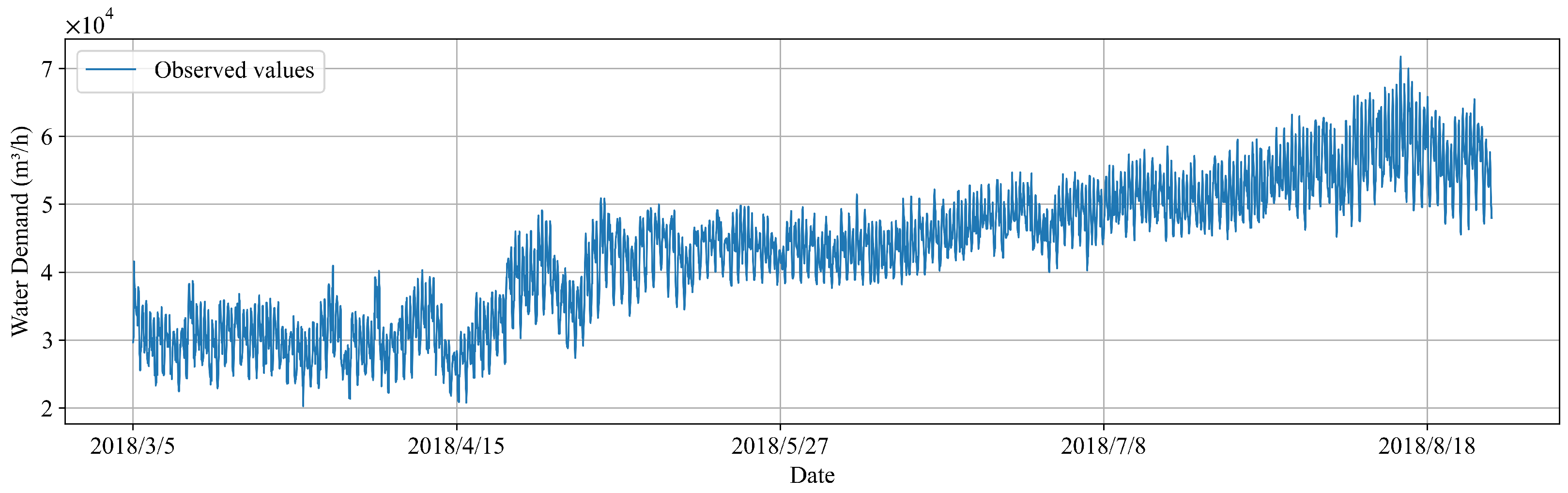
3.1. Dataset Description
3.2. Model Parameter Configuration
3.3. Results and Discussion
3.3.1. Analysis of Attention Mechanism
3.3.2. Comparison of Predictive Performance among Various Models
3.3.3. Contrast with Previous Studies
4. Conclusions
- (1)
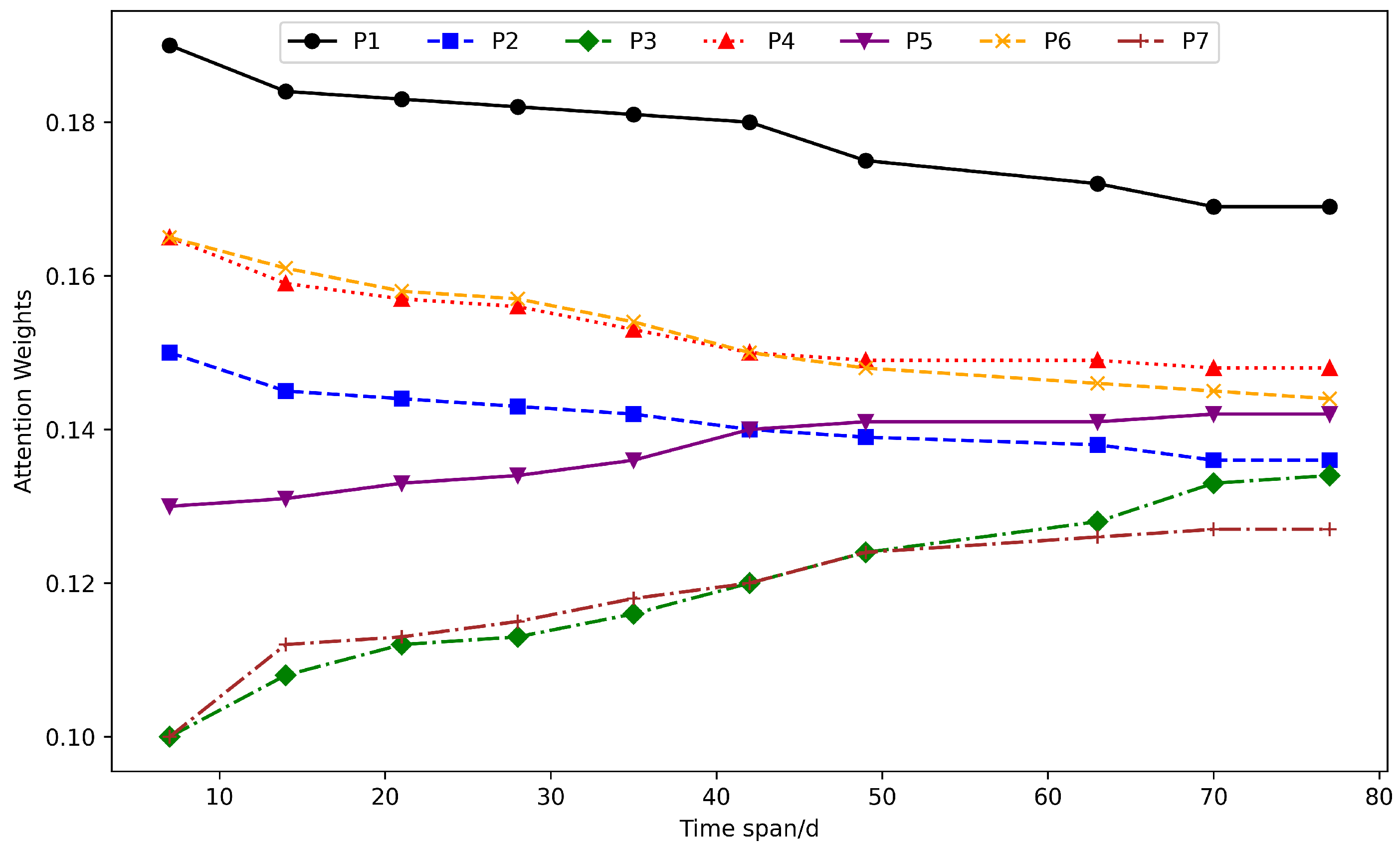
- The attention mechanism exerts a significant influence on linking various input feature sequences to their impact on predictive outcomes. It assigns varying weights to different sequences, with those containing more vital information receiving higher weights. Furthermore, as the temporal span of the dataset extends, the attention weights for each input sequence gradually stabilize amidst dynamic fluctuations. Importantly, the attention mechanism surpasses mere averaging of contribution rates across factors; rather, it autonomously explores the effect of distinct input features on predictive outcomes at each instance. This inherent mechanism notably strengthens the model’s capacity to extract pivotal feature information, thereby facilitating superior predictions.
- (2)
- In terms of the MAE, MAPE, RMSE, and NSE evaluation indicators, the results clearly demonstrate that the proposed method achieves state-of-the-art predictions and exhibits the highest level of robustness across all model tests. The proposed method excels in performance on the test dataset, with MAE, RMSE, MAPE, and NSE values of 544 m3/h, 915 m3/h, 1.00%, and 0.99, respectively, outperforming other benchmark models significantly. Therefore, it can be concluded that our approach is both valid and superior, showcasing satisfactory generalization ability, which could be instrumental in the development of a smart water demand consumption forecasting system.
- (3)
- In this dataset, when the model’s input features are effectively selected, the impact of the attention mechanism might be attenuated. This means that the potential for improvement in model predictive performance could be relatively reduced. In essence, by applying the MIC method to filter the model’s input features, the critical features that are selected undergo a secondary refinement upon integration with the attention mechanism. Consequently, while the model’s performance is indeed enhanced on this foundation, the scope for further enhancement is limited.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, Y.; Zhang, W.; Shen, J.; Mo, Z.; Yi, P. Smart city with Chinese characteristics against the background of big data: Idea, action and risk. J. Clean. Prod. 2017, 173, 60–66. [Google Scholar] [CrossRef]
- Huang, H.; Zhang, Z.; Song, F. An Ensemble-Learning-Based Method for Short-Term Water Demand Forecasting. Water Resour. Manag. 2021, 35, 1757–1773. [Google Scholar] [CrossRef]
- Herrera, M.; Torgo, L.; Izquierdo, J.; Pérez-García, R. Predictive models for forecasting hourly urban water demand. J. Hydrol. 2010, 387, 141–150. [Google Scholar] [CrossRef]
- Sebri, M. Forecasting urban water demand: A meta-regression analysis. J. Environ. Manag. 2016, 183, 777–785. [Google Scholar] [CrossRef]
- Donkor, E.A.; Mazzuchi, T.A.; Soyer, R.; Roberson, J.A. Urban Water Demand Forecasting: Review of Methods and Models. J. Water Resour. Plan. Manag. 2014, 140, 146–159. [Google Scholar] [CrossRef]
- Tiwari, M.K.; Adamowski, J. Urban water demand forecasting and uncertainty assessment using ensemble wavelet-bootstrap-neural network models. Water Resour. Res. 2013, 49, 6486–6507. [Google Scholar] [CrossRef]
- Guo, G.; Liu, S.; Wu, Y.; Li, J.; Zhou, R.; Zhu, X. Short-Term Water Demand Forecast Based on Deep Learning Method. J. Water Resour. Plan. Manag. 2018, 144, 04018076. [Google Scholar] [CrossRef]
- Rak, J.R.; Tchórzewska-Cieślak, B.; Pietrucha-Urbanik, K. A hazard assessment method for waterworks systems operating in self-government units. Int. J. Environ. Res. Public Health 2019, 16, 767. [Google Scholar] [CrossRef]
- Liu, X.; Sang, X.; Chang, J.; Zheng, Y. Multi-model coupling water demand prediction optimization method for megacities based on time series decomposition. Water Resour. Manag. 2021, 35, 4021–4041. [Google Scholar] [CrossRef]
- Braun, M.; Bernard, T.; Piller, O.; Sedehizade, F. 24-Hours Demand Forecasting Based on SARIMA and Support Vector Machines. Procedia Eng. 2014, 89, 926–933. [Google Scholar] [CrossRef]
- Kofinas, D.; Mellios, N.; Papageorgiou, E.; Laspidou, C. Urban Water Demand Forecasting for the Island of Skiathos. Procedia Eng. 2014, 89, 1023–1030. [Google Scholar] [CrossRef]
- Oliveira, P.J.; Steffen, J.L.; Cheung, P. Parameter Estimation of Seasonal Arima Models for Water Demand Forecasting Using the Harmony Search Algorithm. Procedia Eng. 2017, 186, 177–185. [Google Scholar] [CrossRef]
- Ma, X.; Jin, Y.; Dong, Q. A generalized dynamic fuzzy neural network based on singular spectrum analysis optimized by brain storm optimization for short-term wind speed forecasting. Appl. Soft Comput. 2017, 54, 296–312. [Google Scholar] [CrossRef]
- Wong, J.S.; Zhang, Q.; Chen, Y.D. Statistical modeling of daily urban water consumption in Hong Kong: Trend, changing patterns, and forecast. Water Resour. Res. 2010, 46, 3. [Google Scholar] [CrossRef]
- Niknam, A.; Zare, H.K.; Hosseininasab, H.; Mostafaeipour, A.; Herrera, M. A Critical Review of Short-Term Water Demand Forecasting Tools—What Method Should I Use? Sustainability 2022, 14, 5412. [Google Scholar] [CrossRef]
- Xenochristou, M.; Hutton, C.; Hofman, J.; Kapelan, Z. Water Demand Forecasting Accuracy and Influencing Factors at Different Spatial Scales Using a Gradient Boosting Machine. Water Resour. Res. 2020, 56, e2019WR026304. [Google Scholar] [CrossRef]
- Salloom, T.; Yu, X.; He, W.; Kaynak, O. Adaptive Neural Network Control of Underwater Robotic Manipulators Tuned by a Genetic Algorithm. J. Intell. Robot. Syst. 2019, 97, 657–672. [Google Scholar] [CrossRef]
- Ding, C.; Tao, D. Robust Face Recognition via Multimodal Deep Face Representation. IEEE Trans. Multimed. 2015, 17, 2049–2058. [Google Scholar] [CrossRef]
- Minaee, S.; Kalchbrenner, N.; Cambria, E.; Nikzad, N.; Chenaghlu, M.; Gao, J. Deep Learning—Based Text Classification: A Comprehensive Review. ACM Comput. Surv. 2021, 54, 3. [Google Scholar] [CrossRef]
- Zhao, Z.Q.; Zheng, P.; Xu, S.T.; Wu, X. Object Detection With Deep Learning: A Review. IEEE Trans. Neural Networks Learn. Syst. 2019, 30, 3212–3232. [Google Scholar] [CrossRef]
- Zanfei, A.; Menapace, A.; Granata, F.; Gargano, R.; Frisinghelli, M.; Righetti, M. An Ensemble Neural Network Model to Forecast Drinking Water Consumption. J. Water Resour. Plan. Manag. 2022, 148, 04022014. [Google Scholar] [CrossRef]
- Chen, L.; Yan, H.; Yan, J.; Wang, J.; Tao, T.; Xin, K.; Li, S.; Pu, Z.; Qiu, J. Short-term water demand forecast based on automatic feature extraction by one-dimensional convolution. J. Hydrol. 2022, 606, 127440. [Google Scholar] [CrossRef]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural Machine Translation by Jointly Learning to Align and Translate. arXiv 2014, arXiv:1409.0473. [Google Scholar] [CrossRef]
- Zheng, H.; Lin, F.; Feng, X.; Chen, Y. A Hybrid Deep Learning Model With Attention-Based Conv-LSTM Networks for Short-Term Traffic Flow Prediction. IEEE Trans. Intell. Transp. Syst. 2020, 22, 6910–6920. [Google Scholar] [CrossRef]
- Wang, J.; Du, C. Short-term load prediction model based on Attention-BiLSTM neural network and meteorological data correction. Electr. Power Autom. Equip. 2022, 42, 7. [Google Scholar] [CrossRef]
- Du, B.; Huang, S.; Guo, J.; Tang, H.; Wang, L.; Zhou, S. Interval forecasting for urban water demand using PSO optimized KDE distribution and LSTM neural networks. Appl. Soft Comput. 2022, 122, 108875. [Google Scholar] [CrossRef]
- Guo, J.; Sun, H.; Du, B. Multivariable time series forecasting for urban water demand based on temporal convolutional network combining random forest feature selection and discrete wavelet transform. Water Resour. Manag. 2022, 36, 3385–3400. [Google Scholar] [CrossRef]
- Duerr, I.; Merrill, H.R.; Wang, C.; Bai, R.; Boyer, M.; Dukes, M.D.; Bliznyuk, N. Forecasting urban household water demand with statistical and machine learning methods using large space-time data: A Comparative study. Environ. Model. Softw. 2018, 102, 29–38. [Google Scholar] [CrossRef]
- Kinney, J.B.; Atwal, G.S. Equitability, mutual information, and the maximal information coefficient. Proc. Natl. Acad. Sci. USA 2014, 111, 3354–3359. [Google Scholar] [CrossRef]
- Nunes Carvalho, T.M.; Filho, F. Variational Mode Decomposition Hybridized With Gradient Boost Regression for Seasonal Forecast of Residential Water Demand. Water Resour. Manag. 2021, 35, 3431–3445. [Google Scholar] [CrossRef]
- Smyl, S. Forecasting Short Time Series with LSTM Neural Networks. 2016. Available online: https://gallery.azure.ai/Tutorial/Forecasting-Short-Time-Series-with-LSTM-Neural-Networks-2 (accessed on 1 August 2023).
- Nguyen, H.P.; Liu, J.; Zio, E. A long-term prediction approach based on long short-term memory neural networks with automatic parameter optimization by Tree-structured Parzen Estimator and applied to time-series data of NPP steam generators. Appl. Soft Comput. 2020, 89, 106116. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Gao, J.; Gao, X.; Wu, N.; Yang, H. Bi-directional LSTM with multi-scale dense attention mechanism for hyperspectral image classification. Multimed. Tools Appl. 2022, 81, 24003–24020. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Tong, H.; Benesty, M. Xgboost: Extreme Gradient Boosting. 2016. Available online: https://cran.ms.unimelb.edu.au/web/packages/xgboost/vignettes/xgboost.pdf (accessed on 3 August 2023).
- Pan, S.; Zheng, Z.; Guo, Z.; Luo, H. An optimized XGBoost method for predicting reservoir porosity using petrophysical logs. J. Pet. Sci. Eng. 2022, 208, 109520. [Google Scholar] [CrossRef]
- Nguyen, H.; Bui, X.N.; Bac, B.; Cuong, D. Developing an XGBoost model to predict blast-induced peak particle velocity in an open-pit mine: A case study. Acta Geophys. 2019, 67, 477–490. [Google Scholar] [CrossRef]
- Saleh, H.; Mostafa, S.; Alharbi, A.; El-Sappagh, S.; Alkhalifah, T. Heterogeneous Ensemble Deep Learning Model for Enhanced Arabic Sentiment Analysis. Sensors 2022, 22, 3707. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random Search for Hyper-Parameter Optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, J.; Li, C.; Ji, X.; Li, D.; Huang, Y.; Di, F.; Gao, X.; Xu, L. Ultra Short-term Power Load Forecasting Based on Combined LSTM-XGBoost Model. Power Syst. Technol. 2020, 44, 614–620. [Google Scholar] [CrossRef]



| Label | Sequences | MIC |
|---|---|---|
| P1 | 0.863 | |
| P2 | 0.755 | |
| P3 | 0.704 | |
| P4 | 0.792 | |
| P5 | 0.766 | |
| P6 | 0.783 | |
| P7 | 0.708 |
| Hyper-Parameter | Search Range | BiLSTM |
|---|---|---|
| Number of layers | [1, 2, 3] | 2 |
| Number of neurons | from 32 to 128 with an increase 16 | 64 |
| Learning rate | ranging from 0.0001 to 0.01 with an increase of 0.0001 | 0.0043 |
| Activation | tanh, ReLU | ReLU |
| Dropout | True or False | False |
| Hyper-Parameter | Search Range | XGBoost |
|---|---|---|
| n_estimators | ranging from 100 to 150 | 100 |
| max_depth | [2, 3, 4, 5, 6] | 6 |
| eta | ranging from 0.01 to 0.3 with an increase of 0.01 | 0.3 |
| gamma | [0, 1, 2, 3] | 0 |
| subsample | ranging from 0.5 to 1 with an increase of 0.1 | 0.8 |
| colsample_bytree | ranging from 0.5 to 1 with an increase of 0.1 | 1 |
| Model | MAE (m3/h) | RMSE (m3/h) | MAPE (%) | NSE |
|---|---|---|---|---|
| Proposed method | 544 | 915 | 1.00 | 0.99 |
| Attention-BiLSTM | 1128 | 1405 | 1.95 | 0.92 |
| BiLSTM | 1145 | 1475 | 2.00 | 0.88 |
| LSTM | 1235 | 1576 | 2.14 | 0.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shan, S.; Ni, H.; Chen, G.; Lin, X.; Li, J. A Machine Learning Framework for Enhancing Short-Term Water Demand Forecasting Using Attention-BiLSTM Networks Integrated with XGBoost Residual Correction. Water 2023, 15, 3605. https://doi.org/10.3390/w15203605
Shan S, Ni H, Chen G, Lin X, Li J. A Machine Learning Framework for Enhancing Short-Term Water Demand Forecasting Using Attention-BiLSTM Networks Integrated with XGBoost Residual Correction. Water. 2023; 15(20):3605. https://doi.org/10.3390/w15203605
Chicago/Turabian StyleShan, Shihao, Hongzhen Ni, Genfa Chen, Xichen Lin, and Jinyue Li. 2023. "A Machine Learning Framework for Enhancing Short-Term Water Demand Forecasting Using Attention-BiLSTM Networks Integrated with XGBoost Residual Correction" Water 15, no. 20: 3605. https://doi.org/10.3390/w15203605
APA StyleShan, S., Ni, H., Chen, G., Lin, X., & Li, J. (2023). A Machine Learning Framework for Enhancing Short-Term Water Demand Forecasting Using Attention-BiLSTM Networks Integrated with XGBoost Residual Correction. Water, 15(20), 3605. https://doi.org/10.3390/w15203605





