Wetland Management in Recharge Regions of Regional Groundwater Flow Systems with Water Shortage, Nyírség Region, Hungary
Abstract
:1. Introduction
2. Materials and Methods
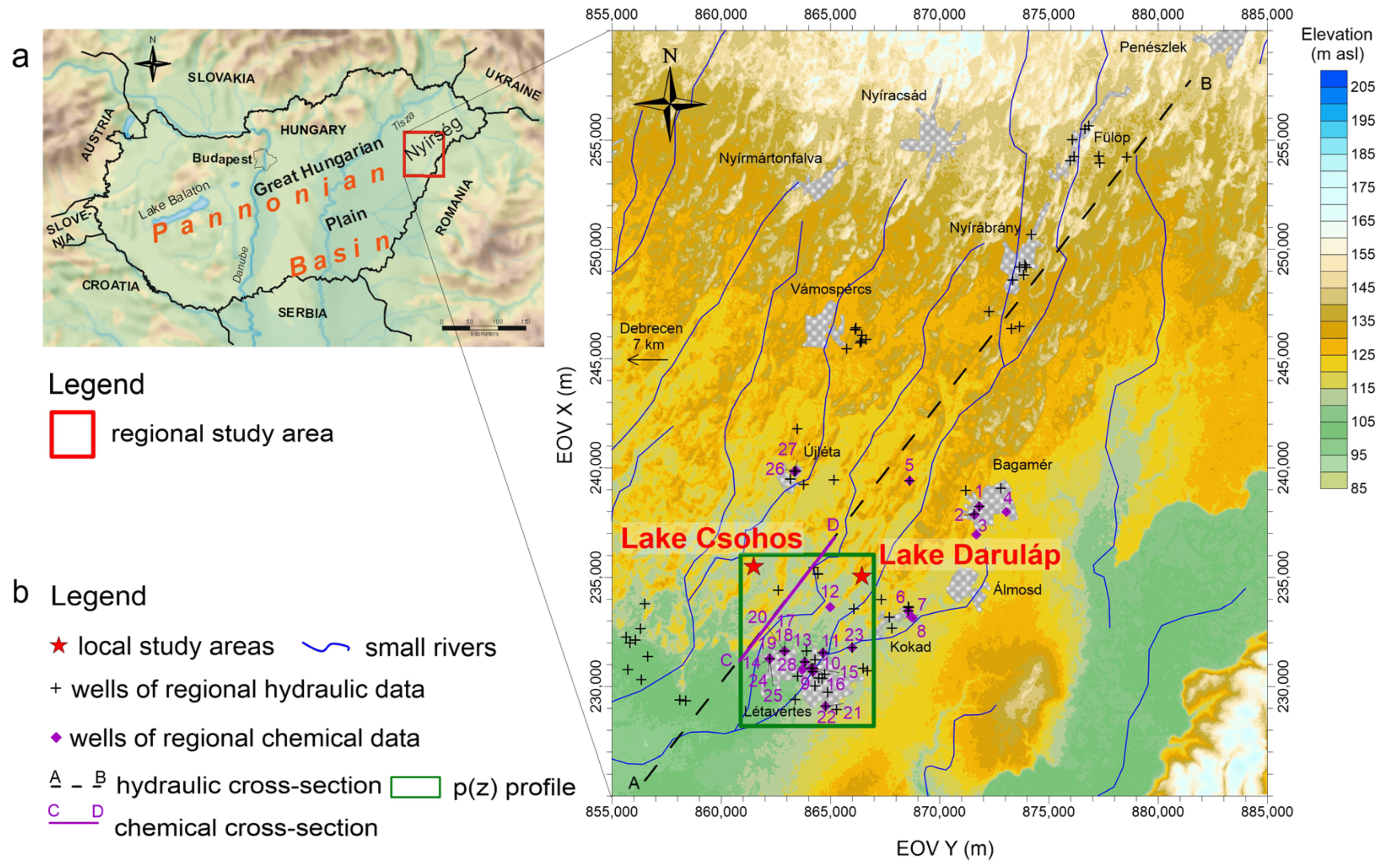
2.1. Study Area
2.2. Methods
2.2.1. Regional-Scale Wetland–Groundwater Characterisation
2.2.2. Local-Scale Wetland–Groundwater Characterisation
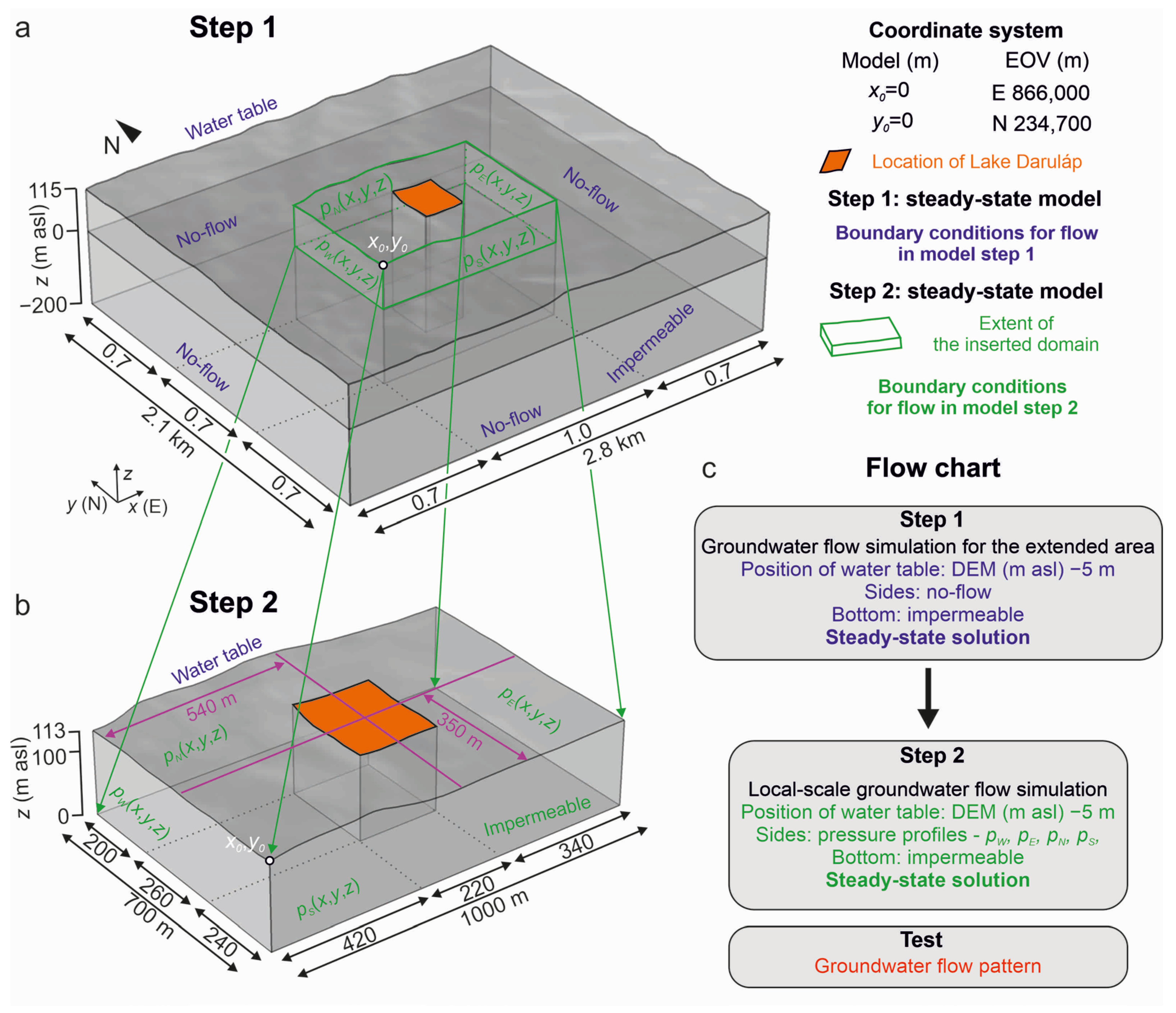
2.2.3. Local-Scale Numerical Simulation
3. Results
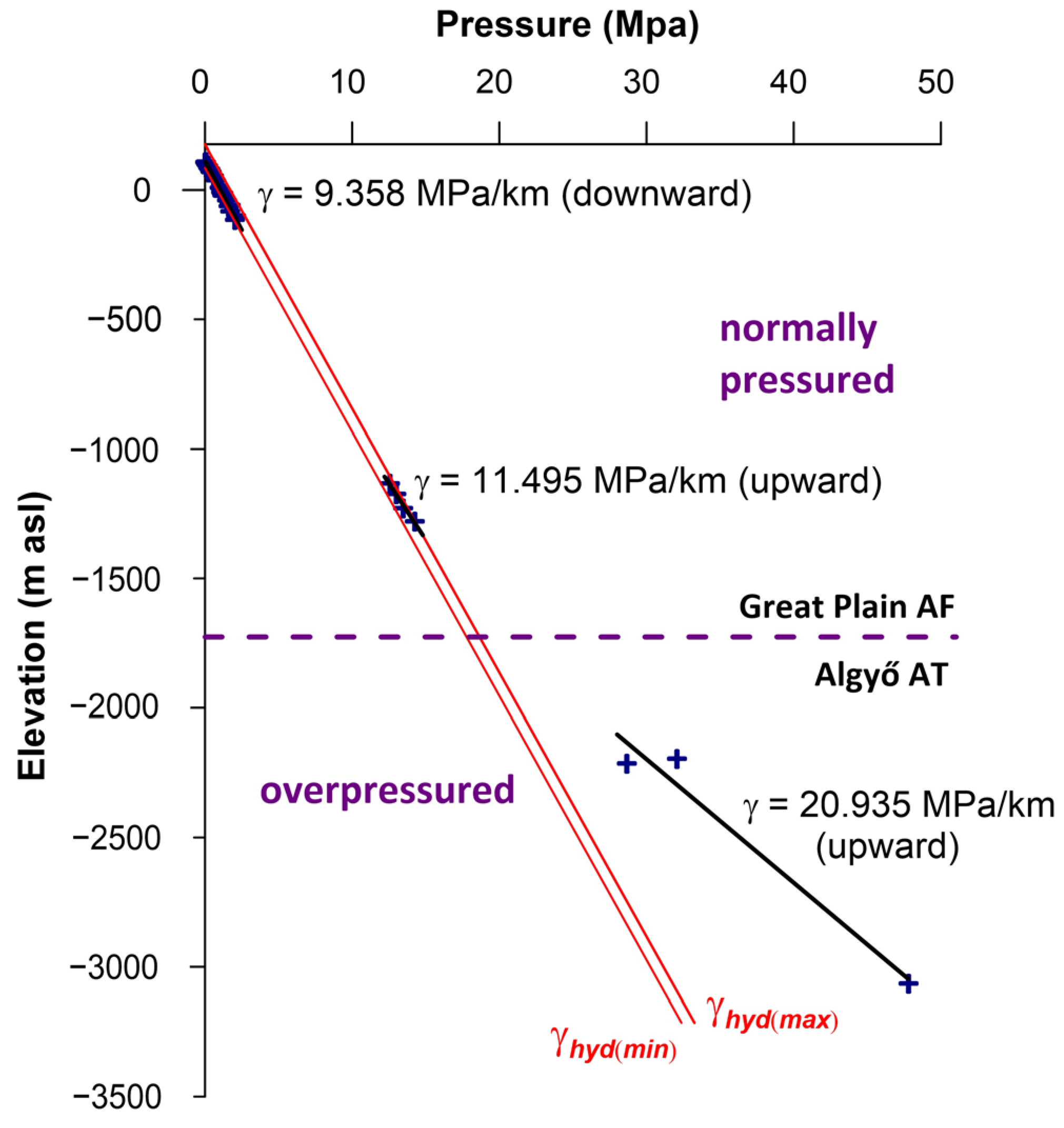
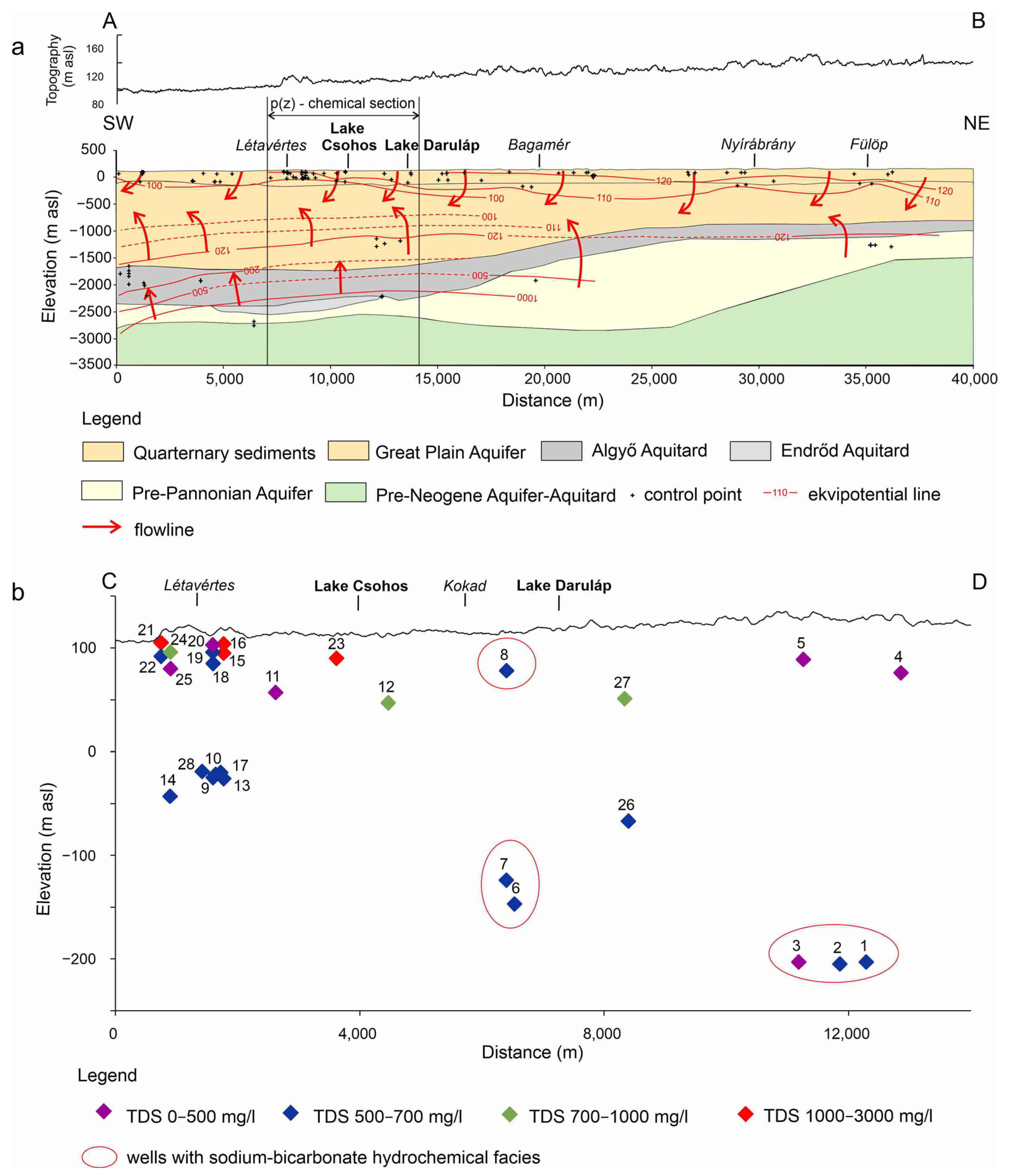
3.1. Regional-Scale Groundwater–Wetland Characterisation
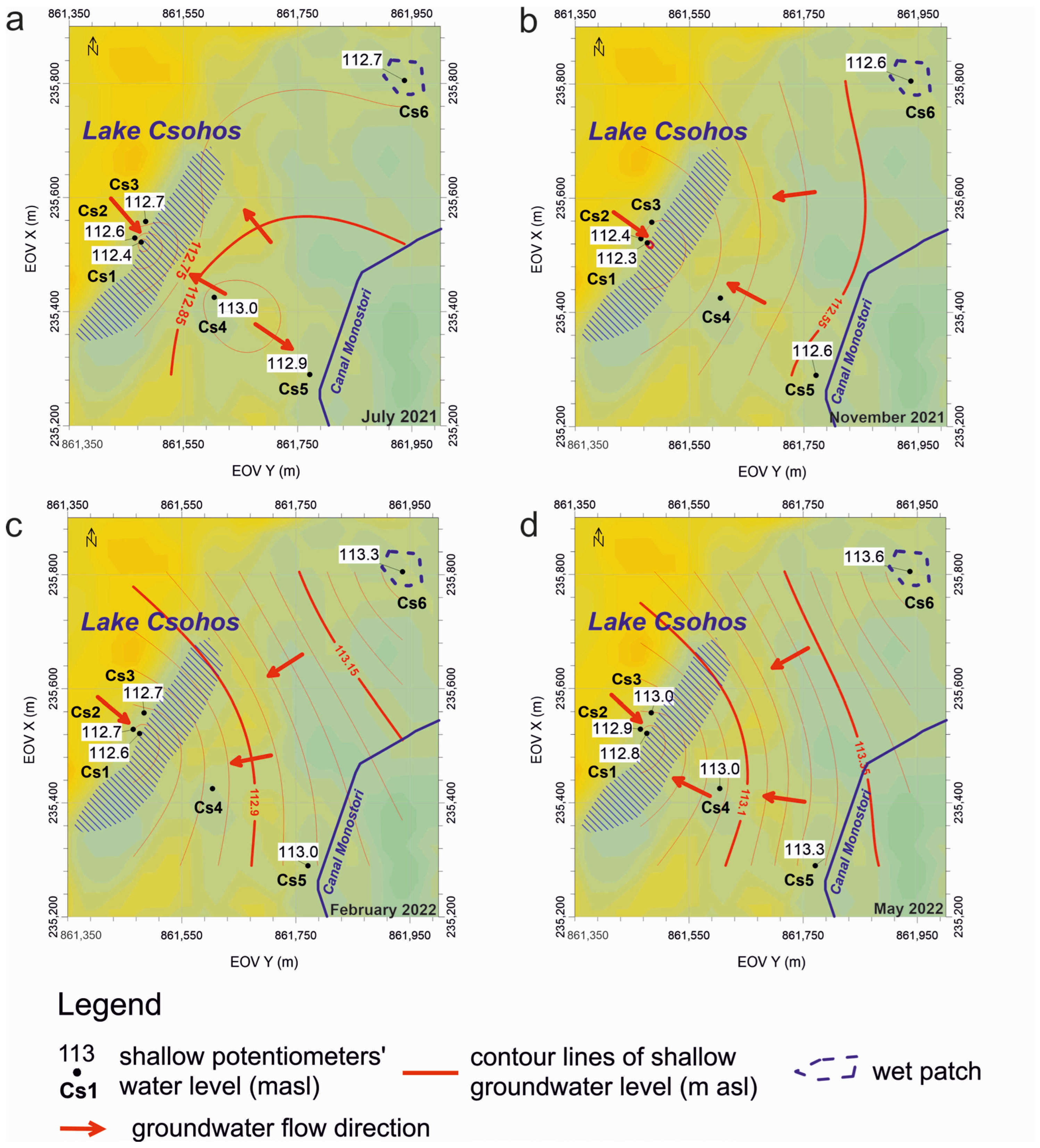
3.2. Local-Scale Investigations at Lake Csohos and Lake Daruláp
3.2.1. Wetland–Groundwater Interaction
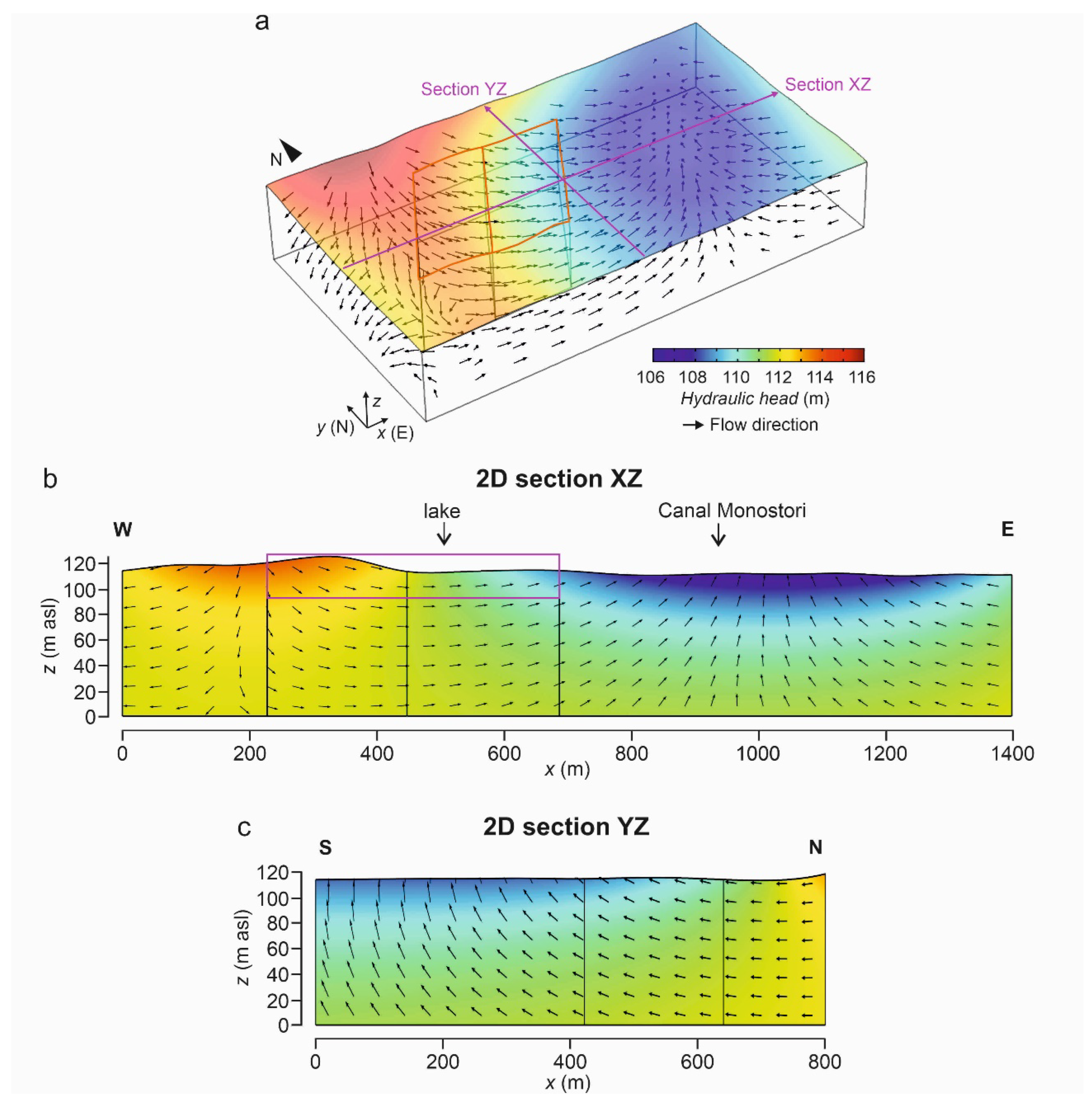
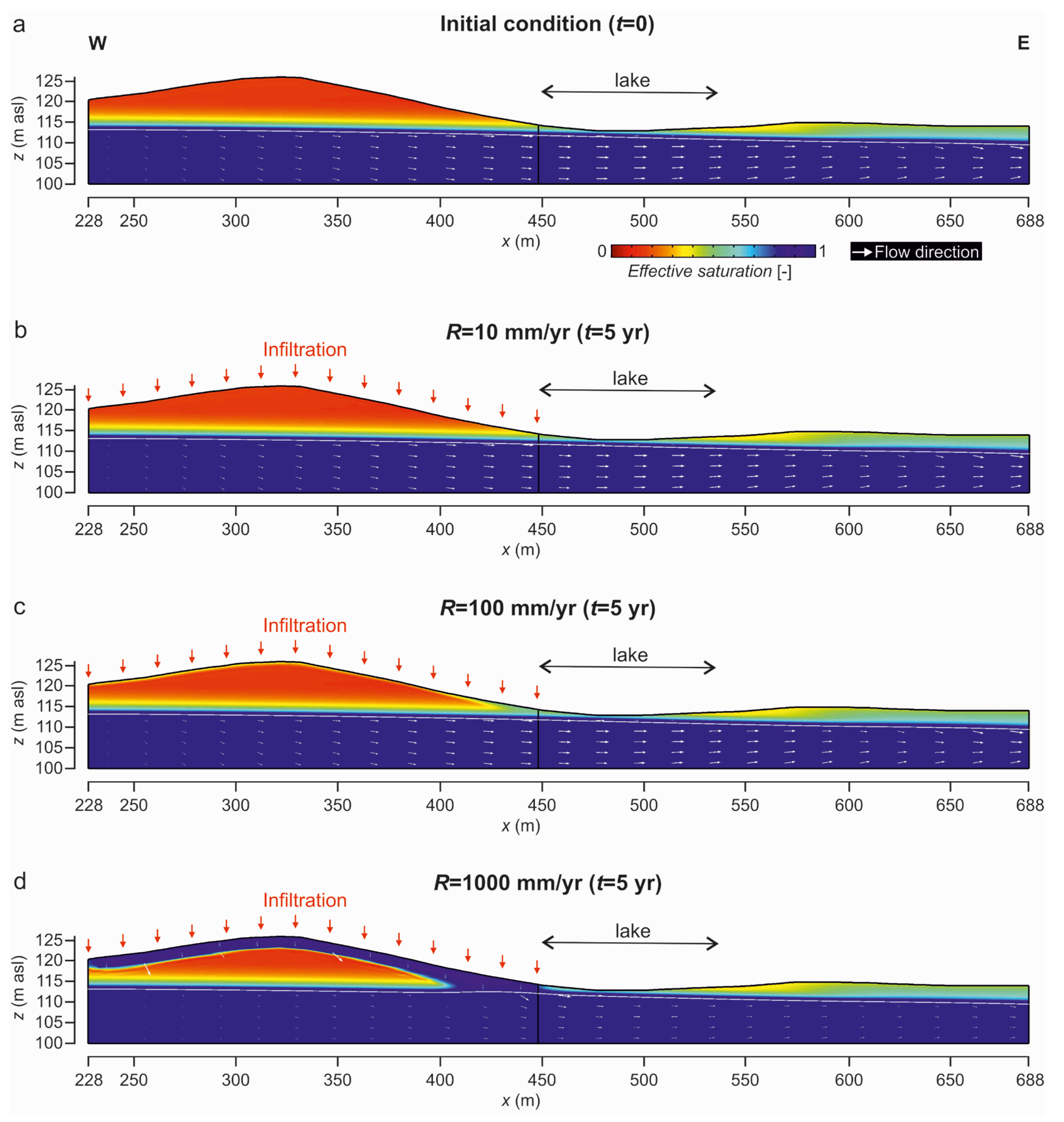
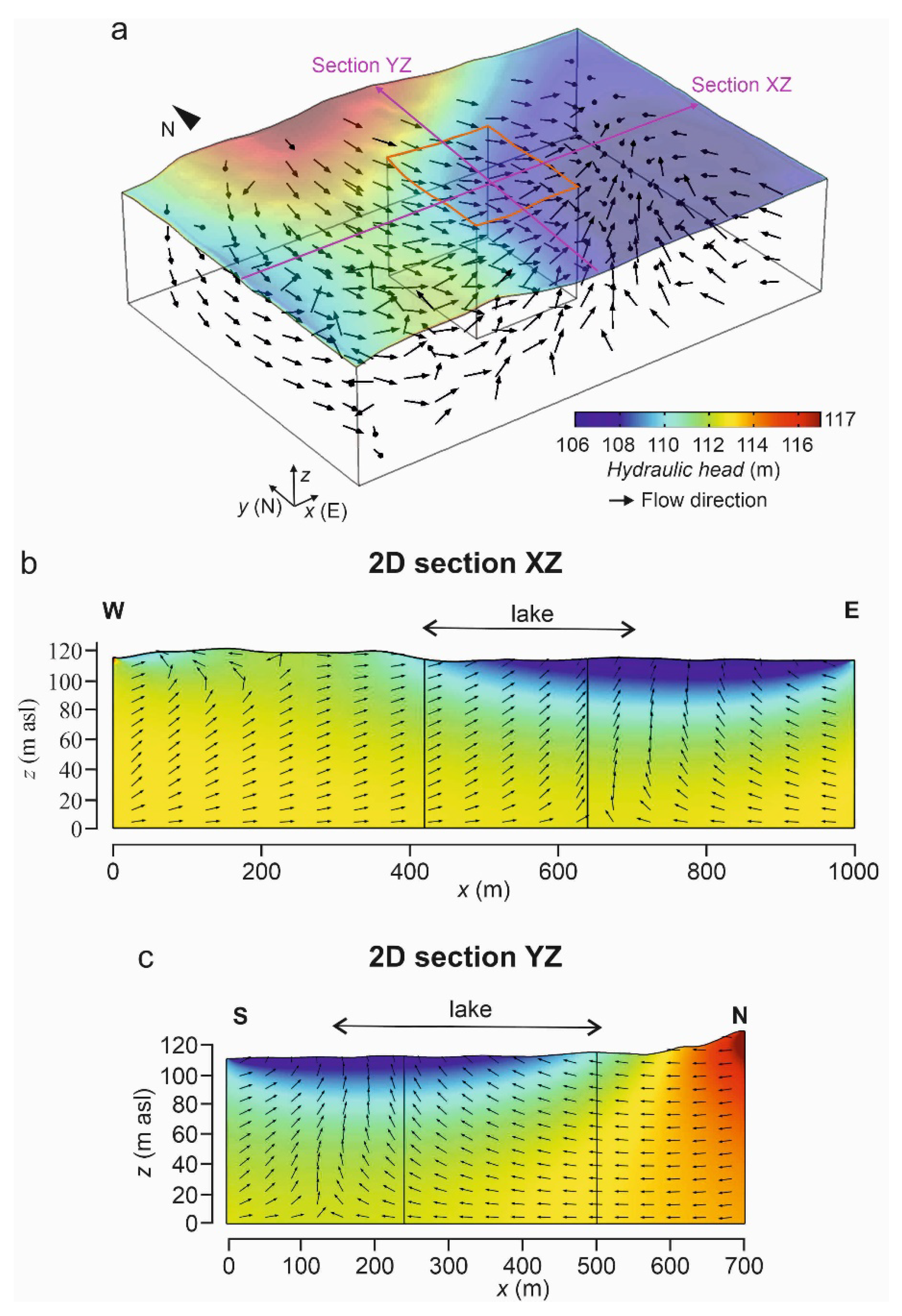
3.2.2. Groundwater Flow Simulation around the Wetlands and the Effect of Deforestation
4. Discussion
4.1. Position of the Wetlands in the Groundwater Flow Systems
4.1.1. Regional Groundwater Flow Conditions around the Wetlands
4.1.2. Wetland–Groundwater Interaction at Local Scale
4.1.3. Significance of Different Scales during Wetland–Groundwater Interaction
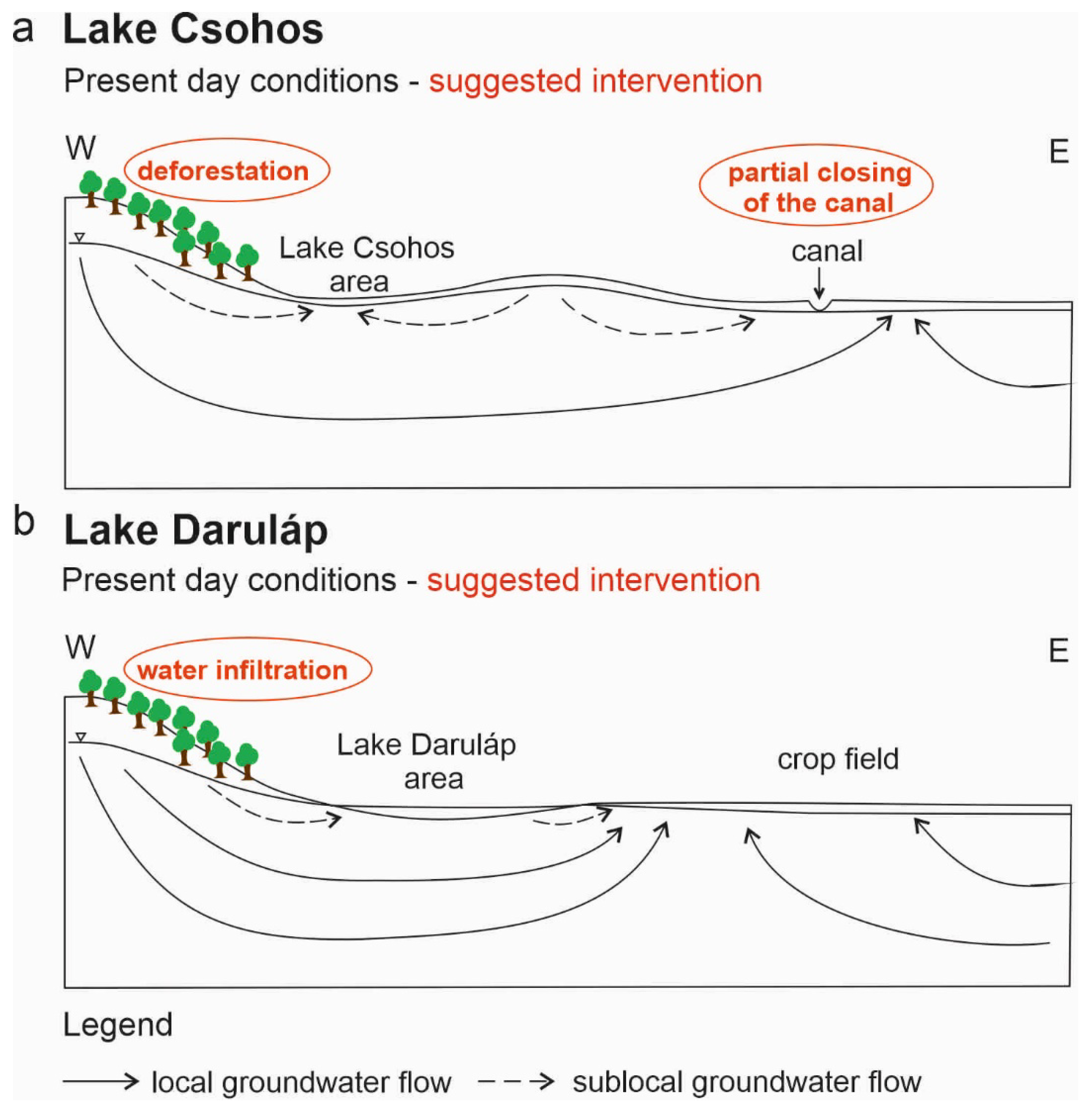
4.2. Potential Solutions to Mitigate Water Decline Affecting the Areas and Ensure Good Wetland Quality
4.3. Limitations of the Investigations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Groundwater Flow in Saturated Porous Media
Appendix A.2. Groundwater Flow in Unsaturated Porous Media
References
- Winter, T.C. Relation of streams, lakes, and wetlands to groundwater flow systems. Hydrogeol. J. 1999, 7, 28–45. [Google Scholar] [CrossRef]
- Brown, J.; Wyers, A.; Aldous, A.B.; Bach, S.L. Groundwater and Biodiversity Conservation: A methods Guide for Integrating Groundwater Needs of Ecosystems and Species into Conservation Plans in the Pacific Northwest; The Nature Conservancy: Arlington, VA, USA, 2007; 123p. [Google Scholar]
- Kløve, B.; Ala-aho, P.; Bertrand, G.; Boukalova, Z.; Ertürk, A.; Goldscheider, N.; Ilmonen, J.; Karakaya, N.; Kupfersberger, H.; Kvœrner, J.; et al. Widerlund. Groundwater dependent ecosystems. Part I: Hydroecological status and trends. Environ. Sci. Policy 2011, 14, 770–781. [Google Scholar] [CrossRef]
- Winter, T.C.; Harvey, J.W.; Franke, O.L.; Alley, W.M. Groundwater and Surface Water: A Single Resource. Circular 1139; US Geological Survey: Denver, CO, USA, 1998; 79p. [Google Scholar]
- Liu, Q.; Mou, X. Interactions Between Surface Water and Groundwater: Key Processes in Ecological Restoration of Degraded Coastal Wetlands Caused by Reclamation. Wetlands 2016, 36, 95–102. [Google Scholar] [CrossRef]
- Shaw, R.D.; Shaw, J.F.H.; Fricker, H.; Prepas, E.E. Integrated Approach to Quantify Groundwater Transport of Phosphorus to Narrow Lake, Alberta. Limnol. Oceanogr. 1990, 35, 870–886. [Google Scholar] [CrossRef]
- Simon, S.; Mádl-Szőnyi, J.; Müller, I.; Pogácsás, G. Conceptual model for surface salinization in an overpressured and a superimposed gravity-flow field, Lake Kelemenszék area, Hungary. Hydrogeol. J. 2011, 19, 701–717. [Google Scholar] [CrossRef]
- Zurek, A.J.; Witczak, S.; Dulinski, M.R.; Wachniew, P.; Rozanski, K.; Kania, J.; Postawa, A.; Karczewski, J.; Moscicki, W.J. Quantification of anthropogenic impact on groundwater-dependent terrestrial ecosystem using geochemical and isotope tools combined with 3-D flow and transport modelling. Hydrol. Earth Syst. Sci. 2015, 19, 1015–1033. [Google Scholar] [CrossRef]
- Van der Kamp, G.; Hayashi, M. Groundwater-wetland ecosystem interaction in the semiarid glaciated plains of North America. Hydrogeol. J. 2009, 17, 203–214. [Google Scholar] [CrossRef]
- Medici, G.; Langman, J.B. Pathways and Estimate of Aquifer Recharge in a Flood Basalt Terrain; A Review from the South Fork Palouse River Basin (Columbia River Plateau, USA). Sustainability 2022, 14, 11349. [Google Scholar] [CrossRef]
- Mádl-Szőnyi, J.; Tóth, J. A hydrogeological type section for the Duna-Tisza Interfluve, Hungary. Hydrogeol. J. 2009, 17, 961–980. [Google Scholar] [CrossRef]
- Meyboom, P. Mass transfer studies to determine the groundwater regime of permanent lakes in hummocky moraine of western Canada. J. Hydrol. 1967, 5, 117–142. [Google Scholar] [CrossRef]
- Erwin, K.L. Wetlands and global climate change: The role of wetland restoration in a changing world. Wetl. Ecol. Manag. 2009, 17, 71–84. [Google Scholar] [CrossRef]
- Kløve, B.; Ala-aho, B.; Bertrand, G.; Gurdak, J.J.; Kupfersberger, H.; Kværner, J.; Muotka, T.; Mykrä, H.; Preda, E.; Rossi, P.; et al. Climate change impacts on groundwater and dependent ecosystems. J. Hydrol. 2014, 518, 250–266. [Google Scholar] [CrossRef]
- Salimi, S.; Almuktar, S.A.A.A.N.; Scholz, M. Impact of climate change on wetland ecosystems: A critical review of experimental wetlands. J. Environ. Manag. 2021, 286, 112160. [Google Scholar] [CrossRef]
- Cuthbert, M.O.; Gleeson, T.; Moosdorf, N.; Befus, K.M.; Schneider, A.; Hartmann, J.; Lehner, B. Global patterns and dynamics of climate–groundwater interactions. Nat. Clim. Chang. 2009, 9, 137–141. [Google Scholar] [CrossRef]
- Kurylyk, B.L.; MacQuarrie, K.T.; Voss, C.I. Climate change impacts on the temperature and magnitude of groundwater discharge from shallow, unconfined aquifers. Water Resour. Res. 2014, 50, 3253–3274. [Google Scholar] [CrossRef]
- Zhou, P.; Wang, G.; Duan, R. Impacts of long-term climate change on the groundwater flow dynamics in a regional groundwater system: Case modeling study in Alashan, China. J. Hydrol. 2020, 590, 125557. [Google Scholar] [CrossRef]
- Trásy-Havril, T.; Szkolnikovics-Simon, S.; Mádl-Szőnyi, J. How Complex Groundwater Flow Systems Respond to Climate Change Induced Recharge Reduction? Water 2022, 14, 3026. [Google Scholar] [CrossRef]
- Mitsch, W.J.; Hernandez, M.E. Landscape and climate change threats to wetlands of North and Central America. Aquat. Sci. 2013, 75, 133–149. [Google Scholar] [CrossRef]
- van Engelenburg, J.; Hueting, R.; Rijpkema, S.; Teuling, A.J.; Uijlenhoet, R.; Ludwig, F. Impact of Changes in Groundwater Extractions and Climate Change on Groundwater-Dependent Ecosystems in a Complex Hydrogeological Setting. Water Resour. Manag. 2018, 32, 259–272. [Google Scholar] [CrossRef]
- Xi, Y.; Peng, S.; Ciais, P.; Chen, Y. Future impacts of climate change on inland Ramsar wetlands. Nat. Clim. Chang. 2021, 11, 45–51. [Google Scholar] [CrossRef]
- Xu, W.; Su, X. Challenges and impacts of climate change and human activities on groundwater-dependent ecosystems in arid areas—A case study of the Nalenggele alluvial fan in NW China. J. Hydrol. 2019, 573, 376–385. [Google Scholar] [CrossRef]
- Engelen, G.B.; Kloosterman, F.H. Hydrological Systems Analysis: Methods and Applications. Water Science and Technology Library; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1996; Volume 20. [Google Scholar]
- Klijn, F.; Witte, J.P.M. Eco-hydrology: Groundwater flow and site factors in plant ecology. Hydrogeol. J. 1999, 7, 65–77. [Google Scholar] [CrossRef]
- Aldous, A.R.; Gannett, M.W. Groundwater, biodiversity, and the role of flow system scale. Ecohydrology 2021, 14, e2342. [Google Scholar] [CrossRef]
- Scherberg, J.; Baker, T.; Selker, J.S.; Henry, R. Design of Managed Aquifer Recharge for Agricultural and Ecological Water Supply Assessed Through Numerical Modeling. Water Resour. Manag. 2014, 28, 4971–4984. [Google Scholar] [CrossRef]
- Dillon, P.; Pavelic, P.; Page, D.; Beringen, H.; Ward, J. Managed Aquifer Recharge: An Introduction. Waterlines Report Series No. 13; National Water Commission: Canberra, Australia, 2009. [Google Scholar]
- Batelaan, O.; De Smedt, F.; Triest, L. Regional groundwater discharge: Phreatophyte mapping, groundwater modelling and impact analysis of land-use change. J. Hydrol. 2003, 275, 86–108. [Google Scholar] [CrossRef]
- Gale, I.N.; Macdonald, D.M.J.; Calow, R.C.; Neumann, I.; Moench, M.; Kulkarni, H.; Mudrakartha, S.; Palanisami, K. Managed Aquifer Recharge: An Assessment of Its Role and Effectiveness in Watershed Management; British Geological Survey: Nottingham, UK, 2006. [Google Scholar]
- Szabó, Z.; Szijártó, M.; Tóth, Á.; Mádl-Szőnyi, J. The Significance of Groundwater Table Inclination for Nature-Based Replenishment of Groundwater-Dependent Ecosystems by Managed Aquifer Recharge. Water 2023, 15, 1077. [Google Scholar] [CrossRef]
- Hungarian Ministry of Internal Affairs Hydrological Directorate. Az Aszály Kockázat Kezelés és a Klímaalkalmazkodási Képesség Javítására Irányuló Vízgazdálkodási Intézkedések Meghatározása; Budapest, Hungary, 31 December 2019; 256p. Available online: https://vizeink.hu/wp-content/uploads/2021/04/Aszaly_VGT3_2021.pdf (accessed on 30 August 2023).
- Czauner, B.; Molnár, F.; Masetti, M.; Arola, T.; Mádl-Szőnyi, J. Groundwater flow system-based dynamic system approach for geofluids and their resources. Water 2022, 14, 1015. [Google Scholar] [CrossRef]
- Kerékgyártó, G. Az Érmelléki löszös hát kistáj településeinek egyedi tájértékei. Agrártudományi Közlemények 2012, 46, 45–50. [Google Scholar]
- Borsy, Z. A Nyírség Természeti Földrajza; Academical Press: Budapest, Hungary, 1961; 227p. [Google Scholar]
- Bihari, Z.; Babolcsai, G.; Bartholy, J.; Ferenczi, Z.; Gerhát-Kerényi, J.; Haszpra, L.; Homoki-Ujváry, K.; Kovács, T.; Lakatos, M.; Németh, Á.; et al. Magyarország éghajlata. In Magyarország Nemzeti Atlasza: Természeti Környezet; Kocsis, K., Ed.; Hungarian Academy of Science, Research Centre for Astronomy and Earth Sciences: Budapest, Hungary, 2018; pp. 58–69. [Google Scholar]
- Ács, F.; Breuer, H.; Szász, G. A tényleges párolgás és a talaj vízkészlet becslése tenyészidőszakban. Agrokémia És Talajt. 2007, 56, 217–236. [Google Scholar] [CrossRef]
- Tóth, J.; Almási, I. Interpretation of observed fluid potential patterns in a deep sedimentary basin under tectonic compression: Hungarian Great Plain, Pannonian Basin. Geofluids 2001, 1, 11–36. [Google Scholar] [CrossRef]
- Szabó, Z. Folyadékáramlási Rendszerek Komplex Értékelése Hajdúszoboszló–Ebes—Balmazújváros Tágabb Térségében. Master’s Thesis, Department of Applied and Environmental Geology, Eötvös Loránd University, Budapest, Hungary, 2018. [Google Scholar]
- Haas, J.; Budai, T.; Csontos, L.; Fodor, L.; Konrád, G.; Koroknai, B. Magyarország Prekainozoos Medencealjzatának Földtana. Magyarázó ”Magyarország Pre-Kainozoos Földtani Térképéhez” (1:500,000); Hungarian Institute of Geology and Geophysics (Magyar Földtani és Geofizikai Intézet): Budapest, Hungary, 2014. [Google Scholar]
- Juhász, G. A pannóniai (sl) formációk térképezése az Alföldön: Elterjedés, fácies és üledékes környezet. Földtani Közlöny 1992, 122, 133–165. [Google Scholar]
- Pogácsás, G.; Lakatos, L.; Újszászi, K.; Vakarcs, G.; Várkonyi, L.; Várnai, P.; Révész, I. Seismic facies, electro facies and Neogene sequence chronology of the Pannonian Basin. Acta Geol. Hung. 1988, 31, 175–207. [Google Scholar]
- Borsy, Z. Blown sand territories in Hungary. Z. Für Geomorphol. Suppl. 1991, 90, 1–14. [Google Scholar]
- Buró, B.; Sipos, G.; Lóki; Andrási, B.; Félegyházi, E.; Négyesi, G. Assessing Late Pleistocene and Holocene phases of aeolian activity on the Nyírség alluvial fan, Hungary. Quatern. Int. 2016, 425, 183–195. [Google Scholar] [CrossRef]
- Szanyi, J. Felszín Alatti Víztermelés Környezeti Hatásai a Dél-Nyírség Példáján. Ph.D. Thesis, University of Szeged, Szeged, Hungary, 2004. [Google Scholar]
- Járó, Z. A hazai erdők vízfogyasztása. Agrártudományi Közlemények 1981, 40, 353–356. [Google Scholar]
- Déri-Takács, J.; Szkolnikovics-Simon, S.; Szijártó, M.; Mádl-Szőnyi, J. Létavértes-Kokad Kutatási Terület Fűzlápjai Vízpótlásának Megalapozása; Report to the Hortobágy National Park Directorate: Budapest, Hungary, 2021. [Google Scholar]
- Tóth, J. Gravitational Systems of Groundwater Flow: Theory, Evaluation, Utilization; Cambridge University Press: Cambridge, UK, 2009; 310p. [Google Scholar]
- Mádlné Szőnyi, J. Felszínalatti Vízáramlások Mintázata Fedetlen és Kapcsolódó Fedett Karbonátos Víztartó Rendszerekben, a Budai-Termálkarszt Tágabb Környezetének Példáján. Ph.D. Thesis, Department of Geology, Eötvös Loránd University, Budapest, Hungary, 2020. [Google Scholar]
- Zimmermann, W.B.J. Multiphysics Modeling With Finite Element Methods; World Scientific Publishing Company: Singapore, 2006; 422p. [Google Scholar]
- Freeze, A.; Cherry, J. Groundwater; Prentice Hall: Eaglewood Cliff, NJ, USA, 1979; 604p. [Google Scholar]
- Farthing, W.M.; Ogden, F.L. Numerical Solution of Richards’ Equation: A Review of Advances and Challenges. Soil Sci. Soc. Am. J. 2017, 81, 1257–1269. [Google Scholar] [CrossRef]
- van Genuchtern, M.T. A closed-form for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Kerék, B.; Vatai, J. Az Alföld földtani kutatásának környezetvédelmi jelentősége. (The importance of environmental research of the Great Hungarian Plain). Agrártudományi Közlemények 2006, 19, 9–16. [Google Scholar]
- Mester, T.; Balla, D.; Szabó, G. Assessment of Groundwater Quality Changes in the Rural Environment of the Hungarian Great Plain Based on Selected Water Quality Indicators. Water Air Soil Pollut. 2020, 231, 536. [Google Scholar] [CrossRef]
- Shedlock, R.J.; Wilcox, D.A.; Thompson, T.A.; Cohen, D.A. Interactions between ground water and wetlands, southern shore of Lake Michigan, USA. J. Hydrol. 1993, 141, 127–155. [Google Scholar] [CrossRef]
- Anibas, C.; Verbeiren, B.; Buis, K.; Chormański, J.; De Doncker, L.; Okruszko, T.; Meire, P.; Batelaan, O. A hierarchical approach on groundwater-surface water interaction in wetlands along the upper Biebrza River, Poland. Hydrol. Earth Syst. Sci. 2012, 16, 2329–2346. [Google Scholar] [CrossRef]
- Czauner, B.; Szabó, Z.; Márton, B.; Mádl-Szőnyi, J. Basin-Scale Hydraulic Evaluation of Groundwater Flow Controlled Biogenic Gas Migration and Accumulation in the Central Pannonian Basin. Water 2023, 15, 3272. [Google Scholar] [CrossRef]
- Czauner, B.; Szkolnikovics-Simon, S.; Mádl-Szőnyi, J. Regional scale normal and abnormal pore pressure regimes and groundwater flow systems—Determination, characterization and climate change-related issues. In Proceedings of the 49th IAH Congress—Groundwater Sustainability and Poverty Reduction, Wuhan, China, 20 September 2022. [Google Scholar]
- Zak, D.; Hupfer, M.; Cabezas, A.; Jurasinski, G.; Audet, J.; Kleeberg, A.; McInnes, R.; Kristiansen, S.M.; Petersen, R.J.; Liu, H.; et al. Sulphate in freshwater ecosystems: A review of sources, biogeochemical cycles, ecotoxicological effects and bioremediation. Earth-Sci. Rev. 2021, 212, 103446. [Google Scholar] [CrossRef]
- Simon, S. Characterization of Groundwater and Lake Interaction in Saline Environment, at Kelemen-szék Lake,Danube-Tisza Interfluve, Hungary. Ph.D. Thesis, Department of Geology, Eötvös Loránd University, Budapest, Hungary, 2010. [Google Scholar]
- Wheeler, B.D.; Proctor, M.C.F. Ecological gradients, subdivisions and terminology of North-West European mires. J. Ecology 2000, 88, 187–203. [Google Scholar] [CrossRef]
- Akinnawo, S.O. Eutrophication: Causes, consequences, physical, chemical and biological techniques for mitigation strategies. Environ. Chall. 2023, 12, 100733. [Google Scholar] [CrossRef]
- Smolders, A.J.P.; Lucassen, E.C.H.E.T.; Bobbink, R.; Roelofs, J.G.M.; Lamers, L.P.M. How nitrate leaching from agricultural lands provokes phosphate eutrophication in groundwater fed wetlands: The sulphur bridge. Biogeochemistry 2010, 98, 1–7. [Google Scholar] [CrossRef]
- Thorslund, J.; Jarsjo, J.; Jaramillo, F.; Jawitz, J.W.; Manzoni, S.; Basu, N.B.; Chalov, S.R.; Cohen, M.J.; Creed, I.F.; Goldenberg, R.; et al. Wetlands as large-scale nature-based solutions: Status and challenges for research, engineering and management. Ecol. Eng. 2017, 108, 489–497. [Google Scholar] [CrossRef]
- Albhaisi, M.; Brendonck, L.; Batelaan, O. Predicted impacts of land use change on groundwater recharge of the upper Berg catchment, South Africa. Water SA 2013, 39, 211–220. [Google Scholar] [CrossRef]
- Hokanson, K.J.; Peterson, E.S.; Devito, K.J.; Mendoza, C.A. Forestland-peatland hydrologic connectivity in water-limited environments: Hydraulic gradients often oppose topography. Environ. Res. Lett. 2020, 15, 034021. [Google Scholar] [CrossRef]
- Haitjema, H.M.; Mitchell-Bruker, S. Are Water Tables a Subdued Replica of the Topography? Ground Water 2005, 43, 781–786. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simon, S.; Déri-Takács, J.; Szijártó, M.; Szél, L.; Mádl-Szőnyi, J. Wetland Management in Recharge Regions of Regional Groundwater Flow Systems with Water Shortage, Nyírség Region, Hungary. Water 2023, 15, 3589. https://doi.org/10.3390/w15203589
Simon S, Déri-Takács J, Szijártó M, Szél L, Mádl-Szőnyi J. Wetland Management in Recharge Regions of Regional Groundwater Flow Systems with Water Shortage, Nyírség Region, Hungary. Water. 2023; 15(20):3589. https://doi.org/10.3390/w15203589
Chicago/Turabian StyleSimon, Szilvia, Judit Déri-Takács, Márk Szijártó, László Szél, and Judit Mádl-Szőnyi. 2023. "Wetland Management in Recharge Regions of Regional Groundwater Flow Systems with Water Shortage, Nyírség Region, Hungary" Water 15, no. 20: 3589. https://doi.org/10.3390/w15203589




