Economic Operation of Variable Speed and Blade Angle-Adjustable Pumping Stations of an Open-Channel Water Transfer Project
Abstract
:1. Introduction
2. Methodology
2.1. Basis of the Model
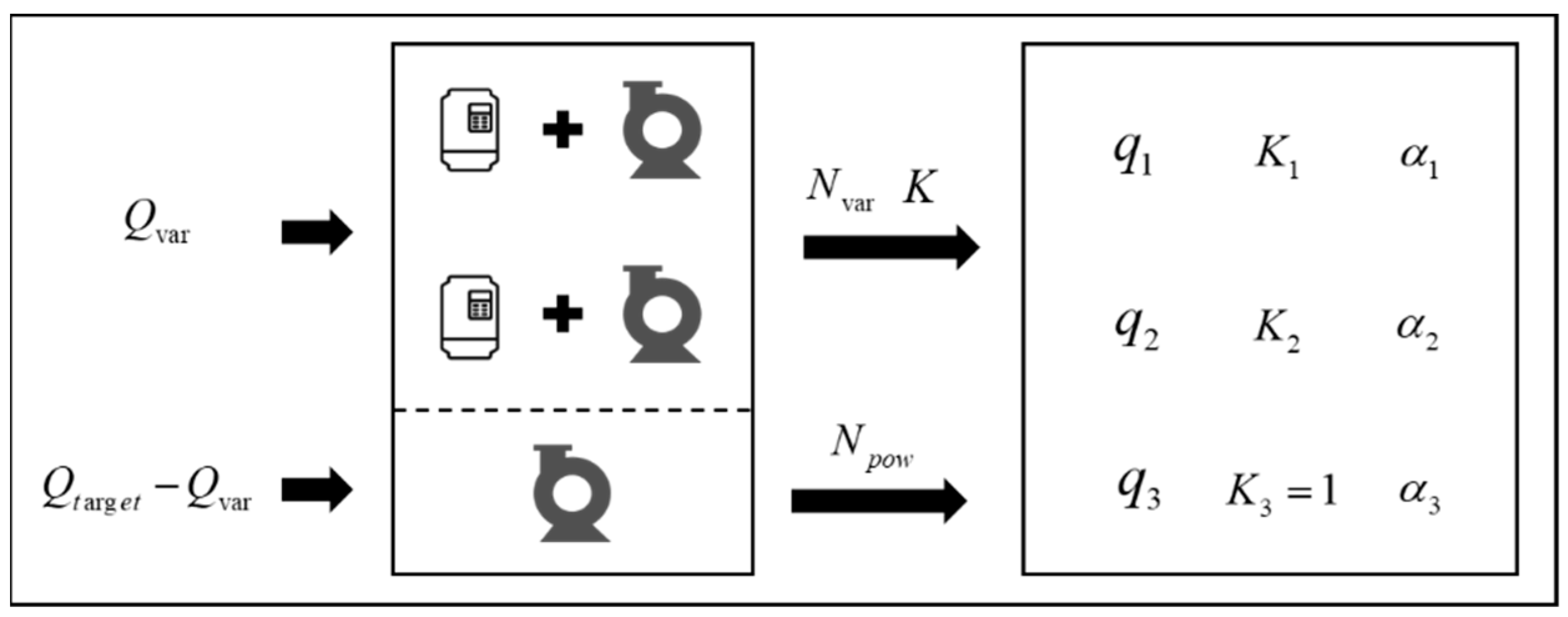
2.2. Discharge Optimization Model for a Single Pumping Station
- (1)
- Decision Variables
- (2)
- Constraints
- (3)
- Objective function
- (4)
- Optimization algorithm
2.3. Head Optimization Model for Cascade Pumping Stations
3. Application and Results
3.1. Study Area
3.2. Discharge Optimization for Single Pumping Station
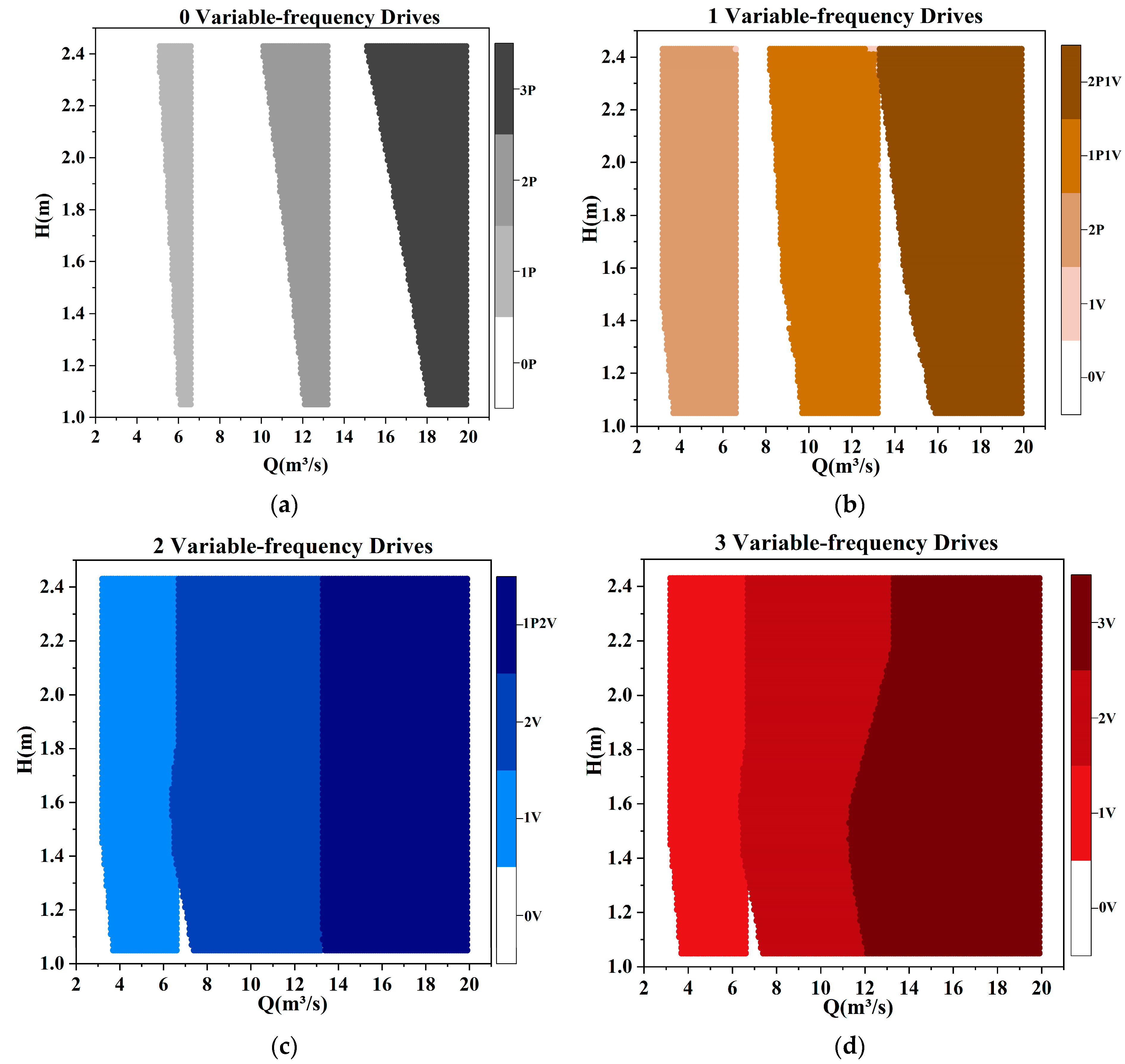
3.2.1. Discharge Range
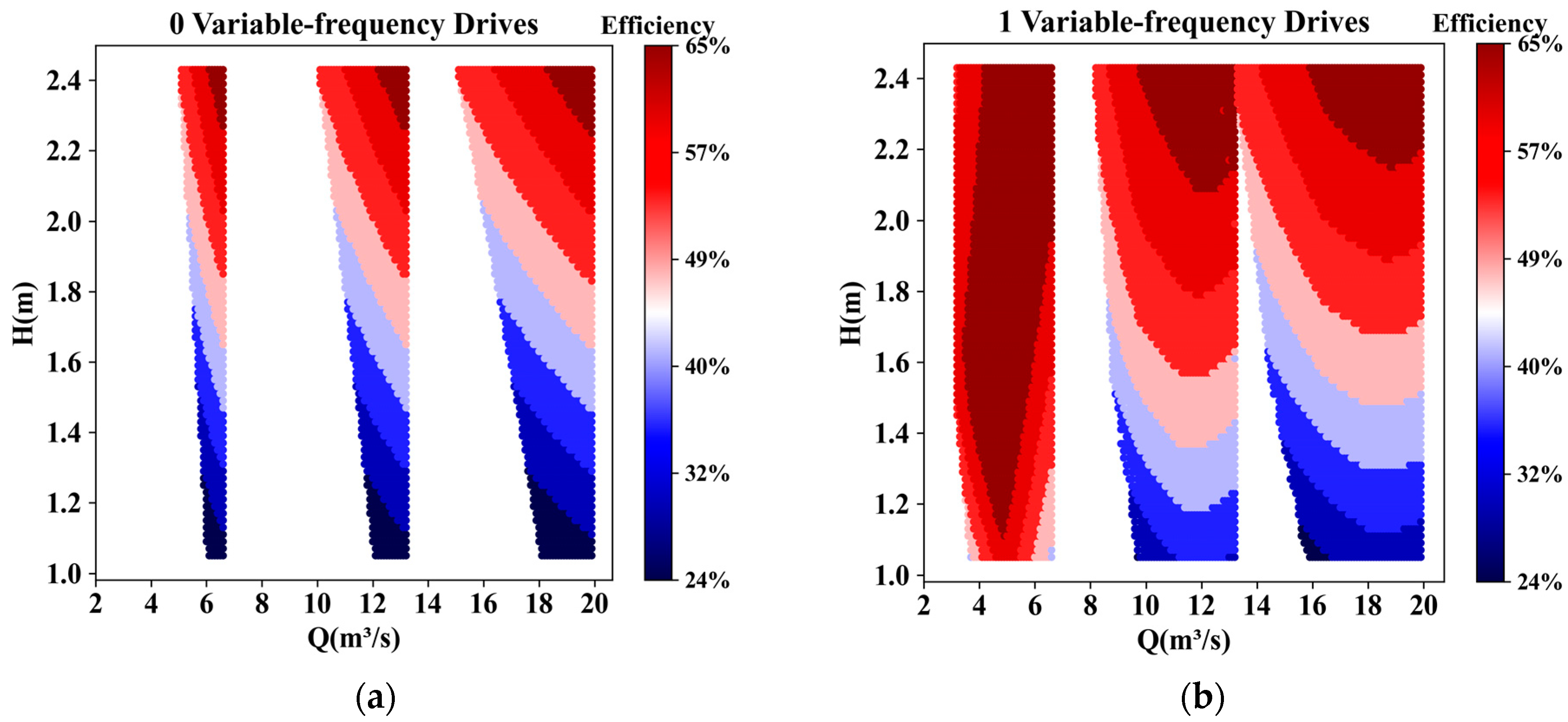
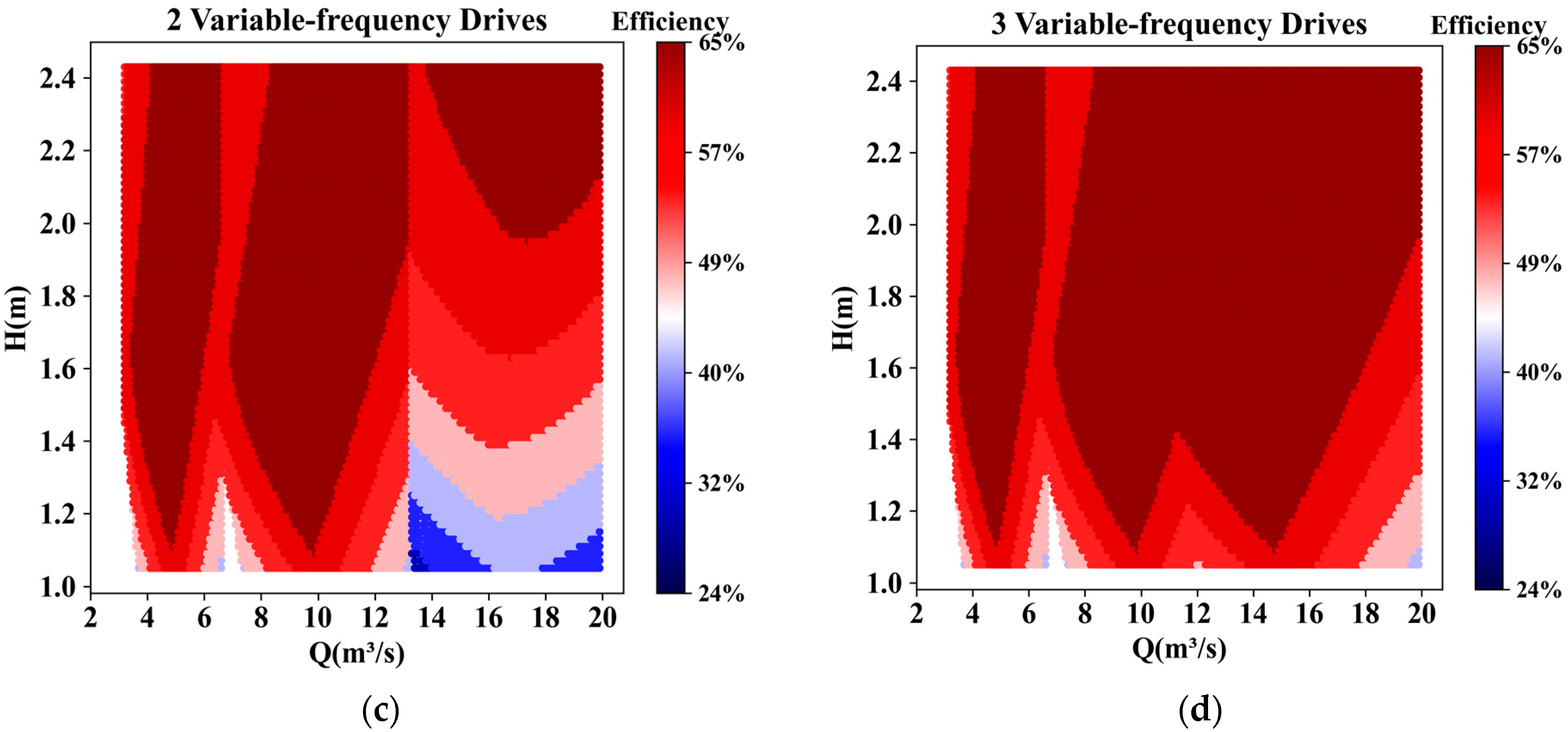
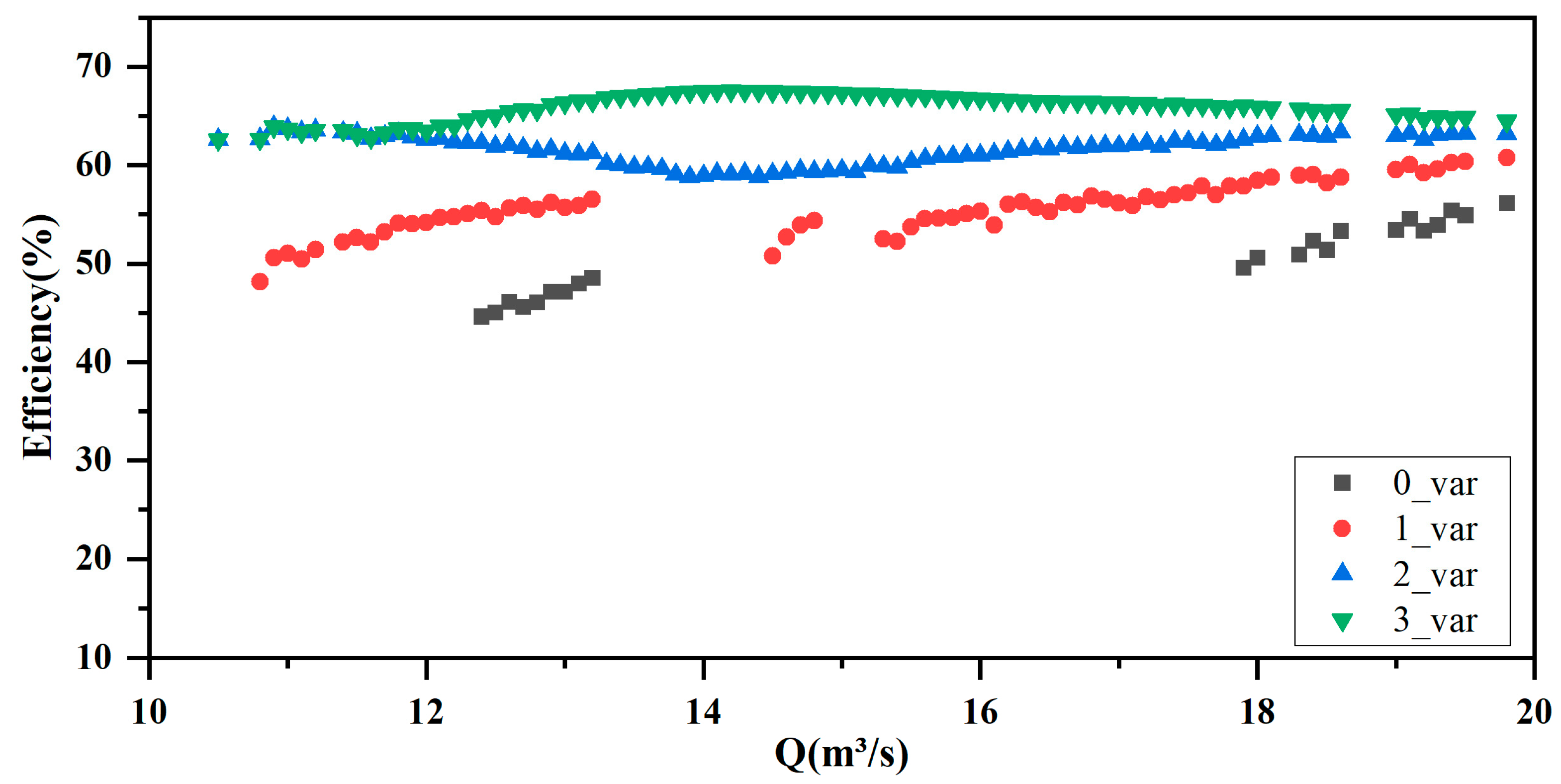
3.2.2. Energy Consumption
3.3. Head Optimization Model for Cascade Pumping Stations
4. Discussion
- (1)
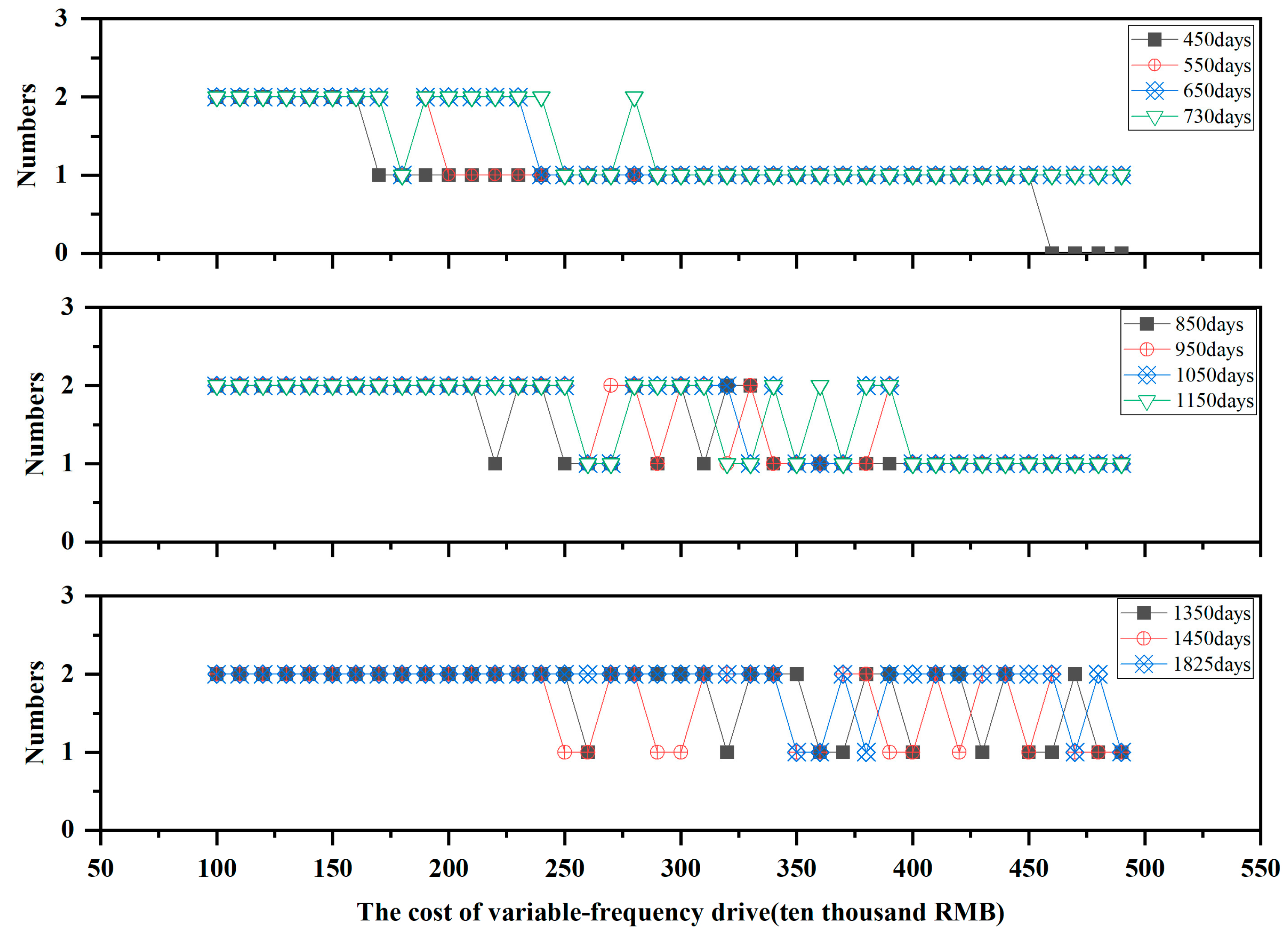
- The influence of VFD cost on the total investment
- (2)
- The influence of running time on the effect of VFDs
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qiao, Q.-S.; Yang, K.-L. Modeling Unsteady Open-Channel Flow for Controller Design. J. Irrig. Drain. Eng. 2010, 136, 383–391. [Google Scholar] [CrossRef]
- Zhang, Z.; Lei, X.; Tian, Y.; Wang, L.; Wang, H.; Su, K. Optimized Scheduling of Cascade Pumping Stations in Open-Channel Water Transfer Systems Based on Station Skipping. J. Water Resour. Plan. Manag. 2019, 145, 05019011. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, Z.; Lei, X.; Jing, X.; Wang, H.; Yan, P. Ecological Scheduling of the Middle Route of South-to-North Water Diversion Project Based on a Reinforcement Learning Model. J. Hydrol. 2021, 596, 126107. [Google Scholar] [CrossRef]
- Wu, P.; Lai, Z.; Wu, D.; Wang, L. Optimization Research of Parallel Pump System for Improving Energy Efficiency. J. Water Resour. Plan. Manag. 2015, 141, 04014094. [Google Scholar] [CrossRef]
- Yan, P.; Zhang, Z.; Lei, X.; Zheng, Y.; Zhu, J.; Wang, H.; Tan, Q. A Simple Method for the Control Time of a Pumping Station to Ensure a Stable Water Level Immediately Upstream of the Pumping Station under a Change of the Discharge in an Open Channel. Water 2021, 13, 355. [Google Scholar] [CrossRef]
- Yan, P.; Zhang, Z.; Hou, Q.; Lei, X.; Liu, Y.; Wang, H. A Novel IBAS-ELM Model for Prediction of Water Levels in Front of Pumping Stations. J. Hydrol. 2023, 616, 128810. [Google Scholar] [CrossRef]
- Arun Shankar, V.K.; Umashankar, S.; Paramasivam, S.; Hanigovszki, N. A Comprehensive Review on Energy Efficiency Enhancement Initiatives in Centrifugal Pumping System. Appl. Energy 2016, 181, 495–513. [Google Scholar] [CrossRef]
- Zhang, L.; Zhuan, X. Optimization on the VFDs’ Operation for Pump Units. Water Resour. Manag. 2019, 33, 355–368. [Google Scholar] [CrossRef]
- Saidur, R. A Review on Electrical Motors Energy Use and Energy Savings. Renew. Sustain. Energy Rev. 2010, 14, 877–898. [Google Scholar] [CrossRef]
- Kong, L.; Li, Y.; Tang, H.; Yuan, S.; Yang, Q.; Ji, Q.; Li, Z.; Chen, R. Predictive Control for the Operation of Cascade Pumping Stations in Water Supply Canal Systems Considering Energy Consumption and Costs. Appl. Energy 2023, 341, 121103. [Google Scholar] [CrossRef]
- Gong, Y.; Cheng, J. Optimization of Cascade Pumping Stations’ Operations Based on Head Decomposition–Dynamic Programming Aggregation Method Considering Water Level Requirements. J. Water Resour. Plan. Manag. 2018, 144, 04018034. [Google Scholar] [CrossRef]
- Giacomello, C.; Kapelan, Z.; Nicolini, M. Fast Hybrid Optimization Method for Effective Pump Scheduling. J. Water Resour. Plan. Manag. 2013, 139, 175–183. [Google Scholar] [CrossRef]
- Córcoles, J.I.; Tarjuelo, J.M.; Moreno, M.A. Methodology to Improve Pumping Station Management of On-Demand Irrigation Networks. Biosyst. Eng. 2016, 144, 94–104. [Google Scholar] [CrossRef]
- Mohammadzade Negharchi, S.; Shafaghat, R.; Najafi, A.; Babazade, D. Evaluation of Methods for Reducing the Total Cost in Rural Water Pumping Stations in Iran: A Case Study. J. Water Supply Res. Technol.-Aqua 2016, 65, 277–293. [Google Scholar] [CrossRef]
- Fernández García, I.; Moreno, M.A.; Rodríguez Díaz, J.A. Optimum Pumping Station Management for Irrigation Networks Sectoring: Case of Bembezar MI (Spain). Agric. Water Manag. 2014, 144, 150–158. [Google Scholar] [CrossRef]
- Sang, G.; Cao, S.; Guo, R.; Zhang, L. Optimization of Cost per Day of Cascade Pumping Station Water-Delivery System. Paiguan Jixie Gongcheng Xuebao J. Drain. Irrig. Mach. Eng. 2013, 31, 688–695. [Google Scholar] [CrossRef]
- Olszewski, P. Genetic Optimization and Experimental Verification of Complex Parallel Pumping Station with Centrifugal Pumps. Appl. Energy 2016, 178, 527–539. [Google Scholar] [CrossRef]
- Sorin, P.; Liviu Valer, H. Reducing Energy Consumption by Upgrading Pumping Stations in Water Distribution Systems. Environ. Eng. Manag. J. 2013, 12, 735–740. [Google Scholar] [CrossRef]
- Cheng, X.; Li, G.; Cheng, C.-T.; Guo, X.-H. Modeling Method of Operation Rules on Cascade Hydroelectric Plants with Hybrid Pumped Storage Power Station. Shuili Xuebao J. Hydraul. Eng. 2013, 44, 388–397. [Google Scholar]
- López-Ibáñez, M.; Prasad, T.D.; Paechter, B. Ant Colony Optimization for Optimal Control of Pumps in Water Distribution Networks. J. Water Resour. Plan. Manag. 2008, 134, 337–346. [Google Scholar] [CrossRef]
- Zheng, H.; Zhang, Z.; Wu, H.; Lei, X. Study on the Daily Optimized Dispatching and Economic Operation of Cascade Pumping Stations in Water Conveyance System. Shuili Xuebao J. Hydraul. Eng. 2016, 47, 1558–1565. [Google Scholar] [CrossRef]
- Naoum-Sawaya, J.; Ghaddar, B.; Arandia, E.; Eck, B. Simulation-Optimization Approaches for Water Pump Scheduling and Pipe Replacement Problems. Eur. J. Oper. Res. 2015, 246, 293–306. [Google Scholar] [CrossRef]
- Sadatiyan Abkenar, S.M.; Stanley, S.D.; Miller, C.J.; Chase, D.V.; McElmurry, S.P. Evaluation of Genetic Algorithms Using Discrete and Continuous Methods for Pump Optimization of Water Distribution Systems. Sustain. Comput. Inform. Syst. 2015, 8, 18–23. [Google Scholar] [CrossRef]
- Tang, Y.; Zheng, G.; Zhang, S. Optimal Control Approaches of Pumping Stations to Achieve Energy Efficiency and Load Shifting. Int. J. Electr. Power Energy Syst. 2014, 55, 572–580. [Google Scholar] [CrossRef]
- Zhuan, X.; Xia, X. Optimal Operation Scheduling of a Pumping Station with Multiple Pumps. Appl. Energy 2013, 104, 250–257. [Google Scholar] [CrossRef]
- Zhang, H.; Liang, Y.; Liao, Q.; Wu, M.; Yan, X. A Hybrid Computational Approach for Detailed Scheduling of Products in a Pipeline with Multiple Pump Stations. Energy 2017, 119, 612–628. [Google Scholar] [CrossRef]
- Ghassemi-Tari, F.; Jahangiri, E. Development of a Hybrid Dynamic Programming Approach for Solving Discrete Nonlinear Knapsack Problems. Appl. Math. Comput. 2007, 188, 1023–1030. [Google Scholar] [CrossRef]
- Feng, X.; Qiu, B.; Wang, Y. Optimizing Parallel Pumping Station Operations in an Open-Channel Water Transfer System Using an Efficient Hybrid Algorithm. Energies 2020, 13, 4626. [Google Scholar] [CrossRef]
- Jing, X.; Zang, Z.; Lei, X.; Mo, Z.; Ma, F.; Kong, L.; Hang, F.; Li, Y. Research on the Influence of Non-electricity Water Transfer Cost on the Discharge Distribution of Parallel Pump Stations. China Rural. Water Hydropower 2023, 134–140. [Google Scholar]
- Marchi, A.; Simpson, A.; Ertugrul, N. Assessing Variable Speed Pump Efficiency in Water Distribution Systems. Drink. Water Eng. Schi. 2011, 5, 15–21. [Google Scholar] [CrossRef]
- Guo, X.; Jia, M.; Xu, C. Artificial colony algorithm for energy saving optimal operation of pumping stations. China Rural. Water Hydropower 2017, 160–164. [Google Scholar]
- Feng, X.; Qiu, B. Optimal Operation Models and Comparison of Their Energy-Saving Effects for Large Pumping Station System. Nongye Gongcheng Xuebao Trans. Chin. Soc. Agric. Eng. 2012, 28, 46–51. [Google Scholar] [CrossRef]
- Shang, Y.; Liu, R.; Li, T.; Zhang, C. Transient Flow Control for an Artificial Open Channel Based on Finite Difference Method. Sci. China Technol. Sci. 2011, 54, 781–792. [Google Scholar] [CrossRef]
- Huang, H.; Liu, Z.; Fan, J.; Mao, W. Study on hydraulic simulation model of main canal of Mid-route of South-to-North Water Transfer Project. Water Resour. Hydropower Eng. 2013, 44, 111–115+122. [Google Scholar]


| Pumping Station Name | Design Head (m) | Rated Speed (r/min) | Pump Parameter | |
|---|---|---|---|---|
| Discharge Range (m3/s) | Head Range (m) | |||
| Tundian | 1.71 | 245 | 5.3–8.2 | 0.07–1.5 |
| Qianliulin | 2.21 | 245 | 4.7–7.4 | 0.67–2.2 |
| Niantou | 2.83 | 245 | 4.45–6.64 | 1.05–2.45 |
| Xingshou | 2.58 | 245 | 4.67–6.86 | 0.18–2.21 |
| Lishishan | 2.21 | 245 | 4.9–7.4 | 0.25–2.04 |
| Xitaishang | 6.18 | 290 | 4.8–10.3 | 4.13–8.18 |
| Number of VFDs | Discharge Range | Average Proportion of Operable Conditions | Relative Increment |
|---|---|---|---|
| 0 | 4.45–19.92 m3/s | 42.80% | - |
| 1 | 3.115–19.92 m3/s | 80.14% | 87.24% |
| 2 | 3.115–19.92 m3/s | 98.35% | 129.8% |
| 3 | 3.115–19.92 m3/s | 98.46% | 130% |
| Number of VFDs | Efficiency | Average Efficiency | Average Absolute Increase | Average Relative Increase |
|---|---|---|---|---|
| 0 | 23.91–63.56% | 45.16% | - | - |
| 1 | 27.25–65.1% | 52.25% | 8.75% | 19.38% |
| 2 | 32.03–65.1% | 57.69% | 12.94% | 28.65% |
| 3 | 43.33–65.1% | 61.09% | 15.86% | 35.12% |
| Operating Conditions | Number of VFDs | Discharge (m3/s) | Speed Ratio | Blade Angle (°) | Pumping Station Efficiency (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1# | 2# | 3# | 1# | 2# | 3# | 1# | 2# | 3# | |||
| Discharge = 6 m3/s; head = 1.45 m | 0 | 6 | 1 | −3.46 | 33.86 | ||||||
| 1 | 6 | 0.84 | 2 | 57.7 | |||||||
| 2 | 6 | 0.84 | 2 | 57.7 | |||||||
| 3 | 6 | 0.84 | 2 | 57.7 | |||||||
| Discharge = 10.1 m3/s; head = 2.41 m | 0 | 5.05 | 5.05 | 1 | 1 | −3.92 | −3.92 | 50.21 | |||
| 1 | 3.46 | 6.64 | 0.81 | 1 | −2.71 | 1.19 | 60.58 | ||||
| 2 | 5.05 | 5.05 | 0.86 | 0.86 | 1.21 | 1.21 | 63.35 | ||||
| 3 | 5.05 | 5.05 | 0.86 | 0.86 | 1.21 | 1.21 | 63.35 | ||||
| Discharge = 16 m3/s, head = 2.05 m | 0 | 5.33 | 5.33 | 5.33 | 1 | 1 | 1 | −3.93 | −3.93 | −3.93 | 44.39 |
| 1 | 3.11 | 6.44 | 6.44 | 0.74 | 1 | 1 | −2.9 | −0.43 | −0.43 | 54.4 | |
| 2 | 4.68 | 4.68 | 6.64 | 0.8 | 0.8 | 1 | 1.22 | 1.22 | 0.2 | 59.89 | |
| 3 | 5.33 | 5.33 | 5.33 | 0.83 | 0.83 | 0.83 | 2 | 2 | 2 | 65.09 | |
| Number of VFDs | Number of Conditions in which the Head Can Be Distributed | Average Efficiency | Absolute Efficiency Gain |
|---|---|---|---|
| 0 | 22 | 50.37% | - |
| 1 | 68 | 55.57% | 7.47% |
| 2 | 85 | 61.52% | 12.04% |
| 3 | 85 | 65.84% | 15.09% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, M.; Zhang, Z.; Chen, Y.; Qu, X.; Yan, P.; Wang, H. Economic Operation of Variable Speed and Blade Angle-Adjustable Pumping Stations of an Open-Channel Water Transfer Project. Water 2023, 15, 3571. https://doi.org/10.3390/w15203571
Du M, Zhang Z, Chen Y, Qu X, Yan P, Wang H. Economic Operation of Variable Speed and Blade Angle-Adjustable Pumping Stations of an Open-Channel Water Transfer Project. Water. 2023; 15(20):3571. https://doi.org/10.3390/w15203571
Chicago/Turabian StyleDu, Mengying, Zhao Zhang, Yichao Chen, Xieyu Qu, Peiru Yan, and Hao Wang. 2023. "Economic Operation of Variable Speed and Blade Angle-Adjustable Pumping Stations of an Open-Channel Water Transfer Project" Water 15, no. 20: 3571. https://doi.org/10.3390/w15203571
APA StyleDu, M., Zhang, Z., Chen, Y., Qu, X., Yan, P., & Wang, H. (2023). Economic Operation of Variable Speed and Blade Angle-Adjustable Pumping Stations of an Open-Channel Water Transfer Project. Water, 15(20), 3571. https://doi.org/10.3390/w15203571







