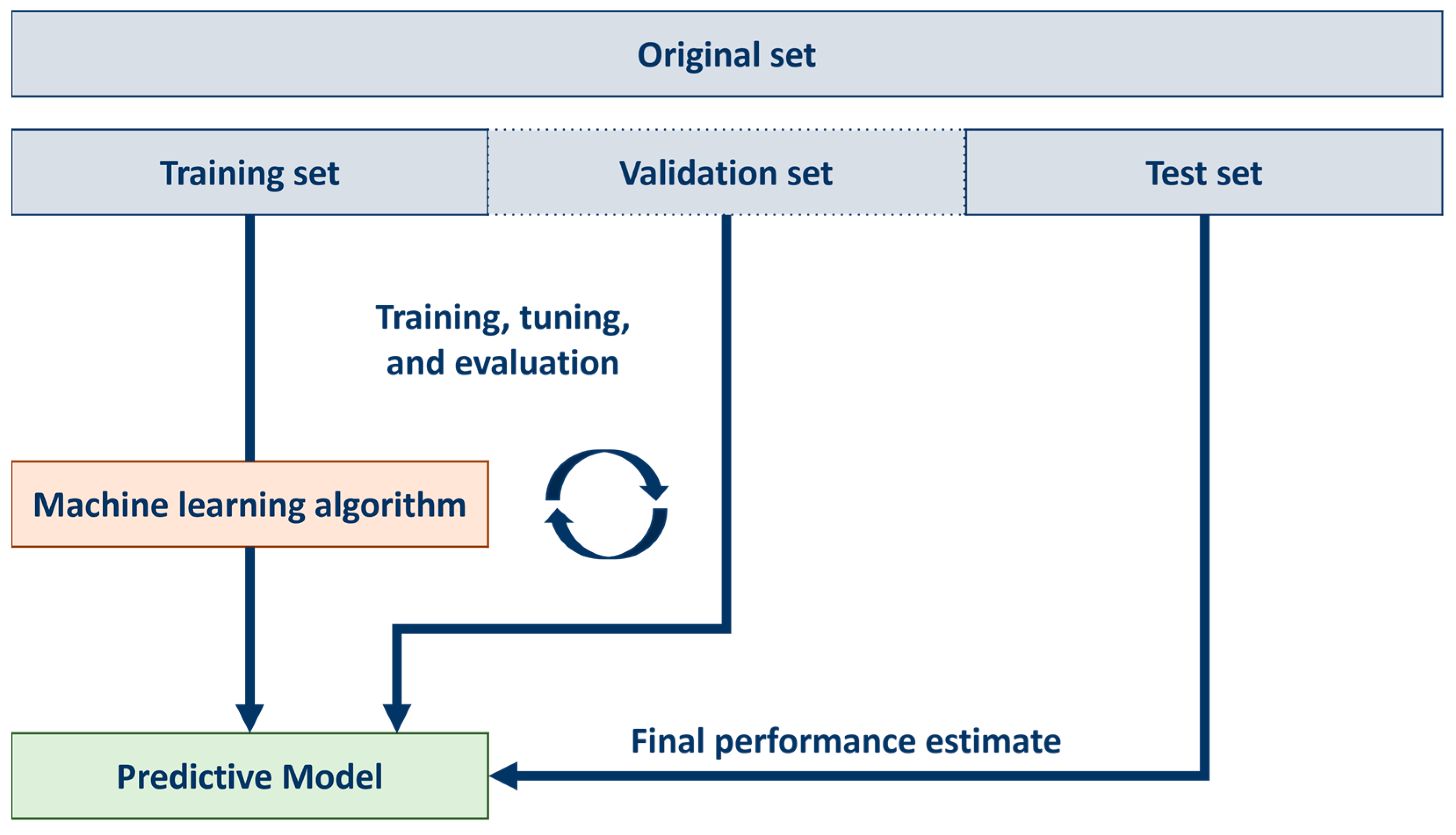
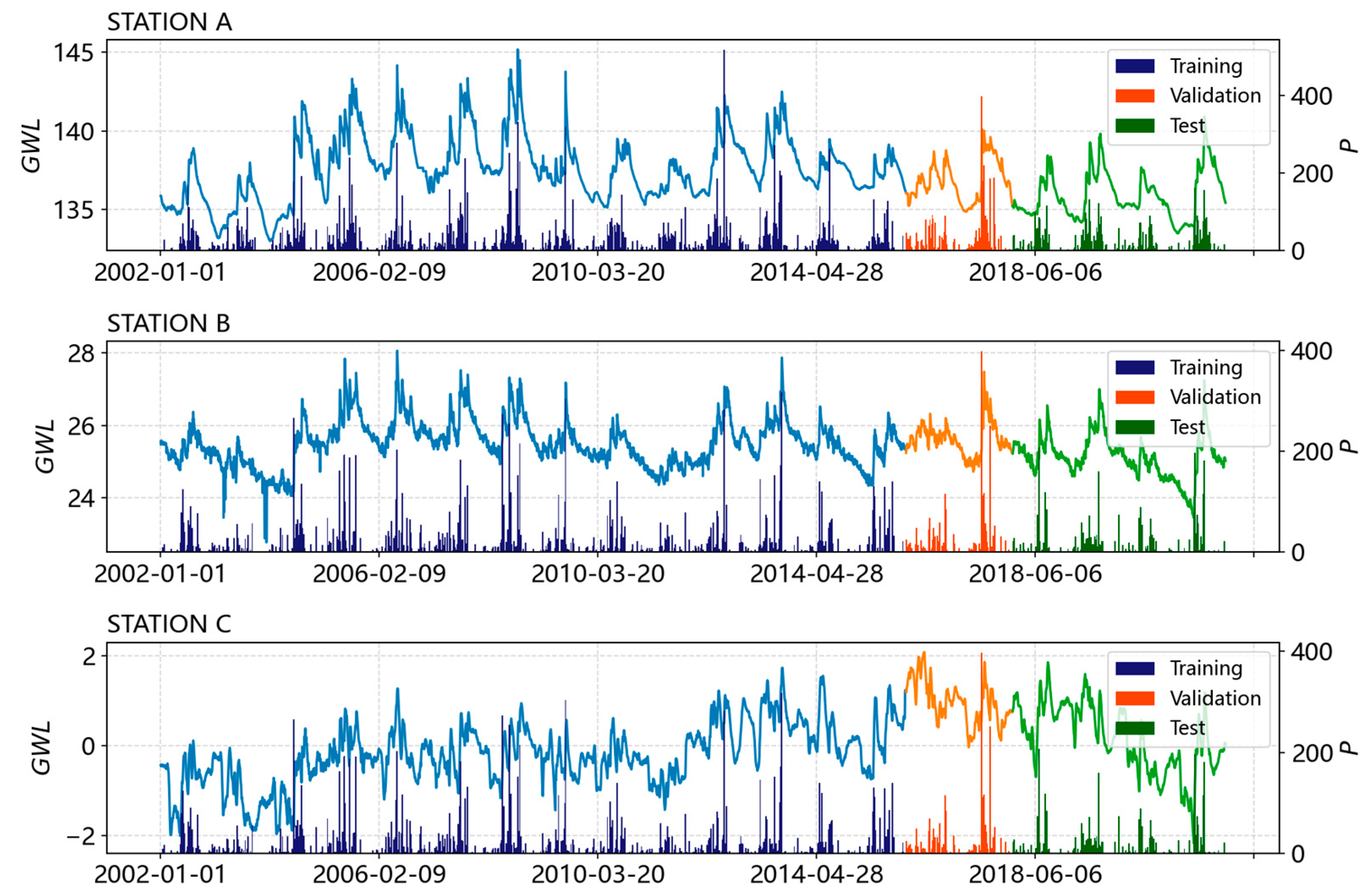
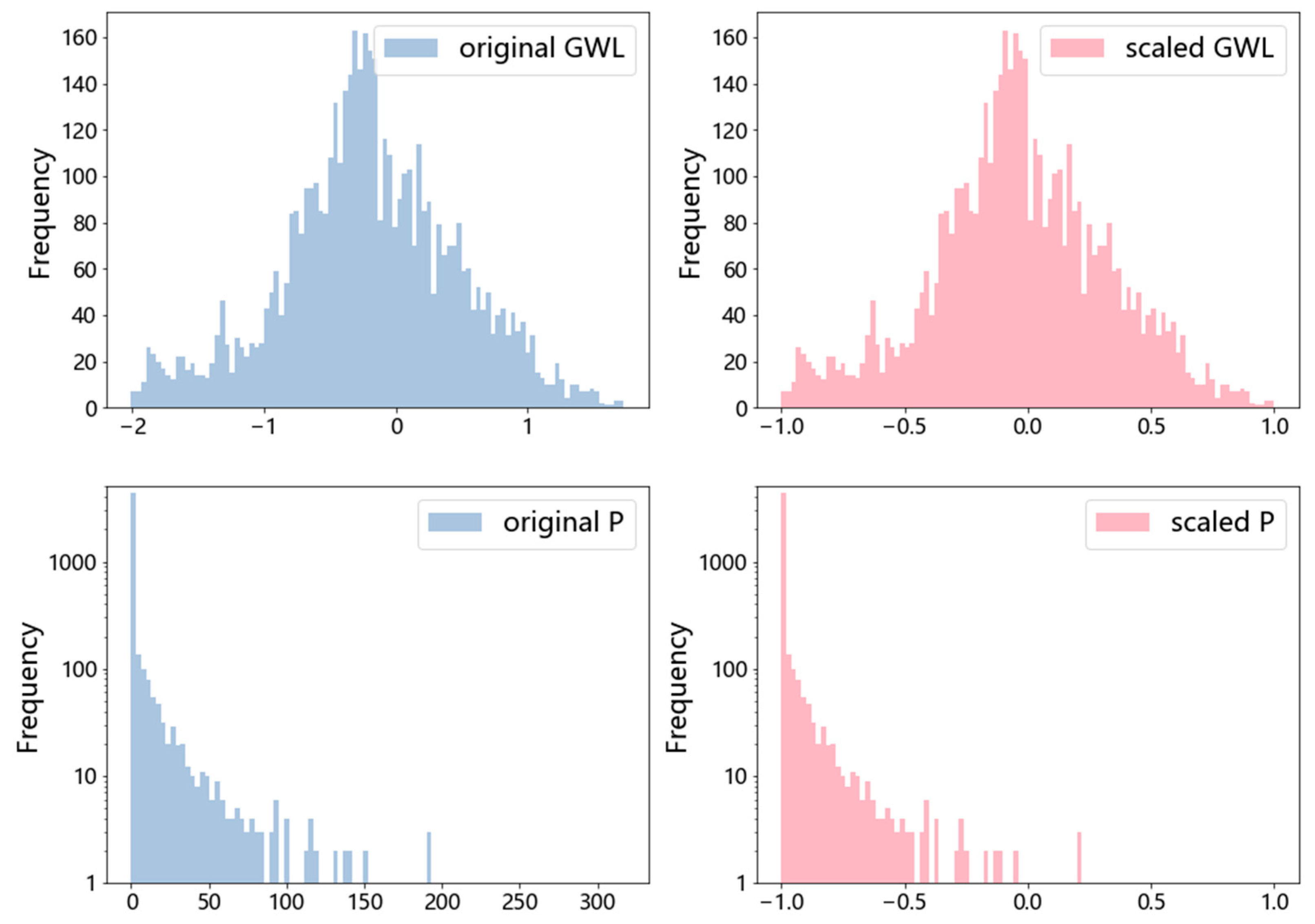
1. Introduction
Due to its geographical and hydrological environment, Taiwan has suffered from insufficient water resources [
1]. An insufficient supply of surface water is conventionally supported with groundwater. However, groundwater is a resource that accumulates over many years. Furthermore, excessive extraction of groundwater leads to land subsidence [
2,
3,
4,
5,
6,
7,
8]. Hence, there remains a need to perform long-term water management. To be able to effectively allocate water resources, groundwater levels must be accurately predicted.
During the process of data collection, data may be missing due to various factors. Therefore, dealing with missing data is a challenge that needs to be overcome in any research field. To maintain data integrity, the missing value imputation (MVI) method is often chosen as a solution. Many missing value imputation methods lack validation. Thus, many studies have utilized machine learning techniques, simulating the learning process of neural networks, to impute missing values. Results have shown that model-based machine learning methods are more effective. Currently, artificial neural networks (ANNs) are widely used in hydrological research as an important tool for groundwater management. However, in recent decades, the thrust of artificial intelligence has gradually changed from machine learning to deep learning [
9]. Missing data is a problem that must be overcome in any research field. In recent years, research on using machine learning to supplement missing value imputation has gradually increased. In 2011, Buuren et al. [
10] applied the MICE framework to a machine learning model and confirmed that the hybrid framework incorporated into the deep learning model can increase accuracy. Stekhoven et al. [
11] established MissForest with a machine learning framework, labeled the data as a test set and training set, and achieved good simulation results.
Imputation models can be divided into discriminative models and generative models. Candes et al. [
12] used matrix completion to restore a low-rank matrix identification model but could not handle sparse matrices with missing data. The denoising autoencoder (DAE) proposed by Vincent et al. [
13] is a generative model. Although it has the ability to resist noise, it cannot handle data with a large amount of information. To solve the disadvantages of the two categories, in 2014, Goodfellow et al. [
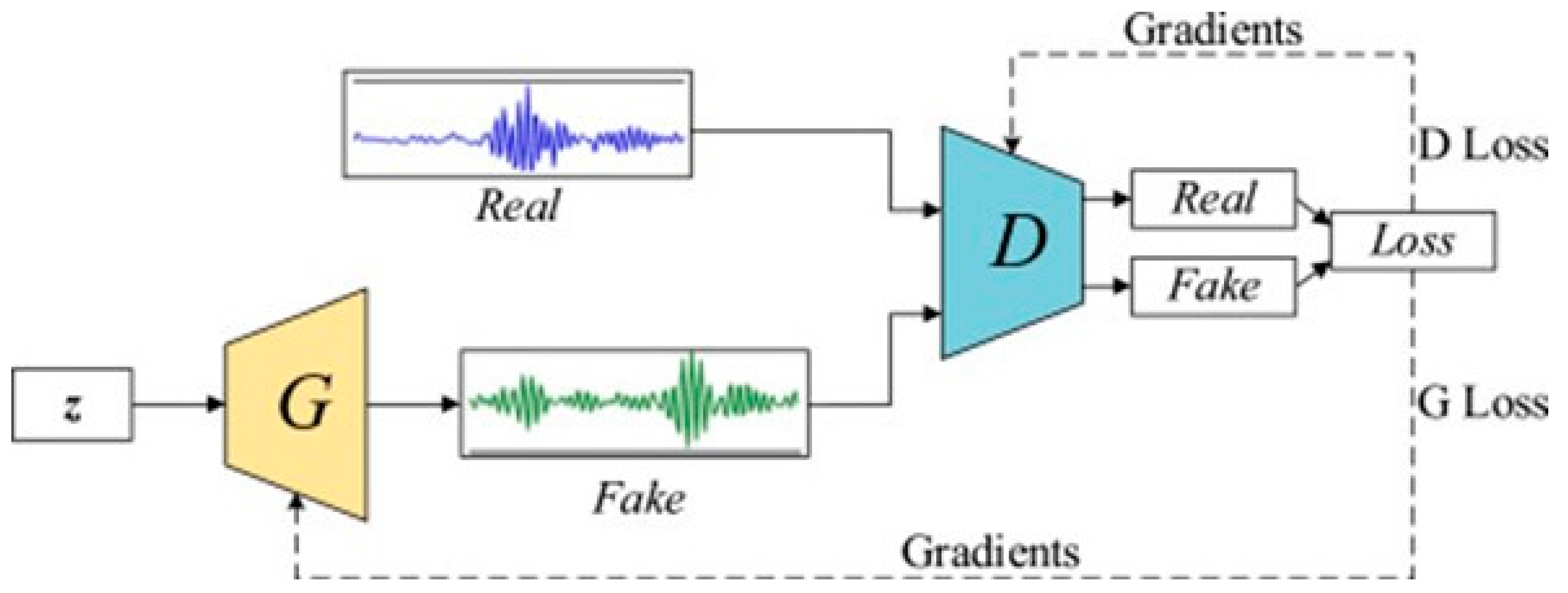
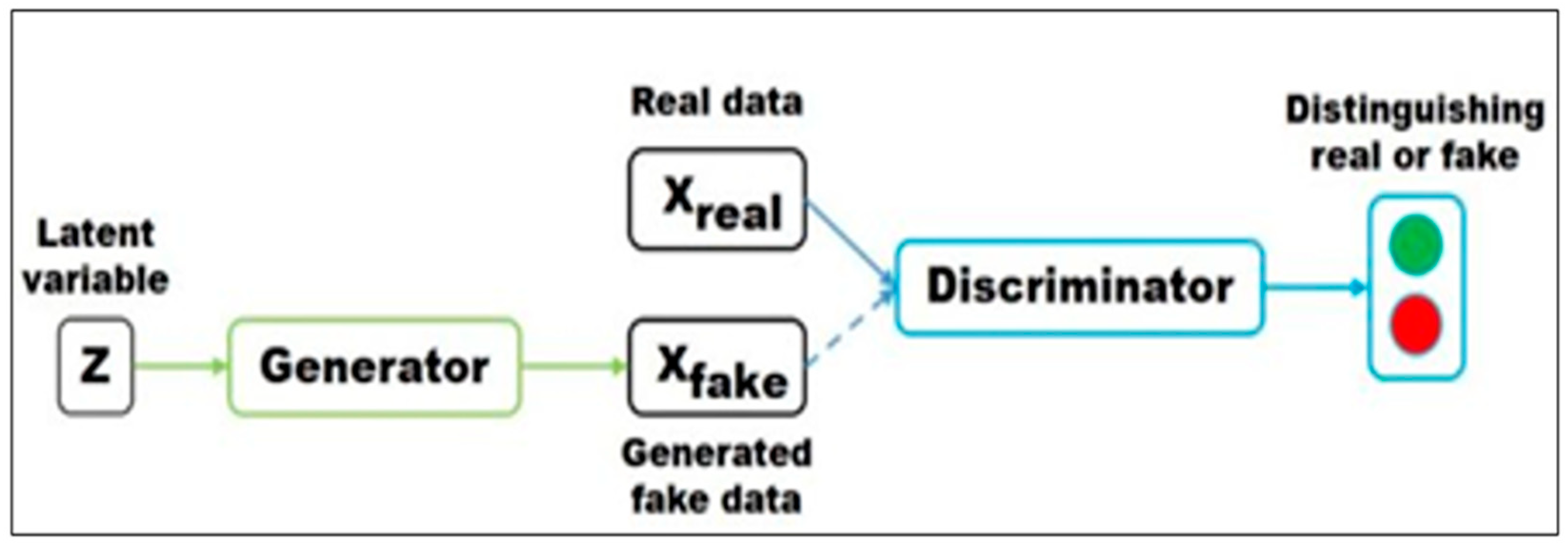
14] created the generative adversarial network (GAN), combining properties of the generative model and discriminative model, as shown in
Figure 1. The two networks compete against each other to achieve Nash equilibrium, which greatly reduces the amount of data needed. It is the first network architecture capable of unsupervised deep learning.
Data missingness can be categorized into three types based on likelihood: missing completely at random (MCAR), missing at random (MAR), and missing not at random (MNAR). In the case of groundwater level data, they fall under the MCAR category. This aligns with the focus of GAIN [
15], which is specifically designed for this type of data. The study employs a framework with a priors (hints) mechanism to address the missing value situation in groundwater hydrology.
Figure 1.
GAN model (source: Pan et al. [
16]).
Figure 1.
GAN model (source: Pan et al. [
16]).
In the past, predecessors utilized widely applied physical models such as the Soil and Water Assessment Tool (SWAT) [
17,
18,
19] and the modular three-dimensional groundwater flow model (MODFLOW) [
20,
21] to predict groundwater levels. In many cases, the lack of physical awareness of implicated processes might create problems in finding applicable models [
22], and two additional barriers are the significant computational demands and the requirement for extensive hydrogeophysical data [
23,
24]. As a result, the modeling process remains fraught with uncertainty and challenges [
25]. Moreover, under comparable simulation conditions, the modeling performance of ANNs surpasses that of MODFLOW [
26]. Over the last decades, ANNs have sparked growing interest among researchers in various water resource issues and have obtained encouraging results [
27,
28,
29,
30], and numerous studies have employed various soft computing techniques such as a self-organizing map (SOM), an adaptive neuro-fuzzy inference system (ANFIS), GMDH, a supervised committee machine with artificial intelligence (SCMAI), boosted regression trees (BRT), and Bayesian networks (BNs) to simulate time series. For instance, ANNs have been utilized for predicting groundwater level time series [
31,
32,
33,
34,
35], estimating hydrogeological groundwater contamination, comprehending inter-annual dynamics of recharge [
36,
37,
38], and capturing the influence of controlling factors on these processes [
39,
40].
Research on time series prediction began with regression equations, such as the autoregressive–moving average (ARMA) and autoregressive integrated moving average (ARIMA) models, which are the most basic modeling approaches [
41,
42]. However, achieving high-precision predictions for nonlinear data using complex models is challenging. Machine learning methods, on the other hand, can construct nonlinear models based on extensive historical data. Through iterative training and learning approximations, they can provide more accurate predictions compared with traditional statistical models. Typical methods include support vector machines (SVMs) [
43], ANNs, and ensemble learning methods [
44,
45]. However, these aforementioned techniques often lack the effective handling of dependencies between variables, leading to limited predictive effectiveness [
46].
Subsequently, LeCun [
47] confirmed that deep learning can effectively mitigate the interference of outliers during the process of data feature extraction, thereby leading to a significant enhancement in technical capabilities across various domains [
48,
49]. As we know, in 1982, Hopfield [
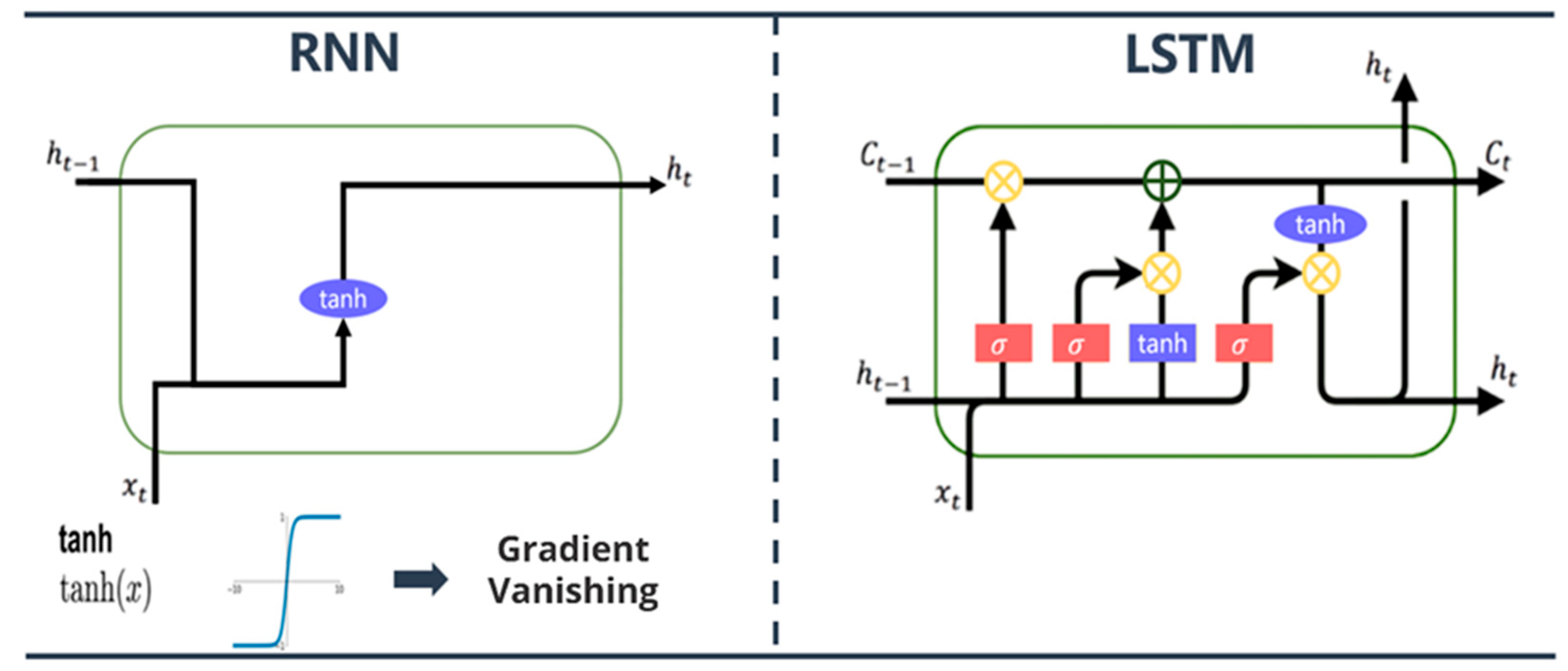
50] published a recurrent neural network (RNN) for sequence data, laying the foundation for deep learning models, and is often seen as the most efficient method of time series prediction. However, RNNs have vanishing gradients and exploding gradients in the process of backward transmission and cannot memorize long sequences. To improve the RNN problem, Hochreiter and Schmidhuber [
51] developed long short-term memory (LSTM) to improve memory function, which is considered one of the most advanced methods for addressing time series prediction problems [
52]. Hence, this study incorporated LSTM to simulate daily water levels.
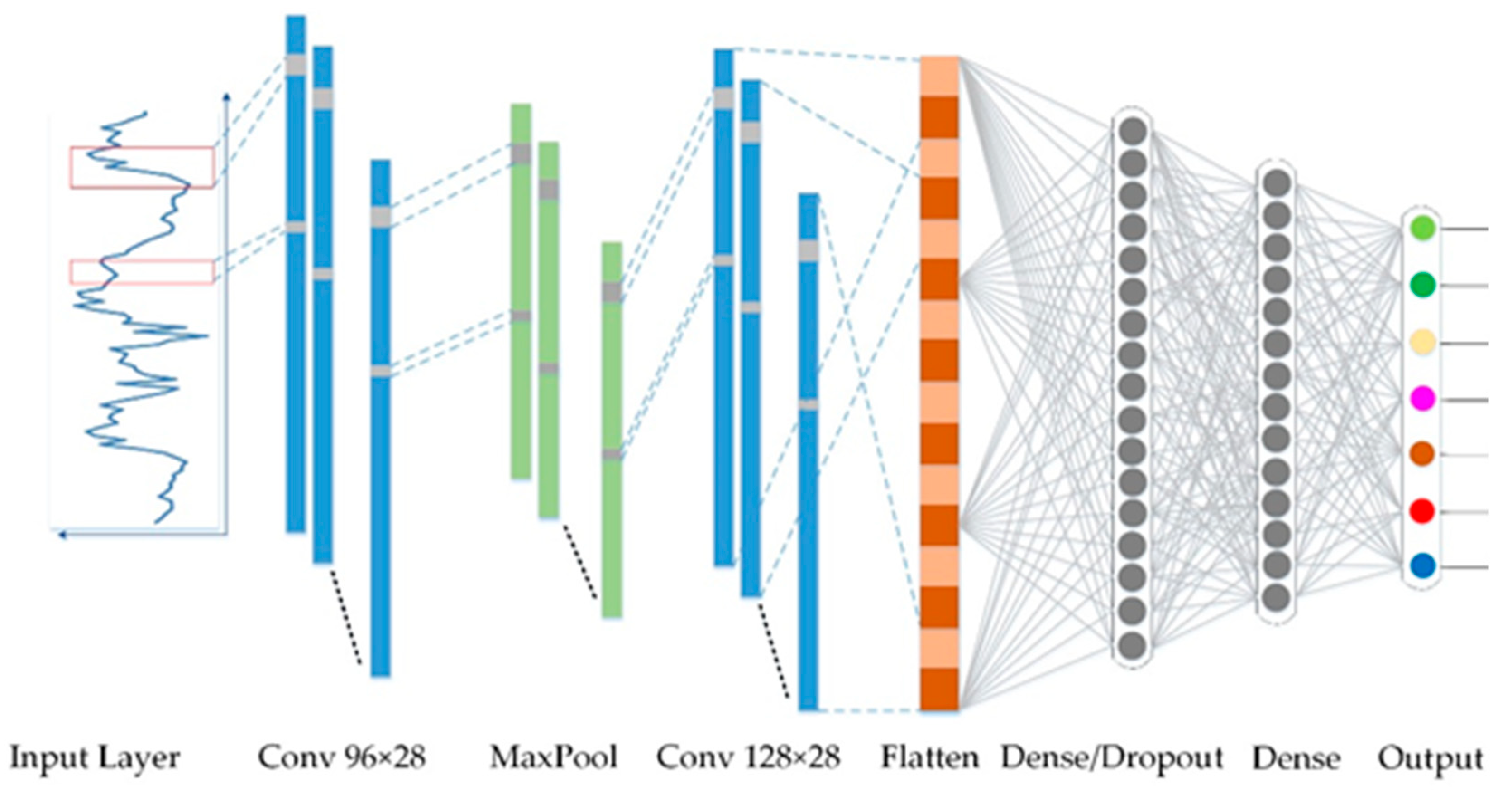
In addition, LeCun et al. [
53] combined the neocognitron to propose a convolutional neural network (CNN) and then applied the model to a one-dimensional CNN with Bengio et al. [
54]. Learning features from sequence data gradually allows the network to achieve excellent performance in signal data and natural language. A CNN mainly extracts spatial information from image-like data, while LSTM was developed for sequence data. In this study, LSTM and a CNN were used to simulate water levels, and the differences between the two methods were compared. This study is expected to reduce the limitations of sequence data research methods and provide more possibilities for water resources research. Therefore, to address the problem of missing hydrological observation data, the purpose of the present study is to use a GAN for imputation. Complete hydrological data can improve the accuracy of groundwater level prediction. Accordingly, the performance of groundwater level prediction was compared using two interdisciplinary methods. One is the LSTM model specially developed for sequence data, while the second model is a CNN, which is good at processing image information.
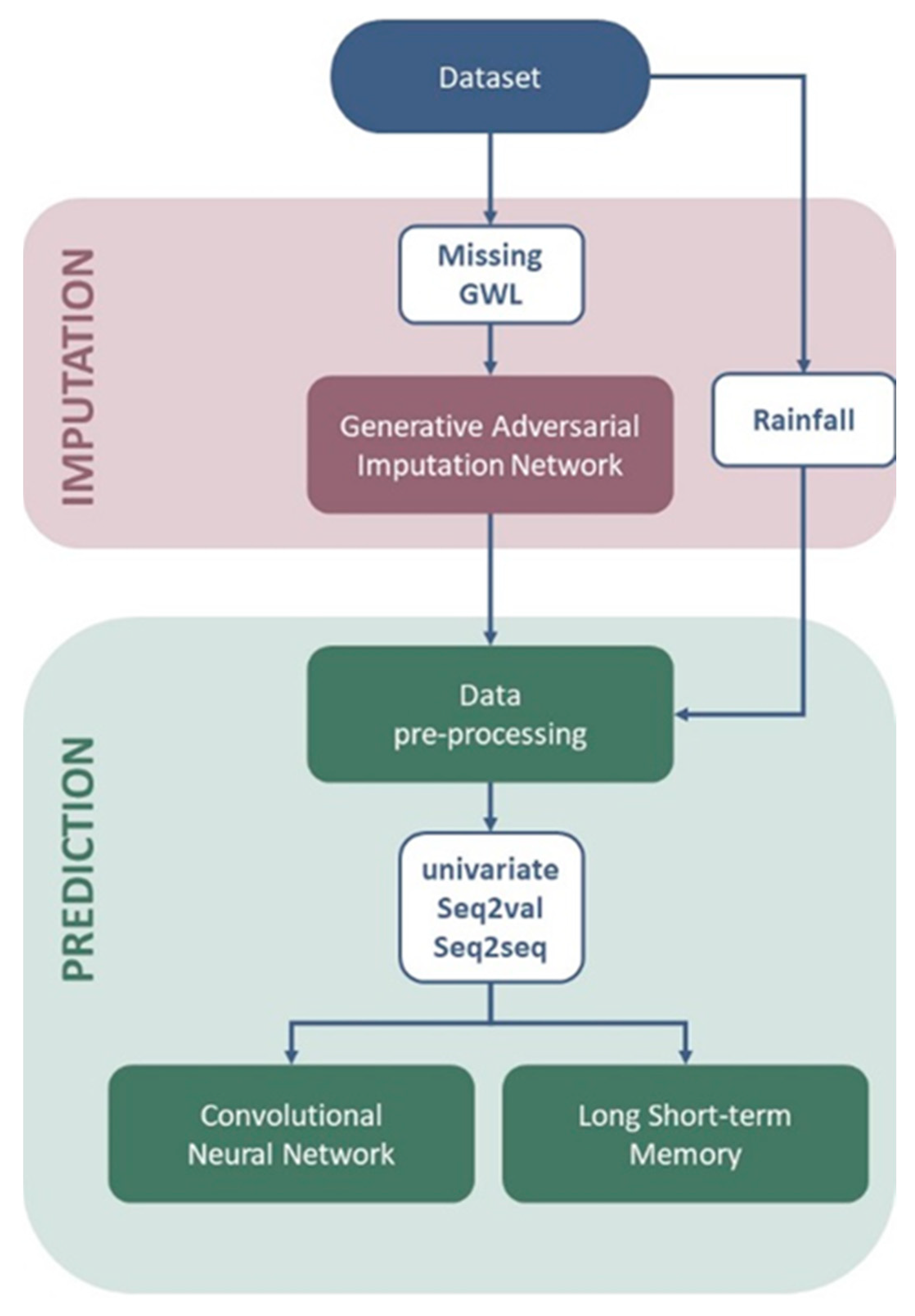
Figure 2 shows the flow of the entire research.
4. Conclusions
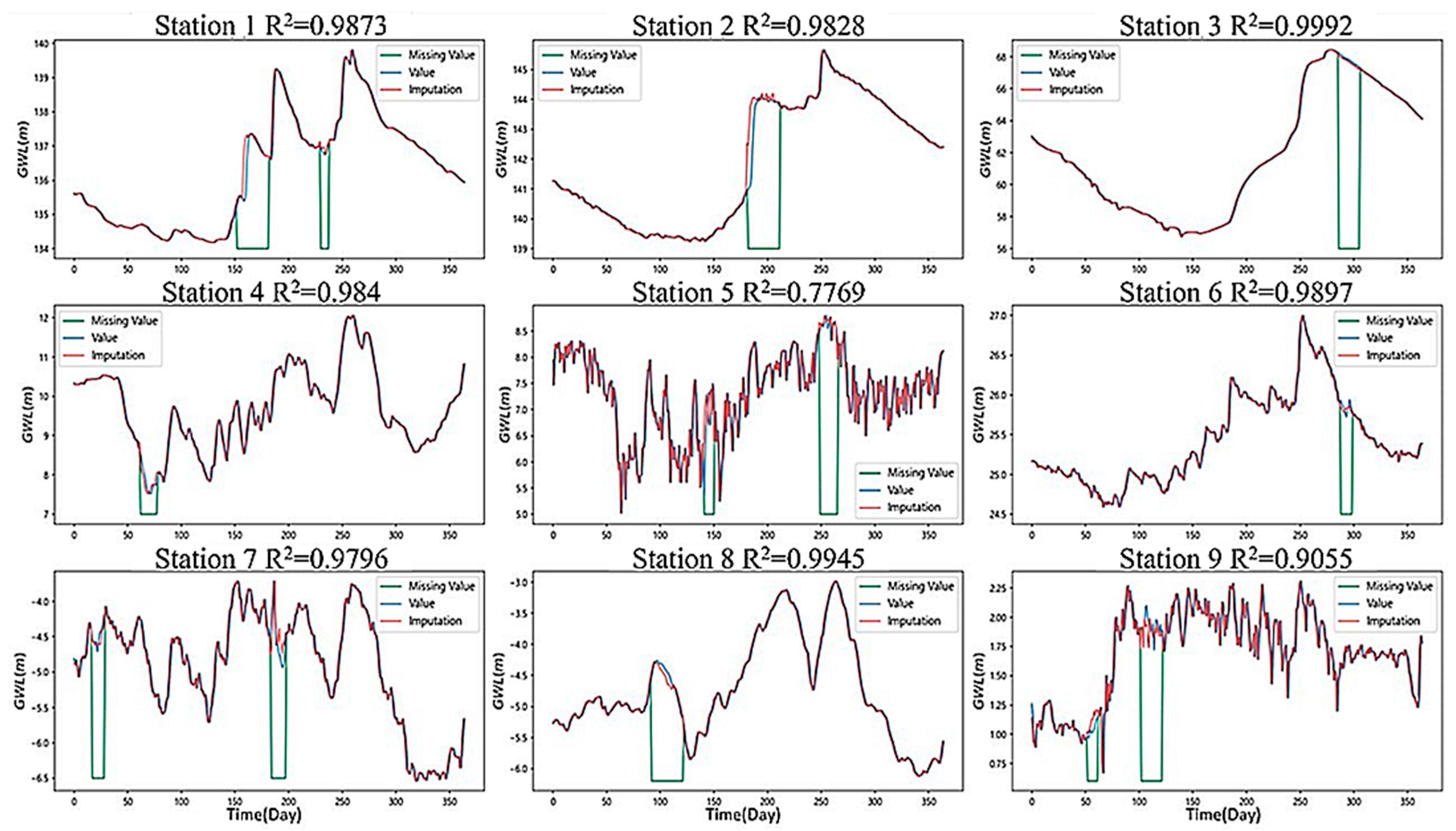
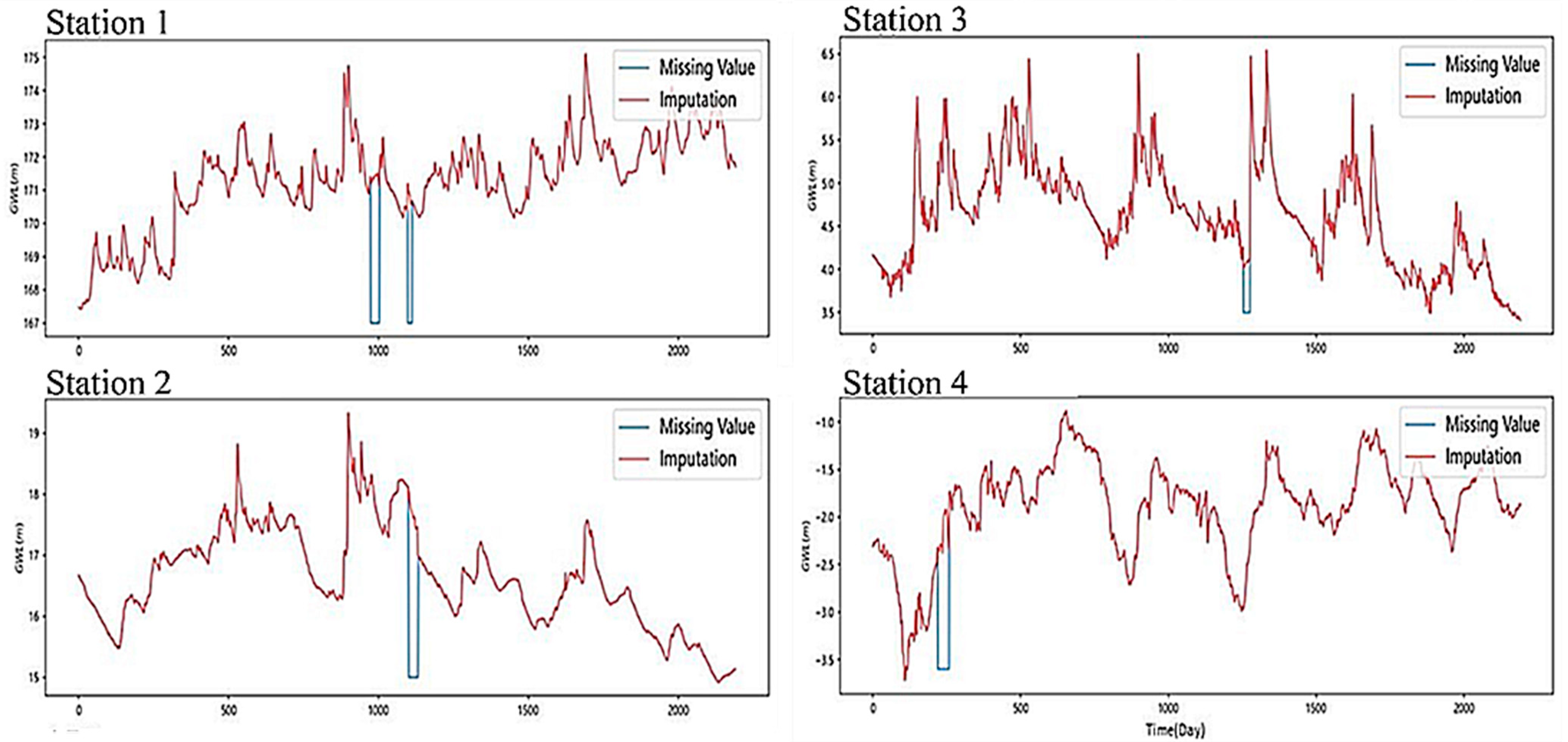
The imputation method using a GAN is composed of a generative model and a discriminative model to fill in the missing data. Our results show that the trend of the sequence region could be reasonably simulated in the smooth section. Although some of the extreme values could not be captured in the undulating section of the groundwater level curve, there was still a certain trend so the feasibility of the model could be determined. Although the GAN could not capture the groundwater level endpoints in every section, the overall simulation performance was still excellent to some extent.
We note that if the characteristics of other models can be incorporated into the basis of the GAN architecture, the performance can be improved. Since the GAN was used in a section with drastic changes, it did not accurately capture the endpoint value. It is recommended to incorporate other mechanisms to strengthen the model to capture the change in the endpoint and improve the ability to respond faster in the sudden rise and fall section.
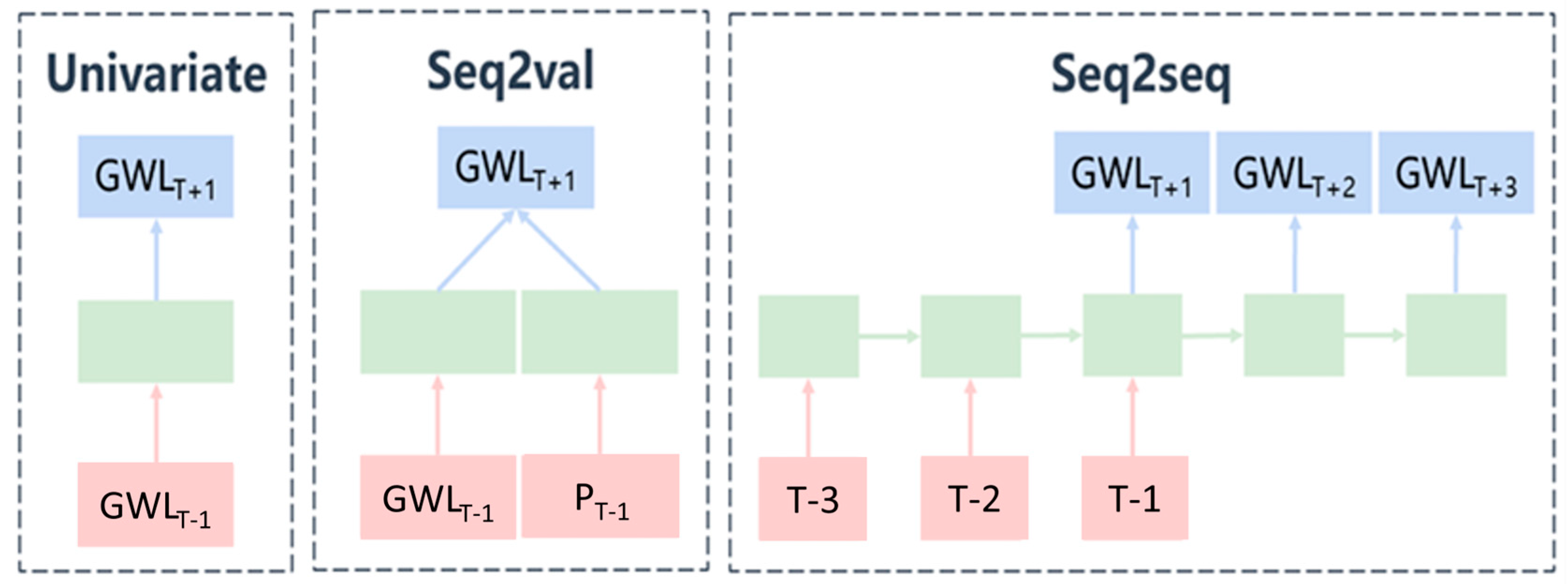
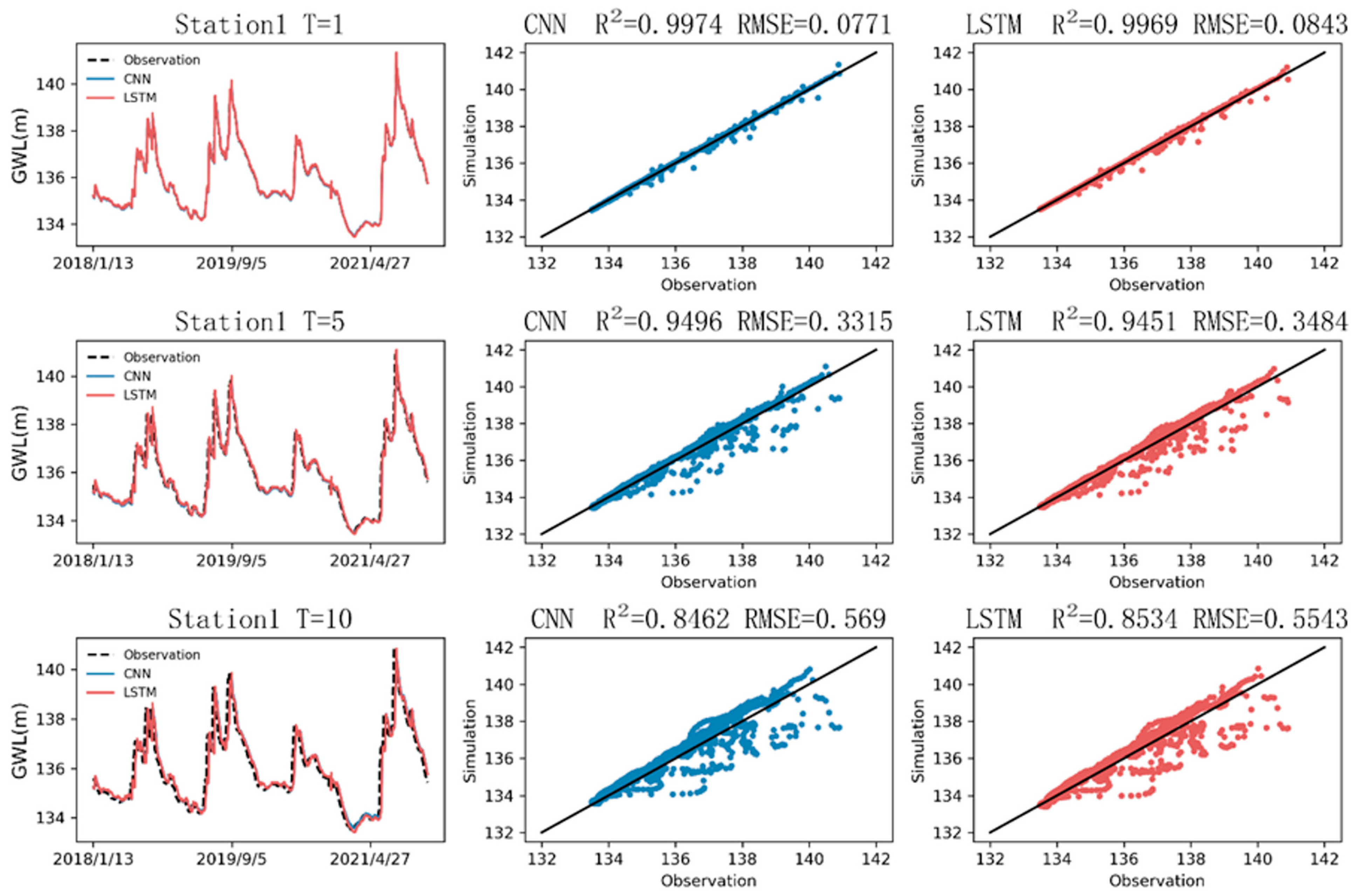
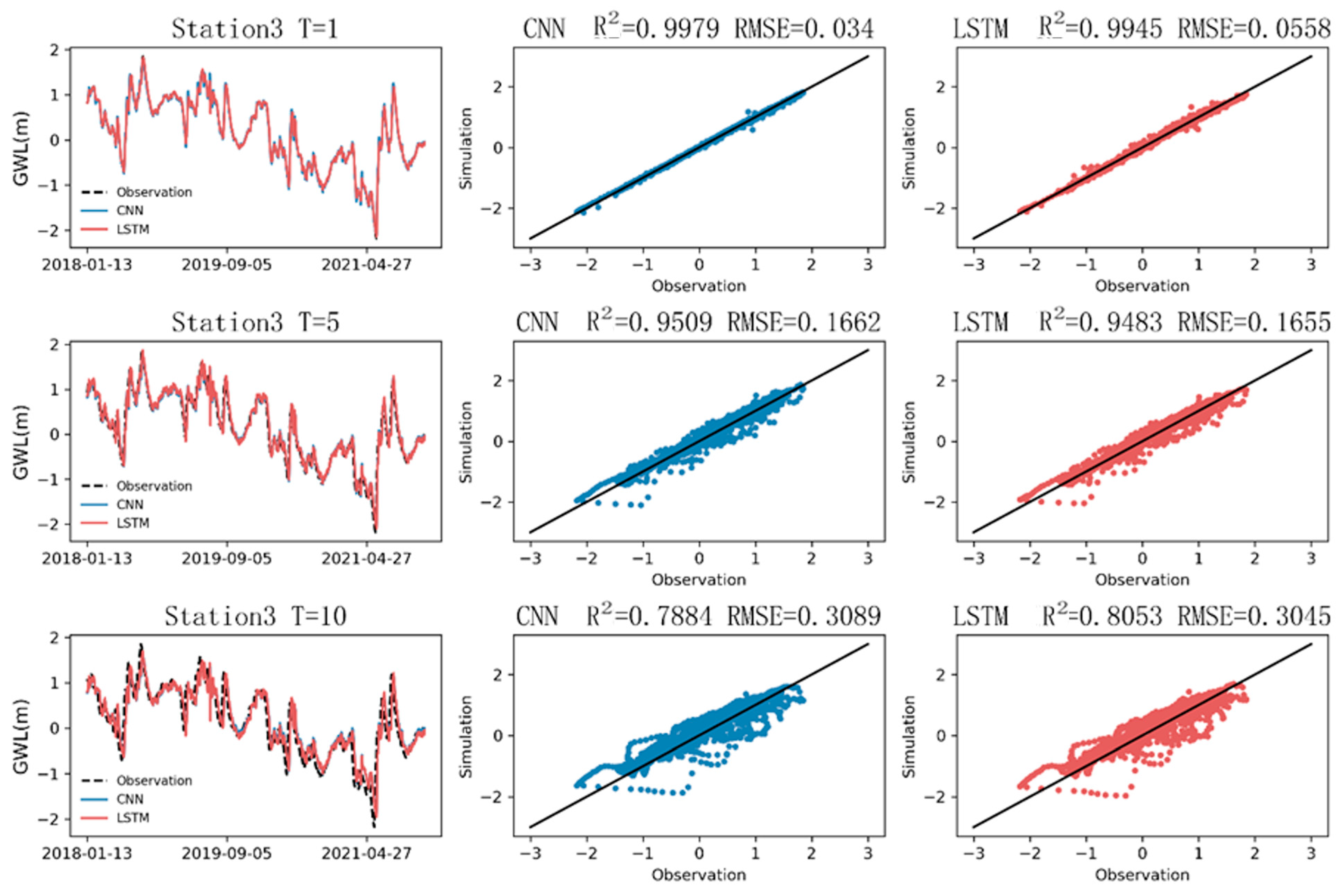
The CNN and LSTM were found to be excellent for hydrological estimation. The coefficient of determination for both was calculated to be approximately 0.99, as indicated in
Table 7, which also lists the values of the RMSE and MAE. Regarding the parameter selection, the simulation results of the univariate analysis (RMSE = 0.007 and MAE = 0.005) were better than those of the Seq2val analysis (RMSE = 0.0321 and MAE = 0.0194). Upon closer inspection, compared with LSTM (RMSE = 0.008 and R = 0.997), the CNN was shown to be slightly better in the evaluation indexes (RMSE = 0.007 and R = 0.998). Both models underestimated the long-term trend. The CNN outperformed LSTM for a shorter stride, but for a longer stride, the drop in accuracy in the CNN was observed to be faster than that in LSTM.
In hydrology, the hysteresis of rainfall recharge has been the subject of many research discussions. From the perspective of the hydrological simulation, the CNN, which is good at processing two-dimensional image information, was shown to be better in accuracy and speed. The model originally developed for 2D data still had good performance when applied to 1D data. Our results suggest that the interdisciplinary deep learning approach may be beneficial for providing a better evaluation of water resources. The accuracy of the CNN is better, while LSTM is better for the simulation of multistep prediction. It is recommended to combine multiple networks to improve their individual deficiencies. Trying to use other parameters to see if the accuracy can be improved is also one of the future research directions of hydrological information.