A Laboratory Simulation Experiment to Assess Permeability and Shear Strength of a Gravel Soil Colluvium
Abstract
:1. Introduction
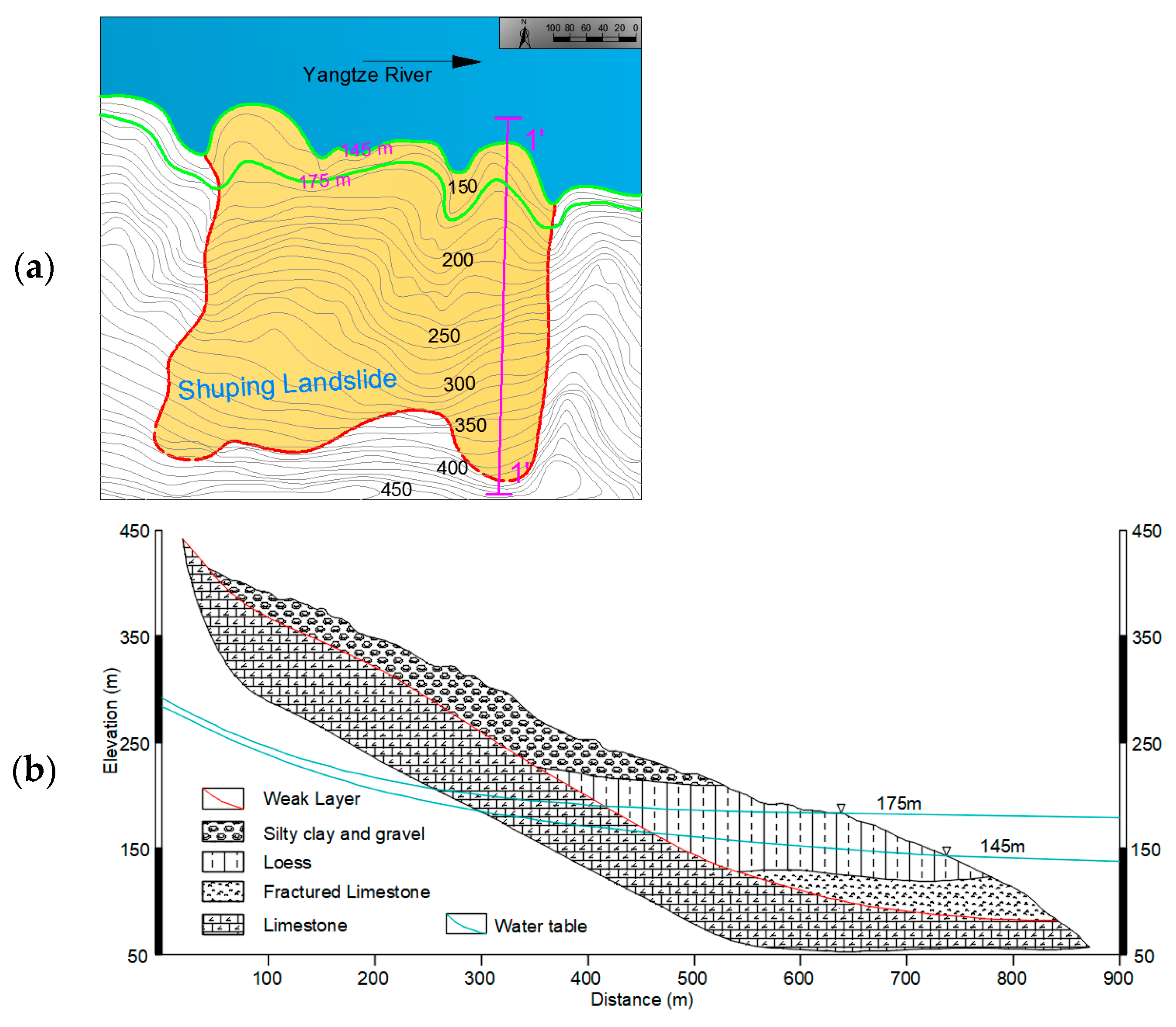
2. Brief Introduction to Shuping Colluvium Landslide
3. Test Plan
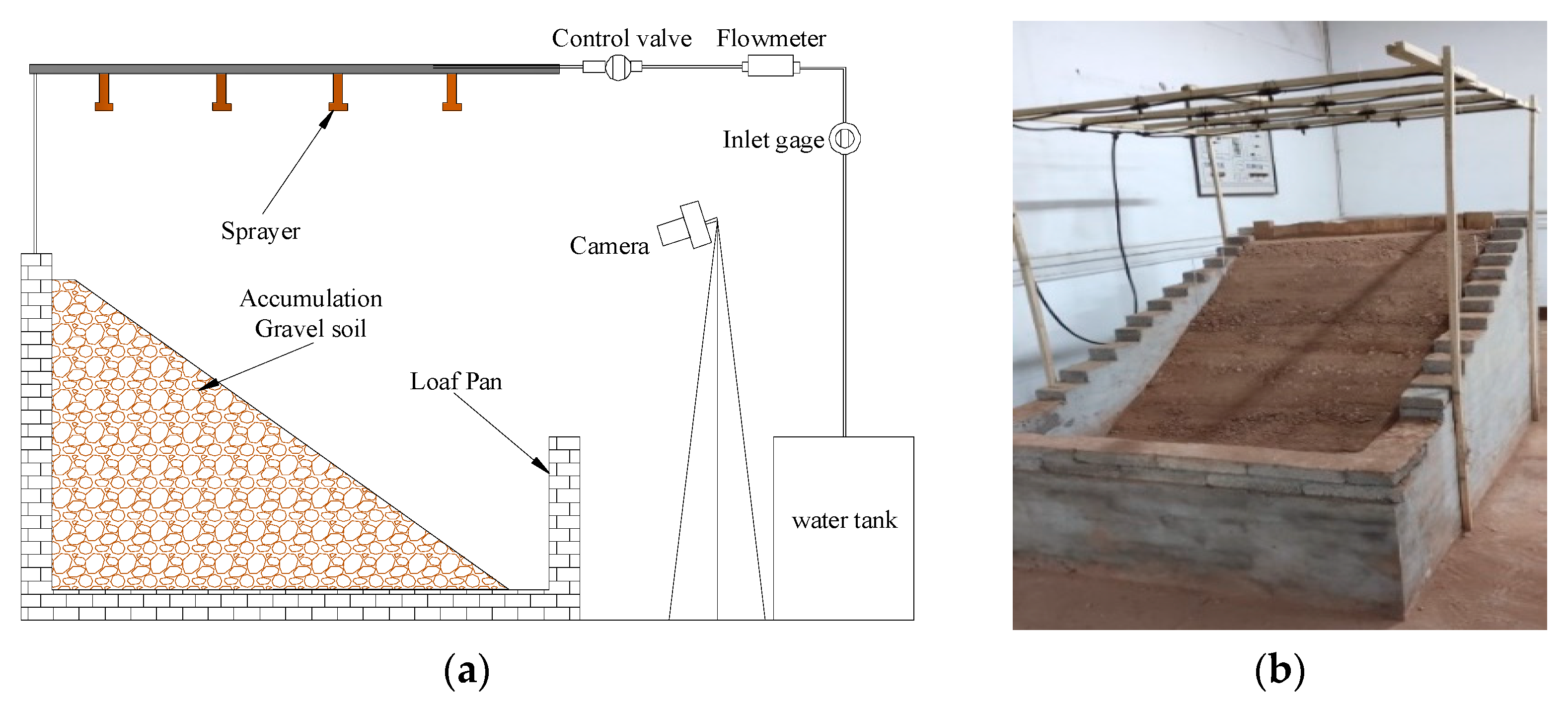
3.1. Model Test Apparatus
3.2. Model Test Material
3.3. Test Program
3.3.1. Rainfall Design
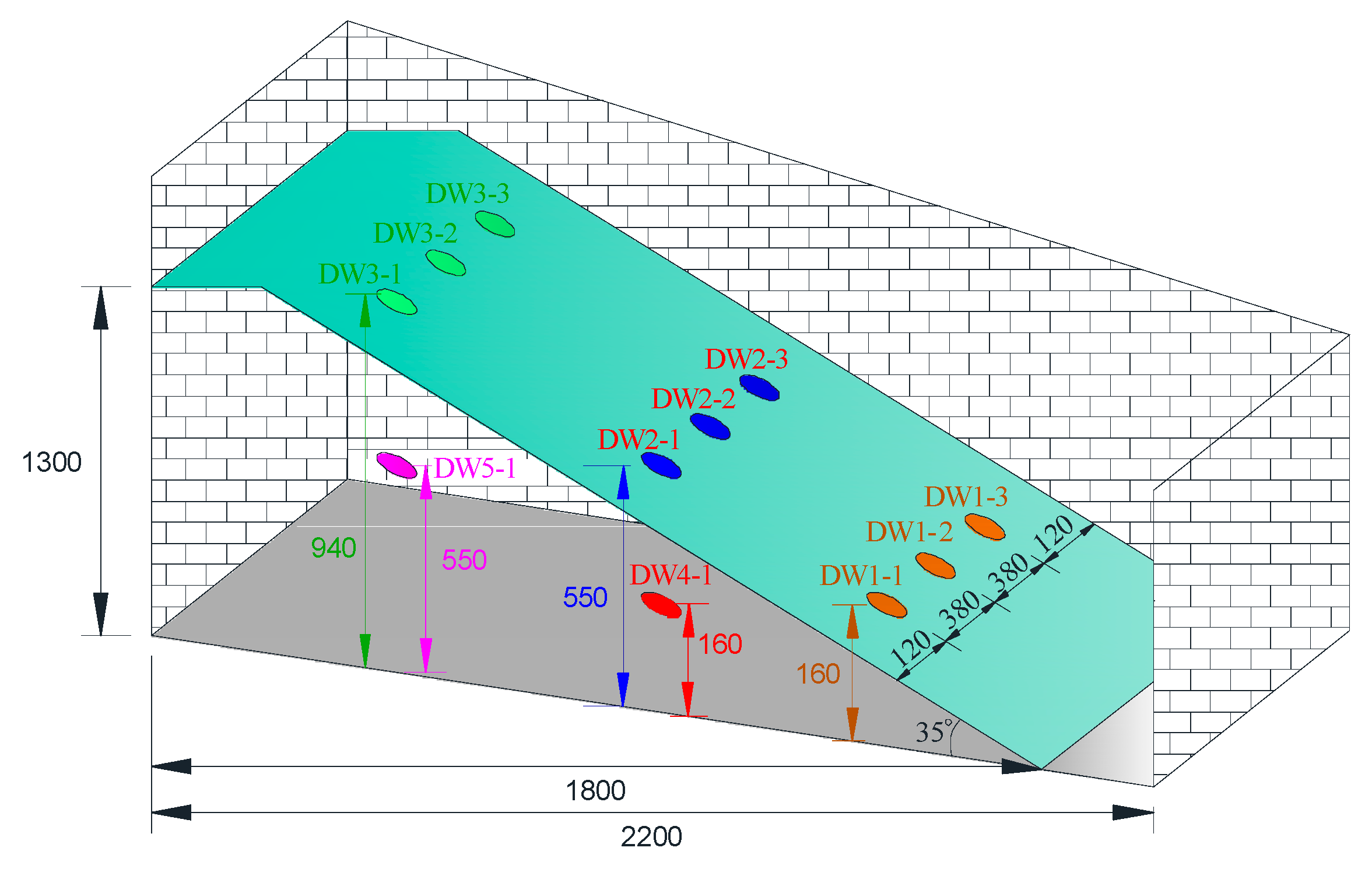
3.3.2. Sampling Point Layout
3.3.3. Test Scheme
4. Analysis of Test Results
4.1. The Deformation and Failure Characteristics of the Landslide Colluvium Model
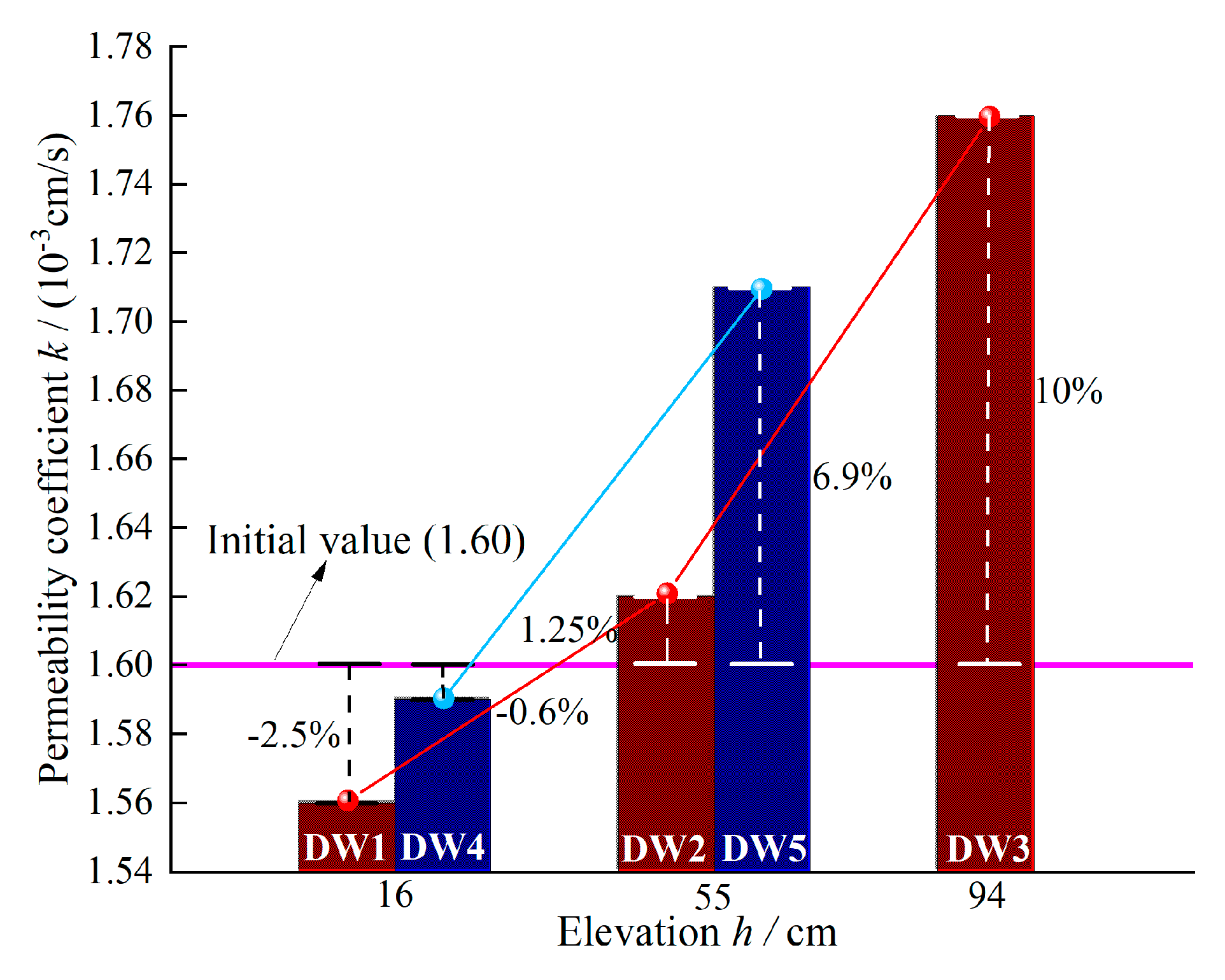
4.2. The Variation Law of Permeability along the Elevation
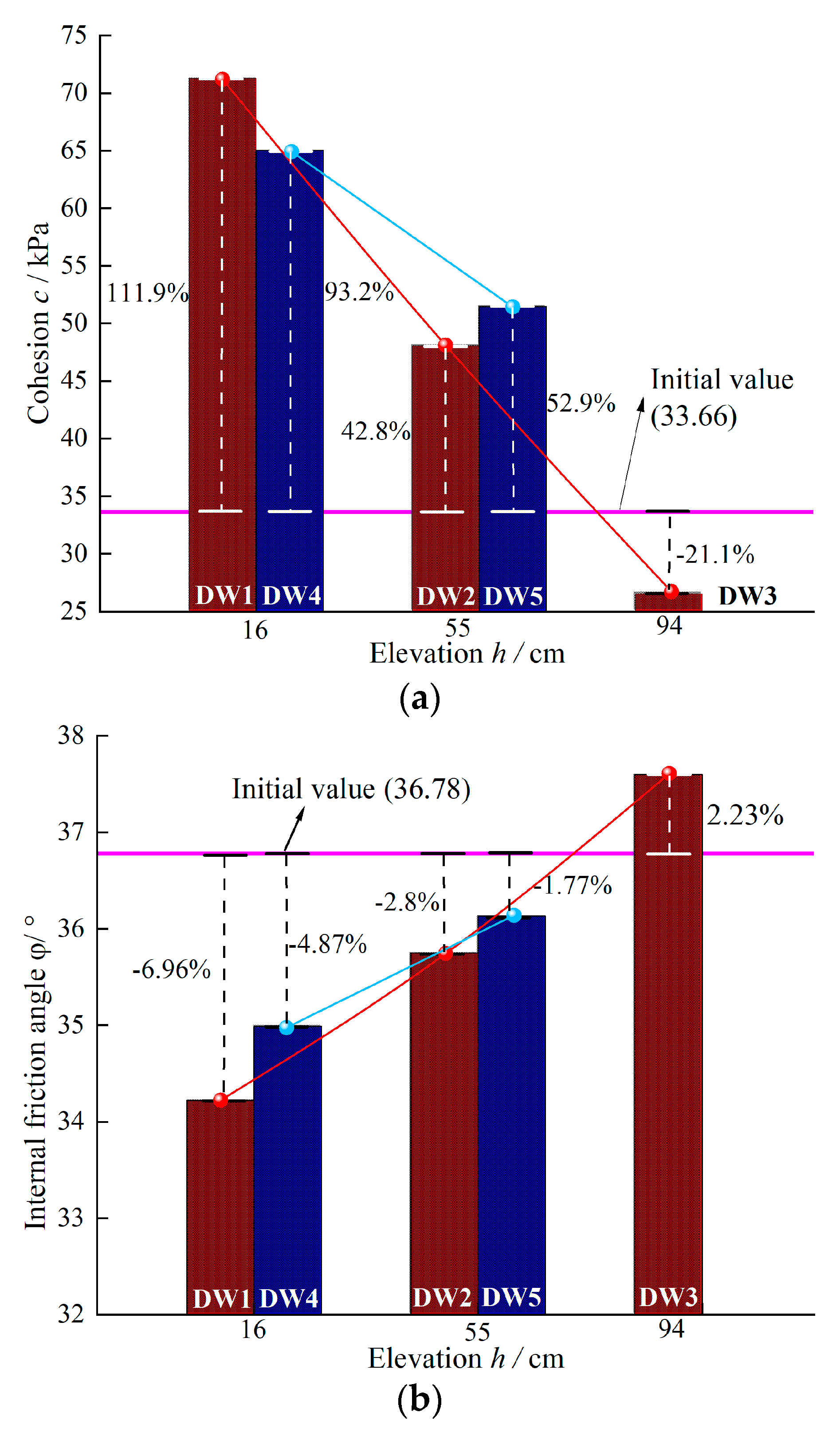
4.3. The Variation Law of Shear Strength Parameters along Elevation
5. Microscopic Analysis of the Variation of Particles in Colluvium along the Elevation
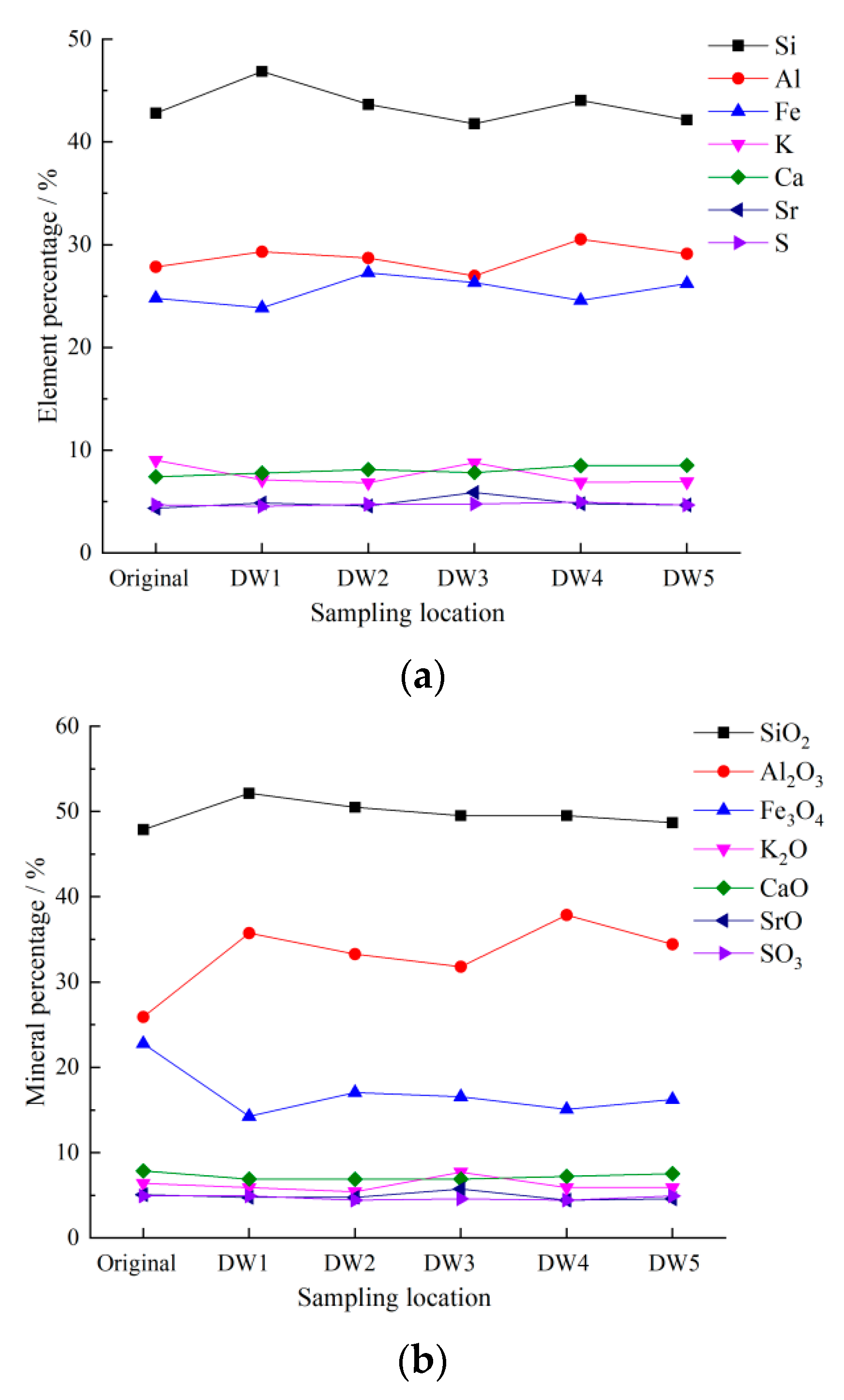
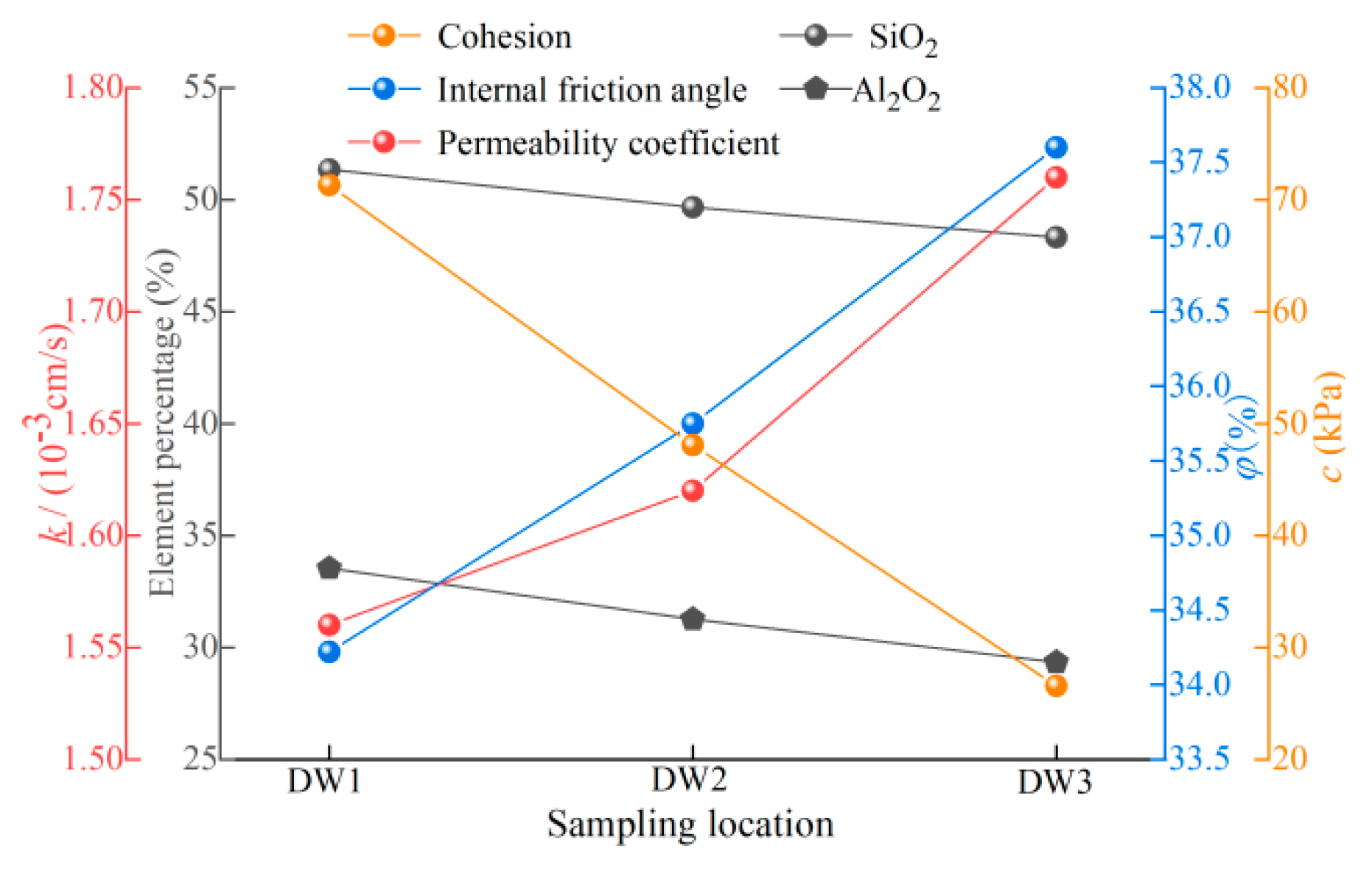
5.1. Variation Characteristics of Element and Mineral Content
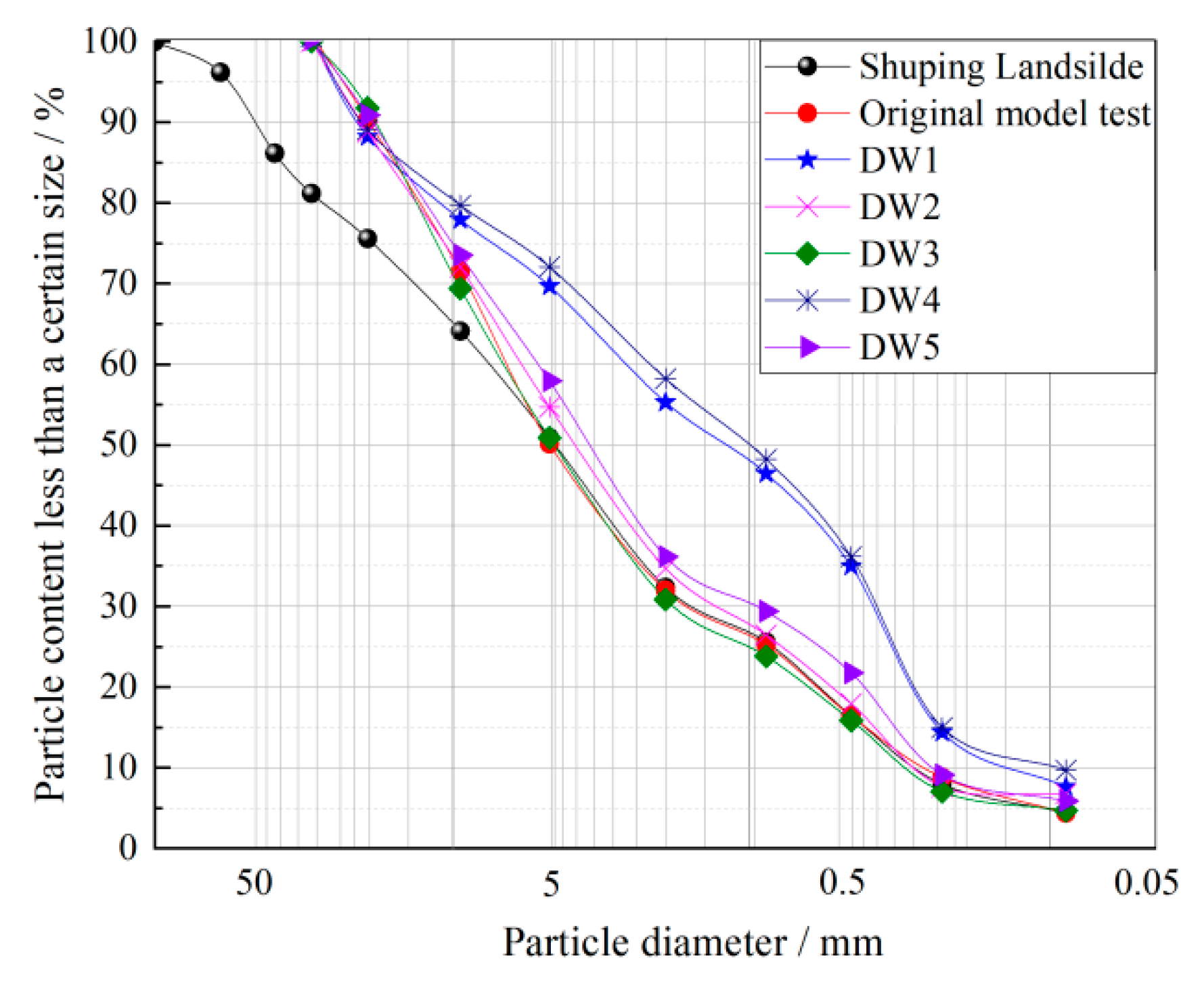
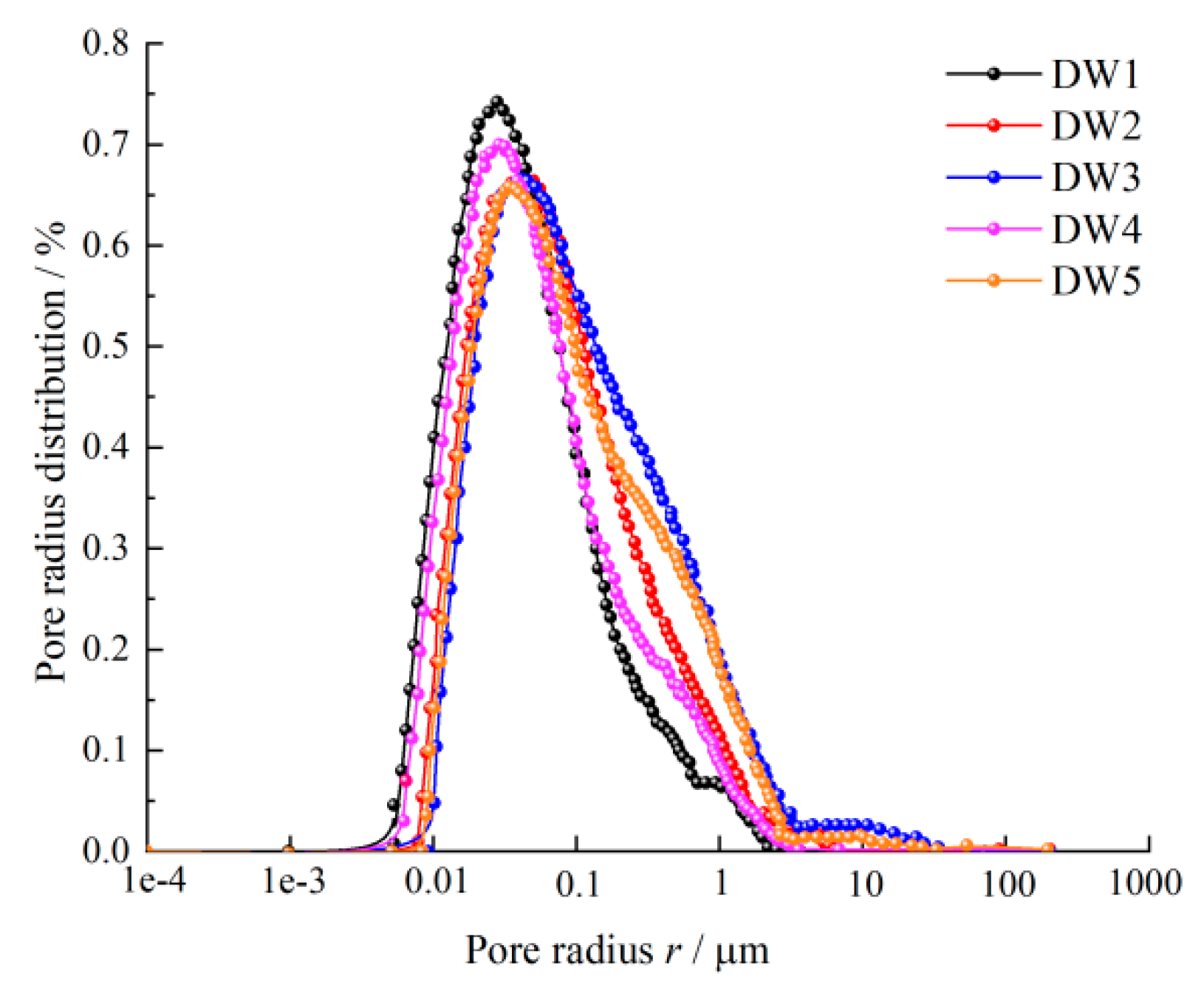
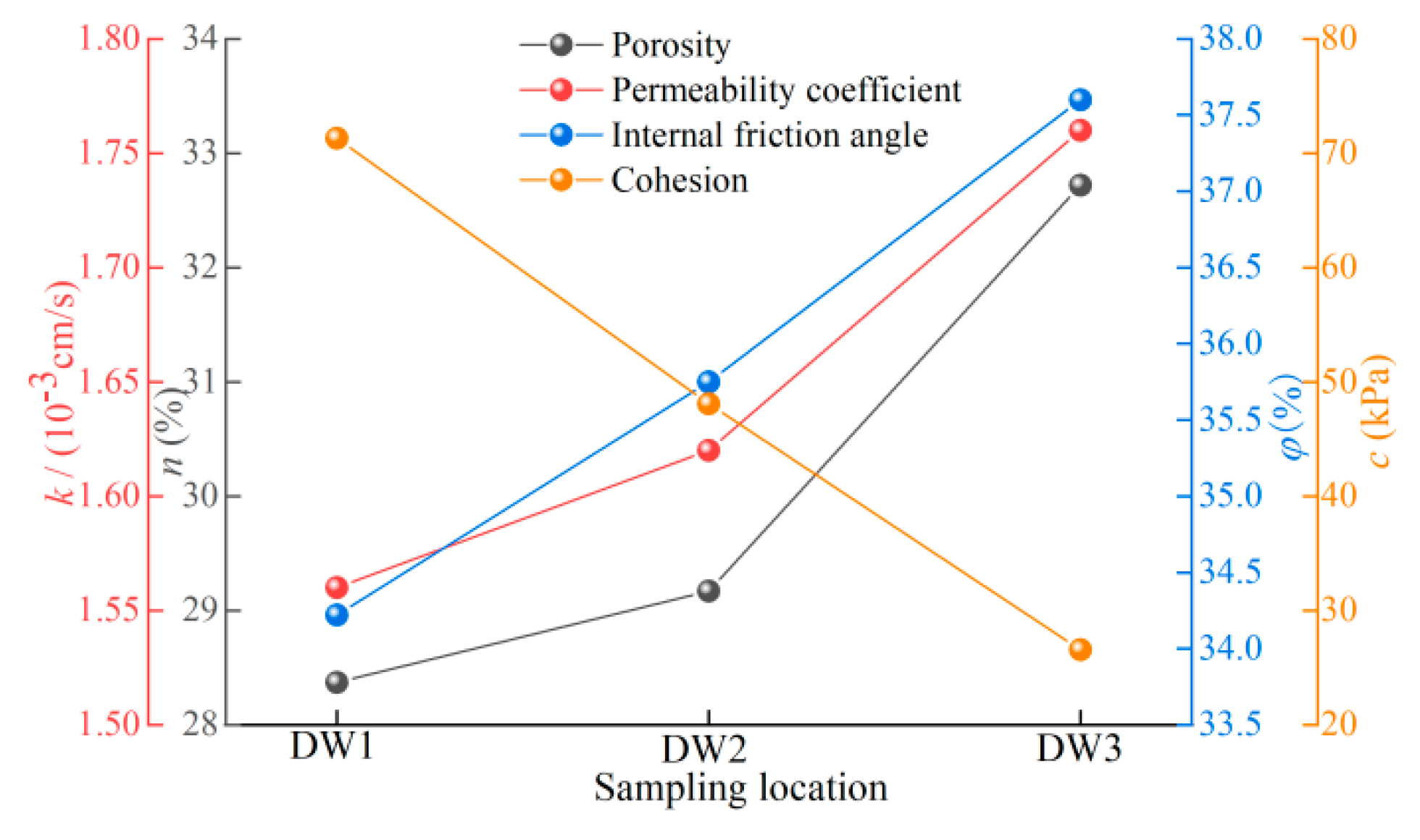
5.2. Particle Gradation and Porosity Variation Characteristics
5.3. Mechanism Analysis of Variation of Parameters along Elevation
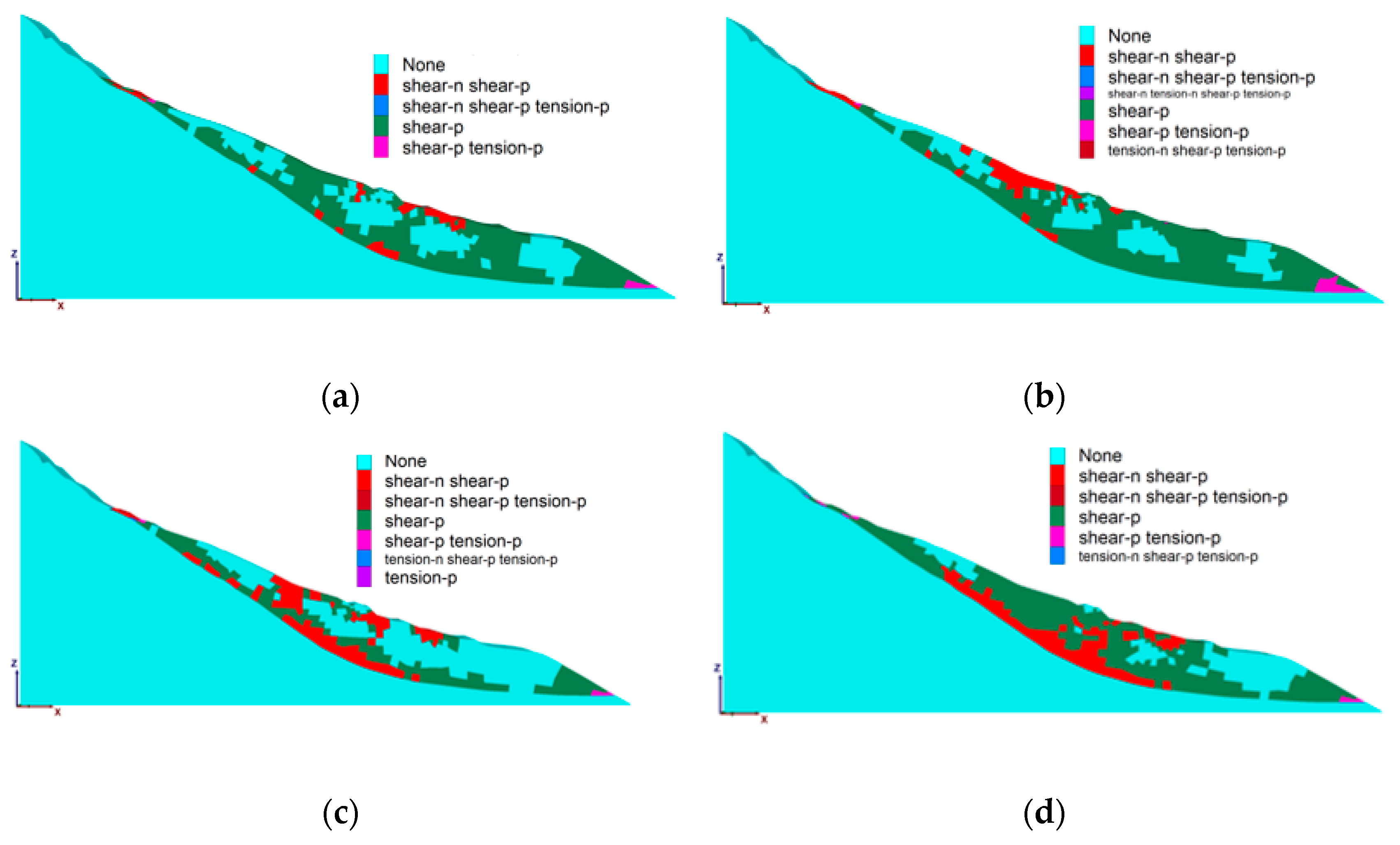
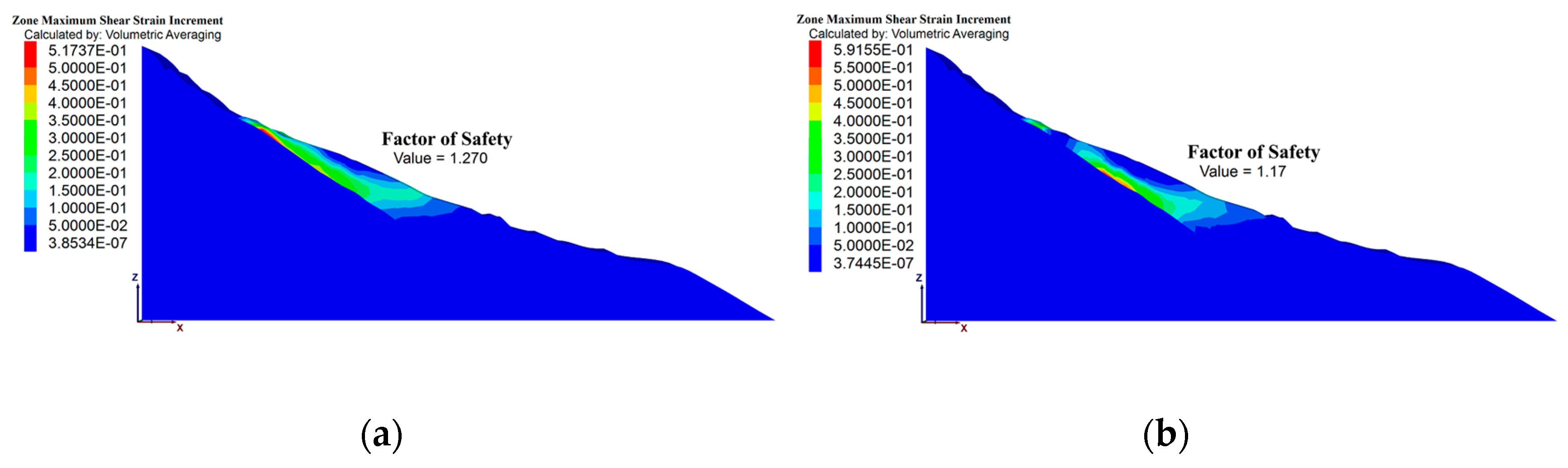
6. Analysis of Landslide Stability of Shuping Colluvium
7. Conclusions
- (1)
- Amidst intermittent rainwater seepage and runoff, notable alterations in the permeability and shear strength parameters of the colluvium transpire along the elevation gradient. With descent from the slope’s summit to its base, the permeability coefficient (k) and internal friction angle (φ) both manifest a linear decline. In contrast, cohesion (c) undergoes a linear increase. The most pronounced impact is attributable to rainfall on cohesion, succeeded by the permeability coefficient, while the internal friction angle experiences the least influence.
- (2)
- When compared to the initial model parameters, characterized by the absence of rainfall, noteworthy variations emerge. Specifically, the permeability coefficient (k) at the downslope surface decreased by 2.5%, while the cohesion (c) increased by a substantial 111.9%, and the internal friction angle (φ) experienced a reduction of 6.96%. In contrast, the upslope surface exhibited a distinct behavior, with a 10% increase in k, a decrease of 21.1% in c, and a 2.23% rise in φ. In terms of the colluvium body’s overall structure, subsequent to rainfall, the permeability coefficient, cohesion, and internal friction angle at the upper slope demonstrated values 1.13, 0.37, and 1.09 times, respectively, in comparison to those at the lower portion. While the internal modifications within the colluvium body followed a pattern akin to that near the surface, the magnitude of these alterations was comparatively less pronounced.
- (3)
- In contrast to the initial state of the colluvium prior to rainfall, a rise in clay mineral content along elevation is observed, followed by a reduction post-rainfall. Notably, the key constituents Si, Al, and the minerals SiO2 and Al2O3 in the clay located at the base of the colluvium model register increments of 4.32%, 1.5%, 4.5%, and 10.34%, respectively. Concurrently, a decline in elevation corresponds to a reduction in both the number and dimensions of pores within the colluvium. This phenomenon underscores that under the influence of rainfall-driven seepage, fine clay particles migrate towards the slope toe, aligning with the seepage direction. Accumulation of fine clay particles at the slope toe leads to the gradual filling of original pores, intensifying particle cementation, resulting in elevated cohesion and diminished permeability coefficient. Simultaneously, the transportation of fine particles triggers a relative surge in coarse particle content upslope, amplifying friction resistance and augmenting the internal friction angle.
- (4)
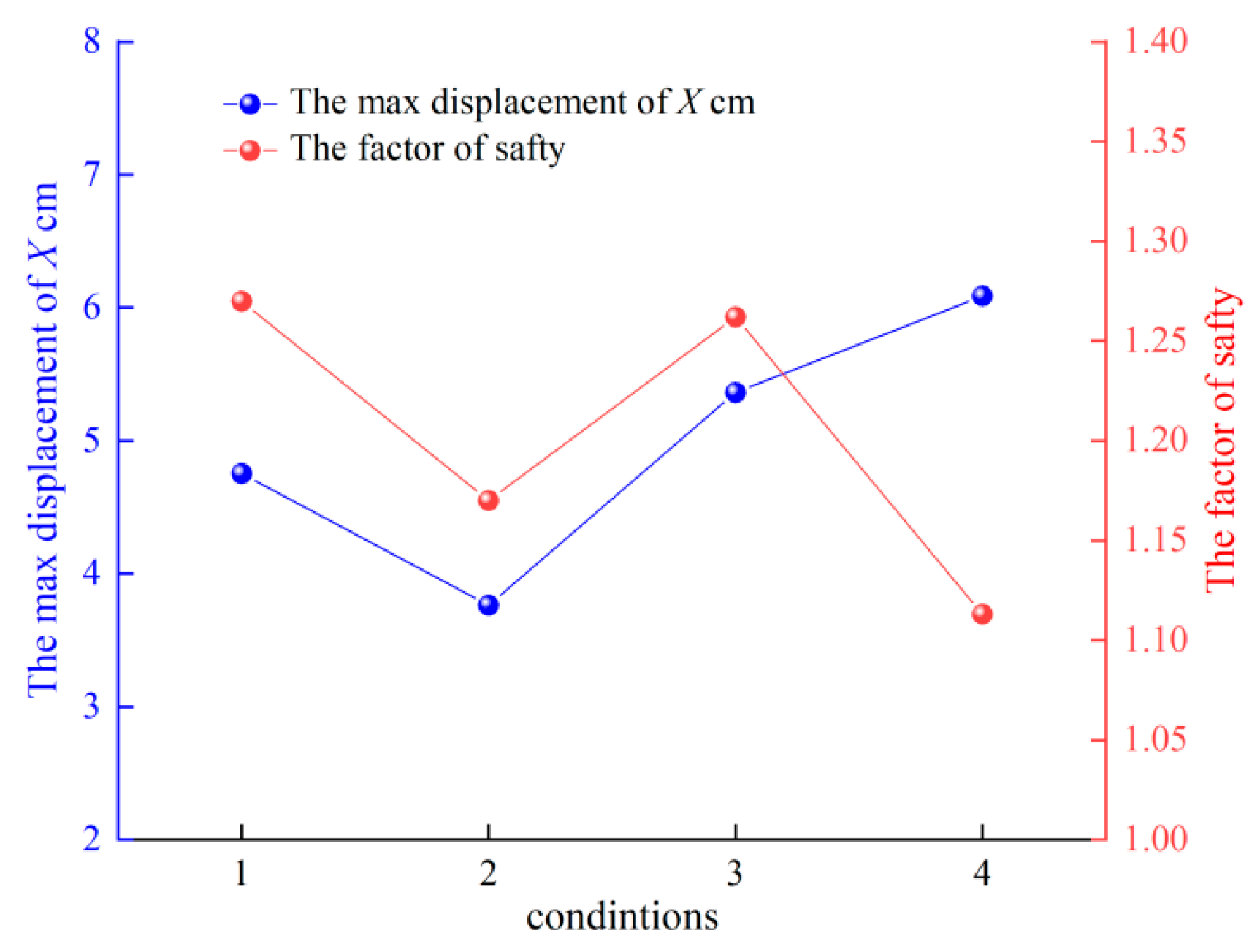
- Considering the combined impact of rainfall and reservoir water level, including the variation of parameters along the landslide elevation, in contrast to scenarios solely involving the effect of reservoir water level at the same elevation, the maximum deformation of the Shuping landslide increased by 12.81% and 42.52% in the X direction at the water levels of 145 m and 175 m, respectively. Nonetheless, the safety factor experienced reductions of 0.63% and 5.13%, respectively. This highlights the significance of accounting for the variability in the physical and mechanical parameters of the landslide along the elevation during numerical calculations. Ignoring this variability can result in an overestimation of the calculated safety factor, subsequently leading to an inflated estimation of colluvium stability. Consequently, incorporating the variability of physical and mechanical parameters induced by rainfall in slope engineering design enhances the reliability of the design outcomes.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jian, W.; Wang, Z.; Yin, K. Mechanism of the Anlesi landslide in the three gorges reservoir, China. Eng. Geol. 2009, 108, 86–95. [Google Scholar] [CrossRef]
- Wang, J.; Su, A.; Xiang, W.; Yeh, H.F.; Xiong, C.; Zou, Z.; Liu, Q. New data and interpretations of the shallow and deep deformation of Huangtupo No. 1 riverside sliding mass during seasonal rainfall and water level fluctuation. Landslides 2016, 13, 795–804. [Google Scholar] [CrossRef]
- Yang, B.; Yin, K.; Xiao, T.; Chen, L.; Du, J. Annual variation of landslide stability under the effect of water level fluctuation and rainfall in the Three Gorges Reservoir, China. Environ. Earth Sci. 2017, 76, 564. [Google Scholar] [CrossRef]
- Dai, Z.; Chen, S.; Li, J. Physical model test of seepage and deformation characteristics of shallow expansive soil slope. Bull. Eng. Geol. Environ. 2020, 79, 4063–4078. [Google Scholar] [CrossRef]
- He, C.; Hu, X.; Tannant, D.D.; Tan, F.; Zhang, Y.; Zhang, H. Response of a landslide to reservoir impoundment in model tests. Eng. Geol. 2018, 247, 84–93. [Google Scholar] [CrossRef]
- He, C.C.; Hu, X.L.; Xu, C.; Wu, S.S.; Zhang, H.; Liu, C. Model test of the influence of cyclic water level fluctuations on a landslide. J. Mt. Sci. 2020, 17, 191–202. [Google Scholar] [CrossRef]
- Wang, L.H.; Yin, S.J.; Xu, X.L. Model test of deformation failure mode of the bank slope deformation of the colluvium under the action of rainfall. Sci. Tech. 2018, 18, 77–82. (In Chinese) [Google Scholar]
- Xiong, X.; Shi, Z.; Xiong, Y.; Peng, M.; Ma, X.; Zhang, F. Unsaturated slope stability around the Three Gorges Reservoir under various combinations of rainfall and water level fluctuation. Eng. Geol. 2019, 261, 105231. [Google Scholar] [CrossRef]
- Lukić, T.; Bjelajac, D.; Fitzsimmons, K.E.; Marković, S.B.; Basarin, B.; Mlađan, D.; Micić, T.; Schaetzl, J.R.; Gavrilov, M.B.; Milanović, M. Factors triggering landslide occurrence on the Zemun loess plateau, Belgrade area, Serbia. Environ. Earth Sci. 2018, 77, 519. [Google Scholar] [CrossRef]
- Li, Q.; Huang, D.; Pei, S.; Qiao, J.; Wang, M. Using Physical Model Experiments for Hazards Assessment of Rainfall-Induced Debris Landslides. J. Earth Sci. 2021, 32, 1113–1128. [Google Scholar] [CrossRef]
- Morar, C.; Lukić, T.; Basarin, B.; Valjarević, A.; Vujičić, M.; Niemets, L.; Telebienieva, I.; Boros, L.; Nagy, G. Shaping Sustainable Urban Environments by Addressing the Hydro-Meteorological Factors in Landslide Occurrence: Ciuperca Hill (Oradea, Romania). Int. J. Environ. Res. Public Health 2021, 18, 5022. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Fenton, G.A. Probabilistic slope stability analysis by finite elements. J. Geotech. Geoenviron. 2004, 130, 507–518. [Google Scholar] [CrossRef]
- Schieber, J. Reverse engineering mother nature-Shale sedimentology from an experimental perspective. Sediment. Geol. 2011, 238, 1–22. [Google Scholar] [CrossRef]
- Huang, J.; Lyamin, A.V.; Griffiths, D.V.; Krabbenhoft, K.; Sloan, S.W. Quantitative risk assessment of landslide by limit analysis and random fields. Comput. Geotech. 2013, 53, 60–67. [Google Scholar] [CrossRef]
- Xiao, H.; Guo, G.; Chen, L. Research on dynamic evaluation model of slope risk based on improved VW-UM. Math. Probl. Eng. 2019, 2019, 5813217. (In Chinese) [Google Scholar] [CrossRef]
- Hua, Y.; Wang, X.; Li, Y.; Xu, P.; Xia, W. Dynamic development of landslide susceptibility based on slope unit and deep neural networks. Landslides 2021, 18, 281–302. [Google Scholar] [CrossRef]
- Yang, H.Q.; Zhang, L.; Pan, Q. Bayesian estimation of spatially varying soil parameters with spatiotemporal monitoring data. Acta Geotech. 2021, 16, 263–278. [Google Scholar] [CrossRef]
- Rana, H.; Sivakumar Babu, G.L. Probabilistic back analysis for rainfall-induced slope failure using MLS-SVR and Bayesian analysis. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2022, 1–14. [Google Scholar] [CrossRef]
- Jiang, S.H.; Papaioannou, I.; Straub, D. Bayesian updating of slope reliability in spatially variable soils with in-situ measurements. Eng. Geol. 2018, 239, 310–320. [Google Scholar] [CrossRef]
- Zhang, W.G.; Meng, F.S.; Chen, F.Y.; Liu, H.L. Effects of spatial variability of weak layer and seismic randomness on rock slope stability and reliability analysis. Soil Dyn. Earthq. Eng. 2021, 146, 106735. [Google Scholar] [CrossRef]
- Mori, H.; Chen, X.; Leung, Y.F.; Shimokawa, D.; Lo, M.K. Landslide hazard assessment by smoothed particle hydrodynamics with spatially variable soil properties and statistical rainfall distribution. Can. Geotech. J. 2020, 57, 1953–1969. [Google Scholar] [CrossRef]
- Li, J.; Luo, W.; Tian, Y.; Wang, Y.; Cassidy, M.J. Modeling of large deformation problem considering spatially variable soils in offshore engineering. Mar. Georesour. Geotec. 2021, 39, 906–918. [Google Scholar] [CrossRef]
- Chen, X.; Li, D.; Tang, X.; Liu, Y. A three-dimensional large-deformation random finite-element study of landslide runout considering spatially varying soil. Landslides 2021, 18, 3149–3162. [Google Scholar] [CrossRef]
- Ding, Y.N.; Li, D.Q.; Zarei, C.; Yi, B.L.; Liu, Y. Probabilistically quantifying the effect of geotechnical anisotropy on landslide susceptibility. Bull. Eng. Geol. Environ. 2021, 80, 6615–6627. [Google Scholar] [CrossRef]
- Xia, Y.X.; Cheng, P.; Liu, M.M.; Hu, J. Numerical Modeling of 3D Slopes with Weak Zones by Random Field and Finite Elements. Appl. Sci. 2021, 11, 9852. [Google Scholar] [CrossRef]
- Luo, X.Q.; Bi, J.F. Theory and Application of Geomechanical Model Test; Shanghai Jiaotong University Press: Shanghai, China, 2011; pp. 90–101. (In Chinese) [Google Scholar]
- Zhi, Y.Y. Experimental Study and Mechanism of MICP Reinforcement for Fractured Rock Mass. Master’s Thesis, China Three Gorges University, Yichang, China, 2020. (In Chinese). [Google Scholar]
- Grunewald, E.; Knight, R. A laboratory study of NMR relaxation times and pore coupling in heterogeneous media. Geophysics 2009, 74, 215–221. [Google Scholar] [CrossRef]
- Zhang, K.G.; Liu, S.G. Soil Mechanics, 3rd ed.; China Architecture and Construction Press: Beijing, China, 2010; pp. 188–210. (In Chinese) [Google Scholar]
- Kozlowski, T.; Ludynia, A. Permeability coefficient of low permeable soils as a single-variable function of soil parameter. Water 2019, 11, 2500. [Google Scholar] [CrossRef]




| Soil Sample Category | Density ρ/g·cm−3 | Content of Stone/% | Water Ratio/% | c/kPa | ° | k/cm·s−1 | Coefficient of Nonuniformity | Coefficient of Curvature |
|---|---|---|---|---|---|---|---|---|
| Shuping landslide | 2.01 | 68 | 23.4 | 20.7 | 23.5 | 1.02 × 10−2 | 30.36 | 1.21 |
| Test landslide colluvium | 2.0 | 68 | 8.0 | 33.66 | 36.78 | 1.60 × 10−3 | 28.0 | 1.90 |
| Point Number | Elevation h/cm | k/cm·s−1 | /k·cm−1 | ||
|---|---|---|---|---|---|
| Surface | DW1 | 16 | 1.56 × 10−3 | −0.025 | / |
| DW2 | 55 | 1.62 × 10−3 | 0.0125 | 1.5 × 10−6 | |
| DW3 | 94 | 1.76 × 10−3 | 0.10 | 3.6 × 10−6 | |
| Interior | DW4 | 16 | 1.59 × 10−3 | −0.006 | / |
| DW5 | 55 | 1.71 × 10−3 | 0.069 | 3.1 × 10−6 | |
| Elevation | 16 cm | 55 cm | 94 cm |
|---|---|---|---|
| Average value | 0.0155 | 0.041 | 0.1 |
| Point Number | Points | c kPa/cm | of c | c kPa/cm | φ/° | of φ | φ °/cm |
|---|---|---|---|---|---|---|---|
| Surface | DW1 | 71.3 | 1.119 | / | 34.22 | −0.0696 | / |
| DW2 | 48.08 | 0.428 | −0.595 | 35.75 | −0.028 | 0.039 | |
| DW3 | 26.56 | −0.211 | −0.552 | 37.6 | 0.0223 | 0.047 | |
| Interior | DW4 | 65.03 | 0.932 | / | 34.99 | −0.0487 | / |
| DW5 | 51.48 | 0.529 | −0.347 | 36.13 | −0.0177 | 0.021 |
| Parameter | 16 cm | 55 cm | 94 cm |
|---|---|---|---|
| Internal friction angle φ/° | 1.026 | 0.479 | −0.211 |
| Cohesion c/kPa | −0.060 | −0.023 | 0.022 |
| Category | /g·cm−3 | /cm·s−1 | /MPa | v | /Pa | /Pa | /kPa | |
|---|---|---|---|---|---|---|---|---|
| Landslide | 2.01 | 1.02 × 10−2 | 300 | 0.255 | 2.04 × 108 | 1.19 × 108 | 20.7 | 23.5 |
| Sliding zone | - | / | 300 | 0.45 | 1 × 109 | 1.03 × 108 | 19.2 | 20.4 |
| Bedrock | 2.61 | / | 5000 | 0.22 | 2.98 × 109 | 2.05 × 109 | 3.38 × 103 | 46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Zhang, J.; Ji, E.; Wang, L.; Huang, P.; Wang, X. A Laboratory Simulation Experiment to Assess Permeability and Shear Strength of a Gravel Soil Colluvium. Water 2023, 15, 3089. https://doi.org/10.3390/w15173089
Xu X, Zhang J, Ji E, Wang L, Huang P, Wang X. A Laboratory Simulation Experiment to Assess Permeability and Shear Strength of a Gravel Soil Colluvium. Water. 2023; 15(17):3089. https://doi.org/10.3390/w15173089
Chicago/Turabian StyleXu, Xiaoliang, Jiafu Zhang, Enyue Ji, Lehua Wang, Peng Huang, and Xiaoping Wang. 2023. "A Laboratory Simulation Experiment to Assess Permeability and Shear Strength of a Gravel Soil Colluvium" Water 15, no. 17: 3089. https://doi.org/10.3390/w15173089
APA StyleXu, X., Zhang, J., Ji, E., Wang, L., Huang, P., & Wang, X. (2023). A Laboratory Simulation Experiment to Assess Permeability and Shear Strength of a Gravel Soil Colluvium. Water, 15(17), 3089. https://doi.org/10.3390/w15173089






