Evolution Characteristics of Meteorological Drought under Future Climate Change in the Middle Reaches of the Yellow River Basin Based on the Copula Function
Abstract
:1. Introduction
2. Materials and Methods
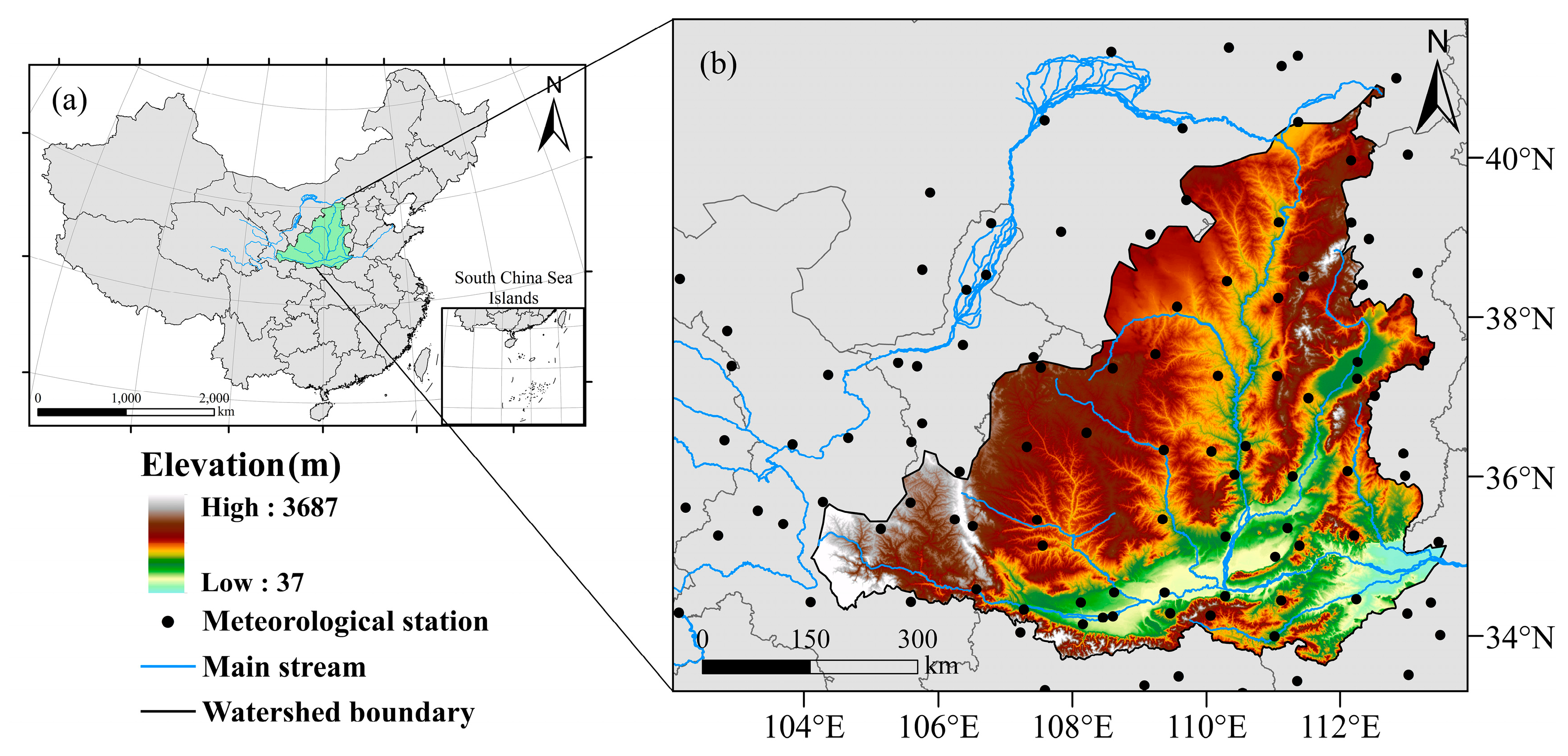
2.1. Study Area
2.2. Datasets
2.2.1. Hydrological Data
2.2.2. CMIP 6 Climate Model
2.3. Methodology
2.3.1. Delta Downscaling
2.3.2. Climate Model Optimization
2.3.3. SPEI
2.3.4. Run-Length Theory
2.3.5. Copula Function
3. Results
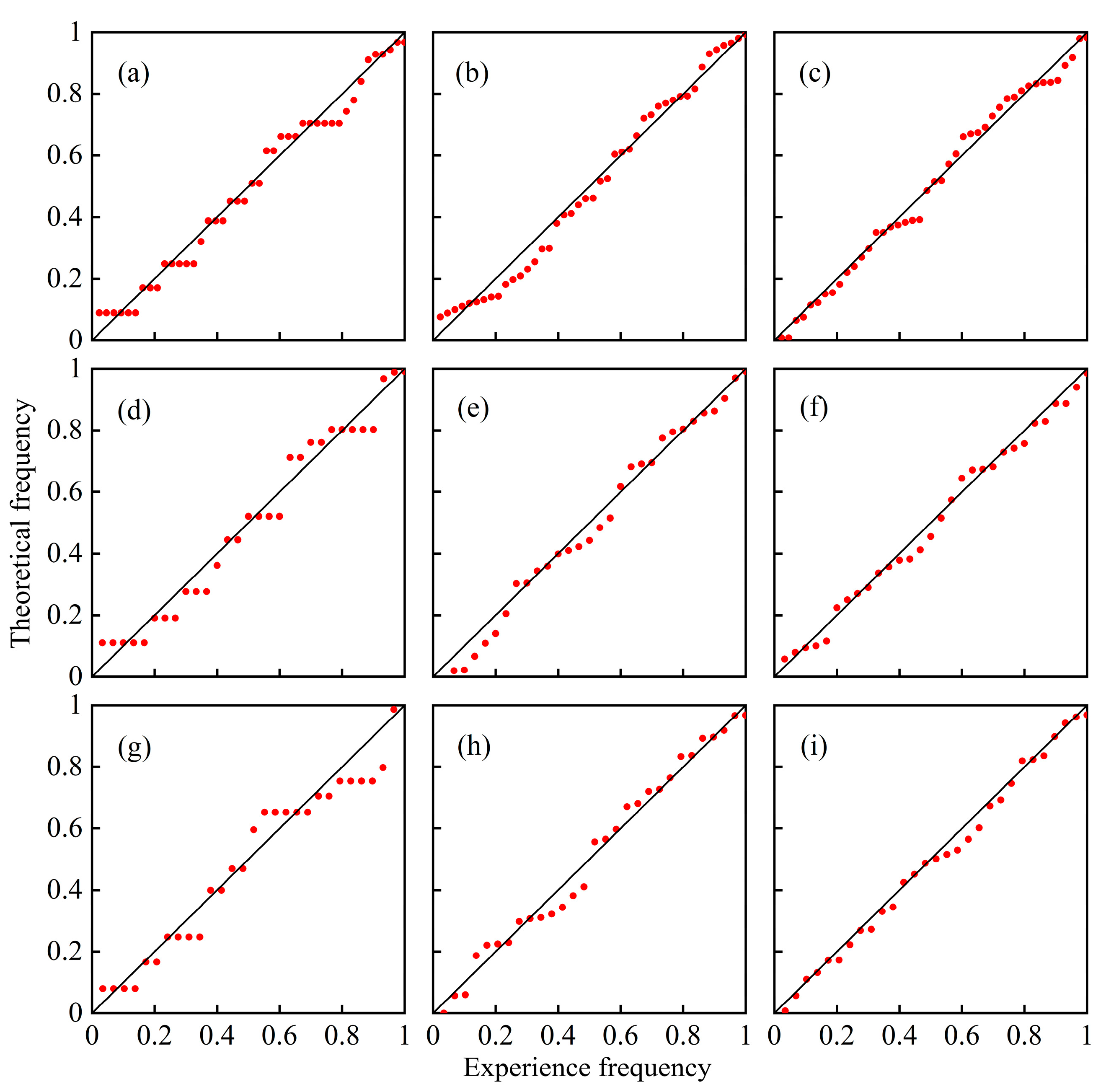
3.1. Climate Model Optimization
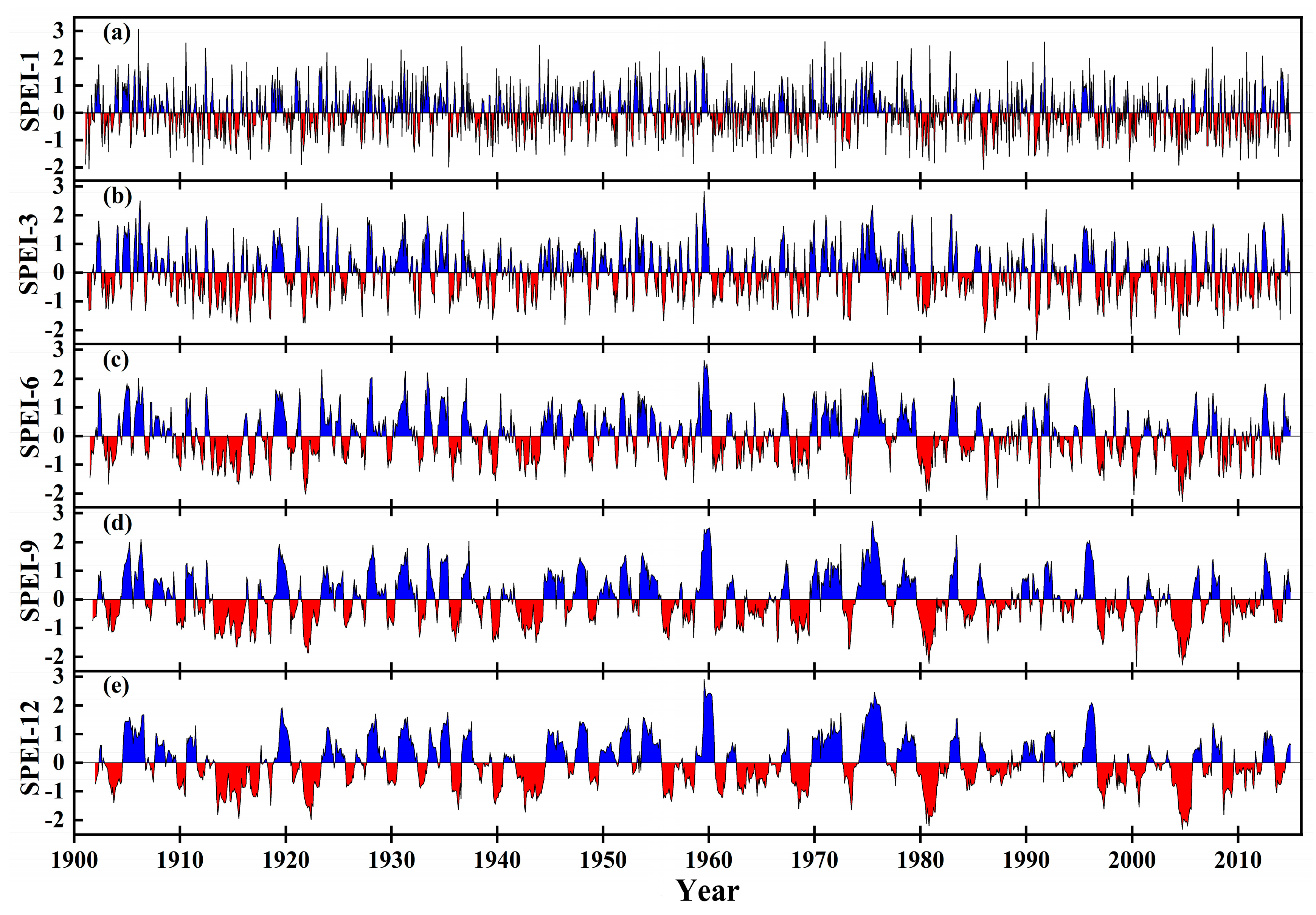
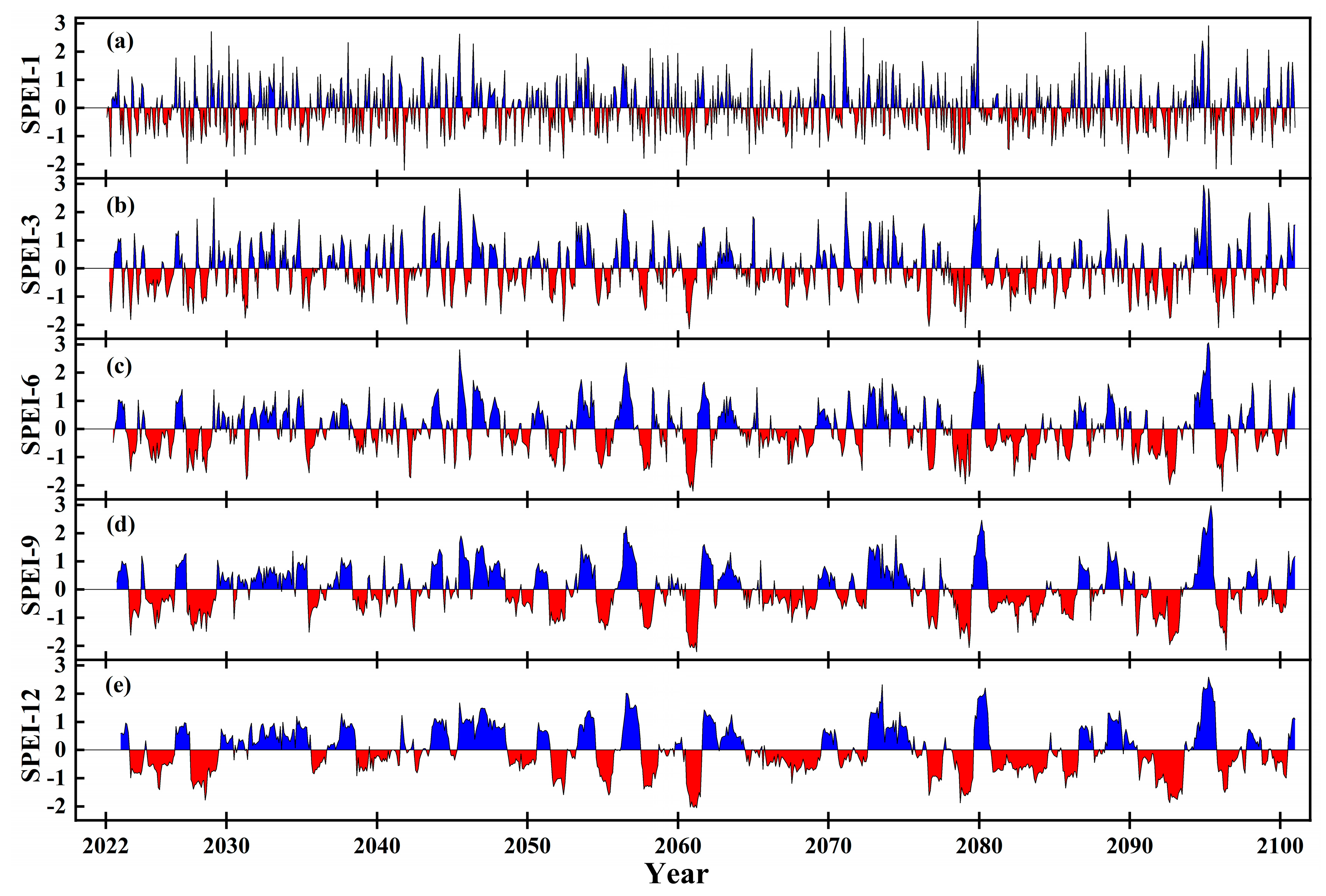
3.2. Variations in the SPEI Meteorological Drought Index
3.3. Identification of Drought Characteristic Variables Using Run-Length Theory
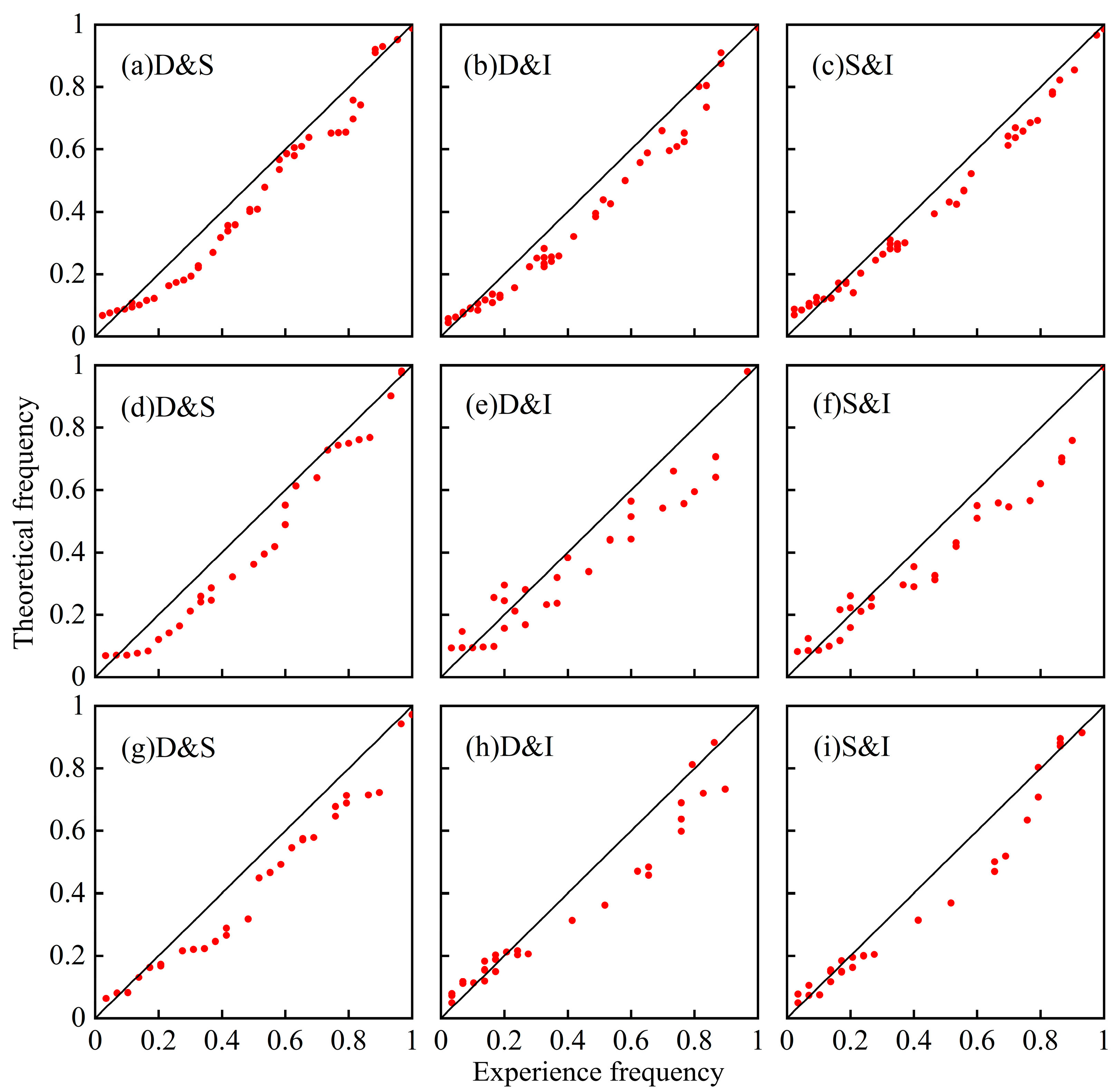
3.4. Drought Analysis Conducted in the YRBM Based on the Copula Function
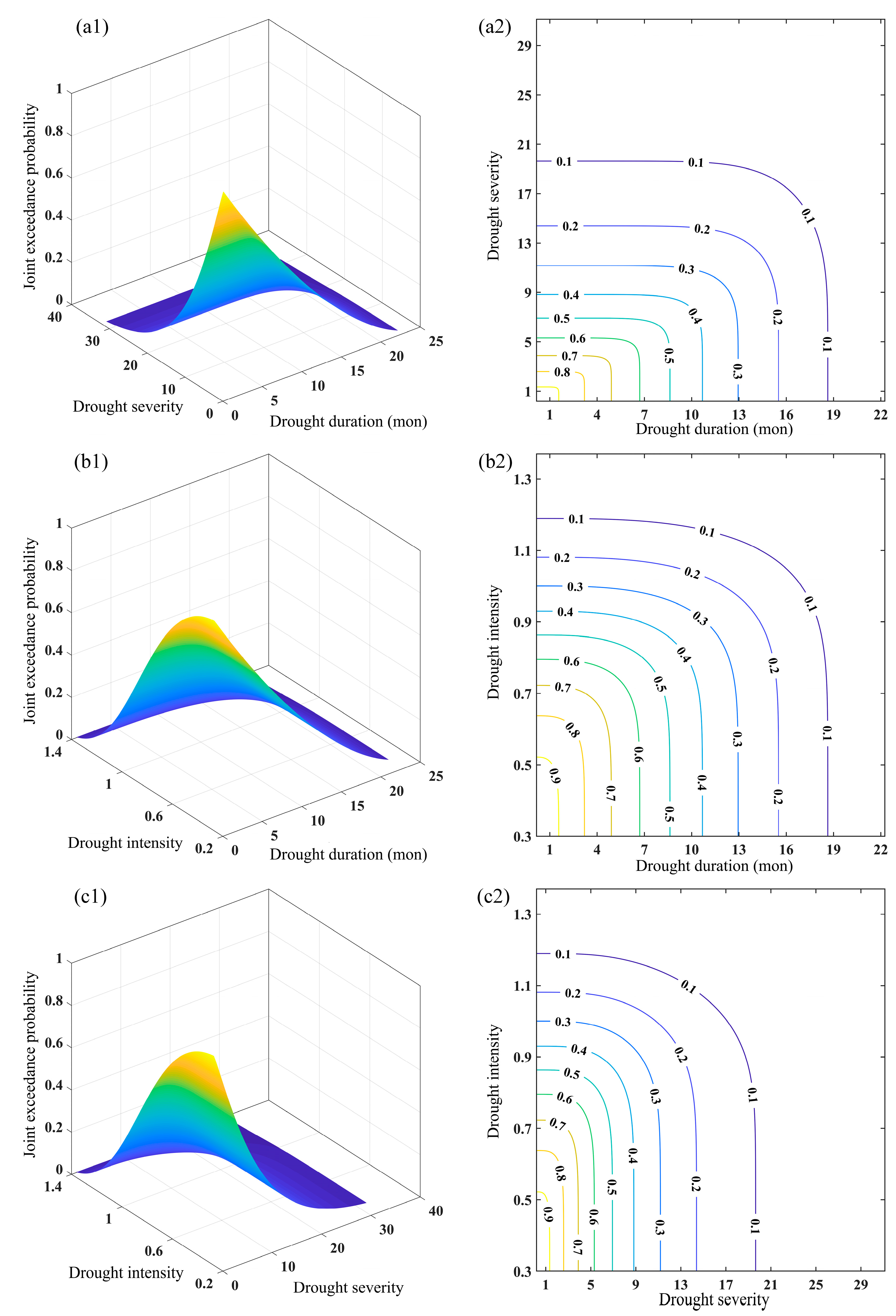
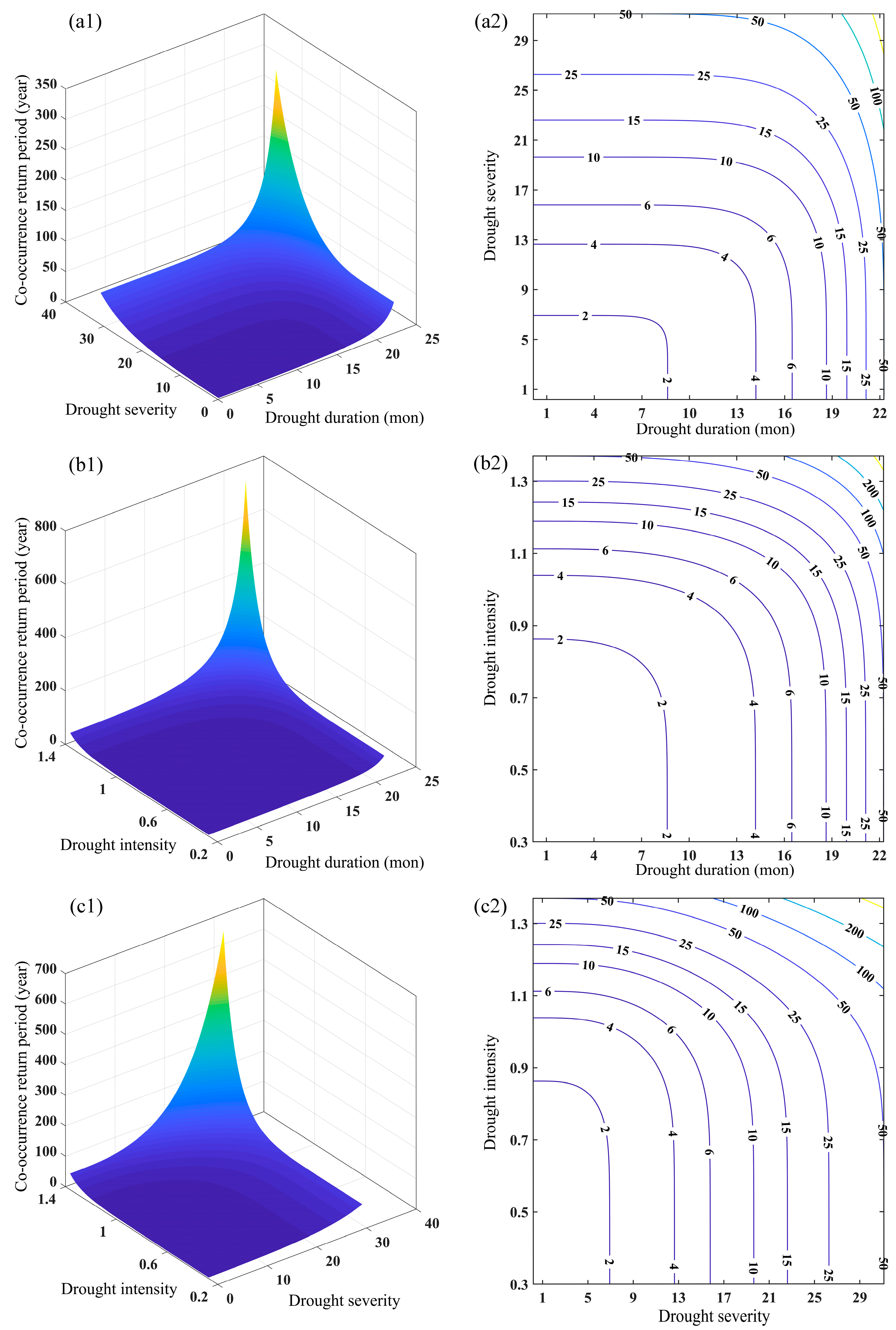
3.5. Joint Distribution and Recurrence Period of Two-Dimensional Drought Characteristic Variables
3.5.1. Historical Joint Probability Distribution and Return Period
3.5.2. SSP245 Joint Probability Distribution and Return Period
3.5.3. SSP585 Joint Probability Distribution and Return Period
3.5.4. Comparative Analysis of Univariate and Multivariate Recurrence Periods
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nooni, I.K.; Hagan, D.F.T.; Wang, G.; Ullah, W.; Lu, J.; Li, S.; Dzakpasu, M.; Prempeh, N.A.; Sian, K.T.C.L.K. Future changes in simulated evapotranspiration across continental Africa based on CMIP6 CNRM-CM6. Int. J. Environ. Res. Public Health 2021, 18, 6760. [Google Scholar] [CrossRef] [PubMed]
- Ukkola, A.M.; De Kauwe, M.G.; Roderick, M.L.; Abramowitz, G.; Pitman, A.J. Robust future changes in meteorological drought in CMIP6 projections despite uncertainty in precipitation. Geophys. Res. Lett. 2020, 47, e2020GL087820. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2022: Mitigation of Climate Change Contribution of Working Group Ⅲ to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2022. [Google Scholar]
- Tian, C.; Yue, X.; Zhou, H.; Lei, Y.; Ma, Y.; Cao, Y. Projections of changes in ecosystem productivity under 1.5 °C and 2 °C global warming. Glob. Planet. Chang. 2021, 205, 103588. [Google Scholar] [CrossRef]
- Xu, J. Reconstructing the suspended sediment load of the Yellow River since 1470 CE using the Drought and Flood Index. Geomorphology 2017, 299, 131–141. [Google Scholar] [CrossRef]
- Hong, J.; Javan, K.; Shin, Y.; Park, J.-S. Future projections and uncertainty assessment of precipitation extremes in Iran from the CMIP6 ensemble. Atmosphere 2021, 12, 1052. [Google Scholar] [CrossRef]
- Song, Y.H.; Shahid, S.; Chung, E. Differences in multi-model ensembles of CMIP5 and CMIP6 projections for future droughts in South Korea. Int. J. Climatol. 2022, 42, 2688–2716. [Google Scholar] [CrossRef]
- Wu, J.; Miao, C.; Wang, Y.; Duan, Q.; Zhang, X. Contribution analysis of the long-term changes in seasonal runoff on the Loess Plateau, China, using eight Budyko-based methods. J. Hydrol. 2017, 545, 263–275. [Google Scholar] [CrossRef]
- Douglas, E.M.; Jacobs, J.M.; Sumner, D.M.; Ray, R.L. A comparison of models for estimating potential evapotranspiration for Florida land cover types. J. Hydrol. 2009, 373, 366–376. [Google Scholar] [CrossRef]
- Yan, X.; Mohammadian, A. Estimating future daily pan evaporation for Qatar using the Hargreaves model and statistically downscaled global climate model projections under RCP climate change scenarios. Arab. J. Geosci. 2020, 13, 938. [Google Scholar] [CrossRef]
- Manabe, S.; Smagorinsky, J.; Strickler, R.F. Simulated climatology of a general circulation model with a hydrologic cycle 1. Mon. Weather Rev. 1965, 93, 769–798. [Google Scholar] [CrossRef]
- Iqbal, Z.; Shahid, S.; Ahmed, K.; Ismail, T.; Khan, N.; Virk, Z.T.; Johar, W. Evaluation of global climate models for precipitation projection in sub-Himalaya region of Pakistan. Atmos. Res. 2020, 245, 105061. [Google Scholar] [CrossRef]
- Gellens, D.; Roulin, E. Streamflow response of Belgian catchments to IPCC climate change scenarios. J. Hydrol. 1998, 210, 242–258. [Google Scholar] [CrossRef]
- Torres, R.R.; Marengo, J.A. Climate change hotspots over South America: From CMIP3 to CMIP5 multi-model datasets. Theor. Appl. Climatol. 2014, 117, 579–587. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef] [Green Version]
- Harding, K.J.; Snyder, P.K. Examining future changes in the character of Central U.S. warm-season precipitation using dynamical downscaling. J. Geophys. Res. Atmos. 2014, 119, 13116–13136. [Google Scholar] [CrossRef] [Green Version]
- Engström, J.; Keellings, D. Drought in the Southeastern USA: An assessment of downscaled CMIP5 models. Clim. Res. 2018, 74, 251–262. [Google Scholar] [CrossRef]
- Ma, Z.; Sun, P.; Zhang, Q.; Zou, Y.; Lv, Y.; Li, H.; Chen, D. The characteristics and evaluation of future droughts across China through the CMIP6 multi-model ensemble. Remote Sens. 2022, 14, 1097. [Google Scholar] [CrossRef]
- Fu, Y.; Lin, Z.; Wang, T. Simulated Relationship between Wintertime ENSO and East Asian Summer Rainfall: From CMIP3 to CMIP6. Adv. Atmos. Sci. 2021, 38, 221–236. [Google Scholar] [CrossRef]
- Wang, L.; Chen, W. A CMIP5 multimodel projection of future temperature, precipitation, and climatological drought in China. Int. J. Climatol. 2014, 34, 2059–2078. [Google Scholar] [CrossRef]
- Zhu, X.; Ji, Z.; Wen, X.; Lee, S.; Wei, Z.; Zheng, Z.; Dong, W. Historical and projected climate change over three major river basins in China from Fifth and Sixth Coupled Model Intercomparison Project models. Int. J. Climtol. 2021, 41, 6455–6473. [Google Scholar] [CrossRef]
- Zhu, H.; Jiang, Z.; Li, L. Projection of climate extremes in China, an incremental exercise from CMIP5 to CMIP6. Sci. Bull. 2021, 66, 2528–2537. [Google Scholar] [CrossRef] [PubMed]
- Yu, T.; Chen, W.; Gong, H.; Feng, J.; Chen, S. Comparisons between CMIP5 and CMIP6 models in simulations of the climatology and interannual variability of the east Asian summer Monsoon. Clim. Dynam. 2022, 60, 2183–2198. [Google Scholar] [CrossRef]
- Qian, L.; Wang, X.; Wang, Z. Modeling the dependence pattern between two precipitation variables using a coupled copula. Environ. Earth Sci. 2020, 79, 486. [Google Scholar] [CrossRef]
- Xu, J.; Gao, Y.; Chen, D.; Xiao, L.; Ou, T. Evaluation of global climate models for downscaling applications centred over the Tibetan Plateau. Int. J. Climatol. 2017, 37, 657–671. [Google Scholar] [CrossRef]
- Storch, H.V. Inconsistencies at the interface of climate impact studies and global climate research. Meteorol. Z. 1992, 4, 72–80. [Google Scholar]
- Chen, J.; Brissette, F.P.; Leconte, R. Coupling statistical and dynamical methods for spatial downscaling of precipitation. Clim. Chang. 2012, 114, 509–526. [Google Scholar] [CrossRef]
- Zhang, Z.; Deng, S.; Zhao, Q.; Zhang, S.; Zhang, X. Projected glacier meltwater and river run-off changes in the Upper Reach of the Shule River Basin, north-eastern edge of the Tibetan Plateau. Hydrol. Process. 2019, 33, 1059–1074. [Google Scholar] [CrossRef]
- Ding, Y.; Peng, S. Spatiotemporal change and attribution of potential evapotranspiration over China from 1901 to 2100. Theor. Appl. Climatol. 2021, 145, 79–94. [Google Scholar] [CrossRef]
- Hay, L.E.; Wilby, R.; Leavesley, G.H. A comparison of delta change and downscaled GCM scenarios for three mountainous basins in the United States. J. Am. Water Resour. Assoc. 2000, 36, 387–397. [Google Scholar] [CrossRef]
- Salahi, B.; Poudineh, E. An evaluation of Delta and SDSM Downscaling Models for simulating and forecasting of average wind velocity in Sistan, Iran. Model. Earth Syst. Environ. 2022, 8, 4441–4453. [Google Scholar] [CrossRef]
- Jian, S.; Wang, A.; Hu, C.; Yan, D. Effect of landscape restoration on evapotranspiration and water use in the Yellow River Basin, China. Acta Geophys. 2023, 175, 106504. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Yang, C.; Wang, N.; Wang, S.; Zhou, L. Performance comparison of three predictor selection methods for statistical downscaling of daily precipitation. Theor. Appl. Climatol. 2018, 131, 43–54. [Google Scholar] [CrossRef]
- Zhao, F.; Ma, S.; Wu, Y.; Qiu, L.; Wang, W.; Lian, Y.; Chen, J.; Sivakumar, B. The role of climate change and vegetation greening on evapotranspiration variation in the Yellow River Basin, China. Agric. For. Meteorol. 2022, 316, 108842. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, S.; Zhao, W.; Liu, Y. The increasing contribution of potential evapotranspiration to severe droughts in the Yellow River basin. J. Hydrol. 2022, 605, 127310. [Google Scholar] [CrossRef]
- Jian, S.; Wang, A.; Su, C.; Wang, K. Prediction of future spatial and temporal evolution trends of reference evapotranspiration in the Yellow River Basin, China. Remote Sens. 2022, 14, 5674. [Google Scholar] [CrossRef]
- Dai, A. Drought under global warming: A review. WIREs Clim. Chang. 2011, 2, 45–65. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Kattel, G.; Zhang, J.; Shang, Y.; Gnyawali, K.R.; Zhang, F.; Miao, L. Slightly enhanced drought in the Yellow River Basin under future warming scenarios. Atmos. Res. 2022, 280, 106423. [Google Scholar] [CrossRef]
- John, R.; Chen, J.Q.; Giannico, V.; Park, H.; Xiao, J.; Shirkey, G.; Ouyang, Z.; Shao, C.; Lafortezza, R.; Qi, J. Grassland canopy cover and aboveground biomass in Mongolia and Inner Mongolia: Spatiotemporal estimates and controlling factors. Remote Sens. Environ. 2018, 213, 34–48. [Google Scholar] [CrossRef]
- Ault, T.R. On the essentials of drought in a changing climate. Science Am. Assoc. Adv. Sci. 2020, 368, 256–260. [Google Scholar] [CrossRef]
- Peng, S.; Gang, C.; Cao, Y.; Chen, Y. Assessment of climate change trends over the Loess Plateau in China from 1901 to 2100. Int. J. Climatol. 2018, 38, 2250–2264. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Mirchi, A.; Madani, K.; Di Baldassarre, G.; Nazemi, A.; Alborzi, A.; Anjileli, H.; Azarderakhsh, M.; Chiang, F.; Hassanzadeh, E.; et al. Anthropogenic drought: Definition, challenges, and opportunities. Rev. Geophys. 2021, 59, e2019RG000683. [Google Scholar] [CrossRef]





| Levels | Types | SPEI |
|---|---|---|
| 1 | Drought-free | (−0.5, +∞) |
| 2 | Mild drought | (−1, −0.5] |
| 3 | Moderate drought | (−1.5, −1] |
| 4 | Severe drought | (−2, −1.5] |
| 5 | Extreme drought | (−∞, −2] |
| Scenario | Drought Characteristics | Preferred Function | Parameters | K-S Results | ||
|---|---|---|---|---|---|---|
| Statistical Magnitude Di | p-Values | Dcritical value (α = 0.05) | ||||
| Historical | D | GenPareto | k = −0.3582, σ = 11.1480, μ = 0.9780 | 0.0890 | 0.8553 | 0.2028 |
| S | Weibull | α = 1.1865, β = 8.9632 | 0.0760 | 0.9488 | ||
| I | Weibull | α = 1.4445, β = 0.3823, γ = 0.5140 | 0.0803 | 0.9239 | ||
| SSP245 | D | Weibull | α = 1.4701, β = 8.6161 | 0.1120 | 0.8062 | 0.2417 |
| S | Gamma | α = 0.7206, β = 9.5242, γ = 1.0798 | 0.0822 | 0.9773 | ||
| I | GenPareto | k = −0.2721, σ = 0.4548, μ = 0.5128 | 0.0787 | 0.9852 | ||
| SSP585 | D | GenPareto | k = −0.5130, σ = 10.8910, μ = 1.1118 | 0.1427 | 0.5488 | 0.2457 |
| S | Gamma | α = 0.8398, β = 8.2235, γ = 1.2677 | 0.0847 | 0.9740 | ||
| I | Gamma | α = 2.0096, β = 0.2074, γ = 0.5157 | 0.0611 | 0.9996 | ||
| Scenario | Pearson | Kendall | Spearman | |
|---|---|---|---|---|
| Historical | D&S | 0.957 | 0.907 | 0.981 |
| D&I | 0.763 | 0.568 | 0.737 | |
| S&I | 0.875 | 0.672 | 0.840 | |
| SSP245 | D&S | 0.948 | 0.897 | 0.976 |
| D&I | 0.684 | 0.542 | 0.703 | |
| S&I | 0.813 | 0.660 | 0.812 | |
| SSP585 | D&S | 0.938 | 0.908 | 0.978 |
| D&I | 0.516 | 0.349 | 0.515 | |
| S&I | 0.757 | 0.463 | 0.604 | |
| Scenario | Copula Function | D&S | D&I | S&I | |||
|---|---|---|---|---|---|---|---|
| AIC | BIC | AIC | BIC | AIC | BIC | ||
| Historical | Gaussian | 12.9753 | 14.7365 | 12.8736 | 14.6348 | 14.375 | 16.1362 |
| t | 15.0016 | 18.524 | 15.085 | 18.6074 | 16.5134 | 20.0358 | |
| Gumbel | 12.6916 | 14.4528 | 12.4755 | 14.2367 | 14.0159 | 15.7771 | |
| Clayton | 12.8362 | 14.5974 | 12.579 | 14.3402 | 13.4885 | 15.2497 | |
| Frank | 13.2127 | 14.9739 | 13.2452 | 15.0064 | 14.5735 | 16.3347 | |
| SSP245 | Gaussian | 12.4804 | 13.8816 | 11.4994 | 12.9006 | 12.2785 | 13.6797 |
| t | 14.4882 | 17.2906 | 13.6228 | 16.4252 | 14.2264 | 17.0288 | |
| Gumbel | 12.1228 | 13.524 | 11.4393 | 12.8405 | 12.2049 | 13.6061 | |
| Clayton | 12.3449 | 13.7461 | 10.9754 | 12.3766 | 11.1935 | 12.5946 | |
| Frank | 12.4856 | 13.8868 | 11.5975 | 12.9987 | 12.1867 | 13.5879 | |
| SSP585 | Gaussian | 12.141 | 13.5083 | 12.0117 | 13.379 | 13.3692 | 14.7365 |
| t | 14.0205 | 16.7551 | 14.1591 | 16.8937 | 15.3742 | 18.1087 | |
| Gumbel | 11.7175 | 13.0848 | 11.8229 | 13.1902 | 13.0324 | 14.3997 | |
| Clayton | 11.4688 | 12.8361 | 11.6899 | 13.0572 | 12.3908 | 13.7581 | |
| Frank | 12.0546 | 13.4219 | 12.2317 | 13.599 | 13.4839 | 14.8512 | |
| Scenario | Return Period | D | S | I | D&S | D&I | S&I | |||
|---|---|---|---|---|---|---|---|---|---|---|
| To | Ta | To | Ta | To | Ta | |||||
| Historical | 10 | 12.76 | 11.38 | 0.98 | 8.98 | 11.29 | 7.41 | 15.38 | 7.14 | 16.70 |
| 20 | 17.01 | 16.22 | 1.14 | 17.77 | 22.89 | 14.35 | 33.06 | 12.38 | 52.16 | |
| 50 | 21.23 | 22.23 | 1.32 | 44.18 | 57.65 | 35.21 | 86.33 | 27.56 | 270.72 | |
| 100 | 23.62 | 26.57 | 1.45 | 88.20 | 115.57 | 70.00 | 175.23 | 52.63 | 1008.44 | |
| SSP245 | 10 | 10.49 | 10.11 | 1.02 | 8.92 | 11.37 | 6.45 | 22.21 | 6.53 | 21.35 |
| 20 | 13.94 | 15.86 | 1.22 | 17.65 | 23.06 | 11.48 | 77.64 | 11.57 | 73.65 | |
| 50 | 17.96 | 23.75 | 1.43 | 43.87 | 58.12 | 26.49 | 443.18 | 26.60 | 416.06 | |
| 100 | 20.74 | 29.86 | 1.56 | 87.57 | 116.54 | 51.50 | 1716.49 | 51.60 | 1605.04 | |
| SSP585 | 10 | 11.46 | 10.19 | 1.05 | 7.46 | 15.17 | 6.33 | 23.75 | 6.52 | 21.49 |
| 20 | 14.71 | 15.48 | 1.24 | 12.84 | 45.27 | 11.33 | 85.26 | 11.55 | 74.66 | |
| 50 | 17.58 | 22.62 | 1.48 | 28.13 | 224.68 | 26.33 | 496.34 | 26.57 | 424.06 | |
| 100 | 19.00 | 28.09 | 1.65 | 53.25 | 820.14 | 51.33 | 1936.70 | 51.57 | 1639.39 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Zhang, Z.; Li, X.; Zheng, B.; Zhang, X. Evolution Characteristics of Meteorological Drought under Future Climate Change in the Middle Reaches of the Yellow River Basin Based on the Copula Function. Water 2023, 15, 2265. https://doi.org/10.3390/w15122265
Zhang G, Zhang Z, Li X, Zheng B, Zhang X. Evolution Characteristics of Meteorological Drought under Future Climate Change in the Middle Reaches of the Yellow River Basin Based on the Copula Function. Water. 2023; 15(12):2265. https://doi.org/10.3390/w15122265
Chicago/Turabian StyleZhang, Guodong, Zhaoxi Zhang, Xiaoyu Li, Baoqiang Zheng, and Xueli Zhang. 2023. "Evolution Characteristics of Meteorological Drought under Future Climate Change in the Middle Reaches of the Yellow River Basin Based on the Copula Function" Water 15, no. 12: 2265. https://doi.org/10.3390/w15122265
APA StyleZhang, G., Zhang, Z., Li, X., Zheng, B., & Zhang, X. (2023). Evolution Characteristics of Meteorological Drought under Future Climate Change in the Middle Reaches of the Yellow River Basin Based on the Copula Function. Water, 15(12), 2265. https://doi.org/10.3390/w15122265





