Combining Synthetic and Observed Data to Enhance Machine Learning Model Performance for Streamflow Prediction
Abstract
1. Introduction
2. Materials and Methods
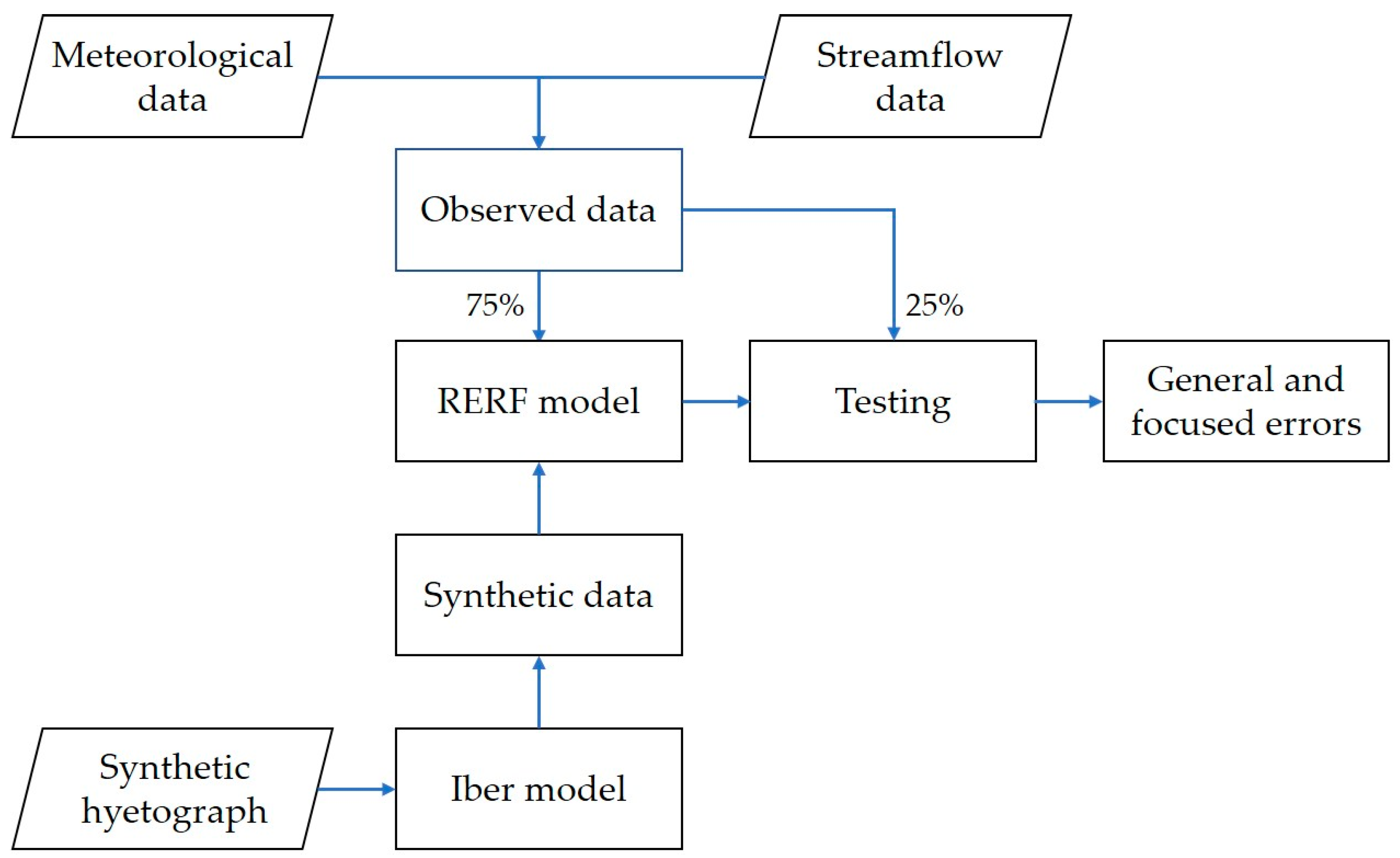
2.1. Methodology
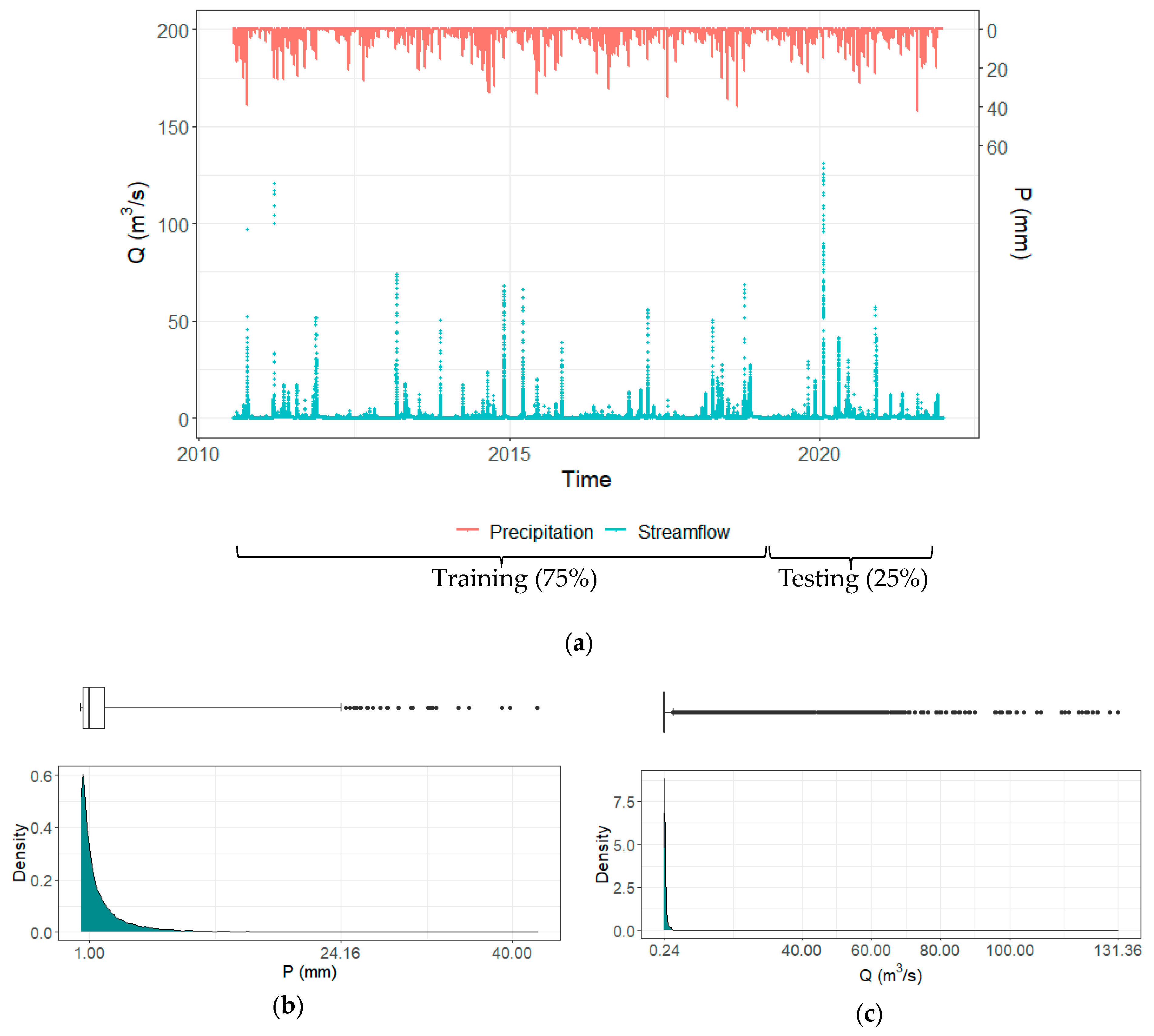
- Rainfall and discharge data were collected from the meteorological and streamflow stations, respectively, to set every input and output of the models. This data set was further divided chronologically: 75% for training and 25% for testing (the most recent data).
- The numerical model based on Iber was calibrated, taking into account high events of the training set.
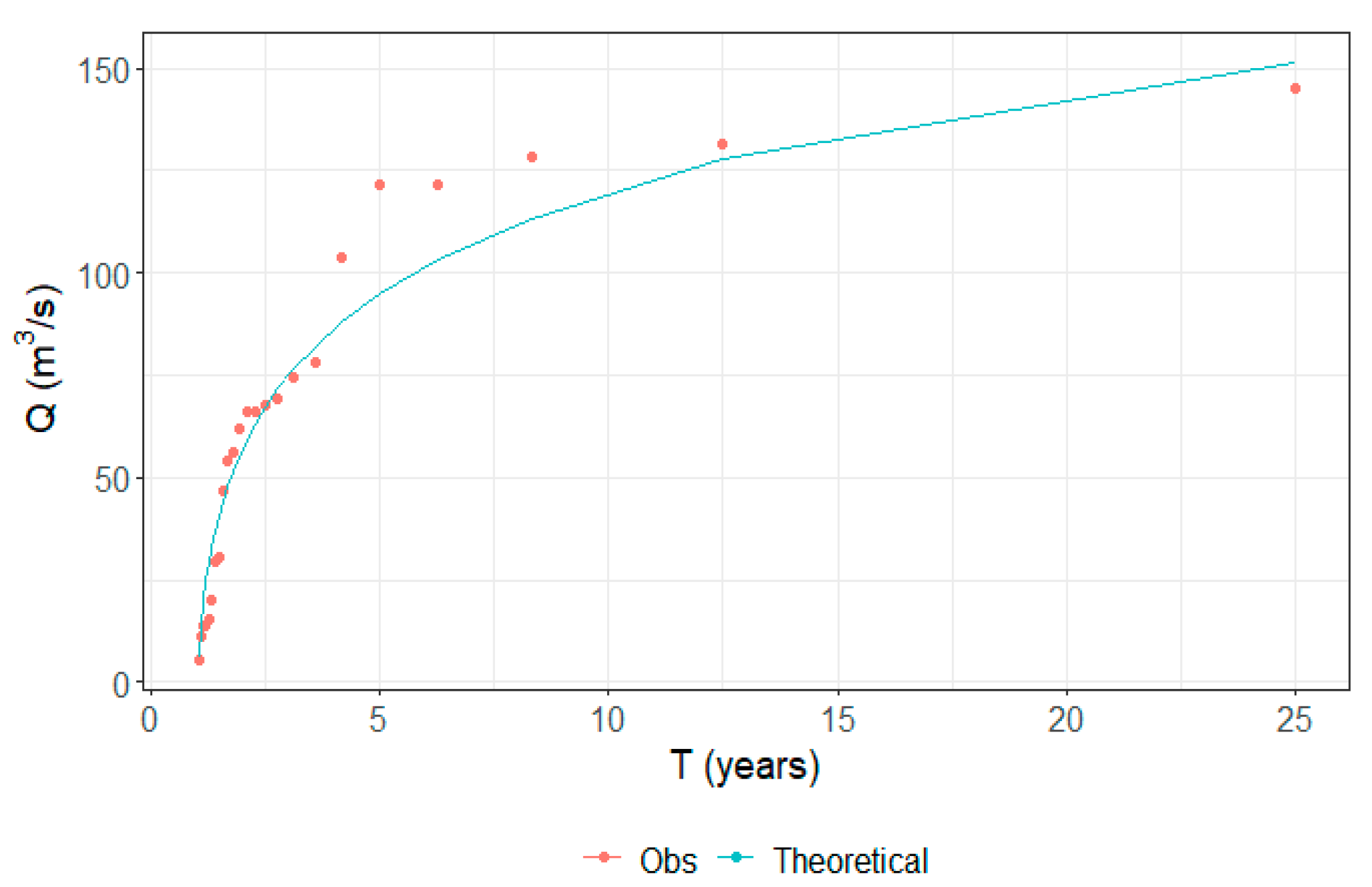
- Synthetic hyetographs with different periods of return were built using the Alternating Block Method (ABM) and intensity-duration-frequency (IDF) equations. They are employed in the calibrated Iber model to obtain synthetic hydrographs with higher streamflow values than those registered in the measured training set.
- Two RERF models were built using only the training data from the stations (RERF1) and a combination of the training set and the synthetic cases (RERF2).
- The testing set was evaluated considering both models, taking into account general errors and metrics focused on the most important values in the context of an imbalanced domain.
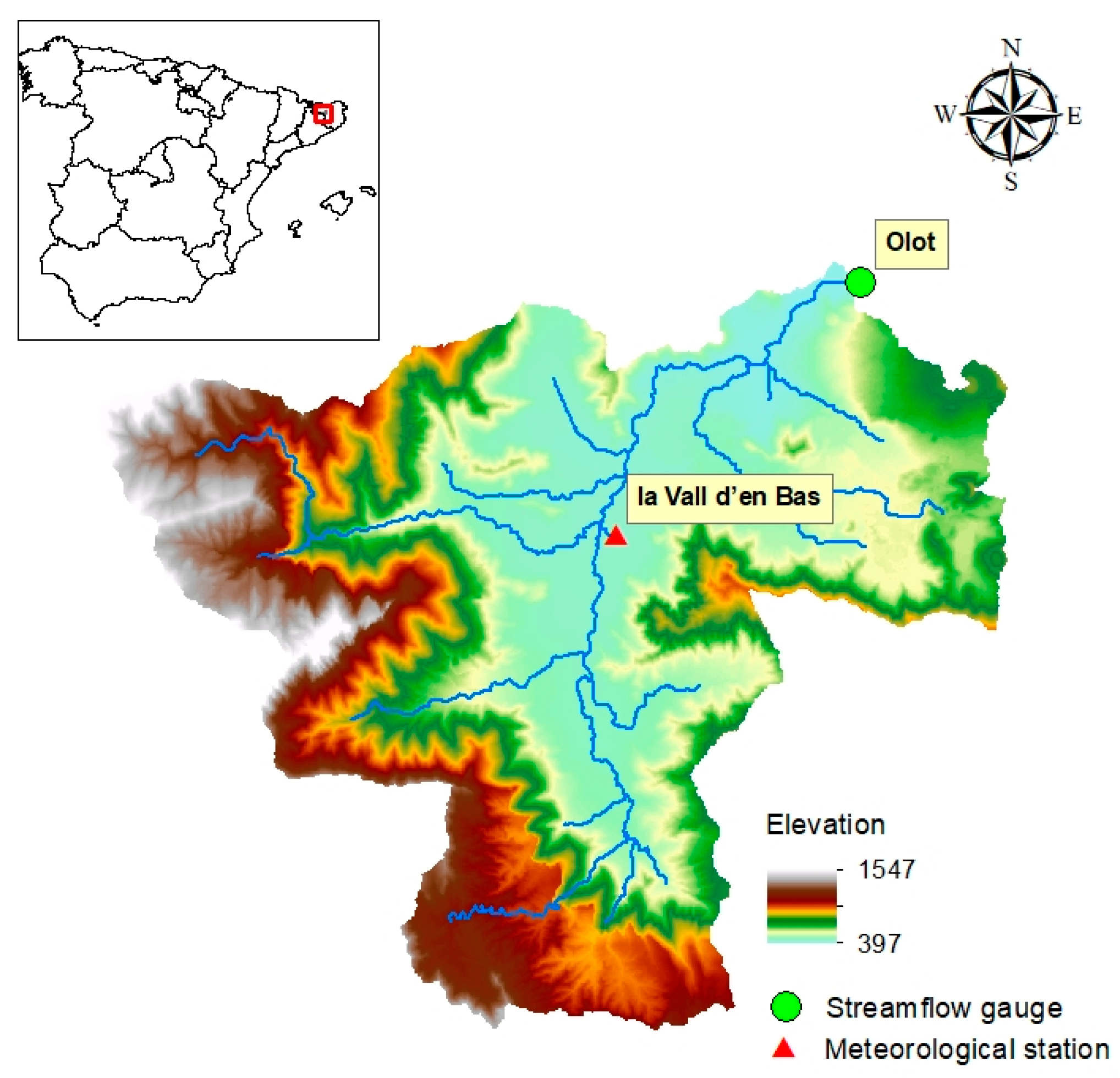
2.2. Study Area
2.3. Data
2.4. Iber Model
2.5. Synthetic Cases
2.6. Regression-Enhanced Random Forest (RERF)
- The k-fold cross-validation method with 10-folds is applied using Lasso regression and the training set following Equation (1) to obtain a suitable penalization parameter (λ). After that, the Lasso model is trained considering the determined λ and the entire training set to establish the coefficients of Equation (5):where Y is the set of outputs (observed streamflow at time t), X is the set of inputs, and βλ are the Lasso coefficients. This study uses the R package glmnet (version 4.1-7) [75] to train the Lasso model.
- 2.
- An RF model is built using the same inputs given in (1) and the error from the Lasso regression (ϵλ) as the output according to (6):The RF model uses the default parameters for the number of trees (ntree) and the number of features (mtry) from the randomForest package of R language [76] and it is denoted by Tntree,mtry (X).
- 3.
- Finally, the RERF model is given by the sum of the Lasso and the RF model (7). In this sense, according to Zhang et al. [24], it is possible to find linear relations between the inputs and the output, making an approximated extrapolation possible.
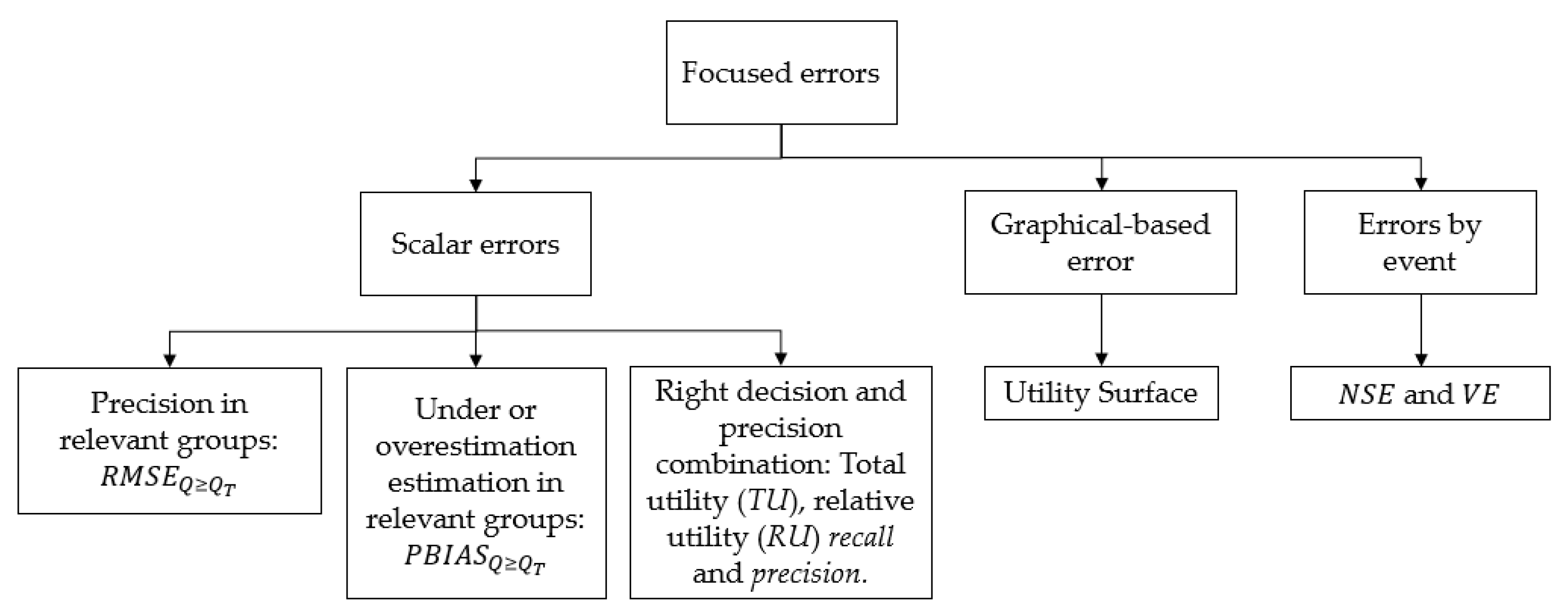
2.7. General and Focused Errors
2.7.1. Scalar Errors
2.7.2. Graphical-Based Errors
2.7.3. Errors by Event
3. Results and Discussion
3.1. Synthetic Cases
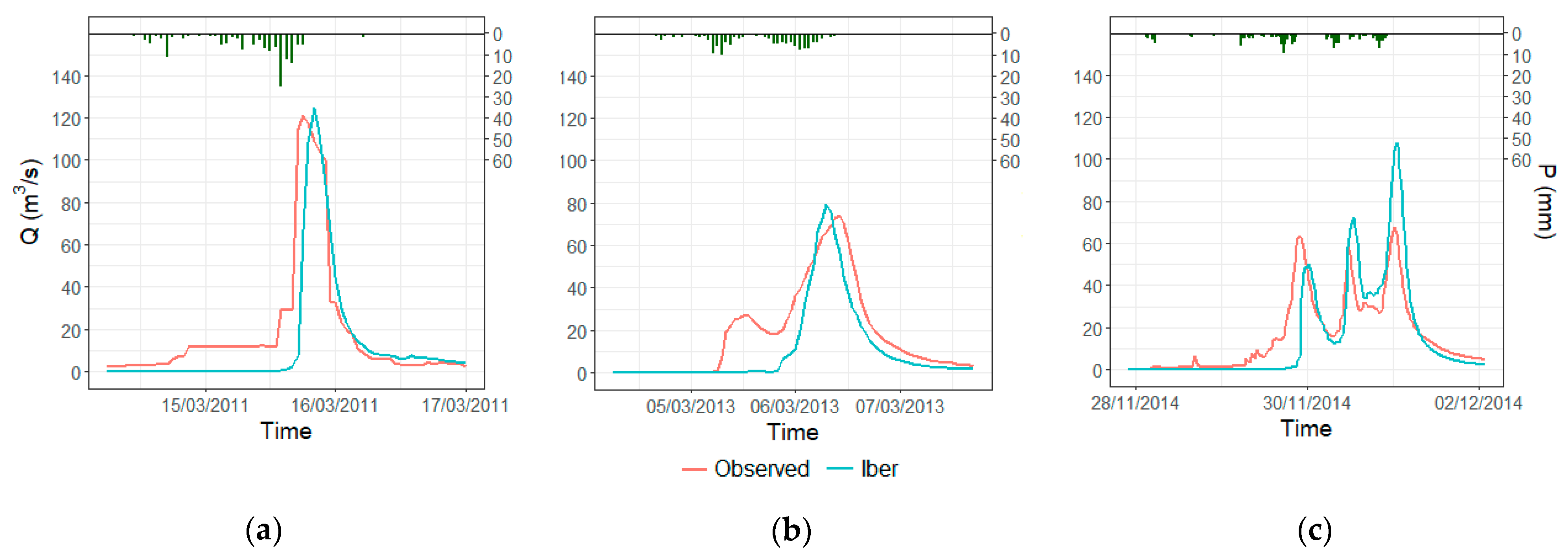
3.2. General Errors
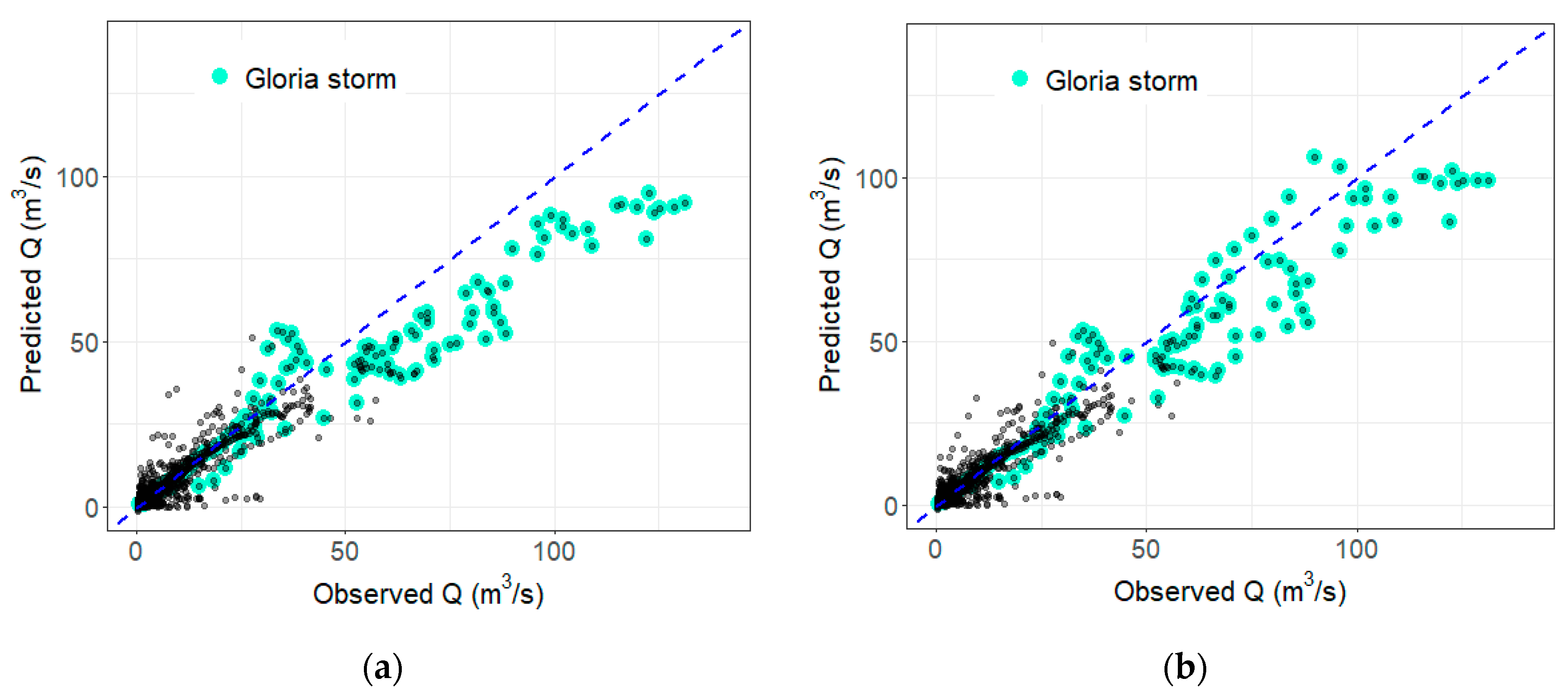
3.3. Focused Errors
3.4. Overall Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
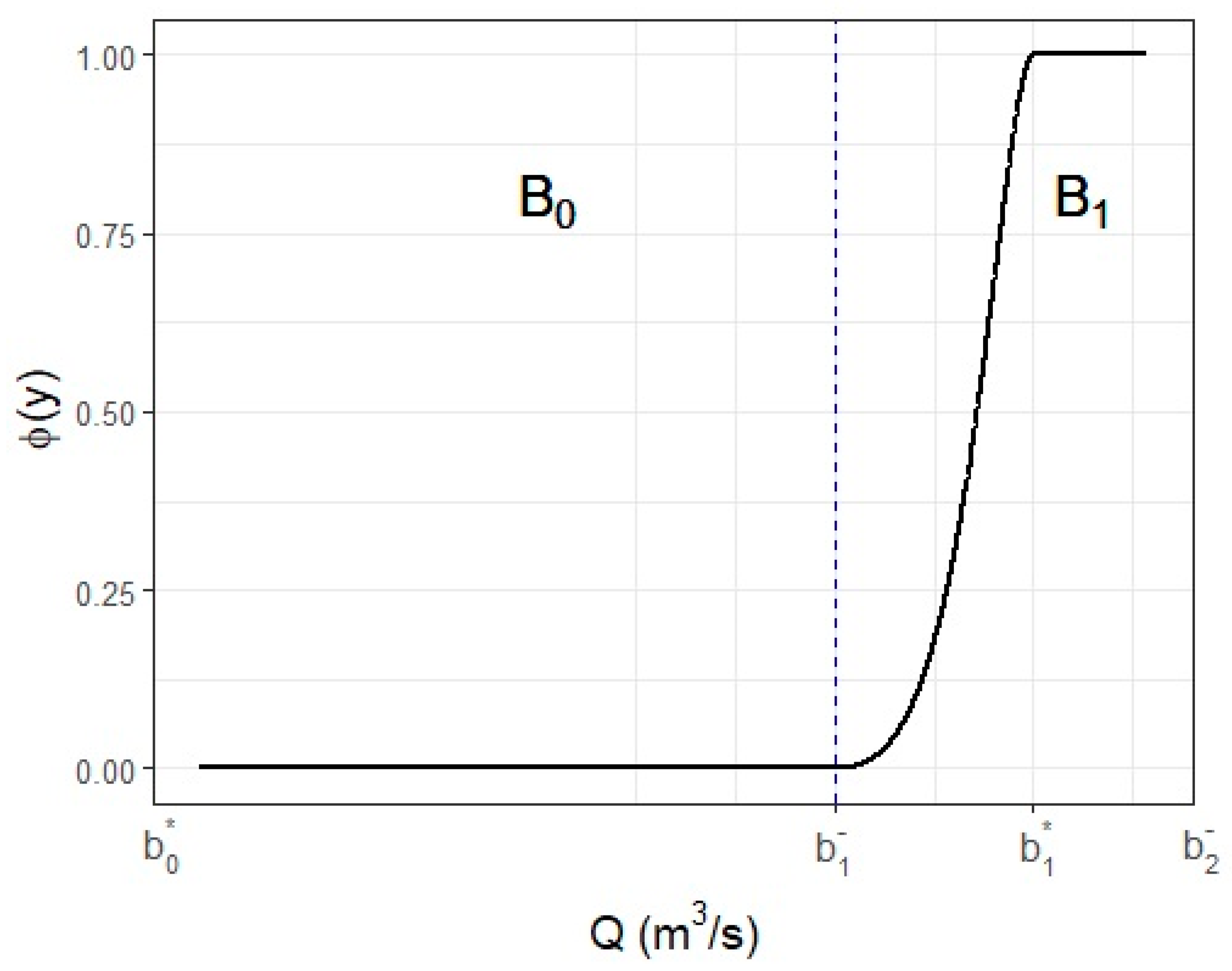
Appendix B
References
- Stefanidis, S.; Stathis, D. Assessment of Flood Hazard Based on Natural and Anthropogenic Factors Using Analytic Hierarchy Process (AHP). Nat. Hazards 2013, 68, 569–585. [Google Scholar] [CrossRef]
- UNISDR. Global Assessment Report on Disaster Risk Reduction; United Nations: Geneva, Switzerland, 2015; ISBN 9789211320428. [Google Scholar]
- Jongman, B.; Kreibich, H.; Apel, H.; Barredo, J.I.; Bates, P.D.; Feyen, L.; Gericke, A.; Neal, J.; Aerts, J.C.J.H.; Ward, P.J. Comparative Flood Damage Model Assessment: Towards a European Approach. Nat. Hazards Earth Syst. Sci. 2012, 12, 3733–3752. [Google Scholar] [CrossRef]
- Laudan, J.; Zöller, G.; Thieken, A.H. Flash Floods versus River Floods-a Comparison of Psychological Impacts and Implications for Precautionary Behaviour. Nat. Hazards Earth Syst. Sci. 2020, 20, 999–1023. [Google Scholar] [CrossRef]
- Hapuarachchi, H.A.P.; Wang, Q.J.; Pagano, T.C. A Review of Advances in Flash Flood Forecasting. Hydrol. Process. 2011, 25, 2771–2784. [Google Scholar] [CrossRef]
- Kobiyama, M.; Goerl, R.F. Quantitative Method to Distinguish Flood and Flash Flood as Disasters. SUISUI Hydrol. Res. Lett. 2007, 1, 11–14. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Kanae, S.; Seneviratne, S.I.; Handmer, J.; Nicholls, N.; Peduzzi, P.; Mechler, R.; Bouwer, L.M.; Arnell, N.; Mach, K.; et al. Flood Risk and Climate Change: Global and Regional Perspectives. Hydrol. Sci. J. 2014, 59, 1–28. [Google Scholar] [CrossRef]
- Zanchetta, A.D.L.; Coulibaly, P. Hybrid Surrogate Model for Timely Prediction of Flash Flood Inundation Maps Caused by Rapid River Overflow. Forecasting 2022, 4, 126–148. [Google Scholar] [CrossRef]
- Cools, J.; Innocenti, D.; O’Brien, S. Lessons from Flood Early Warning Systems. Environ. Sci. Policy 2016, 58, 117–122. [Google Scholar] [CrossRef]
- Giannaros, C.; Dafis, S.; Stefanidis, S.; Giannaros, T.M.; Koletsis, I.; Oikonomou, C. Hydrometeorological Analysis of a Flash Flood Event in an Ungauged Mediterranean Watershed under an Operational Forecasting and Monitoring Context. Meteorol. Appl. 2022, 29, e2079. [Google Scholar] [CrossRef]
- Casagrande, L.; Tomasella, J.; dos Santos Alvalá, R.C.; Bottino, M.J.; de Oliveira Caram, R. Early Flood Warning in the Itajaí-Açu River Basin Using Numerical Weather Forecasting and Hydrological Modeling. Nat. Hazards 2017, 88, 741–757. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.W. Flood Prediction Using Machine Learning Models: Literature Review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Bourdin, D.R.; Fleming, S.W.; Stull, R.B. Streamflow Modelling: A Primer on Applications, Approaches and Challenges. Atmosphere-Ocean 2012, 50, 507–536. [Google Scholar] [CrossRef]
- Majone, B.; Avesani, D.; Zulian, P.; Fiori, A.; Bellin, A. Analysis of High Streamflow Extremes in Climate Change Studies: How Do We Calibrate Hydrological Models? Hydrol. Earth Syst. Sci. 2022, 26, 3863–3883. [Google Scholar] [CrossRef]
- Huang, X.; Li, Y.; Tian, Z.; Ye, Q.; Ke, Q.; Fan, D.; Mao, G.; Chen, A.; Liu, J. Evaluation of Short-Term Streamflow Prediction Methods in Urban River Basins. Phys. Chem. Earth 2021, 123, 103027. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Shalev, G.; Klambauer, G.; Hochreiter, S.; Nearing, G. Benchmarking a Catchment-Aware Long Short-Term Memory Network (LSTM) for Large-Scale Hydrological Modeling. Hydrol. Earth Syst. Sci. Discuss. 2019, 2019, 1–32. [Google Scholar] [CrossRef]
- Jehanzaib, M.; Ajmal, M.; Achite, M.; Kim, T.W. Comprehensive Review: Advancements in Rainfall-Runoff Modelling for Flood Mitigation. Climate 2022, 10, 147. [Google Scholar] [CrossRef]
- Di Nunno, F.; de Marinis, G.; Granata, F. Short-Term Forecasts of Streamflow in the UK Based on a Novel Hybrid Artificial Intelligence Algorithm. Sci. Rep. 2023, 13, 7036. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Herrnegger, M.; Hochreiter, S. A Glimpse into the Unobserved: Runoff Simulation for Ungauged Catchments with LSTMs. In Workshop on Modelling and Decision-Making in the Spatiotemporal Domain, 32nd Conference on Neural Information Processing Systems; NeuRIPS: Montréal, QC, Canada, 2018; Available online: http://www.openreview.net/forum?id=Bylhm72oKX (accessed on 20 February 2023).
- Kim, T.; Yang, T.; Gao, S.; Zhang, L.; Ding, Z.; Wen, X.; Gourley, J.J.; Hong, Y. Can Artificial Intelligence and Data-Driven Machine Learning Models Match or Even Replace Process-Driven Hydrologic Models for Streamflow Simulation?: A Case Study of Four Watersheds with Different Hydro-Climatic Regions across the CONUS. J. Hydrol. 2021, 598, 126423. [Google Scholar] [CrossRef]
- Gauch, M.; Mai, J.; Gharari, S.; Lin, J. Data-Driven vs. Physically-Based Streamflow Prediction Models. In Proceedings of the 9th International Workshop on Climate Informatics, Paris, France, 2–4 October 2019. [Google Scholar]
- Bhasme, P.; Vagadiya, J.; Bhatia, U. Enhancing Predictive Skills in Physically-Consistent Way: Physics Informed Machine Learning for Hydrological Processes. J. Hydrol. 2022, 615, 128618. [Google Scholar] [CrossRef]
- Duan, S.; Ullrich, P.; Shu, L. Using Convolutional Neural Networks for Streamflow Projection in California. Front. Water 2020, 2, 28. [Google Scholar] [CrossRef]
- Zhang, H.; Nettleton, D.; Zhu, Z. Regression-Enhanced Random Forests. arXiv 2019, arXiv:1904.10416v1. [Google Scholar]
- Slater, L.J.; Arnal, L.; Boucher, M.-A.; Chang, A.Y.-Y.; Moulds, S.; Murphy, C.; Nearing, G.; Shalev, G.; Shen, C.; Speight, L.; et al. Hybrid Forecasting: Blending Climate Predictions with AI Models. Hydrol. Earth Syst. Sci. 2023, 27, 1865–1889. [Google Scholar] [CrossRef]
- Wi, S.; Steinschneider, S. Assessing the Physical Realism of Deep Learning Hydrologic Model Projections Under Climate Change. Water Resour. Res. 2022, 58, e2022WR032123. [Google Scholar] [CrossRef]
- Khandelwal, A.; Xu, S.; Li, X.; Jia, X.; Stienbach, M.; Duffy, C.; Nieber, J.; Kumar, V. Physics Guided Machine Learning Methods for Hydrology. arXiv 2020, arXiv:2012.02854v1. [Google Scholar]
- Hoedt, P.-J.; Kratzert, F.; Klotz, D.; Halmich, C.; Holzleitner, M.; Nearing, G.; Hochreiter, S.; Klambauer, G. MC-LSTM: Mass-Conserving LSTM. In Proceedings of the 38th International Conference on Machine Learning, Virtual, 18–24 July 2021. [Google Scholar]
- Xie, K.; Liu, P.; Zhang, J.; Han, D.; Wang, G.; Shen, C. Physics-Guided Deep Learning for Rainfall-Runoff Modeling by Considering Extreme Events and Monotonic Relationships. J. Hydrol. 2021, 603, 127043. [Google Scholar] [CrossRef]
- Asadieh, B.; Krakauer, N.Y. Global Change in Streamflow Extremes under Climate Change over the 21st Century. Hydrol. Earth Syst. Sci. 2017, 21, 5863–5874. [Google Scholar] [CrossRef]
- Cho, K.; Kim, Y. Improving Streamflow Prediction in the WRF-Hydro Model with LSTM Networks. J. Hydrol. 2022, 605, 127297. [Google Scholar] [CrossRef]
- Konapala, G.; Kao, S.C.; Painter, S.L.; Lu, D. Machine Learning Assisted Hybrid Models Can Improve Streamflow Simulation in Diverse Catchments across the Conterminous US. Environ. Res. Lett. 2020, 15, 104022. [Google Scholar] [CrossRef]
- Abebe, A.J.; Price, R.K. Managing Uncertainty in Hydrological Models Using Complementary Models. Hydrol. Sci. J. 2003, 48, 679–692. [Google Scholar] [CrossRef]
- Lu, D.; Konapala, G.; Painter, S.L.; Kao, S.C.; Gangrade, S. Streamflow Simulation in Data-Scarce Basins Using Bayesian and Physics-Informed Machine Learning Models. J. Hydrometeorol. 2021, 22, 1421–1438. [Google Scholar] [CrossRef]
- Liu, B.; Tang, Q.; Zhao, G.; Gao, L.; Shen, C.; Pan, B. Physics-Guided Long Short-Term Memory Network for Streamflow and Flood Simulations in the Lancang–Mekong River Basin. Water 2022, 14, 1429. [Google Scholar] [CrossRef]
- Young, C.C.; Liu, W.C.; Wu, M.C. A Physically Based and Machine Learning Hybrid Approach for Accurate Rainfall-Runoff Modeling during Extreme Typhoon Events. Appl. Soft Comput. J. 2017, 53, 205–216. [Google Scholar] [CrossRef]
- Liu, J.; Yuan, X.; Zeng, J.; Jiao, Y.; Li, Y.; Zhong, L.; Yao, L. Ensemble Streamflow Forecasting over a Cascade Reservoir Catchment with Integrated Hydrometeorological Modeling and Machine Learning. Hydrol. Earth Syst. Sci. 2022, 26, 265–278. [Google Scholar] [CrossRef]
- Mohammadi, B.; Moazenzadeh, R.; Christian, K.; Duan, Z. Improving Streamflow Simulation by Combining Hydrological Process-Driven and Artificial Intelligence-Based Models. Environ. Sci. Pollut. Res. 2021, 28, 65752–65768. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Yang, D.; Chen, J.; Santisirisomboon, J.; Lu, W.; Zhao, B. A Physical Process and Machine Learning Combined Hydrological Model for Daily Streamflow Simulations of Large Watersheds with Limited Observation Data. J. Hydrol. 2020, 590, 125206. [Google Scholar] [CrossRef]
- Feng, D.; Lawson, K.; Shen, C. Mitigating Prediction Error of Deep Learning Streamflow Models in Large Data-Sparse Regions with Ensemble Modeling and Soft Data. Geophys. Res. Lett. 2021, 48, e2021GL092999. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, D.; Wang, G.; Qiu, J.; Long, K.; Du, Y.; Xie, H.; Wei, Z.; Shangguan, W.; Dai, Y. A Hybrid Deep Learning Algorithm and Its Application to Streamflow Prediction. J. Hydrol. 2021, 601, 126636. [Google Scholar] [CrossRef]
- Branco, P.; Ribeiro, R.P.; Torgo, L.; Krawczyk, B.; Moniz, N. SMOGN: A Pre-Processing Approach for Imbalanced Regression. Proc. Mach. Learn. Res. 2017, 74, 36–50. [Google Scholar]
- Ribeiro, R.P.; Moniz, N. Imbalanced Regression and Extreme Value Prediction. Mach. Learn. 2020, 109, 1803–1835. [Google Scholar] [CrossRef]
- Snieder, E.; Abogadil, K.; Khan, U.T. Resampling and Ensemble Techniques for Improving ANN-Based High-Flow Forecast Accuracy. Hydrol. Earth Syst. Sci. 2021, 25, 2543–2566. [Google Scholar] [CrossRef]
- Granata, F.; Di Nunno, F.; de Marinis, G. Stacked Machine Learning Algorithms and Bidirectional Long Short-Term Memory Networks for Multi-Step Ahead Streamflow Forecasting: A Comparative Study. J. Hydrol. 2022, 613, 128431. [Google Scholar] [CrossRef]
- Témez, J. Cálculo Hidromteorológico de Caudales Máximos En Pequeñas Cuencas Naturales; Ministerio de Obras Públicas y Urbanismo, Dirección General de Carreteras: Madrid, Spain, 1978. [Google Scholar]
- ICGC. Available online: http://www.icc.cat/vissir3/ (accessed on 24 November 2022).
- CLC Copernicus Land Monitoring Service. Available online: https://land.copernicus.eu/pan-european/corine-land-cover/clc2018 (accessed on 24 November 2022).
- Roux, H.; Amengual, A.; Romero, R.; Bladé, E.; Sanz-Ramos, M. Evaluation of Two Hydrometeorological Ensemble Strategies for Flash-Flood Forecasting over a Catchment of the Eastern Pyrenees. Nat. Hazards Earth Syst. Sci. 2020, 20, 425–450. [Google Scholar] [CrossRef]
- Lana, X.; Casas-Castillo, M.C.; Rodríguez-Solà, R.; Serra, C.; Martínez, M.D.; Kirchner, R. Rainfall Regime Trends at Annual and Monthly Scales in Catalonia (NE Spain) and Indications of CO2 Emissions Effects. Theor. Appl. Climatol. 2021, 146, 981–996. [Google Scholar] [CrossRef]
- Llasat, M.C.; Llasat-Botija, M.; Rodriguez, A.; Lindbergh, S. Flash Floods in Catalonia: A Recurrent Situation. Adv. Geosci. 2010, 26, 105–111. [Google Scholar] [CrossRef]
- INUNCAT. Plan Especial de Emergencias Para Inundaciones. 2017. Available online: https://www.proteccioncivil.es/catalogo/naturales/jornada-normativa-inundaciones-0612/planesccaa/cataluna/INUNCAT.pdf (accessed on 24 November 2022).
- Rogers, G.; Sorensen, J.H. Diffusion of Emergency Warning: Comparing Empirical and Simulation Results; Springer Science + Business Media: New York, NY, USA, 1991. [Google Scholar] [CrossRef]
- Aboelata, M.; Bowles, D.S.; Mcclelland, D.M. A Model for Estimating Dam Failure Life Loss. In Proceedings of the Australian Committee on Large Dams Risk Workshop, Launceston, Tasmania, Australia, October 2003; Available online: https://www.researchgate.net/profile/David-Bowles-3/publication/228771403_A_model_for_estimating_dam_failure_life_loss/links/0912f51007ae49d483000000/A-model-for-estimating-dam-failure-life-loss.pdf (accessed on 20 February 2023).
- Hofflinger, A.; Somos-Valenzuela, M.A.; Vallejos-Romero, A. Response Time to Flood Events Using a Social Vulnerability Index (ReTSVI). Nat. Hazards Earth Syst. Sci. 2019, 19, 251–267. [Google Scholar] [CrossRef]
- Jimeno-Sáez, P.; Senent-Aparicio, J.; Pérez-Sánchez, J.; Pulido-Velazquez, D. A Comparison of SWAT and ANN Models for Daily Runoff Simulation in Different Climatic Zones of Peninsular Spain. Water 2018, 10, 192. [Google Scholar] [CrossRef]
- Muñoz, P.; Orellana-Alvear, J.; Willems, P.; Célleri, R. Flash-Flood Forecasting in an Andean Mountain Catchment—Development of a Step-Wise Methodology Based on the Random Forest Algorithm. Water 2018, 10, 1519. [Google Scholar] [CrossRef]
- Leahy, P.; Kiely, G.; Corcoran, G. Structural Optimisation and Input Selection of an Artificial Neural Network for River Level Prediction. J. Hydrol. 2008, 355, 192–201. [Google Scholar] [CrossRef]
- Badrzadeh, H.; Sarukkalige, R.; Jayawardena, A.W. Hourly Runoff Forecasting for Flood Risk Management: Application of Various Computational Intelligence Models. J. Hydrol. 2015, 529, 1633–1643. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Society. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- de Ville, B. Decision Trees. Wiley Interdiscip Rev. Comput. Stat. 2013, 5, 448–455. [Google Scholar] [CrossRef]
- Sanz-Ramos, M.; Amengual, A.; Bladé, E.; Romero, R.; Roux, H. Flood Forecasting Using a Coupled Hydrological and Hydraulic Model (Based on FVM) and Highresolution Meteorological Model. In Proceedings of the E3S Web of Conferences 40: River Flow 2018-Ninth International Conference on Fluvial Hydraulics, Lyon-Villeurbanne, France, 5–8 September 2018; EDP Sciences: Les Ulis, France, 2018; Volume 40. [Google Scholar]
- Cea, L.; Bladé, E. A Simple and Efficient Unstructured Finite Volume Scheme for Solving the Shallow Water Equations in Overland Flow Applications. Water Resour. Res. 2015, 51, 5464–5486. [Google Scholar] [CrossRef]
- Bladé, E.; Cea, L.; Corestein, G.; Escolano, E.; Puertas, J.; Vázquez-Cendón, E.; Dolz, J.; Coll, A. Iber: Herramienta de Simulación Numérica Del Flujo En Ríos. Rev. Int. De Metodos Numer. Para Calc. Y Diseno Ing. 2014, 30, 1–10. [Google Scholar] [CrossRef]
- Sanz-Ramos, M.; Bladé, E.; González-Escalona, F.; Olivares, G.; Aragón-Hernández, J.L. Interpreting the Manning Roughness Coefficient in Overland Flow Simulations with Coupled Hydrological-Hydraulic Distributed Models. Water 2021, 13, 3433. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1988; ISBN 0071001743. [Google Scholar]
- Ministerio de Medio Ambiente y Medio Rural y Marino. Guía Metodológica Para el Desarrollo del Sistema Nacional de Cartografía de Zonas Inundables; Ministerio de Medio Ambiente, y Medio Rural y Marino: Madrid, Spain, 2011; ISBN 9788449111365. Available online: https://www.miteco.gob.es/es/agua/publicaciones/guia_metodologica_ZI.aspx (accessed on 6 March 2023).
- Aparicio Mijares, F.J. Fundamentos de Hidrología de Superficie; Editorial Limusa and Grupo Noriega de Editores: México D.F., México, 1989; ISBN 9681830148. [Google Scholar]
- Sikorska, A.E.; Viviroli, D.; Seibert, J. Effective Precipitation Duration for Runoff Peaks Based on Catchment Modelling. J. Hydrol. 2018, 556, 510–522. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Venkatesan, E.; Mahindrakar, A.B. Forecasting Floods Using Extreme Gradient Boosting A New Approach. Int. J. Civ. Eng. Technol. 2019, 10, 1336–1346. [Google Scholar]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. A Brief Review of Random Forests for Water Scientists and Practitioners and Their Recent History in Water Resources. Water 2019, 11, 910. [Google Scholar] [CrossRef]
- Lantz, B. Machine Learning with R; Packt Publishing: Birmingham, UK, 2013; ISBN 9781782162148. [Google Scholar]
- Díaz-Uriarte, R.; Alvarez de Andrés, S. Gene Selection and Classification of Microarray Data Using Random Forest. BMC Bioinform. 2006, 7, 3. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Package RandomForest—Breiman and Culter’s Random Forest for Classification and Regression. Version 4.7-1.1. 2022. Available online: https://cran.r-project.org/web/packages/randomForest/randomForest.pdf (accessed on 9 December 2022).
- Shu, C.; Burn, D.H. Artificial Neural Network Ensembles and Their Application in Pooled Flood Frequency Analysis. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Dazzi, S.; Vacondio, R.; Mignosa, P. Flood Stage Forecasting Using Machine-Learning Methods: A Case Study on the Parma River (Italy). Water 2021, 13, 1612. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of Different Efficiency Criteria for Hydrological Model Assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Branco, P. Utility-Based Predictive Analytics. Ph.D. Thesis, Programa Doutoral em Informática das Universidades do Minho, Aveiro e Porto, Portugal, 2018. [Google Scholar]
- Carpenter, T.M.; Sperfslage, J.A.; Georgakakos, K.P.; Sweeney, T.; Fread, D.L. National Threshold Runoff Estimation Utilizing GIS in Support of Operational Flash Flood Warning Systems. J. Hydrol. 1999, 224, 21–44. [Google Scholar] [CrossRef]
- Toth, E. Estimation of Flood Warning Runoff Thresholds in Ungauged Basins with Asymmetric Error Functions. Hydrol. Earth Syst. Sci. 2016, 20, 2383–2394. [Google Scholar] [CrossRef]
- Yue, S.; Ouarda, T.B.M.J.; Bobée, B.; Legendre, P.; Bruneau, P. The Gumbel Mixed Model for Flood Frequency Analysis. J. Hydrol. 1999, 226, 88–100. [Google Scholar] [CrossRef]
- Cardoso de Salis, H.H.; Monteiro da Costa, A.; Moreira Vianna, J.H.; Azeneth Schuler, M.; Künne, A.; Sanches Fernandes, L.F.; Leal Pacheco, F.A. Hydrologic Modeling for Sustainable Water Resources Management in Urbanized Karst Areas. Int. J. Environ. Res. Public Health 2019, 16, 2542. [Google Scholar] [CrossRef]
- Ribeiro, R.P. Utility-Based Regression. Ph.D. Thesis, Department of Computer Science, Faculty of Sciences, University of Porto, Porto, Portugal, 2011. [Google Scholar]
- Borchers, H.W. Package Pracma: Practical Numerical Math Functions. Version 2.4.2. 2022. Available online: https://cran.r-project.org/web/packages/pracma/pracma.pdf (accessed on 9 December 2022).
- Bivand, R.S.; Pebesma, E.J.; Gómez-Rubio, V. Applied Spatial Data Analysis with R; Springer: Berlin/Heidelberg, Germany, 2008; ISBN 9780387781709. [Google Scholar]
- Nash, J.E.; Sutcliffe, J. V River Flow Forecasting through Conceptual Models Part I—A Disscussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Criss, R.E.; Winston, W.E. Do Nash Values Have Value? Discussion and Alternate Proposals. Hydrol. Process. 2008, 22, 2723–2725. [Google Scholar] [CrossRef]
- Yilmaz, M.U.; Onoz, B. A Comparative Study of Statistical Methods for Daily Streamflow Estimation at Ungauged Basins in Turkey. Water 2020, 12, 459. [Google Scholar] [CrossRef]
- Motovilov, Y.G.; Gottschalk, L.; Engeland, K.; Rodhe, A. Validation of a Distributed Hydrological Model against Spatial Observations. Agric. For. Meteorol. 1999, 98–99, 257–277. [Google Scholar] [CrossRef]






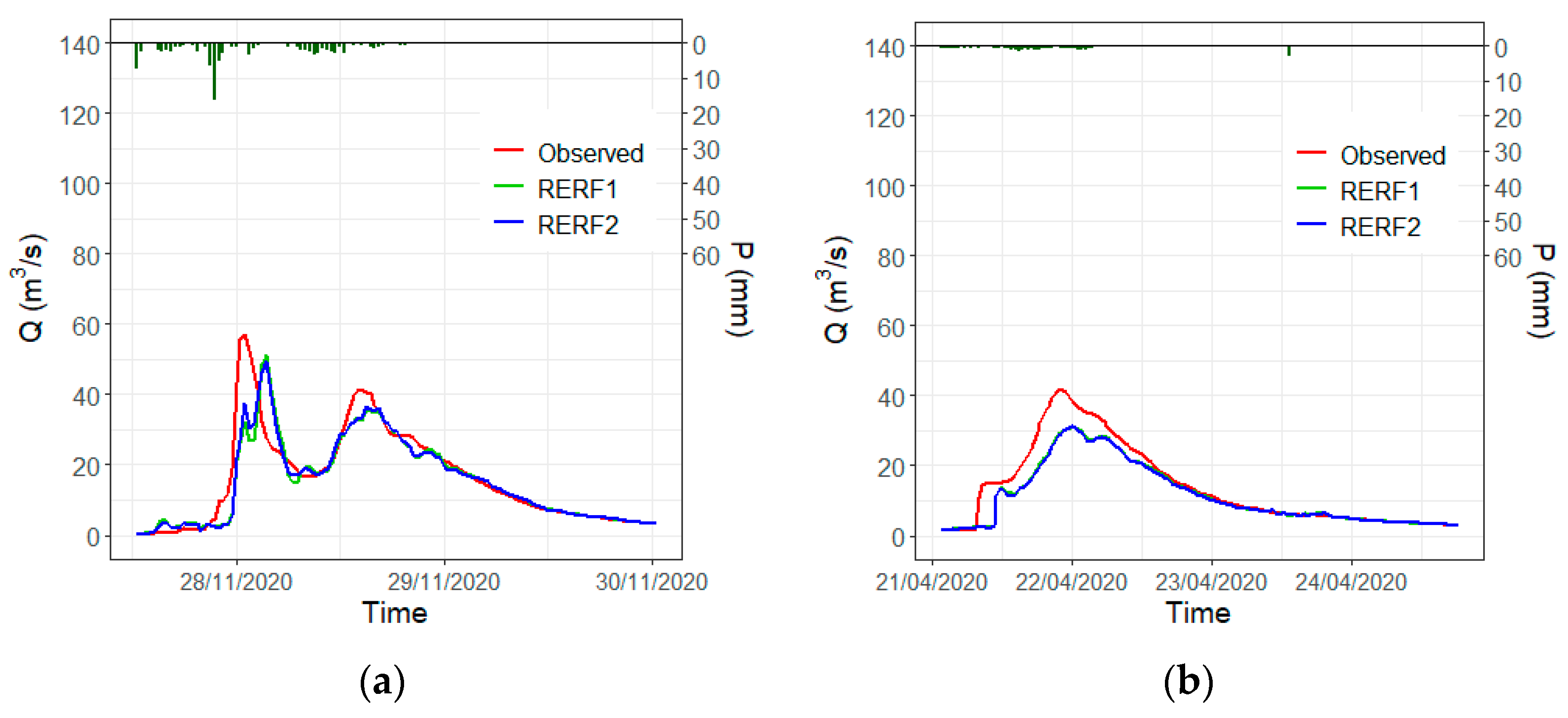
| MAE (m³/s) | RMSE (m³/s) | MAPE (%) | R² | |
|---|---|---|---|---|
| RERF1 | 0.14 | 1.17 | 11.10 | 0.94 |
| RERF2 | 0.13 | 1.01 | 11.05 | 0.94 |
| Total Utility | Relative Utility | Recall | Precision | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (m³/s) | (m³/s) | (m³/s) | (%) | (%) | (%) | |||||
| RERF1 | 9.22 | 21.19 | 25.97 | −15.2 | −25.9 | −24.8 | 105.25 | 0.53 | 0.69 | 0.73 |
| RERF2 | 7.86 | 16.60 | 19.96 | −11.8 | −16.7 | −15.2 | 116.37 | 0.58 | 0.77 | 0.80 |
| Percentage Change | −14.78% | −21.63% | −23.15% | −22.37% | −35.52% | −38.71% | 10.56% | 10.56% | 11.39% | 10.09% |
| NSE | VE | |||||
|---|---|---|---|---|---|---|
| Gloria Storm | 2nd Event | 3rd Event | Gloria Storm | 2nd Event | 3rd Event | |
| RERF1 | 0.86 | 0.77 | 0.85 | 0.77 | 0.81 | 0.82 |
| RERF2 | 0.91 | 0.81 | 0.84 | 0.82 | 0.83 | 0.81 |
| Percentage Change | 6.13% | 5.84% | −1.18% | 6.44% | 1.95% | −1.06% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-Chacón, S.R.; Salazar, F.; Bladé, E. Combining Synthetic and Observed Data to Enhance Machine Learning Model Performance for Streamflow Prediction. Water 2023, 15, 2020. https://doi.org/10.3390/w15112020
López-Chacón SR, Salazar F, Bladé E. Combining Synthetic and Observed Data to Enhance Machine Learning Model Performance for Streamflow Prediction. Water. 2023; 15(11):2020. https://doi.org/10.3390/w15112020
Chicago/Turabian StyleLópez-Chacón, Sergio Ricardo, Fernando Salazar, and Ernest Bladé. 2023. "Combining Synthetic and Observed Data to Enhance Machine Learning Model Performance for Streamflow Prediction" Water 15, no. 11: 2020. https://doi.org/10.3390/w15112020
APA StyleLópez-Chacón, S. R., Salazar, F., & Bladé, E. (2023). Combining Synthetic and Observed Data to Enhance Machine Learning Model Performance for Streamflow Prediction. Water, 15(11), 2020. https://doi.org/10.3390/w15112020






