Dynamic Response Law and Failure Mechanism of Slope with Weak Interlayer under Combined Action of Reservoir Water and Seismic Force
Abstract
:1. Introduction
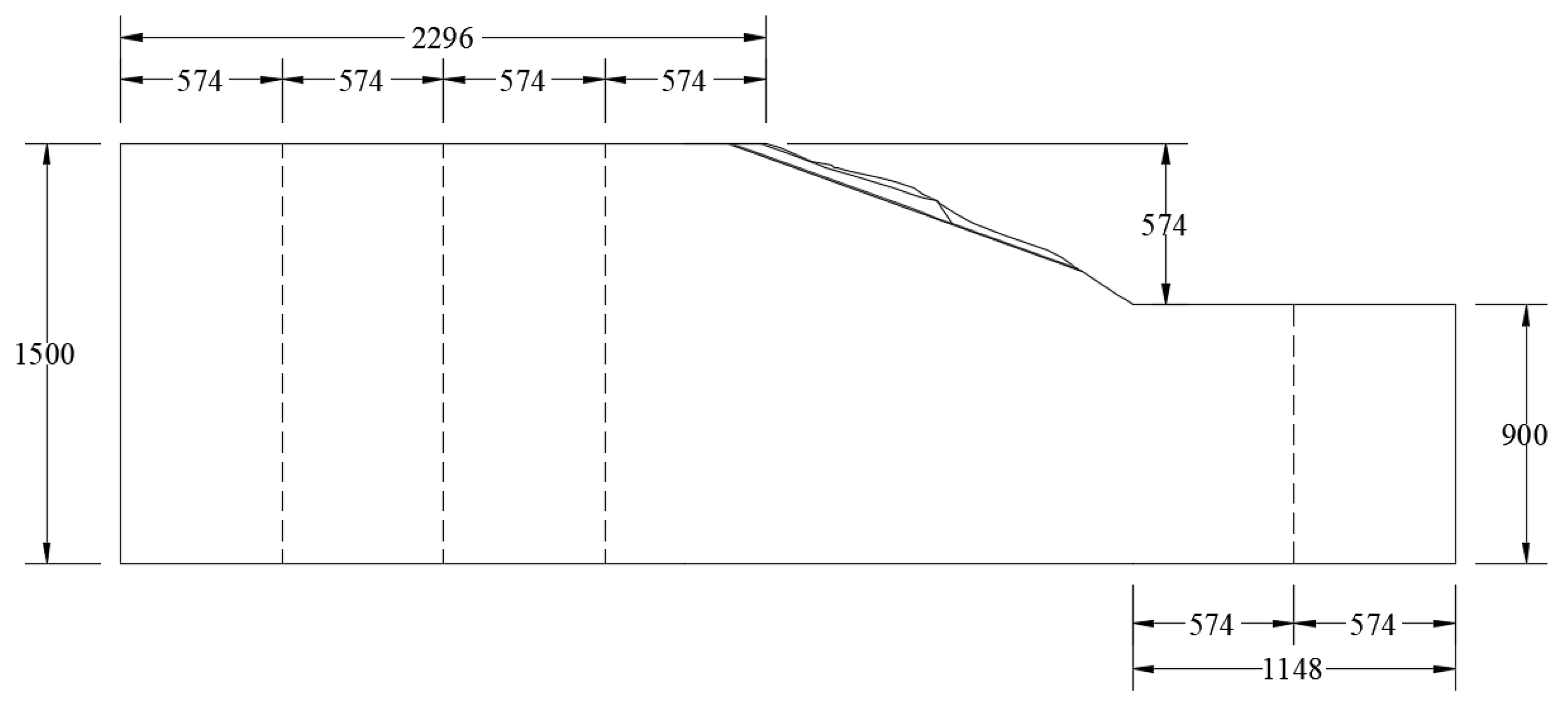
2. Shaking Table Model Test Scheme
2.1. General Situation of Engineering Geological Environment
2.2. Determining the Physical Parameters of Each Rock Layer
2.3. Similar Relationships and Material Ratios
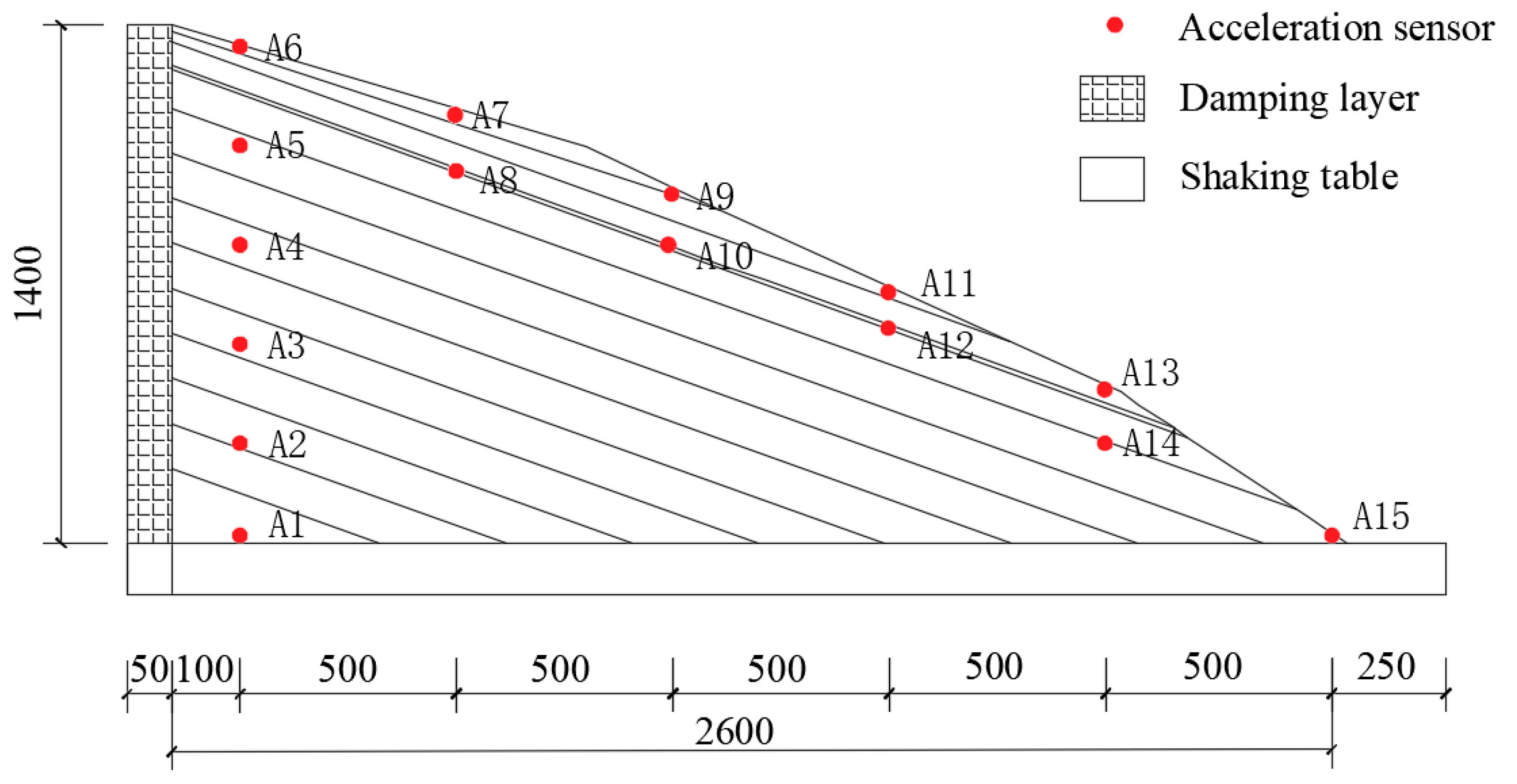
2.4. Layout of Monitoring Points
2.5. Seismic Input and Loading Scheme
3. Shaking Table Test Results and Analysis
3.1. Dynamic Response Analysis during Earthquake
- It can be seen that when the input seismic acceleration was the same, the PGA at the normal water level was greater than that with no water, indicating that the mudding effect of reservoir water had a significant amplification effect on the PGA of the slope. The sedimentation of reservoir water also had a certain influence on the PGA distribution of the slope, and the enlarged area of PGA in the slope obviously increased after sedimentation. This is because after the front section of the weak interlayer was cemented, the cohesive force of the weak interlayer decreased, and the slope surface was damaged under the action of seismic waves, so the acceleration amplification effect at the slope angle was more obvious.
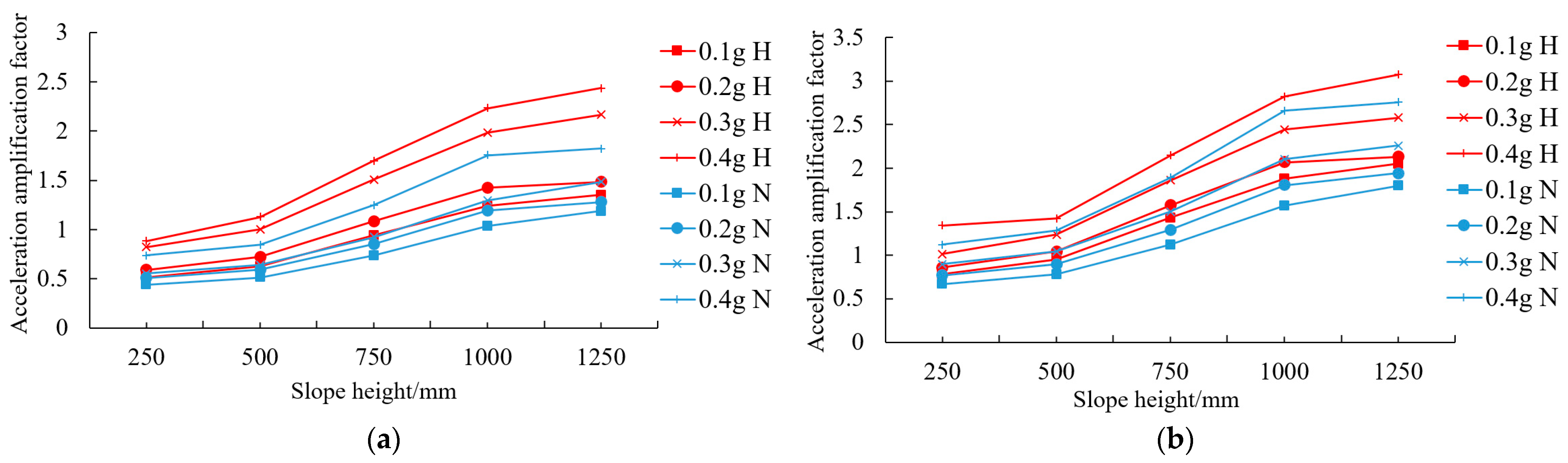
- When both horizontal and vertical seismic waves were input, the acceleration response of the slope increased from the bottom to the top along the slope surface, reaching the maximum value at the top of the slope, with the maximum amplification factor of 2.5 with the input of vertical seismic waves, 3.25 with the input of horizontal seismic waves, and 0.83 times at the peak dynamic response of vertical seismic waves. By observing the slope of the folding line of the amplification coefficient change in PGA, it can be seen that, when increasing the slope height of the same height, the change in PGA at the slope angle of 250–500 mm is not significant. PGA rapidly increases in the middle part of the slope at 500–1000 mm, and the increase rate slows down again at 1000–1250 mm. Analyzing this phenomenon indicates that the impact of earthquakes on the slope is mainly evident in the middle part of the slope, and it can be considered that the middle part of the slope should be reinforced. It can reduce the PGA growth rate.
- Upon comparing normal water storage conditions with no water level conditions, it can be observed that an increase in water level significantly increases the PGA amplification coefficient of the slope surface. When inputting vertical seismic waves, the peak value of PGA without water level is 1.82, and under normal water storage conditions, the peak value of PGA is 2.43, an increase of 33%. When inputting horizontal seismic waves, the PGA peak without water level is 2.76, and under normal water storage conditions, the PGA peak is 3.07, an increase of 11%. By analyzing the above data, it can be found that changes in water level have a significant impact on the dynamic response of the slope; especially, when inputting vertical seismic waves, the change in PGA is more severe. This indicates that, when analyzing the dynamic response of the slope, reservoir water and vertical earthquakes are two important factors affecting the stability of the slope.
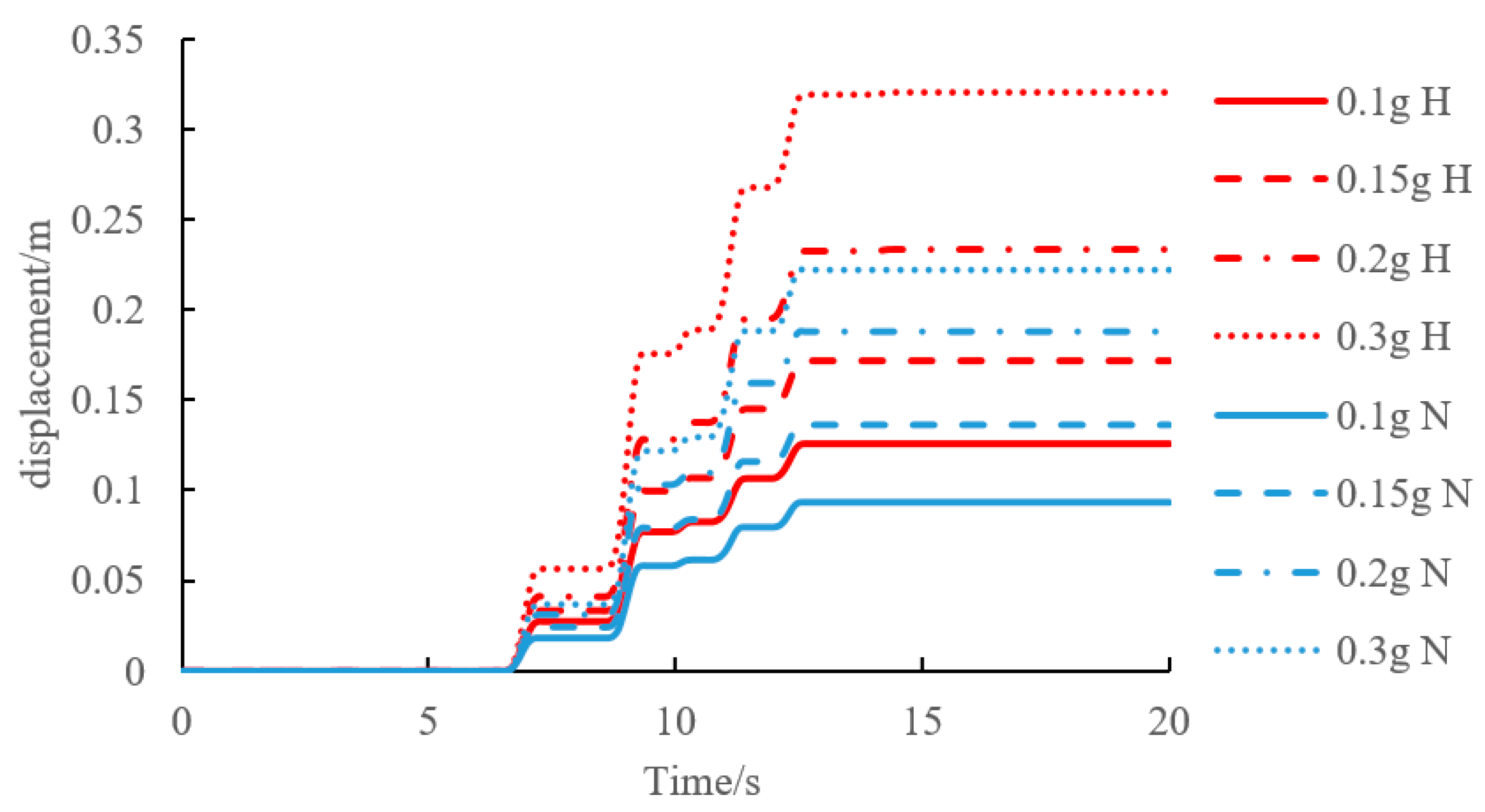
3.2. Analysis of Permanent Displacement during Earthquake
4. Numerical Simulation Analysis
4.1. Analysis Software and Constitutive Model Selection
4.2. The Establishment and Calculation of Numerical Model
4.3. Effect of Reservoir Water and Earthquake on Weak Sandwich Slope
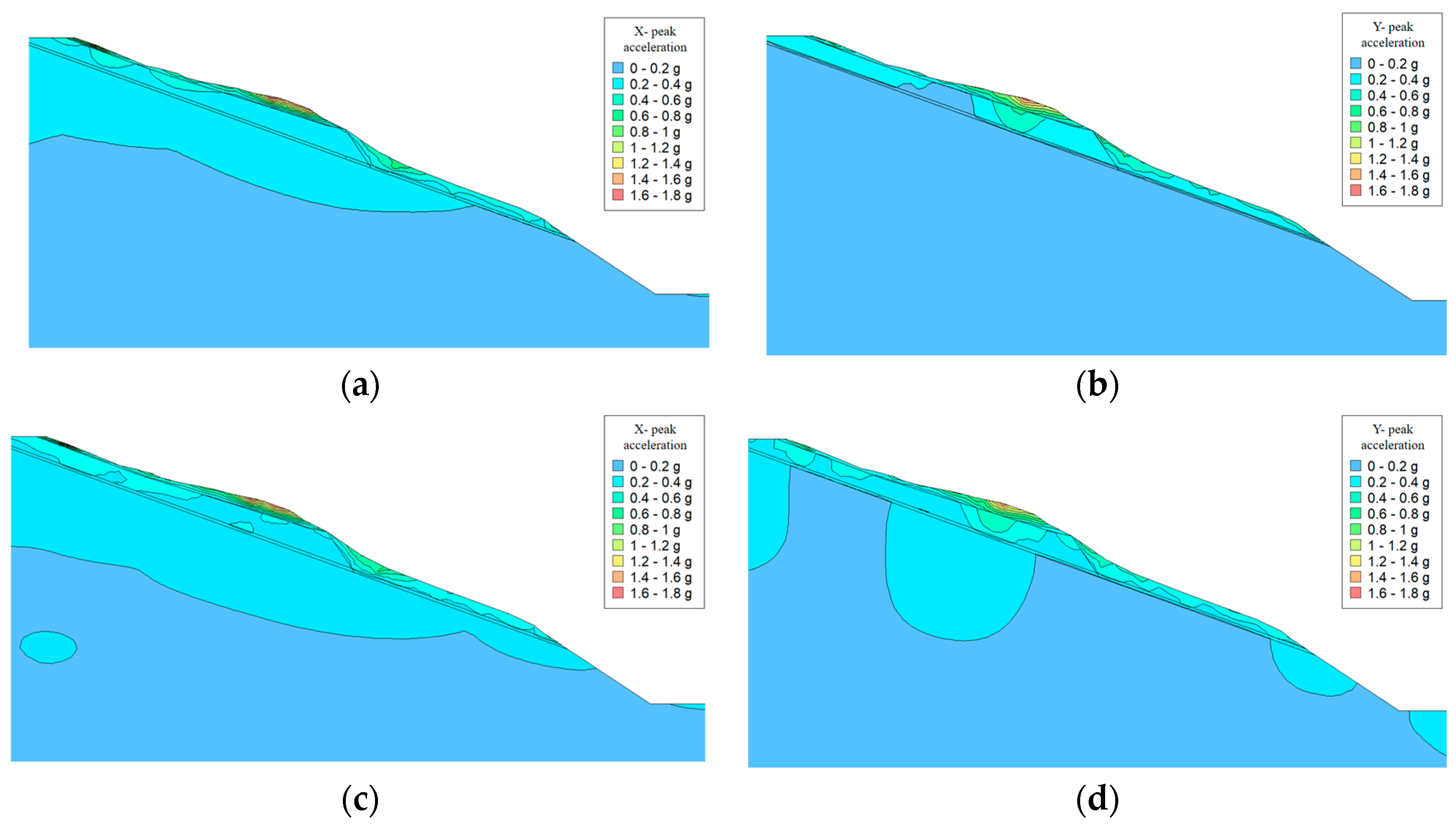
4.3.1. Acceleration Response Analysis
- By analyzing the PGA variation curves of different vertical seismic actions in the X direction, it can be seen from Figure 13a that the influence of reservoir water mud was mainly 300 m away from the bottom of the slope. With the increase in the input vertical seismic acceleration, the PGA within 300 m of the bottom of the slope changed most obviously among the four monitoring points on the slope surface. Compared with the normal water level and no water, only the PGA gap within 300 m of the bottom of the slope was large, and the PGA in other areas was very similar. This shows that when the weak interlayer in the front of a slope is muddled, the dynamic response of the slope will increase, i.e., the muddied, weak interlayer in the X direction can amplify the seismic wave.
- By analyzing the PGA variation curves of different vertical seismic actions in the Y direction, it can be seen from Figure 13b that the influence of reservoir water mud was mainly 400 m from the bottom of the slope, and the PGA in other areas were very similar with the normal water level and with no water, which indicates that vertical seismic waves mainly affect the middle of a slope. When the weak interlayer in front of the slope was muddy, the dynamic response in the Y direction was mainly reflected in the middle and upper part of the slope. The maximum PGA value in the Y direction was 3.0, which could reach 0.85 times the maximum PGA value in the X direction, which was 3.5. These were very similar to the results of the model test, which showed that the numerical simulation had a high level of reliability.
4.3.2. Permanent Displacement Analysis
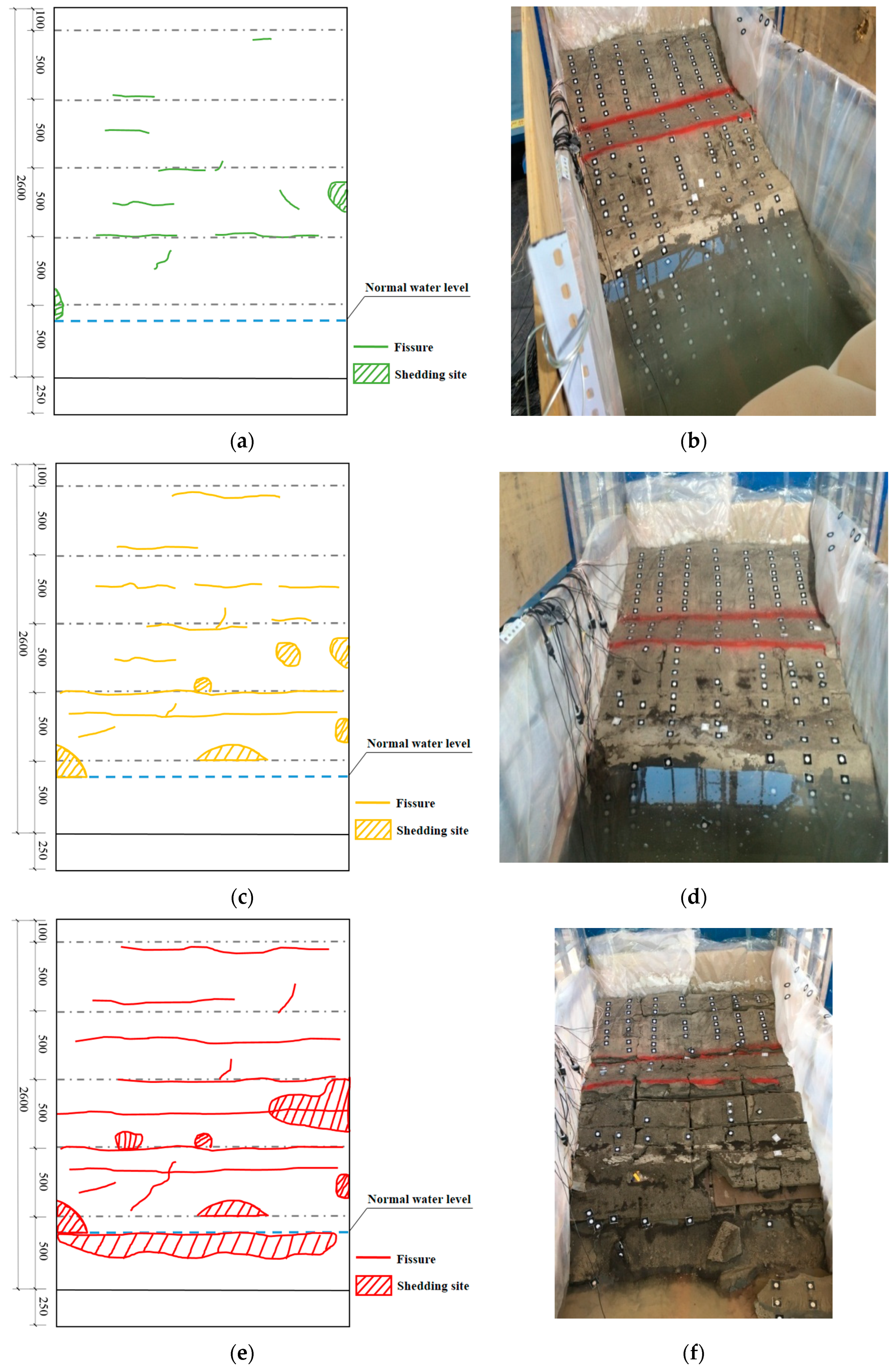
5. Failure Pattern and Instability Mechanism Analysis
5.1. Slope Failure Pattern
5.2. Induced Factors and Failure Mechanism of Slope Slip
6. Conclusions
- Seismic waves are affected by weak interlayers, which overlap repeatedly between a weak interlayer and a slope surface. The acceleration amplification effect is about 1.8 times larger than that of a homogeneous slope. The acceleration response of the input vertical and horizontal seismic waves in a slope is magnified from the bottom to the top along the slope surface and reaches the maximum value at the top of the slope. A vertical earthquake has a significant influence on the dynamic response of a slope. The magnification factor of peak acceleration can reach 0.83 times the horizontal peak acceleration. An increase in the intensity of a vertical earthquake is more likely to induce damage on the top and in the middle of a slope.
- When considering the mud action of reservoir water on weak interlayers, with the increase in the input seismic acceleration, sliding failure first occurs in the mud area located in the weak interlayer. The shear entrance and shear exit of slope sliding are located in the middle and at the foot of the slope, respectively, which indicates that the stability of the weak interlayer directly affected by reservoir water is the worst.
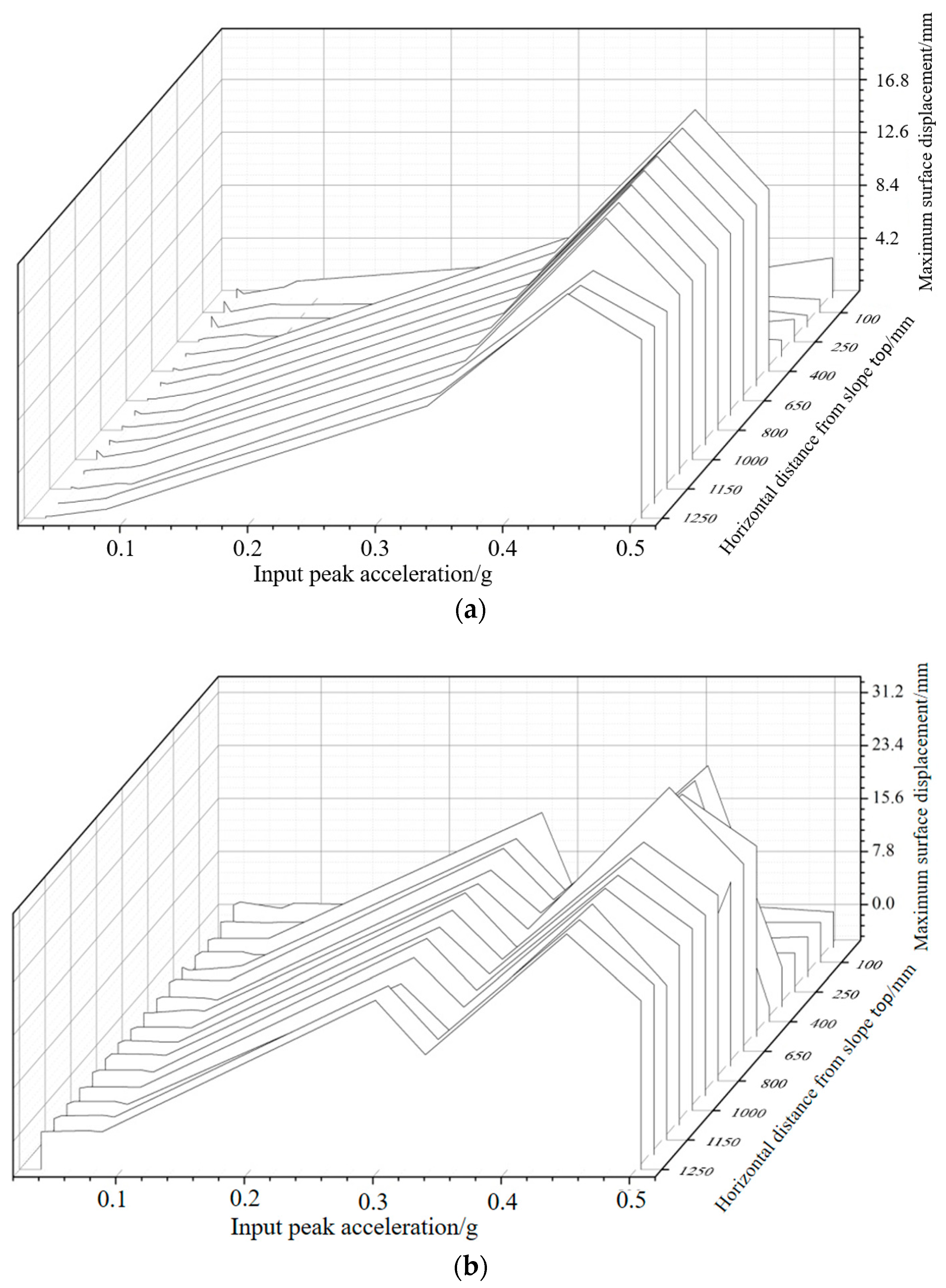
- The displacement of a slope can be generalized into three stages with the increase in a seismic wave. The first stage is elastic deformation, when the displacement increases uniformly from 0 to 0.3 g. In the second stage, when the displacement is 0.3–0.45 g, the displacement first decreases and then increases, which is the plastic deformation stage. The maximum displacement of the slope surface also appears, up to 31.2 mm. The third stage is when the surface displacement decreases sharply after reaching 0.45 g, which is the sliding destabilization stage, indicating that the slope begins to slide and destabilize at this time.
- The failure mode of the slope is as follows: cracking occurs in the upper part of the slope due to an earthquake. With the increase in the intensity of the earthquake and reservoir water infiltration, the crack propagation is aggravated, and sliding damage occurs gradually in the front section of the slope. Finally, accumulation occurs at the foot of the slope. The failure mode of the slope model reveals that the sliding surface is controlled by a weak interlayer. When a strong earthquake and the water level in the reservoir area jointly affect the weak-interlayer slope, the slope is in the plastic deformation and instability stage. The stability of the slope may be overestimated, and sliding instability easily occurs. Therefore, monitoring and treatment must be carried out.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.M. Research status and development trend of rock slope stability with weak interlayer. Chin. J. Eng. Geol. 2020, 28, 626–638. [Google Scholar] [CrossRef]
- Niu, Y.; Yang, X.Z.; Zhao, J.L.; Ji, W.K. Seismic stability analysis of slope with sandwich based on upper limit analysis. J. Highw. Transp. Sci. Technol. 2019, 36, 38–45. [Google Scholar]
- Lin, M.L.; Lin, C.H.; Li, C.H.; Liu, C.Y.; Hung, C.H. 3D modeling of the ground deformation along the fault rupture and its impact on engineering structures: Insights from the 1999 Chi-Chi earthquake, Shigang District, Taiwan. Eng. Geol. 2021, 281, 105993. [Google Scholar] [CrossRef]
- Li, S.D.; Li, X.; Zhang, J.; He, J.M.; Li, S.H.; Wang, Y.C. Research on formation mechanism of Tangjiashan landslide and overall stability of barrier dam. Chin. J. Rock Mech. Eng. 2010, 29 (Suppl. S1), 2908–2915. [Google Scholar]
- Xu, L.; Pei, X.J.; Wu, J.H. Stability evaluation and treatment of Zhengjiashan Landslide in Sichuan Earthquake stricken area. J. Chang. Inst. Technol. (Nat. Sci. Ed.) 2010, 11, 68–70+81. [Google Scholar]
- Haeri, S.M.; Kavand, A.; Rahmani, I.; Torabi, H. Response of a group of piles to liquefaction-induced lateral spreading by large scale shake table testing. Soil Dyn. Earthq. Eng. 2012, 38, 25–45. [Google Scholar] [CrossRef]
- Panah, A.K.; Eftekhari, Z. Shaking table tests on polymeric-strip reinforced-soil walls adjacent to a rock slope. Geotext. Geomembr. 2021, 49, 737–756. [Google Scholar] [CrossRef]
- Wang, H.L.; Jiang, Z.H.; Xu, W.Y.; Wang, R.B.; Xie, W.C. Physical model test on deformation and failure mechanism of deposit landslide under gradient rainfall. Bull. Eng. Geol. Env. 2022, 81, 66. [Google Scholar] [CrossRef]
- Xiao, J.F.; Li, Y.A.; Hu, Y.; Zhang, S.; Cai, J.M. Model tests on deformation characteristics of ancient bank landslide under water level fluctuation and rainfall. Rock Soil Mech. 2021, 42, 471–480. [Google Scholar] [CrossRef]
- Mburu, J.W.; Li, A.-J.; Lin, H.-D.; Lu, C.-W. Investigations of Unsaturated Slopes Subjected to Rainfall Infiltration Using Numerical Approaches—A Parametric Study and Comparative Review. Sustainability 2022, 14, 14465. [Google Scholar] [CrossRef]
- Zhang, M.S.; Dong, Y.; Sun, P.P. Impact of reservoir impoundment-caused groundwater level changes on regional slope stability: A case study in the Loess Plateau of Western China. Environ. Earth Sci. 2012, 66, 1715–1725. [Google Scholar] [CrossRef]
- Manenti, S.; Amicarelli, A.; Palazzolo, N.; Bordoni, M.; Creaco, E.; Meisina, C. Post-Failure Dynamics of Rainfall-Induced Landslide in Oltrepò Pavese. Water 2020, 12, 2555. [Google Scholar] [CrossRef]
- Wang, R.; Wan, J.; Cheng, R.; Wang, Y.; Wang, Z. Physical and Numerical Simulation of the Mechanism Underpinning Accumulation Layer Deformation, Instability, and Movement Caused by Changing Reservoir Water Levels. Water 2023, 15, 1289. [Google Scholar] [CrossRef]
- Jiang, Z.H.; Wang, H.L.; Xie, W.C. Deformation mechanism of deposit landslide induced by fluctuations of reservoir water level based on physical model tests. Environ. Earth Sci. 2021, 80, 410. [Google Scholar] [CrossRef]
- Upomo, T.C.; Chang, M.; Kusumawardani, R.; Prayitno, G.A.; Kuo, C.-P.; Nugroho, U. Assessment of Petobo Flowslide Induced by Soil Liquefaction during 2018 Palu–Donggala Indonesian Earthquake. Sustainability 2023, 15, 5371. [Google Scholar] [CrossRef]
- Kim, H.; Kim, D.; Lee, Y.; Kim, H. Effect of Soil Box Boundary Conditions on Dynamic Behavior of Model Soil in 1 g Shaking Table Test. Appl. Sci. 2020, 10, 4642. [Google Scholar] [CrossRef]
- WANG, K.L.; LIN, M.L. Initiation and displacement of landslide induced by earthquake—A study of shaking table model slope test. Eng. Geol. 2011, 122, 106–114. [Google Scholar] [CrossRef]
- Yang, H.; Cui, S.; Pei, X.; Fan, X.; Lei, J. Multiple earthquake-induced progressive failure of bedding slopes with a saturated weak layer: Shaking table model tests. Soil Dyn. Earthq. Eng. 2023, 170, 107906. [Google Scholar] [CrossRef]
- Wang, L.W.; Wen, H.; Zhang, Z.P.; Du, Y.X.; Fu, X.D. Seismic dynamic response analysis and stability evaluation of Ganjiazhai Landslide based on QUAKE/W and SLOPE/W. Sci. Technol. Eng. 2018, 18, 274–280. [Google Scholar]
- Yan, Z.X.; Gao, L.; Peng, N.B.; Ren, Z.H.; Guo, B. Study on seismic dynamic response of bedding rock slope. Rock Soil Mech. 2012, 33 (Suppl. S2), 85–90. [Google Scholar] [CrossRef]
- Jin, Y.; Kim, D.; Jeong, S.; Kim, H. Analysis of Multilayered Ground Amplification Characteristics by Scaled-Down Model Tests. Appl. Sci. 2022, 12, 3432. [Google Scholar] [CrossRef]
- Huang, D.; Xie, Z.Z.; Song, Y.X.; Meng, Q.J.; Luo, S.L. Centrifuge model test study on the toppling deformation of the anti-dip soft-hard interbedded rock slopes. Chin. J. Rock Mech. Eng. 2021, 40, 1357–1368. [Google Scholar] [CrossRef]
- Málaga-Chuquitaype, C. Estimation of peak displacements in steel structures through dimensional analysis and the efficiency of alternative ground-motion time and length scales. Eng. Struct. 2015, 101, 264–278. [Google Scholar] [CrossRef]
- Guo, M.-Z.; Gu, K.-S.; Wang, C. Dynamic Response and Failure Process of a Counter-Bedding Rock Slope under Strong Earthquake Conditions. Symmetry 2022, 14, 103. [Google Scholar] [CrossRef]
- Buckingham, E. On physically similar systems, illustrations of the use of dimensional equations. Phys. Rev. 1914, 4, 345–376. [Google Scholar] [CrossRef]
- Cai, G.-Q.; Su, Y.-L.; Zhou, A.-N.; Yin, F.-J.; Shi, Y.-H. An elastic-viscoplastic model for time-dependent behavior of unsaturated soils. Comput. Geotech. Vol. 2023, 159, 105415. [Google Scholar] [CrossRef]
- Rizzitano, S.; Cascone, E.; Biondi, G. Oupling of topographic and stratigraphic effects on seismic response of slopes through 2D linear and equivalent linear analyses. Soil Dyn. Earthq. Eng. 2014, 67, 66–84. [Google Scholar] [CrossRef]
- Zhang, J.W.; Zhou, A.H.; Chi, M.J.; Wang, Y.S.; Chen, S. Study on optimal boundary range in numerical simulation of slope seismic response. J. Disaster Prev. Mitig. Eng. 2022, 42, 34–41. [Google Scholar] [CrossRef]





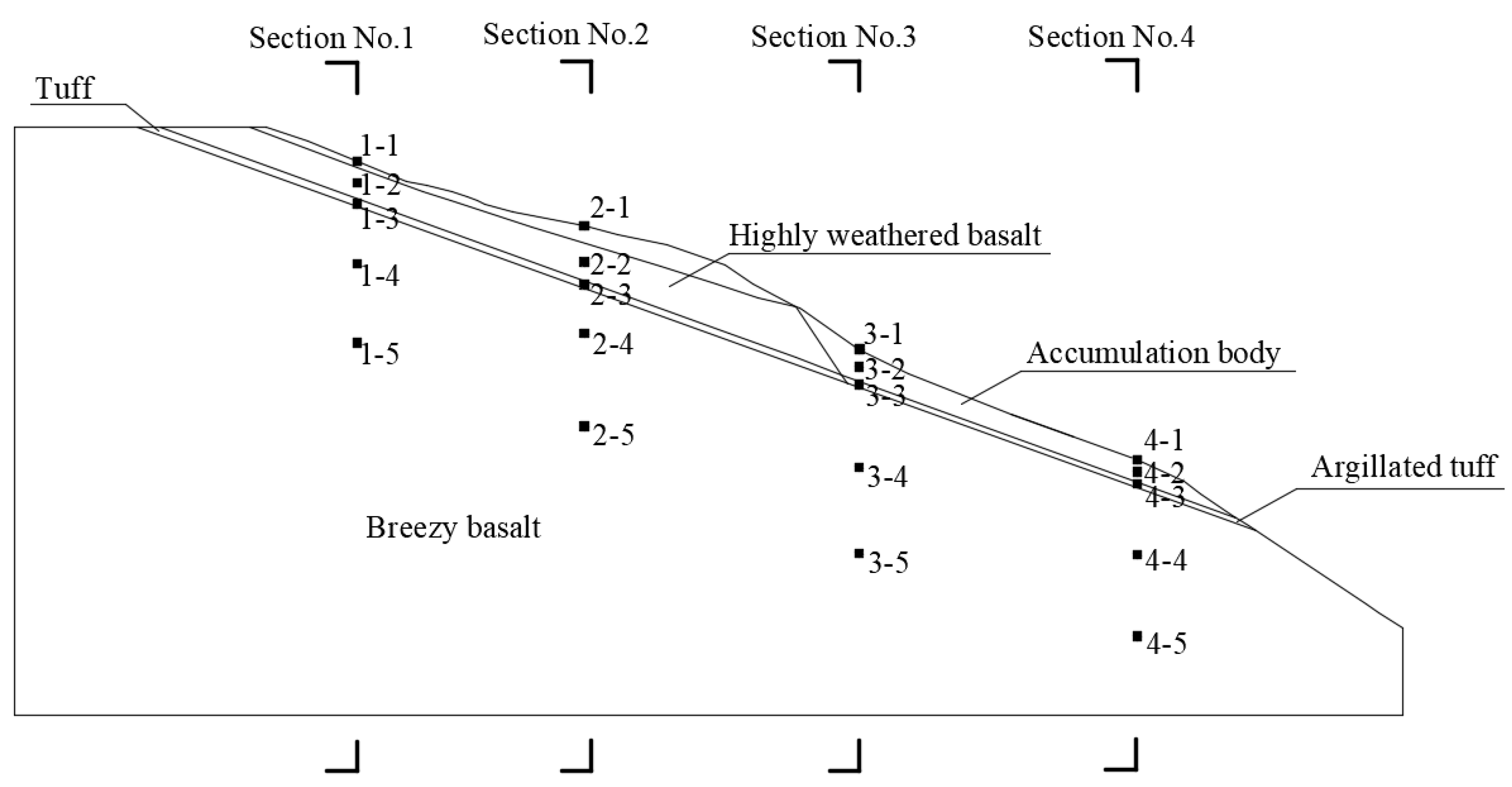



| Material Name | Volume Weight | Elasticity Modulus E/MPa | Poisson’s Ratio μ | Cohesion c/Mpa | Frictional Angle |
|---|---|---|---|---|---|
| Accumulation body | 24 | 25 | 0.38 | 0.03 | 31 |
| Highly weathered basalt | 30 | 1000 | 0.26 | 0.8 | 35 |
| Tuff | 29 | 80 | 0.30 | 0.09 | 28 |
| Argillated tuff | 30 | 40 | 0.33 | 0.05 | 24 |
| Breezy basalt | 30 | 20,000 | 0.23 | 1.5 | 43 |
| Physical Quantity | Similar Relationships | Similarity Ratio |
|---|---|---|
| Geometric dimension L | 400 | |
| Accelerated speed a | 1 | |
| Material density ρ | 1 | |
| Cohesion c | 400 | |
| Friction angle | 1 | |
| Unit weight | 1 | |
| Elastic modulus E | 400 | |
| Poisson’s ratio | 1 |
| Material Name | Material Ratio | Cohesion c/kPa | Friction Angle /° |
|---|---|---|---|
| Accumulator | Talc powder: Sand 2.4:1.6 | 1.55 | 31.8 |
| Strongly weathered basalt | Steel slag: Sand: Gypsum: Water 5:4:1.3:2.2 | 9.3 | 34.4 |
| Microweathered basalt | Iron powder: Barite powder: Water: Cement 30.0:10.0:3.5:1.4 | 14.3 | 43.4 |
| Tuff | Hardboard | 0.9 | 26.6 |
| Loading Conditions | Earthquake Direction | Seismic Peak Acceleration/g | Reservoir Water Status |
|---|---|---|---|
| 1 | Vertical earthquake | 0.1 g | Normal water level |
| 2 | No water level | ||
| 3 | 0.2 g | Normal water level | |
| 4 | No water level | ||
| 5 | 0.3 g | Normal water level | |
| 6 | No water level | ||
| 7 | 0.4 g | Normal water level | |
| 8 | No water level | ||
| 9 | Horizontal earthquake | 0.1 g | Normal water level |
| 10 | No water level | ||
| 11 | 0.2 g | Normal water level | |
| 12 | No water level | ||
| 13 | 0.3 g | Normal water level | |
| 14 | No water level | ||
| 15 | 0.4 g | Normal water level | |
| 16 | No water level |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ning, W.; Tang, H. Dynamic Response Law and Failure Mechanism of Slope with Weak Interlayer under Combined Action of Reservoir Water and Seismic Force. Water 2023, 15, 1956. https://doi.org/10.3390/w15101956
Ning W, Tang H. Dynamic Response Law and Failure Mechanism of Slope with Weak Interlayer under Combined Action of Reservoir Water and Seismic Force. Water. 2023; 15(10):1956. https://doi.org/10.3390/w15101956
Chicago/Turabian StyleNing, Wenpeng, and Hua Tang. 2023. "Dynamic Response Law and Failure Mechanism of Slope with Weak Interlayer under Combined Action of Reservoir Water and Seismic Force" Water 15, no. 10: 1956. https://doi.org/10.3390/w15101956






