Machine Learning Framework with Feature Importance Interpretation for Discharge Estimation: A Case Study in Huitanggou Sluice Hydrological Station, China
Abstract
1. Introduction
2. Methodology
2.1. Study Area and Data Sources
2.2. Methods
2.2.1. Exploratory Data Analysis (EDA)
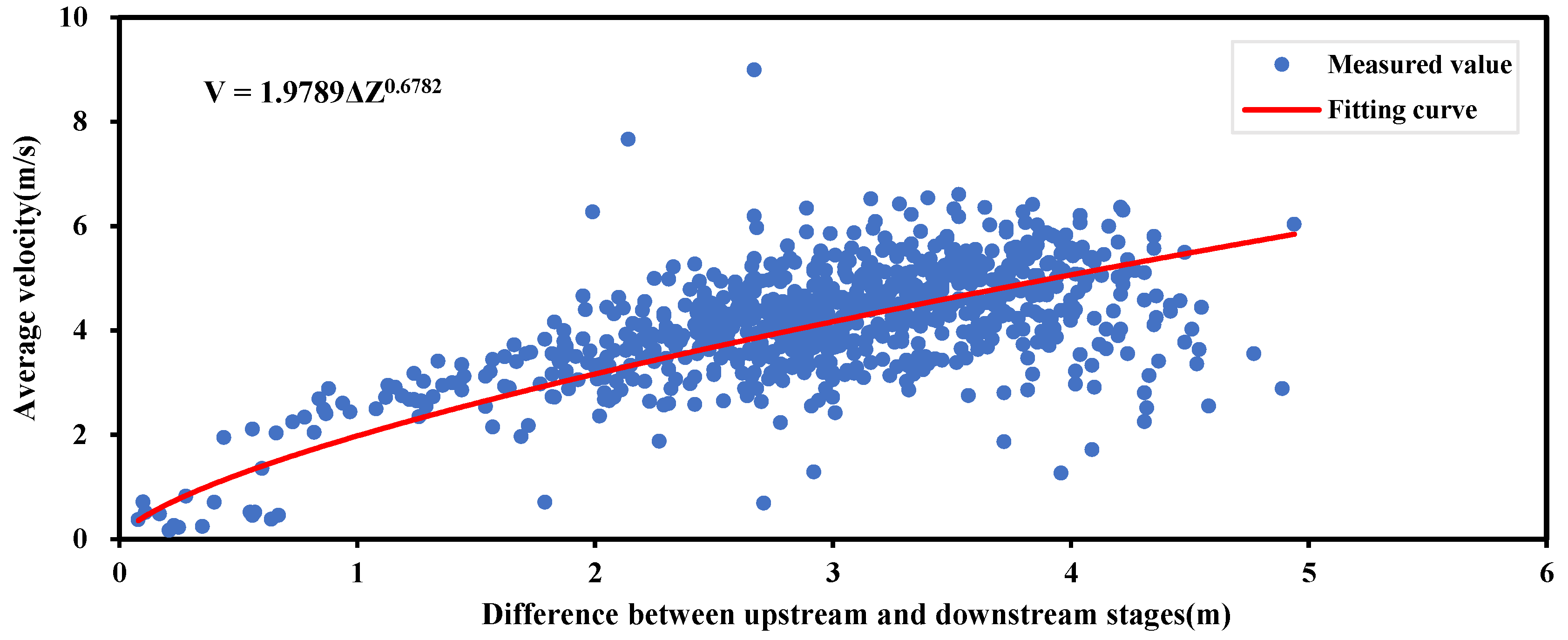
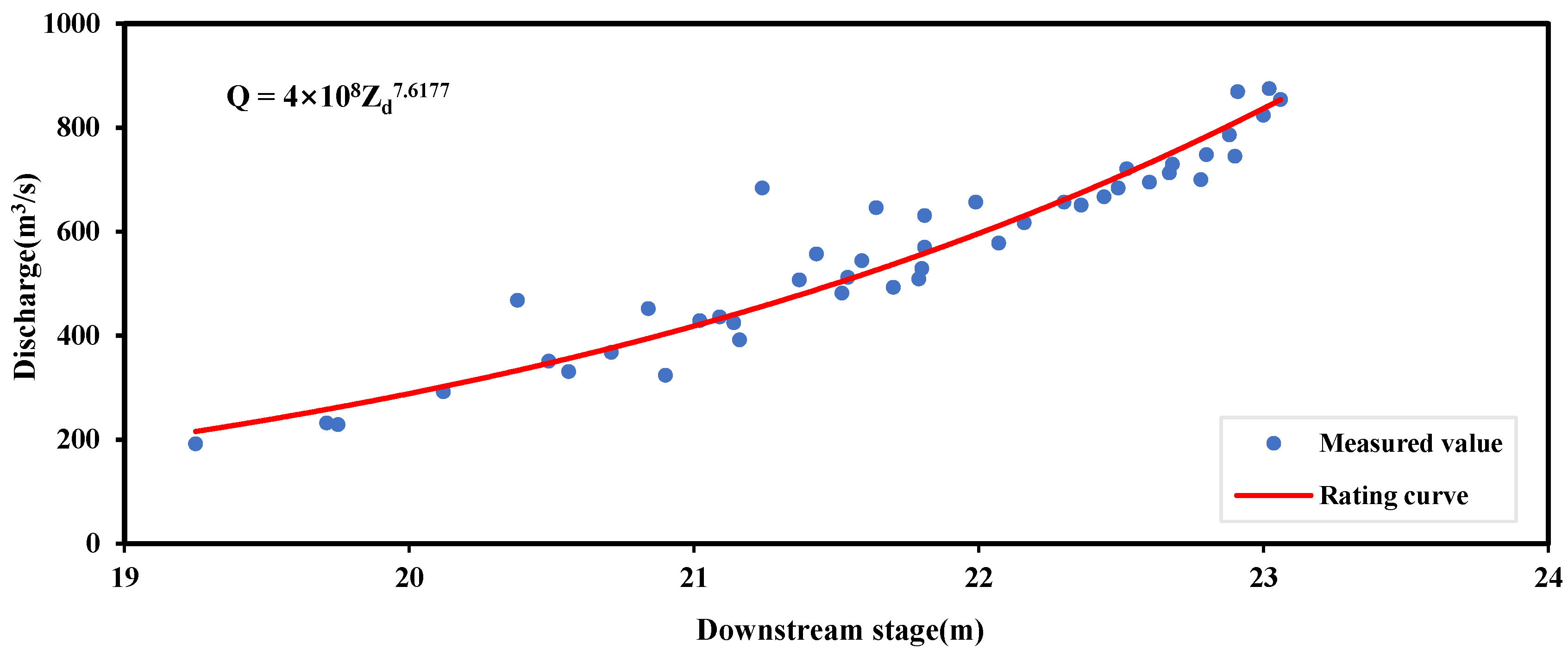
2.2.2. Conventional Method: Stage–Discharge Rating Curve (SDRC)
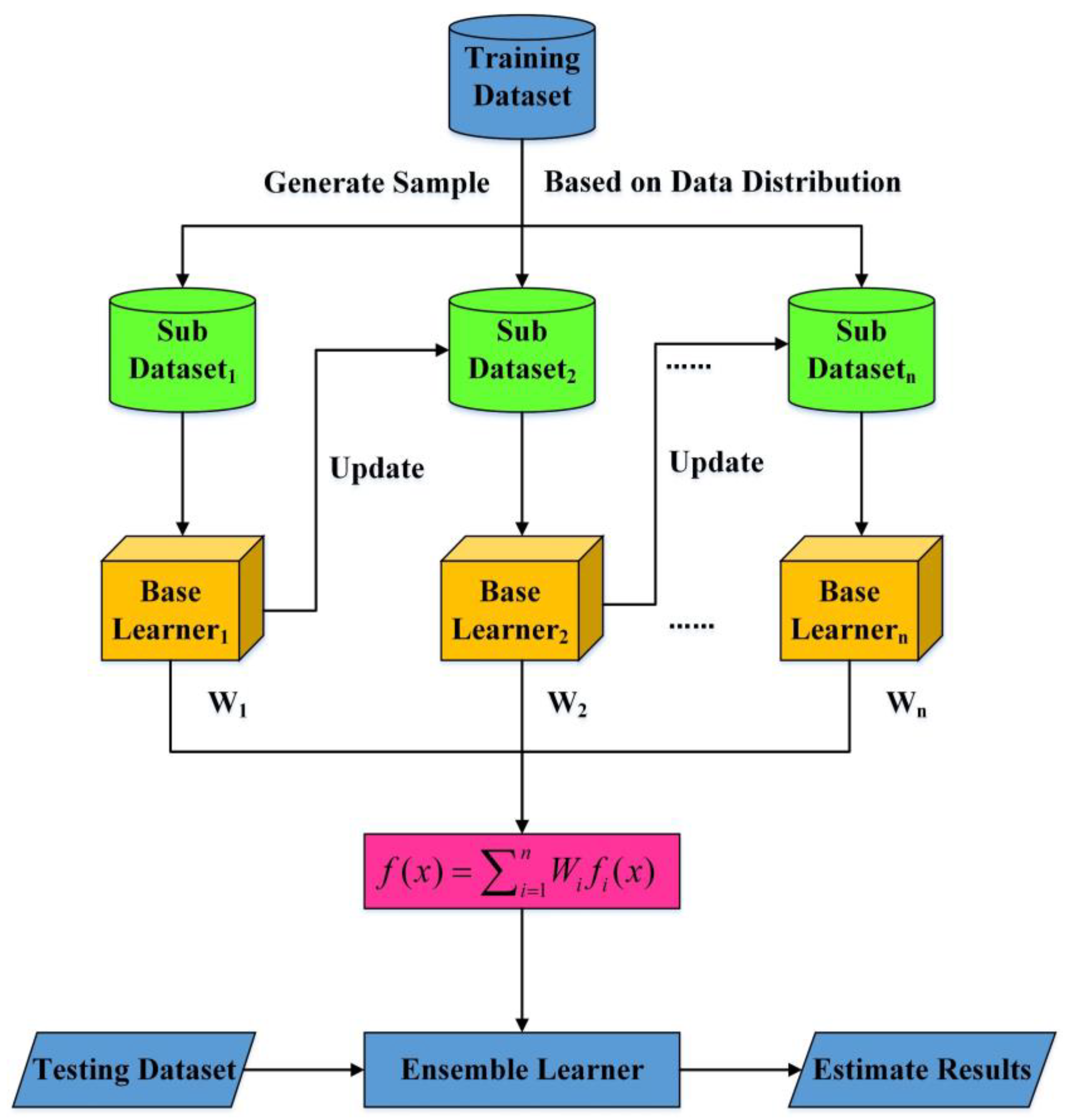
2.2.3. Ensemble Learning Random Forest (ELRF) Algorithm
2.2.4. Ensemble Learning Gradient Boosting Decision Tree (ELGBDT) Algorithm
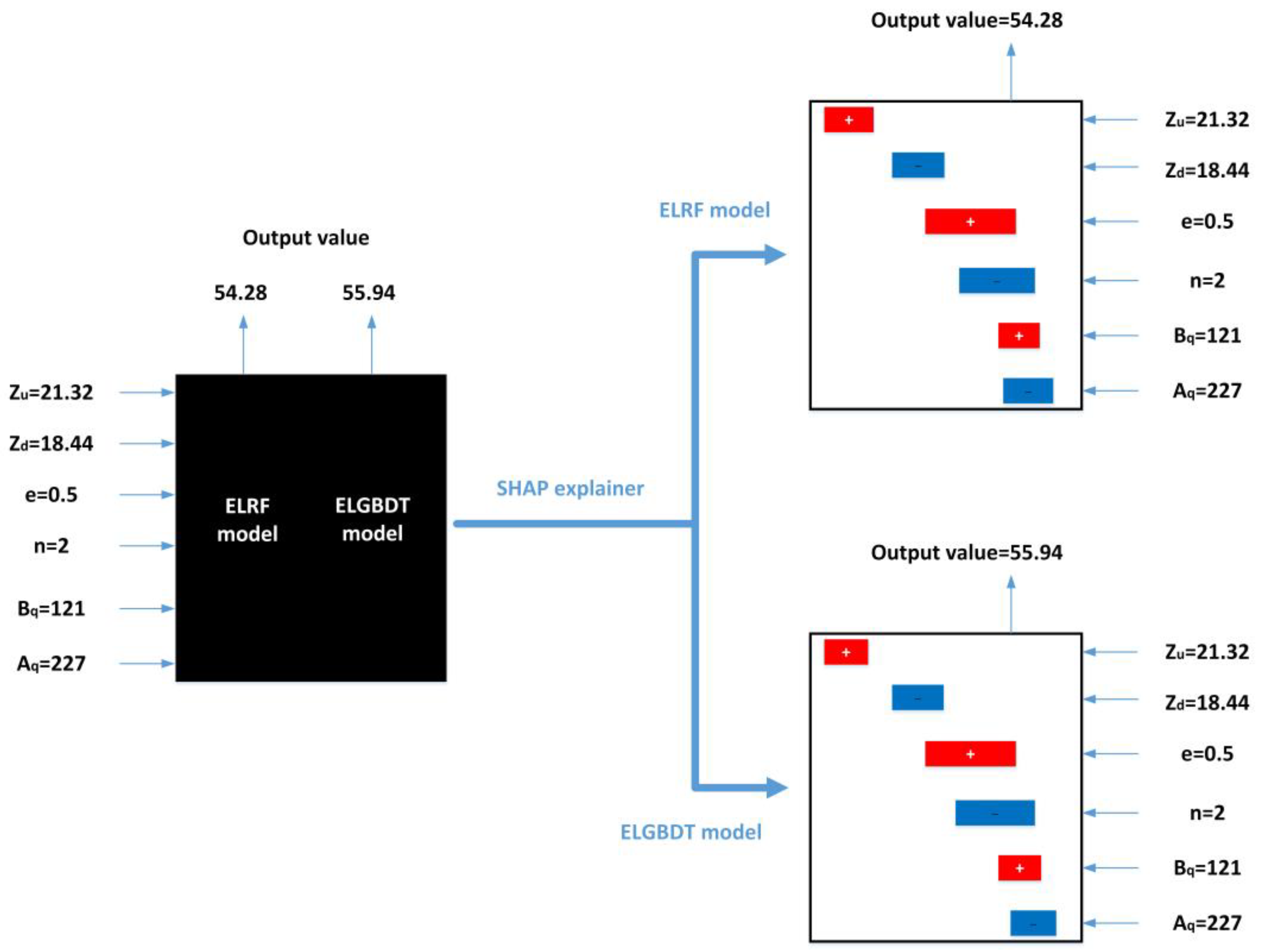
2.2.5. SHAP Algorithm
2.2.6. Bayesian Optimization Algorithm
2.3. Performance Evaluation Methods
3. Results
3.1. Data Exploration and Analysis
3.2. Conventional SDRC Fitting
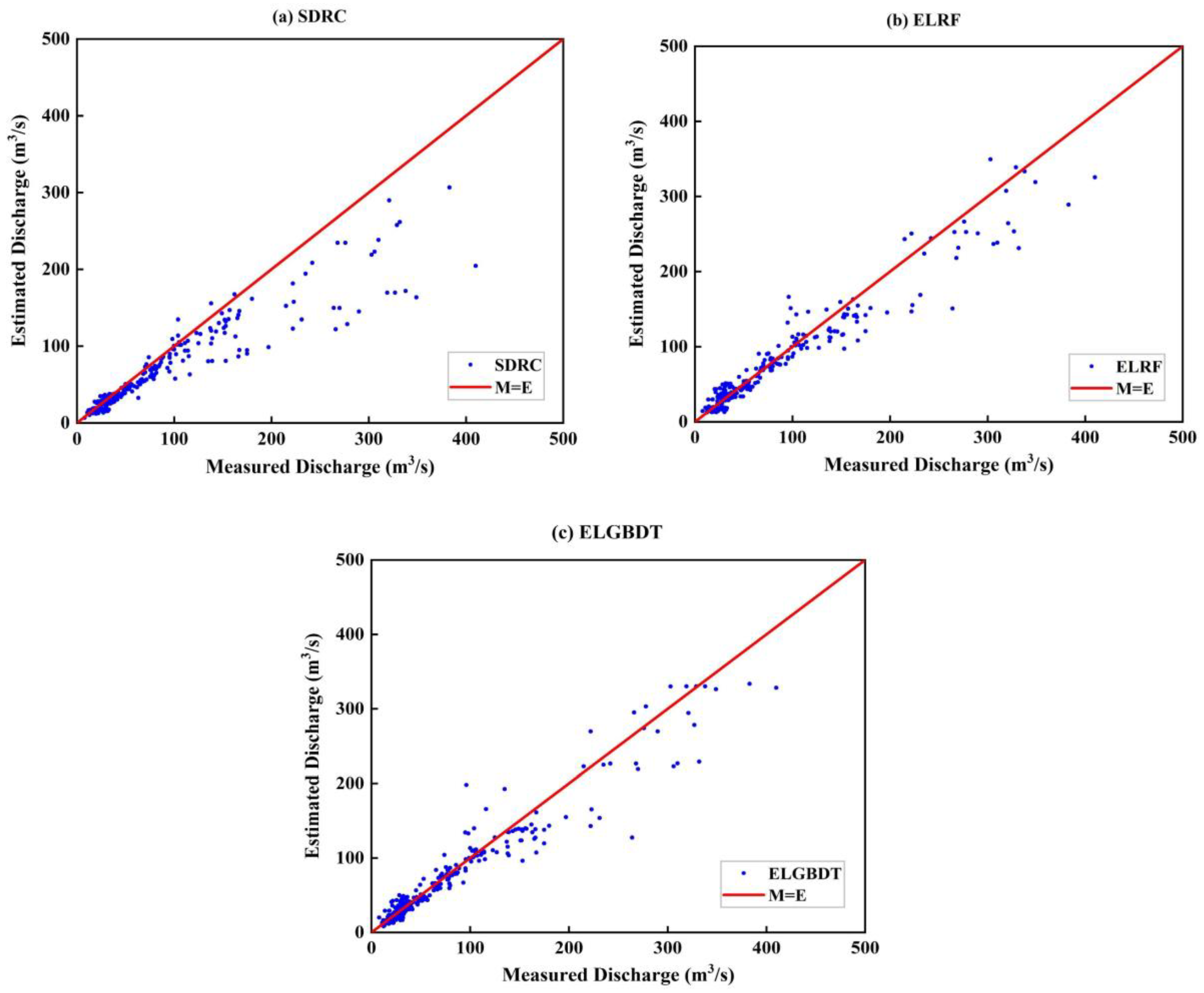
3.3. Model Estimation
3.3.1. Bayesian Hyperparameter Optimization
3.3.2. Model Evaluation
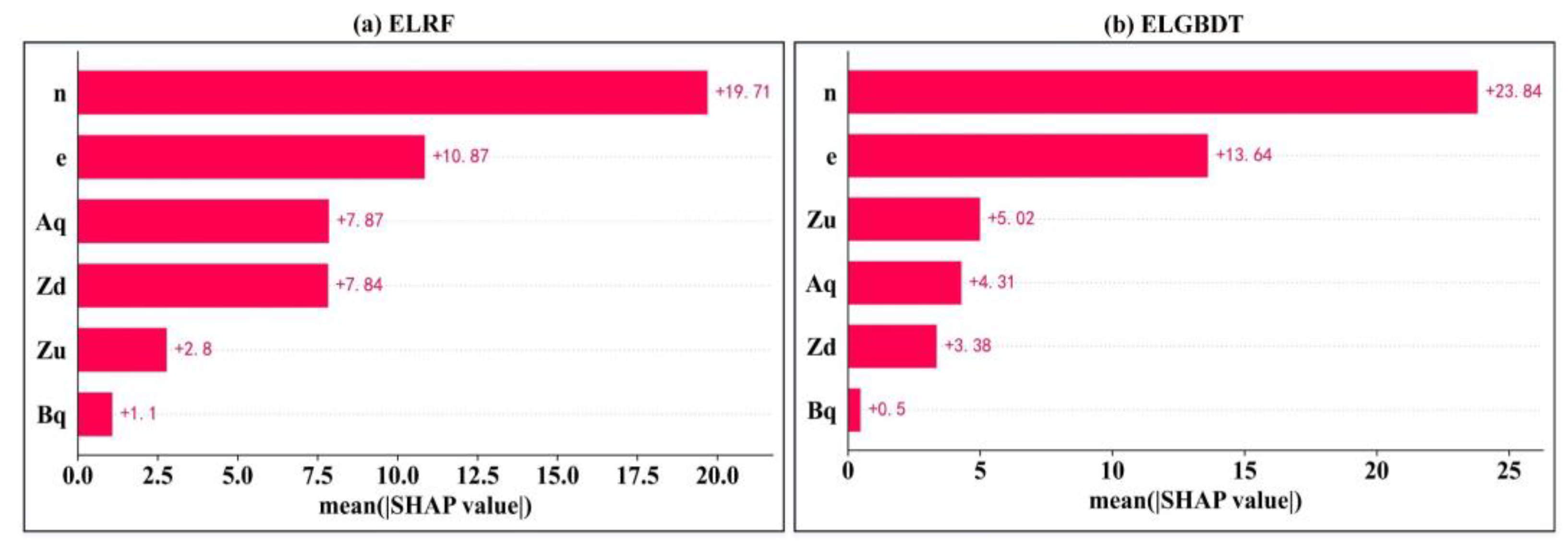
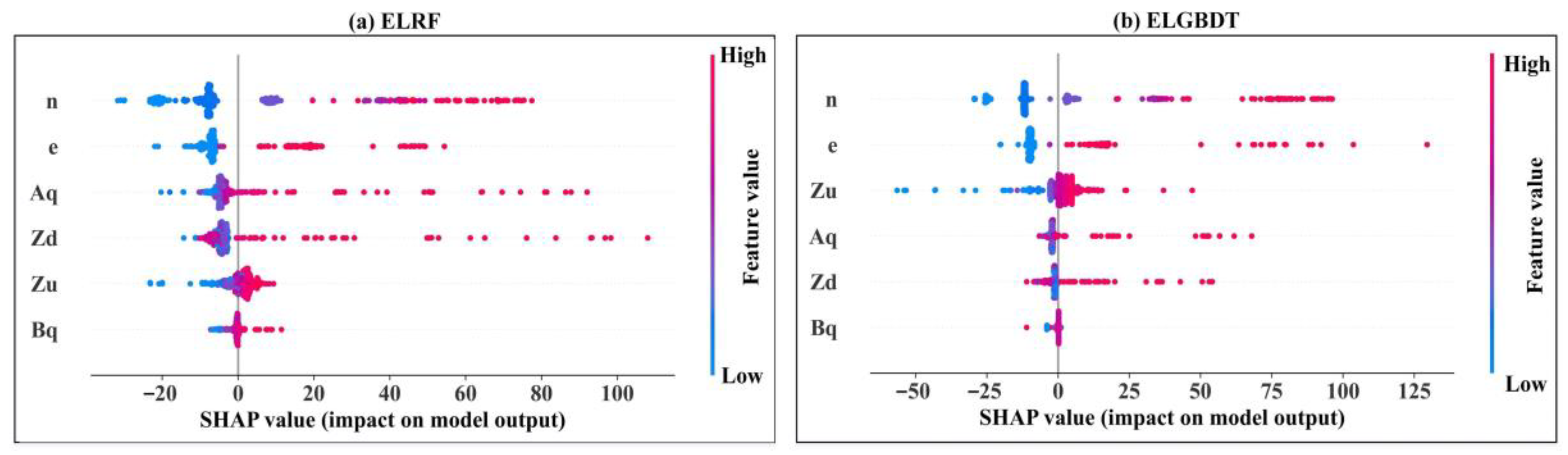
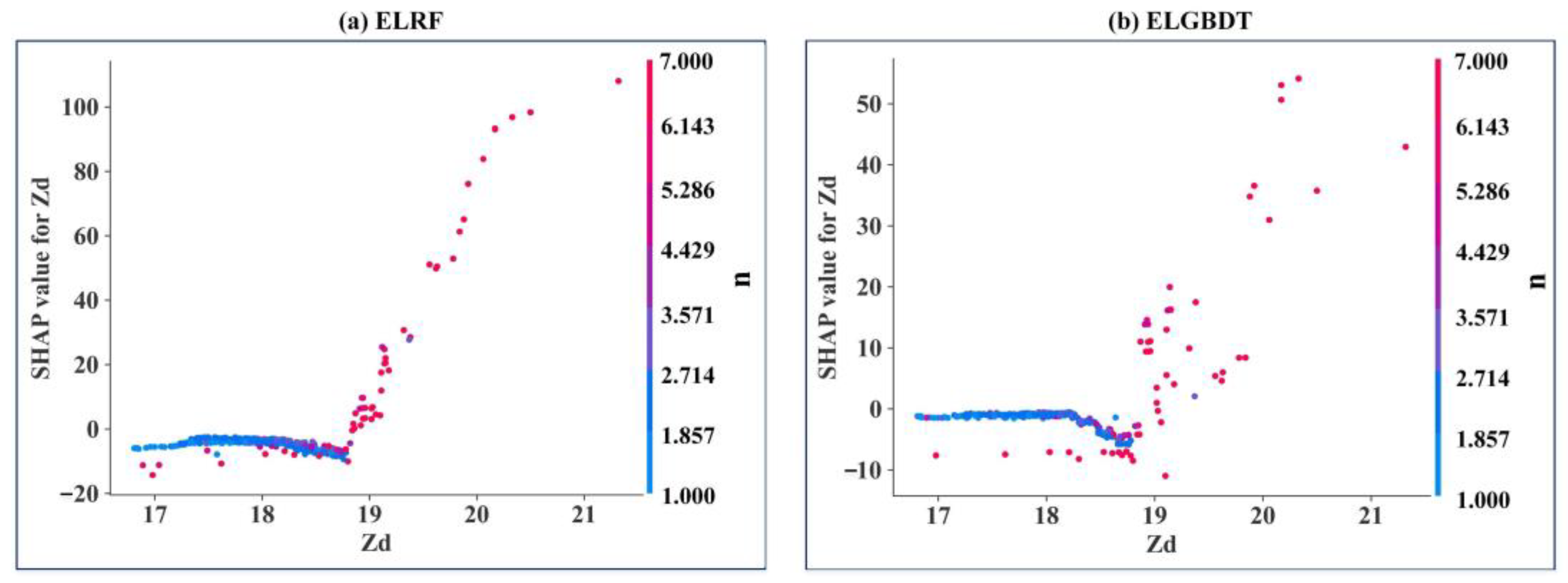
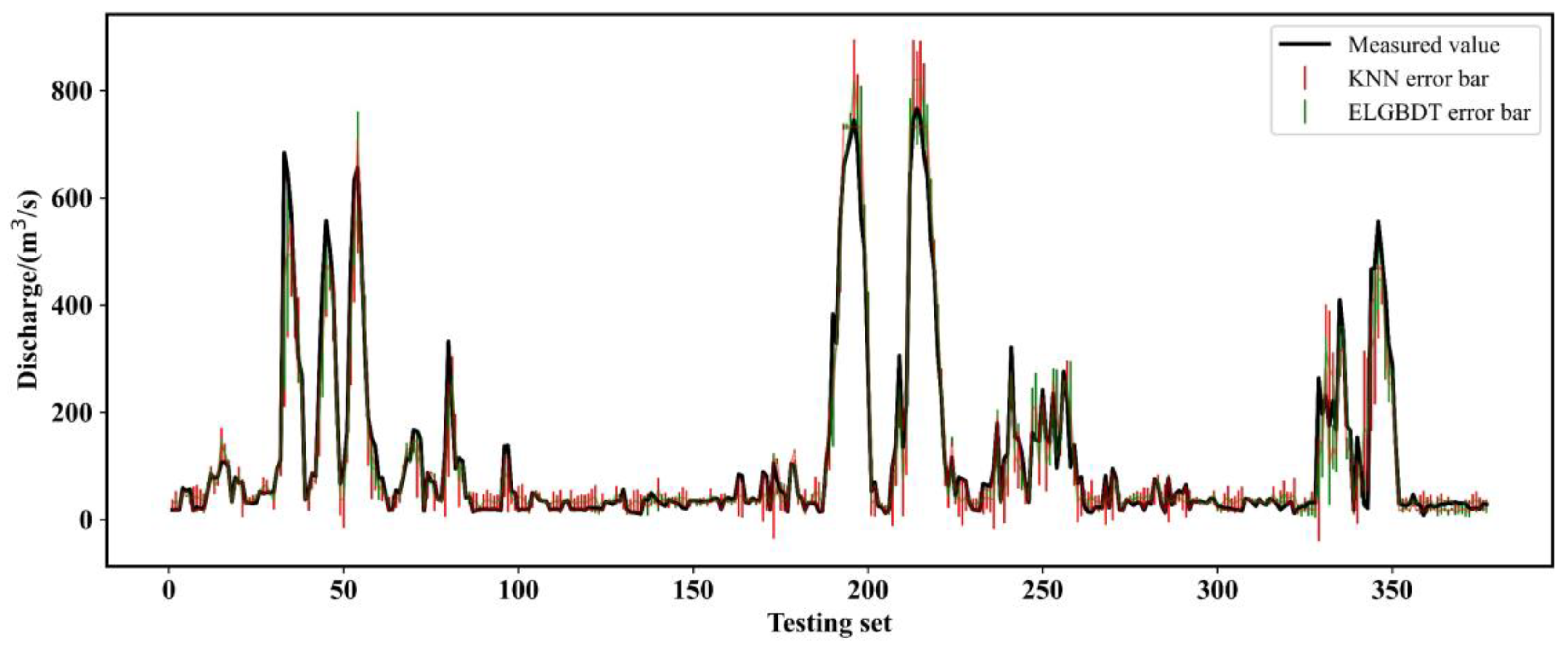
3.4. Model Feature Importance Interpretation
4. Discussion
5. Conclusions
- (1)
- The performance of the model is improved by Bayesian optimization. ELRF and ELGBDT models estimate discharge with almost identical accuracy. The accuracy of the ensemble ML model is superior to that of the SDRC method in the submerged orifice flow state. The R2, RMSE, and CC values of the ensemble ML model are 0.912, 19.578, and 0.971, respectively. The RE distribution parameter and violin plot of the ensemble ML model are the best, and this model has the strongest generalization ability.
- (2)
- The SHAP method reveals the interactions between all variables and how this relationship is reflected in the model. In the ensemble ML model, the sluice gate opening number (n) is the strongest influential variable, and the discharge measurement cross-section width (Bq) is the weakest influential variable. The estimated average discharge of the ensemble ML model is less than 100 m3/s. The variables can be appropriately analyzed, resulting in a better model with higher performance indicators.
- (3)
- Compared with the SDRC method and single ML model, the ensemble ML model has higher accuracy and better stability, which indicates that the ensemble ML model can express more complex nonlinear transformations accurately and effectively.
- (4)
- The accuracy of the ensemble ML model is the highest without considering the flow state. The R2, RMSE, and CC values of the ensemble ML model are 0.963, 31.268, and 0.984, which indicates that the ensemble ML model has a strong adaptive ability.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nezamkhiavy, K.; Nezamkhiavy, S. Estimate stage-discharge relation for rivers using artificial neural networks-Case study: Dost Bayglu hydrometry station over Qara Su River. Int. J. Water Resour. Environ. Eng. 2014, 6, 232–238. [Google Scholar]
- Roushangar, K.; Alizadeh, F. Scenario-based prediction of short-term river stage-discharge process using wavelet-EEMD-based relevance vector machine. J. Hydroinform. 2019, 21, 56–76. [Google Scholar] [CrossRef]
- Azamathulla, H.M.; Ghani, A.A.; Leow, C.S.; Chang, N.A.; Zakaria, N.A. Gene-Expression Programming for the Development of a Stage-Discharge Curve of the Pahang River. Water Resour. Manag. 2011, 25, 2901–2916. [Google Scholar] [CrossRef]
- Ghimire, B.; Reddy, M.J. Development of Stage-Discharge Rating Curve in River Using Genetic Algorithms and Model Tree; International Workshop on Advances in Statistical Hydrology: Taormina, Italy, 2010. [Google Scholar]
- Guven, A.; Aytek, A. New Approach for Stage–Discharge Relationship: Gene-Expression Programming. J. Hydrol. Eng. 2009, 14, 812–820. [Google Scholar] [CrossRef]
- Ajmera, T.K.; Goyal, M.K. Development of stage-discharge rating curve using model tree and neural networks: An application to Peachtree Creek in Atlanta. Expert Syst. Appl. 2012, 39, 5702–5710. [Google Scholar] [CrossRef]
- Tawfik, M.; Ibrahim, A.; Fahmy, H. Hysteresis sensitive neural network for modeling rating curves. J. Comput. Civ. Eng. 1997, 11, 206–211. [Google Scholar] [CrossRef]
- Bhattacharya, B.; Solomatine, D.P. Neural network and M5 model trees in modeling water level–discharge relationship. J. Neurocomput. 2005, 63, 381–396. [Google Scholar] [CrossRef]
- Petersen-Øverleir, A. Modelling stage-discharge relationships affected by hysteresis using the Jones formula and nonlinear regression. Hydrol. Sci. J. 2006, 51, 365–388. [Google Scholar] [CrossRef]
- Wolfs, V.; Willems, P. Development of discharge-stage curves affected by hysteresis using time varying models, model trees and neural networks. Environ. Model. Softw. 2014, 55, 107–119. [Google Scholar] [CrossRef]
- Lohani, A.K.; Goel, N.K.; Bhatia, K.K.S. Takagi-Sugeno fuzzy inference system for modeling stage-discharge relationship. J. Hydrol. 2006, 331, 146–160. [Google Scholar] [CrossRef]
- Kashani, M.H.; Daneshfaraz, R.; Ghorbani, M.A.; Najafi, M.R.; Kisi, O. Comparison of different methods for developing a stage -discharge curve of the Kizilirmak River. J. Flood Risk Manag. 2015, 8, 71–86. [Google Scholar] [CrossRef]
- Birbal, P.; Azamathulla, H.; Leon, L.; Kumar, V.; Hosein, J. Predictive modelling of the stage-discharge relationship using Gene-Expression Programming. Water Supply 2021, 21, 3503–3514. [Google Scholar] [CrossRef]
- Alizadeh, F.; Gharamaleki, A.F.; Jalilzadeh, R. A two-stage multiple-point conceptual model to predict river stage-discharge process using machine learning approaches. J. Water Clim. Chang. 2021, 12, 278–295. [Google Scholar] [CrossRef]
- Lin, H.; Jiang, Z.; Liu, B.; Chen, Y. Research on stage-discharge relationship model based on information entropy. Water Policy 2021, 23, 1075–1088. [Google Scholar] [CrossRef]
- Jain, S.K.; Chalisgaonkar, D. Setting up stage–discharge relations using ANN. J. Hydraul. Eng. 2000, 5, 428–433. [Google Scholar] [CrossRef]
- Sharma, P.; Said, Z.; Kumar, A.; Nižetić, S.; Pandey, A.; Hoang, A.T.; Huang, Z.; Afzal, A.; Li, C.; Le, A.T.; et al. Recent Advances in Machine Learning Research for Nanofluid-Based Heat Transfer in Renewable Energy System. Energy Fuels 2022, 36, 6626–6658. [Google Scholar] [CrossRef]
- Fu, J.; Zhong, P.; Chen, J.; Xu, B.; Zhu, F.; Zhang, Y. Water Resources Allocation in Transboundary River Basins Based on a Game Model Considering Inflow Forecasting Errors. Water Resour. Manag. 2019, 33, 2809–2825. [Google Scholar] [CrossRef]
- Wang, G.; Sun, J.; Ma, J.; Xu, K.; Gu, J. Sentiment classification: The contribution of ensemble learning. Decis. Support Syst. 2014, 57, 77–93. [Google Scholar] [CrossRef]
- Nourani, V.; Elkiran, G.; Abba, S.I. Wastewater treatment plant performance analysis using artificial intelligence—An ensemble approach. Water Sci. Technol. 2018, 78, 2064–2076. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Sang, X.; Chang, J.; Zheng, Y.; Han, Y. Sensitivity analysis and prediction of water supply and demand in Shenzhen based on an ELRF algorithm and a self-adaptive regression coupling model. Water Supply 2021, 22, 278–293. [Google Scholar] [CrossRef]
- Whitehead, M.; Yaeger, L. Building a General Purpose Cross-Domain Sentiment Mining Model. In Proceedings of the 2009 WRI World Congress on Computer Science and Information Engineering, Los Angeles, CA, USA, 31 March–2 April 2009; pp. 472–476. [Google Scholar] [CrossRef]
- Wilson, T.; Wiebe, J.; Hwa, R. Recognizing strong and weak opinion clauses. Comput. Intell. 2006, 22, 73–99. [Google Scholar] [CrossRef]
- Polikar, R. Ensemble based systems in decision making. IEEE Circuits Syst. Mag. 2006, 6, 21–45. [Google Scholar] [CrossRef]
- Lary, D.J.; Alavi, A.H.; Gandomi, A.H.; Walker, A.L. Machine learning in geosciences and remote sensing. Geosci. Front. 2016, 7, 3–10. [Google Scholar] [CrossRef]
- Bauer, E.; Kohavi, R. An empirical comparison of voting classification algorithms: Bagging, boosting, and variants. Mach. Learn. 1999, 36, 105–139. [Google Scholar] [CrossRef]
- Schapire, R.E. The strength of weak learnability. Mach. Learn. 1990, 5, 197–227. [Google Scholar] [CrossRef]
- Cmv, A.; Jie, D.B. Accurate and efficient sequential ensemble learning for highly imbalanced multi-class data. Neural Netw. 2020, 128, 268–278. [Google Scholar] [CrossRef]
- Reig, S.; Norman, S.; Morales, C.G.; Das, S.; Steinfeld, A.; Forlizzi, J. A Field Study of Pedestrians and Autonomous Vehicles. In Proceedings of the 10th International ACM Conference on Automotive User Interfaces and Interactive Vehicular Applications, Toronto, ON, Canada, 23–25 September 2018. [Google Scholar] [CrossRef]
- Morales, C.G.; Carter, E.J.; Tan, X.Z.; Steinfeld, A. Interaction Needs and Opportunities for Failing Robots. In Proceedings of the 2019 on Designing Interactive Systems Conference, San Diego, CA, USA, 23–28 June 2019. [Google Scholar] [CrossRef]
- Morales, C.G.; Gisolfi, N.; Edman, R.; Miller, J.K.; Dubrawski, A. Provably Robust Model-Centric Explanations for Critical Decision-Making. arXiv 2021, arXiv:2110.13937. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should I Trust You?”: Explaining the Predictions of Any Classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4765–4774. [Google Scholar]
- Alvarez-Melis, D.; Jaakkola, T. On the Robustness of Interpretability Methods. arXiv 2018, arXiv:1806.08049. [Google Scholar]
- Wang, J.; Wang, L.; Zheng, Y.; Yeh, C.; Jain, S.; Zhang, W. Learning-from-disagreement: A model comparison and visual analytics framework. arXiv 2022, arXiv:2201.07849. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Erion, G.G.; Lee, S.I. Consistent individualized feature attribution for tree ensembles. arXiv 2018, arXiv:1802.03888. [Google Scholar]
- Zarei, A.R.; Moghimi, M.M.; Mahmoudi, M.R. Parametric and non-parametric trend of drought in arid and semi-arid regions using RDI index. Water Resour. Manag. 2016, 30, 5479–5500. [Google Scholar] [CrossRef]
- Žerovnik, J.; Rupnik Poklukar, D. Elementary methods for computation of quartiles. Teaching Statistics 2017, 39, 88–91. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Gordon, A.D.; Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees. Biometrics 1984, 40, 874. [Google Scholar] [CrossRef]
- Tandon, A.; Yadav, S.; Attri, A.K. Non-linear analysis of short term variations in ambient visibility. Atmos. Pollut. Res. 2013, 4, 199–207. [Google Scholar] [CrossRef]
- Liu, J.; Wu, C. A gradient-boosting decision-tree approach for firm failure prediction: An empirical model evaluation of Chinese listed companies. J. Risk Model Valid. 2017, 11, 43–64. [Google Scholar] [CrossRef]
- Friedman, J. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.L. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian Optimization of Machine Learning Algorithms. In Proceedings of the 25th International Conference on Neural Information Processing Systems, Lake Tahoe Nevada, CA, USA, 3–6 December 2012; pp. 2951–2959. [Google Scholar] [CrossRef]
- Alruqi, M.; Sharma, P. Biomethane Production from the Mixture of Sugarcane Vinasse, Solid Waste and Spent Tea Waste: A Bayesian Approach for Hyperparameter Optimization for Gaussian Process Regression. Fermentation 2023, 9, 120–134. [Google Scholar] [CrossRef]
- Garrido-Merchán, E.C.; Hernández-Lobato, D. Dealing with Categorical and Integer-valued Variables in Bayesian Optimization with Gaussian Processes. Neurocomputing 2020, 380, 20–35. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Bzdok, D.; Krzywinski, M.; Altman, N. Points of significance: Machine learning: Supervised methods. Nat. Methods 2018, 15, 5–6. [Google Scholar] [CrossRef] [PubMed]







| Dataset | Number of Cases | Variable | Minimum | Maximum | Mean | Median | Standard Deviation |
|---|---|---|---|---|---|---|---|
| Training | 897 | Zu (m) | 17.07 | 23.06 | 21.13 | 21.31 | 0.81 |
| Zd (m) | 16.77 | 22.97 | 18.26 | 18.16 | 0.87 | ||
| e (m) | 0.10 | 6.86 | 0.52 | 0.30 | 0.89 | ||
| n | 1 | 7 | 3 | 2 | 2 | ||
| Bq (m) | 97.5 | 158 | 118.1 | 119 | 7.1 | ||
| Aq (m2) | 28.1 | 856 | 200.7 | 188 | 109.1 | ||
| Qm (m3/s) | 2.49 | 875 | 66.9 | 36.6 | 107.4 | ||
| Testing | 384 | Zu (m) | 18.43 | 22.96 | 21.15 | 21.27 | 0.69 |
| Zd (m) | 17.08 | 22.92 | 18.52 | 18.18 | 1.20 | ||
| e (m) | 0.10 | 6.76 | 0.91 | 0.30 | 1.55 | ||
| n | 1 | 7 | 3 | 2 | 2 | ||
| Bq (m) | 89.1 | 156 | 120.8 | 121 | 8.9 | ||
| Aq (m2) | 63.5 | 818 | 241.9 | 195 | 153.3 | ||
| Qm (m3/s) | 7.75 | 767 | 116.9 | 45.6 | 163.3 |
| Model | R2 | RMSE | CC |
|---|---|---|---|
| SDRC | 0.801 | 33.354 | 0.947 |
| ELRF | 0.911 | 19.578 | 0.971 |
| ELGBDT | 0.912 | 19.955 | 0.967 |
| Model | CIUL (%) | UQ (%) | Median (%) | LQ (%) | CILL (%) |
|---|---|---|---|---|---|
| SDRC | 52.90 | 25.80 | 14.02 | 7.74 | 0 |
| ELRF | 50.07 | 24.54 | 13.50 | 7.53 | 0 |
| ELGBDT | 49.38 | 24.25 | 14.81 | 7.49 | 0 |
| Model | R2 | RMSE | CC | Mean RE |
|---|---|---|---|---|
| ELRF | 0.959 | 31.451 | 0.982 | 0.174 |
| ELGBDT | 0.963 | 31.268 | 0.984 | 0.173 |
| Model | R2 | RMSE | CC | Mean RE |
|---|---|---|---|---|
| SVM | 0.928 | 42.409 | 0.966 | 0.217 |
| KNN | 0.943 | 38.284 | 0.973 | 0.195 |
| ELGBDT | 0.963 | 31.268 | 0.984 | 0.173 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, S.; Niu, G.; Sang, X.; Sun, X.; Yin, J.; Chen, H. Machine Learning Framework with Feature Importance Interpretation for Discharge Estimation: A Case Study in Huitanggou Sluice Hydrological Station, China. Water 2023, 15, 1923. https://doi.org/10.3390/w15101923
He S, Niu G, Sang X, Sun X, Yin J, Chen H. Machine Learning Framework with Feature Importance Interpretation for Discharge Estimation: A Case Study in Huitanggou Sluice Hydrological Station, China. Water. 2023; 15(10):1923. https://doi.org/10.3390/w15101923
Chicago/Turabian StyleHe, Sheng, Geng Niu, Xuefeng Sang, Xiaozhong Sun, Junxian Yin, and Heting Chen. 2023. "Machine Learning Framework with Feature Importance Interpretation for Discharge Estimation: A Case Study in Huitanggou Sluice Hydrological Station, China" Water 15, no. 10: 1923. https://doi.org/10.3390/w15101923
APA StyleHe, S., Niu, G., Sang, X., Sun, X., Yin, J., & Chen, H. (2023). Machine Learning Framework with Feature Importance Interpretation for Discharge Estimation: A Case Study in Huitanggou Sluice Hydrological Station, China. Water, 15(10), 1923. https://doi.org/10.3390/w15101923










