Evaluation of Soil Infiltration Variability in Compacted and Uncompacted Soil Using Two Devices
Abstract
:1. Introduction
- The method used to determine infiltration in compacted and non-compacted soil track is statistically significant.
- The selected research area in terms of the degree of compaction has a significant effect on the degree of infiltration capacity of the soil.
- The phenomenon of “water repellency” can be alleviated by extending the measurement time.
2. Materials and Methods
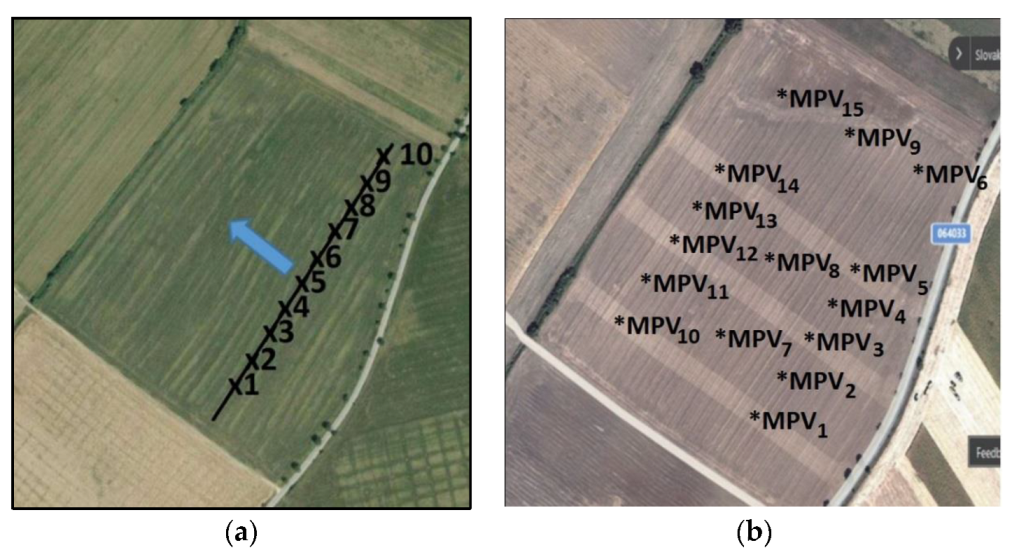
2.1. Locality Characteristics
| Crop Variability | ||
|---|---|---|
| Harvest Years | Crop | Average Yield (t·ha−1) |
| 2009 | Spring barley cv. Kango | 5.0 |
| 2011 | Winter wheat cv. Augustus | 6.2 |
| 2014 | Spring barley cv. Kango | 4.8 |
| 2016 | Winter wheat cv. HYFI | 7.9 |
| 2017 | Winter barley cv. Wintmalt | 6.7 |
| 2019 | Winter wheat cv. RGT Reform | 7.8 |
| 2021 | Spring barley cv. IS Maltigo | 3.0 |
| Soil cone index (soil strength) | ||
| Zone * | Variability, MPa | |
| A | 0.59–2.5 | |
| B | 0.78–2.35 | |
| C | 0.9–3.45 | |
2.2. Characteristics of Measuring Technology
2.3. Statistical Evaluation of Results
3. Results and Discussion
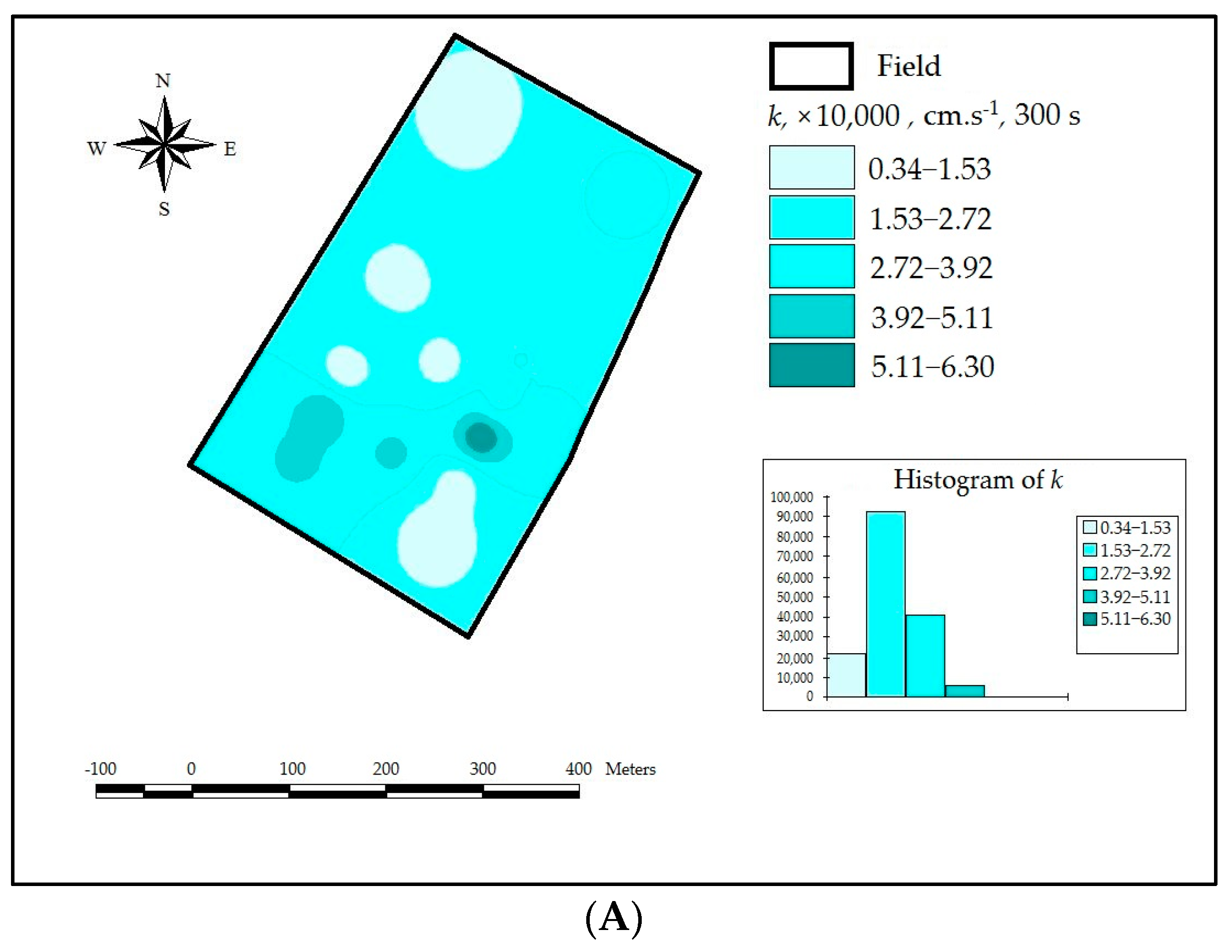
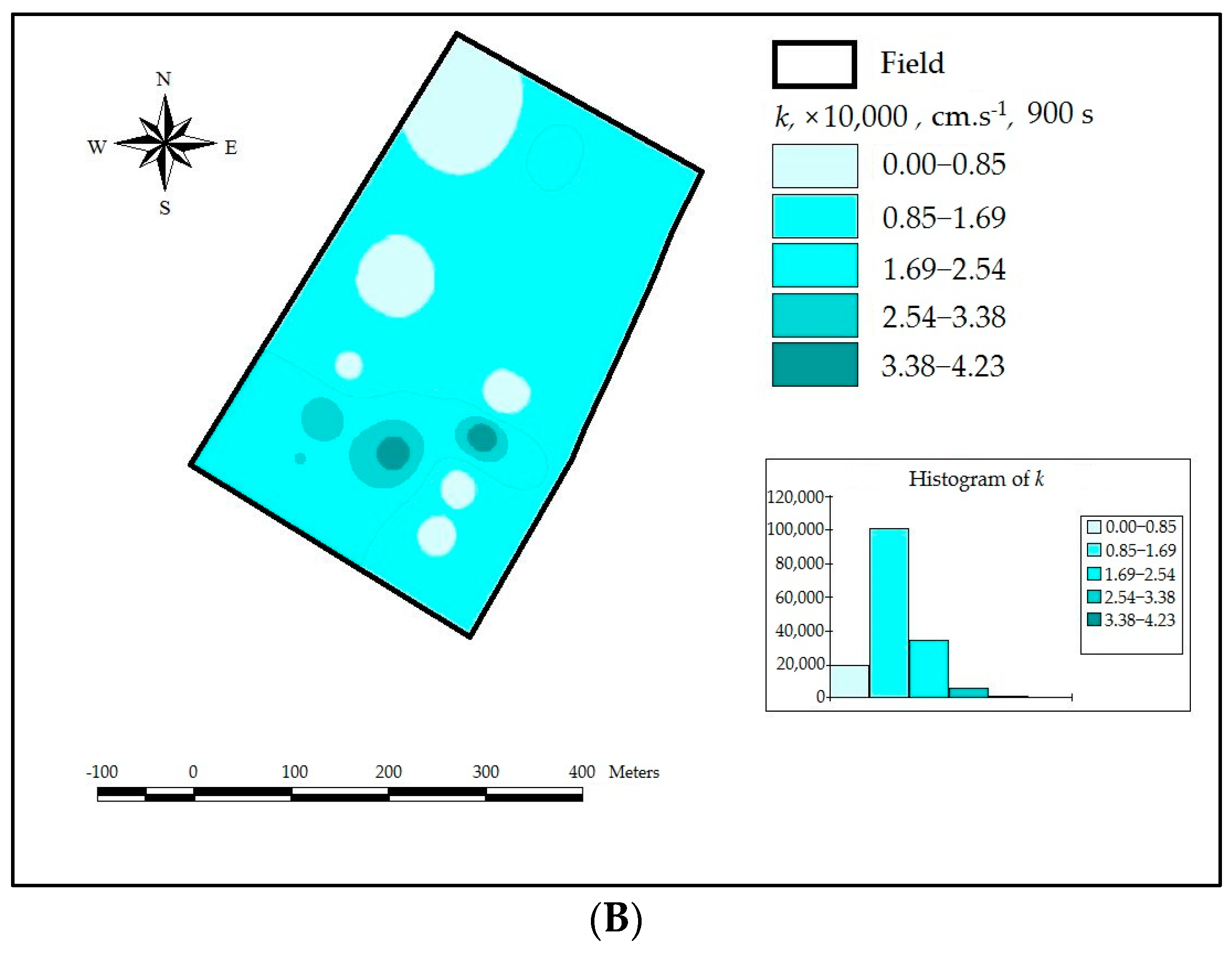
3.1. Spatial Variability of Hydraulic Conductivity
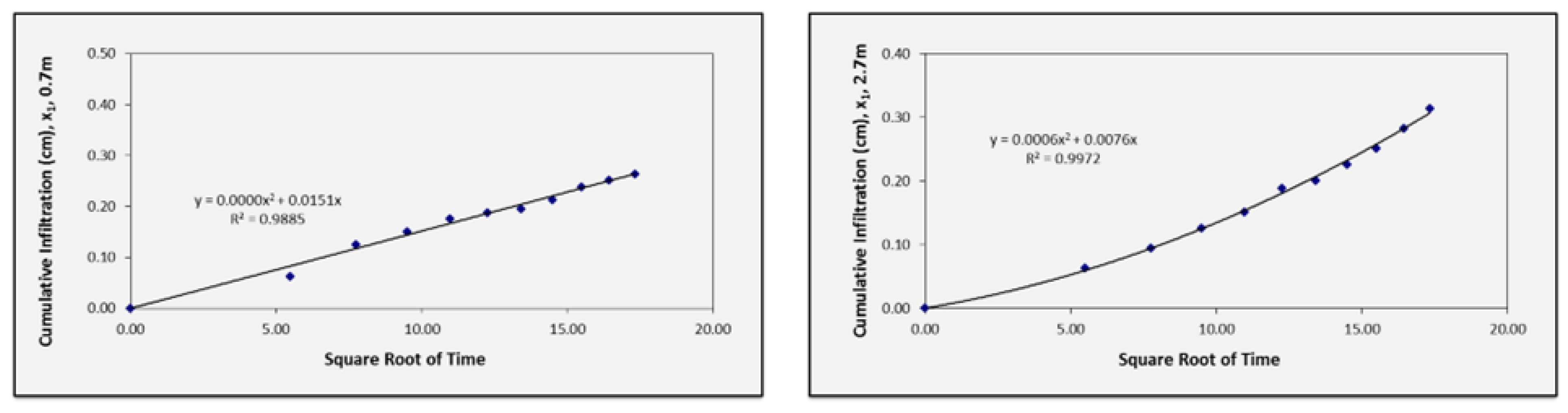
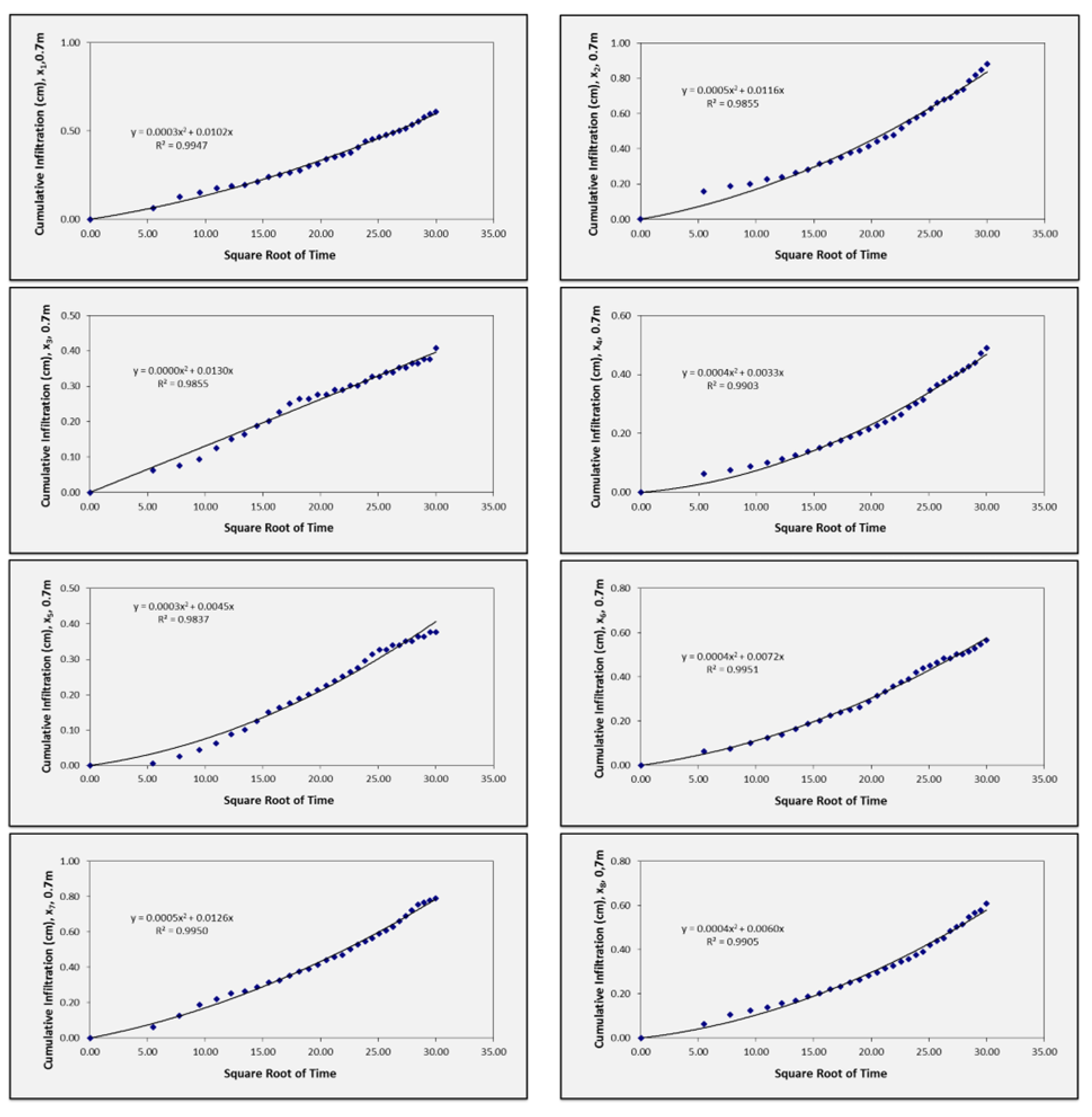
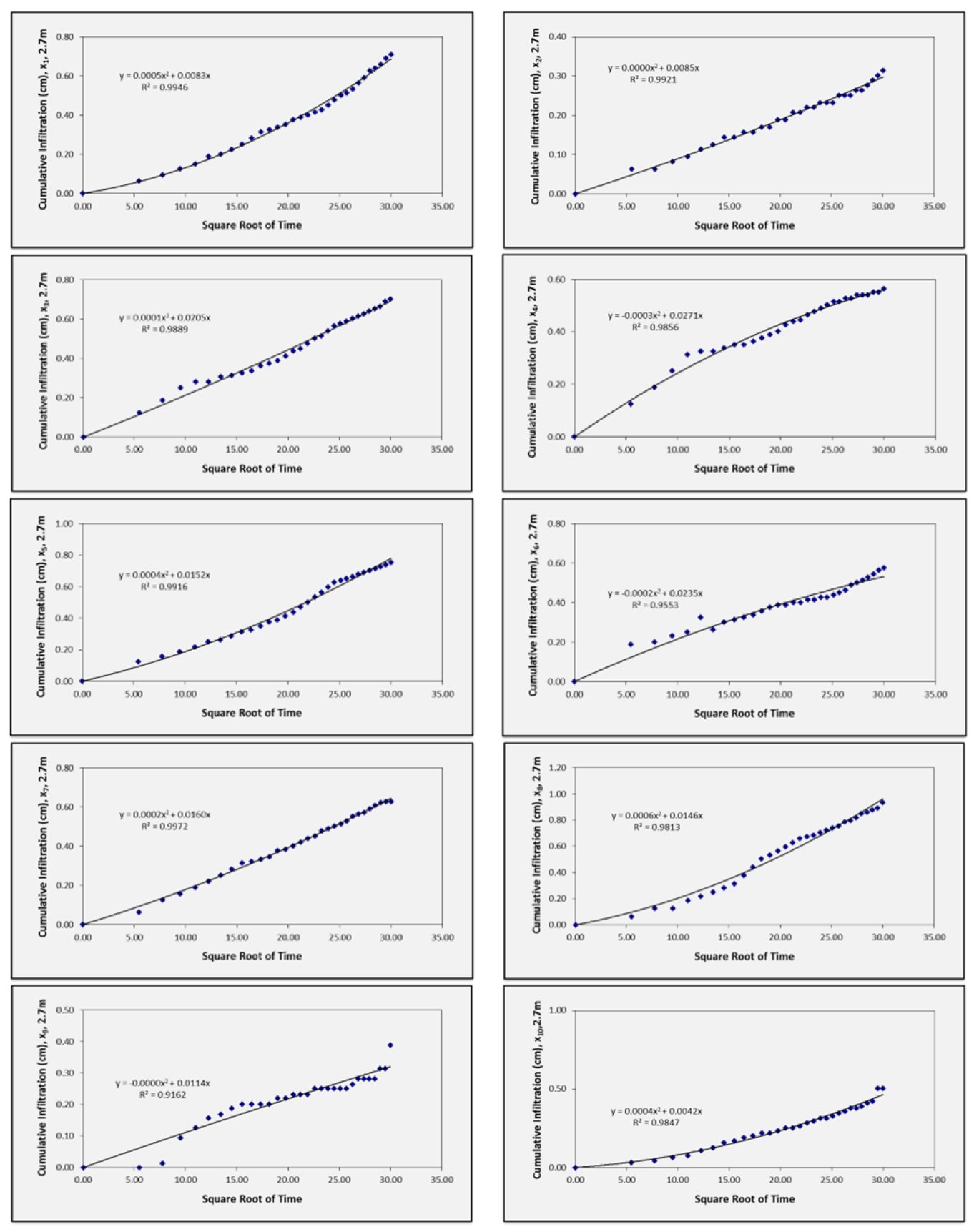
3.2. Results of Mini Disk Infiltrometer Measurements (Method One)
3.3. Results of Double Ring Infiltrometer Measurements (Method Two)
4. Conclusions
- -
- The used infiltration monitoring method showed differences in the measured values, with the difference factor reaching values of up to 0.24. The results obtained by the double ring infiltrometer method indicate higher values than the mini disk infiltrometer measurements.
- -
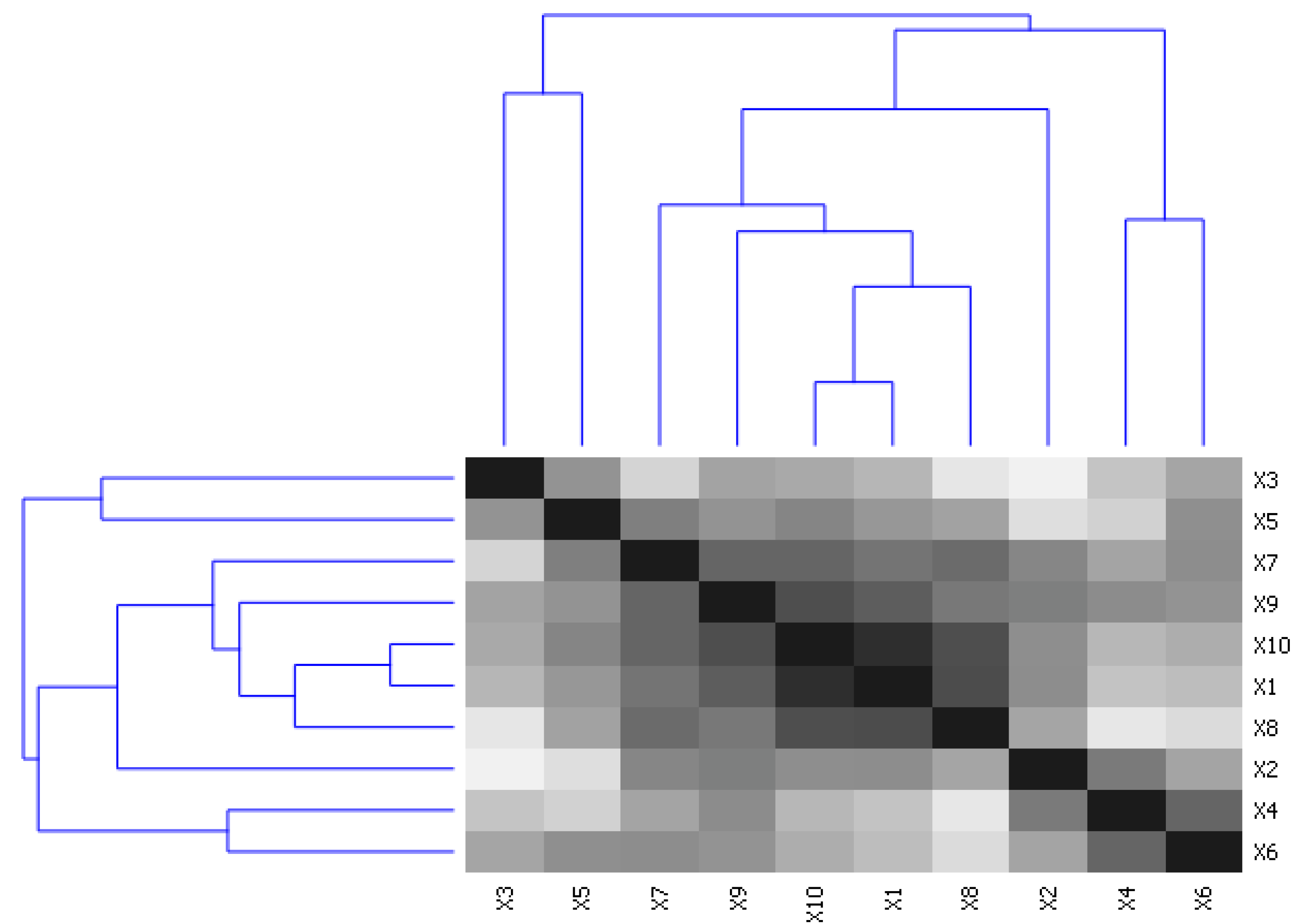
- From the point of view of monitoring the statistical significance of the location of the soil infiltration capacity measurement, the hypothesis was not confirmed. However, when evaluating the results with the first method (mini disk infiltrometer) in a hierarchical grouping in both lines and at all ten monitoring points, the results show a substantial deviation of three monitoring points from the others, which were located in the zones of long-term soil compaction.
- -
- The time interval of the soil infiltration capacity monitoring showed differences in the case of compacted and non-compacted soil; however, they were not significant when statistically considered. The hypothesis regarding the phenomenon of water repellency has been confirmed, which means that the effect of water repellency can be reduced by extending the measurement time interval.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Velebný, V.; Novák, V.; Skalová, J. Soil Water Regime, 1st ed.; Slovak Technical University: Bratislava, Slovakia, 2000; p. 208. (In Slovak) [Google Scholar]
- Jobbágy, J.; Krištof, K.; Bárek, V. Melioration in Agriculture: Soil Properties, Drainage and Irrigation, 1st ed.; Slovak University of Agriculture in Nitra: Nitra, Slovakia, 2017; p. 253. (In Slovak) [Google Scholar]
- Butler, D.; James, D.C.; Makropoulos, C.; Davies, J. Urban Drainage, 4th ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Kukan, P.; Jobbágy, J.; Buc, M.; Findura, P. Infiltration ability of soil as an indicator of its variability. In Proceedings of the Xth International Conference of Young Scientists, Prague, Czech Republic, 16–18 September 2008; pp. 130–135. [Google Scholar]
- Radinja, M.; Vidmar, I.; Atanasova, N.; Mikoš, M.; Šraj, M. Determination of Spatial and Temporal Variability of Soil Hydraulic Conductivity for Urban Runoff Modelling. Water 2019, 11, 941. [Google Scholar] [CrossRef]
- Šraj, M.; Dirnbek, L.; Brilly, M. The influence of effective rainfall on modelled runoff hydrograph. J. Hydrol. Hydromech. 2010, 58, 3–14. [Google Scholar] [CrossRef]
- Rossman, L. Storm Water Management Model User’s Manual Version 5.1; US EPA Office of Research and Development: Washington, DC, USA, 2015. [Google Scholar]
- Deb, S.K.; Shukla, M.K. Variability of hydraulic conductivity due to multiple factors. Am. J. Environ. Sci. 2012, 8, 489–502. [Google Scholar] [CrossRef]
- Fodor, N.; Sándor, R.; Orfanus, T.; Lichner, L.; Rajkai, K. Evaluation method dependency of measured saturated hydraulic conductivity. Geoderma 2011, 165, 60–68. [Google Scholar] [CrossRef]
- Kanso, T.; Tedoldi, D.; Gromaire, M.-C.; Ramier, D.; Saad, M.; Chebbo, G. Horizontal and Vertical Variability of Soil Hydraulic Properties in Roadside Sustainable Drainage Systems (SuDS)-Nature and Implications for Hydrological Performance Evaluation. Water 2018, 10, 987. [Google Scholar] [CrossRef]
- Gadi, V.K.; Tang, Y.-R.; Das, A.; Monga, C.; Garg, A.; Berretta, C.; Sahoo, L. Spatial and temporal variation of hydraulic conductivity and vegetation growth in green infrastructures using infiltrometer and visual technique. Catena 2017, 155, 20–29. [Google Scholar] [CrossRef]
- Bockhorn, B.; Klint, K.E.S.; Locatelli, L.; Park, Y.-J.; Binning, P.J.; Sudicky, E.; Bergen Jensen, M. Factors affecting the hydraulic performance of infiltration based SUDS in clay. Urban Water J. 2017, 14, 125–133. [Google Scholar] [CrossRef]
- Hills, C.R. The determination of the infiltration capacity of field soil using cylinder infiltrometer. Br. Geomorphol. Res. Group Tech. Bull. 1970, 3, 24. [Google Scholar]
- Ghosh, B.; Pekkat, S. A critical evaluation of measurement-induced variability in infiltration characteristics for a river sub-catchment. Measurement 2019, 132, 47–59. [Google Scholar] [CrossRef]
- Robichaud, P.R.; Lewis, S.; Ashmun, L. New Procedure for Sampling Infiltration to Assess Post-Fire Soil Water Repellency; Research Note RMRS-RN-33; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2008. [Google Scholar]
- Köhne, J.M.; Júnior, J.A.; Köhne, S.; Tiemeyer, B.; Lennartz, B.; Kruse, J. Double-ring and tension infiltrometer measurements of hydraulic conductivity and mobile soil regions. Pesqui. Agropecuária Trop. 2011, 41, 336–347. [Google Scholar]
- Schulin, R. Bodenschutz-Kutz; Institut f. Terrestrische Ökologie. ETHZ: Zürich, Switzerland, 1995. (In German) [Google Scholar]
- Davis, J.R.; Frey, A.W. Measurement of infiltration rates in irrigated furrows. Trans. ASAE 1963, 6, 4. [Google Scholar]
- Rataj, V.; Galambošová, J.; Macák, M.; Nozdrovický, L. Precision Agriculture: System—Machines—Experiences, 1st ed.; Profi Press: Prague, Czech Republic, 2014; 160p. (In Slovak) [Google Scholar]
- Godwin, R.; Misiewicz, P.; White, D.; Smith, E.; Chamen, T.; Galambošová, J.; Stobart, R. Results from recent traffic systems research and the implications for future work. Acta Technol. Agric. 2015, 3, 57–63. [Google Scholar] [CrossRef]
- SHMU. Meteorological Data from Podhájska. Available online: http://www.shmu.sk/sk/?page=2049&id=996 (accessed on 19 February 2019).
- Kolinany. Available online: https://www.kolinany.eu/download_file_f.php?id=73729 (accessed on 21 February 2013).
- SHMU. Meteorological Data. Available online: https://www.shmu.sk/sk/?page=1&id=klimat_operativneudaje2&identif=11858&rok=2020&obdobie=1991-2020 (accessed on 19 February 2020).
- SHMU. Meteorological Data. Available online: https://www.shmu.sk/sk/?page=1&id=klimat_operativneudaje1&identif=11858&rok=2020&obdobie=1991-2020&sub=1 (accessed on 19 February 2020).
- Ditzler, C.; Scheffer, K.; Monger, H.C. (Eds.) Soil Science Division Staff Soil Survey Manual; USDA Handb.; Government Printing Office: Washington, DC, USA, 2017; Volume 18, ISBN 978-1410204172. [Google Scholar]
- Rataj, V.; Kumhálová, J.; Macák, M.; Barát, M.; Galambošová, J.; Chyba, J.; Kumhála, F. Long-Term Monitoring of Different Field Traffic Management Practices in Cereals Production with Support of Satellite Images and Yield Data in Context of Climate Change. Agronomy 2022, 12, 128. [Google Scholar] [CrossRef]
- Ritchey, E.L.; McGrath, J.M.; Gehring, D. Determining Soil Texture by Feel; Agriculture and Natural Resources Publication, University of Kentucky, College of Agriculture, Food and Environment: Lexington, KY, USA, 2015; p. 139. [Google Scholar]
- Topcon GRS-1. Operator’s Manual. Available online: https://www.topptopo.dk/files/manual/GRS-1_OM.PDF (accessed on 21 February 2009).
- METER Group Inc. Mini Disk Infiltrometer; METER Group Inc.: Pullman, WA, USA, 2018. [Google Scholar]
- Kirkham, M.B. Principles of Soil and Plant Water Relations; Elsevier Academic Press: Burlington, MA, USA, 2005; pp. 145–172. [Google Scholar]
- Zhang, R. Determination of Soil Sorptivity and Hydraulic Conductivity from the Disk Infiltrometer. Soil Sci. Soc. Am. J. 1997, 61, 1024–1030. [Google Scholar] [CrossRef]
- Carsel, R.F.; Parrish, R.S. Developing joint probability distributions of soil water retention characteristics. Water Resour. Res. 1988, 24, 755–769. [Google Scholar] [CrossRef]
- Dohnal, M.; Dusek, J.; Vogel, T. Improving hydraulic conductivity estimates from Minidisk Inltrometer measurements for soils with wide pore-size distributions. Soil Sci. Soc. Am. J. 2010, 74, 804–811. [Google Scholar] [CrossRef]
- Kutilek, M.; Nielsen, D.R. Soil Hydrology; Catena-Verlag: Cremlingen-Destedt, Germany, 1994; 370p. [Google Scholar]
- DRIM. Double Ring Infiltrometer Manual; Eijkelkamp: Giesbeek, The Netherlands, 2015; Available online: https://www.eijkelkamp.com/download.php?file=M0904e_Double_ring_infiltrometer_68ab.pdf (accessed on 25 February 2015).
- Philip, J.R. The theory of infiltration: 1. The infiltration equation and its solution. Soil Sci. 1957, 83, 345–358. [Google Scholar] [CrossRef]
- Köhne, J.M.; Júnior, J.A.; Köhne, S.; Lennartz, B. Double-ring and tension infiltrometer measurements of saturated hydraulic conductivity and dye tracer movement. Geophys. Res. Abstr. 2006, 8, 01368. [Google Scholar]
- Liu, H.; Lei, T.W.; Yhao, J.; Zuan, C.P.; Fan, Y.T.; Qu, L.Q. Effects of rainfall intensity and antecedent soil water content on soil infiltrability under rainfall conditions using the run off-on-out method. J. Hydrol. 2011, 396, 24–32. [Google Scholar] [CrossRef]
- Chromíková, J.; Heviánková, S.; Kyncl, M.; Korabík, M.; Marschalko, M. Artificial Recharge-measurement of soil infiltration in Rožňov pod Radhoštěm. GeoScience Eng. 2018, 63, 13–19. [Google Scholar] [CrossRef]
- Radinja, M.; Banovec, P.; Comas Matas, J.; Atanasova, N. Modelling and Evaluating Impacts of Distributed Retention and Infiltration Measures on Urban Runoff. Acta Hydrotech. 2017, 30, 51–64. [Google Scholar]
- Jobbágy, J.; Krištof, K.; Findura, P.; Angelovič, M.; Folkman, M. Evaluation of infiltration capacity of the soil during application of additional irrigation. Savrem. Poljopr. Teh. 2014, 40, 69–76. [Google Scholar] [CrossRef]
- DeBano, L.F. Water Repellent Soils: A State-of-the-Art; General Technical Report PSW-GTR-46; U.S. Department of Agriculture, Forest Service, Pacific Southwest Forest and Range Experiment Station: Berkeley, CA, USA, 1981. [Google Scholar]
- DeBano, L.F. Water repellency in soils: A historical overview. J. Hydrol. 2000, 231–232, 4–32. [Google Scholar] [CrossRef]
- Lucas-Borja, M.E.; Zema, D.A.; Plaza-Álvarez, P.A.; Zupanc, V.; Baartman, J.; Sagra, J.; González-Romero, J.; Moya, D.; de las Heras, J. Effects of Different Land Uses (Abandoned Farmland, Intensive Agriculture and Forest) on Soil Hydrological Properties in Southern Spain. Water 2019, 11, 503. [Google Scholar] [CrossRef]
- de Jonge, L.W.; Jacobsen, O.H.; Moldrup, P. Soil Water Repellency: Effects of Water Content, Temperature, and Particle Size. Soil Sci. Soc. Am. J. 1999, 63, 437. [Google Scholar] [CrossRef]
- Leelamanie, D.A.L.; Karube, J. Effects of organic compounds, water content and clay on the water repellency of a model sandy soil. Soil Sci. Plant Nutr. 2007, 53, 711–719. [Google Scholar] [CrossRef]
- Lichner, L.; Orfánus, T.; Nováková, K.; Šír, M.; Tesař, M. The impact of vegetation on hydraulic conductivity of sandy soil. Soil Water Res. 2007, 2, 59–66. [Google Scholar] [CrossRef]
- Stolte, J.; Van Venrooij, B.; Zhang, G.; Trouwborst, K.O.; Liu, G.; Ritsema, C.J.; Hessel, R. Land-use induced spatial heterogeneity of soil hydraulic properties on the Loess Plateau in China. Catena 2003, 54, 59–76. [Google Scholar] [CrossRef]
- Šindelář, R.; Kroulík, M.; Mašek, J.; Prochádzka, P.; Hula, J.; Kovaříček, P. Evaluation of the water infiltration into the soil. In Proceedings of the IX International scientific conference of young scientists, Nitra, Slovakia, 10–11 October 2007. [Google Scholar]
- Shipitalo, M.J.; Dick, W.A.; Edwards, W.M. Conservation tillage and macropore factors that affect water movement and the fate of chemicals. Soil Tillage Res. 2000, 53, 167–183. [Google Scholar] [CrossRef]
- Ginting, D.; Moncrief, J.F.; Gupta, S.C. Performance of a Variable Tillage Systems Based on Interaction with Landscape and Soil. Precis. Agric. 2003, 4, 19–34. [Google Scholar] [CrossRef]
- Rose, C.W. Agricultural Physics; Permagon Press Ltd.: Headington Hill Hall, Oxford/London, UK, 1966; 248p. [Google Scholar]
- Brady, N.C.; Weil, R.R. The Nature and Properties of Soils, 12th ed.; Prentice Hall Publishers: London, UK, 1999; 740p. [Google Scholar]
- Pimentel, D.; Harvey, C.; Resosudarmo, P.; Sinclair, K.; Kurz, D.; McNair, M.; Crist, S.; Shpritz, L.; Fitton, L.; Saffouri, R.; et al. Environmental and economic costs of soil erosion and conservation benefits. Science 1995, 267, 1117–1123. [Google Scholar] [CrossRef] [PubMed]
- Lal, R. Soil erosion and the global carbon budget. Environ. Int. 2003, 29, 437–450. [Google Scholar] [CrossRef] [PubMed]



| Soil Properties | ||
|---|---|---|
| Code | Code Description | Properties |
| 01 | Climate region code | warm, dry, lowland |
| 50 | Main soil unit code | pseudogley brown soil on loamy and polygenic clays, medium–heavy |
| 0 | Slope and exposure code | plain without surface water erosion |
| 0 | Soil skeleton and depth code | deep soil without skeleton |
| 2 | Soil grain size code | medium–heavy soils (clay) |
| Soil texture | ||
| Clay | 51% | |
| Sand | 30% | |
| Silt | 19% | |
| Weather Properties | ||
| Precipitation, mm | Average (1991–2020) | Sum, 2020 |
| 521 | 578.4 | |
| Temperature, °C | Average (1991–2020) | Range, 2020 |
| −2 ÷ 24 | −4 ÷ 27 | |
| MP | C1 | k, ×10−4 cm·s−1 | C1 | k, ×10−4 cm·s−1 | C1 | k, ×10−4 cm·s−1 | C1 | k, ×10−4 cm·s−1 |
|---|---|---|---|---|---|---|---|---|
| Measurement Data for MP—0.7 m | Measurement Data for MP—2.7 m | |||||||
| T = 300 s | T = 900 s | T = 300 s | T = 900 s | |||||
| x1 | 0.0000 | 0.00 | 0.0003 | 1.07 | 0.0006 | 2.14 | 0.0005 | 1.79 |
| x2 | −0.0003 | −1.07 | 0.0005 | 1.79 | 0.0000 | 0.00 | 0.0000 | 0.00 |
| x3 | 0.0004 | 1.43 | 0.0000 | 0.00 | −0.0005 | −1.79 | 0.0001 | 0.36 |
| x4 | 0.0000 | 0.00 | 0.0004 | 1.43 | −0.0006 | −2.14 | −0.0003 | −1.07 |
| x5 | 0.0007 | 2.50 | 0.0003 | 1.07 | 0.0000 | 0.00 | 0.0004 | 1.43 |
| x6 | 0.0004 | 1.43 | 0.0004 | 1.43 | −0.0008 | −2.86 | −0.0002 | −0.71 |
| x7 | 0.0003 | 1.07 | 0.0005 | 1.79 | 0.0005 | 1.79 | 0.0002 | 0.71 |
| x8 | 0.0001 | 0.36 | 0.0004 | 1.43 | 0.0011 | 3.93 | 0.0006 | 2.14 |
| x9 | 0.0001 | 0.36 | 0.0003 | 1.07 | 0.0006 | 2.14 | 0.0000 | 0.00 |
| x10 | 0.0001 | 0.36 | 0.0003 | 1.07 | 0.0006 | 2.14 | 0.0004 | 1.43 |
| Aver | 0.83 | 1.22 | 1.73 | 0.98 | ||||
| St. dev. | 0.79 | 0.49 | 1.27 | 0.77 | ||||
| CV (%) | 94.59 | 39.99 | 73.37 | 78.71 | ||||
| MP | A1 | ks × 10−3 cm·s−1 | A1 | ks × 10−3 cm·s−1 | A1 | ks × 10−3 cm·s−1 | A1 | ks × 10−3 cm·s−1 |
|---|---|---|---|---|---|---|---|---|
| Measurement Data, MB—0.7 m | Measurement Data, MB—2.7 m | |||||||
| T = 300 s | T = 900 s | T = 300 s | T = 900 s | |||||
| x1 | 0.0028 | 4.20 | 0.0025 | 3.75 | 0.0014 | 2.10 | 0.0049 | 7.35 |
| x2 | 0.0048 | 7.20 | 0.0021 | 3.15 | 0.0022 | 3.30 | 0.0001 | 0.15 |
| x3 | 0.0016 | 2.40 | 0.0003 | 0.45 | 0.02 | 30.00 | 0.0091 | 13.65 |
| Aver. | 4.60 | 2.45 | 11.80 | 7.05 | ||||
| St. dev. | 1.98 | 1.44 | 12.88 | 5.52 | ||||
| CV (%) | 43.04 | 58.58 | 109.14 | 78.23 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jobbágy, J.; Krištof, K.; Angelovič, M.; Zsembeli, J. Evaluation of Soil Infiltration Variability in Compacted and Uncompacted Soil Using Two Devices. Water 2023, 15, 1918. https://doi.org/10.3390/w15101918
Jobbágy J, Krištof K, Angelovič M, Zsembeli J. Evaluation of Soil Infiltration Variability in Compacted and Uncompacted Soil Using Two Devices. Water. 2023; 15(10):1918. https://doi.org/10.3390/w15101918
Chicago/Turabian StyleJobbágy, Ján, Koloman Krištof, Michal Angelovič, and József Zsembeli. 2023. "Evaluation of Soil Infiltration Variability in Compacted and Uncompacted Soil Using Two Devices" Water 15, no. 10: 1918. https://doi.org/10.3390/w15101918
APA StyleJobbágy, J., Krištof, K., Angelovič, M., & Zsembeli, J. (2023). Evaluation of Soil Infiltration Variability in Compacted and Uncompacted Soil Using Two Devices. Water, 15(10), 1918. https://doi.org/10.3390/w15101918









