Temporal Fluctuations in Household Water Consumption and Operating Pressure Related to the Error of Their Water Meters

Abstract

The growing population is creating a rising demand for water, particularly in developing countries. As the urban population seeks to improve their standard of living, the authorities responsible for providing domestic utility services face increased pressure to provide higher-quality and secure services. To meet this challenge, the performance of all systems must be improved, and a better understanding of user behavior and water consumption patterns must be achieved. Modern routing and water quality models need accurate demand information. This research will analyze household water consumption patterns over time and their correlation with pressure levels. The results will inform a new methodology for managing and delivering services, considering the global error of gauges in the study area. The goal is to ensure sufficient and effective capacity to provide appropriate services for community development.

1. Introduction

The design of a water supply network consists of sizing the pipes that must provide a water demand to the consumers. Demands are used as part of the data needed for the design. In the field of project design, two models are commonly employed to cope with these demands. The first model considers permanent or static consumption factors [1], while the second model considers the time evolution or dynamic consumption factors. Despite the widespread use of these models, they assume that the consumption factors they represent are accurate. However, it is widely recognized that domestic water consumption is not consistently generated over time, but rather occurs in short bursts with extended periods of non-consumption [1]. To face this intermittent water supply, many water distribution networks include domestic tanks that allow users to store water during supplying hours [2]. This sporadic consumption pattern can result in longer residence times in the lateral pipes of distribution networks, which can negatively impact the quality of the water reaching the end users [3]. Blokker et al. [4] stated that residence time of water (water age) in a network is a good measure of the quality, and this parameter can be easily calculated if the information about demand patterns is accurate.

The accuracy of water quality modeling in distribution networks can be improved by considering both main pipes and secondary pipes, rather than relying solely on skeletonized models that are limited to main pipes and the time variation of global demand for the entire network [5]. Grayman et al. [6] demonstrated that defining a district metering area in looped networks hardly affects the water quality, and Matchell and Boxall [3] observed that additional effects such as demand patterns or mixing schemes can cause differences in water quality. In this sense, Piazza et al. [7] compared the advective model used by EPANET to a dynamic dispersion model. In the comparison, the latter performed better in the presence of variable flow regimes. The differences between real measurements and calculated values are bigger for low values of the Reynolds number [8]. To effectively optimize drinking water networks, it is crucial to understand the behavior of the subscribers, including the volume of water they consume and the accuracy of their water meters [5]. This information provides insight into the volume of water that is consumed and the extent to which the billing process reflects this consumption.

Criminisi et al. [9] related the accuracy of domestic water meters with the behavior of water tanks. They observed that the errors in the water meters were highly affected by the presence of water tanks. If the tanks are almost full, the flow entering them is very small, and the errors in the meters are high. On the contrary, if these tanks are periodically filled and emptied, the error reduces because the flow rate is higher in tanks than in appliances. They also observed in situ that errors in water meters dramatically increase with water meter age.

In this study, a set of domestic water meters was studied to analyze the errors and relate them with both age and water tank behavior. This study seeks to answer the question of whether household water meters have flow errors and what impact these errors may have on water consumption and the billing process. By identifying any flow errors, this research aims to ensure sufficient and effective capacity for providing appropriate services to the community. In addition as mentioned above, knowledge of demand patterns allows quantifying water quality in a network, especially when there are domestic tanks and an intermittent water supply scheme.

2. Methodology

The current study was conducted through the collection of two types of data in two main phases. The first phase involves the installation of remote stations and the respective procedures for collecting and analyzing data, whereas the second phase is the removal of the water meters for testing and data analysis, which will capture the primary field processes. The data collection was carried out both digitally and manually by a materials team.

2.1. First Phase (Consumption and Pressure Curves and Their Evolution over Time)

The present study was conducted in the cantonal capital city of Loja, which is situated at an altitude of 2100 m above sea level and at a latitude of 4° south and a longitude of 79° west. The water supply network under investigation is located in the “El Sagrario” parish of Loja city, registered as “Route 46” in the municipal registry. The distribution network starts at an underground chamber serving as a control point and data collection node (base node). The “Route 46” water distribution network supplies water to the residential areas of La Estancia, Zamora Huayco, and Las Minas, covering an area of 30.60 ha, forming a hydro-metric district for this study. These areas are composed of public or private residential developments that are in the process of consolidation, largely disconnected from one another. The population density is 93 inhabitants per ha, and the areas are predominantly located in close proximity to the consolidated region. The urban environments are currently undergoing a process of densification and transformation, with a mono-functional residential landscape dominated by pre-planned urbanization. Accessibility is moderate due to the proximity to a primary road system, while the community interaction within public spaces is low. A visual representation of the study area is presented in Figure 1.

For the purpose of compiling field data, this information was used to graphically interpret the curves. Remote stations were installed in 5 different households for an average of 30 days, with data being recorded every 60 s to create a database for the main analysis. Each station was placed next to each household’s water meter, thereby capturing the flow generated by the users and the pressure of the network [10].

Registration of Water Consumption

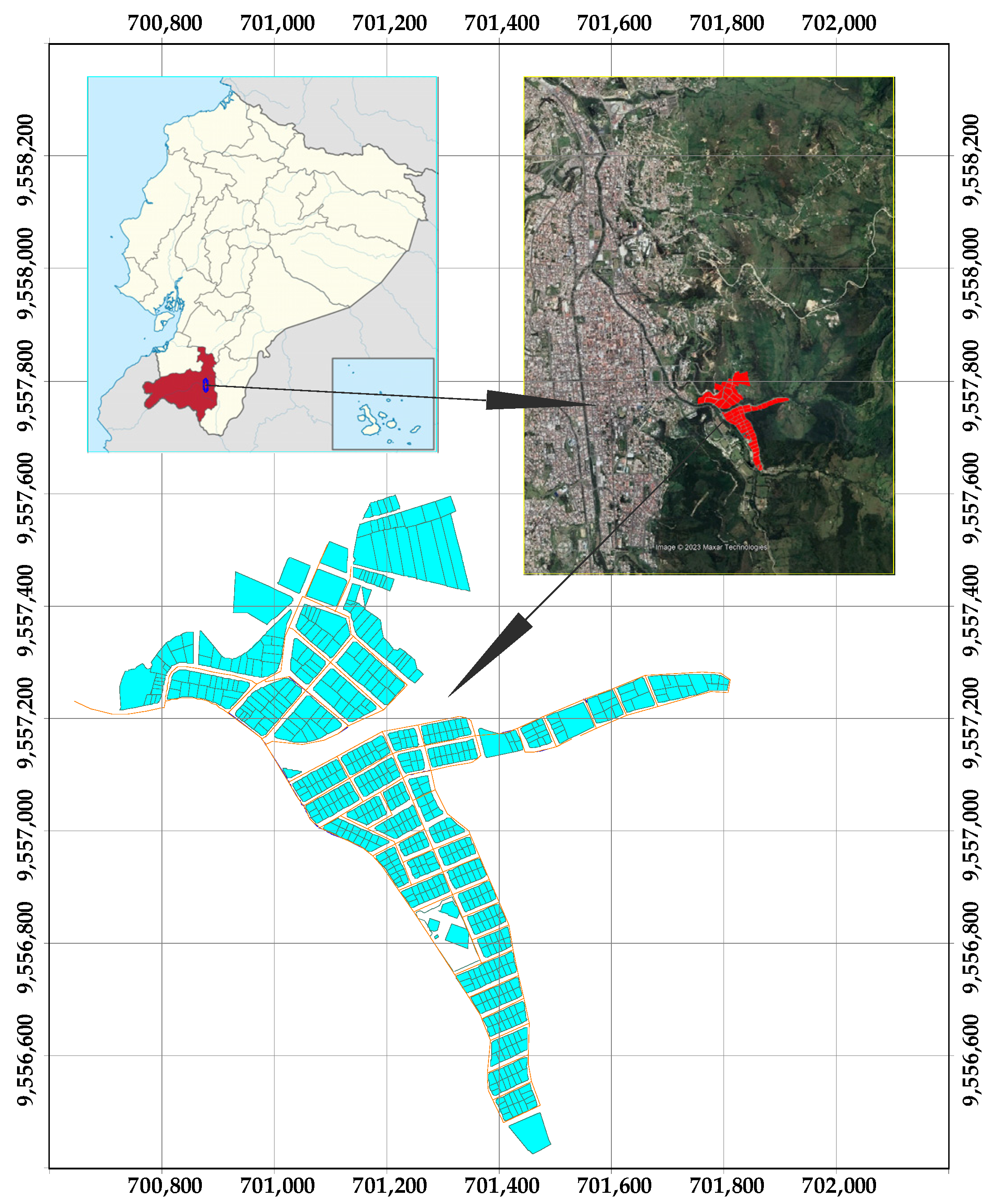
The registration of water consumption and supply pressure took place from 1 December 2014 to 29 July 2015. The area selected for the study is mainly residential (86%), with 4% being commercial subscribers and 10% being other uses. Most of the lots in the area correspond to single-family houses (69%). In a recent survey, 31% of users stated that they had continuous service, and the remaining 69% had some kind of interruption in their service. For this reason, most of the houses included a tank to guarantee the supply of water so that water from the network fills the tanks, and users consume from them.

It is worth noting that there were instances where data recording stopped due to technical failures of servers [11]. The data recorded during the day allowed for the projection of a comparative consumption and pressure curve over time. The trends generated by consumption and pressure are shown in Figure 2. The actual demand of a home and its occupants is very different from the time history curve. It can be observed in Figure 2 that the flow circulating through the matrix or core network is very different from domestic demands, as shown in Figure 3.

Most of the flow data recorded contained zero units of domestic consumption, while the consumption of the primary grid remained constant. From the analysis of the patterns in each graph, the following observations can be made: In Figure 3, there are fairly long periods of zero flow rate and a specific consumption pattern in certain hours or peak periods [12]. The pressure curve remains constant at night, resulting in a consistent pressure, but when domestic consumption begins, there is a pressure drop and a low pressure value from the beginning of consumption until consumption subsides, leading to a full restoration of pressure in the network [13]. It can be clearly seen from the previous two graphs that the pressure drops at around 5:00 a.m. when domestic consumption increases and continues to decline until 8:00 p.m. when consumption subsides, resulting in an absolute recovery of pressure in the network [14]. This time frame (5:00 p.m. to 8:00 p.m.) is considered to be when the pressure significantly decreases due to direct correlation with consumption.

2.2. Second Phase (Global Determination of Domestic Water Meter Error)

This part of the investigation aimed to determine the global error of domestic water meters in the study area and its evolution over time [15]. The goal was to analyze both the percentage of economic losses for the institution responsible and the cost incurred by users as a result of this error. Like all mechanical devices, water meters wear out and lose their metrological properties over time, and their accuracy depends on factors such as the amount of water measured, circulating currents, installation position, quality of building materials, water composition, and possible resistance materials [16]. The only way to determine if a meter is accurately recording the flow of water is through testing. Previous studies did not take into account the starting flow [17], which leads to incorrect calculations of the global error and does not account for registered volume consumption at low flows. The purpose of determining this error is to understand the actual or approximate behavior of users as they become aware of the working range and performance of the water meters.

The development of this phase of research involved the random removal of operational domestic water meters from participating dwellings. To maintain the privacy of the water meter manufacturers, the brand and model will not be disclosed [18]. The experiments were conducted on a hydraulic bench using small-diameter gauges. The different types of water meters were tested in their respective homes, and each meter was a multiple-nozzle meter. With a total of 56 used water meters and an additional 180 new water meters, a total of 236 water meters were tested, providing a sufficient base of information for the analysis.

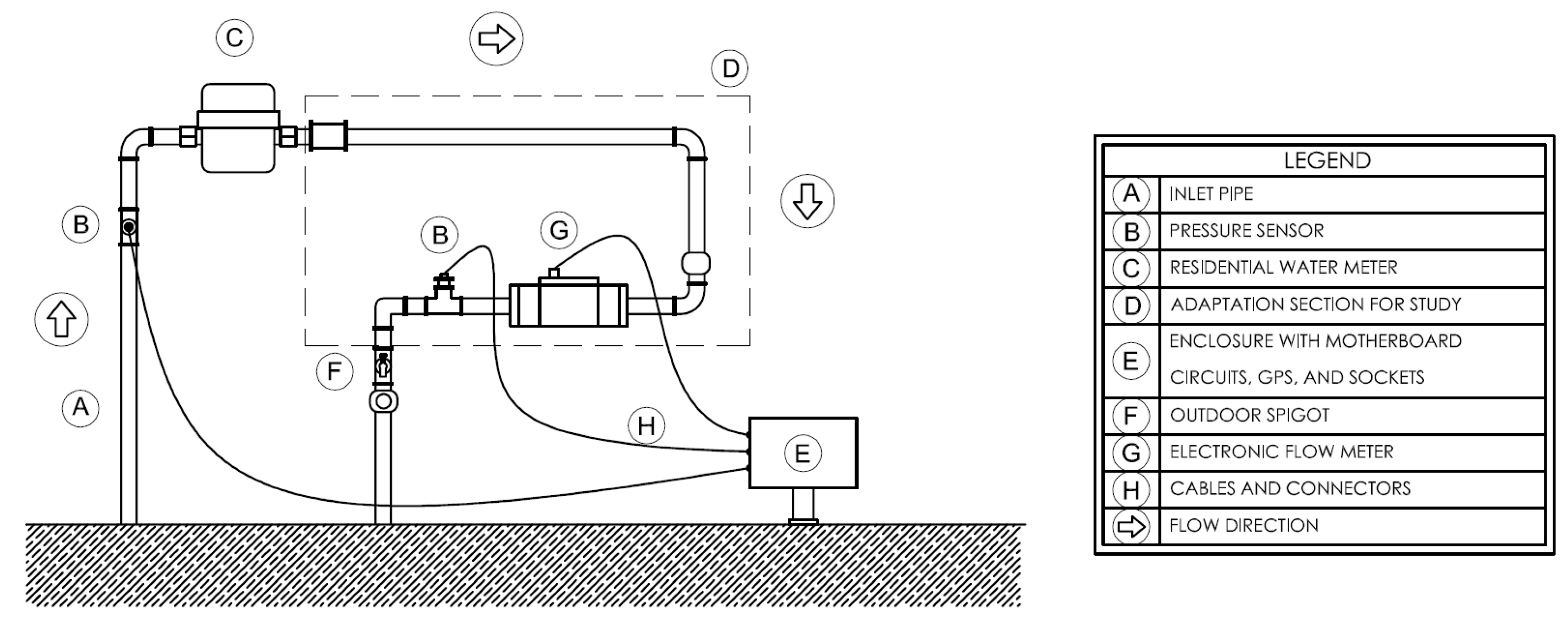
2.2.1. Description of the Experiments

Efficient management of hydrometric systems requires consideration of the available water meters, as they provide a direct indicator of the amount of water consumed by users [19]. To determine the error present in water meters, experiments were performed to measure the error. Properly defining the procedure is crucial for achieving greater accuracy and validity of the results. It is important to carry out error tests systematically and with the highest possible accuracy, as incorrect test procedures can lead to incorrect conclusions and result in significant economic losses [20]. The focus of this section will be on the procedures and test equipment used in the results.

The results of the experiments generated a cloud of points that served as the starting point for creating a curve. When the trend could be determined, points that did not fit the trend were discarded, leaving only those that followed a defined range [21]. The measurement error was determined by comparing the volume circulated in a calibrated tank to the volume recorded by the water meter. This was performed in three phases [4]: a visual reading of the meter’s total accumulated volume before the trial ($V_i$), the injection of a known volume of water ($V_r$) into the hydraulic bench, and a refresh of the visual reading of the meter’s total accumulated volume after the known volume had passed ($V_f$). See Figure 4.

The measurement error is determined by the test performed using Equation (1):

$$E_{\%}=\left(\frac{V_m-V_r}{V_r}\right)\times 100$$

(1)

where E% is the percent error of the measurement device; $V_m=V_f-V_i$; $V_f$ is the accumulated volume of the meter after the test; $V_i$ is the cumulative volume of the meter before testing; and $V_r$ is the tested real volume.

The measurement error in water distribution systems is a result of comparing the volume recorded by the meter with the real volume stored in the tank during a test. If the recorded volume is greater than the actual stored volume, it is referred to as overcounting [22]. On the other hand, if it is less, it is referred to as undercounting.

2.2.2. Assay Procedure

To calculate the error in the water meters and create the error curve, the following procedure was followed: the water meters were carefully removed from their respective houses to prevent any damage during transportation. Before installing them on the bench, the meters were checked for any blockages. The hydropneumatic system was then turned on, and the shut-off valve was closed at the beginning of the test. The water meters were connected in series, with consideration given to the flow direction to avoid any inaccuracies during testing.

The valve at the beginning of the meter was opened while the one at the end was kept closed to prevent any leaks. If there were any leaks, the meter was removed and re-installed to ensure no leaks existed. The manual readings ($V_i$) were taken before the test and recorded with an accuracy of 0.1 L. The sample flow was regulated by manually opening the tap and the check valve. The flow was maintained consistently throughout the test. Once the desired volume ($V_r$) was reached, the volumetric tank was stopped, and the new volumes ($V_f$) were recorded and reported by the water meters. The readings were correctly interpreted by the technical manager [23]. Finally, the hydropneumatic system was turned off, the last key was opened and depressurized (see Figure 4, H of the legend), and each meter was dismantled and removed for re-installation in the houses.

2.2.3. Mathematical Models Used to Assess the Precision of Household Flow Meter

To estimate the accuracy of the flow recording of the household flow meters, mathematical models are used. The relationship between pressure and discharge, which is an integral component of the continuity equation, is a critical aspect of hydraulic models based on pressure simulation methods. In this study, a model was proposed to evaluate the flow of a known volume through a hydraulic pumping line, where 8 flow meters were assessed simultaneously. The model considers the presence of a local storage tank located at the end of the hydraulic line.

The proposed model was modified from that of Criminisi et al. as outlined in [9]. The modified model accurately represents the tank intake process by taking into account the characteristics of the water level in the calibrated cylindrical storage tank. By implementing this model, a deeper understanding of the accuracy and reliability of the flow meters can be gained, leading to potential enhancements in their performance.

The expected volume that should flow through the system can be calculated using these equations and compared with the volume recorded by each meter. If a difference is detected, it would indicate an error in the measurement and could be used to adjust or calibrate the meter accordingly.

In the context of domestic flow meters, the initial and final volume of water passing through each meter is recorded. The difference between these volumes should correspond to the volume that filled the calibrated storage tank. However, discrepancies between the measured and actual volumes can indicate either overcounting or undercounting.

In order to address this issue, a proposed model integrates the tank continuity equation (Equation (2)) and the emitter law of the float valve based on Torricelli’s principle (Equation (3)). This model considers the negligible magnitude of the kinetic component and provides a more accurate assessment of the flow meter performance.

$$Q_{up}-R=\frac{dV}{dt}=A·\frac{dh}{dt}$$

(2)

In addition, the emitter law of the float valve based on Torricelli’s principle, with the assumption that the kinetic component of the surface of the tank is of minimal significance, is described by Equation (3):

$$Q_{up}=C_v{a}_v\sqrt{2g \left(H-z_r\right)}$$

(3)

Here, (R) and (Q_up) represent the water needs of the user and the outflow, respectively, while (t) refers to time, and (V) refers to the storage volume, which is determined by the area (A) and (h), the variable water depth. The emitter coefficient of the float valve is represented by ($C_v)$; the outlet area of the valve is represented by ($a_v)$; (H) represents the hydraulic head above the distribution network; $(z_r)$ represents the height of the float valve; and (g) is the acceleration due to gravity.

Criminisi et al. [9], put forward a proposal for an exponential law for the emitter coefficient of a float valve, as stated in Equation (4):

$$C_v=f\left(h\right)=\left\{\begin{array}{cc}C\times v \to & if h>h_{min}\\ C\times v\times {\left\{\frac{h_{max}-h}{h_{max}-h_{min}}\right\}}^m \to & if h\le h_{min}\end{array}\right\}$$

(4)

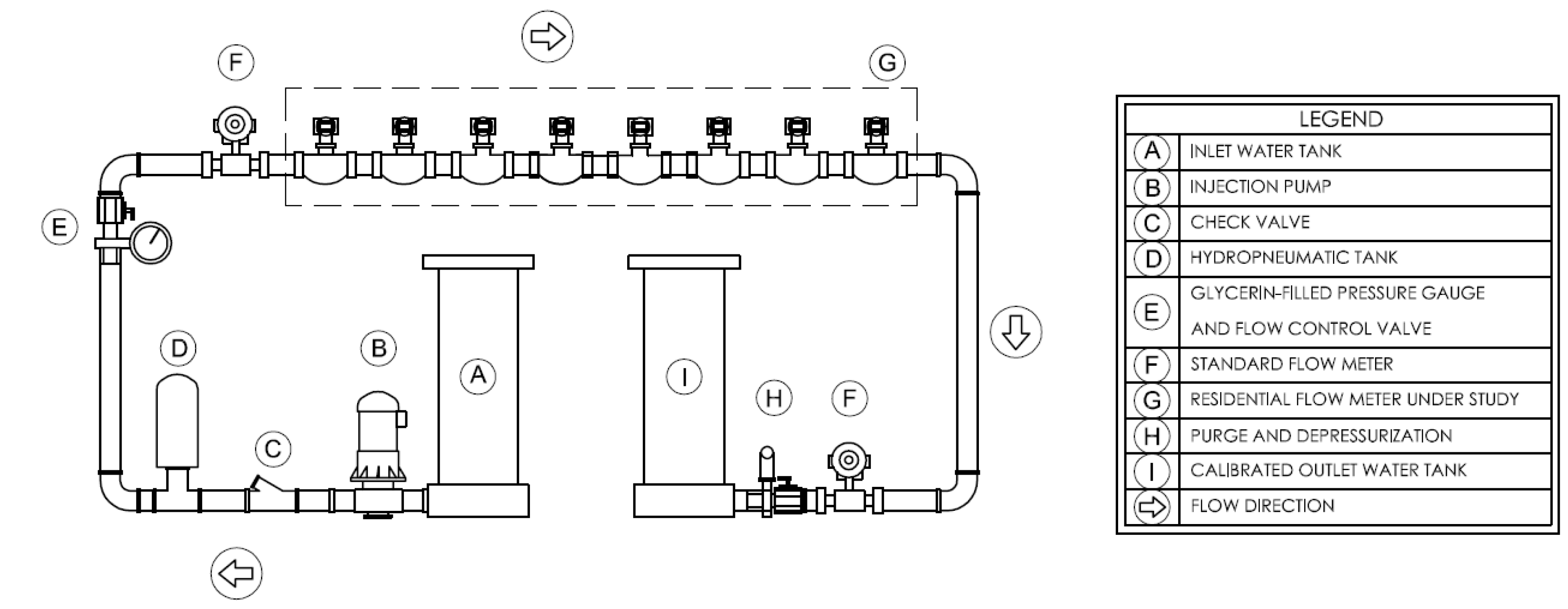
2.2.4. Hydraulic Water Meter Bench

The hydraulic water meter bench that was tested had a capacity of 8 water meters connected in series, with diameters ranging from 13 mm to 40 mm (Figure 4). The bench was equipped with a pressure gauge filled with glycerin, gate wrenches, media valves, a flow regulator wrench, and a calibrated storage tank [24]. The bench was supplied by a suction tank through a hydropneumatic system that used a 25 mm PVC pipe [25].

2.2.5. Water Meters Tested

A total of 56 water meters were tested at random, and additional information was obtained from 180 newly tested water meters, giving a total of 236 tested water meters [26]. The tested water meters were instances of a multi-beam model, designed to regulate the flow of water through a series of channels in the meter’s chamber or capsule. The water’s flow is influenced by symmetrical and balanced jets, which cause the rotation and measurement of the water’s volume [27].

To install pressure data loggers and an electronic flow meter in households, minor adjustments were required in the house connections (Figure 5).

2.2.6. Limitation of the Study

The research was focused on measuring domestic water usage, which could be impacted by poor maintenance of pipes resulting in water being lost before it reaches the meters. This can lead to errors in the values collected. Furthermore, the accuracy of the measurements in the study may not be optimal due to the lack of modern equipment for obtaining precise values [28]. Finally, the apathy that may be observed among the households involved in the study could affect the research results, as the individuals may provide incorrect information that could mislead the research team.

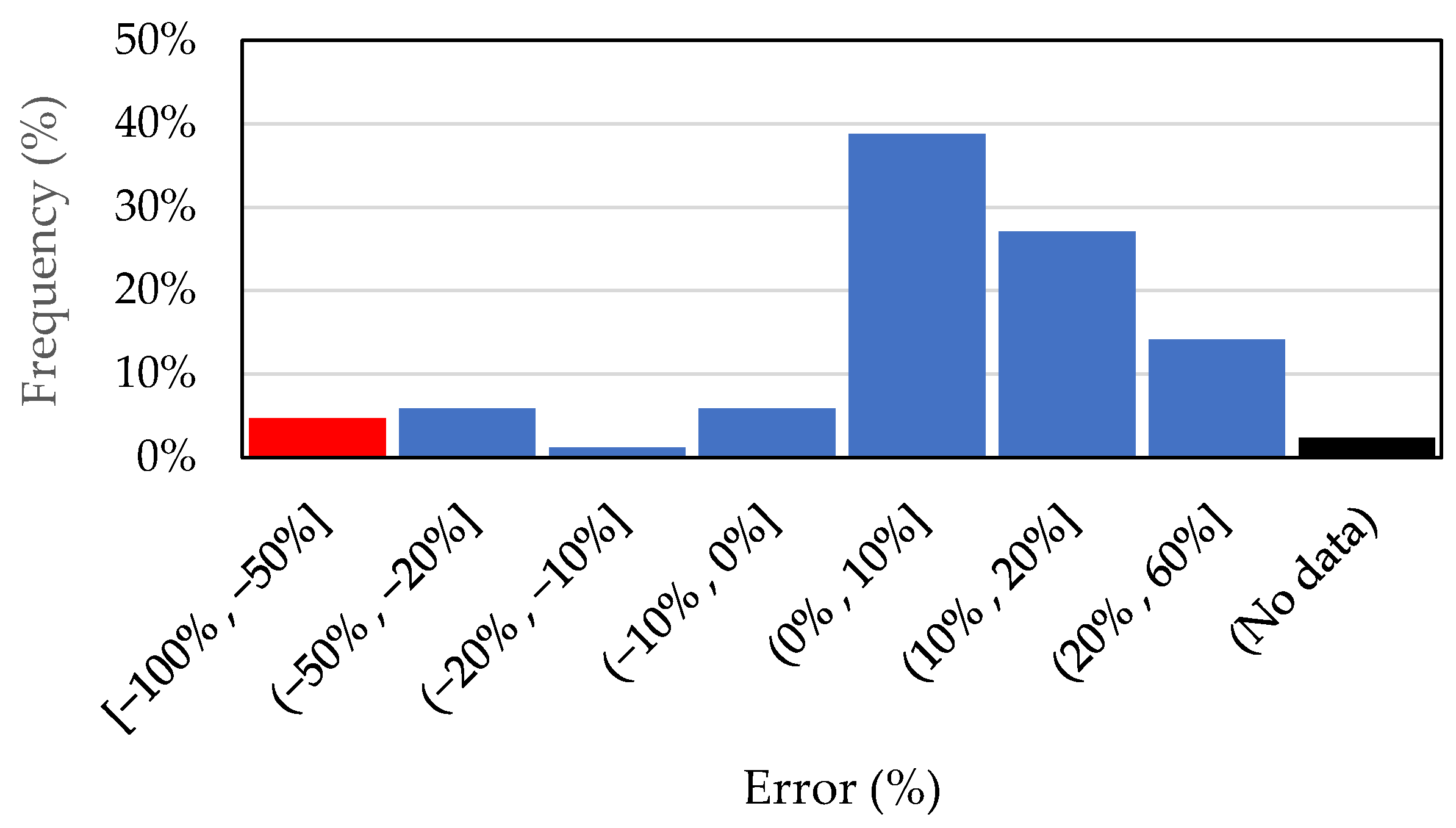
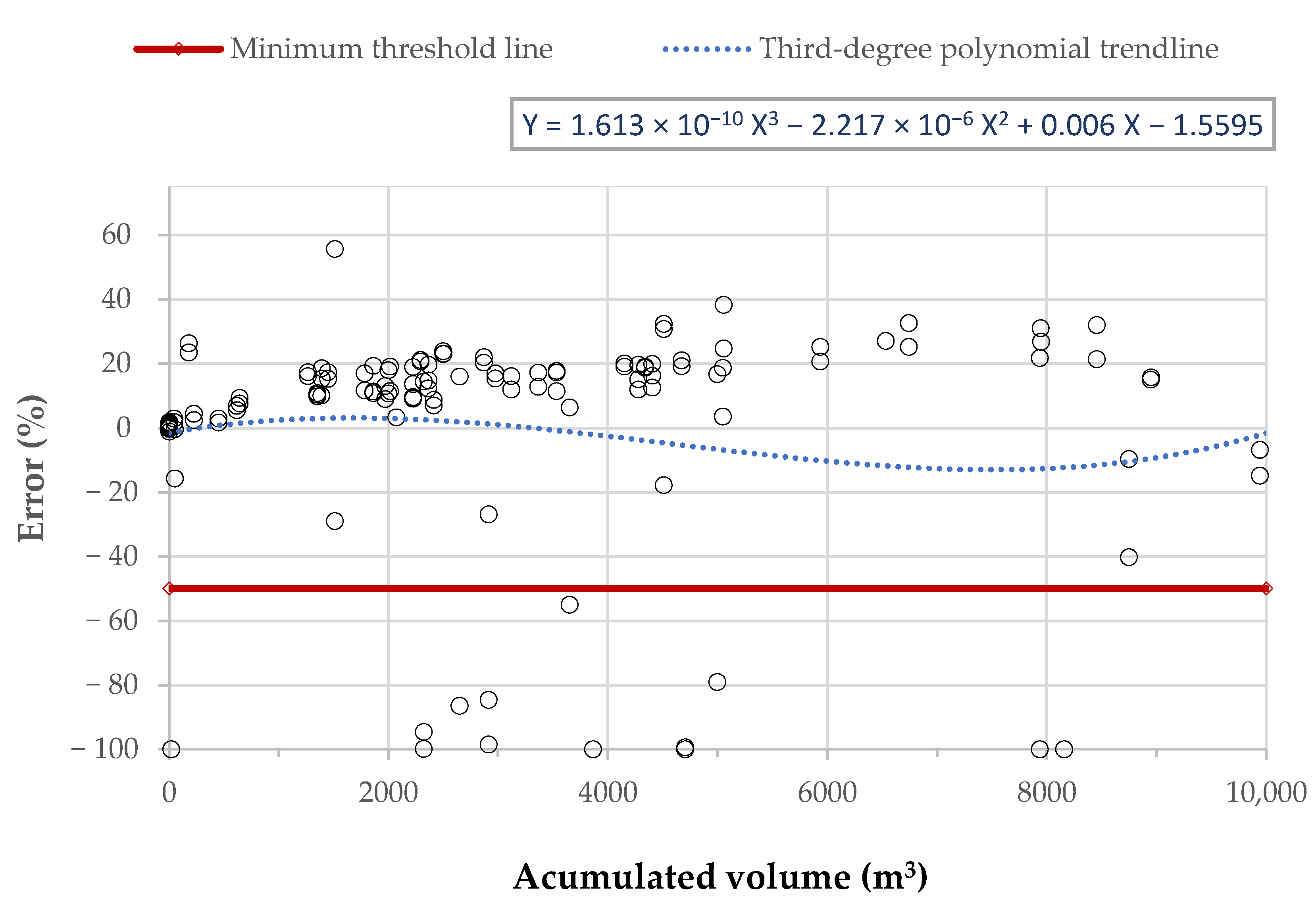
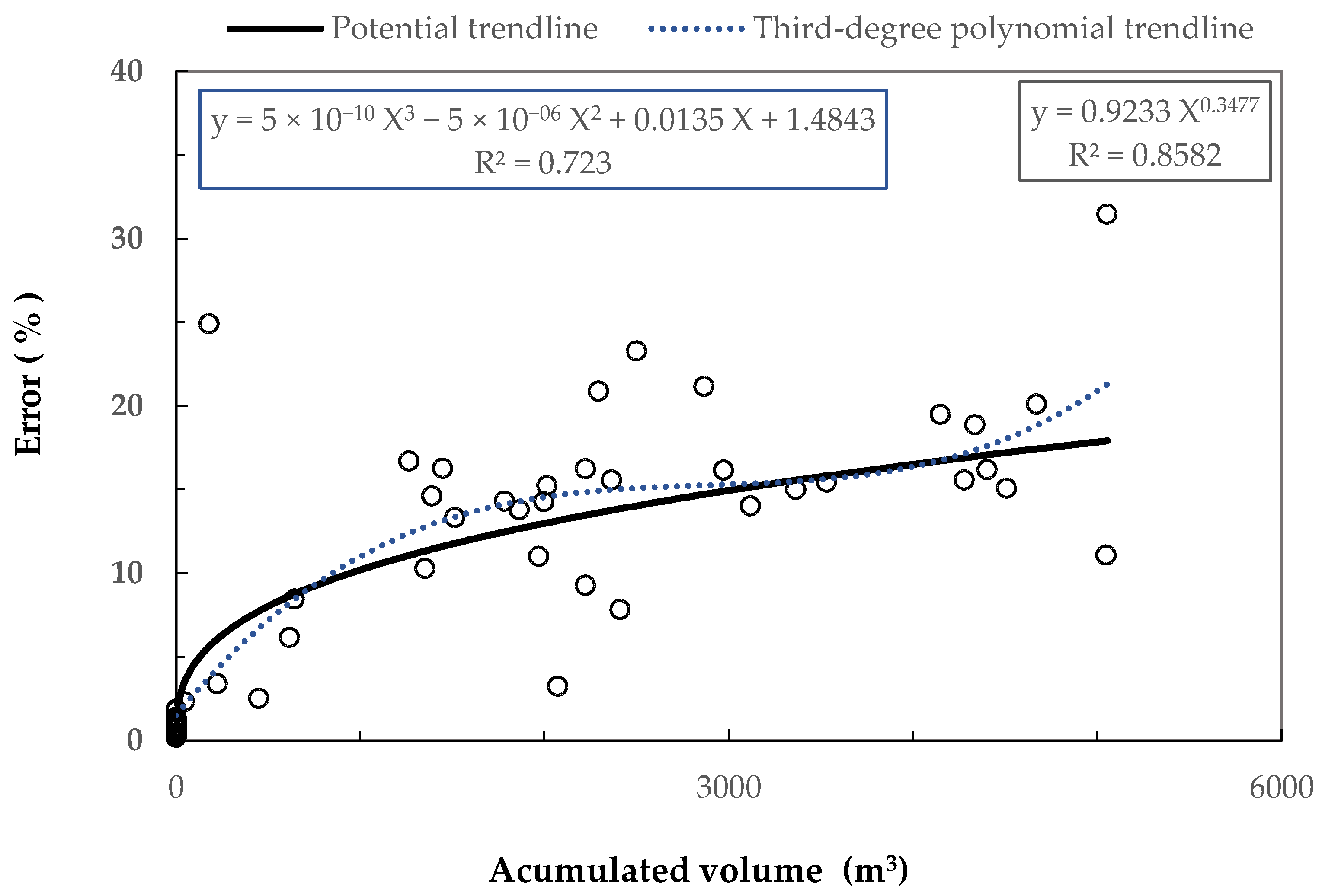
3. Results

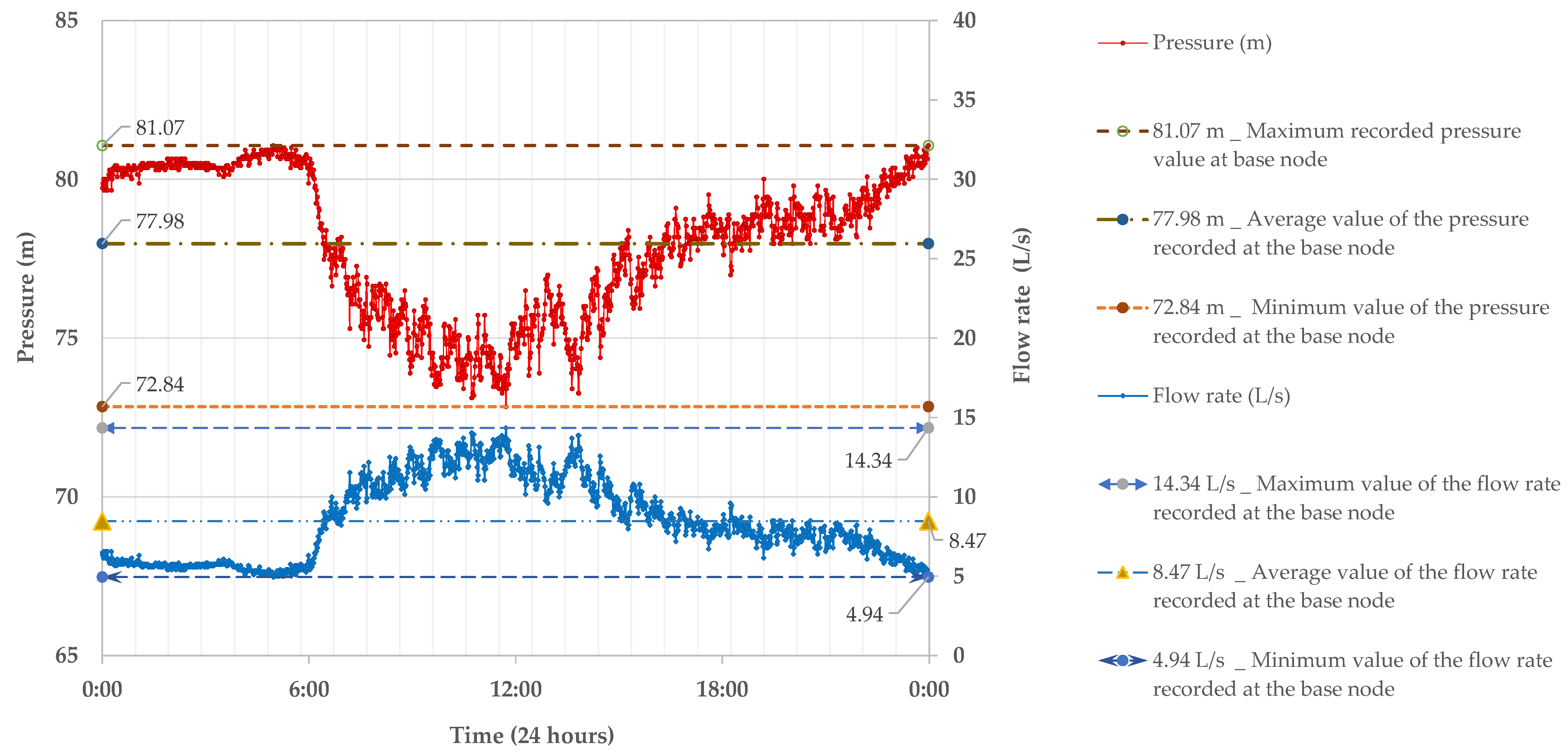
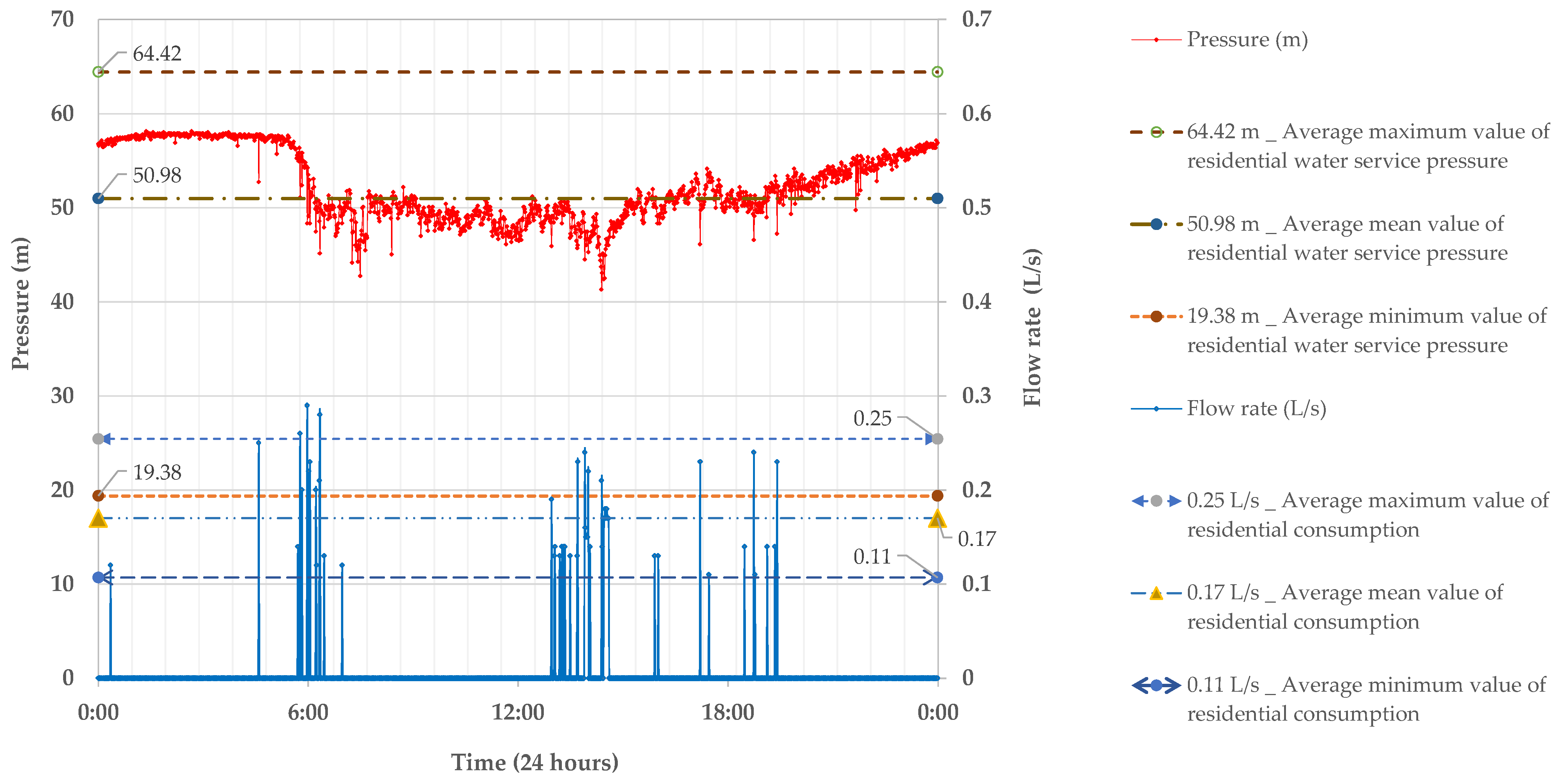
Expected and Obtained Data

The obtained data were analyzed, and sufficient information was gathered to construct a global error curve. However, it is important to note that not all values obtained can be plotted, as some of the water meters are in poor condition and tend to provide incorrect readings. These water meters can produce values that are too high or too low compared to the actual test values. Additionally, readings from water meters that are damaged or in poor condition and no longer provide accurate readings were also discarded [26]. To eliminate these values, a histogram was created to demonstrate the frequency of errors in the water meters.

As seen in Figure 6, in most cases the errors generated by the water meters are quite high at 0%. Following that, water meters with no data (2.4%) or with values with a big negative error were discarded due to the limited number of occurrences. The database obtained was sufficiently reliable to create an error curve [9]. After analyzing the results, ranges of error levels were established for the cumulative volumes in the water meters, resulting in the elimination of any erroneous information. The ranges are defined as 3 levels: the first for water meters with a cumulative volume of less than 1000 cubic meters, the second level between 1000 cubic meters and 5000 cumulative cubic meters, and the third for volumes greater than 5000 cubic meters. These are volumes accumulated from the installation of the residential flow meters and not only during the testing. A maximum and minimum error rate were defined for each of these ranges, with the first having an error rate of 0–8%, the second having an error rate of 8–25%, and the third having an error rate of 20–50% [29].

For better understanding, three graphs were created. The first graph contains all the data obtained from the tests, the second graph displays the data that were discarded due to malfunctions, and the third graph displays the global error curve after discarding the data outside of the defined ranges [30].

Figure 7 shows the errors generated by the tested meters. The visual representation confirms the values due to their wide spread, which tends towards negative values and represents a global error of undercounting. This is due to the high number of water meters that are corrupted [31]. To generate Figure 8 from the study’s data, flow meters exceeding 5375 cubic meters (the optimal criterion for replacement) [32] and those with negative measurement errors (below 0%) were excluded. Figure 8 illustrates the relationship between accumulated volume and meter error for meters with overcounting.

According to previous research, data falling outside of established ranges can indicate that the water meters are not functioning properly. Specifically, when data consistently show high values that extend towards sub-metering, it suggests that the meters are in a negatively damaged state [33]. This means that they are over-measuring and producing inaccurate readings, which can lead to overcharging of customers and higher revenue for the water supply company. Therefore, it is crucial to monitor and maintain the accuracy and reliability of water meters to ensure that they are functioning properly and providing accurate readings.

The final result is the curve generated from the accepted values for the study, as they provide an objective baseline for the analysis of errors in the cumulative volume readings [16]. This is illustrated in Figure 9.

The use of a statistical program allows for the determination of the trend in error points for each meter, which increases as the volume accumulates over time. The curve approach was found to be the best after comparing it to alternative models [34].

Table 1. Models of the trend of errors.

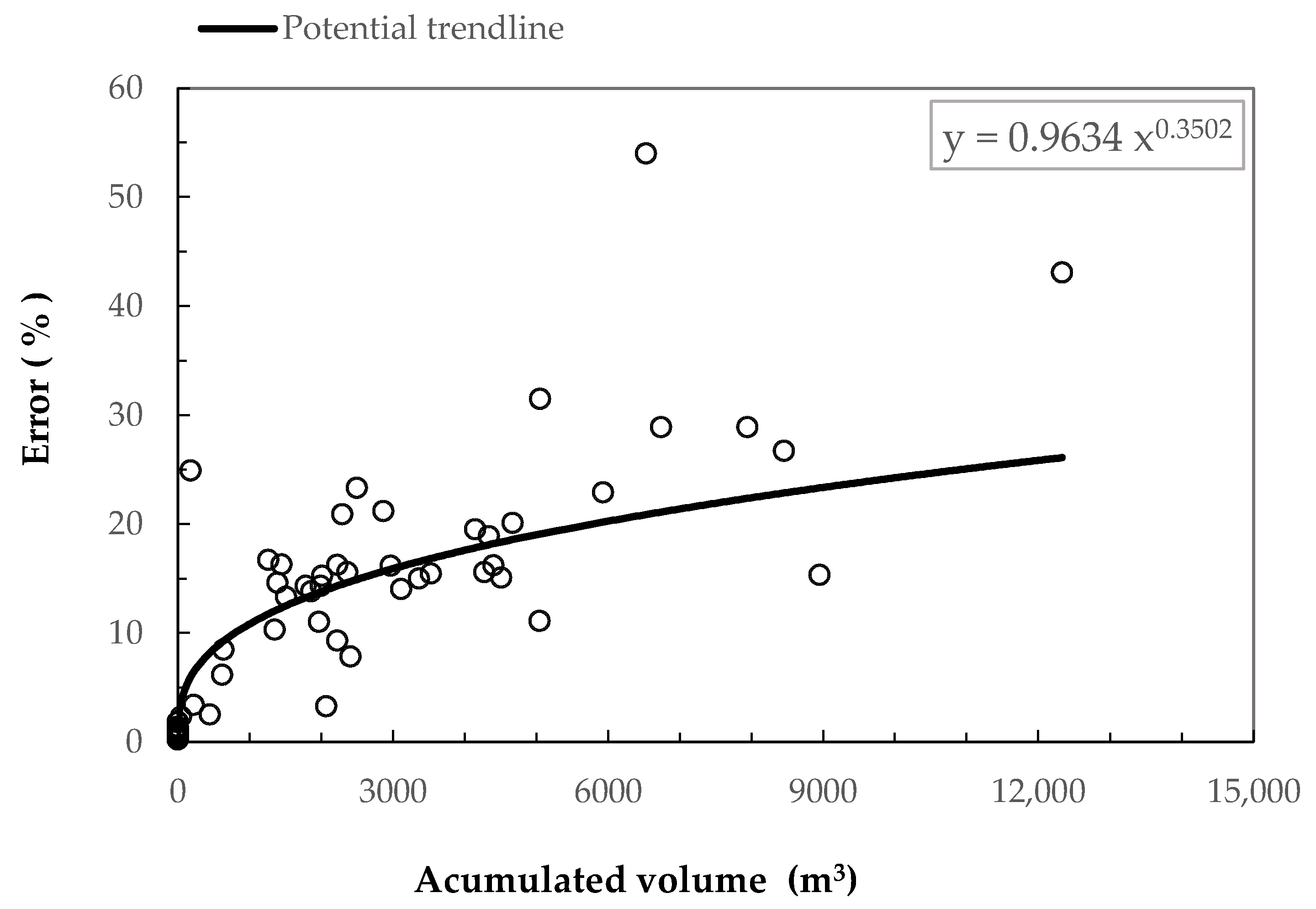
Comparison of Alternative Models
Model	Correlation	Square Root
Multiplicative	0.9418	88.70%
Double square root	0.9343	87.29%
Square root of X	0.9115	83.09%
Square root-Y Log-X	0.8958	80.25%
Logarithmic-Y square root-X	0.8876	78.79%

displays the alternative models that best fit, with the multiplicative model, also known as trend potential, as the most fitting.

The analysis of the data using the statistical program has resulted in a strong correlation between the variables, as indicated by the correlation coefficient of 0.94. The fitted model, represented by the R-square of 88.70%, provides insight into the over-metering trend from the first day of operation of the meter [35]. As the volume registered by the meter increases over its lifetime, so does the error percentage. This information can be used to calculate the error associated with any home meter simply by registering its volume using Equation (5):

$$E_{\%}=0.9634 V_f^{0.3502}$$

(5)

where Ε% is the percentage error of the counter and Vf is the accumulated volume of the meter.

By using this formula, it is possible to approximate the actual value that each water meter should be registering. As an illustration,

Table 2. Percentage of error according to the volume recorded during operation.

Volume (m3)	Error (%)
100	4.82
500	8.48
1000	10.81
3000	15.88
5000	18.99
8000	22.38
10,000	24.20

shows the errors generated by water meters based on their recorded volumes.

An illustration of the overcharging scenario is as follows: If a water meter has recorded a volume of 500 m³, its error is 8.3%. This means that for every 1000 L consumed in this household, the bill includes 80.3 L that is being paid for in excess. On the other hand, households with a meter reading of 5000 m³ per 1000 L of consumption would be overcharged by 185 L.

4. Discussion of Results

After conducting the two phases of the study, the results have provided motivation for continued work towards improving process designs and better management of distribution networks [21]. Based on the research findings, it can be concluded that current design simulations are run using point-of-use constants that are not entirely accurate, as shown in Figure 2 and Figure 3. Consequently, domestic consumption patterns are sporadic and not constant [20]. The traditional demand curve is still deemed appropriate for all network designs, but a more accurate model that provides a demand curve for each household could be developed using hydraulic simulation programs such as a version of EPANET, which is available for free.

It is important to note that the study’s findings are limited to the analysis of the generated curves from distribution networks [1] and do not apply to areas where water supply is not continuous. In addition, the results indicate a tendency for water meters in the study environment to over-measure, which has a direct impact on consumers who are paying for water they do not actually consume [33]. As shown in Figure 6, positive errors meaning over-measurement represent 80% of the water meters analyzed.

This leads to higher revenue for the water supply company for services that were never provided and a water balance issue within the network. Unclaimed funds from over-billed consumption may be redirected to other sectors, such as through leaks or illegal connections, resulting in inefficiencies in the distribution system. The goal of this research is to provide guidelines for future interventions and to improve the quality of life and service for the community [11].

5. Conclusions

In conclusion, the accuracy and reliability of household water meters are crucial factors in understanding the behavior of distribution networks and optimizing drinking water networks. The proposed mathematical model, which integrates the tank continuity equation and the emitter law of the float valve based on Torricelli’s principle, provides a deeper understanding of the accuracy and reliability of flow meters. The results of the study indicate a tendency to overcount due to over-measuring. This happens in the 80% of the water meters. This fact not only affects consumers but also results in higher revenue for water supply companies. Incorporating household-specific demand curves can lead to a more accurate representation of water usage. To ensure sufficient and effective capacity to provide appropriate services for community development, it is important to consider both main pipes and secondary pipes in water quality modeling.

Based on the results of this study, the main question in the introduction regarding whether household water meters have flow errors can be answered. It was found that the overall error tends toward overcounting due to over-measuring.

An important relationship between the age of a water meter and the magnitude of meter errors was uncovered in this study. Specifically, the findings indicate that older meters tend to exhibit higher levels of overcounting, resulting in significant inaccurate billing. This trend can be attributed to the degradation of mechanical components over time, which can cause decreased meter accuracy. Figure 9 shows a strong dependency of error on the accumulated volume, that is, on the age of the water meter. The average error in water meters with 0 m³ to 1000 m³ of accumulated volume is 2.35%. This value increases up to 15.12% for water meters with accumulated volumes between 1000 m³ and 5000 m³ and 29.15% for water meter with more than 5000 m³ of accumulated volume.

Therefore, ensuring the accuracy and reliability of flow meters is crucial for an accurate reflection of consumption and billing processes. Moreover, incorporating household-specific demand curves can lead to a more precise representation of water usage, optimizing drinking water networks.

Based on these results, it is recommended that water supply companies evaluate their current meter replacement regulations. The systematic replacement of older meters with newer models can significantly improve the overall accuracy and reliability of the metering system, resulting in more equitable billing practices and greater efficiency in water distribution networks.

On the other hand, it was noted that the study has limitations such as poor maintenance of pipes leading to water leaks, lack of modern measuring devices, and the possibility of incorrect information provided by households. Despite these limitations, the study provides valuable insights into the water distribution system and highlights the need for improved water management practices.

To sum up, this research provides guidelines for future interventions in water distribution systems, with the goal of improving the quality of life and service for communities. It highlights the importance of ensuring accurate water meter readings to ensure fair and efficient billing practices.