Numerical Modelling on Physical Model of Ringlet Reservoir, Cameron Highland, Malaysia: How Flow Conditions Affect the Hydrodynamics
Abstract
1. Introduction
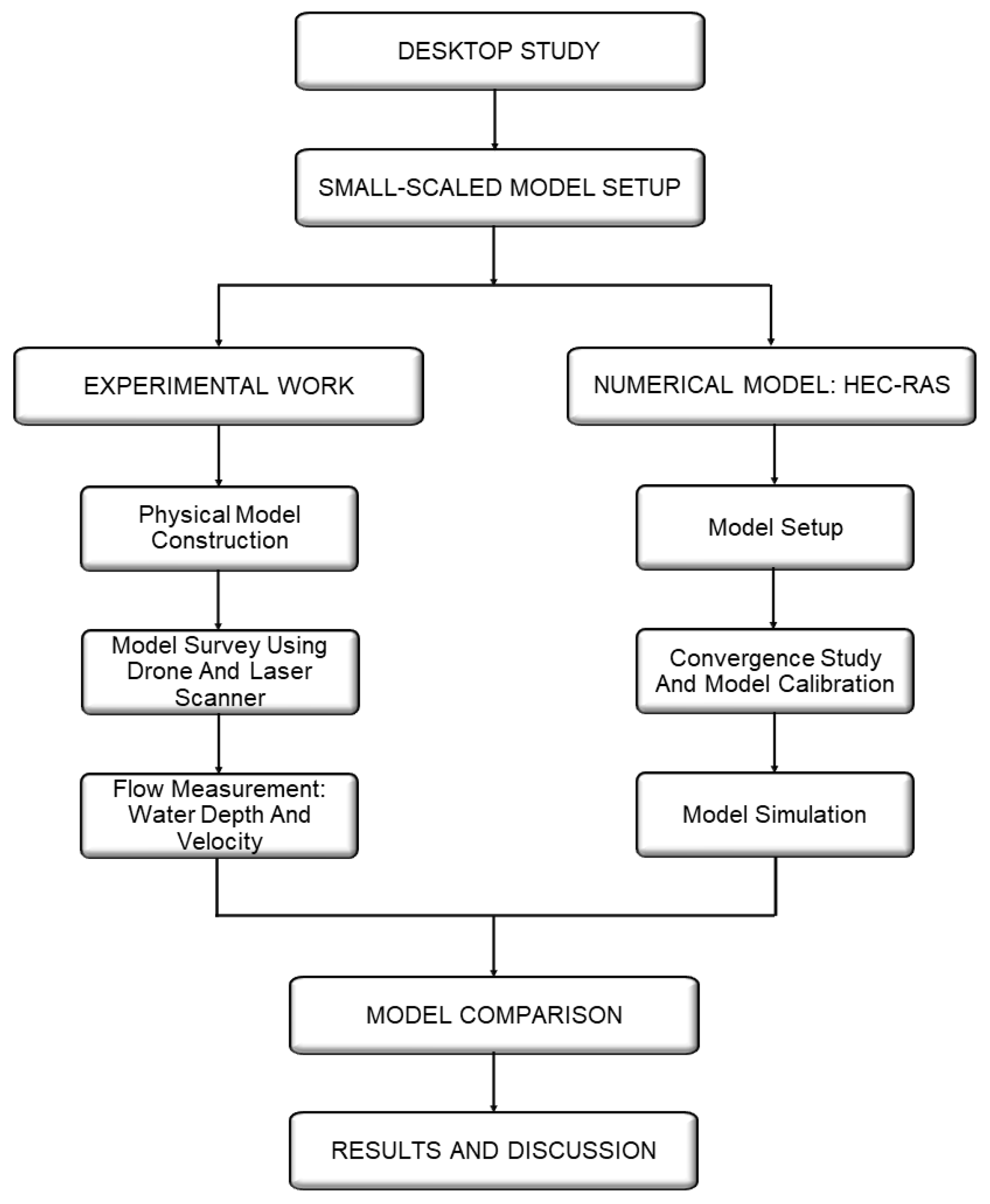
2. Methodology
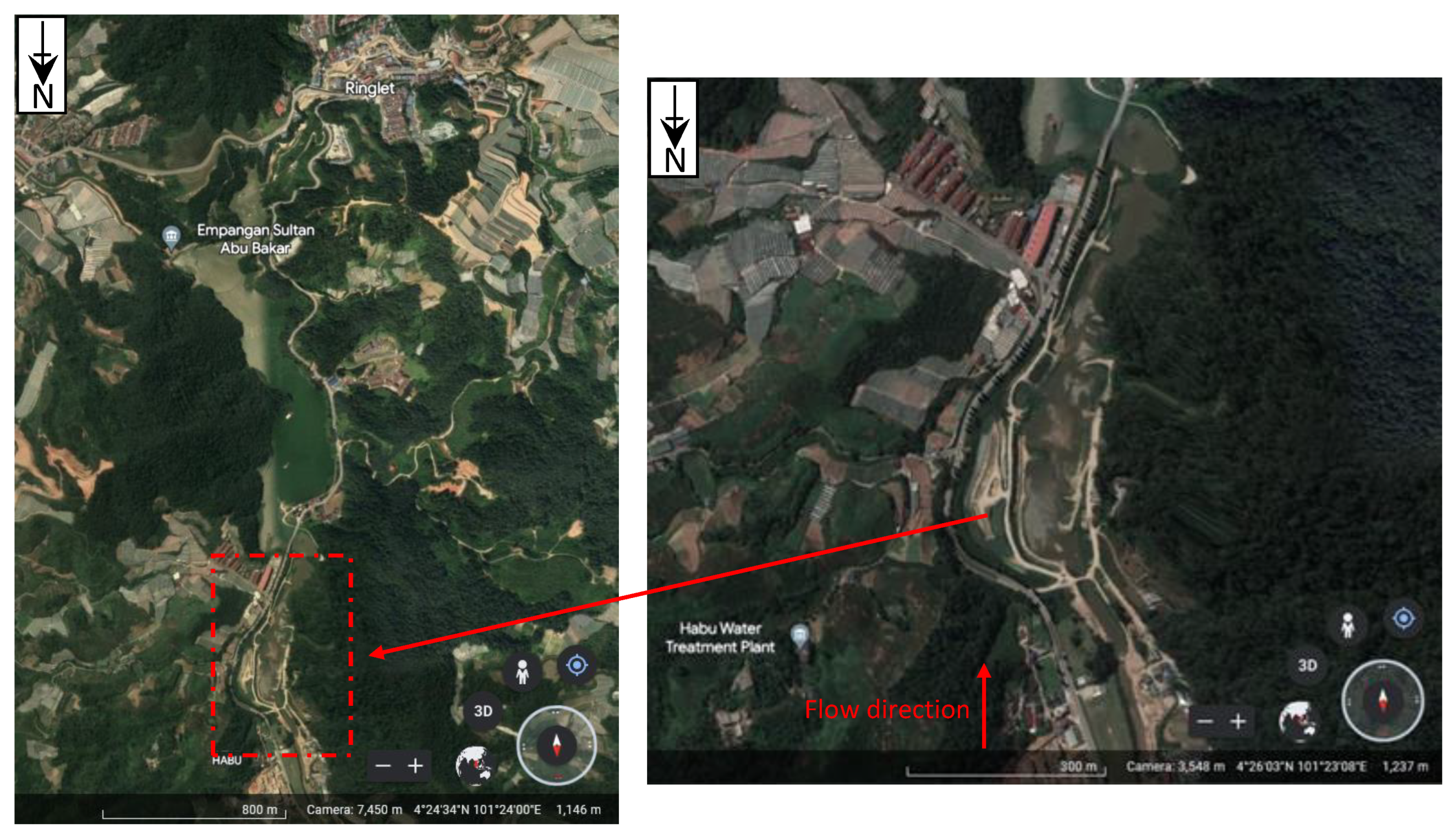
2.1. Study Area
2.2. Experimental Works
2.2.1. Physical Model Construction
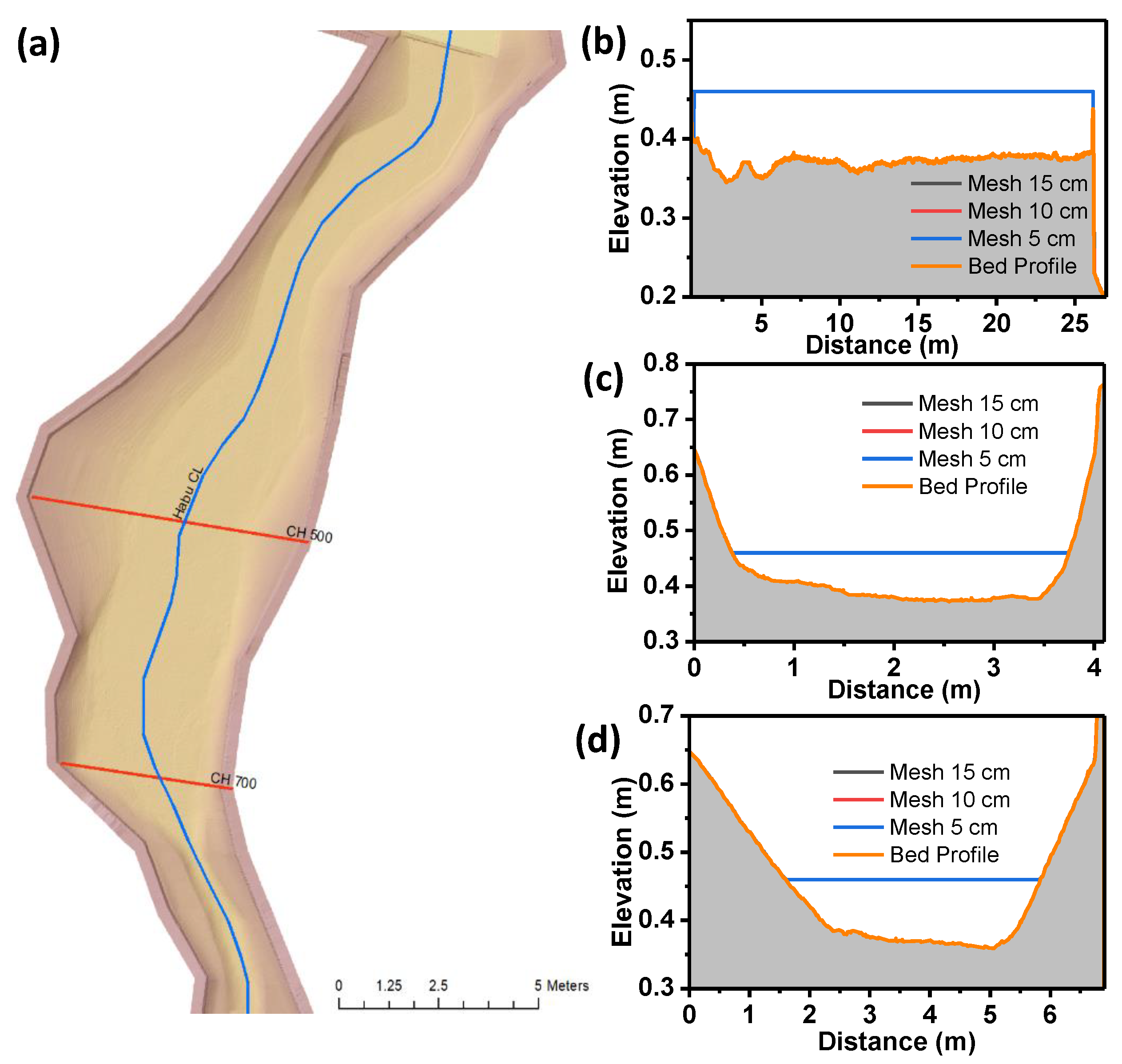
2.2.2. Model Surveying
2.2.3. Flow Measurements
2.3. Numerical Model (HEC-RAS)
2.3.1. Model Setup
2.3.2. Convergence Study and Model Calibration
2.3.3. Model Simulation
3. Results and Discussions
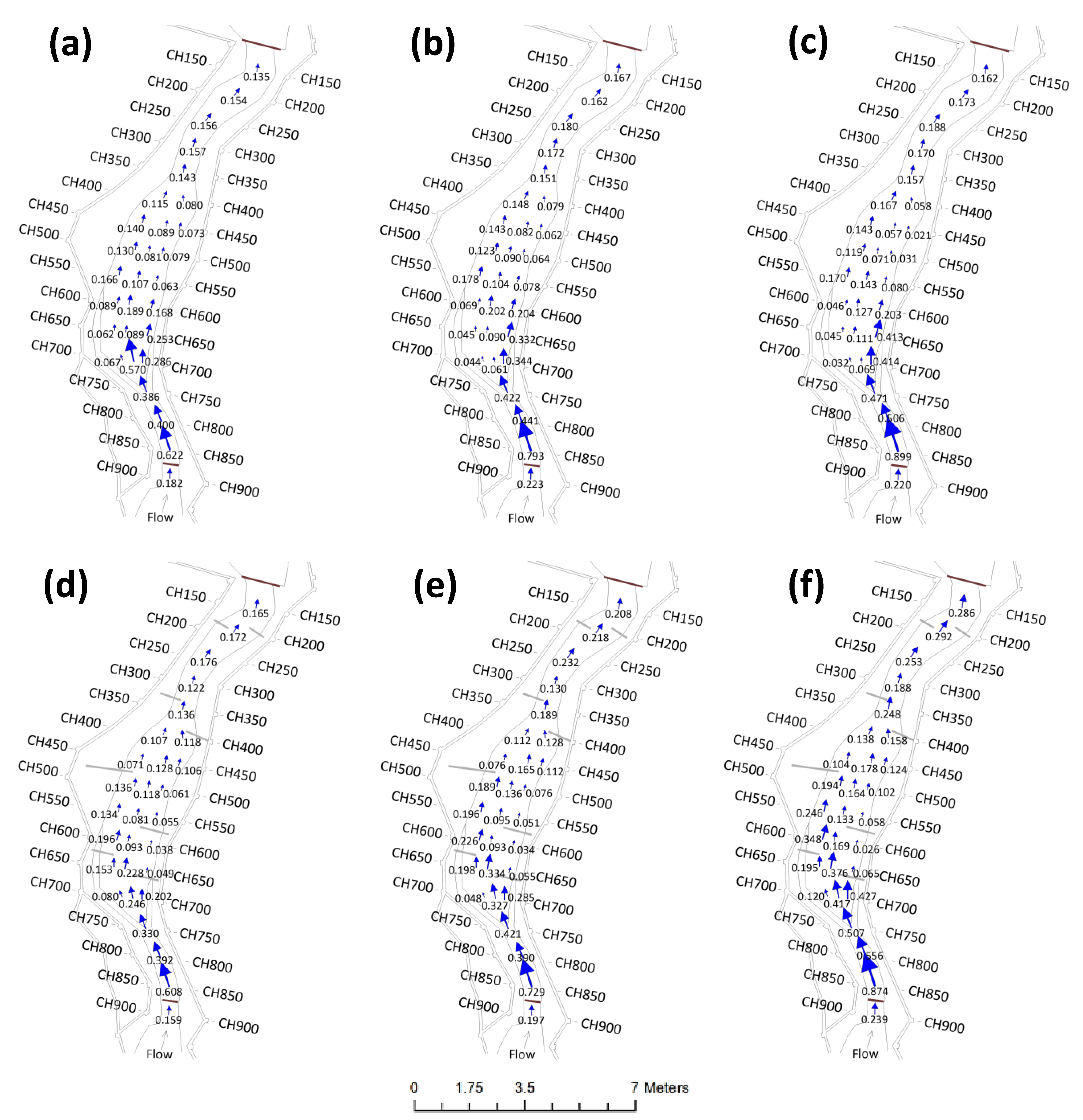
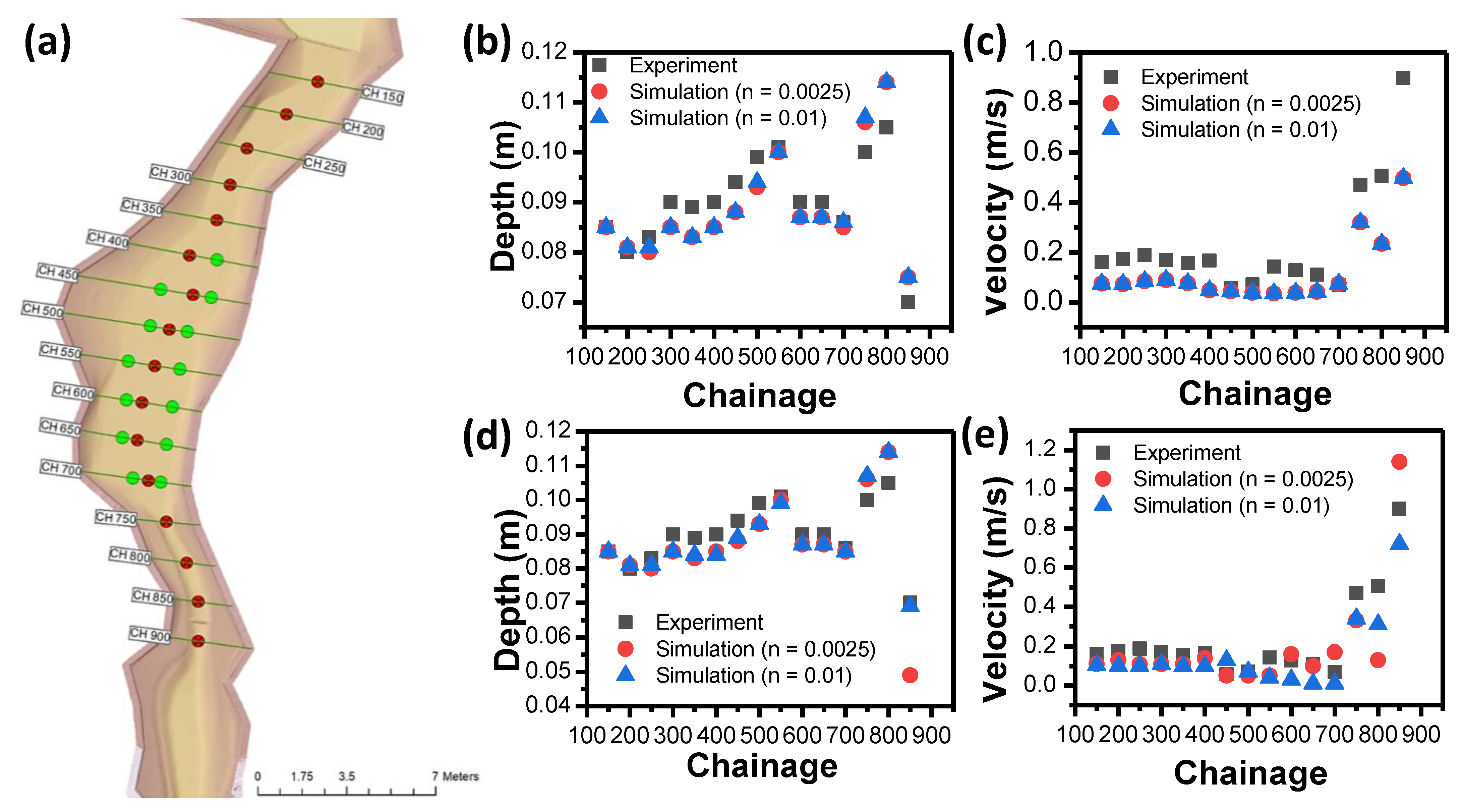
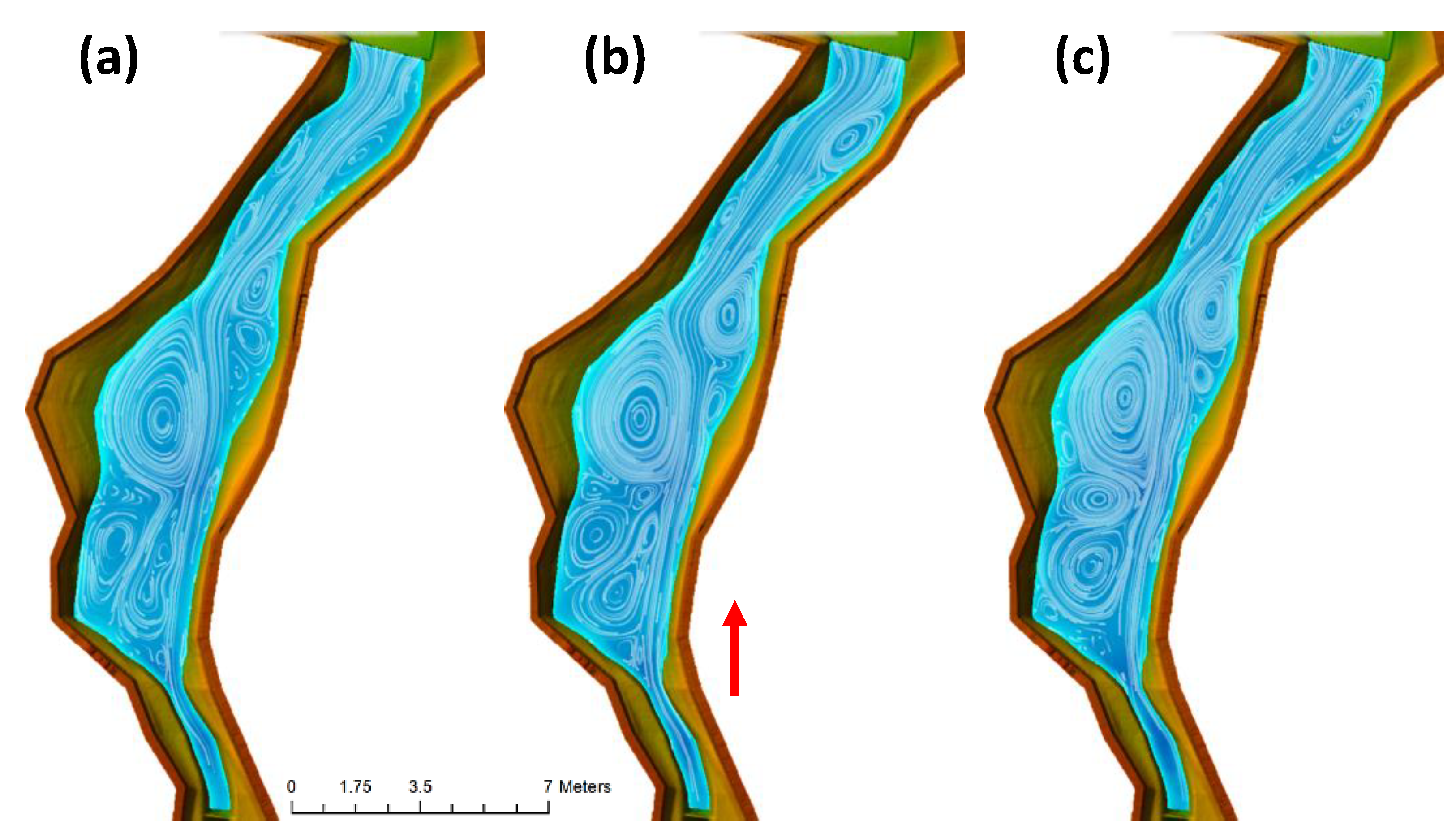
3.1. Physical Model
3.2. HEC-RAS
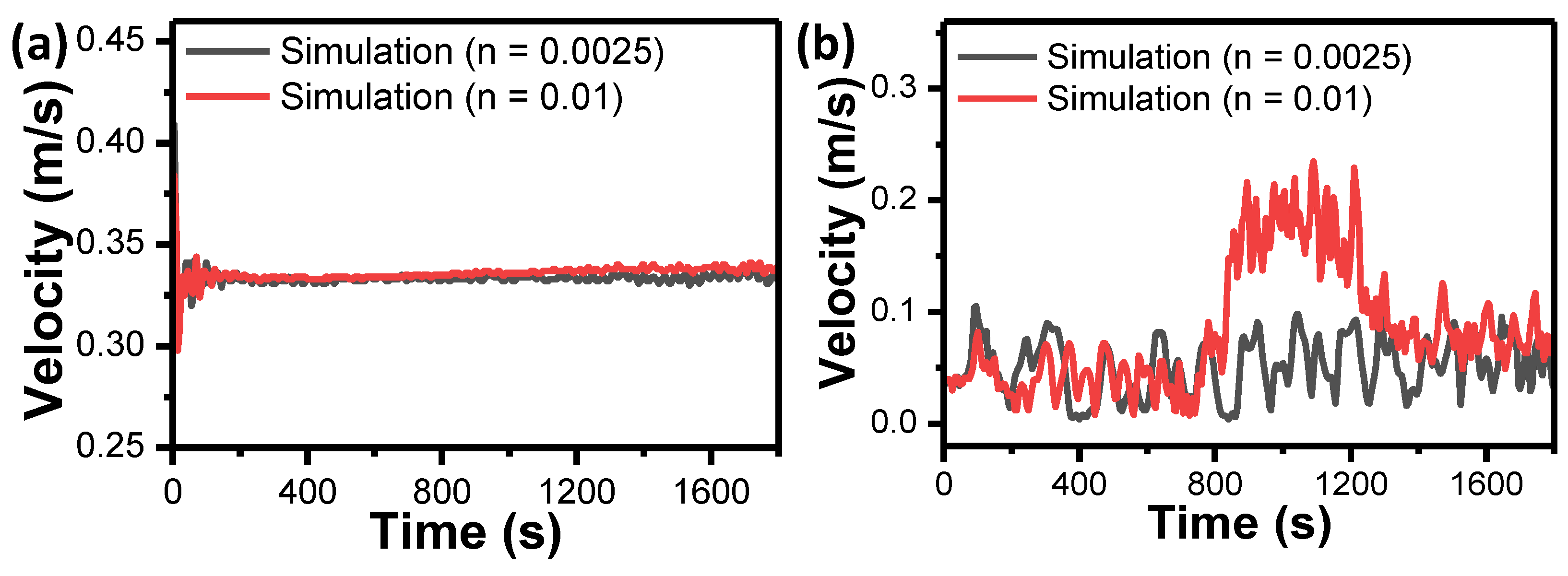
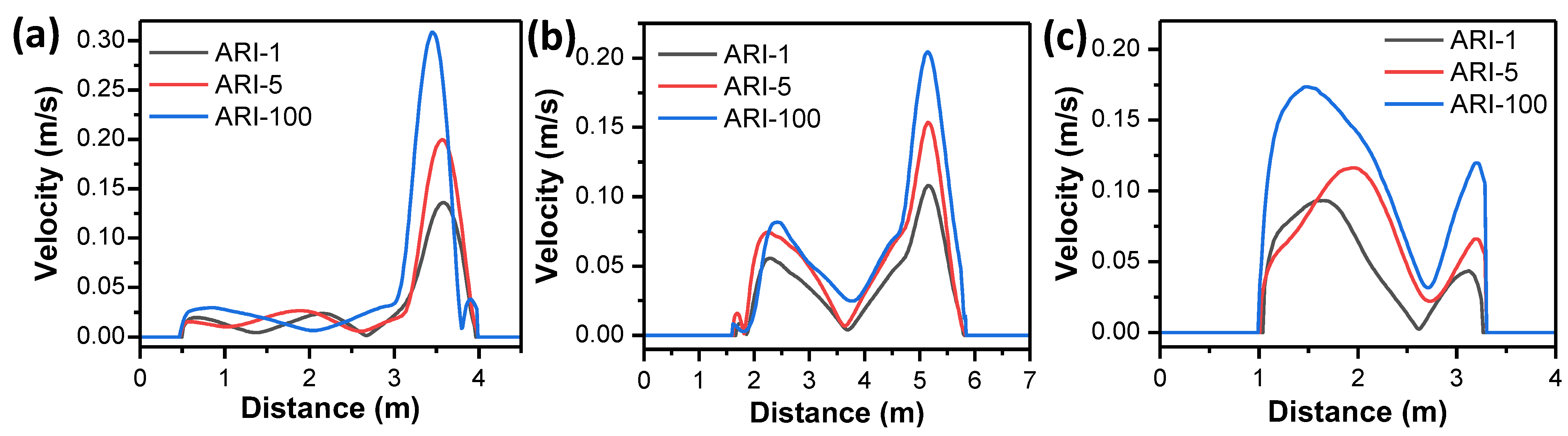
3.2.1. Convergence Study
3.2.2. Model Calibration
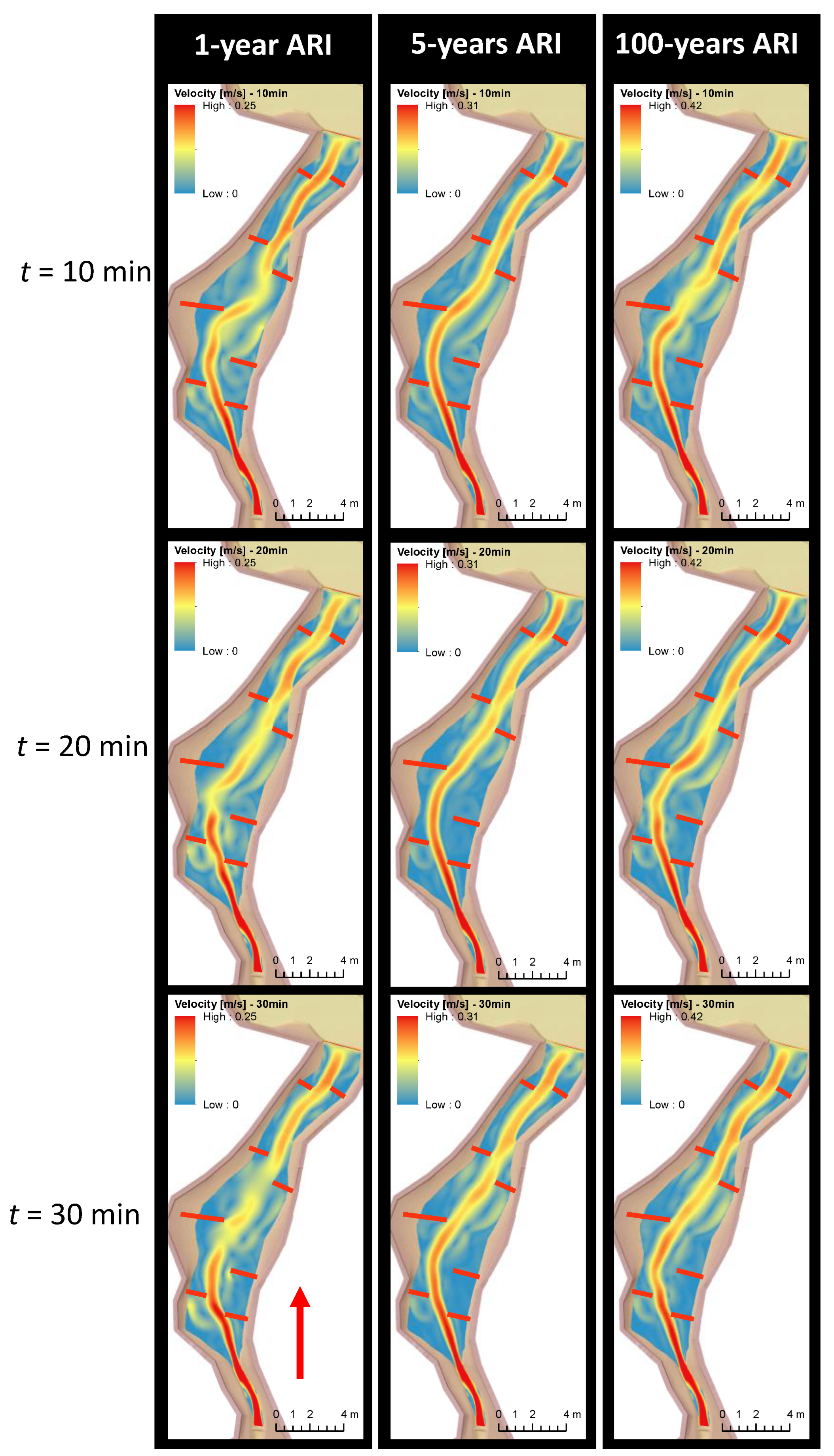
3.3. Simulation
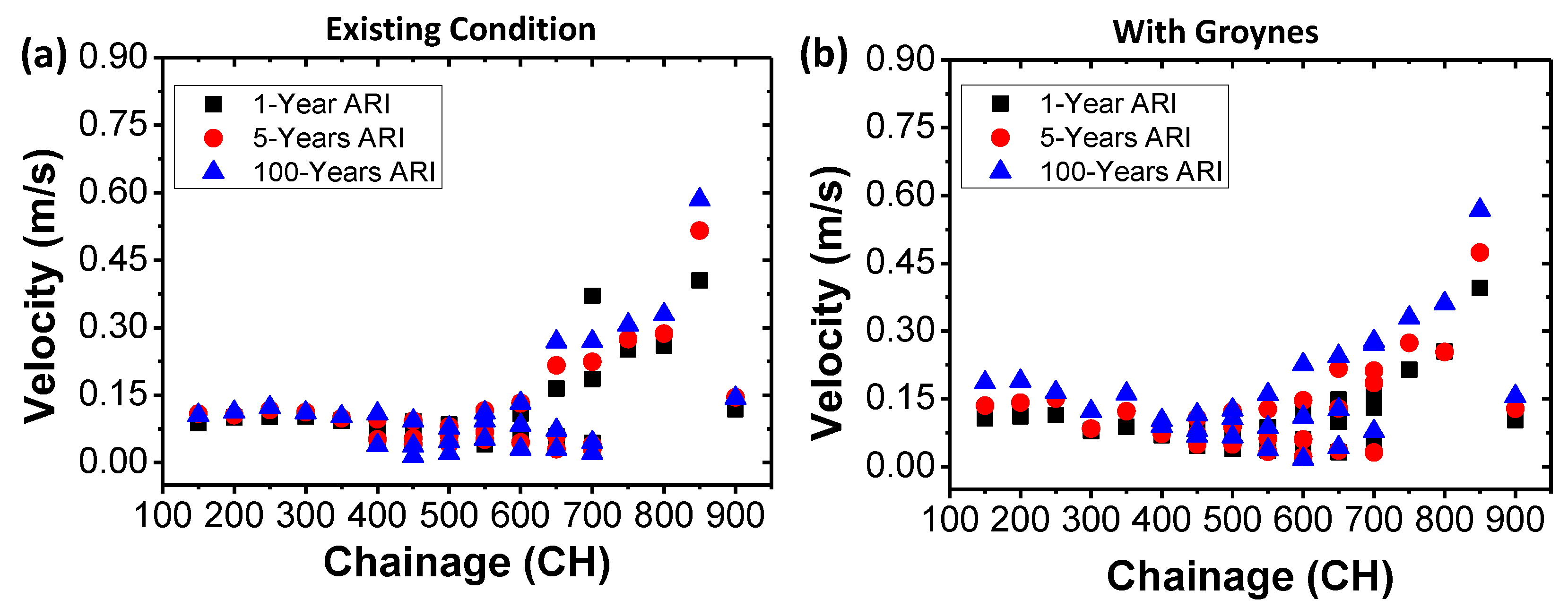
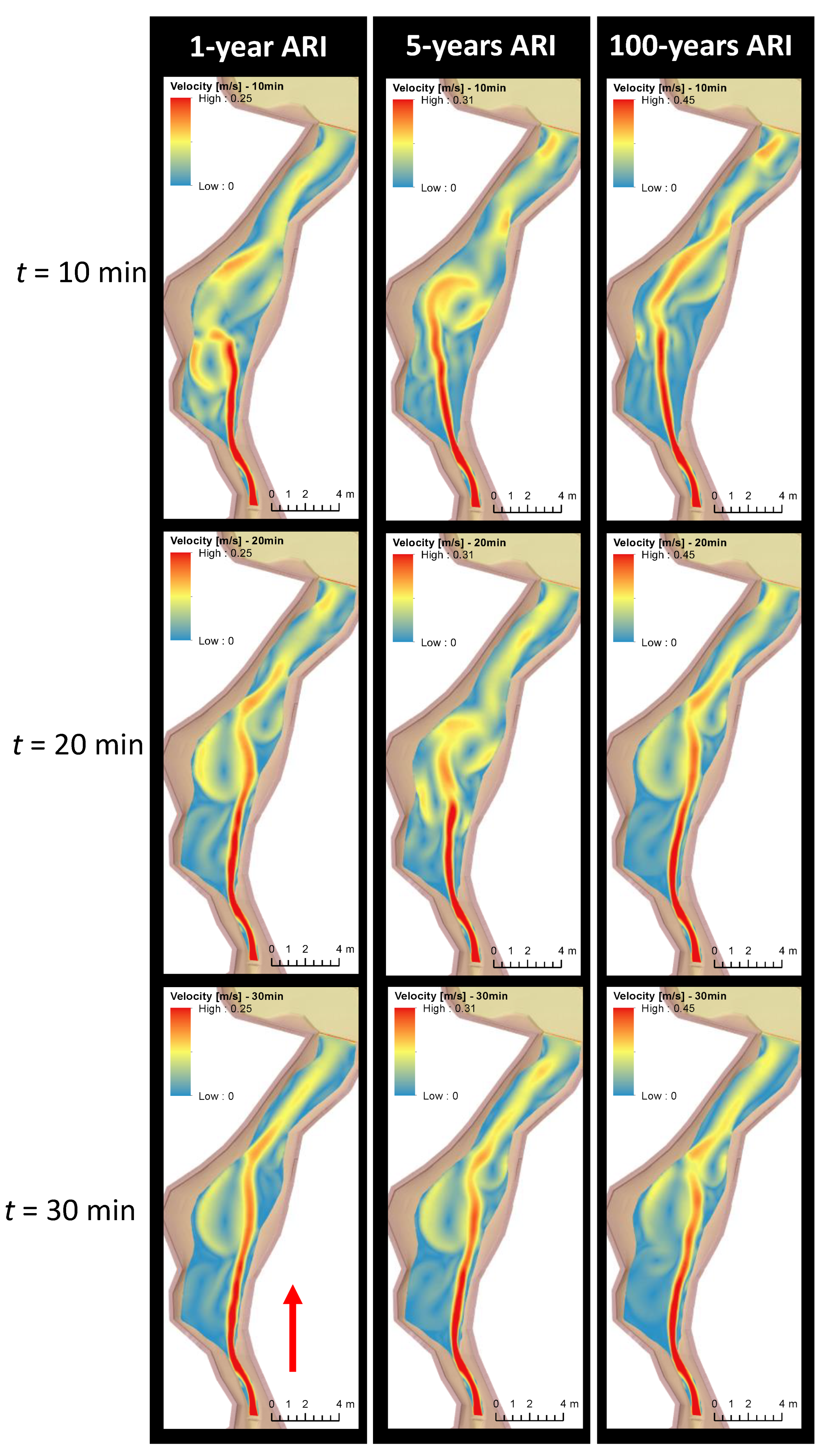
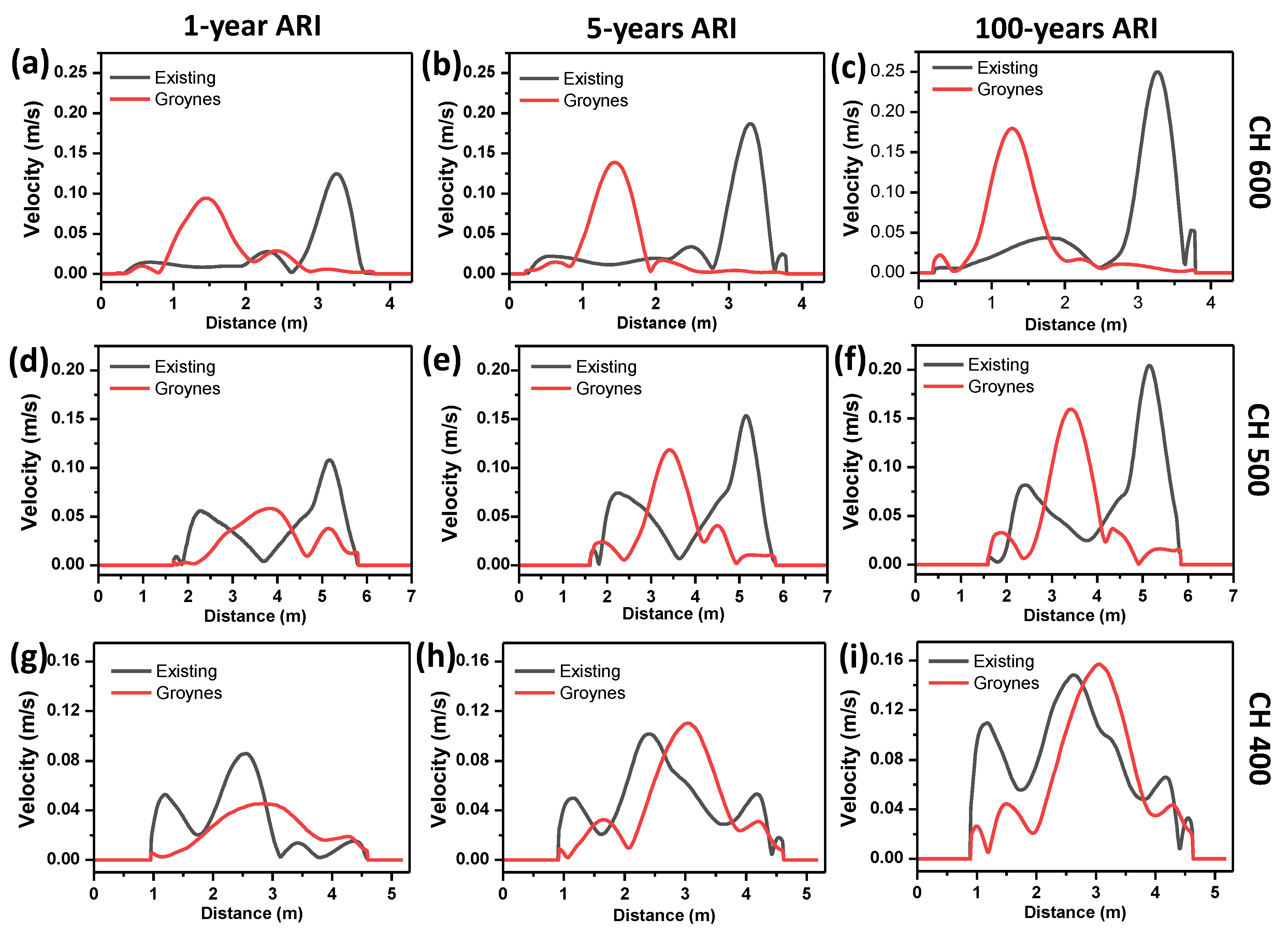
3.3.1. Habu Existing Conditions
3.3.2. Habu with Groynes Installed
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maass, A.; Hufschmidt, M.M.; Dorfman, R.; Thomas, J.H.A.; Marglin, S.A.; Fair, G.M. Design of Water-Resource Systems; Harvard University Press: Cambridge, MA, USA, 1962. [Google Scholar]
- Annandale, G.W.; Morris, G.L.; Karki, P. Extending the Life of Reservoirs: Sustainable Sediment Management for Dams and Run-of-River Hydropower; The World Bank: Washington, DC, USA, 2016; p. 188. [Google Scholar]
- Branche, E. The multipurpose water uses of hydropower reservoir: The SHARE concept. Comptes Rendus Phys. 2017, 18, 469–478. [Google Scholar] [CrossRef]
- IEA. Hydroelectricity. 2022. Available online: https://www.iea.org/reports/hydroelectricity (accessed on 13 March 2023).
- Huang, C.-C.; Lai, J.-S.; Lee, F.-Z.; Tan, Y.-C. Physical Model-Based Investigation of Reservoir Sedimentation Processes. Water 2018, 10, 352. [Google Scholar] [CrossRef]
- Basson, G. Reservoir sedimentation—An overview of global sedimentation rates and predicted sediment deposition. In Proceedings of the Oral Contribution to the International CHR Workshop-Expert Consultation: Erosion, Transport and Deposition of Sediments, Bern, Switzerland, 28–30 April 2008; pp. 74–79. [Google Scholar]
- Garcia, M. Sedimentation Engineering: Processes, Measurements, Modeling, and Practice; ASCE: Reston, VA, USA, 2008; pp. 2–12. [Google Scholar]
- Padhy, M.K.; Saini, R.P. A review on silt erosion in hydro turbines. Renew. Sustain. Energy Rev. 2008, 12, 1974–1987. [Google Scholar] [CrossRef]
- Sidek, L.M.; Luis, I.J. Sustainability of Hydropower Reservoir as Flood Mitigation Control: Lesson Learned from Ringlet Reservoir, Cameron Highlands, Malaysia. 2014. In Proceedings of the 2nd International Conference on Water Resources (ICWR2012), Langkawi, Malaysia, 5–7 November 2012. [Google Scholar]
- Sidek, L.M.; Luis, I.J.; Desa, M.N.M.; Julien, P.Y. Challenge In Running Hydropower As Source Of Clean Energy: Ringlet Reservoir, Cameron Highlands Case Study. In Proceedings of the National Graduate Conference 2012 (NatGrad2012), Kajang, Malaysia, 8–10 November 2012. [Google Scholar]
- Kositgittiwong, D.; Chinnarasri, C.; Julien, P. Numerical simulation of flow velocity profiles along a stepped spillway. Proc. Inst. Mech. Eng. E J. Process Mech. Eng. 2013, 227, 327–335. [Google Scholar] [CrossRef]
- Zhang, Y.; Han, L.; Chen, L.; Wang, C.; Chen, B.; Jiang, A. Study on the 3D Hydrodynamic Characteristics and Velocity Uniformity of a Gravity Flow Circular Flume. Water 2021, 13, 927. [Google Scholar] [CrossRef]
- McCoy, A.; Constantinescu, G.; Weber Larry, J. Numerical Investigation of Flow Hydrodynamics in a Channel with a Series of Groynes. J. Hydraul. Eng. 2008, 134, 157–172. [Google Scholar] [CrossRef]
- Choufu, L.; Abbasi, S.; Pourshahbaz, H.; Taghvaei, P.; Tfwala, S. Investigation of Flow, Erosion, and Sedimentation Pattern around Varied Groynes under Different Hydraulic and Geometric Conditions: A Numerical Study. Water 2019, 11, 235. [Google Scholar] [CrossRef]
- Desa, S.M.; Samion, M.K.H.; Hamzah, A.F.; Manan, E.A.; Noh, M.N.M. Physical Modelling Study on Sediment Removal of Sungai Habu and Sungai Ringlet, Cameron Highlands. In ICDSME 2019—Water Resources Development and Management; Springer: Singapore, 2020; pp. 184–196. [Google Scholar]
- Al-Qaisi, D.A.; Alqaisi, M.; Abdulridha, R. Analysis of the hydraulic characteristics of al mahawil stream using hecras: A field study. Pollut. Res. 2020, 39, 856–863. [Google Scholar]
- Mojtahedi, A.; Basmenji, A.B. Numerical and Field Investigation of the Impacts of the Bank Protection Projects on the Fluvial Hydrodynamics (Case Study: Ghezel Ozan River). Int. J. Eng. Technol. 2017, 9, 492–497. [Google Scholar] [CrossRef]
- Walker, D.J.; Dong, P.; Anastasiou, K. Sediment Transport near Groynes in the Nearshore Zone. J. Coast. Res. 1991, 7, 1003–1011. [Google Scholar]
- Luis, J.; Sidek, L.M.; Desa, M.N.M.; Julien, P.Y. Hydropower Reservoir for Flood Control: A Case Study on Ringlet Reservoir, Cameron Highlands, Malaysia. J. Flood Eng. 2013, 4, 87–102. [Google Scholar]
- Berhad, T.N. TNB’s Nenggiri Dam to Play Multi-Fold Role. 2021. Available online: https://www.thesundaily.my/local/tnb-s-nenggiri-dam-to-have-multifold-roles-YG7811573 (accessed on 23 March 2023).
- Teh, S.H. Soil Erosion Modeling Using RUSLE and GIS on Cameron Highlands, Malaysia for Hydropower Development. Master’s Thesis, The School for Renewable Energy Science, Akureyri, Iceland, 2011. [Google Scholar]
- Luis, J.; Sidek, L.M.; Desa, M.N.M.; Julien, P.Y. Sustainability of hydropower as source of renewable and clean energy. IOP Conf. Ser. Earth Environ. Sci. 2013, 16, 012050. [Google Scholar] [CrossRef]
- Raj, J.K. Land use changes, soil erosion and decreased base flow of rivers at Cameron Highlands, Peninsular Malaysia. Bull. Geol. Soc. Malays. 2002, 45, 3–10. [Google Scholar] [CrossRef]
- Razad, A.Z.A.; Abbas, N.A.; Sidek, L.M.; Alexander, J.L.; Jung, K. Sediment management strategies for hydropower reservoirs in active agricultural area. Int. J. Eng. Technol. 2018, 7, 228–233. [Google Scholar]
- Vangelis, H.; Zotou, I.; Kourtis, I.M.; Bellos, V.; Tsihrintzis, V.A. Relationship of Rainfall and Flood Return Periods through Hydrologic and Hydraulic Modeling. Water 2022, 14, 3618. [Google Scholar] [CrossRef]
- Morales-Marin, L.A.; French, J.R.; Burningham, H.; Battarbee, R.W. Three-dimensional hydrodynamic and sediment transport modeling to test the sediment focusing hypothesis in upland lakes. Limnol. Oceanogr. 2018, 63, S156–S176. [Google Scholar] [CrossRef]
- Kang, T.; Jang, C.-L.; Kimura, I.; Lee, N. Numerical Simulation of Debris Flow and Driftwood with Entrainment of Sediment. Water 2022, 14, 3673. [Google Scholar] [CrossRef]
- Ma, C.; Xu, X.; Yang, J.; Cheng, L. Safety Monitoring and Management of Reservoir and Dams. Water 2023, 15, 1078. [Google Scholar] [CrossRef]
- El Kadi Abderrezzak, K.; Die Moran, A.; Mosselman, E.; Bouchard, J.-P.; Habersack, H.; Aelbrecht, D. A physical, movable-bed model for non-uniform sediment transport, fluvial erosion and bank failure in rivers. J. Hydro-Environ. Res. 2014, 8, 95–114. [Google Scholar] [CrossRef]
- Isaac, N.; Eldho, T.I.; Gupta, I.D. Numerical and physical model studies for hydraulic flushing of sediment from Chamera-II reservoir, Himachal Pradesh, India. ISH J. Hydraul. Eng. 2014, 20, 14–23. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, L.; Liu, J.; Lin, J.; Cui, Q. A Data Assimilation Approach to the Modeling of 3D Hydrodynamic Flow Velocity in River Reaches. Water 2022, 14, 3598. [Google Scholar] [CrossRef]
- Yossef, M. The Effect of Groynes on Rivers: Literature Review; Cluster Publicatienummer 03.03.04; Delft University of Technology: Delft, The Netherlands, 2002. [Google Scholar]
- Michioku, K.; Osawa, Y.; Kanda, K. Performance of a groyne in controlling flow, sediment and morphology around a tributary confluence. E3S Web Conf. 2018, 40, 04006. [Google Scholar] [CrossRef]
- Farzad Mohammadi, N.M. Technical Evaluation of the Performance of River Groynes Installed in Sezar and Kashkan Rivers, Lorestan, Iran. J. Appl. Environ. Biol. Sci. 2015, 5, 258–268. [Google Scholar]
- Baker, C.; Johnson, T.; Flynn, D.; Hemida, H.; Quinn, A.; Soper, D.; Sterling, M. Chapter 4—Computational techniques. In Train Aerodynamics; Baker, C., Johnson, T., Flynn, D., Hemida, H., Quinn, A., Soper, D., Sterling, M., Eds.; Butterworth-Heinemann: Oxford, UK, 2019; pp. 53–71. [Google Scholar]
- Katopodes, N.D. Chapter 8—Methods for Two-Dimensional Shallow-Water Flow. In Free-Surface Flow; Katopodes, N.D., Ed.; Butterworth-Heinemann: Oxford, UK, 2019; pp. 500–567. [Google Scholar]
- U.S. Army Corps of Engineers. HEC-RAS 2D Modeling User’s Manual; U.S. Army Corps of Engineers: Washington, DC, USA, 2021.
- Sjölund, L. A Study of Sedimentation Problems in the Lower Reaches of the River Österdalälven. Master’s Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2018. [Google Scholar]
- Shields, A.B. Application of Similarity Principles and Turbulence Research to Bed-Load Movement; California Institute of Technology: Pasadena, CA, USA, 1936. [Google Scholar]
- Camnasio, E.; Orsi, E.; Schleiss, A.J. Experimental study of velocity fields in rectangular shallow reservoirs. J. Hydraul. Res. 2011, 49, 352–358. [Google Scholar] [CrossRef]
- Yossef Mohamed, F.M.; de Vriend Huib, J. Sediment Exchange between a River and Its Groyne Fields: Mobile-Bed Experiment. J. Hydraul. Eng. 2010, 136, 610–625. [Google Scholar] [CrossRef]







| Location | Conditions | ARI (Year) | Test Series | Flow Rate | |
|---|---|---|---|---|---|
| Prototype (m3/s) | Model (l/s) | ||||
| Habu | H1 Existing | 1 | H1-1 | 23.5 | 4.7 |
| 5 | H1-5 | 34.5 | 7.0 | ||
| 100 | H1-100 | 55.5 | 11.3 | ||
| H2 with Groynes | 1 | H2-1 | 23.5 | 4.7 | |
| 5 | H2-5 | 34.5 | 7.0 | ||
| 100 | H2-100 | 55.5 | 11.3 | ||
| Condition | (Years) | (L/s) | |||
|---|---|---|---|---|---|
| H1 Existing | 1 | 4.7 | 0.062 | 0.622 | 0.180 |
| 5 | 7.0 | 0.044 | 0.793 | 0.181 | |
| 100 | 11.3 | 0.021 | 0.899 | 0.188 | |
| H2 Groynes | 1 | 4.7 | 0.038 | 0.608 | 0.161 |
| 5 | 7.0 | 0.034 | 0.729 | 0.195 | |
| 100 | 11.3 | 0.026 | 0.874 | 0.248 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mat Desa, S.; Jamal, M.H.; Mohd, M.S.F.; Samion, M.K.H.; Rahim, N.S.; Muda, R.S.; Sa’ari, R.; Kasiman, E.H.; Mustaffar, M.; Ishak, D.S.M.; et al. Numerical Modelling on Physical Model of Ringlet Reservoir, Cameron Highland, Malaysia: How Flow Conditions Affect the Hydrodynamics. Water 2023, 15, 1883. https://doi.org/10.3390/w15101883
Mat Desa S, Jamal MH, Mohd MSF, Samion MKH, Rahim NS, Muda RS, Sa’ari R, Kasiman EH, Mustaffar M, Ishak DSM, et al. Numerical Modelling on Physical Model of Ringlet Reservoir, Cameron Highland, Malaysia: How Flow Conditions Affect the Hydrodynamics. Water. 2023; 15(10):1883. https://doi.org/10.3390/w15101883
Chicago/Turabian StyleMat Desa, Safari, Mohamad Hidayat Jamal, Mohd Syazwan Faisal Mohd, Mohd Kamarul Huda Samion, Nor Suhaila Rahim, Rahsidi Sabri Muda, Radzuan Sa’ari, Erwan Hafizi Kasiman, Mushairry Mustaffar, Daeng Siti Maimunah Ishak, and et al. 2023. "Numerical Modelling on Physical Model of Ringlet Reservoir, Cameron Highland, Malaysia: How Flow Conditions Affect the Hydrodynamics" Water 15, no. 10: 1883. https://doi.org/10.3390/w15101883
APA StyleMat Desa, S., Jamal, M. H., Mohd, M. S. F., Samion, M. K. H., Rahim, N. S., Muda, R. S., Sa’ari, R., Kasiman, E. H., Mustaffar, M., Ishak, D. S. M., & Mokhtar, M. Z. (2023). Numerical Modelling on Physical Model of Ringlet Reservoir, Cameron Highland, Malaysia: How Flow Conditions Affect the Hydrodynamics. Water, 15(10), 1883. https://doi.org/10.3390/w15101883





