Optimization of an Empirical Model for Microorganism-Immobilized Media to Predict Nitrogen Removal Efficiency
Abstract
:1. Introduction
2. Materials and Methods
2.1. Microorganism-Immobilized Media
2.2. Evaluation of Modified Ludzack–Ettinger Process with Microorganism-Immobilized Media
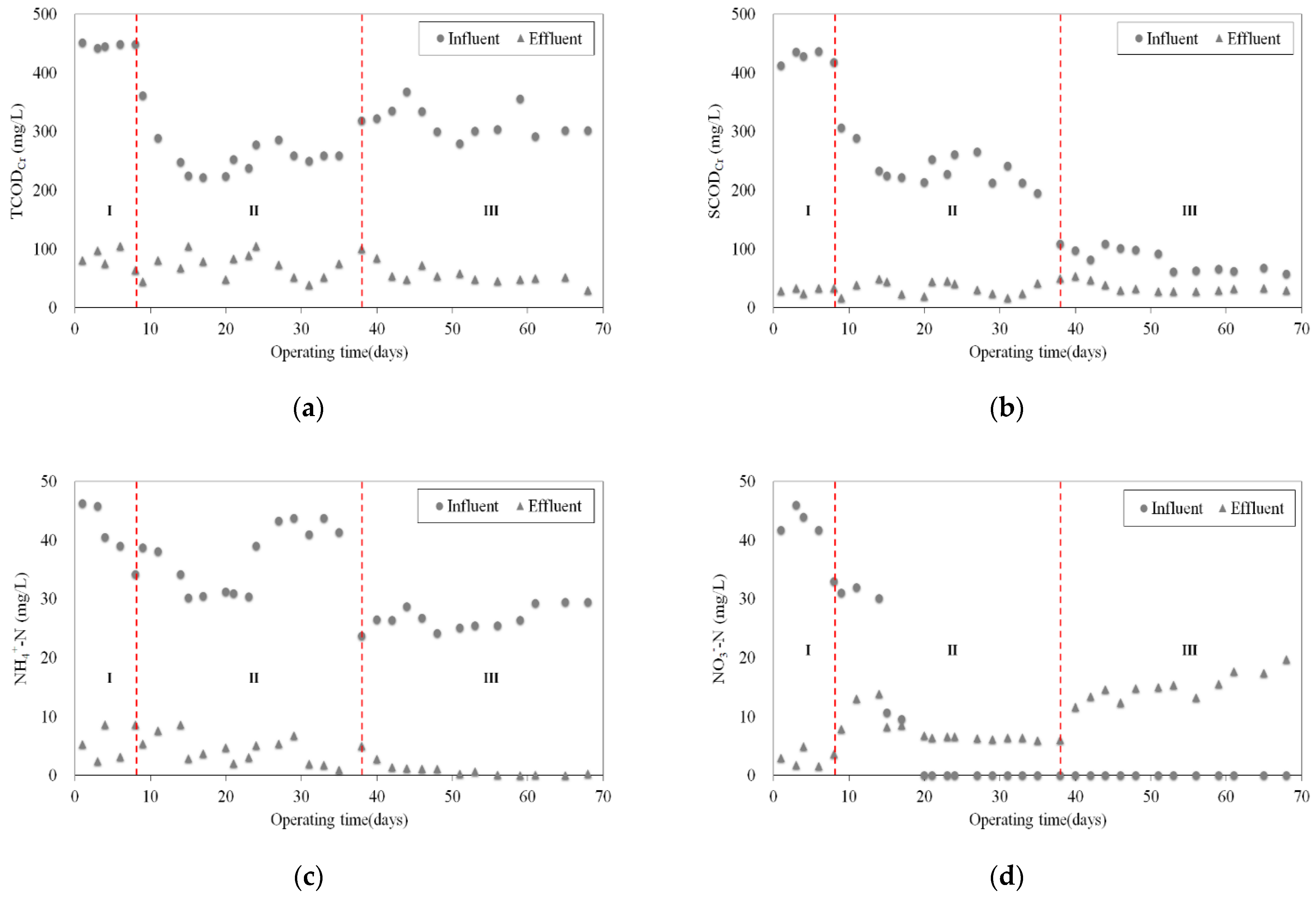
- Mode I: Chemical oxygen demand (CODCr) 450 mg/L, NH4+-N 50 mg/L, NO3−-N 40 mg/L, total phosphorous (T-P) 4.0 mg/L, alkalinity 350 mg/L as CaCO3, aerobic HRT 12 h, anoxic HRT 4.8 h;
- Mode II: CODCr 250 mg/L, NH4+-N 40 mg/L, NO3−-N 0 mg/L, T-P 4.5 mg/L, alkalinity 250 mg/L as CaCO3, aerobic HRT 8 h, anoxic HRT 3.2 h;
- Mode III: CODCr 280~368 mg/L, NH4+-N 57~109 mg/L, NO3−-N 24~30 mg/L, T-P 2.7~7.2 mg/L, alkalinity 280~355 mg/L as CaCO3, aerobic HRT 6 h, anoxic HRT 2.4 h.
2.3. Experimental Design by Box–Behnken Method
2.4. Development of Treated Water Quality Prediction Model
- -
- Operation factor: anoxic HRT 2.4 h, aerobic HRT 4.7 h;
- -
- Summer influent data (1st): total nitrogen (TN) 36.0 mg/L, C/N ratio 4.42;
- -
- Winter influent data (2nd): TN 39.0 mg/L, C/N ratio 3.87.
3. Results
3.1. Lab-Scale Reactor Operation Results
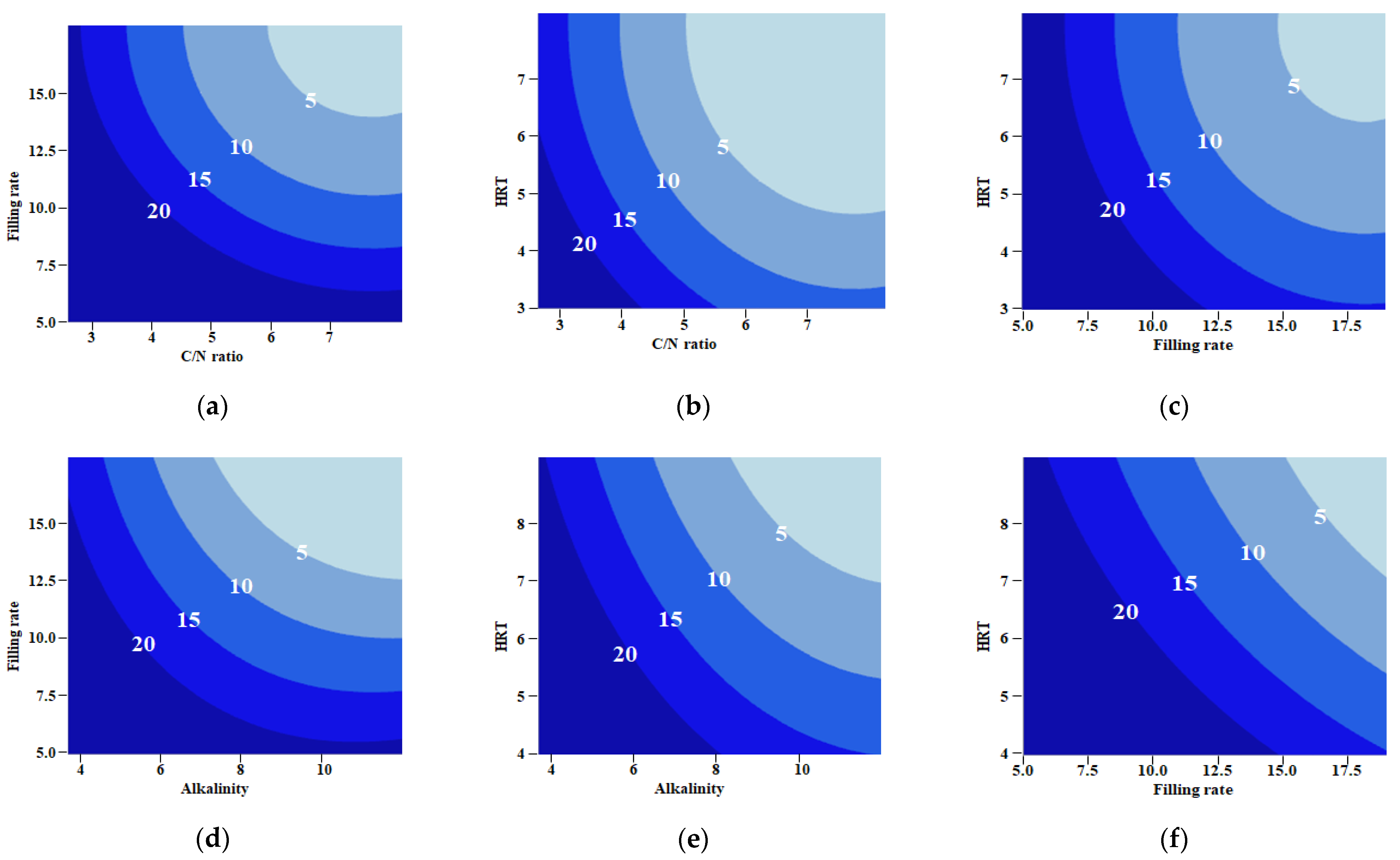
3.2. Model Development by Box–Behnken Method
3.2.1. Anoxic Conditions
3.2.2. Aerobic Conditions
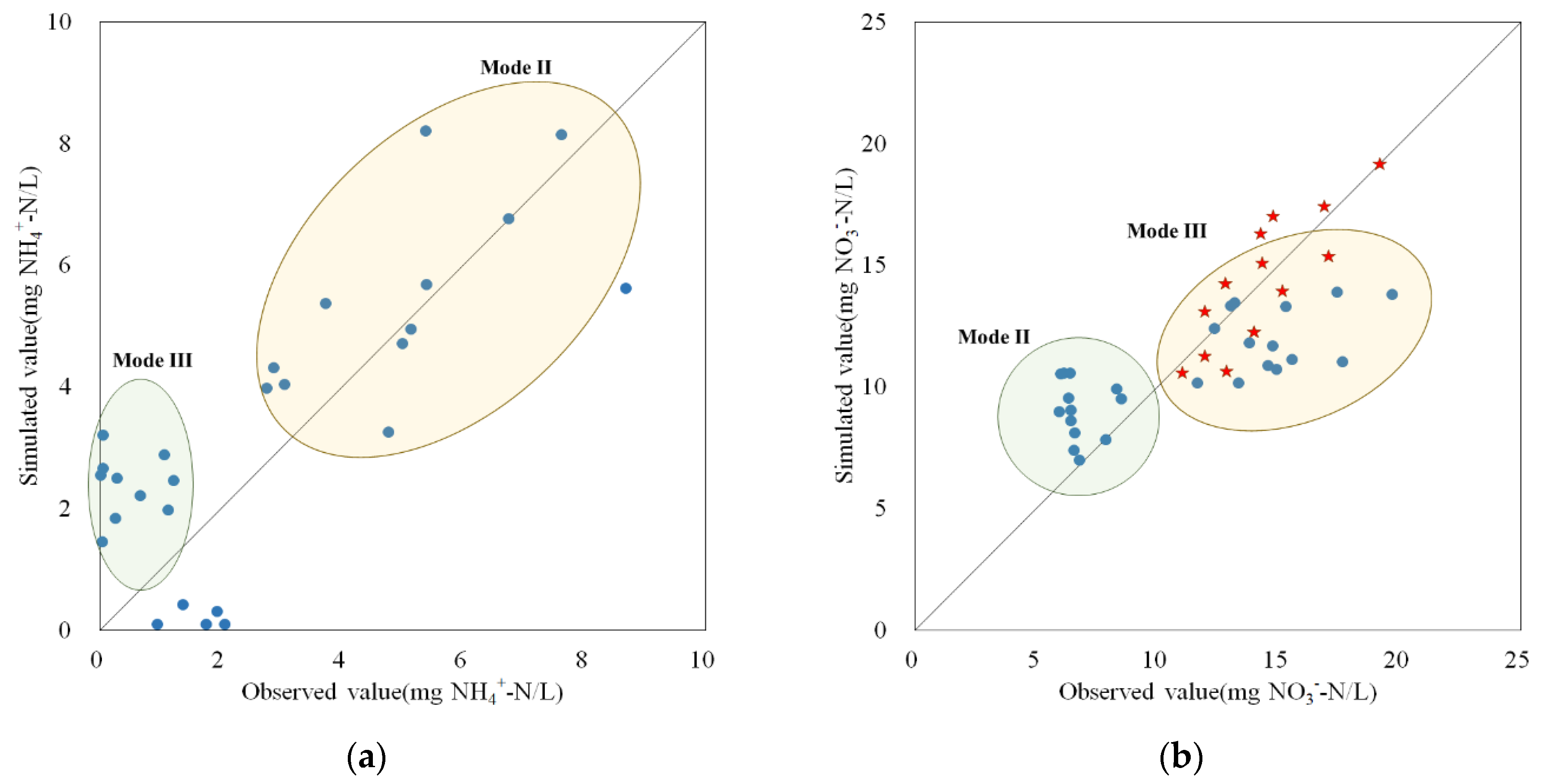
3.2.3. Model Evaluation (Congruence, Significance)
- -
- Denitrification: NO3−-Nin—50 mg/L, HRT—5 h, C/N ratio—5, filling rate—15%;
- -
- Nitrification: NH4+-Nin—50 mg/L, HRT—9 h, alkalinity—9 mg as CaCO3/L, filling rate—15%.
3.3. Model Validation versus Lab Test Results
3.4. Sewage Treatment Plant Water Quality Prediction through Model Application
4. Conclusions
- -
- In the case of the aerobic model, the NH4+-N predicted value was estimated at 1.5 mg/L higher than the measured value. When the model is used to predict the HRT (size) of the reactor, this should be considered to avoid overdesigning.
- -
- In the case of applying an anoxic model, it is possible to obtain more accurate predictions by applying readily biodegradable organic matter through the COD fraction by inputting the C/N ratio among the variables.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lam, M.K.; Lee, K.T. Immobilization as a feasible method to simplify the separation of microalgae from water for biodiesel production. Chem. Eng. J. 2012, 191, 263–268. [Google Scholar] [CrossRef]
- Covarrubias, S.A.; De-Bashan, L.E.; Moreno, M.; Bashan, Y. Alginate beads provide a beneficial physical barrier against native microorganisms in wastewater treated with immobilized bacteria and microalgae. Appl. Microbiol. Biotechnol. 2012, 93, 2669–2680. [Google Scholar] [CrossRef] [PubMed]
- Boelee, N.; Temmink, H.; Janssen, M.; Buisman, C.; Wijffels, R. Balancing the organic load and light supply in symbiotic microalgal–bacterial biofilm reactors treating synthetic municipal wastewater. Ecol. Eng. 2014, 64, 213–221. [Google Scholar] [CrossRef]
- Shen, Y.; Gao, J.; Li, L. Municipal wastewater treatment via co-immobilized microalgal-bacterial symbiosis: Microorganism growth and nutrients removal. Bioresour. Technol. 2017, 243, 905–913. [Google Scholar] [CrossRef]
- Leenen, E.J.; Dos Santos, V.A.; Grolle, K.C.; Tramper, J.; Wijffels, R. Characteristics of and selection criteria for support materials for cell immobilization in wastewater treatment. Water Res. 1996, 30, 2985–2996. [Google Scholar] [CrossRef]
- Lertsutthiwong, P.; Boonpuak, D.; Pungrasmi, W.; Powtongsook, S. Immobilization of nitrite oxidizing bacteria using biopolymeric chitosan media. J. Environ. Sci. 2013, 25, 262–267. [Google Scholar] [CrossRef]
- Tee, P.F.; Abdullah, M.O.; Tan, I.A.W.; Rashid, N.K.A.; Amin, M.A.M.; Nolasco-Hipolito, C.; Bujang, K. Review on hybrid energy systems for wastewater treatment and bio-energy production. Renew. Sustain. Energy Rev. 2016, 54, 235–246. [Google Scholar] [CrossRef]
- Wang, J.-H.; Chen, Y.-P.; Dong, Y.; Wang, X.-X.; Guo, J.-S.; Shen, Y.; Yan, P.; Ma, T.-F.; Sun, X.-Q.; Fang, F.; et al. A new method to measure and model dynamic oxygen microdistributions in moving biofilms. Environ. Pollut. 2017, 229, 199–209. [Google Scholar] [CrossRef]
- Beni, A.A.; Esmaeili, A. Design and optimization of a new reactor based on biofilm-ceramic for industrial wastewater treatment. Environ. Pollut. 2019, 255, 113298. [Google Scholar] [CrossRef]
- Karadag, D.; Köroğlu, O.E.; Ozkaya, B.; Cakmakci, M. A review on anaerobic biofilm reactors for the treatment of dairy industry wastewater. Process Biochem. 2015, 50, 262–271. [Google Scholar] [CrossRef]
- Zhang, W.; Yin, K.; Li, B.; Chen, L. A glutathione S-transferase from Proteus mirabilis involved in heavy metal resistance and its potential application in removal of Hg2+. J. Hazard. Mater. 2013, 261, 646–652. [Google Scholar] [CrossRef] [PubMed]
- Cassidy, M.B.; Lee, H.; Trevors, J.T. Environmental applications of immobilized microbial cells: A review. J. Ind. Microbiol. Biotechnol. 1996, 16, 79–101. [Google Scholar] [CrossRef]
- Rostron, W.M.; Stuckey, D.C.; A Young, A. Nitrification of high strength ammonia wastewaters: Comparative study of immobilisation media. Water Res. 2001, 35, 1169–1178. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.L. Immobilization Techniques for Biocatalysts and Water Pollution Control; Science Press: Beijing, China, 2000. [Google Scholar]
- Zheng, S.; Yang, M.; Park, Y.H.; Liu, F. Washout of a yeast population during continuous treatment of salad-oil-manufacturing wastewater. Bioresour. Technol. 2003, 86, 235–237. [Google Scholar] [CrossRef] [PubMed]
- Dong, Y.; Zhang, Z.; Jin, Y.; Li, Z.; Lu, J. Nitrification performance of nitrifying bacteria immobilized in waterborne Polyurethane at low ammonia nitrogen concentrations. J. Environ. Sci. 2011, 23, 366–371. [Google Scholar] [CrossRef] [PubMed]
- Abu Bakar, S.N.H.; Abu Hasan, H.; Mohammad, A.W.; Abdullah, S.R.S.; Haan, T.Y.; Ngteni, R.; Yusof, K.M.M. A review of moving-bed biofilm reactor technology for palm oil mill effluent treatment. J. Clean. Prod. 2018, 171, 1532–1545. [Google Scholar] [CrossRef]
- Shin, D.-C.; Kim, J.-S.; Park, C.-H. Study on physical and chemical characteristics of microorganism immobilized media for advanced wastewater treatment. J. Water Process Eng. 2019, 29, 100784. [Google Scholar] [CrossRef]
- Henze, M.; Grady, C.; Gujer, W.; Marais, G.; Matsuo, T. A general model for single-sludge wastewater treatment systems. Water Res. 1987, 21, 505–515. [Google Scholar] [CrossRef] [Green Version]
- Hvala, N.; Vrečko, D.; Burica, O.; Strazžar, M.; Levstek, M. Simulation study supporting wastewater treatment plant upgrading. Water Sci. Technol. 2002, 46, 325–332. [Google Scholar] [CrossRef]
- Nuhoglu, A.; Keskinler, B.; Yildiz, E. Mathematical modelling of the activated sludge process—the Erzincan case. Process Biochem. 2005, 40, 2467–2473. [Google Scholar] [CrossRef]
- Wanner, O.; Eberl, H.; Morgenroth, E.; Noguera, D.; Picioreanu, C.; Rittman, B.; Loosdrecht, M.V. Mathematical Modeling of Biofilms; IWA Task Group on Biofilm Modeling, Scientific and Technical Report; IWA Publishing: London, UK, 2006; p. 18. [Google Scholar]
- Shin, D.-C.; Yoon, S.-C.; Park, C.-H. Biological characteristics of microorganisms immobilization media for nitrogen removal. J. Water Process Eng. 2019, 32, 100979. [Google Scholar] [CrossRef]
- Baş, D.; Boyacı, I.H. Modeling and optimization I: Usability of response surface methodology. J. Food Eng. 2007, 78, 836–845. [Google Scholar] [CrossRef]
- Ceylan, H.; Kubilay, S.; Aktas, N.; Sahiner, N. An approach for prediction of optimum reaction conditions for laccase-catalyzed bio-transformation of 1-naphthol by response surface methodology (RSM). Bioresour. Technol. 2008, 99, 2025–2031. [Google Scholar] [CrossRef] [PubMed]
- Alim, M.; Lee, J.-H.; Akoh, C.; Choi, M.-S.; Jeon, M.-S.; Shin, J.-A.; Lee, K.-T. Enzymatic transesterification of fractionated rice bran oil with conjugated linoleic acid: Optimization by response surface methodology. LWT 2008, 41, 764–770. [Google Scholar] [CrossRef]
- Sridhar, R.; Sivakumar, V.; Maran, J.P.; Thirugnanasambandham, K. Influence of operating parameters on treatment of egg processing effluent by electrocoagulation process. Int. J. Environ. Sci. Technol. 2013, 11, 1619–1630. [Google Scholar] [CrossRef] [Green Version]
- Nourani, M.; Baghdadi, M.; Javan, M.; Bidhendi, G.N. Production of a biodegradable flocculant from cotton and evaluation of its performance in coagulation-flocculation of kaolin clay suspension: Optimization through response surface methodology (RSM). J. Environ. Chem. Eng. 2016, 4, 1996–2003. [Google Scholar] [CrossRef] [Green Version]
- Davarnejad, R.; Nasiri, S. Slaughterhouse wastewater treatment using an advanced oxidation process: Optimization study. Environ. Pollut. 2017, 223, 1–10. [Google Scholar] [CrossRef]
- Cifuentes, A.; Xu, X.; Kok, W.; Poppe, H. Optimum conditions for preparative operation of capillary zone electrophoresis. J. Chromatogr. A 1995, 716, 141–156. [Google Scholar] [CrossRef] [Green Version]
- IWA Task Group on Mathematical Modeling for Design and Operation of Biological Wastewater Treatment. Activated Sludge Models ASM1, ASM2, ASM2d, ASM3; IWA Publishing: London, UK, 2000. [Google Scholar]
- Gujer, W.; Henze, M.; Mino, T.; Matsuo, T.; Wentzel, M.C.; Marais, G.V.R. The activated sludge model no. 2: Biological phosphorus removal. Water Sci. Technol. 1995, 31, 1–11. [Google Scholar] [CrossRef]

| Variable | Level | |||
|---|---|---|---|---|
| −1 | 0 | 1 | ||
| Nitrification | NH4+-N Conc. (mg/L) | 25 | 50 | 75 |
| CODCr (mg/L) | 50 | 100 | 150 | |
| NH4+-N/Alk. | 4 | 7 | 10 | |
| Filling rate (%) | 5 | 12.5 | 20 | |
| HRT (h) | 4 | 7 | 10 | |
| Denitrification | NO3−-N Conc. (mg/L) | 40 | 80 | 120 |
| C/N ratio | 2 | 5 | 8 | |
| Filling rate (%) | 5 | 12.5 | 20 | |
| Classification | Operating Factor | Effluent T-N (mg/L) | Remarks | |||||
|---|---|---|---|---|---|---|---|---|
| MLSS (mg/L) | Filling Rate (%) | HRT (h) | ||||||
| Anoxic | Aerobic | Anoxic | Aerobic | |||||
| 1st data | Observed | 2500 | - | - | 2.4 | 4.7 | 14.0 | |
| Simulated | - | 15 | 20 | 2.4 | 4.7 | 9.75 | ||
| 8.43 | C/N ratio: 5.0 | |||||||
| 2nd data | Observed | 2850 | - | - | 2.4 | 4.7 | 14.3 | |
| Simulated | - | 15 | 20 | 2.4 | 4.7 | 13.56 | ||
| 9.84 | C/N ratio: 5.0 | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shin, D.; Chung, W.; Lee, J. Optimization of an Empirical Model for Microorganism-Immobilized Media to Predict Nitrogen Removal Efficiency. Water 2023, 15, 83. https://doi.org/10.3390/w15010083
Shin D, Chung W, Lee J. Optimization of an Empirical Model for Microorganism-Immobilized Media to Predict Nitrogen Removal Efficiency. Water. 2023; 15(1):83. https://doi.org/10.3390/w15010083
Chicago/Turabian StyleShin, Dongchul, Wonsik Chung, and Jongkeun Lee. 2023. "Optimization of an Empirical Model for Microorganism-Immobilized Media to Predict Nitrogen Removal Efficiency" Water 15, no. 1: 83. https://doi.org/10.3390/w15010083
APA StyleShin, D., Chung, W., & Lee, J. (2023). Optimization of an Empirical Model for Microorganism-Immobilized Media to Predict Nitrogen Removal Efficiency. Water, 15(1), 83. https://doi.org/10.3390/w15010083







