Study of the Internal Cyclonic Flow Characteristics of Cyclones with Different Guide Vane Heights
Abstract
:1. Introduction
2. Construction of a Mathematical Model of Guide Vane Cyclones
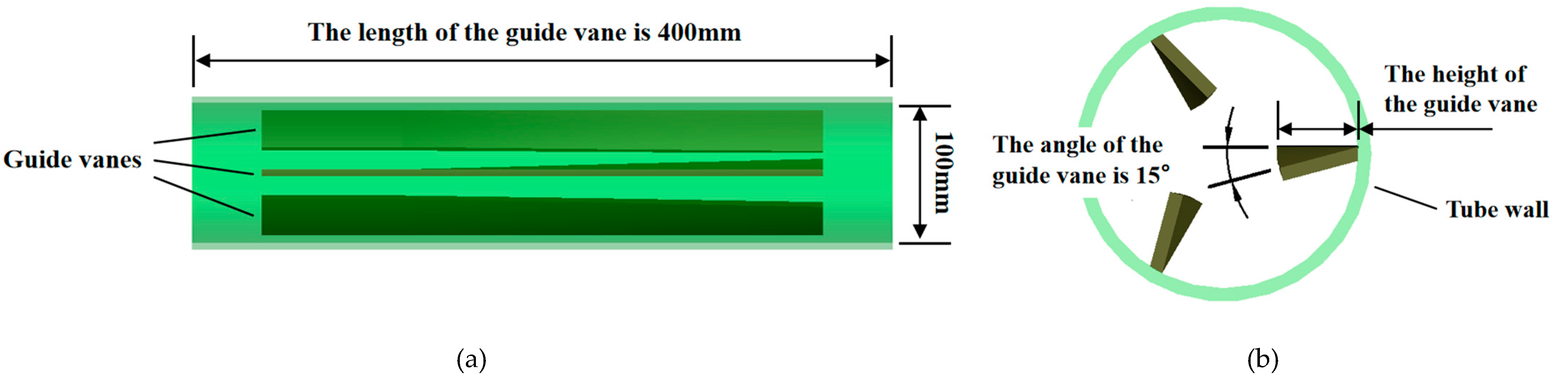
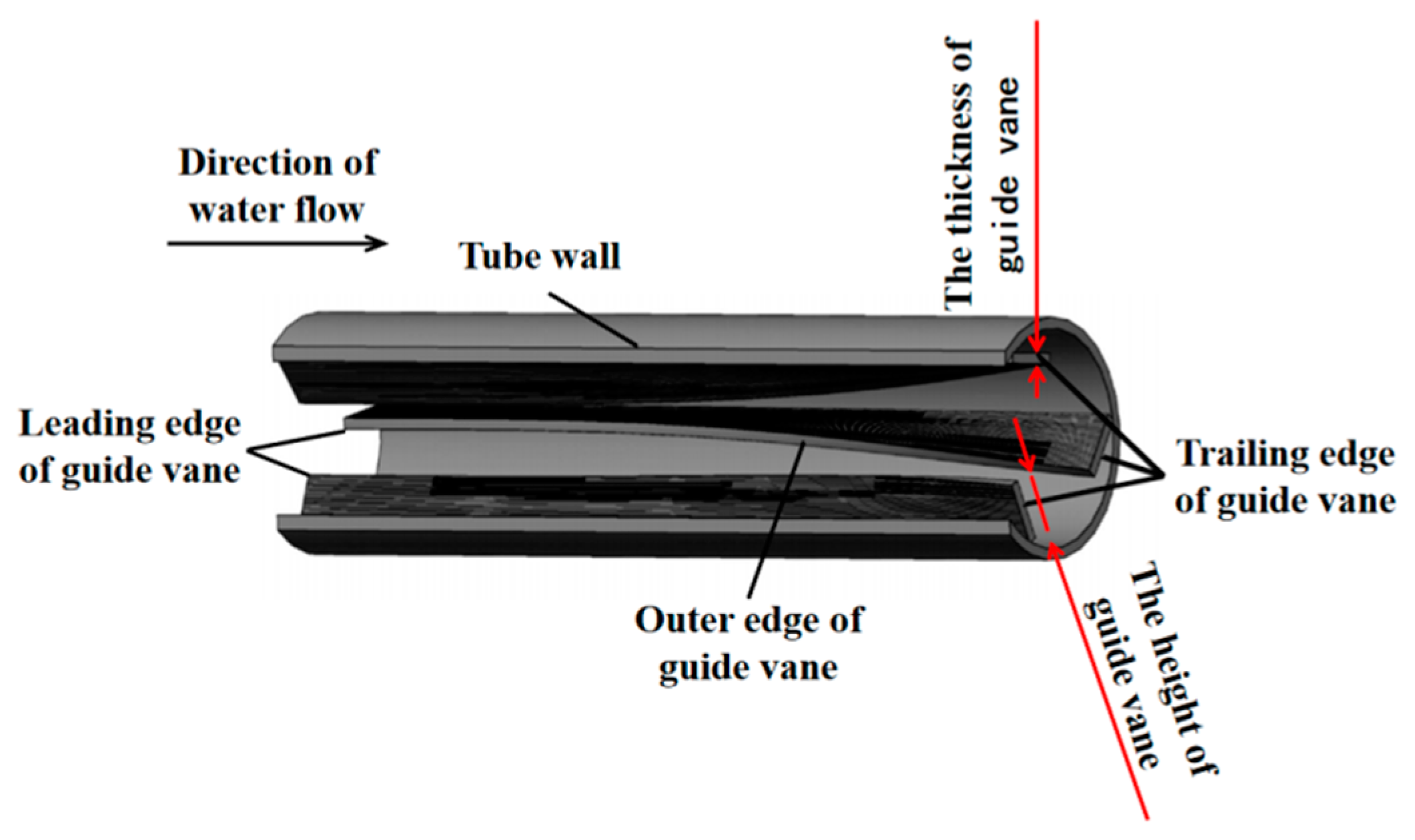
2.1. Geometric Modelling
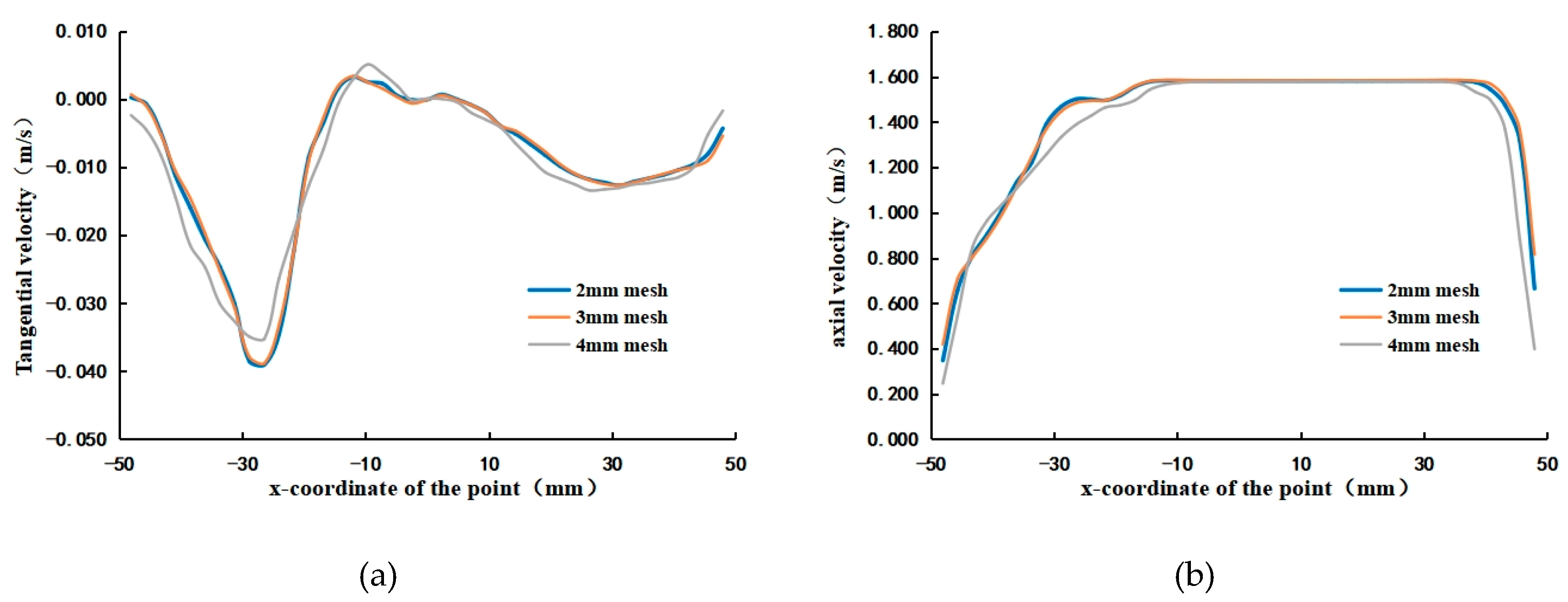
2.2. Mesh Division
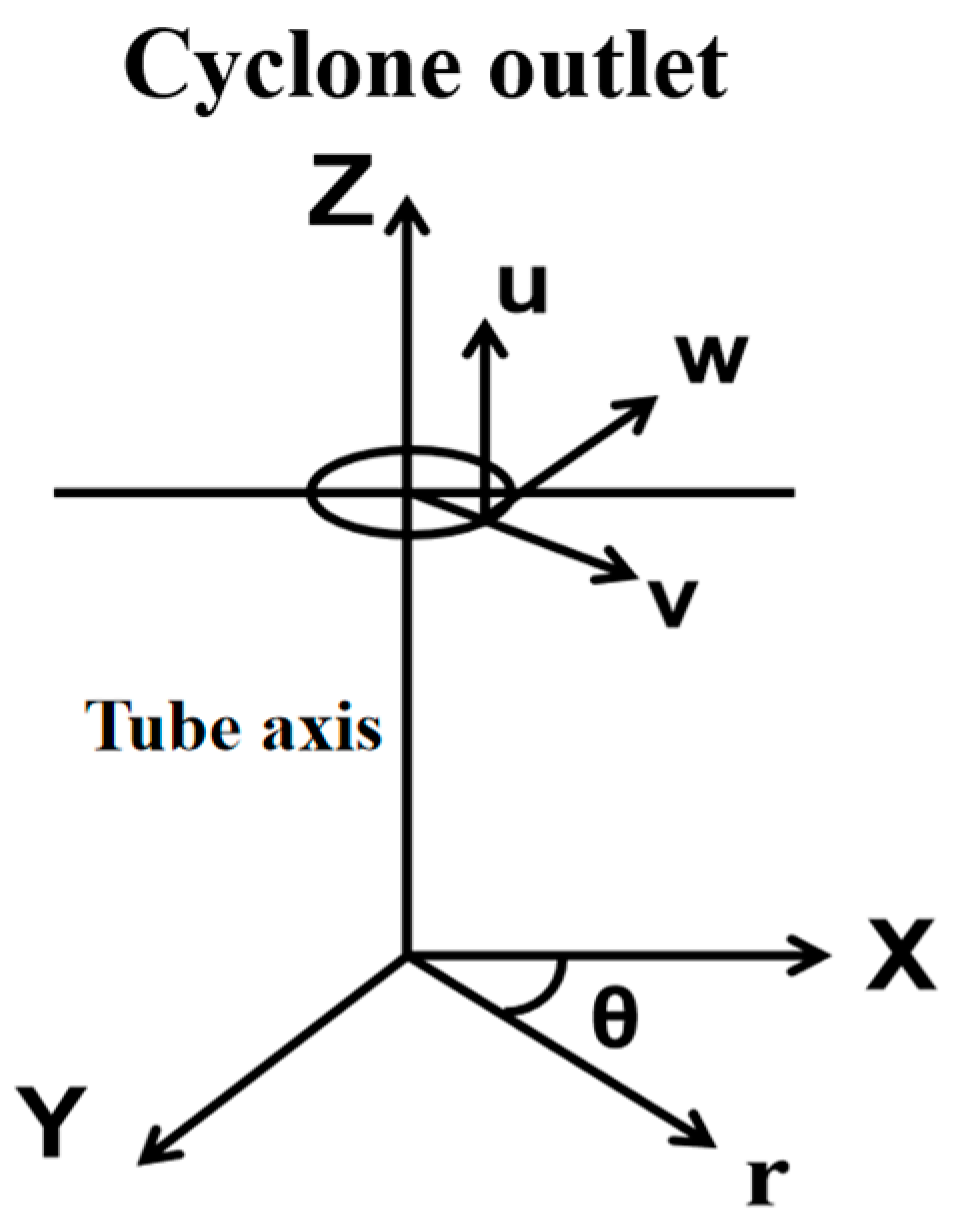
2.3. Model Selection and Its Control Equations
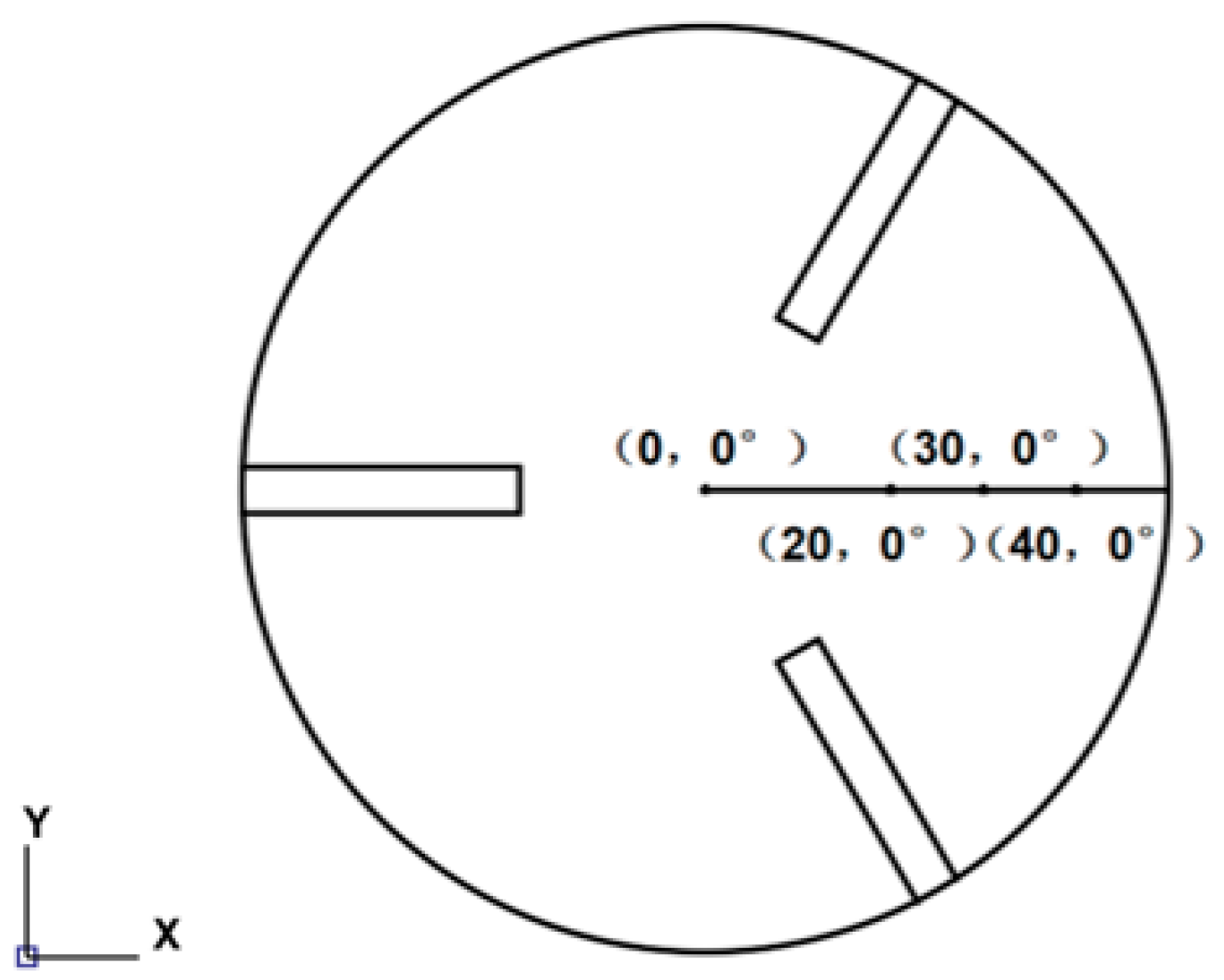
3. Research Programme
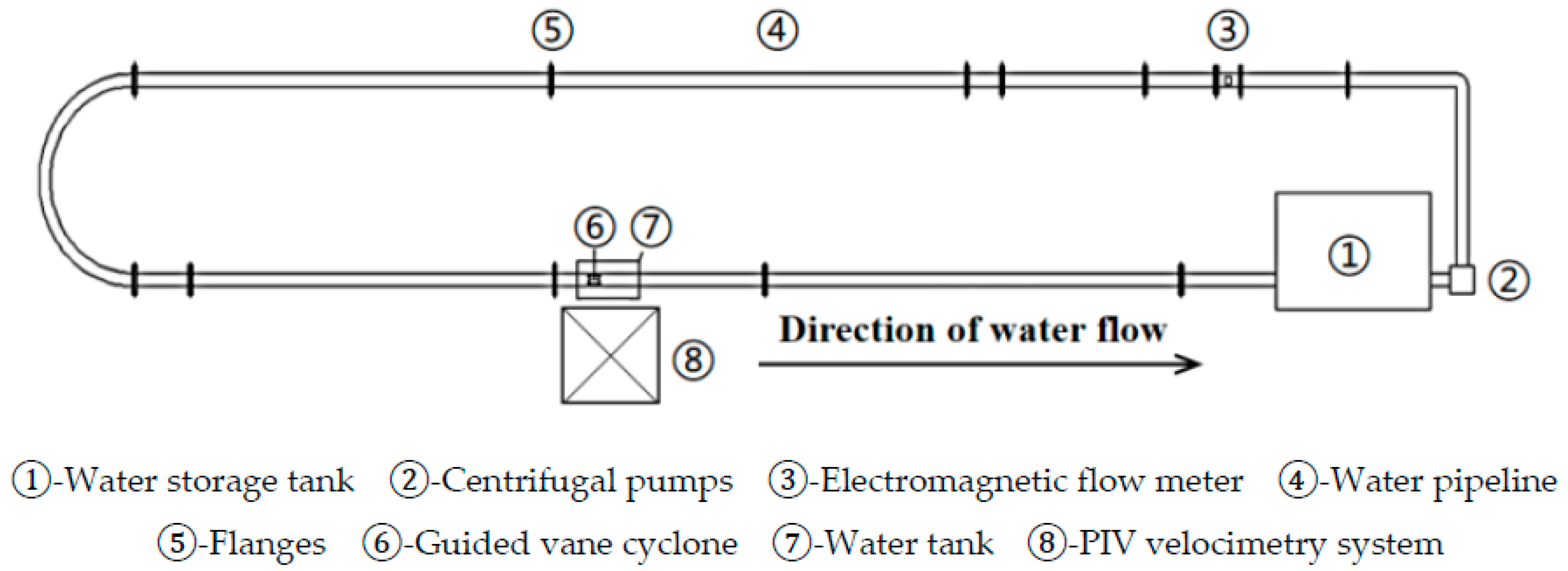
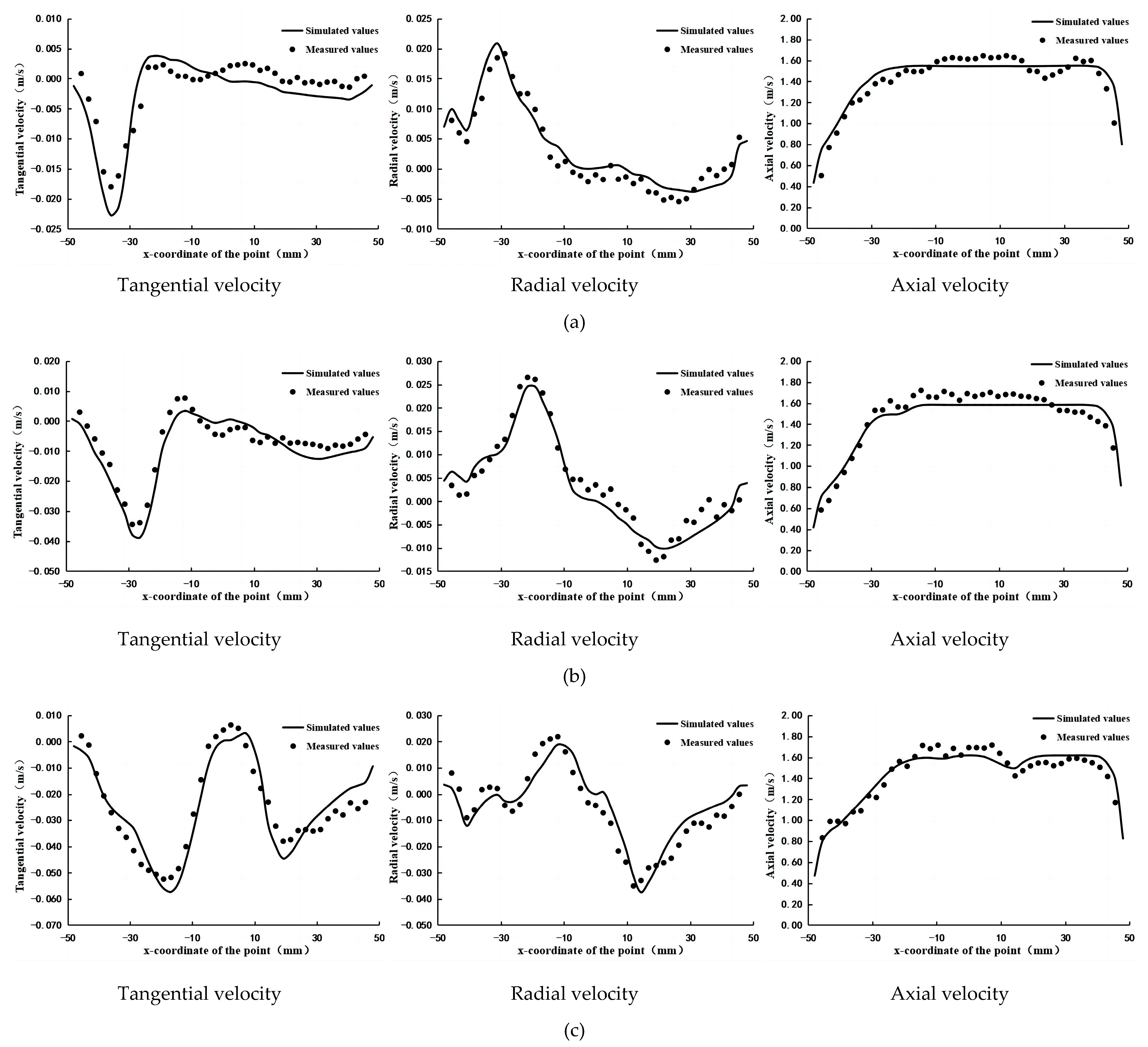
4. Experimental Verification of Simulation Results
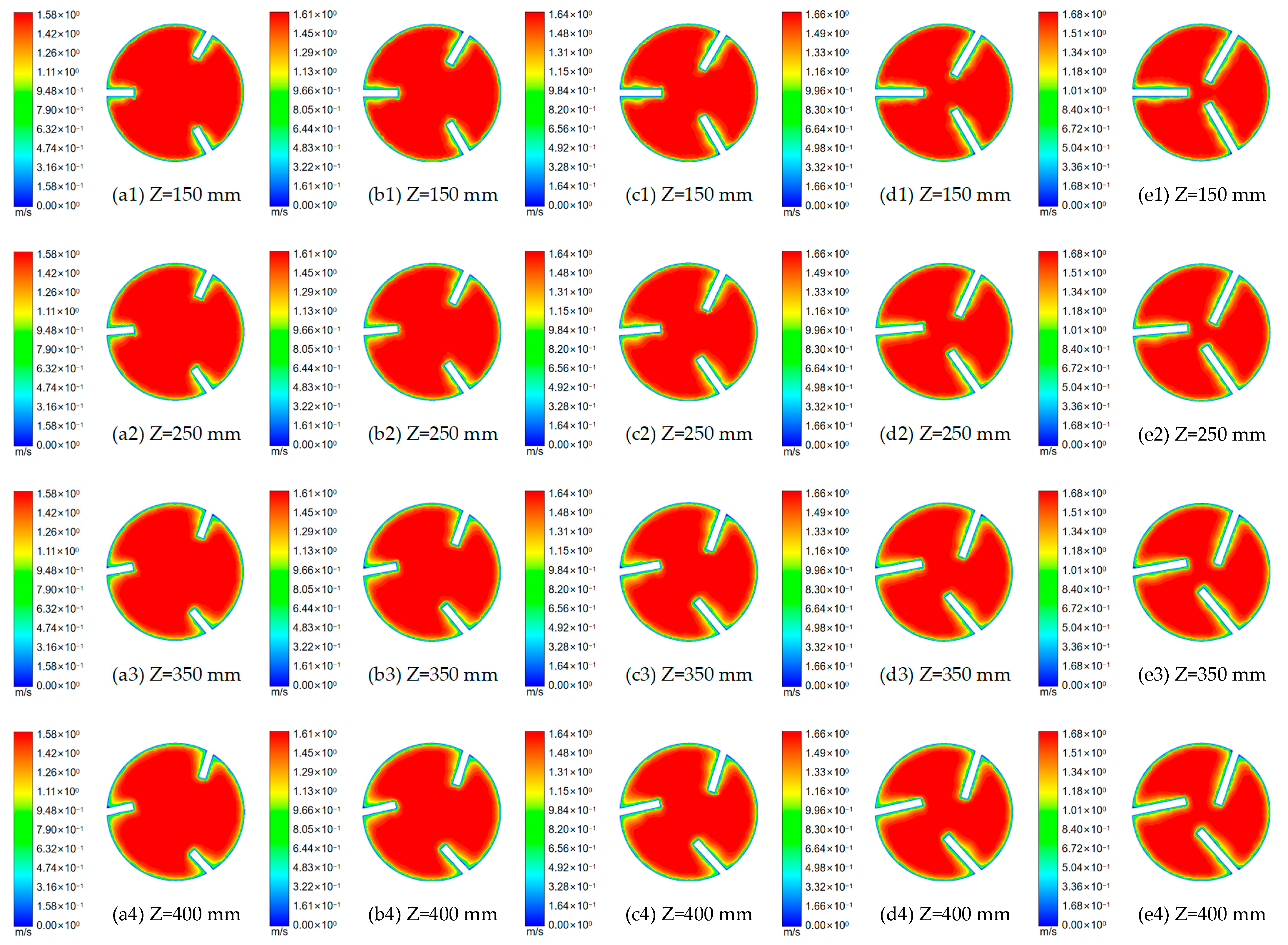
5. Simulation Results and Analysis
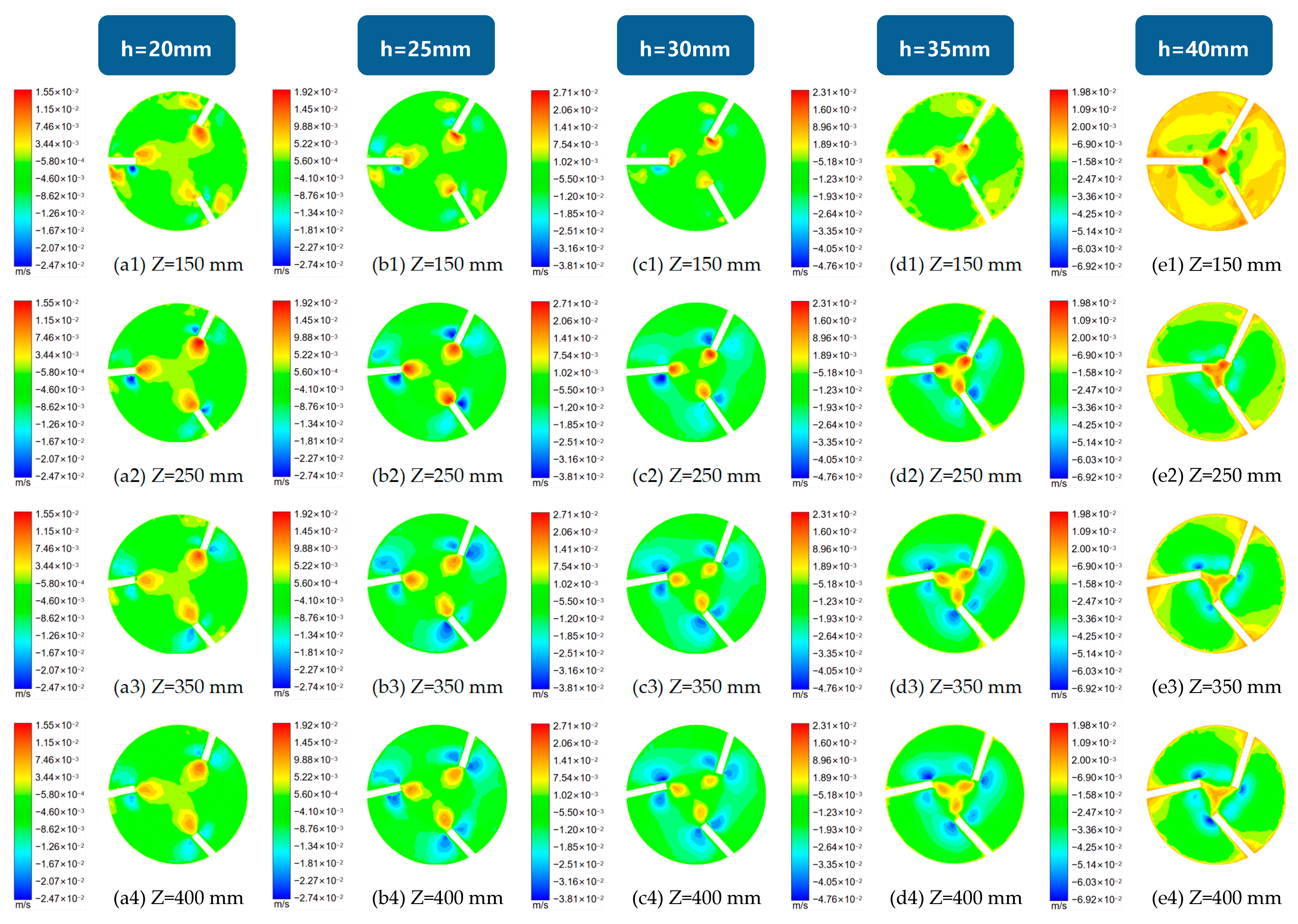
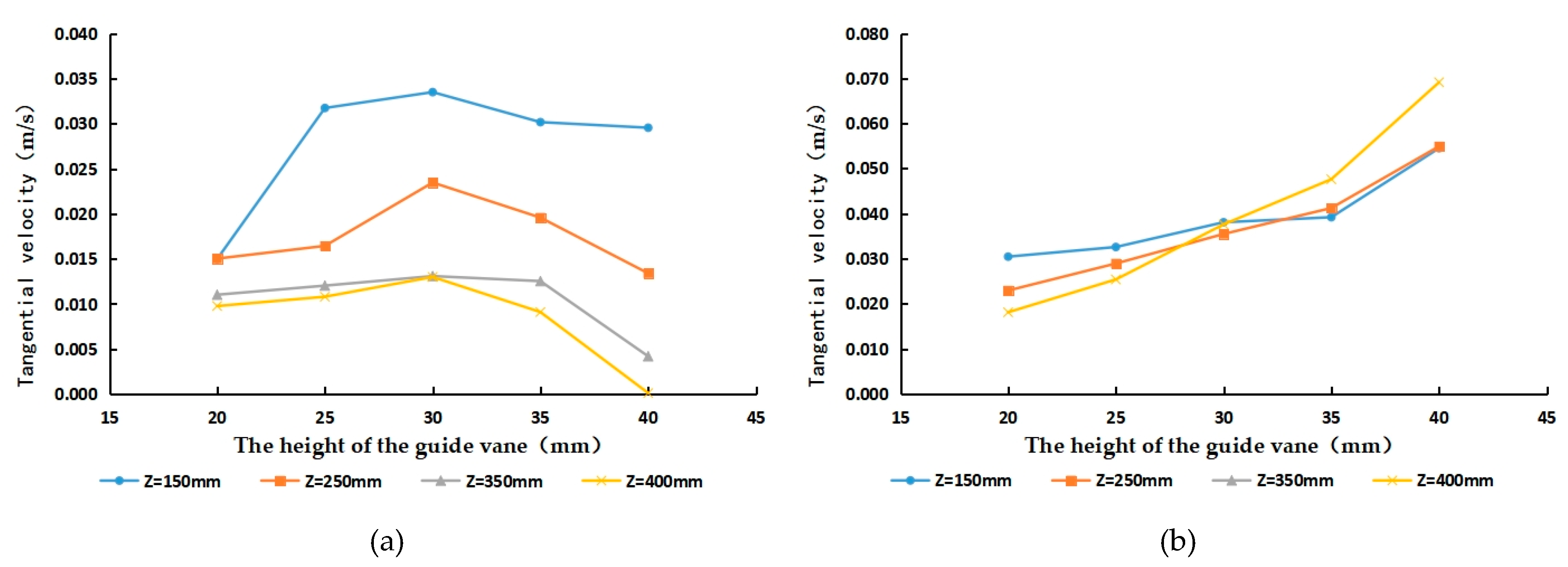
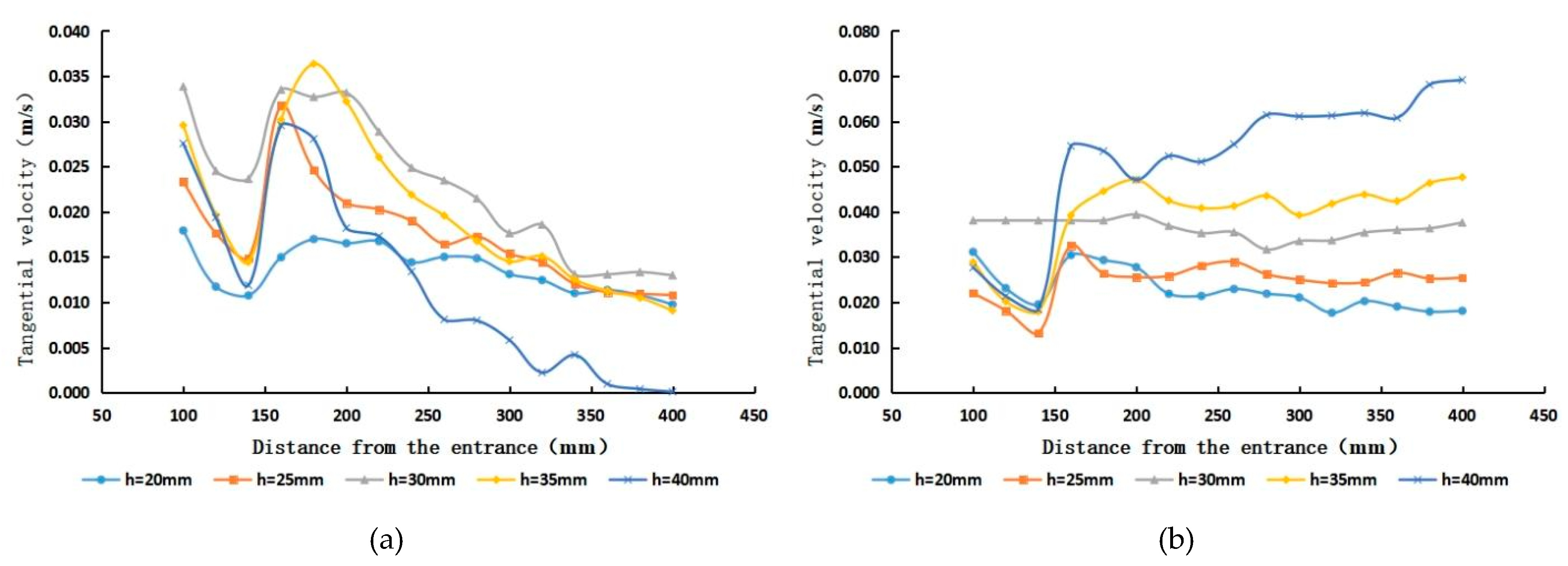
5.1. Analysis of the Internal Tangential Velocity Characteristics of Cyclones with Different Guide Vane Heights
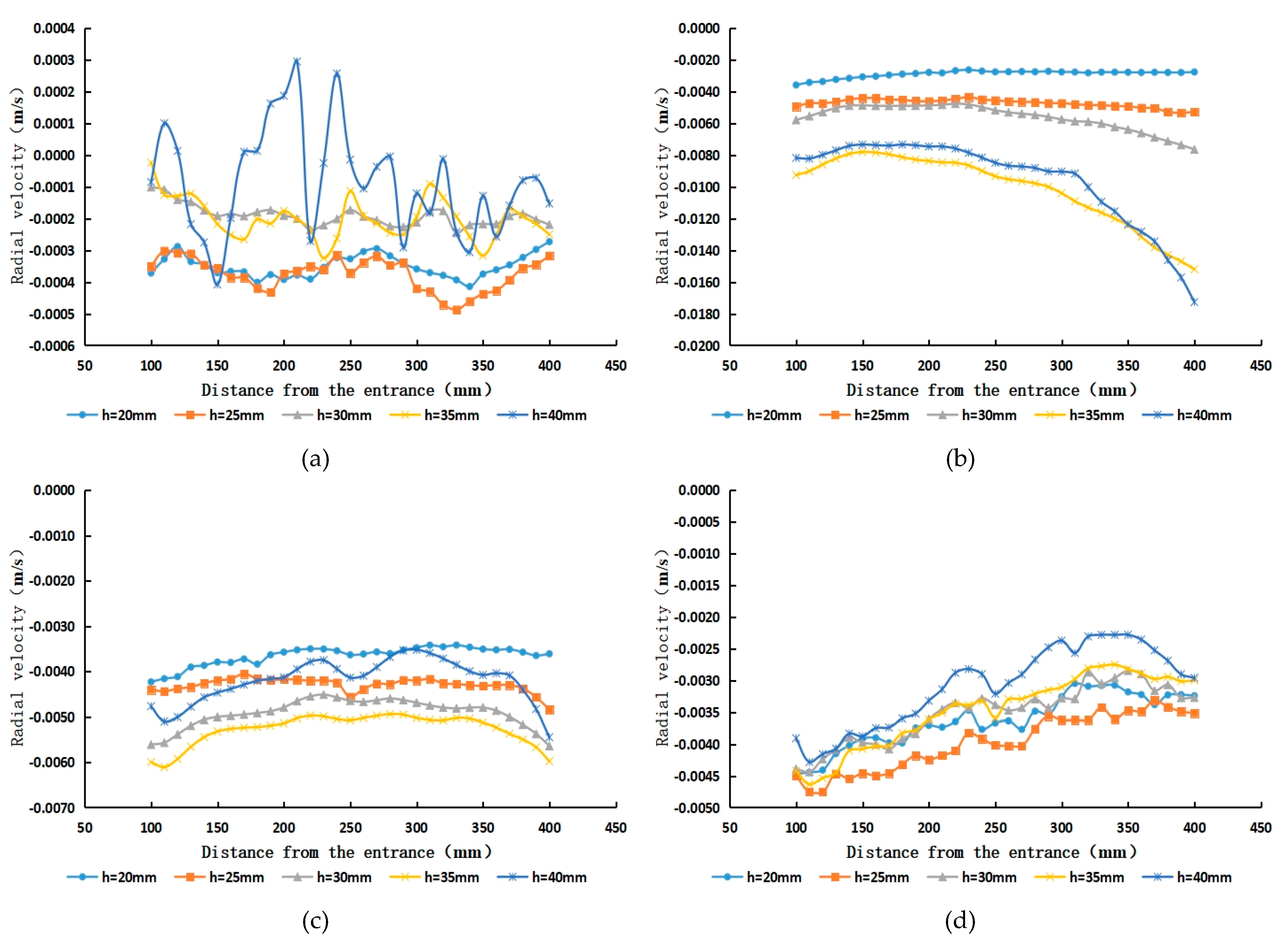
5.2. Analysis of the Internal Radial Velocity Characteristics of Cyclones with Different Guide Vane Heights
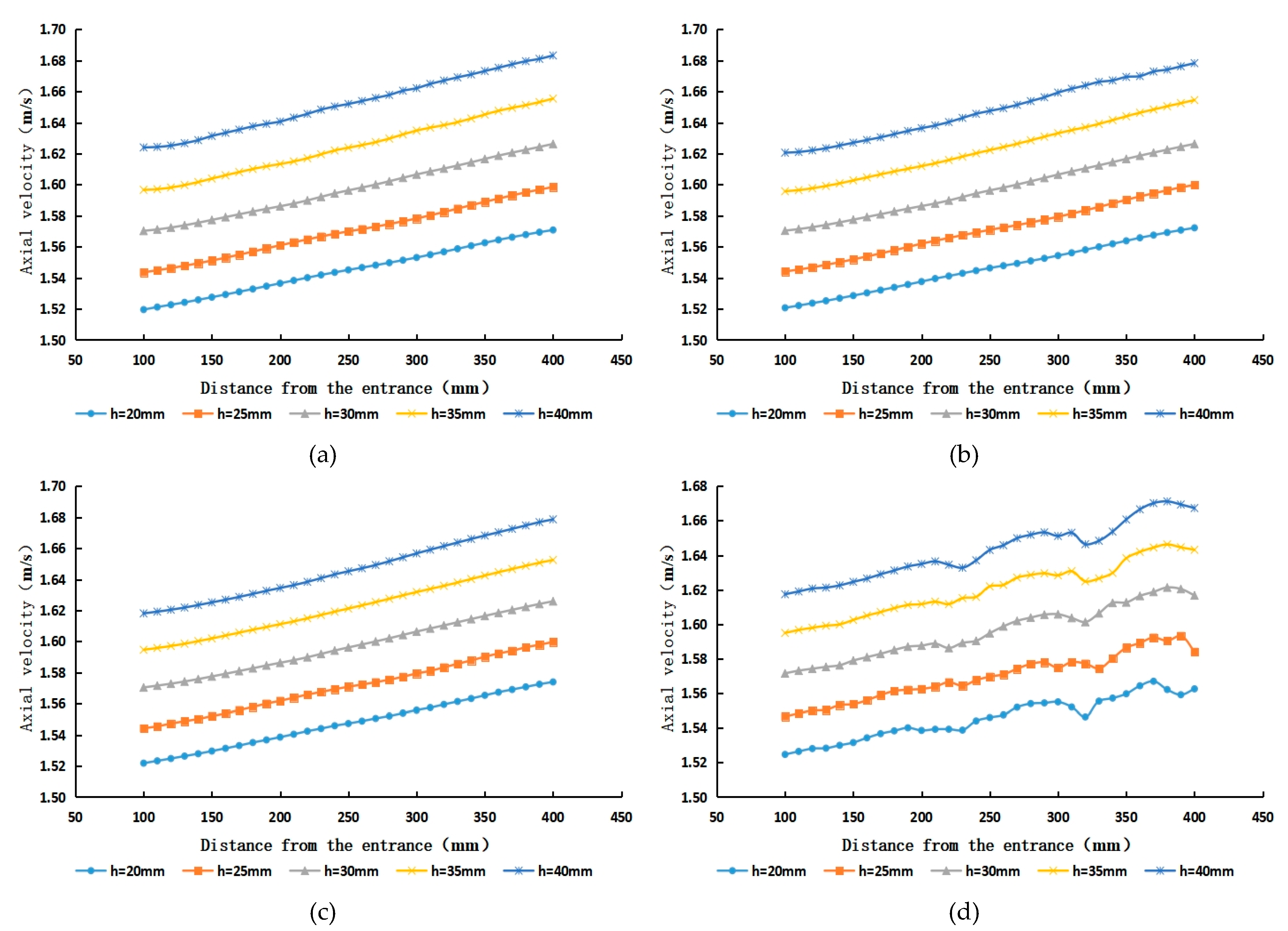
5.3. Analysis of the Internal Axial Velocity Characteristics of Cyclones with Different Guide Vane Heights
6. Discussion and Conclusions
- The tangential velocity in the centre of the cyclone pipe is mainly in the anticlockwise direction, and the flow velocity increases with the increase in the guide vane height and then decreases. When the ratio between the height of the guide vane and the inner diameter of the cyclone is in the range of 0.5 to 0.7, it can produce a high−strength and more stable spiral flow. When the height of the guide vane is 30 mm and the height−to−diameter ratio is near 0.6, the tangential velocity reaches its maximum and the intensity of the spiral flow generated is the highest, which enables more particle of different sizes to enter the suspended flow at this time and provides a better sand removal effect.
- The radial velocity increases as the height of the guide vane increases, and the radial velocity region pointing towards the tube wall increases, while the radial velocity region pointing towards the tube axis decreases.
- The overall distribution of axial flow velocity is similar to that of turbulent flow in a circular tube. The axial flow velocity inside the cyclone increases gradually along the course due to the influence of the water−retaining area of the guide vane and increases accordingly when the height of the guide vane increases.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Deng, A.; Chen, J.; Hu, H.; Zhang, G. Analysis of reservoir siltation in China. J. Hydraul. Eng. 2022, 53, 325–332. [Google Scholar]
- Cao, W.; Liu, C. Advance and prospect in research on reservoir sediment control and functional restoration. J. Hydraul. Eng. 2018, 49, 1079–1086. [Google Scholar]
- Liu, J.; Zhang, Z. Evaluation and countermeasure analysis of the impact of sedimentation in reservoir. Shaanxi Water Resour. 2018, 49, 1079–1086. [Google Scholar]
- Yan, Z.; Wang, Y.; Jiang, S. An Overview of Reservoir Siltation Control Techniques. In Proceedings of the Inaugural Meeting of the Professional Committee on Reservoir Sediment Treatment and Resource Utilization Technology of the Chinese Society of Dam Engineering; 2017; pp. 119–126. [Google Scholar]
- Parshall, R.L. Model and prototype studies of sand traps. Trans. Am. Soc. Civ. Eng. 1952, 117, 204–212. [Google Scholar] [CrossRef]
- Robinson, A.R. Vortex tube sand trap. Trans. Am. Soc. Civ. Eng. 1962, 127, 391–425. [Google Scholar] [CrossRef]
- Kreith, F.; Sonju, O.K. The decay of a turbulent swirl in a pipe. J. Fluid Mech. 1965, 22, 257–271. [Google Scholar] [CrossRef]
- Kitoh, O. Experimental study of turbulent swirling flow in a straight pipe. J. Fluid Mech. 1991, 225, 445–479. [Google Scholar] [CrossRef]
- Atkinson, E. Vortex-tube sediment extractors. I: Trapping efficiency. J. Hydraul. Eng. 1994, 120, 1110–1125. [Google Scholar] [CrossRef]
- Wang, Q. Experimental Study on Development of Secondary Flow and its Sediment Sluicing Effect. Yellow River 1987, 5, 12–17. [Google Scholar]
- Chen, Y.; Guo, T.; Gao, E. Mechanistic study of reservoir sediment removal by vortex flow pipes. Water Resour. Hydropower Eng. 1993, 53–56. [Google Scholar]
- Wang, S.; Rao, Y.; Zhang, L.; Ma, W.; Zhao, S. Research Situation and Progress on Flow Characteristics of Spiral Flow in Horizontal Pipe. J. Tai Yuan Univ. Technol. 2013, 44, 232–236. [Google Scholar]
- Wang, S.; Rao, Y.; Wu, Y.; Wang, B. Experimental Research on Gas-Liquid Two-Phase Spiral Flow in a Horizontal Pipe. J. Exp. Mech. 2013, 14, 77–86. [Google Scholar]
- Zhang, Y.; Zhang, Q.; Zhang, L. Experimental Study on Inlet Velocity Field of the Spiral Flow Desiltor. Pearl River 2019, 40, 111–115, 145. [Google Scholar]
- Xihuan, S.; Wenyan, W.; Pengling, W. Outlet cross-section velocity distribution and rotation efficiency of spiral pipe flow generator. J. Northwest AF Univ. 2000, 28, 37–41. [Google Scholar]
- Wu, P. Experimental Study on Energy Gradient of Sediment Transportation in Spiral Pipe Flow. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2002, 18, 60–63. [Google Scholar]
- Li, Y.; Sun, X.; Yan, Q. Experimental study on the characteristics of spiral flow in a local generator. J. Hydroelectr. Eng. 2011, 30, 72–77. [Google Scholar]
- Li, Y.; Gao, Y.; Jia, X.; Lu, Y.; Sun, X.; Zhang, X.; Li, J. Velocity characteristics of spiral flow in downstream section of guide vane cyclone. J. Drain. Irrig. Mach. Eng. 2020, 38, 807–813. [Google Scholar]
- Li, Y.; Zhang, T.; Li, F. Study on Hydraulic Characteristics of Hydrocyclones with Different Guide Vane Heights in Motion. J. Taiyuan Univ. Technol. 2020, 51, 706–711. [Google Scholar]
- Zhou, F.; Wang, C.; Qiu, X. Numerical Simulation of Flow around Standard Model of High-rise Building. Sci. Technol. Eng. 2022, 22, 5852–5859. [Google Scholar]





| Computational Models | Advantages | Disadvantages |
|---|---|---|
| Standard k-ε | Wide range of application, economic and reasonable, with high accuracy; its convergence and calculation accuracy can meet general engineering calculation requirements; suitable for design selection and parameter study. | Poor simulation of complex flows with high curvature and sharp changes in pressure gradients; deficiencies in the simulation of cyclonic and bypass flows. |
| RNG k-ε | Moderately complex flows, such as separation flows, secondary flows and cyclonic flows, can be simulated for complex shear flows involving fast strains and moderate vortices. | The strong cyclonic processes cannot be predicted due to the limitations of the vortex viscous homogeneity assumption. |
| Realisable k-ε | Similar to the RNG, the calculation is more accurate than the RNG and allows for better simulation of circular jets. | Strong cyclonic processes cannot be predicted due to the limitations of the vortex viscous homogeneity assumption. Turbulent eddy viscosity coefficients are strain rate dependent and therefore less efficient to calculate. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, S.; Li, Y.; Song, X.; Zhang, J. Study of the Internal Cyclonic Flow Characteristics of Cyclones with Different Guide Vane Heights. Water 2023, 15, 78. https://doi.org/10.3390/w15010078
Tao S, Li Y, Song X, Zhang J. Study of the Internal Cyclonic Flow Characteristics of Cyclones with Different Guide Vane Heights. Water. 2023; 15(1):78. https://doi.org/10.3390/w15010078
Chicago/Turabian StyleTao, Siyuan, Yongye Li, Xiaoteng Song, and Jiaxuan Zhang. 2023. "Study of the Internal Cyclonic Flow Characteristics of Cyclones with Different Guide Vane Heights" Water 15, no. 1: 78. https://doi.org/10.3390/w15010078





