1. Introduction
To mitigate the damage and losses caused by expected flooding following heavy rains, one of the most important steps is to use historical, albeit mostly very limited, data on extreme events to establish acceptable levels of protection [
1] (p. 26). The magnitudes of historical floods specific to a given area are being used for fitting a function-establishing connection between their return periods [
2] and return levels. The latter participates in designing drainage systems for stormwater to be carried [
3] in order to prevent or reduce the damage and losses in the area.
The return period is the inverse of the annual exceedance probability (AEP) of the event of a given magnitude and, unfortunately, is frequently confused with the period of years for which the exceedance probability of this event is considered [
4,
5,
6,
7,
8]. The importance of the correct understanding of this statistic is explained in great detail in [
4], mostly based on R. Vogel et al. [
9,
10]. The remarkable example of the true meaning of a 2% exceedance probability during a 50-year period is worth citing in this context as follows: “Earthquake engineers, for example, relate the strength of new buildings to ground shaking from the “maximum considered earthquake” in an area, which has a 2 percent chance of being exceeded in a 50-year period. That equates to 98 percent reliability that such an earthquake will not happen within the 50-year time frame (equivalent to protecting against an earthquake with a 2475-year average return period)” [
4].
Another example that is closer to our theme of extreme events in hydrology is brought in the following USGS document [
11]: “The 1-percent AEP flood has a 1-percent chance of occurring in any given year; however, during the span of a 30-year mortgage, a home in the 1-percent AEP (100-year) floodplain has a 26-percent chance of being flooded at least once during those 30 years! The value of 26 percent is based on probability theory that accounts for each of the 30 years having a 1-percent chance of flooding.”
A vivid example of the undesirable consequences of the misunderstood term “100-year flood” illustrates the urgent need for further clarifications as follows: “Fifteen years ago, after the Midwest was swamped with what was pronounced a “100-year” or even a “500-year” flood, some folks figured they would never again see such a disaster in their lifetime. Some even dropped their flood insurance. Big mistake. Now, with the region struck by a supposedly once-in-a-lifetime flood for the second time since 1993, some scientists and disaster officials say the use of terms like “100-year flood” should be re-evaluated because they are often misunderstood and can give the public a false sense of security” [
12]. Remarkably, that even in the guidelines referred to above, a “once in 25 years” term is used in lieu of an “annual exceedance probability” of 1:25 [
1] (p. 25).
We look forward to contributing to the correct understanding of extreme events statistics by the wider public in general and relevant policymakers in particular. In this paper, we consider periods of 50 and 100 years, over which the exceedance probabilities of extreme events have a special interest. This special interest is due to the widespread use of these durations as return periods, characterizing the intensity of extreme events both in building codes and in narratives in the media. Therefore, we see our task as clarifying the true meaning of the frequency of extreme events in periods equal to 50 and 100 years. We will label the exceedance probabilities in 50- and 100-year periods as P50y and P100y (respectively), to distinguish them from AEP (annual exceedance probability).
To illustrate, we use the data of an extreme event closely related to flooding-heavy precipitation. Digitized records of rainfall intensity from historical rain gauges (1938–2005) at 88 locations [
13] supplemented and continued by data from 85 automated weather stations [
14,
15] available from the Israel Meteorological Service help us illustrate the true value of
P50y and
P100y and their proposed uses as convenient measures for comparative analysis of the intensity of extreme events.
2. Methods
Let us recall the basics. The term “a 100-year flood” has been introduced in the 1960’s as a short name for a flood magnitude with a 1% annual probability to occur or be exceeded in any given year [
11]; in simpler words, annual exceedance probability (AEP)
p = 1%, or 0.0.1, or 1/100. The inverse of AEP is called return period, or recurrence interval,
T:
and expressed as a number of years. Thus, for
p = 1%,
T = 100 years. This number can be best understood as the average period between two adjacent events on an infinite time axis. To each return period corresponds a certain intensity (magnitude) called a “return level” or “return value”. The higher the intensity of an event the longer its return period.
Let us call the exceedance probability of an event with a given intensity for a given period of N years P[N]y, while at N = 1, P1y is AEP, or p.
To calculate P[N]y, it is necessary to add up all the probabilities that such an event will occur or will be exceeded in any year, or any 2 years, or any 3 years, and so on, for the given N-year period. This is a very burdensome path. Instead, the easiest way is to calculate an exceedance probability P[N]y as a complement to 1 of a non-exceedance probability over the same period, as shown next.
An annual non-exceedance probability
q is a complement of an annual exceedance probability
p to 1:
A non-exceedance probability
Q over an
N-year period,
Q[
N]y (or reliability [
2]) is the product of the annual non-exceedance probabilities
q, assuming that all annual maxima are independent and identically distributed (
i.i.d.):
where:
N is the length of the period, in years;
Q[N]y is the non-exceedance probability of the event over the N-year period;
q is the annual non-exceedance probability of the event;
p is the annual exceedance probability of the event;
T is the return period of the event, in years.
The exceedance probability
P[
N]y and non-exceedance probability
Q[
N]y for the same period of years
N are complementary to each other and add up to 1, just like
p and
q for one year (Formula (2)). Therefore:
with
P[
N]y × 100% for a percentage expression.
Now, let us derive the annual exceedance probability p and the return period T for the event with the required exceedance probability P[N]y over N years. Formulas (4b) and (4c) provide, correspondingly:
Surely, a simplest way for finding T is using Formula (5a) to obtain p and then calculating T as its inverse (Formula (1)).
3. Results
3.1. Examples of Calculating P[N]y as a Function of T and Vice Versa
In the examples below, we chose the cases, which are widely used, for example, in the urban planned drainage system design or in the insurance industry, when the mortgage period should be secured for the possible weather interventions [
2,
4,
6].
Example A. The exceedance probability over a 100-year period (
N = 100 years) for a 500-year event (
T = 500 years) is (with help of Formula (4c)):
Example B. A return period
T of an event with a required exceedance probability over 100 years,
P100y = 1%, or 0.01, is an inverse of an annual exceedance probability
p, which is (with help of Formula (5a)):
The return period
T is its inverse:
Example C. Let us require an exceedance probability of an extreme event to be 2% over a 50-year period:
P50y = 2%, or 0.02. The corresponding return period
T would be the following (with help of Formula (5b)):
Example D. To provide a 10% exceedance probability of an extreme event over a 100-year period (
P100y = 10%, or 0.1), a corresponding return period
T should be the following (with Formula (5b)):
3.2. Graphical Representation of Exceedance Probabilities over a Period of Years P[N]y
3.2.1. Exceedance Probabilities P[N]y as Functions of a Length of the Period of N Years
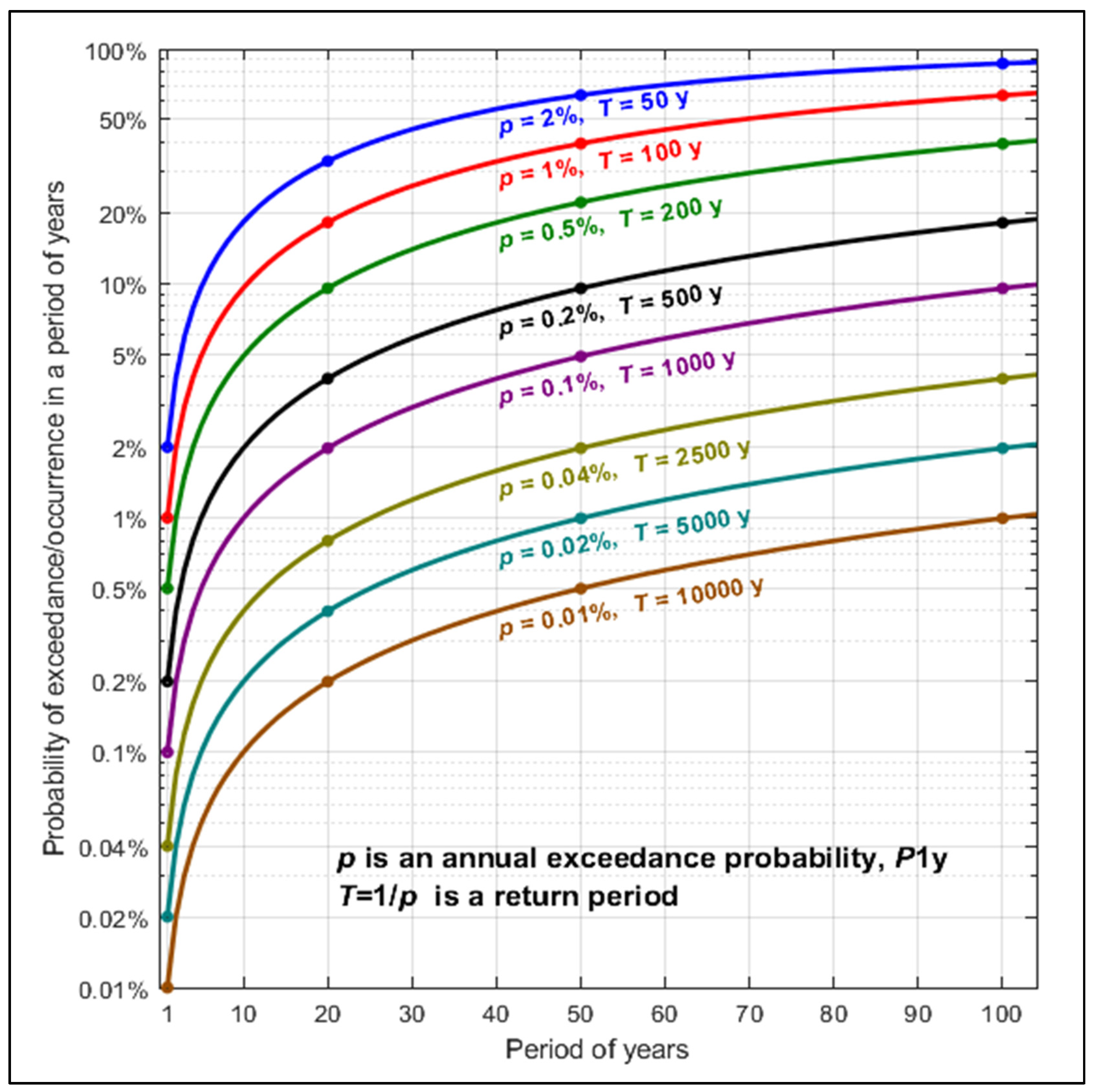
Figure 1 (designed with help of Formula (4c)) allows us to graphically derive the exceedance probabilities
P[
N]y over any period of
N years, up to
N = 100 years, for events with some specified return periods
T:
T = {50, 100, 200, 500, 1000, 2500, 5000, 10,000} years. For example, a 50-year event (
T = 50 years) has about a 63.6% chance to occur or be exceeded within a 50-year period: for
N = 50 years,
P50y ≈ 63.6%. A 100-year event (
T = 100 years) has a similar, slightly lower chance to occur or be exceeded for a 100-year period: for
N = 100 years,
P100y ≈ 63.4%.
3.2.2. The 50- and 100-year Exceedance Probabilities as Functions of a Return Period
The 50- and 100-year exceedance probabilities (
P50y and
P100y, respectively) will be applied in this paper as convenient statistics illustrating frequencies and intensities of extreme events. Therefore,
Figure 2 presents
P50y and
P100y (shown in
Figure 1 for a limited set of return periods) as continuous functions of a return period
T, up to
T = 10,000 years.
For example,
Figure 2 demonstrates that the events with return periods shorter than 20 years (
T < 20 years) have about a 100% chance to occur or be exceeded within a 100-year period and a higher than 90% chance to occur or be exceeded within a 50-year period.
Figure 2 allows a reader to graphically derive which return period should correspond to the return level of any structure in order to ensure its required reliability [
2], and vice versa, what reliability would correspond to a given return period. In part,
Figure 2 allows a reader to easily identify the numbers presented in the example [
2] (p. 78–1) as follows: given a 100-year extreme event, the reliability of the structure over its planned 50-year lifetime would only be 60.5% (which is much less than imaginable 99%), because, for
T = 100 years,
P50y = 39.5%.
Let us find with help of
Figure 2 the return period corresponding to the return level securing a 99% reliability for a 100-year lifetime period of some construction. The exceedance probability
P100y is as follows:
P100y = 100% − 99% = 1%. Thus, the return period must be about 10,000 years. This value was already calculated above (Example B in
Section 3.1).
3.3. Application
3.3.1. Study Area
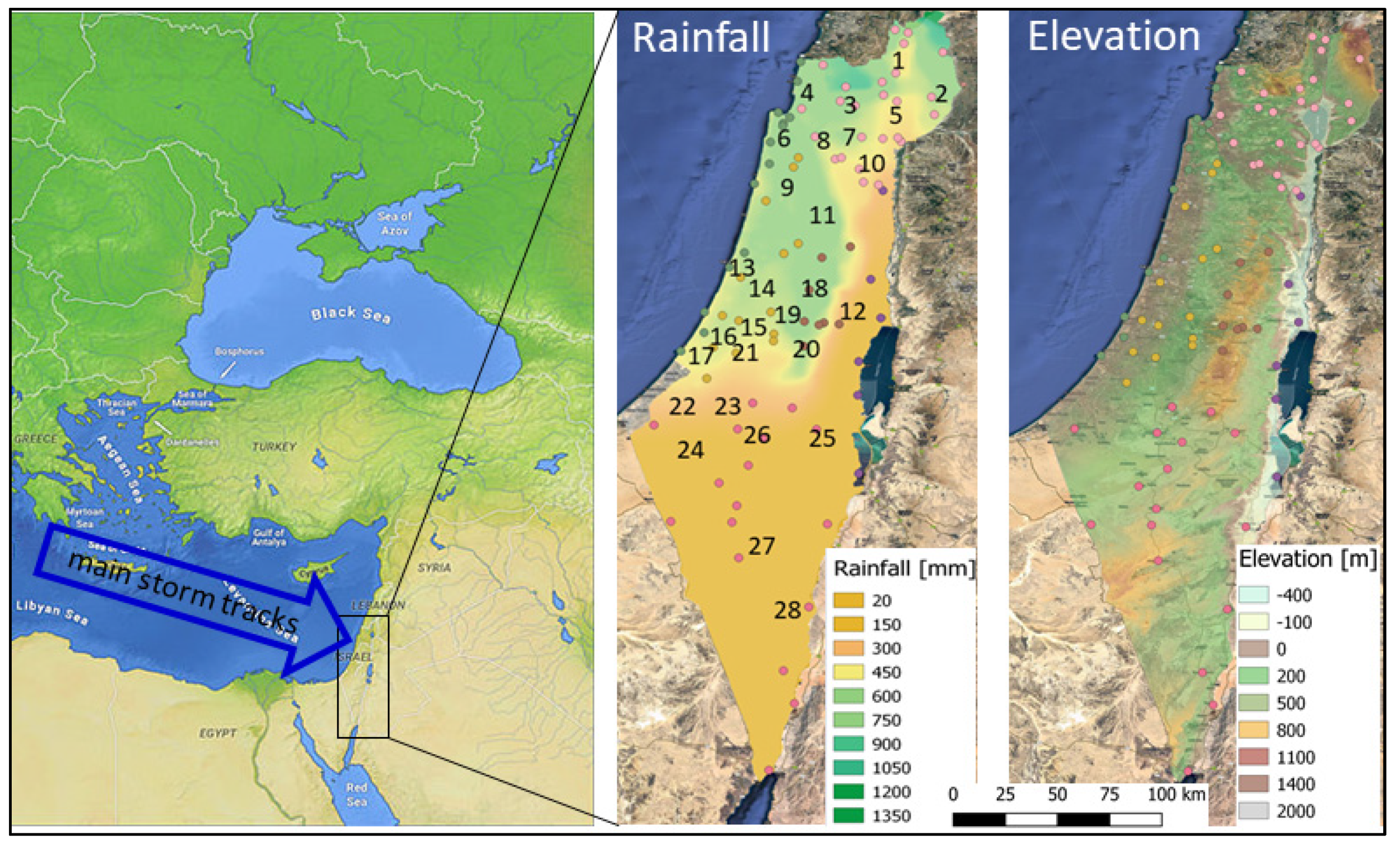
We will now demonstrate the application of
P50y and
P100y to the 10- to 120-min rainfall intensities, recorded at historical and automated weather stations in Israel. Israel is located in the southeastern Mediterranean and is ~400 km from north to south and a maximum of ~100 km from west to east (
Figure 3).
The topography of this small country is very diverse and includes the long coastal plain, mountain ridge, the Dead Sea Valley (with its lowest point at ~430 m below mean sea level), and the Negev desert in the south. The climate here is Mediterranean, which means hot and dry summers and mild and wet winters. Most of the precipitation is brought by westerly winds. Average annual rainfall totals range from 1350 mm (~53 inches) in the very north to 20 mm (<1 inch) in the very south.
3.3.2. Long-Term Series of Annual Maxima of Rainfall Intensities
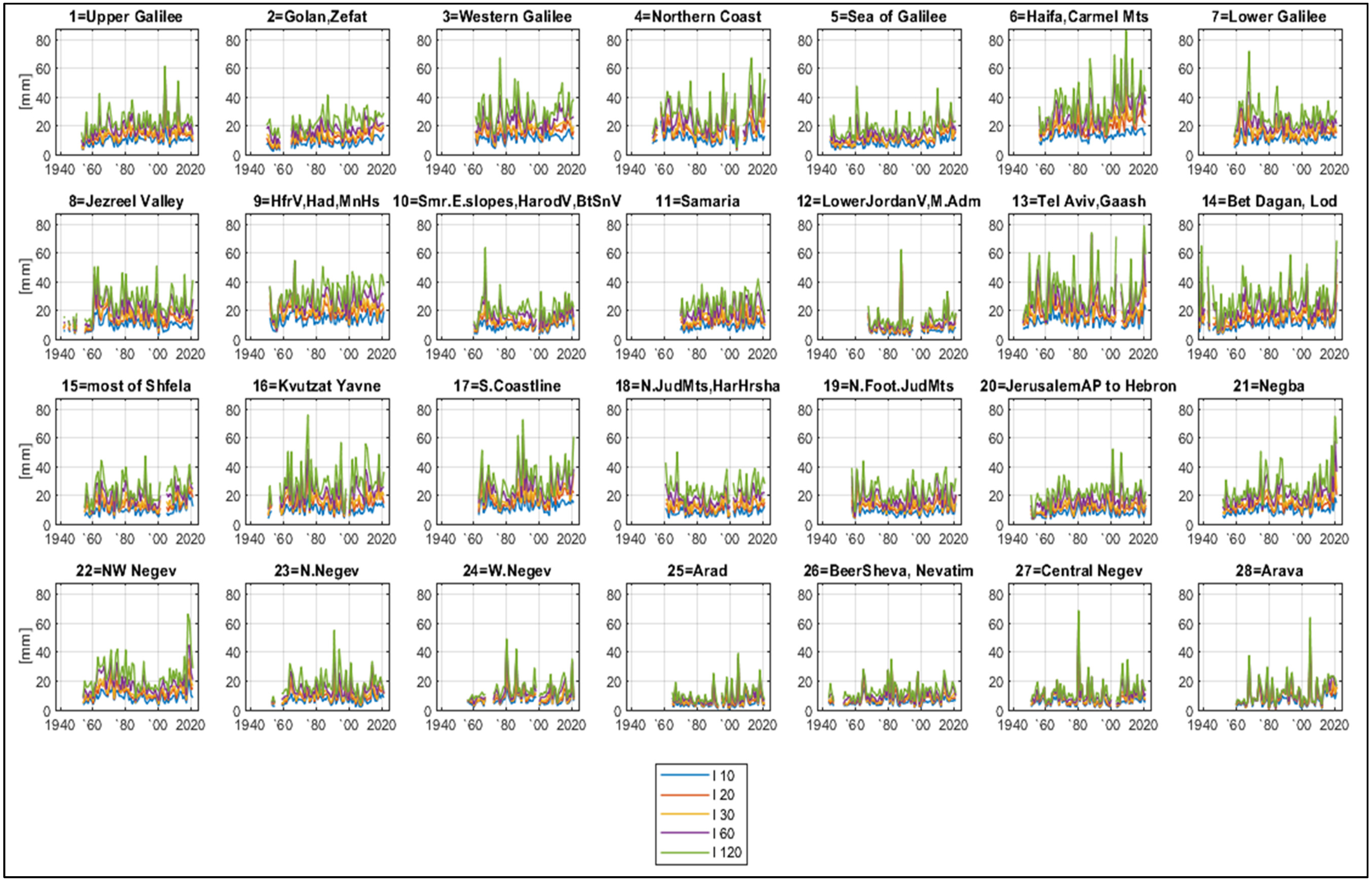
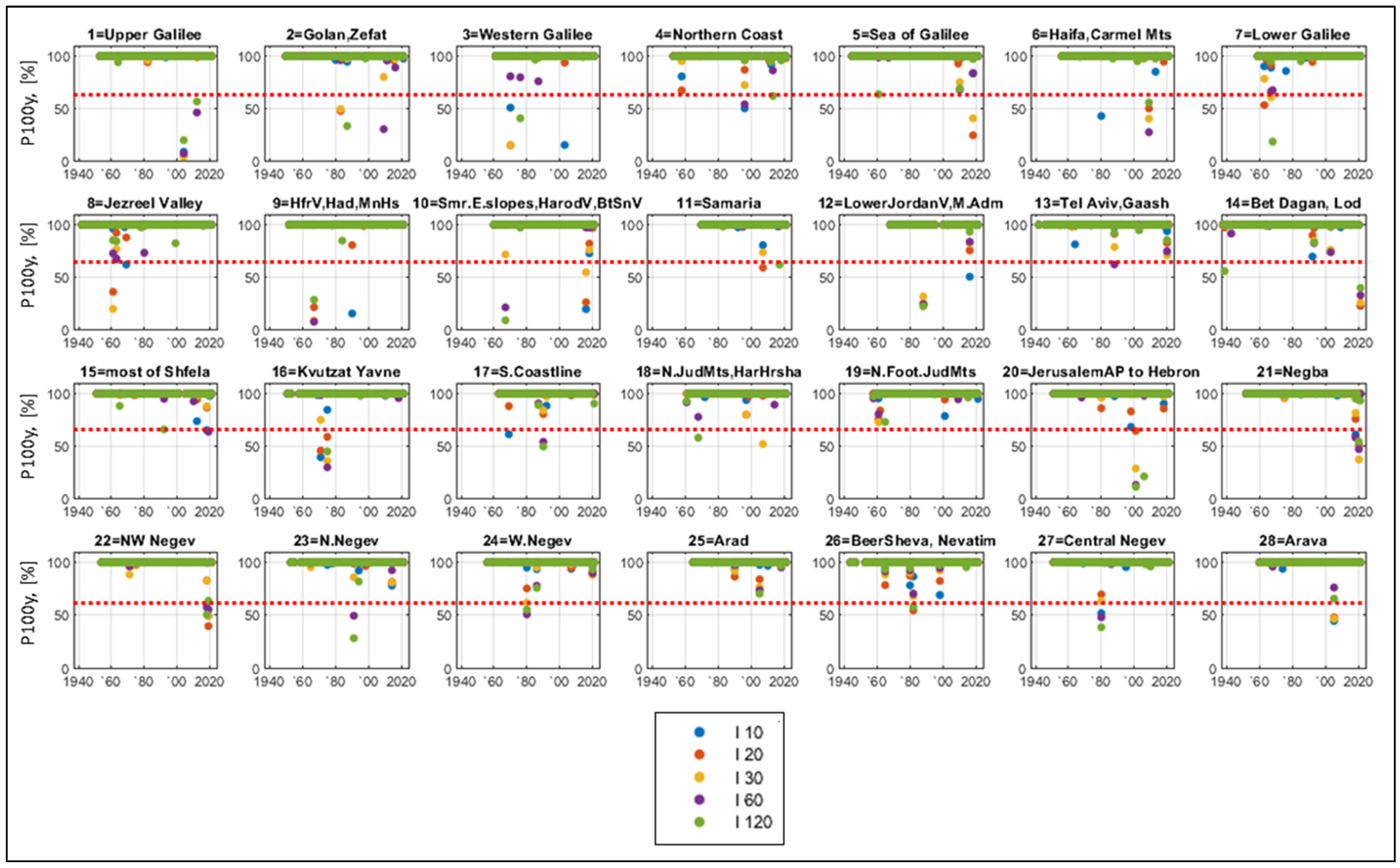
To compile long-term series of annual maxima of rainfall intensities (RI), shown in
Figure 4 for each of the 28 regions (
Figure 3) for the period 1938–2021, we used the following:
Historical data (HD): The long-term digitized records from the rainfall strip-charts of the 90+ historical stations (each record started in 1938 at the earliest and ended in 2005 at the latest) [
13];
Automated 1-min data (A1): The 1-min rainfall data (started sometimes in 2006 and mostly in 2009) calibrated for high intensities from the 80+ automated stations, up to 2021 [
14];
Automated 10-min data (A10): The 10-min rainfall data [
15], mostly for the short period from around 2006 to around 2008, to fill as much as possible the gap between HD and A1 (despite some underestimation of A10 due to coarser time resolution as compared to A1 and lack of calibration for high intensities).
These data records were clustered into 28 regions, according to close or similar (from the topo-climatic point of view) station locations. From the overlapping records, the highest RI was picked up. The obtained data series show no common trend. Therefore, overall, a general stationarity was assumed. This assumption will allow us to fit a stationary distribution to each long-term series.
Figure 4 shows that in coastal and coastal plain regions (regions 4, 6, 13, 14, 16, 17 in
Figure 3), the RI is the highest and have multiple peaks; in northern and central mountainous areas, the RI is lower; the eastern and southern semi-arid and arid regions typically have very low RI with occasional high annual peaks.
3.3.3. Estimating the Return Periods
In order to apply the 50- and 100-year exceedance probabilities to the long-term RI series, we first need to calculate their return periods
T. This was performed separately for each RI series, i.e., for each region (out of 28 regions) and for each interval (out of the following five intervals: 10, 20, 30, 60, and 120 min). The generalized extreme value (GEV) distribution parameters were estimated and tested (
Figure 5) and then applied as follows [
17]:
where:
F is the cumulative distribution function (CDF) of the GEV distribution;
x is the return value (return level). In our application, it is the rainfall intensity RI;
μ is a location parameter;
σ is a scale parameter;
k is a shape parameter.
Figure 5 shows GEV parameters estimated with the maximum likelihood estimation (MLE) method (assuming the independent identically distributed (
i.i.d.) annual maxima) and
p-values. The
p-values, evaluated with the Anderson–Darling goodness-of-fit test, show that all GEV distributions were fit well to the RI data.
High values of a shape parameter k indicate the heavy-tailed distributions; that is, the presence of outliers that we observed in semi-arid and arid regions. The high values of a location parameter μ describe rainy regions while the lowest—arid regions. For the latter, low values of a scale parameter σ indicate that most data are very close to their location parameter (regions numbered from 25 to 28).
For each RI, its return period
T was calculated with the estimated GEV parameters as follows:
where
F was found with Formula (6).
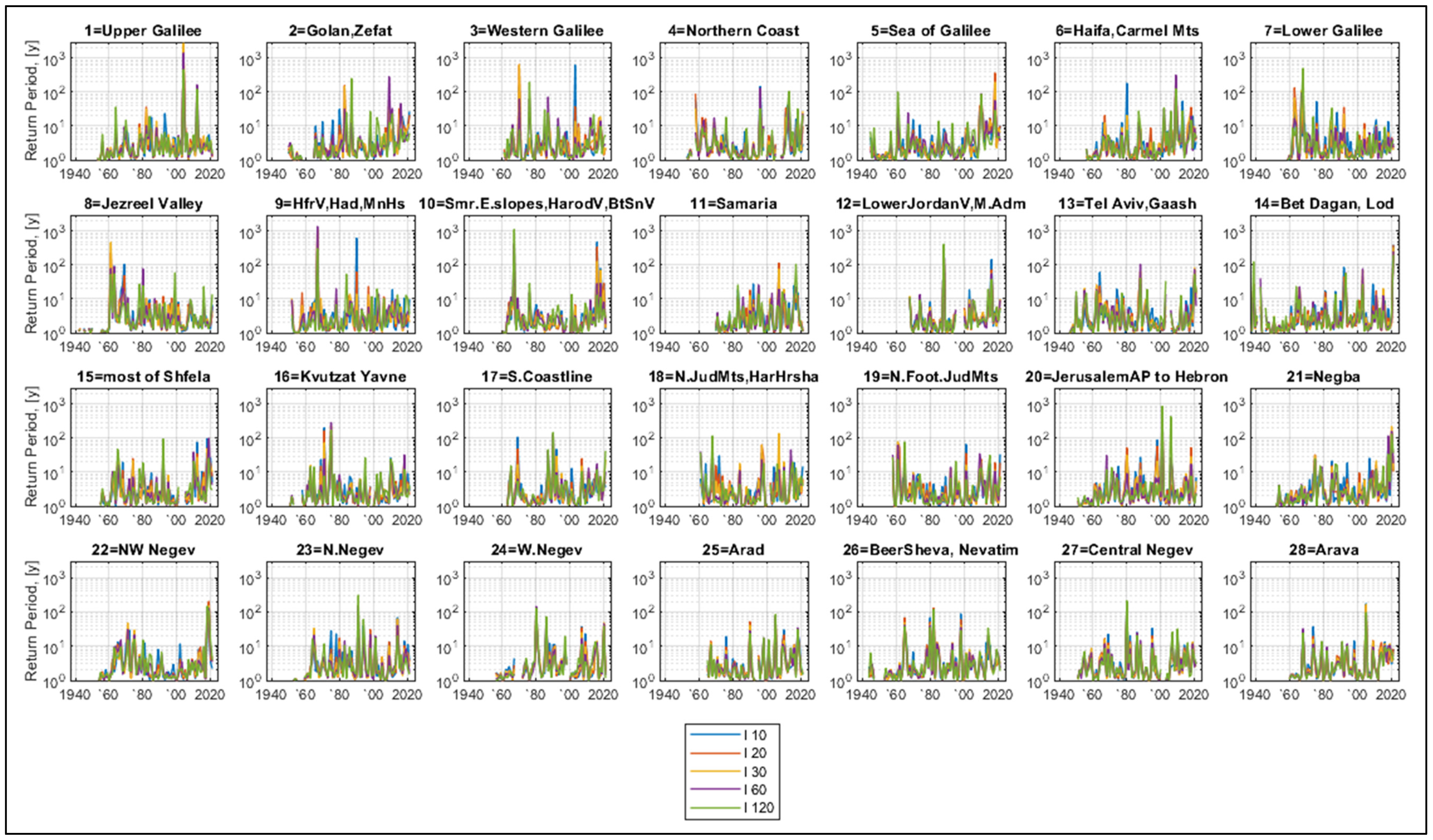
The long-term series of return periods for all RI annual maxima (
Figure 4) are shown in
Figure 6. It is worth mentioning that
Figure 6 resembles
Figure 4 and thus does not contribute much to a visual analysis.
3.3.4. The Exceedance Probabilities over 50- and 100-year Periods
Figure 7 shows the exceedance probabilities of the short-interval rainfall intensities in Israel for a period of 100 years. In most cases, they get stuck close to 100%, which indicates annual maxima with a low return period. In some years, 100-year probabilities are visually very small, which means the years with the most intense annual rainstorms, correspond to the longest return periods. As mentioned above, a 100-year probability of less than 63% corresponds to return periods longer than 100 years, which is longer than the observational period. We see that in most regions, such rainstorms occurred more than once. Moreover, in regions 1–3, 6, 7, 9–12,14, 16–18, and 20–22, they occurred twice and more, being separated by sometimes only a few years, while in region 22 they occurred two years in a row.
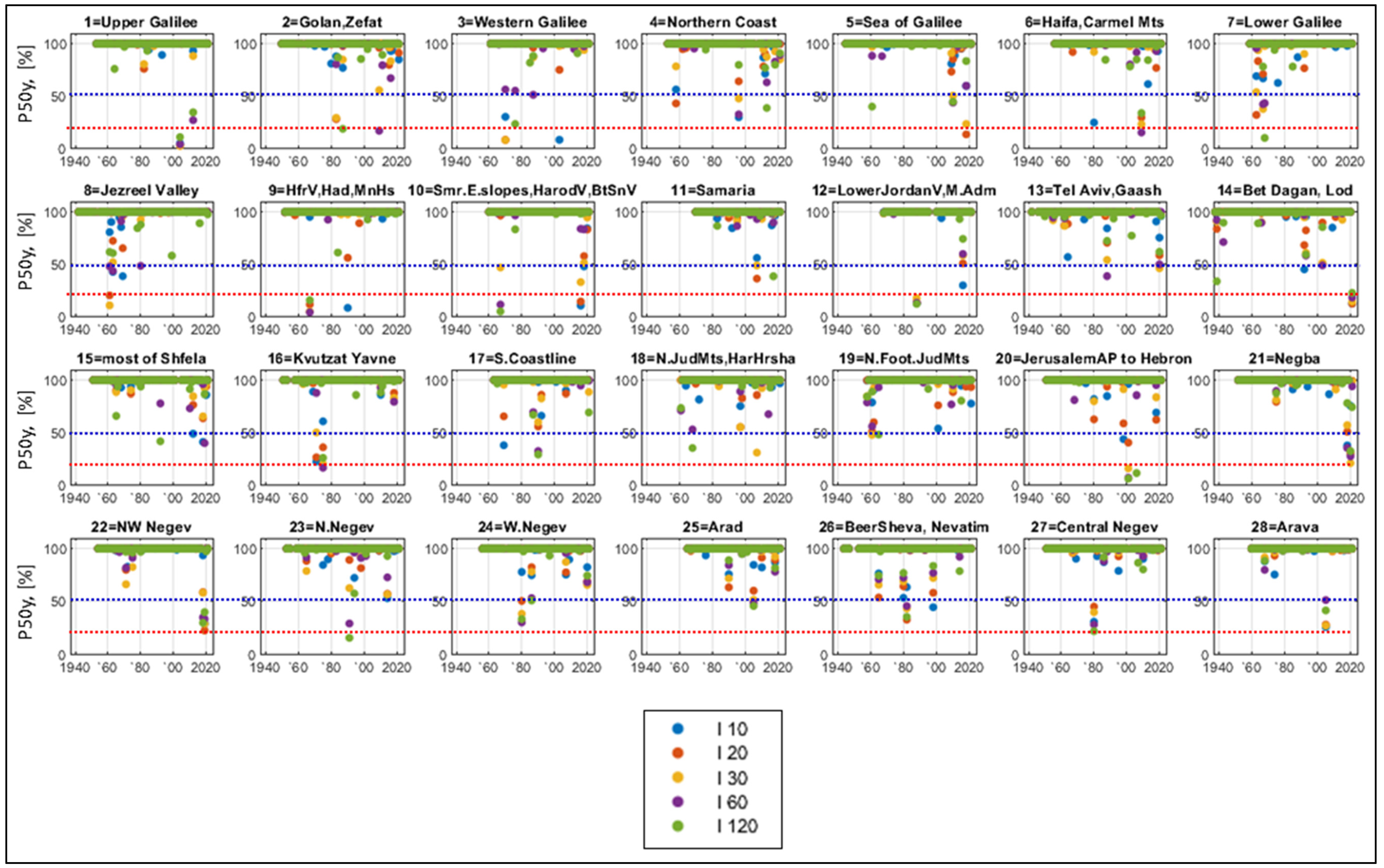
Now, consider the exceedance probabilities for 50 years,
P50y (
Figure 8). The
P50y values are lower than the
P100y, and therefore more convenient in visual analysis because they more clearly identify the years of the events with the highest short-interval rainfall intensities (i.e., the events with the longest return periods). The
P50y values below 50% (shown by blue lines in
Figure 8) correspond to the events with return periods longer than 72 years, which is longer than most of the observational periods. Nevertheless,
Figure 8 shows that in almost all regions (except the arid ones) such events were separated by a only few years. The
P50y values below 20% correspond to the events with return periods longer than 225 years. Still, they occurred in 12 out of 28 regions, while in regions 2, 3, 9, 10, and 20 they occurred even twice during the observational period.
4. Summary, Discussion and Conclusions
This work describes, in simple terms, the deriving and meaning of the exceedance probability of an event over a period of years. The main purpose of this paper is to show the difference between the annual exceedance probability and the exceedance probability over a period of years through the process of calculating both. While the annual exceedance probability is only valid for one year, the exceedance probability over a period of years is the sum of all the probabilities of occurrence or exceedance of an extreme event in any year or in any two years, etc. as detailed in the Methods section.
Since the number of these probabilities increases with increasing the period of years, the probability of an extreme event to be exceeded over a longer period also increases. Therefore, the reliability (which is the complement of the exceedance probability to 100%) of any construction decreases with the increase in the planned lifetime.
Regarding meteorological and hydrological phenomena, such as heavy rainfall, strong wind, deep floodings, etc., we propose to equip the engineers and policymakers with the 50- and 100-year exceedance probabilities. While in common use in the insurance industry, these terms need to be acknowledged by the wider public. Specifically, it is important in the urban drainage design codes, because each 2–3 years, coastal zones suffer from flood damages, which are still named “1-in-50-year” or “1-in-100-year” events. Drainage systems, constructed for return levels corresponding to the 50- and 100-year return periods, or to the 2% and 1% annual exceedance probabilities, are unable to carry out water volumes corresponding to the 2% and 1% exceedance probabilities over a period of years. Completing the usually misinterpreted “50-year return period” norm (meaning a ~64% probability within any period of 50 years) with the “P50y = 2%” norm (meaning the return level corresponding to the return period of about 2500 years) will secure a true 2% exceedance probability for any 50-year period.
The 50- and 100-year exceedance probabilities can serve as the statistics supplementary to the return periods, but are much more convenient for visual data analysis. This statement is illustrated in the present work with the long-term data of the rainfall intensity annual maxima. In most years, the P50y and P100y values are stuck close to 100% percent, and only in some years are distinguishably lower, indicating years with the most extreme events, that is, the events with the longest return periods.
Author Contributions
Conceptualization, I.O.-T. and E.F.; methodology, I.O.-T. and E.F.; software, I.O.-T. and E.F.; validation, I.O.-T. and E.F.; formal analysis, I.O.-T. and E.F.; data preparation, I.O.-T.; resources, E.F.; data curation, I.O.-T. and E.F.; writing—original draft preparation, I.O.-T.; writing—review and editing, E.F.; visualization, I.O.-T. and E.F.; supervision, E.F.; funding acquisition, E.F. All authors have read and agreed to the published version of the manuscript.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The IMS data used for the application of the 50- and 100-year exceedance probabilities, last accessed on 31 July 2021.
Acknowledgments
We thank the Israel Meteorological Service for providing the rainfall data.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- United Nations Department of Economic and Social Affairs. Guidelines for Reducing Flood Losses; United Nations: New York, NY, USA, 2002. [Google Scholar]
- Vogel, R.M.; Castellarin, A. Chapter 78: Risk, Reliability, and Return Periods and Hydrologic Design. In Handbook of Applied Hydrology, 2nd ed.; Singh, V.P., Ed.; McGraw-Hill Education: New York, NY, USA, 2016; pp. 78-1–78-10. [Google Scholar]
- NDS Water Management. How to Calculate Drainage. Available online: https://www.ndspro.com/PDFs/Tech-Spec-Guides/definitive-drainage-guide.pdf (accessed on 29 September 2022).
- Oleson, T. The ‘100-year flood’ fallacy: Return periods misleading in communication of flood risk. American Geosciences Institute Earth Magazine, 8 December 2014. [Google Scholar]
- United States Geological Survey. The 100-Year Flood. In USGS Water Science School online program; 7 June 2018. Available online: https://www.usgs.gov/special-topics/water-science-school/science/100-year-flood (accessed on 29 September 2022).
- Federal Emergency Management Agency. The 100 Year Flood Myth. Available online: https://training.fema.gov/hiedu/docs/hazrm/handout%203-5.pdf (accessed on 29 September 2022).
- Hillhouse, G. The 100-Year Flood Is Not What You Think It Is. Practical Engineering, 28 February 2016. [Google Scholar]
- Mace, R. A 100-year Flood Doesn’t Mean You Won't See One Again for 99 Years. The Conversation, 17 June 2021. [Google Scholar]
- Vogel, R.; Hecht, J.; Read, L. Nonstationary Approaches to Hydrologic Design. In Proceedings of the European Geosciences Union General Assembly 2014 (EGU2014), Vienna, Austria, 27 April–2 May 2014. [Google Scholar]
- Vogel, R.; Farmer, W.; Boehlert, B. Blunders and Bias in Flood and Drought Frequency Analysis. In Proceedings of the European Geosciences Union General Assembly 2014 (EGU2014), Vienna, Austria, 27 April–2 May 2014. [Google Scholar]
- Holmes, R.R., Jr.; Dinicola, K. 100-Year Flood—It’s All About Chance. USGS Gen. Inform. Product 2010, 106. Available online: https://pubs.usgs.gov/gip/106/pdf/100-year-flood-handout-042610.pdf (accessed on 29 September 2022).
- Experts: Term ‘100-Year’ Flood Misleads Public. NBC News. 1 July 2008. Available online: https://www.nbcnews.com/id/wbna25463476 (accessed on 29 September 2022).
- Israel Meteorological Service. Rainfall Intensities. Available online: https://ims.gov.il/he/node/293 (accessed on 31 July 2021).
- Israel Meteorological Service. 1-Minute Rain. Available online: https://data.gov.il/dataset/1minrain (accessed on 31 July 2021).
- Israel Meteorological Service. 10-Minute Data. Available online: https://ims.data.gov.il/ims/7 (accessed on 31 July 2021).
- Osetinsky-Tzidaki, I.; Fredj, E. The 50- and 100-yr Probabilities of Occurrence as the New and Convenient Measures for the Extreme Events Intensity: An Application to Extreme Precipitation in Israel. In Proceedings of the 102nd American Meteorological Society Annual Meeting (AMS102), Virtual, 23–27 January 2022. [Google Scholar]
- NASA Global Modeling and Assimilation Office. Generalized Extreme Value Distribution and Calculation of Return Value. Available online: https://gmao.gsfc.nasa.gov/research/subseasonal/atlas/GEV-RV-html/GEV-RV-description.html#:~:text=The%20return%20value%20is%20defined,%3D%201%2D1%2FT (accessed on 29 September 2022).
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).