1. Introduction
Authorities are increasingly implementing environmentally sustainable solutions in new and existing developments, and urban drainage systems are no exception. In this field, Sustainable Urban Drainage Systems (SUDS) have multiple advantages [
1]: they provide energy savings, they mitigate climate change by reducing greenhouse gases, they reduce the urban heat island effect, and they improve community livability by enhancing, among others, aesthetics, recreation possibilities, and biodiverse habitats. In addition, from the stormwater management point of view, SUDS reduce the volume and peak of generated runoff, being recognised as a sustainable strategy to mitigate floods in urban environments [
2,
3,
4,
5,
6,
7,
8].
However, both stormwater management and flood mitigation require efficient mathematical models in order to promote sustainable urban environments [
3]. However, the increasing number of hydrological model applications in urban environments, together with the greater sustainability challenges, makes it essential to go further in the hydrological processes present in urban areas; hence, these models need to be further explored in order to face existing and new challenges [
9].
Regarding stormwater network contribution, runoff is currently the main parameter to characterise the hydrological response of an urban plot [
10]. Hence, runoff simulation is a key component of the modelling process, together with the confluence process to the stormwater network. In that regard, hydrologic methods compute catchment runoff based on precipitation excess, with infiltration being the main process that creates precipitation losses. This infiltration can be computed based on several methods, although the relative efficiency of a particular method with respect to others cannot be determined in a definite manner [
11].
On the other hand, models integrating SUDS are becoming increasingly common, as they provide an analysis of SUDS’ impact at a catchment scale [
12]. These models have been extensively used as optimisation tools for different SUDS configurations, making them an extremely helpful decision resource to explore the hydraulic performance of several SUDS types, study their implementation, and check different setups [
3]. Yet, further research is recommended in order to improve modelling techniques for evaluating the performance of SUDS [
13].
Permeable Pavements (PP) are one of such SUDS and can be used in walkways, roads, playgrounds, or parking lots, among others [
14]. PPs are quite different from other SUDS types, as they ensure a hard surface while providing infiltration and detention capacity, thus reducing additional land requirement for detention facilities and being an alternative for impervious surfaces. This is especially important in urban areas with high land price and highly impervious sites with little or no space for stormwater detention [
15,
16]. Those implementation factors, together with their environmental benefits, have boosted its implementation [
17].
Currently, there are several computational models available to simulate the hydrodynamic behaviour of PPs [
14,
18], with some of them being integrated into wider urban drainage models [
19]. However, as mentioned previously, methods for calculating infiltration in a certain subcatchment are diverse. Moreover, with the implementation of PP models, infiltration can also be computed with the recent, in addition to the traditional, thus overlapping several infiltration methods in the same model. Hence, in a particular urban plot, a traditional method can be selected to compute infiltration, but in the adjoining plot or even in a particular area of the former plot, a PP model may be applied to compute infiltration.
This is a quite common practice in order to study how a certain PP implementation affects the runoff created in a certain urban area. Palla and Gnecco [
20] compared runoff peak/volume/delay in a
do nothing scenario with several
conversion scenarios where PPs were applied. Jato-Espino et al. [
21] tested the efficiency of PPs reducing the stormwater volume in the existing drainage system, for which actual/PP scenarios were defined. In addition, Lee et al. [
22] created before/after PP situations to check how different climate change scenarios affected to the runoff reduction rate of PPs.
The previous cases are just some examples of how PP efficiency is analysed with a model defining a hypothetical PP scenario. Nevertheless, to analyse the effect of PPs, the same catchment has to be modelled with two different methods, a traditional one, to test current conditions, and the PP model, to test the hypothetical or future scenario. However, can results obtained from different models be directly compared in order to draw certain conclusions? The authors consider that an equivalency or link between models shall be established in order to obtain robust conclusions.
For that purpose, it is common to compare the performance of several models and decide which one is the most suitable for a certain application. In those cases, conclusions are often based on field data. Wilcox et al. [
23] compared runoff prediction capabilities, without calibration, for the Soil Conservation Service Curve Number (SCS-CN) and Green–Ampt (GA) models in rural catchments based on real data from six catchments. They concluded that the SCS-CN model, although simpler, performs as well as more complex models. More recently, Ajmal et al. [
24] compared the SCS-CN model with a proposed nonlinear model based on one parameter. Proposed nonlinear models, overall, performed better than the SCS-CN model for studied watersheds. In addition, Hu et al. [
25] developed a new urban hydrological model that represents nonlinear rainfall–runoff relationships for different urban surfaces and compared it with two commonly used urban hydrological models: the Horton and SCS-CN models. The results showed that their proposed model outperformed the other two models in terms of total runoff and peak flow.
However, measured data are not the only way to produce relevant outcomes: infiltration models can also be compared on a theoretical basis. Zhang and Guo [
26] compared the runoff reduction performance of a certain area when infiltration was controlled by the PP model or by the GA model. They found inconsistent results for the PP model for low pavement heights, low drains, and large time steps, so they recommended using the GA method to model PPs. On the other hand, Baiamonte [
27] established, assuming constant rainfall intensity, an analytical link between SCS-CN and GA infiltration models, which allowed for an interoperability between both.
Despite its limitations, the SCS-CN method is a popular model compared to those traditional ones because it is simple, predictable, and stable and also because it relies on only one parameter that responds to major properties producing runoff in a watershed [
28]. On the other hand, the Storm Water Management Model (SWMM), which implements a PP model, is one of the most popular among researchers due to the diversity of hydrologic and hydraulic computation methods [
12]. For instance, the four examples mentioned previously that compared scenarios with and without PP, selected the CN method to control runoff for those subcatchments without PP and the PP model from SWMM to control runoff from PP scenarios. All four compare computed runoff in both subcatchments in order to reach some more general conclusions. However, there is not an obvious link between both models, and hence the comparison cannot be validated.
Consequently, this study explores, on a theoretical basis, the relation between the runoff computed by those two models, the SCS-CN and PP models defined in SWMM, in order to establish, if possible, an equivalency between them, which would be beneficial to derive more consistent outcomes in broader analysis related to the hydraulic benefits of PPs. As SCS-CN relies on one parameter, an equivalent parameter has been selected for the PP model based on a previous sensitivity analysis performed by the authors [
29]: pavement permeability. This parameter plays an equivalent role. It is a superficial parameter that controls inflow to the layers below and is also easy to relate and compare against rainfall intensity. More specifically, and from a practical point of view, urban planners, practitioners, and researchers will be able to compare PP implementation runoff scenarios computed on the same model, especially pervious/impervious, by just considering one single parameter, pavement permeability, as this parameter can be linked to a certain CN.
Accordingly, the specific objectives of the article are as follows: (a) explore, on a theoretical basis, the relation between CN and pavement permeability, in order to obtain equivalent runoff hydrographs; (b) analyse the influence of storm depth, pavement slope, catchment shape, and PP type on that relation; and (c) set the conditions in which PP can be used to model runoff equivalent to that modelled by a certain CN.
2. Materials and Methods
This section describes the methodology used in the steps followed during the research process: (1) define the general experimental design, (2) describe the CN method used as a baseline scenario, (3) describe the infiltration provided by both the CN method and the PP module in SWMM, (4) define the model used to obtain the data during the experimental design, and (5) define criteria to compare obtained hydrographs along with the calibration procedure to obtain pavement permeability values.
2.1. Experimental Design
As the objective of this study was to compare runoff created with two different models by linking one parameter from each model, namely, pavement permeability and CN, the study was designed to compute the hydrograph for a certain CN, used as a baseline, and, based on that hydrograph, calibrate the pavement permeability from the PP model. Hence, both models were linked by means of those two parameters: pavement permeability from the PP model and CN from the SCS-CN model. The selected tool to compare both models was SWMM. The model definitions and SWMM implementations are given in
Section 2.2 and
Section 2.3, while model setup used to compare both methods is given in
Section 2.4. The study was also designed to explore how storm depth, pavement slope, catchment shape, and PP type influence that relation.
In order to study the effect of the storm depth, a single design storm was selected, as it is common to rely on them for drainage infrastructure design purposes. Selected return periods were 2, 10, and 100 years, all three with a duration of 6 h [
30]. The selected method to define such a storm was the alternating block method [
31], based on previously defined IDF curves. Details of the selected IDF curves and defined storm depths are given in
Section 2.4.
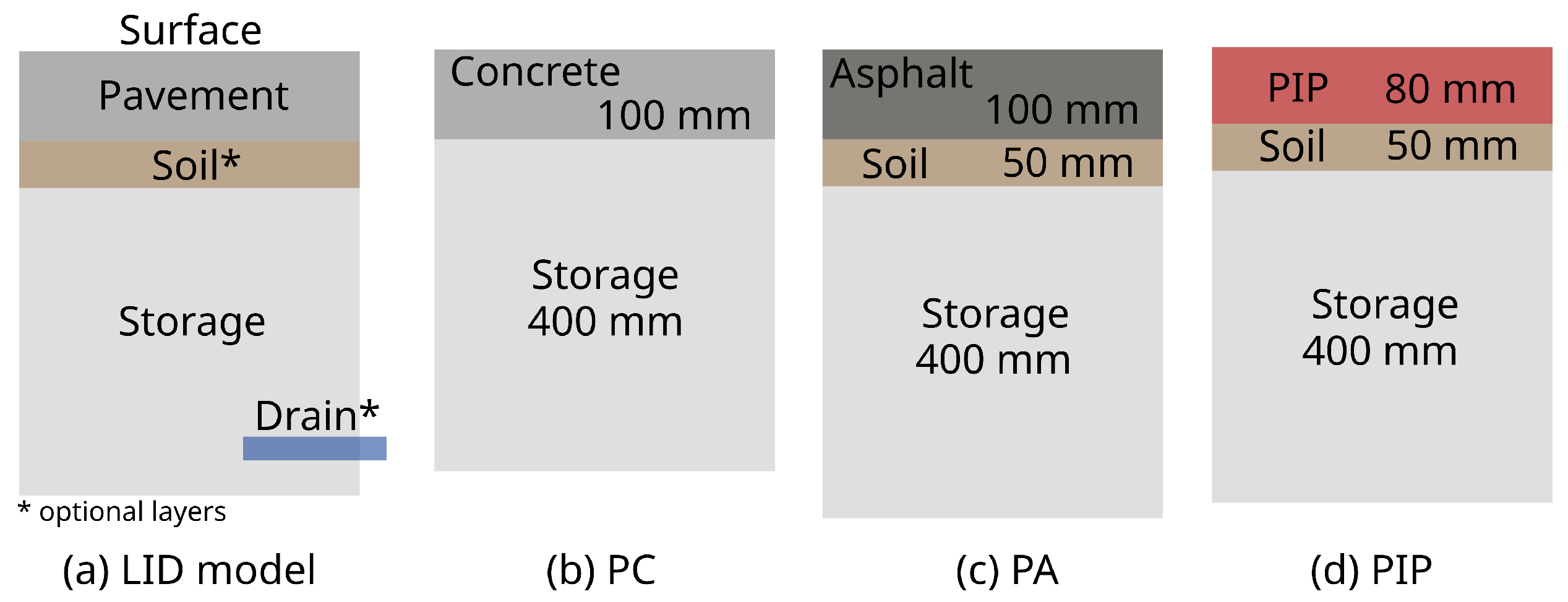
To study the effect of pavement type, three typical permeable cross-sections were selected (see
Figure 1): Permeable Concrete (PC), Permeable Asphalt (PA), and Permeable Interlocking Pavers (PIP). Although layer thickness may vary greatly depending on project conditions such as traffic loadings or subgrade bearing capacity, a common layout for urban conditions was defined based on a Spanish standard [
32], where 10 cm of asphalt was defined over 40 cm of aggregate. In addition, typical pavement and soil layer thicknesses were selected from the SUDS manual [
6]. With this approach, and based on the layout definition provided by SWMM (see
Figure 1a), a storage layer of 400 mm depth was defined for all three sections. All but PC were considered with a soil layer of 50 mm. Pavement layer was defined 100 mm thick for PC and PA, but 80 mm for PIP.
To analyse the slope effect, three slopes were selected from the typical range of PPs [
33,
34]: 1%, 2%, and 6%. As SUDS units are relatively small, the proposed area for the study was 100 m
2. However, three types of catchment were defined to check the effect of the catchment shape:
narrow,
squared, and
wide catchments. As the defined area was 100 m
2, shape defining widths were 1 m for the
narrow shape, 10 m for the
squared shape, and 100 m for the
wide shape.
To study the CN effect’s variation, a total of 12 CNs were selected between 40 and 100 for each previously mentioned case. In fact, 12 intervals were selected for that range, and to avoid overlapping points, each of the previous cases was given a random CN from that interval. Considering the three storm depths, three PP types, 3 shapes, 3 slopes, and 12 CNs, for a total of 972 points or relations between CN and pavement permeability, were obtained.
Based on those experimental variables, baseline runoff hydrographs with the SCS-CN method were generated, and their runoff hydrographs were computed. Afterwards, the PP hydrographs were calibrated and, thus, pavement permeability values were obtained. The correlation, obtained for a single event, will later be tested for a continuous event, using continuous 1-year data series.
Data analysis in this study was made with R [
35], an open source programming language. Data communication between R and SWMM was carried out with the
swmmr package [
36]. For model calibration, DE algorithm was used, implemented in the DEoptim package [
37].
2.2. Curve Number Method
The CN method from the Soil Conservation Service (SCS), currently the NRCS-CN method, was developed as a method of runoff computation designed for small agricultural watersheds. The method is included in
Section 4 of the National Engineering Handbook (NEH-4) published by the SCS, U.S. Department of Agriculture [
38]. At first, CN was developed from many experimental watersheds and is now extensively used to calculate direct runoff created by a precipitation event. In spite of being originally intended for agricultural sites, its applicability has also been extended to the urban environment [
39].
The SCS-CN method is based on two fundamental hypotheses and the water balance equation,
, where
P is total rainfall,
is initial abstraction,
F is actual infiltration, and
R is the amount of direct surface runoff. The first hypothesis assumes proportional equalities between direct runoff and potential runoff,
, and actual infiltration and maximum retention,
. The term
represents the effective rainfall or
, and
is the maximum potential losses to runoff in
or maximum potential difference between effective rainfall and runoff. If that hypothesis and water balance equation are combined, the widely used Equation (
1) for runoff (
R) computation is obtained, which is dimensionally homogeneous:
The second hypothesis assumes there is some initial abstraction in the beginning of the rainfall,
, and it is related to potential maximum retention,
, by the factor
. Thus,
. Despite the controversy around the value of
, the original method gives a median of 0.2 for
, as given in Equation (
2):
The value of
is transformed to CN by an identity, see Equation (
3), in order to have a soils/land/cover coefficient with a direct positive relationship to calculated
R. The underlying difference between
and CN is that the former is a dimensional quantity [L], whereas the latter is a non-dimensional quantity and varies conveniently from 0 to 100. Although CN theoretically varies from 0 to 100, values between 40 and 98 are practical design values validated by experience [
28]. The original expression gave
in inches; thus, in metric units, the formula for CN differs from the original [
40]:
Using the method requires selecting a CN from tables or experience, based on soils land use, hydrologic condition, and initial moisture status. The U.S. Forest Service developed CNs for forested lands, and SCS elaborated woodland runoff CNs. Moreover, CNs for urban lands were built by weighting representative CNs for impervious land types and open spaces in good condition. Current editions of NEH-4 contain a variety of CN tables and charts for an array of additional soils and land uses [
40].
2.3. Storm Water Management Model
SWMM is a dynamic rainfall–runoff simulation model used for single-event or long-term (continuous) simulation of runoff quantity and quality from primarily urban areas [
41]. Being a distributed model, SWMM divides a urban plot into several subcatchments. As urban areas usually contain a mix of land surfaces, subcatchments can be partitioned into two primary categories: pervious surfaces, allowing infiltration into the soil, and impervious surfaces, over which no infiltration occurs.
A third category can also be added, that corresponding to a SUDS, named Low-Impact Development (LID) control in SWMM, which can be globally defined in the model and, later, included into any subcatchment. It is also possible that the entire subcatchment is occupied by the LID control; in that case, there will not be any pervious or impervious surfaces. This article will just consider two types of surfaces: a pervious area and an LID area completely occupied by PP.
The runoff created in a subcatchment by a rainfall is estimated with a nonlinear reservoir model in SWMM, as shown in
Figure 2. Subcatchment inflows are runoff (
) from other subcatchments and precipitation (
i), but the first will not be considered here. Outflows are evaporation (
e), infiltration (
f), runoff (
q), and drain outflow (
). In
Figure 2,
d or
are water level elevations over the infiltration surface; they account for reservoir volume, and
or
indicate the minimum water level to produce runoff or outflow from the reservoir, respectively.
In order to compute runoff with the SCS-CN method, a standard pervious area was selected, as shown in
Figure 2a. The CN method is new to SWMM5 as an alternative to computing infiltration. The model implemented it because most practitioners were familiar with it, but also because there are several tabulated CNs available for numerous soil groups and land uses. The original CN method is a lumped loss method that combines interception, depression storage, and infiltration losses. The method calculates, for a rainfall event, the total rainfall excess. More details about its implementation in SWMM can be found in the hydrology manual [
41].
In order to compute runoff with the PP model, an area completely occupied by PP was selected, as shown in
Figure 2b. Conceptually, SWMM represents a generic LID unit via multiple horizontal layers, which later are integrated in order to create several LID control types [
42]. Specifically, PP is created by combining the following layers (
Figure 2): Surface, Pavement, Soil, Storage, and Drain. Two of those layers are optional, Soil and Drain. The model solves a simple mass balance equation for each layer in order to compute hydrological processes into the LID control. Those balances yield the water volume increase or decrease over time by computing the difference between the inflow water flux rate and outflow flux rate [
42]. More details about LID units in SWMM can be found in the user’s manual [
43].
As shown in
Figure 2, the LID model has some differences with a standard subcatchment in SWMM. As mentioned previously, a nonlinear reservoir model is also applied to the LID area, but with some differences. Firstly, we need to consider that inflows (precipitation) are equal in both subcatchments. Secondly, potential evaporation rates are computed in the climatological module of SWMM, and thus, it is equal to both. However, evaporation rates differ because LID areas usually have more water available, as layers below the surface are considered. Hence, the main difference between the two models lies in the infiltration, which is computed differently. That makes computed runoff differ in both areas, even if the evaporation rate remains equal.
The above shows how different computation in a LID area is compared to a pervious area. In the LID area, runoff generation potential relies not just on the native soil properties, but also on the PP layers and their characteristics. For this article, pavement permeability was the selected as the parameter to calibrate runoff, as it is a property of the upper layer and its values are easy to link to an inflow.
2.4. Model Setup
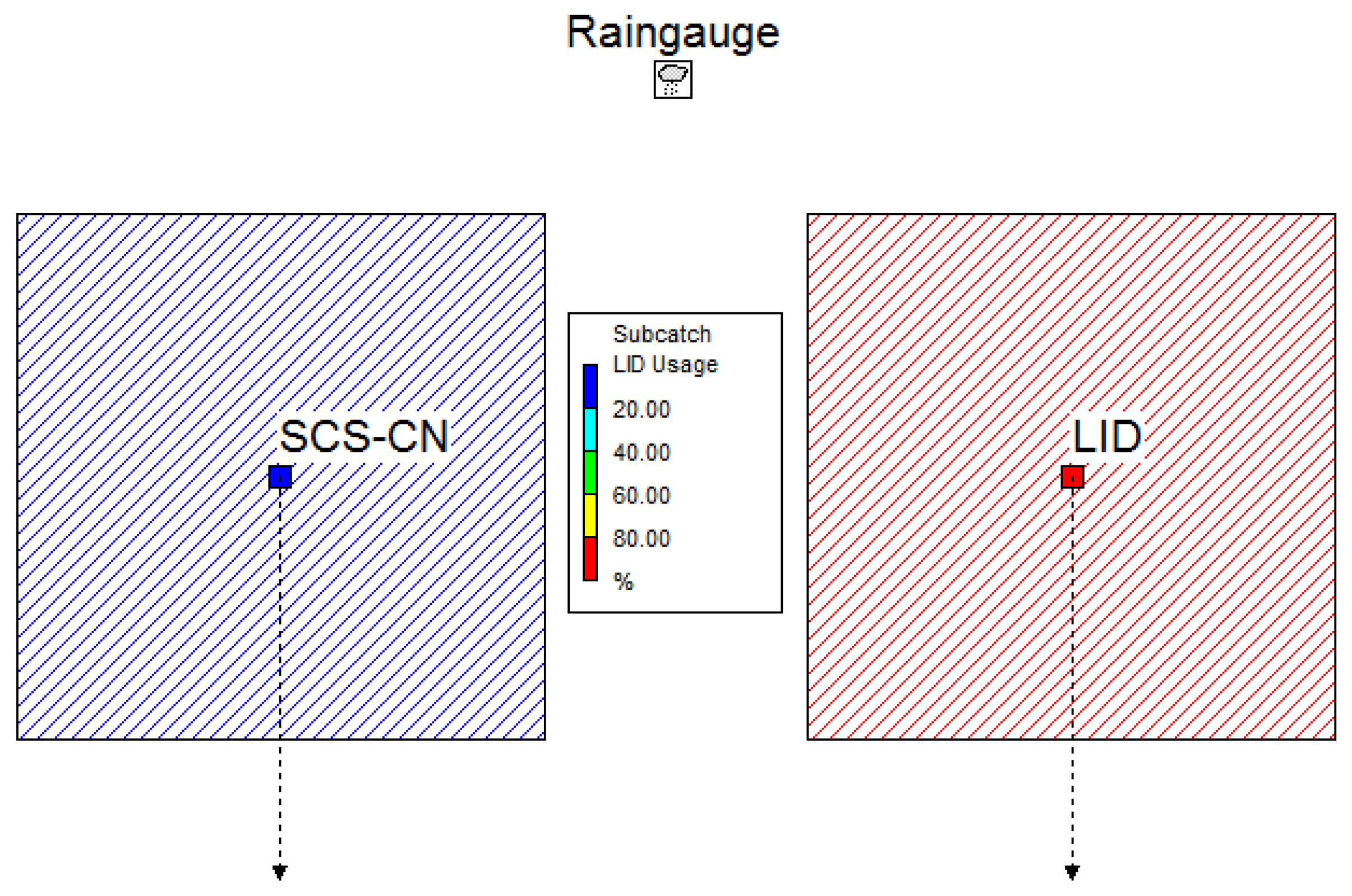
The model setup was designed to compare the performance, in terms of runoff creation capacity, of two different models: the SCS-CN model and the LID model for PPs. To measure and compare runoff hydrographs from two models, two equivalent catchments were created, as shown in
Figure 3. The SCS-CN catchment was defined with the general SWMM model and infiltration was calculated with the CN method. The LID catchment was defined as entirely occupied by PP.
SCS-CN catchment characteristics were defined in the catchment properties, while LID properties were set to zero, as they are overwritten by LID properties when modelled as an entirely LID occupied catchment. The used parameters are given in
Table 1. The Manning value for SCS-CN subcatchment was set to zero to avoid any delay in the runoff [
41]. Initial abstraction depth was fixed at 1 mm, based on previous studies for urban areas, taking the value for traditional pavements [
44].
Although a unique LID control type, PP, was studied, three typical cross-sections were analysed (see
Figure 1) to explore if there was any difference in the obtained permeability value. All three types were considered without any drain. Layer properties were identical for all three types, see
Table 2, but impervious surface fraction was 0.90 for PIP [
45]. For all parameters, standard values were used, taken from the SWMM manual [
46].
All three PP types were implemented identically into the LID subcatchment, as shown in
Table 3.
Climatological data for this study were gathered from the Igeldo weather station (43190 N, 200 W) and Miramon weather station (431720 N, 15816 W), both placed in Donostia/San Sebastián (Spain), which is located in the Bay of Biscay.
The first station was chosen because of its large historical data. In order to study the hydraulic response of the PP, a single event of a 6-hour duration was selected, with a volume of mm for a 100-year return period (named 6hT100), mm for a 10-year return period (named 6hT10), and mm for a 2-year return period (named 6hT2). Those events were obtained from IDF curves created based on Igeldo station data, used to generate a design storm with the alternating block method and considering 15 min time steps.
The second weather station, Miramon, was selected because it had 10 min interval temperature and precipitation data, best suited to perform a continuous or long-term analysis. Thus, in order to test results obtained with the previous single event, data from 2019 were gathered. Annual precipitation is
mm, with 206 dry days (minimum measured values was 0.1 mm). The average temperature for 2019 was 14.2 °C. The Hargreaves method [
47] was used to compute evaporation rates based on daily max–min temperatures and the latitude.
For the continuous event, computed time steps were 2:00 min for Wet Weather and 10:00 min for Dry Weather; the reporting time step was 10:00 min. For the single event, the time step for both cases was 1:00 min and the same as the reporting time step.
2.5. Hydrograph Performance and Calibration
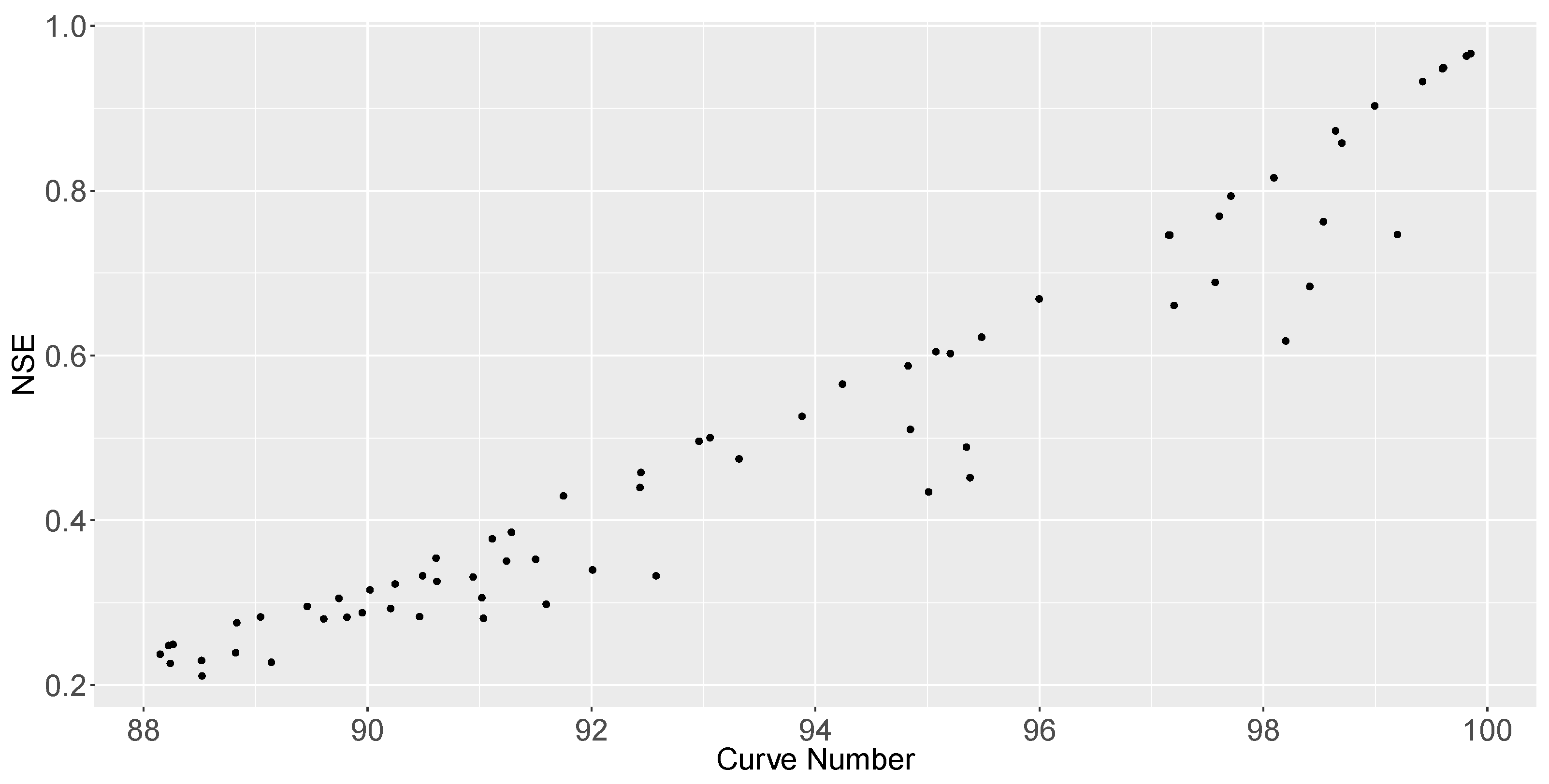
Calibration performance was checked by evaluating the Nash–Sutcliffe adimensional coefficient or NSE [
48], given by Equation (
4) below. Usually, observed and modelled data are compared but, as this research calibrated the parameters for LID to simulate the flows produced by SCS-CN and, therefore, both are modelled, the hydrograph from the SCS-CN area was considered as a baseline scenario and the hydrograph from the LID area as the scenario to be compared. Hence,
R is the observed runoff in SCS-CN area,
is its average, and
is LID area runoff. NSE values range from
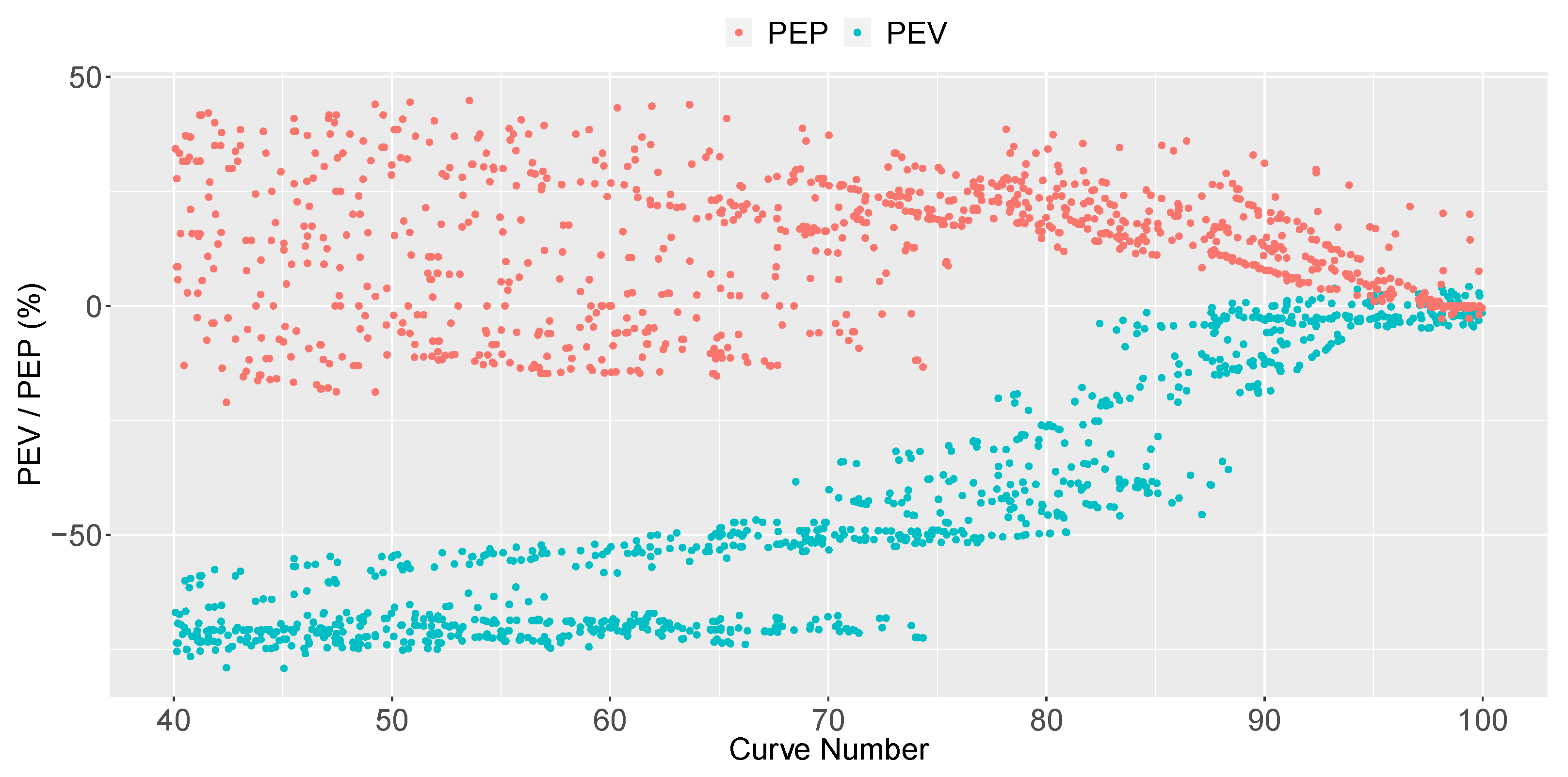
to 1, where a value equal to 1 indicates a perfect fit.
On the other hand, once the calibration parameter was fixed, the resulting runoff hydrographs from both areas were also compared to obtain more information. As it is common to study peak flow and volume for single events [
49], percent error in peak (PEP) and percent error in volume (PEV) were analysed, as shown in Equations (
5) and (
6), the
R values being from the SCS-CN subcatchment and the
L values from the LID subcatchment:
The calibrated parameter in this study was Pavement Permeability from the Pavement layer of the LID control. The objective function selected for calibration was the NSE defined in Equation (
4). For minima searching of the objective function, the Differential Evolution (DE) algorithm was applied, which is one type of meta-heuristic optimization technique based on function evaluation, successfully implemented in multiple areas, as it has prove to be a useful tool for global optimization [
50]. In addition, DE is particularly well-suited to find the global optimum of a real-valued function of real-valued parameters, and does not require that the function be either continuous or differentiable [
51]. In this study, lower and upper bounds of the parameter to be optimized were (0, 200), and the selected maximum number of iterations (population generation) was 20. These values were validated with a previous test.
4. Conclusions
This study compares the hydraulic performance of the PP model given in SWMM and the widespread CN model by linking one parameter from each model: pavement permeability from the first and CN from the latter. The comparison has been performed with SWMM, analysing the influence of several variables involved in the PP’s design: storm depth, pavement layout, catchment shape, and pavement slope. However, it should be noted that the research was not designed to test or compare the performance of any of the mentioned models separately; the aim of the research was to link both models numerically, based on a theoretical comparison.
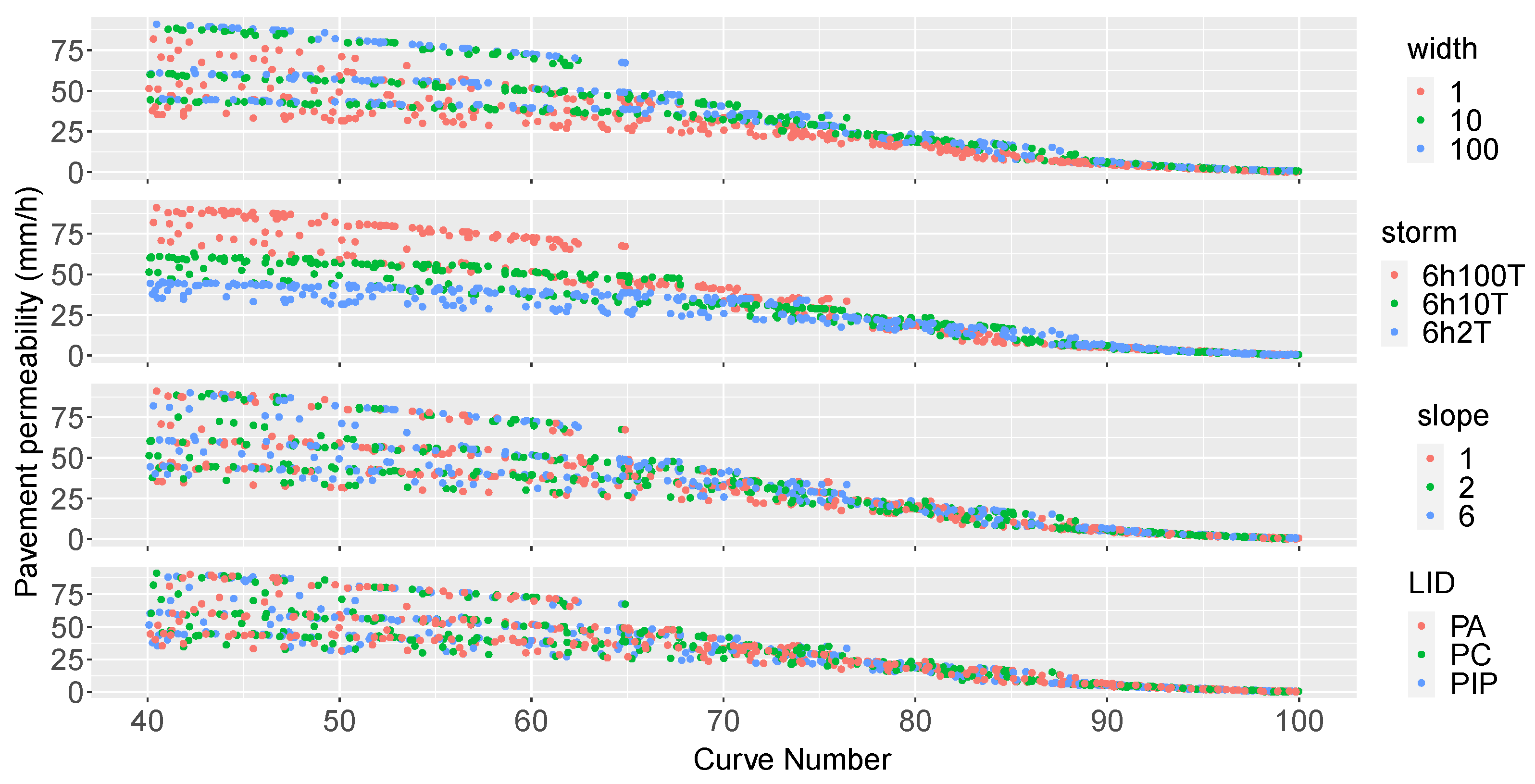
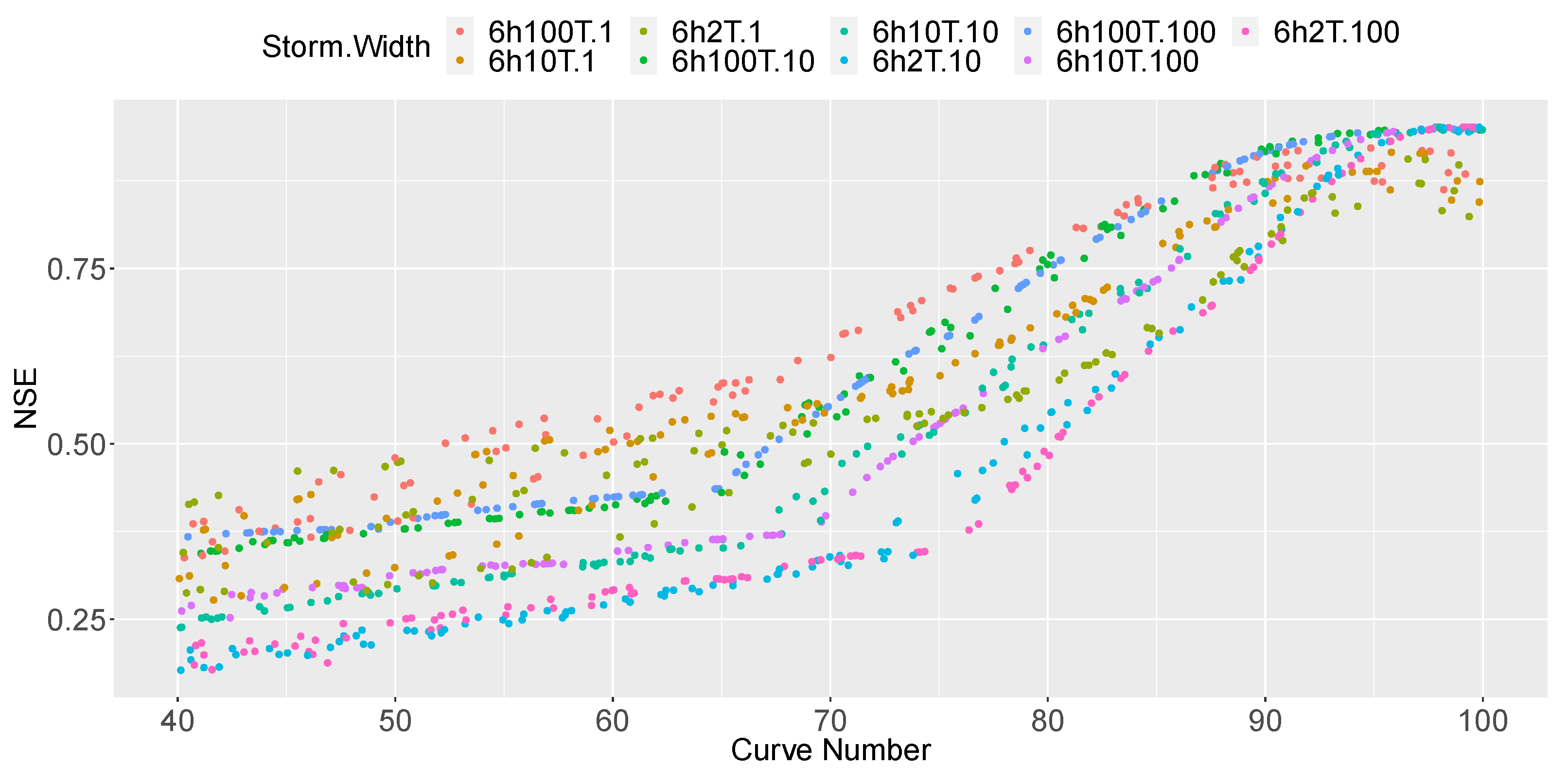
The article explores how different the models are and, thus, how the runoff modelled in each case differs from the other, as infiltration computations varies. Because of that disparity, the article demonstrates that we cannot consider an equivalence between the runoff hydrographs for pervious surfaces or low CNs. In addition, the article shows that catchment width and storm depth considerably influence the infiltration process, and thus the equivalency between models is significantly influenced by these variables. The article also shows that pavement slope and PP layout do not have impact on that equivalency.
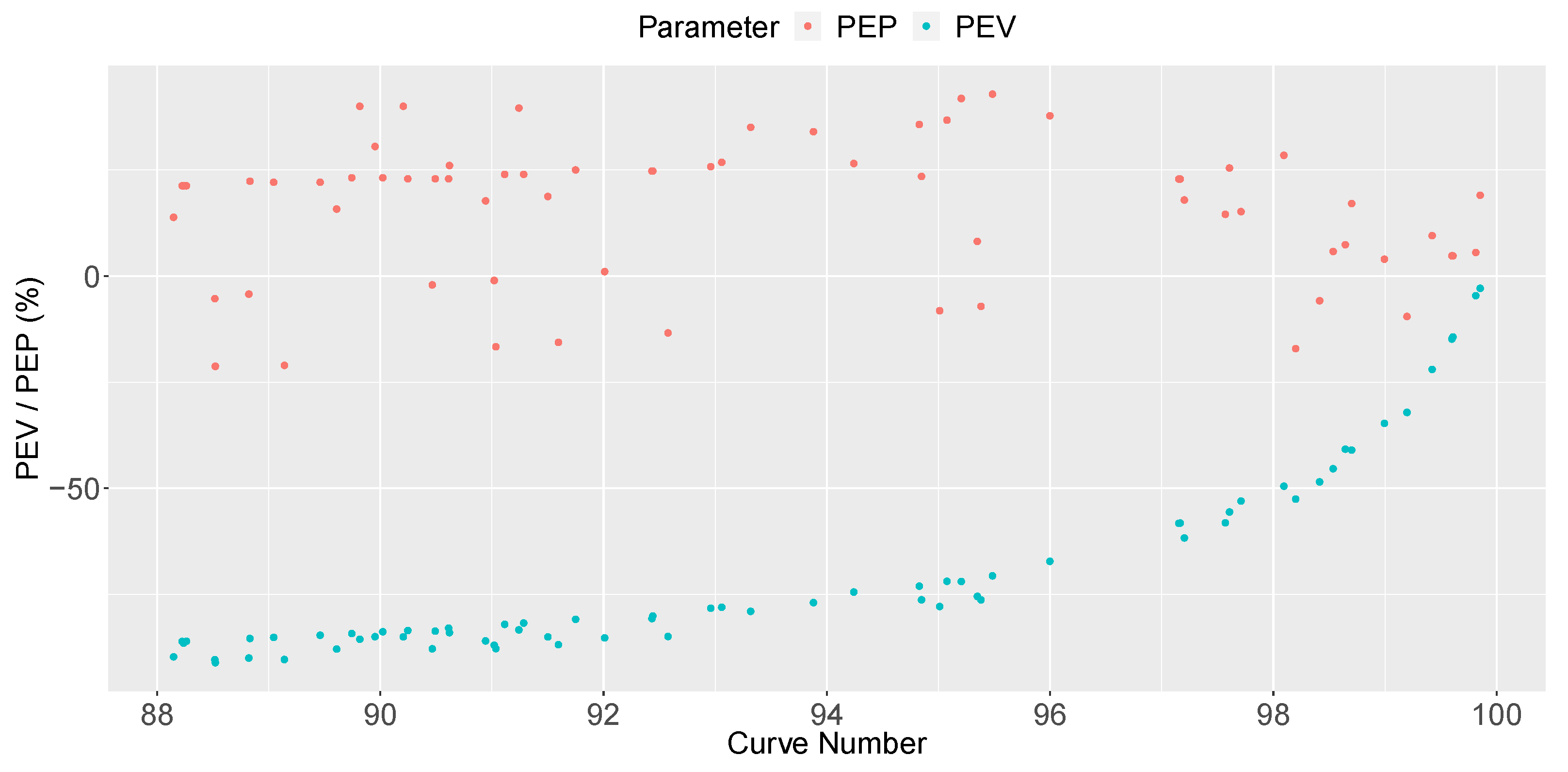
However, this study shows that it is possible to generate runoff hydrographs with the PP model given in SWMM equivalent to those created with the SCS-CN method in some cases. In fact, the article gives a relation between a certain CN and the pavement permeability that creates an equivalent runoff hydrograph: [mm/h] = . This relation would be valid for single events when CNs are higher than 88 and would not be influenced by the PP layout, catchment shape, storm depth, nor the pavement slope. Equivalent hydrographs would have an NSE higher than 0.60, and peak/volume performances would be in the range of .
This was the primary goal of the article: to find an equivalency for both methods. That relation can be useful, when modelling, to compare runoff created in a certain catchment with and without PP, that is, to analyse the influence of a particular PP design based on runoff data gathered with the same model, providing more robust conclusions in broader studies. Although the conducted analysis makes the relation valid just for the PP model definition given in SWMM, it may be useful for any other PP model, or even SUDS, where infiltration is controlled by a similar surface parameter equivalent to pavement permeability; however, further studies are required.
From a purely practical perspective, it would not be necessary to change the model to check those two scenarios, as PP could also serve as an impervious surface. In addition, PP layouts are defined once in SWMM and can be implemented in several catchments. Thus, it would be enough to change one unique parameter, namely pavement permeability, just once to change the catchment response: for example, from a completely impervious surface type to a catchment with a PP, no matter how many PPs are implemented in the model.
The article also shows that the mentioned equivalency is not valid if a continuous event is modelled. In that case, the PP is much worse at obtaining a hydrograph similar to that created by the SCS-CN. Hence, a continuous event shall not be modelled using the mentioned equivalency if it does not have a CN higher than 98. In this case, the selected test event yields NSE values higher than 0.60, peak errors lower than , and volume errors higher than . However, the above-mentioned benefits remain valid: the same model can be used to test PP implementation.
Further research is recommended for other LID types, where the permeable pavement parameter does not exist and surface permeability is controlled by other parameters. Thus, it would be interesting to further study what the relation would look like for other types of SUDS, as those are also studied when implementing SUDS in urban environments. It also would be interesting to investigate if LID control implementation in SWMM may become simpler, as many parameters need to be changed in order to modify a catchment completely occupied by an LID to another one with a different infiltration model. Further studies are also recommended to check the links between SUDS and other models, such as the Rational one, which is also common among practitioners.
In summary, the article compares two widespread models used in urban environments that simulate runoff hydrographs and specifies under which conditions equivalent hydrographs can be obtained. Consequently, the article is expected to be useful for practitioners analysing how the implementation of certain PPs affects the runoff created in one or several areas.