Uncertainty with Varying Subsurface Permeabilities Reduced Using Coupled Random Field and Extended Theory of Porous Media Contaminant Transport Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theory of Porous Media (TPM)
2.2. Extended Theory of Porous Media (eTPM)
2.2.1. Immiscible Constituents
2.2.2. Miscible Concentration
2.3. Field Equations and Constitutive Theory
2.4. Evaluation of the Entropy Inequality
2.5. Adaption of the Entropy Inequality
2.6. The Chemical Potential as a Free Helmholz Energy Function for a Contaminant
2.7. Stresses and Interaction Forces
2.8. Numerical Treatment
- Balance of momentum for the mixture
- Balance of mass for the mixture
- Balance of mass for the contaminant
2.9. Stabilized Boundary Conditions for Contaminant Transport
2.10. Random Field Method
2.11. Physical Sandbox Experiment
2.12. Field Scale Simulation
3. Results and Discussion
3.1. Validation with the Physical Sandbox Experiment
3.2. Transport of Contaminant in Groundwater through Three-Layer Heterogeneous Alluvial System
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BaRE | Bayesian recursive estimation |
| CI | confidence interval |
| eTPM | extended Theory of Porous Media |
| GLUE | Generalized likelihood uncertainty estimation |
| MCMC | Markov chain Monte Carlo |
| MSE | mean square error |
| RF | random fields |
| REV | representative elementary volume |
| TPM | Theory of Porous Media |
| TDS | total dissolved solids |
References
- Patil, S.; Chore, H. Contaminant transport through porous media: An overview of experimental and numerical studies. Adv. Environ. Res. 2014, 3, 45–69. [Google Scholar] [CrossRef] [Green Version]
- Seyedpour, S.; Kirmizakis, P.; Brennan, P.; Doherty, R.; Ricken, T. Optimal remediation design and simulation of groundwater flow coupled to contaminant transport using genetic algorithm and radial point collocation method (RPCM). Sci. Total. Environ. 2019, 669, 389–399. [Google Scholar] [CrossRef] [Green Version]
- Rosén, L.; Back, P.E.; Söderqvist, T.; Norrman, J.; Brinkhoff, P.; Norberg, T.; Volchko, Y.; Norin, M.; Bergknut, M.; Döberl, G. SCORE: A novel multi-criteria decision analysis approach to assessing the sustainability of contaminated land remediation. Sci. Total. Environ. 2015, 511, 621–638. [Google Scholar] [CrossRef]
- Wu, J.; Zeng, X. Review of the uncertainty analysis of groundwater numerical simulation. Chin. Sci. Bull. 2013, 58, 3044–3052. [Google Scholar] [CrossRef] [Green Version]
- Zadeh, L.A. Toward a generalized theory of uncertainty (GTU)—An outline. Inf. Sci. 2005, 172, 1–40. [Google Scholar] [CrossRef]
- Liu, P.; Shu, L. Uncertainty on numerical simulation of groundwater flow in the riverside well field. J. Jilin Univ. (Earth Sci. Ed.) 2008, 38, 639–643. [Google Scholar]
- Merz, B.; Thieken, A.H. Flood risk curves and uncertainty bounds. Nat. Hazards 2009, 51, 437–458. [Google Scholar] [CrossRef] [Green Version]
- Yang, P.; Yuan, D.; Yuan, W.; Kuang, Y.; Jia, P.; He, Q. Formations of groundwater hydrogeochemistry in a karst system during storm events as revealed by PCA. Chin. Sci. Bull. 2010, 55, 1412–1422. [Google Scholar] [CrossRef]
- Singh, A.; Mishra, S.; Ruskauff, G. Model averaging techniques for quantifying conceptual model uncertainty. Groundwater 2010, 48, 701–715. [Google Scholar] [CrossRef]
- Fiori, A.; Zarlenga, A.; Bellin, A.; Cvetkovic, V.; Dagan, G. Groundwater contaminant transport: Prediction under uncertainty, with application to the MADE transport experiment. Front. Environ. Sci. 2019, 7, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Prasad, K.L.; Rastogi, A. Estimating net aquifer recharge and zonal hydraulic conductivity values for Mahi Right Bank Canal project area, India by genetic algorithm. J. Hydrol. 2001, 243, 149–161. [Google Scholar] [CrossRef]
- Ehlers, W. Poröse Medien: Ein Kontinuumsmechanisches Modell auf der Basis der Mischungstheorie; Universität-GH Essen: Duisburg, Germany, 1989. [Google Scholar]
- Ehlers, W. Foundations of multiphasic and porous materials. In Porous Media; Springer: Berlin/Heidelberg, Germany, 2002; pp. 3–86. [Google Scholar]
- De Boer, R. Theory of Porous Media: Highlights in the Historical Development and Current State; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Ehlers, W.; Bluhm, J. Porous Media: Theory, Experiments and Numerical Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Ricken, T.; Schröder, J.; Bluhm, J.; Maike, S.; Bartel, F. Theoretical formulation and computational aspects of a two-scale homogenization scheme combining the TPM and FE2 method for poro-elastic fluid-saturated porous media. Int. J. Solids Struct. 2022, 241, 111412. [Google Scholar] [CrossRef]
- Bowen, R. Toward a thermodynamics and mechanics of mixtures. Arch. Ration. Mech. Anal. 1967, 24, 370–403. [Google Scholar] [CrossRef]
- Schmidt, A.; Henning, C.; Herbrandt, S.; Könke, C.; Ickstadt, K.; Ricken, T.; Lahmer, T. Numerical studies of earth structure assessment via the theory of porous media using fuzzy probability based random field material descriptions. GAMM-Mitteilungen 2019, 42, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Seyedpour, S.M.; Ricken, T. Modeling of contaminant migration in groundwater: A continuum mechanical approach using in the theory of porous media. PAMM 2016, 16, 487–488. [Google Scholar] [CrossRef]
- Seyedpour, S.; Janmaleki, M.; Henning, C.; Sanati-Nezhad, A.; Ricken, T. Contaminant transport in soil: A comparison of the Theory of Porous Media approach with the microfluidic visualisation. Sci. Total. Environ. 2019, 686, 1272–1281. [Google Scholar] [CrossRef]
- Huggi, V.; Rastogi, A. Estimation of solute transport parameters of groundwater systems using genetic algorithm. Water Energy Int. 2003, 60, 38–45. [Google Scholar]
- Hassan, A.E.; Bekhit, H.M.; Chapman, J.B. Uncertainty assessment of a stochastic groundwater flow model using GLUE analysis. J. Hydrol. 2008, 362, 89–109. [Google Scholar] [CrossRef]
- Tsai, F.T.; Li, X. Inverse groundwater modeling for hydraulic conductivity estimation using Bayesian model averaging and variance window. Water Resour. Res. 2008, 44, 1–15. [Google Scholar] [CrossRef]
- Rackwitz, R. Reviewing probabilistic soils modelling. Comput. Geotech. 2000, 26, 199–223. [Google Scholar] [CrossRef]
- Geyer, S.; Papaioannou, I.; Graham-Brady, L.; Straub, D. The spatial averaging method for non-homogeneous random fields with application to reliability analysis. Eng. Struct. 2022, 253, 1–14. [Google Scholar] [CrossRef]
- Vanmarcke, E.H. Probabilistic modeling of soil profiles. J. Geotech. Eng. Div. 1977, 103, 1227–1246. [Google Scholar] [CrossRef]
- Henning, C.; Ricken, T. Polymorphic uncertainty quantification for stability analysis of fluid saturated soil and earth structures. PAMM 2017, 17, 59–62. [Google Scholar] [CrossRef] [Green Version]
- Henning, C.; Herbrandt, S.; Ickstadt, K.; Ricken, T. Combining Finite Elements and Random Fields to Quantify Uncertainty in a Multi-phase Structural Analysis. PAMM 2018, 18, 1–4. [Google Scholar] [CrossRef]
- Fiori, A. On the influence of local dispersion in solute transport through formations with evolving scales of heterogeneity. Water Resour. Res. 2001, 37, 235–242. [Google Scholar] [CrossRef]
- Suciu, N. Spatially inhomogeneous transition probabilities as memory effects for diffusion in statistically homogeneous random velocity fields. Phys. Rev. E 2010, 81, 1–8. [Google Scholar] [CrossRef]
- Biot, M.A. General theory of three-dimensional consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Ricken, T.; Bluhm, J. Evolutional growth and remodeling in multiphase living tissue. Comput. Mater. Sci. 2009, 45, 806–811. [Google Scholar] [CrossRef]
- Ricken, T.; Sindern, A.; Bluhm, J.; Widmann, R.; Denecke, M.; Gehrke, T.; Schmidt, T.C. Concentration driven phase transitions in multiphase porous media with application to methane oxidation in landfill cover layers. ZAMM-J. Appl. Math. Mech. Angew. Math. Mech. 2014, 94, 609–622. [Google Scholar] [CrossRef]
- Ricken, T.; Thom, A.; Gehrke, T.; Denecke, M.; Widmann, R.; Schulte, M.; Schmidt, T.C. Biological Driven Phase Transitions in Fully or Partly Saturated Porous Media. In Views on Microstructures in Granular Materials; Springer: Berlin/Heidelberg, Germany, 2020; pp. 157–183. [Google Scholar]
- Ricken, T.; Dahmen, U.; Dirsch, O. A biphasic model for sinusoidal liver perfusion remodeling after outflow obstruction. Biomech. Model. Mechanobiol. 2010, 9, 435–450. [Google Scholar] [CrossRef]
- Thom, A.; Ricken, T. In Silico Modeling of Coupled Physical-Biogeochemical (P-BGC) Processes in Antarctic Sea Ice. PAMM 2021, 20, 1–3. [Google Scholar] [CrossRef]
- Ricken, T.; Werner, D.; Holzhütter, H.; König, M.; Dahmen, U.; Dirsch, O. Modeling function–perfusion behavior in liver lobules including tissue, blood, glucose, lactate and glycogen by use of a coupled two-scale PDE–ODE approach. Biomech. Model. Mechanobiol. 2015, 14, 515–536. [Google Scholar] [CrossRef] [PubMed]
- Job, G.; Herrmann, F. Chemical potential—A quantity in search of recognition. Eur. J. Phys. 2006, 27, 353–371. [Google Scholar] [CrossRef] [Green Version]
- Seyedpour, S. Simulation of Contaminant Transport in Groundwater: From Pore-Scale to Large-Scale; Shaker Verlag: Herzogenrath, Germany, 2021. [Google Scholar]
- Werner, D. Two Scale Multi-Component and Multi-Phase Model for the Numerical Simulation of Biological Growth Processes in Saturated Porous Medi—At the Example of Fatty Liver in Human; Shaker Verlag: Herzogenrath, Germany, 2017. [Google Scholar]
- Vanmarcke, E. Random Fields: Analysis and Synthesis; World Scientific: Singapore, 2010. [Google Scholar]
- Schlather, M.; Malinowski, A.; Oesting, M.; Boecker, D.; Strokorb, K.; Engelke, S.; Martini, J.; Ballani, F.; Moreva, O.; Menck, P.J.; et al. Random-Fields: Simulation and Analysis of Random Fields. R package version 3.1.4. 2015.
- Seyedpour, S.; Valizadeh, I.; Kirmizakis, P.; Doherty, R.; Ricken, T. Optimization of the Groundwater Remediation Process Using a Coupled Genetic Algorithm-Finite Difference Method. Water 2021, 13, 1–18. [Google Scholar] [CrossRef]
- Sreekanth, J.; Datta, B. Comparing hydraulic conductivity through both inverted auger hole and constant head methods. Water Resour. Manag. 2014, 28, 1573–1650. [Google Scholar]
- Henning, C.; Ricken, T. Polymorphic Uncertainty Quantification of Computational Soil and Earth Structure Simulations via the Variational Sensitivity Analysis. PAMM 2019, 19, 1–2. [Google Scholar] [CrossRef]



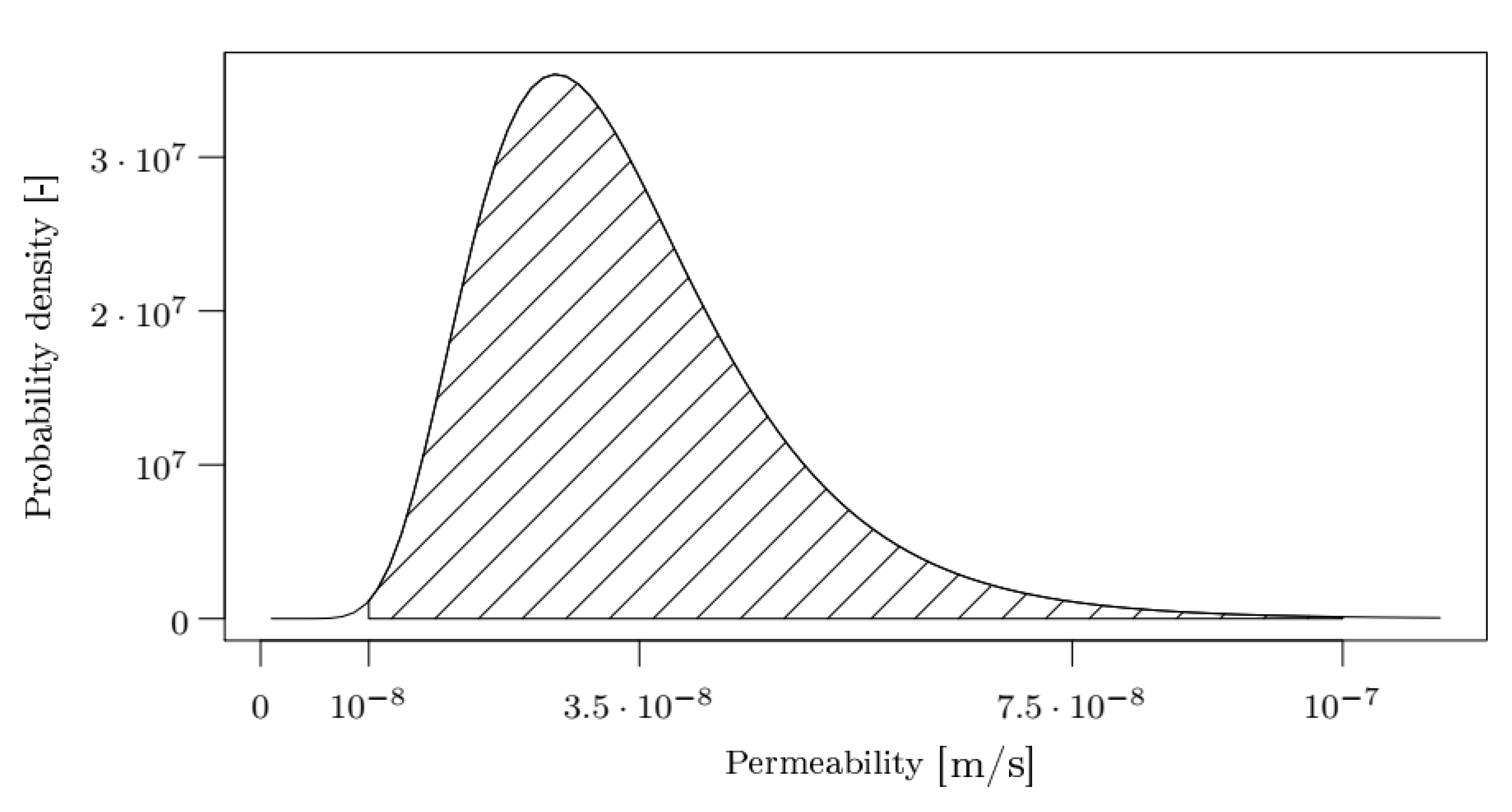
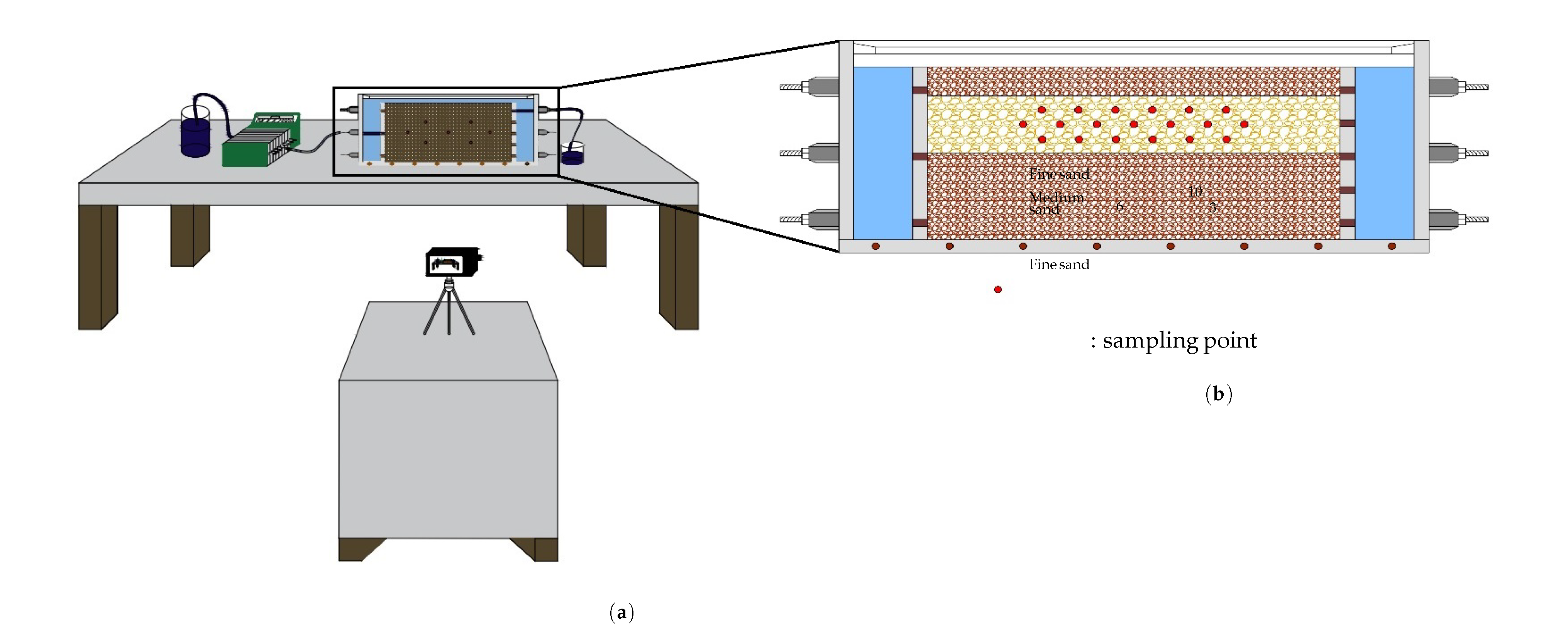



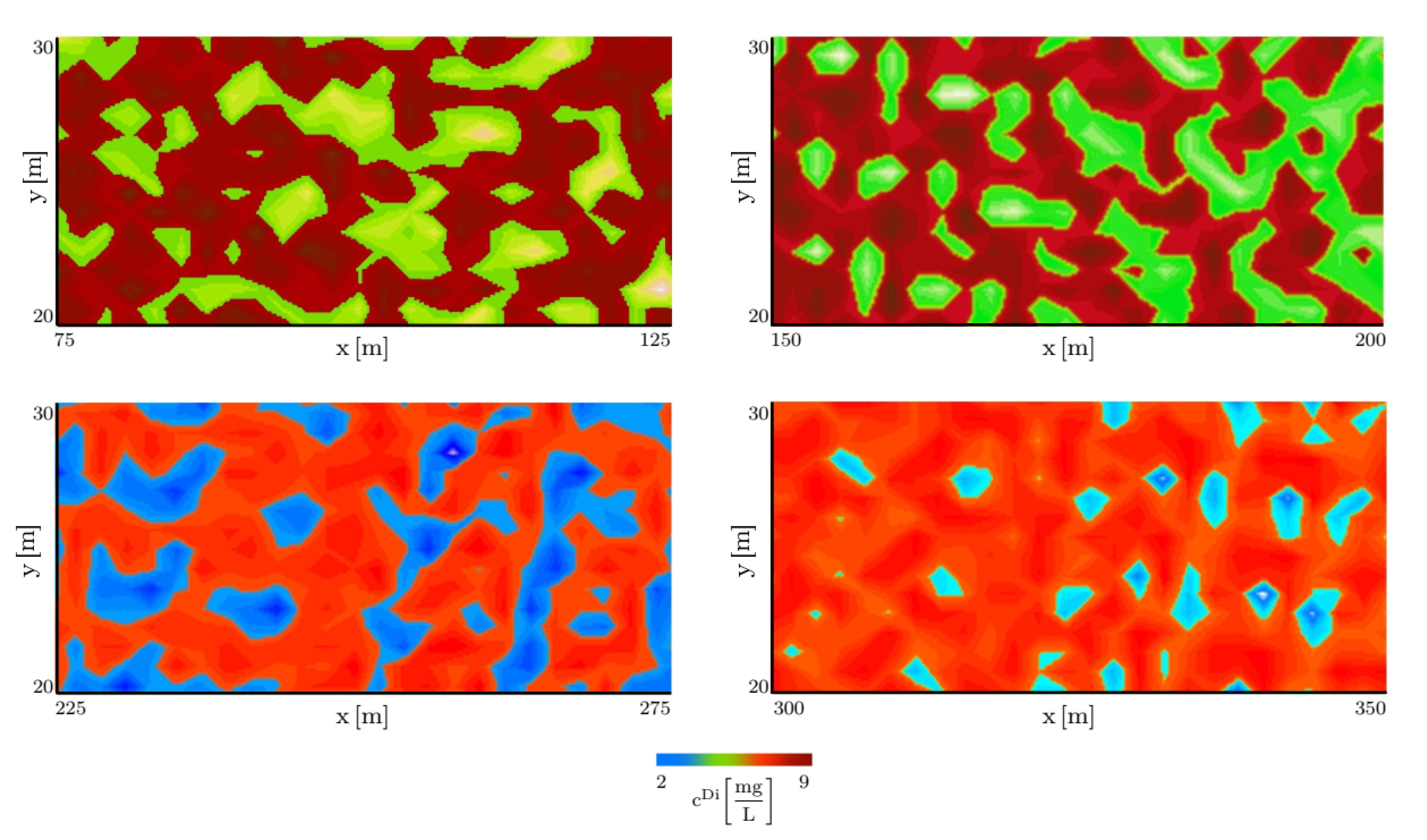

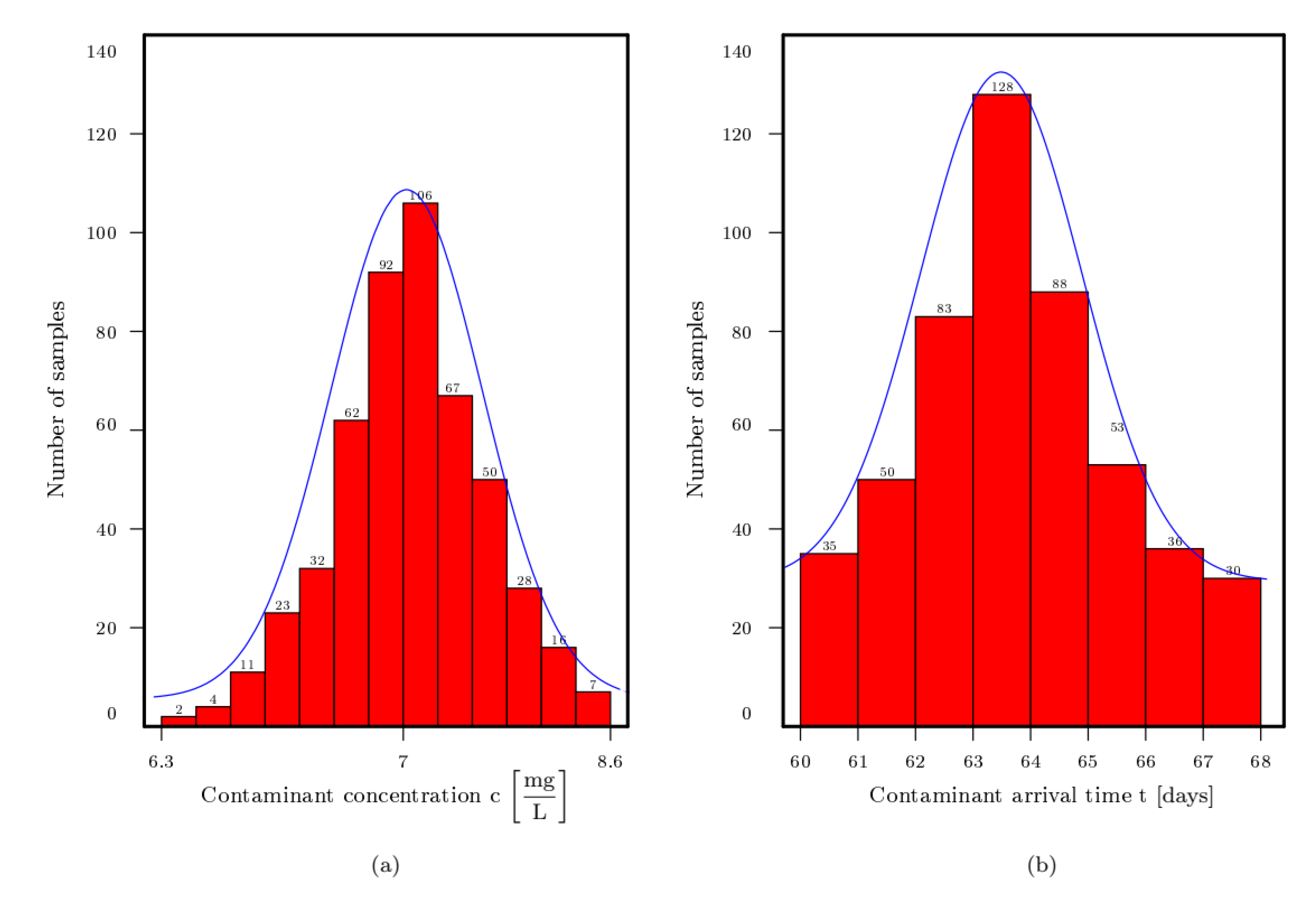
| Soil Layer | Height | Value Interval | |||
|---|---|---|---|---|---|
| 3 | 15 | 8 | |||
| 2 | 20 | 8 | |||
| 1 | 15 | 8 |
| Size (mm) | Hydraulic Conductivity (m/sec) | Porosity (%) | Hydraulic Gradient (-) | |
|---|---|---|---|---|
| Sand | 0.075–0.5 | 21 | −0.0003 | |
| High permeability Sand | 0.5–2.36 | 43 | −0.0005 |
| Parameter | Simulation | Physical Sandbox |
|---|---|---|
| Number of layers | 3 | 3 |
| Height of layers (m) | 50 | 50 |
| Permeability (m/sec) | – | – |
| Grain size distribution (mm) | - | 0.075–2.36 |
| Porosity (%) | - | 21–43 |
| Flow rate (lt/h) | 16 | 16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seyedpour, S.M.; Henning, C.; Kirmizakis, P.; Herbrandt, S.; Ickstadt, K.; Doherty, R.; Ricken, T. Uncertainty with Varying Subsurface Permeabilities Reduced Using Coupled Random Field and Extended Theory of Porous Media Contaminant Transport Models. Water 2023, 15, 159. https://doi.org/10.3390/w15010159
Seyedpour SM, Henning C, Kirmizakis P, Herbrandt S, Ickstadt K, Doherty R, Ricken T. Uncertainty with Varying Subsurface Permeabilities Reduced Using Coupled Random Field and Extended Theory of Porous Media Contaminant Transport Models. Water. 2023; 15(1):159. https://doi.org/10.3390/w15010159
Chicago/Turabian StyleSeyedpour, S. M., C. Henning, P. Kirmizakis, S. Herbrandt, K. Ickstadt, R. Doherty, and T. Ricken. 2023. "Uncertainty with Varying Subsurface Permeabilities Reduced Using Coupled Random Field and Extended Theory of Porous Media Contaminant Transport Models" Water 15, no. 1: 159. https://doi.org/10.3390/w15010159
APA StyleSeyedpour, S. M., Henning, C., Kirmizakis, P., Herbrandt, S., Ickstadt, K., Doherty, R., & Ricken, T. (2023). Uncertainty with Varying Subsurface Permeabilities Reduced Using Coupled Random Field and Extended Theory of Porous Media Contaminant Transport Models. Water, 15(1), 159. https://doi.org/10.3390/w15010159







