Baseflow Trends for Midsize Carpathian Catchments in Poland and Slovakia in 1970–2019
Abstract
1. Introduction
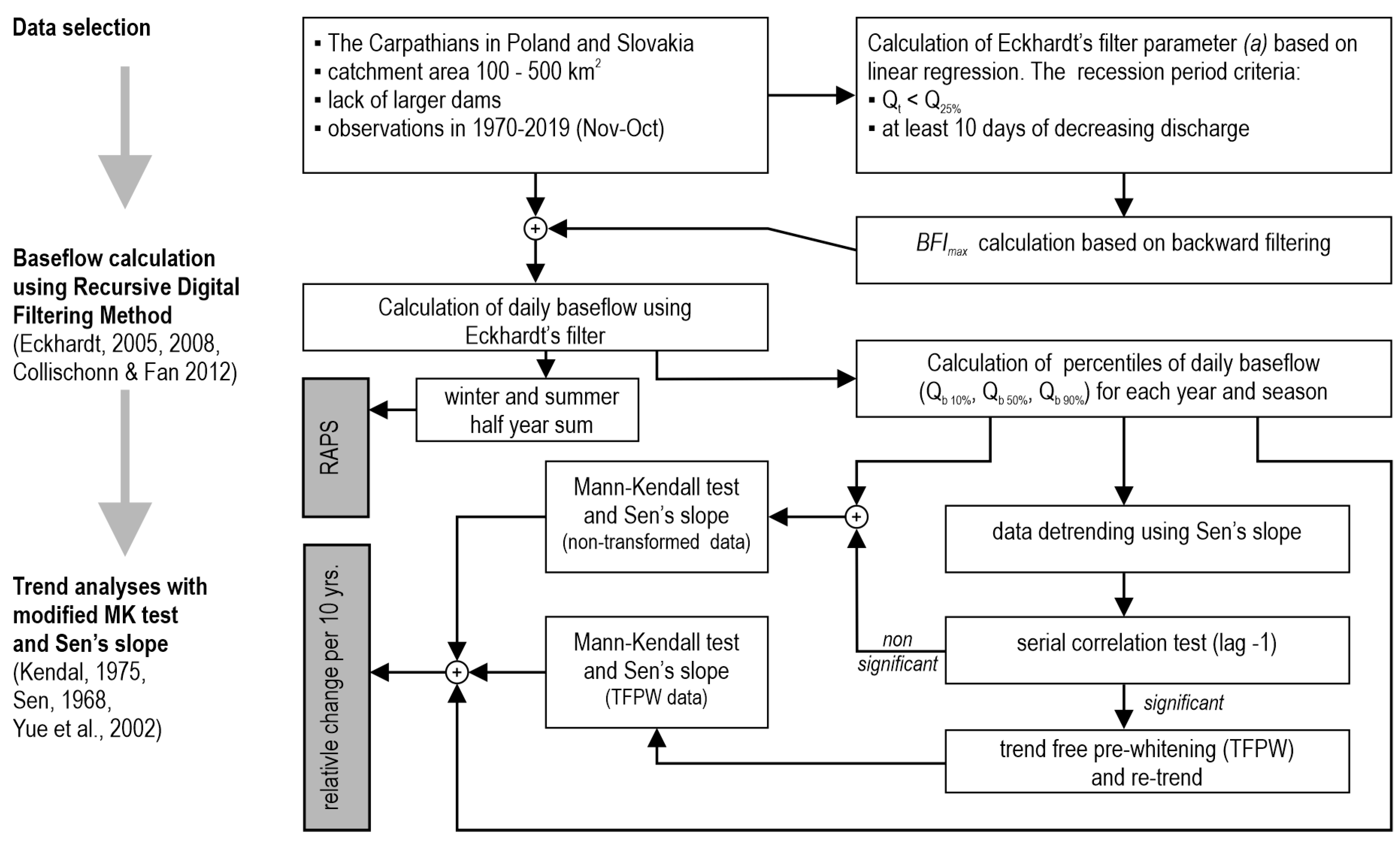
2. Material and Methods
2.1. The Studied Catchments
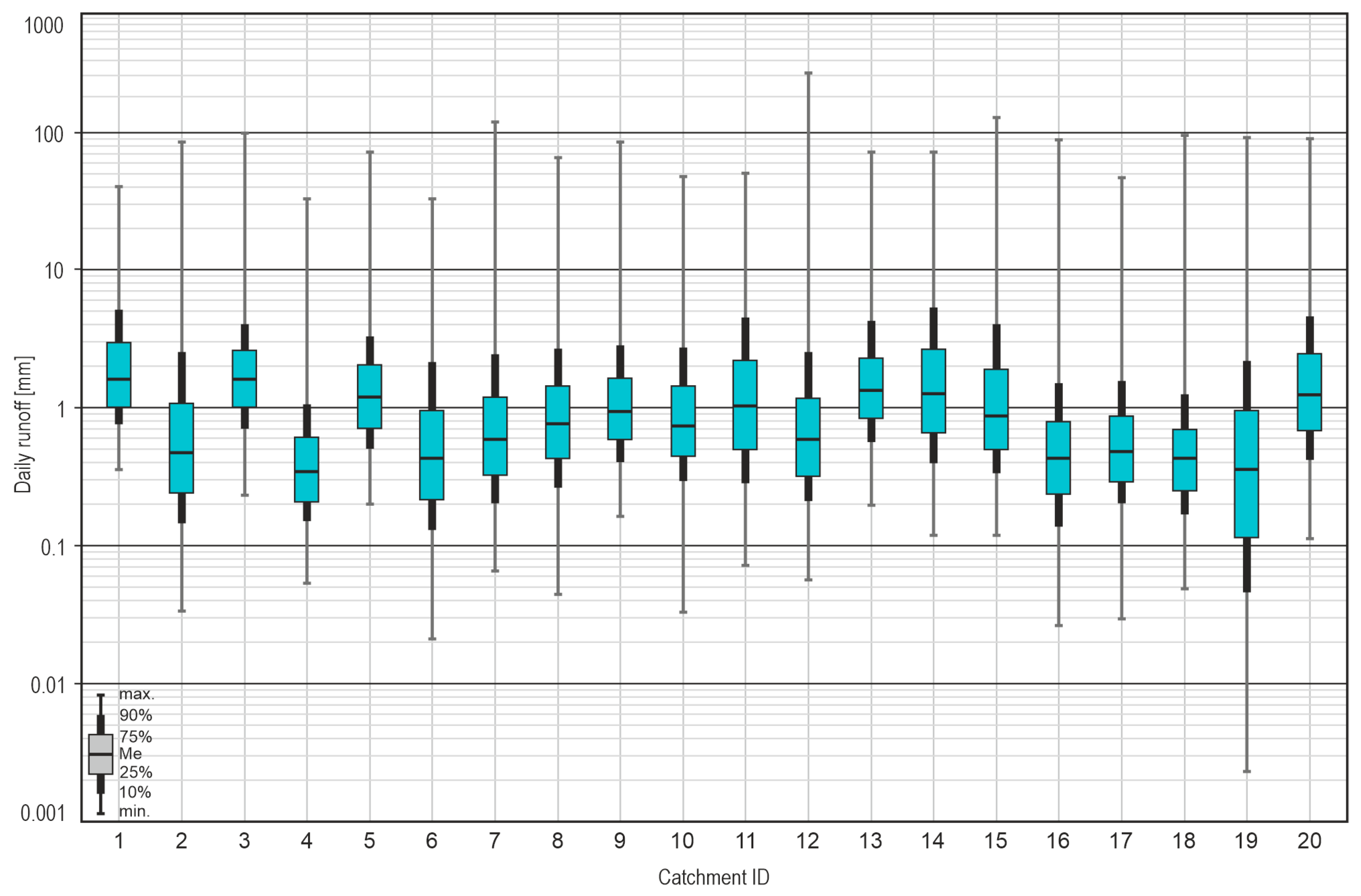
2.2. Baseflow Calculation
2.3. Trend Estimation
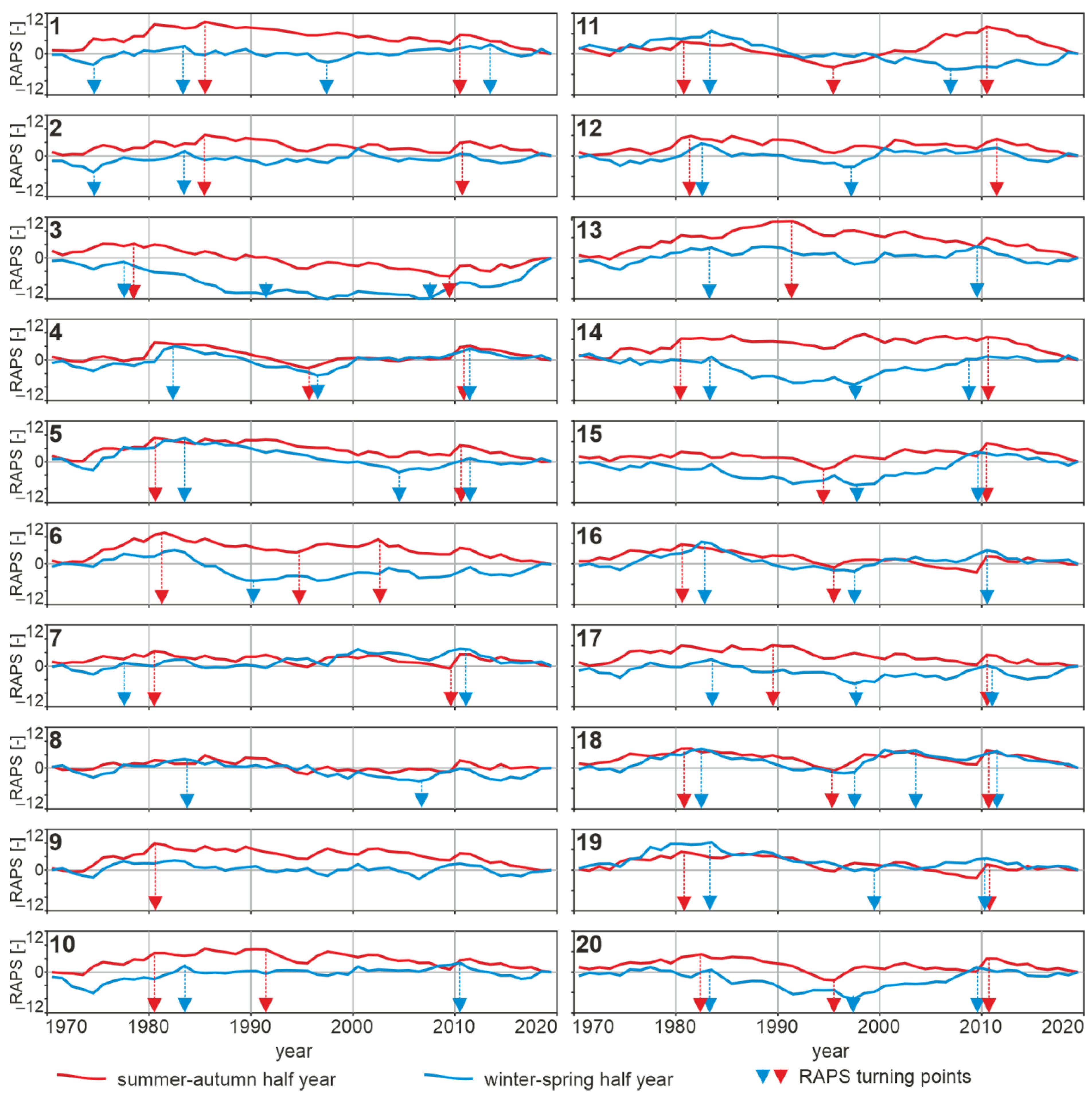
2.4. Rescaled Adjusted Partial Sums
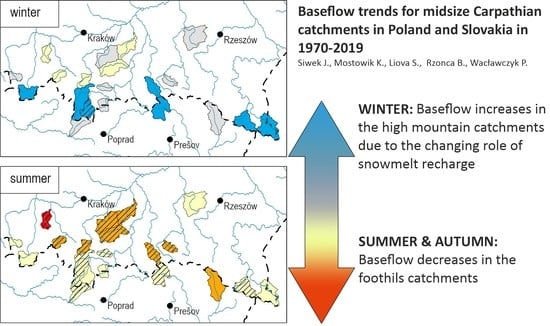
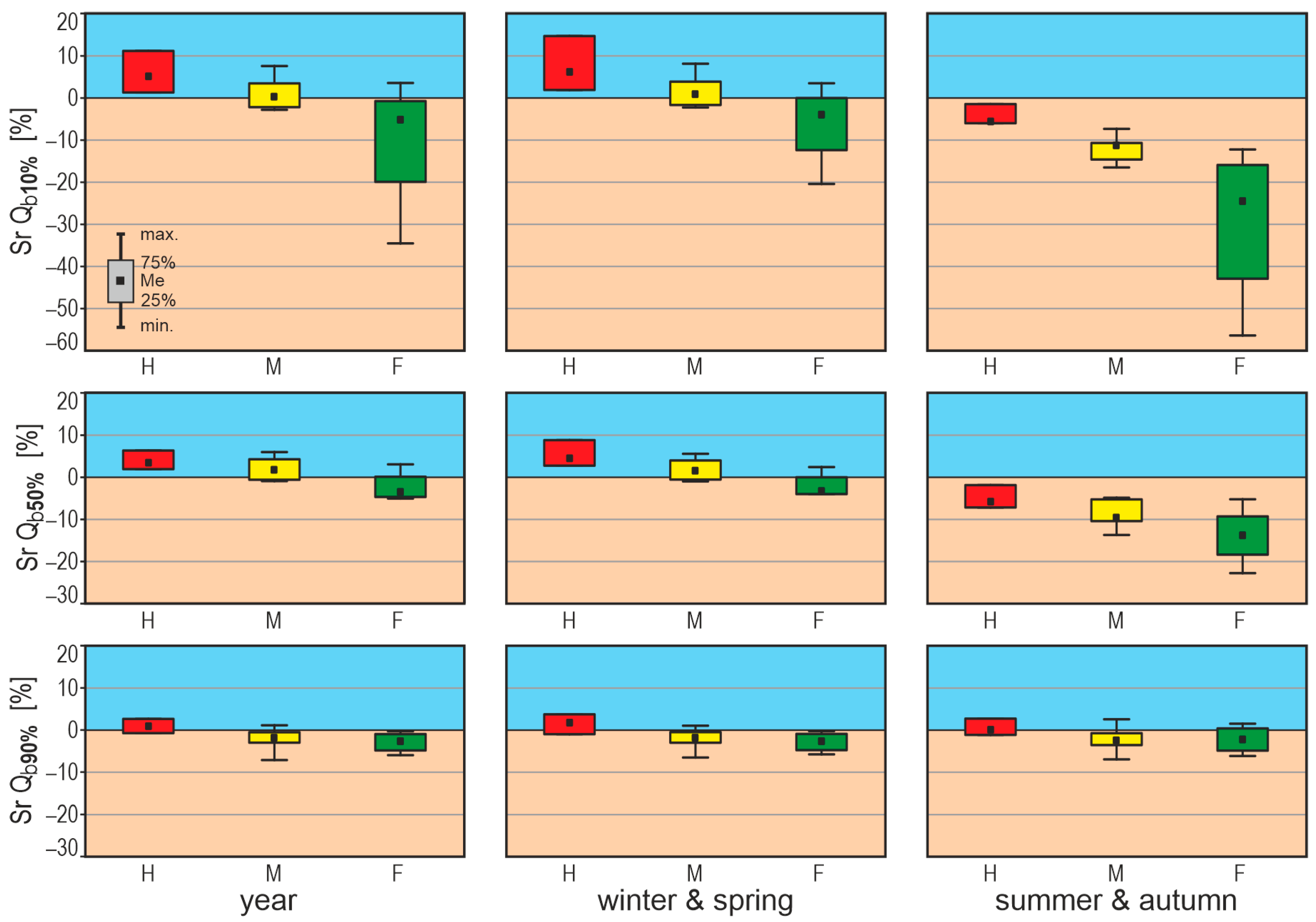
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bates, B.; Kundzewicz, Z.W.; Wu, S.; Palutikof, J. Climate Change and Water; Technical Paper of the Intergovernmental Panel on Climate Change; IPCC Secretariat: Geneva, Switzerland, 2008. [Google Scholar]
- Blöschl, G.; Hall, J.; Viglione, A.; Perdigão, R.A.P.; Parajka, J.; Merz, B.; Lun, D.; Arheimer, B.; Aronica, G.T.; Bilibashi, A.; et al. Changing climate shifts timing of European floods. Science 2017, 357, 588–590. [Google Scholar] [CrossRef] [PubMed]
- Blöschl, G.; Hall, J.; Viglione, A.; Perdigão, R.A.P.; Parajka, J.; Merz, B.; Lun, D.; Arheimer, B.; Aronica, G.T.; Bilibashi, A.; et al. Changing climate both increases and decreases European river floods. Nature 2019, 573, 108–111. [Google Scholar] [CrossRef] [PubMed]
- UNESCO World Water Assessment Programme. The United Nations World Water Development Report 2020: Water and Climate Change; UNESCO: Paris, France, 2020. [Google Scholar]
- Wu, W.Y.; Lo, M.H.; Wada, Y.; Famiglietti, J.S.; Reager, J.T.; Yeh, P.J.-F.; Ducharne, A.; Yang, Z.-L. Divergent effects of climate change on future groundwater availability in key mid-latitude aquifers. Nat. Commun. 2020, 11, 3710. [Google Scholar] [CrossRef] [PubMed]
- Milly, P.C.D.; Dunne, K.A.; Vecchia, A.V. Global pattern of trends in streamflow and water availability in a changing climate. Nature 2005, 438, 347–350. [Google Scholar] [CrossRef]
- Stahl, K.; Hisdal, H.; Hannaford, J.; Tallaksen, L.; Van Lanen, H.; Sauquet, E.; Demuth, S.; Fendekova, M.; Jódar, J. Streamow trends in Europe: Evidence from a dataset of near-natural catchments. Hydrol. Earth Syst. Sc. 2010, 14, 2367–2382. [Google Scholar] [CrossRef]
- Van Vliet, M.T.H.; Franssen, W.H.P.; Yearsley, J.R.; Ludwig, F.; Haddeland, I.; Lettenmaier, D.P.; Kabat, P. Global river discharge and water temperature under climate change. Glob. Environ. Change 2013, 23, 450–464. [Google Scholar] [CrossRef]
- Birsan, M.V.; Zaharia, L.; Chendes, V.; Branescu, E. Seasonal trends in Romanian streamflow. Hydrol. Process. 2014, 28, 4496–4505. [Google Scholar] [CrossRef]
- Bard, A.; Renard, B.; Lang, M.; Giuntoli, I.; Korck, J.; Koboltschnig, G.; Janža, M.; D’Amico, M.; Volken, D. Trends in the hydrologic regime of Alpine rivers. J. Hydrol. 2015, 529, 1823–1837. [Google Scholar] [CrossRef]
- Piniewski, M.; Marcinkowski, P.; Kundzewicz, Z.W. Trend detection in river flows indices in Poland. Acta Geophys. 2018, 66, 347–360. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Leonard, M.; Do, H.X.; Westra, S.; Seneviratne, S.I. Observed trends in global indicators of mean and extreme streamflow. Geophys. Res. Lett. 2019, 46, 756–766. [Google Scholar] [CrossRef]
- Mostowik, K.; Siwek, J.; Kisiel, M.; Kowalik, K.; Krzysik, M.; Plenzler, J.; Rzonca, B. Runoff trends in a changing climate in the Eastern Carpathians (Bieszczady Mountains, Poland). Catena 2019, 182, 104174. [Google Scholar] [CrossRef]
- Górnik, M. Changing trends of river flows in the Upper Vistula Basin (East-Central Europe). Acta Geophys. 2020, 68, 495–504. [Google Scholar] [CrossRef]
- Green, T.R.; Taniguchi, M.; Kooi, H.; Gurdak, J.J.; Allen, D.M. Beneath the surface of global change: Impacts of climate change on groundwater. J. Hydrol. 2011, 405, 532–560. [Google Scholar] [CrossRef]
- Buczyński, S.; Wcislo, M. Predicting climate-induced changes in groundwater resources on the basis of hydrogeological model research: Case study of the Carpathian flysch belt. Episodes 2013, 36, 105–114. [Google Scholar] [CrossRef] [PubMed]
- Famiglietti, J.S. The global groundwater crisis. Nat. Clim. Change 2014, 4, 945–948. [Google Scholar] [CrossRef]
- Freiwald, P.; Patorski, R.; Witek, K. Hydrogeological cycles in the light of monitoring studies in the Carpathians. Acta Sci. Pol. Form. Circumiectus 2014, 13, 11–19. (In Polish) [Google Scholar]
- Kløve, B.; Ala-Aho, P.; Bertrand, G.; Gurdak, J.J.; Kupfersberger, H.; Kvarner, J.; Muotka, T.; Mykra, H.; Preda, E.; Rosii, P.; et al. Climate change impacts on groundwater and dependent ecosystems. J. Hydrol. 2014, 518, 250–266. [Google Scholar] [CrossRef]
- Hellwig, J.; Stahl, K. An assessment of trends and potential future changes in groundwater-baseflow drought based on catchment response times. Hydrol. Earth Syst. Sci. 2018, 22, 6209–6224. [Google Scholar] [CrossRef]
- Bierkens, M.F.P.; Wada, Y. Non-renewable groundwater use and groundwater depletion: A review. Environ. Res. Lett. 2019, 14, 063002. [Google Scholar] [CrossRef]
- Li, B.; Rodell, M.; Sheffield, J.; Wood, E.; Sutanudjaja, E. Long-term, non-anthropogenic groundwater storage changes simulated by three global-scale hydrological models. Sci. Rep. 2019, 9, 10746. [Google Scholar] [CrossRef]
- Mekonnen, M.; Hoekstra, A. Four billion people facing severe water scarcity. Sci. Adv. 2016, 2, e1500323. [Google Scholar] [CrossRef] [PubMed]
- Bucak, T.; Trolle, D.; Andersen, H.E.; Thodsen, H.; Erdoğan, Ş.; Levi, E.E.; Filiz, N.; Jeppesen, E.; Beklioglu, M. Future water availability in the largest freshwater Mediterranean lake is at great risk as evidenced from simulations with the SWAT model. Sci. Total Environ. 2017, 581–582, 413–425. [Google Scholar] [CrossRef] [PubMed]
- Rodell, M.; Famiglietti, J.S.; Wiese, D.N.; Reager, J.T.; Beaudoing, H.K.; Landerer, F.W.; Lo, M.H. Emerging trends in global freshwater availability. Nature 2018, 557, 651–659. [Google Scholar] [CrossRef] [PubMed]
- Mankin, J.S.; Seager, R.; Smerdon, J.E.; Cook, B.I.; Park Williams, A. Mid-latitude freshwater availability reduced by projected vegetation responses to climate change. Nat. Geosci. 2019, 12, 983–988. [Google Scholar] [CrossRef]
- Ficklin, D.L.; Robeson, S.M.; Knouft, J.H. Impacts of recent climate change on trends in baseflow and stormflow in United States watersheds. Geophys. Res. Lett. 2016, 43, 5079–5088. [Google Scholar] [CrossRef]
- Buttle, J.M. Mediating stream baseflow response to climate change: The role of basin storage. Hydrol. Process. 2018, 32, 363–378. [Google Scholar] [CrossRef]
- Tan, X.; Liu, B.; Tan, X. Global changes in baseflow under the impacts of changing climate and vegetation. Water Resour. Res. 2020, 56, e2020WR027349. [Google Scholar] [CrossRef]
- Chen, H.; Teegavarapu, R.S.V. Spatial and temporal variabilities in baseflow characteristics across the continental USA. Theor. Appl. Climatol. 2021, 143, 1615–1629. [Google Scholar] [CrossRef]
- Lei, Y.; Jiang, X.; Geng, W.; Zhang, J.; Zhao, H.; Ren, L. The Variation Characteristics and Influencing Factors of Base Flow of the Hexi Inland Rivers. Atmosphere 2021, 12, 356. [Google Scholar] [CrossRef]
- Duncan, H.P. Baseflow separation—A practical approach. J. Hydrol. 2019, 527, 308–313. [Google Scholar] [CrossRef]
- Völker, J.; Borchardt, D. Drinking Water Quality at Risk: A European Perspective. In Atlas of Ecosystem Services; Schröter, M., Bonn, A., Klotz, S., Seppelt, R., Baessler, C., Eds.; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Pepin, N.; Bradley, R.S.; Diaz, H.F.; Baraer, E.B.; Caceres, N.; Forsythe, N.; Fowler, H.; Greenwood, C.; Hashmi, M.Z.; Liu, X.D.; et al. Elevation-dependent warming in mountain regions of the world. Nat. Clim. Change 2015, 5, 424–430. [Google Scholar] [CrossRef]
- Wypych, A.; Ustrnul, Z.; Schmatz, D.R. Long-term variability of air temperature and precipitation conditions in the Polish Carpathians. J. Mt. Sci. 2018, 15, 237–253. [Google Scholar] [CrossRef]
- Tomczyk, A.M.; Bednorz, E. The extreme year—analysis of thermal conditions in Poland in 2018. Theor. Appl. Climatol. 2020, 139, 251–260. [Google Scholar] [CrossRef]
- Bokwa, A.; Wypych, A.; Ustrnul, Z. Climate Changes in the Vertical Zones of the Polish Carpathians in the Last 50 Years. In The Carpathians: Integrating Nature and Society Towards Sustainability. Environmental Science and Engineering; Kozak, J., Ostapowicz, K., Bytnerowicz, A., Wyżga, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 89–109. [Google Scholar] [CrossRef]
- Spinoni, J.; Szalai, S.; Szentimrey, T.; Lakatos, M.; Bihari, Z.; Nagy, A.; Nemeth, A.; Kovacs, A.; Mihic, D.; Dacic, M.; et al. Climate of the Carpathian Region in the period 1961–2010: Climatologies and trends of 10 variable. Int. J. Climatol. 2015, 35, 1322–1341. [Google Scholar] [CrossRef]
- Kubiak-Wójcicka, K. Variability of Air Temperature, Precipitation and Outflows in the Vistula Basin (Poland). Resources 2020, 9, 103. [Google Scholar] [CrossRef]
- Twardosz, R.; Cebulska, M. Temporal variability of the highest and the lowest monthly precipitation totals in the Polish Carpathian Mountains (1881–2018). Theor. Appl. Climatol. 2020, 140, 327–341. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Seneviratne, I. European drought trends. Proc. IAHS 2015, 369, 75–79. [Google Scholar] [CrossRef]
- Madsen, H.; Lawrence, D.; Lang, M.; Martinkova, M.; Kjeldsen, T. R Review of trend analysis and climate change projections of extreme precipitation and floods in Europe. J. Hydrol. 2014, 519, 3634–3650. [Google Scholar] [CrossRef]
- Szwed, M. Variability of precipitation in Poland under climate change. Theor. Appl. Climatol. 2019, 135, 1003–1015. [Google Scholar] [CrossRef]
- Eckhardt, K.; Ulbrich, U. Potential impacts of climate change on groundwater recharge and streamflow in a central European low mountain range. J. Hydrol. 2003, 284, 244–252. [Google Scholar] [CrossRef]
- Chełmicki, W.; Skąpski, R.; Soja, R. The flow regime of Polish Carpathian rivers. Folia Geogr. Geogr. Phys. 1998/1999, 29–30, 67–80. (In Polish) [Google Scholar]
- Viviroli, D.; Dürr, H.H.; Messerli, B.; Meybeck, M.; Weingartner, R. Mountains of the world, water towers for humanity: Typology, mapping, and global significance. Water Resour. Res. 2007, 43, W07447. [Google Scholar] [CrossRef]
- Łajczak, A. Deltas in dam-retained lakes in the Carpathian part of the Vistula drainage basin. Pr. Geogr. 2006, 116, 99–110. [Google Scholar]
- Wyżga, B. A review on channel incision in the Polish Carpathian rivers during the 20th century. In Gravel-Bed Rivers VI: From Process Understanding to River Restoration; Habersack, H., Piégay, H., Rinaldi, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Griffiths, P.; Kuemmerle, T.; Baumann, M.; Radeloff, V.; Abrudan, I.V.; Lieskovsky, J.; Munteanu, C.; Ostapowicz, K.; Hostert, P. Forest disturbances, forest recovery, and changes in forest types across the Carpathian ecoregion from 1985 to 2010 based on Landsat image composites. Remote Sens. Environ. 2014, 151, 72–88. [Google Scholar] [CrossRef]
- Wiejaczka, Ł.; Olędzki, J.; Bucała-Hrabia, A.; Kijowska-Strugała, M. A spatial and temporal analysis of land use changes in two mountain valleys: With and without dam reservoir (Polish Carpathians). Quaest. Geogr. 2017, 36, 129–137. [Google Scholar] [CrossRef]
- Solon, J.; Borzyszkowski, J.; Bidłasik, M.; Richling, A.; Badora, K.; Balon, J.; Brzezińska-Wójcik, T.; Chabudziński, Ł.; Dobrowolski, R.; Grzegorczyk, I.; et al. Physico-geographical mesoregions of Poland: Verification and adjustment of boundaries on the basis of contemporary spatial data. Geogr. Pol. 2018, 91, 143–170. [Google Scholar] [CrossRef]
- Eckhardt, K. How to construct recursive digital filters for baseflow separation. Hydrol. Process. 2005, 19, 507–515. [Google Scholar] [CrossRef]
- Collischonn, W.; Fan, F.M. Defining parameters for Eckhardt’s digital baseflow filter. Hydrol. Process. 2013, 27, 2614–2622. [Google Scholar] [CrossRef]
- Kissel, M.; Schmalz, M. Comparison of Baseflow Separation Methods in the German Low Mountain Range. Water 2020, 12, 1740. [Google Scholar] [CrossRef]
- Eckhardt, K. A comparison of baseflow indices, which were calculated with seven different baseflow separation methods. J. Hydrol. 2008, 352, 168–173. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1975; p. 202. [Google Scholar]
- Garbrecht, J.; Fernandez, G.P. Visualization of trends and fluctuations in climatic records. JAWRA J. Am. Water Resour. Assoc. 1994, 30, 297–306. [Google Scholar] [CrossRef]
- Shelton, M.L. Seasonal hydroclimate change in the Sacramento River basin, California. Phys. Geogr. 1998, 19, 239–255. [Google Scholar] [CrossRef]
- Kos, Ž.; Đurin, B.; Dogančić, D.; Kranjčić, N. Hydro-Energy Suitability of Rivers Regarding Their Hydrological and Hydrogeological Characteristics. Water 2021, 13, 1777. [Google Scholar] [CrossRef]
- Herbich, P.; Prażak, J.; Przytuła, E. Dynamics of the shallow groundwater retention in the hydrogeological units. Biuletyn PIG 2009, 436, 159–164. (In Polish) [Google Scholar]
- Kowalczyk, A.; Szydło, M.; Stępińska-Drygała, I.; Wesołowski, P.; Bejger, M.; Gołębiewski, M. Hydrogeological Droughts in Poland in the Period 1981–2015; PIG–PIB: Warszawa, Poland, 2017. (In Polish) [Google Scholar]
- Bartnik, A.; Moniewski, P. Multiannual variability of spring discharge in southern Poland. Episodes 2019, 42, 187–198. [Google Scholar] [CrossRef]
- Rzepecka, Z.; Biryło, M.; Kuczyńska-Siehień, J.; Nastula, J.; Pajak, K. Analysis of groundwater level variations and water balance in the area of the Sudety mountains. Acta Geodyn. Geomater. 2017, 14, 307–315. [Google Scholar] [CrossRef]
- Śliwińska, J.; Biryło, M.; Rzepecka, Z.; Nastula, J. Analysis of Groundwater and Total Water Storage Changes in Poland Using GRACE Observations, In-situ Data, and Various Assimilation and Climate Models. Remote Sens. 2019, 11, 2949. [Google Scholar] [CrossRef]
- Piniewski, M.; Szcześniak, M.; Mezghani, A.; Kundzewicz, Z.W. Hydroclimatic Projections for the Upper Vistula Basin. In Flood Risk in the Upper Vistula Basin; Kundzewicz, Z., Stoffel, M., Niedźwiedź, T., Wyżga, B., Eds.; GeoPlanet: Earth and Planetary Sciences; Springer: Berlin/Heidelberg, Germany, 2016; pp. 331–340. [Google Scholar] [CrossRef]
- Piniewski, M.; Szcześniak, M.; Huang, S.; Kundzewicz, Z.W. Projections of runoff in the Vistula and the Odra river basins with the help of the SWAT model. Hydrol. Res. 2018, 49, 303–317. [Google Scholar] [CrossRef]
- Raczyński, K.; Dyer, J. Multi-annual and seasonal variability of low-flow river conditions in southeastern Poland. Hydrol. Sci. J. 2020, 65, 2561–2576. [Google Scholar] [CrossRef]
- Kędra, M. Sensitivity of mountain catchments to global warming: A case study of the San Basin, Poland. Water Environ. J. 2020, 34, 648–660. [Google Scholar] [CrossRef]
- Boczoń, A.; Kowalska, A.; Dudzińska, M.; Wróbel, M. Drought in Polish Forests in 2015. Pol. J. Environ. Stud. 2016, 25, 1857–1862. [Google Scholar] [CrossRef] [PubMed]
- Büntgen, U.; Urban, O.; Krusic, P.J.; Rybnicek, M.; Kolar, T.; Kyncl, T.; Ac, A.; Konasova, E.; Caslavsky, J.; Esper, J.; et al. Recent European drought extremes beyond Common Era background variability. Nat. Geosci. 2021, 14, 190–196. [Google Scholar] [CrossRef]
- Rzonca, B.; Siwek, J.; Zawiło, M.; Bryndza, M.; Dojtrowska, I.; Lasota, J.; Piech, K.; Bryła, M. Drought in the Bieszczady Mts in 2015. Rocz. Bieszcz. 2016, 24, 263–279. (In Polish) [Google Scholar]
- Staśko, S.; Buczyński, S. Drought and its effects on spring discharge regimes in Poland and Germany during the 2015 drought. Hydrol. Sci. J. 2018, 63, 741–751. [Google Scholar] [CrossRef]
- Tomczyk, A.M.; Bednorz, E.; Szyga-Pluta, K. Changes in Air Temperature and Snow Cover in Winter in Poland. Atmosphere 2021, 12, 68. [Google Scholar] [CrossRef]
- Kędra, M. Regional Response to Global Warming: Water Temperature Trends in Semi-Natural Mountain River Systems. Water 2020, 12, 283. [Google Scholar] [CrossRef]
- Lakatos, M.; Weidinger, T.; Hoffmann, L.; Bihari, Z.; Horváth, Á. Computation of daily Penman–Monteith reference evapotranspiration in the Carpathian Region and comparison with Thornthwaite estimates. Adv. Sci. Res. 2020, 16, 251–259. [Google Scholar] [CrossRef]
- Pińskwar, I.; Choryński, A.; Graczyk, D.; Kundzewicz, Z.W. Observed changes in extreme precipitation in Poland: 1991–2015 versus 1961–1990. Theor. Appl. Climatol. 2019, 135, 773–787. [Google Scholar] [CrossRef]
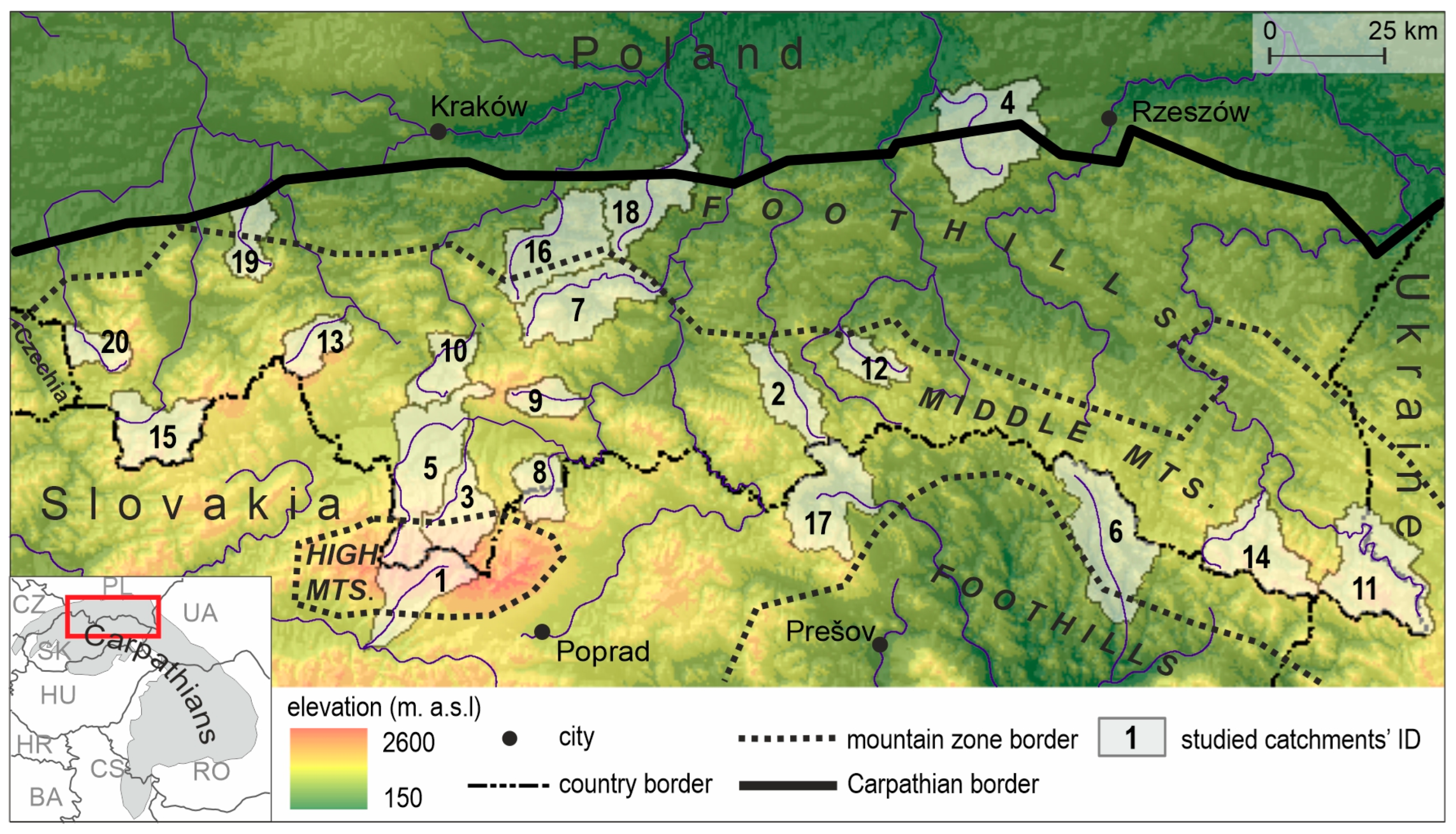
| No | River | Gauging Station | Area [km2] | Mean Elev. [m a.s.l.] | Average Annual Runoff [mm] | Land Cover [%] | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Forest | Arable Land | Pasture and Grassland | Urban and Industrial | Other | ||||||
| 1 | Belá | Liptovský Hrádok | 244 | 1286 | 876 | 41.0 | 10.5 | 40.4 | 3.5 | 4.6 |
| 2 | Biała | Grybów | 207 | 560 | 425 | 55.2 | 31.8 | 11.7 | 1.3 | 0.0 |
| 3 | Biały Dunajec | Szaflary | 210 | 1047 | 806 | 43.8 | 11.2 | 28.7 | 13.2 | 3.1 |
| 4 | Brzeźnica | Brzeźnica | 482 | 272 | 216 | 25.6 | 61.4 | 4.4 | 8.3 | 0.3 |
| 5 | Dunajec | Nowy Targ | 435 | 869 | 648 | 28.4 | 28.2 | 34.6 | 7.2 | 1.6 |
| 6 | Laborec | Koškovce | 438 | 447 | 341 | 66.2 | 25.2 | 5.8 | 2.8 | 0.0 |
| 7 | Łososina | Jakubkowice | 347 | 538 | 425 | 40.1 | 54.6 | 1.1 | 4.2 | 0.0 |
| 8 | Niedziczanka | Niedzica | 137 | 800 | 481 | 56.1 | 19.6 | 21.1 | 3.1 | 0.1 |
| 9 | Ochotnica | Tylamnowa | 106 | 805 | 519 | 68.1 | 25.1 | 5.6 | 1.2 | 0.0 |
| 10 | Raba | Mszana Dolna | 157 | 628 | 473 | 43.7 | 26.2 | 18.4 | 11.7 | 0.0 |
| 11 | San | Dwernik | 418 | 780 | 702 | 76.9 | 1.3 | 21.1 | 0.4 | 0.3 |
| 12 | Sękówka | Gorlice | 122 | 516 | 478 | 72.0 | 17.8 | 8.2 | 2.0 | 0.0 |
| 13 | Skawica | Skawica Dolna | 136 | 790 | 769 | 75.4 | 10.8 | 9.2 | 4.6 | 0.0 |
| 14 | Solinka | Terka | 309 | 789 | 849 | 91.4 | 2.1 | 5.6 | 0.7 | 0.2 |
| 15 | Soła | Rajcza | 254 | 787 | 644 | 72.5 | 12.1 | 13.0 | 2.4 | 0.0 |
| 16 | Stradomka | Stradomka | 363 | 358 | 295 | 26.9 | 70.6 | 0.8 | 1.7 | 0.0 |
| 17 | Topľa | Bardejov | 326 | 601 | 291 | 64.9 | 20.6 | 11.4 | 3.0 | 0.1 |
| 18 | Uszwica | Borzęcin | 266 | 290 | 304 | 30.6 | 59.1 | 2.6 | 7.7 | 0.0 |
| 19 | Wieprzówka | Rudze | 152 | 409 | 353 | 31.0 | 53.4 | 1.4 | 12.8 | 1.4 |
| 20 | Wisła | Ustroń | 107 | 709 | 781 | 74.6 | 16.2 | 1.3 | 7.6 | 0.3 |
| ID | River | a | BFImax [%] | Baseflow | |||
|---|---|---|---|---|---|---|---|
| BFI [%] | Annual [mm] | Max | Min | ||||
| 1 | Belá | 0.99 | 63 | 57 | 497 | Jun | Feb |
| 2 | Biała | 0.96 | 36 | 30 | 128 | Apr | Oct |
| 3 | Biały Dunajec | 0.98 | 65 | 59 | 479 | Jun | Feb |
| 4 | Brzeźnica | 0.98 | 57 | 50 | 107 | Mar | Sep |
| 5 | Dunajec | 0.98 | 59 | 52 | 339 | May | Feb |
| 6 | Laborec | 0.96 | 47 | 41 | 141 | Apr | Sep |
| 7 | Łososina | 0.97 | 43 | 37 | 157 | Apr | Oct |
| 8 | Niedziczanka | 0.98 | 48 | 42 | 202 | Apr | Feb |
| 9 | Ochotnica | 0.98 | 58 | 52 | 271 | Apr | Feb |
| 10 | Raba | 0.97 | 51 | 44 | 210 | Apr | Oct |
| 11 | San | 0.95 | 50 | 44 | 307 | Apr | Aug |
| 12 | Sękówka | 0.98 | 37 | 29 | 141 | Apr | Oct |
| 13 | Skawica | 0.97 | 54 | 47 | 361 | Apr | Oct |
| 14 | Solinka | 0.95 | 52 | 46 | 393 | Apr | Aug |
| 15 | Soła | 0.97 | 42 | 36 | 233 | Apr | Oct |
| 16 | Stradomka | 0.96 | 51 | 44 | 131 | Apr | Oct |
| 17 | Topľa | 0.97 | 62 | 56 | 163 | Apr | Sep |
| 18 | Uszwica | 0.98 | 44 | 35 | 108 | Apr | Oct |
| 19 | Wieprzówka | 0.93 | 36 | 31 | 108 | Apr | Nov |
| 20 | Wisła | 0.96 | 53 | 47 | 364 | Apr | Oct |
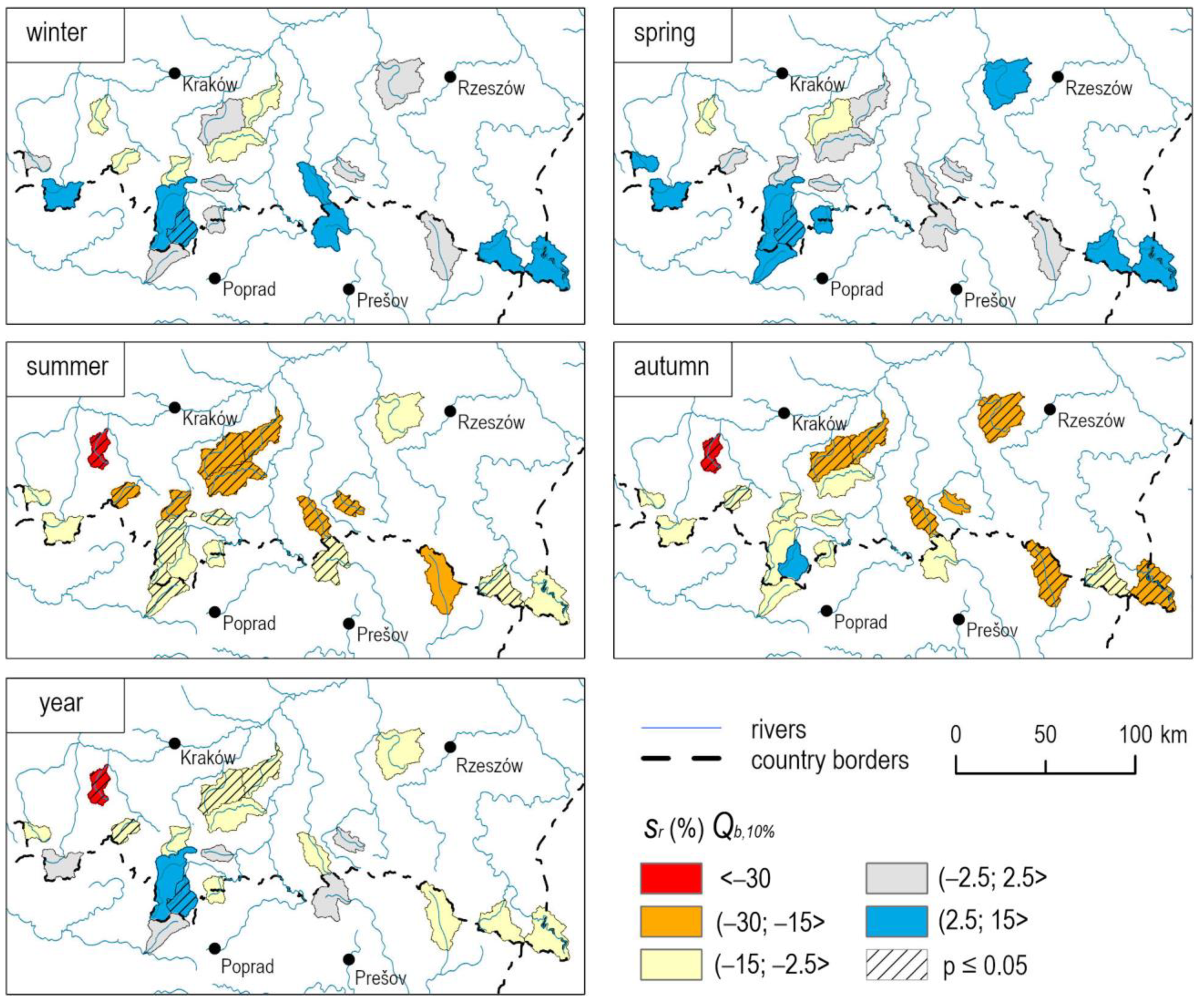
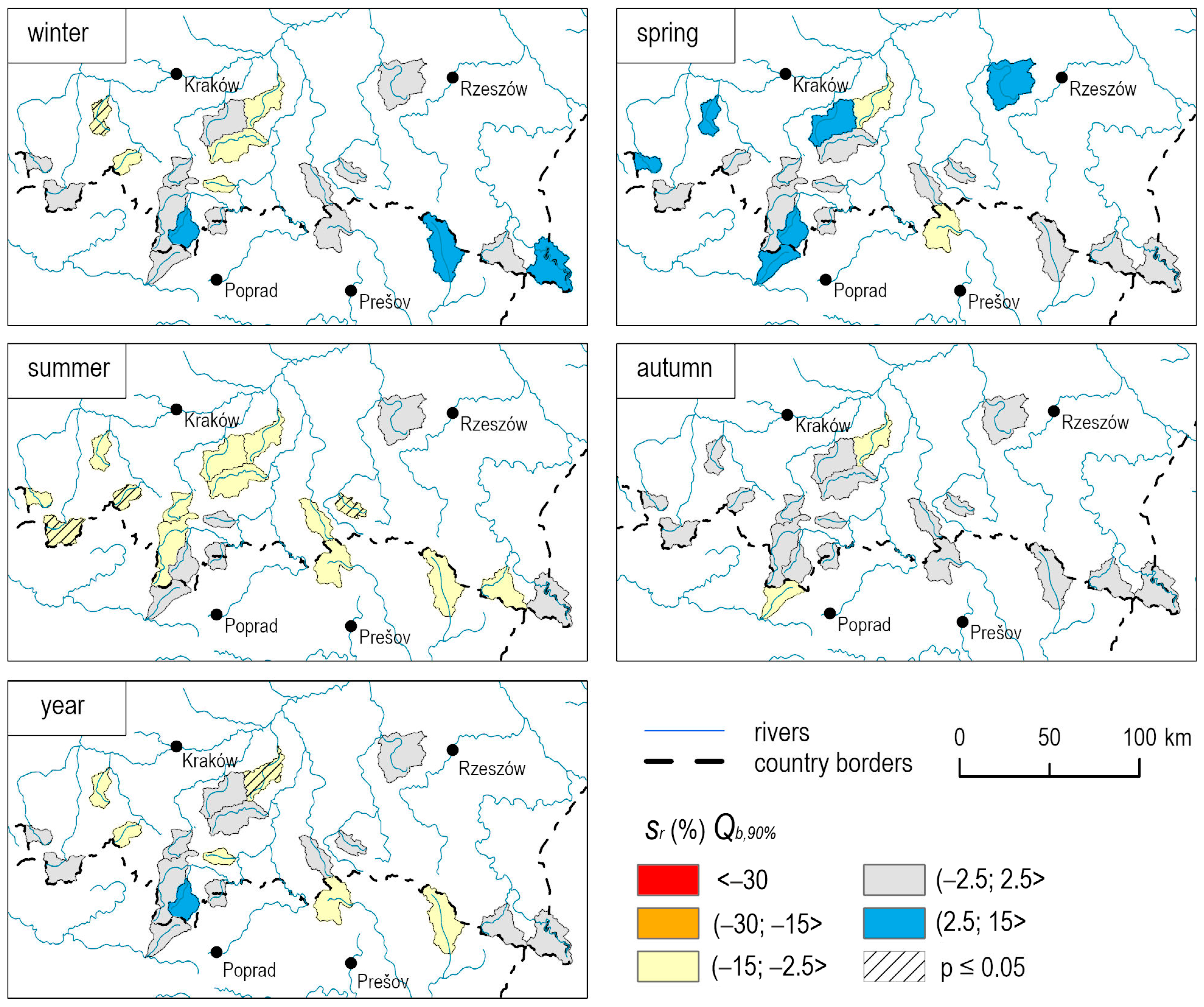
| River | Qb, 10% | Qb, 50% | Qb, 90% | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Yr | W | SP | SU | A | Yr | W | SP | SU | A | Yr | W | SP | SU | A | |
| 1.Bela | 0.01 | 0.00 | 0.02 | −0.10 | −0.03 | −0.02 | 0.00 | 0.04 | −0.16 | −0.04 | −0.05 | 0.01 | 0.09 | −0.04 | −0.06 |
| 2.Biała | 0.00 | 0.00 | 0.00 | −0.02 | −0.01 | −0.02 | 0.01 | 0.01 | −0.04 | −0.01 | 0.00 | 0.00 | −0.02 | −0.04 | 0.00 |
| 3.Biały Dunajec | 0.05 | 0.06 | 0.08 | −0.04 | 0.03 | 0.01 | 0.05 | 0.03 | −0.06 | 0.05 | 0.07 | 0.05 | 0.09 | 0.01 | 0.04 |
| 4.Brzeźnica | 0.00 | 0.00 | 0.01 | −0.01 | −0.01 | 0.00 | 0.00 | 0.00 | −0.01 | −0.01 | 0.00 | 0.00 | 0.02 | −0.01 | 0.00 |
| 5.Dunajec | 0.02 | 0.01 | 0.03 | −0.06 | −0.02 | −0.02 | 0.02 | −0.03 | −0.06 | −0.01 | −0.03 | 0.00 | 0.03 | −0.07 | −0.02 |
| 6.Laborec | 0.00 | 0.00 | 0.00 | −0.01 | −0.01 | −0.01 | −0.01 | −0.01 | −0.02 | −0.01 | −0.03 | 0.04 | −0.02 | −0.04 | 0.00 |
| 7.Łososina | −0.01 | −0.01 | 0.00 | −0.03 | −0.01 | −0.02 | 0.00 | −0.01 | −0.04 | −0.01 | −0.01 | −0.02 | −0.02 | −0.06 | 0.00 |
| 8.Niedziczanka | −0.01 | 0.00 | 0.01 | −0.03 | −0.01 | −0.01 | 0.01 | −0.03 | −0.01 | −0.01 | 0.01 | 0.01 | 0.02 | 0.01 | 0.00 |
| 9.Ochotnica | −0.01 | 0.00 | 0.01 | −0.05 | −0.03 | −0.01 | 0.00 | −0.02 | −0.04 | −0.02 | −0.03 | −0.03 | 0.00 | −0.03 | −0.01 |
| 10.Raba | −0.01 | −0.01 | 0.00 | −0.04 | −0.01 | −0.02 | 0.00 | 0.01 | −0.06 | −0.01 | 0.00 | −0.02 | 0.03 | −0.08 | −0.02 |
| 11.San | −0.01 | 0.01 | 0.02 | −0.02 | −0.03 | −0.02 | 0.03 | −0.06 | −0.03 | −0.05 | −0.02 | 0.05 | −0.01 | −0.01 | 0.02 |
| 12.Sękówka | 0.00 | 0.00 | 0.00 | −0.02 | −0.01 | −0.02 | −0.01 | 0.00 | −0.04 | −0.01 | 0.00 | 0.00 | −0.01 | −0.06 | 0.00 |
| 13.Skawica | −0.04 | −0.02 | 0.01 | −0.08 | −0.04 | −0.06 | −0.03 | −0.02 | −0.11 | −0.04 | −0.04 | −0.08 | 0.03 | −0.14 | −0.03 |
| 14.Solinka | −0.02 | 0.01 | 0.03 | −0.03 | −0.03 | −0.04 | 0.02 | −0.06 | −0.07 | −0.05 | −0.02 | 0.04 | 0.04 | −0.07 | 0.01 |
| 15.Soła | 0.00 | 0.01 | 0.02 | −0.01 | −0.01 | −0.01 | 0.02 | 0.01 | −0.03 | 0.01 | 0.01 | −0.01 | 0.02 | −0.09 | 0.01 |
| 16.Stradomka | −0.01 | 0.00 | −0.01 | −0.03 | −0.02 | −0.02 | −0.01 | −0.01 | −0.04 | −0.01 | −0.01 | −0.01 | 0.04 | −0.06 | 0.00 |
| 17.Topla | 0.00 | 0.01 | 0.00 | −0.02 | 0.00 | −0.02 | 0.01 | −0.01 | −0.03 | −0.01 | −0.04 | 0.01 | −0.08 | −0.05 | −0.01 |
| 18.Uszwica | −0.01 | 0.00 | 0.00 | −0.02 | −0.02 | −0.02 | 0.00 | −0.02 | −0.04 | −0.01 | −0.03 | −0.02 | −0.02 | −0.04 | −0.01 |
| 19.Wieprzówka | −0.01 | 0.00 | −0.01 | −0.01 | −0.02 | −0.02 | −0.02 | −0.01 | −0.03 | −0.02 | −0.03 | −0.05 | 0.04 | −0.06 | 0.00 |
| 20.Wisła Ustroń | −0.01 | −0.01 | 0.02 | −0.03 | −0.02 | −0.02 | 0.03 | 0.01 | −0.07 | −0.02 | −0.01 | −0.01 | 0.09 | −0.06 | −0.01 |
| River | Q 10% | Q 50% | Q 90% | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Yr | W | SP | SU | A | Yr | W | SP | SU | A | Year | W | SP | SU | A | |
| 1.Bela | 0.01 | 0.00 | 0.03 | −0.09 | −0.04 | −0.01 | 0.01 | 0.08 | −0.18 | −0.01 | −0.04 | 0.02 | 0.09 | −0.32 | 0.02 |
| 2.Biała | −0.01 | 0.01 | 0.00 | −0.03 | −0.02 | −0.03 | 0.01 | −0.02 | −0.07 | −0.03 | −0.06 | 0.08 | −0.06 | −0.19 | 0.03 |
| 3.Biały Dunajec | 0.07 | 0.07 | 0.08 | −0.04 | 0.02 | 0.02 | 0.08 | 0.02 | −0.10 | 0.07 | 0.09 | 0.06 | 0.20 | −0.06 | 0.17 |
| 4.Brzeźnica | −0.01 | 0.00 | 0.01 | −0.02 | −0.02 | 0.00 | 0.01 | 0.01 | −0.01 | −0.01 | −0.04 | 0.00 | 0.00 | −0.02 | 0.01 |
| 5.Dunajec | 0.01 | 0.01 | 0.05 | −0.07 | −0.03 | −0.01 | 0.01 | −0.06 | −0.12 | −0.01 | −0.07 | −0.03 | −0.06 | −0.20 | 0.05 |
| 6.Laborec | −0.01 | 0.00 | 0.00 | −0.01 | −0.01 | −0.03 | −0.01 | −0.02 | −0.03 | −0.02 | −0.11 | 0.15 | −0.22 | −0.13 | −0.03 |
| 7.Łososina | −0.02 | −0.01 | 0.00 | −0.02 | −0.02 | −0.03 | −0.01 | 0.00 | −0.07 | −0.02 | −0.04 | −0.09 | −0.10 | −0.17 | 0.03 |
| 8.Niedziczanka | −0.01 | −0.01 | 0.01 | −0.02 | −0.01 | 0.00 | 0.01 | −0.01 | −0.03 | 0.01 | −0.05 | 0.01 | −0.06 | −0.08 | 0.01 |
| 9.Ochotnica | −0.02 | 0.00 | −0.03 | −0.06 | −0.03 | −0.03 | −0.01 | 0.00 | −0.08 | −0.05 | −0.06 | −0.06 | −0.09 | −0.16 | −0.06 |
| 10.Raba | −0.02 | 0.00 | −0.02 | −0.05 | −0.02 | −0.04 | 0.00 | 0.00 | −0.10 | −0.02 | −0.01 | −0.03 | 0.05 | −0.22 | −0.02 |
| 11.San | −0.02 | 0.02 | 0.00 | −0.03 | −0.03 | −0.05 | 0.04 | −0.06 | −0.06 | −0.09 | 0.07 | 0.28 | 0.03 | −0.03 | 0.00 |
| 12.Sękówka | −0.01 | −0.01 | −0.02 | −0.03 | −0.02 | −0.04 | 0.01 | −0.02 | −0.06 | −0.02 | 0.02 | 0.04 | 0.10 | −0.15 | 0.02 |
| 13.Skawica | −0.06 | −0.02 | −0.03 | −0.09 | −0.05 | −0.09 | −0.06 | −0.01 | −0.14 | −0.06 | −0.16 | −0.24 | 0.00 | −0.54 | 0.08 |
| 14.Solinka | −0.04 | 0.01 | 0.02 | −0.05 | −0.04 | −0.08 | 0.00 | −0.07 | −0.12 | −0.11 | 0.02 | 0.12 | 0.11 | −0.31 | 0.00 |
| 15.Soła | −0.01 | 0.02 | 0.02 | −0.02 | −0.01 | −0.01 | 0.02 | 0.00 | −0.06 | 0.00 | 0.00 | −0.01 | 0.16 | −0.34 | 0.19 |
| 16.Stradomka | −0.02 | 0.00 | −0.01 | −0.03 | −0.03 | −0.03 | −0.02 | −0.02 | −0.06 | −0.02 | −0.05 | −0.03 | 0.02 | −0.14 | 0.00 |
| 17.Topla | 0.00 | 0.01 | −0.01 | −0.02 | −0.01 | −0.02 | 0.01 | −0.04 | −0.05 | −0.01 | −0.08 | 0.05 | −0.19 | −0.09 | −0.02 |
| 18.Uszwica | −0.02 | 0.00 | −0.01 | −0.03 | −0.03 | −0.02 | −0.01 | 0.00 | −0.06 | −0.03 | −0.10 | −0.03 | −0.05 | −0.15 | 0.00 |
| 19.Wieprzówka | −0.02 | −0.01 | −0.02 | −0.02 | −0.03 | −0.04 | −0.03 | −0.02 | −0.06 | −0.04 | −0.08 | −0.17 | −0.01 | −0.22 | 0.04 |
| 20.Wisła Ustroń | −0.03 | 0.00 | 0.02 | −0.05 | −0.02 | −0.06 | 0.02 | −0.03 | −0.13 | −0.04 | 0.06 | 0.00 | 0.22 | −0.23 | 0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siwek, J.; Mostowik, K.; Liova, S.; Rzonca, B.; Wacławczyk, P. Baseflow Trends for Midsize Carpathian Catchments in Poland and Slovakia in 1970–2019. Water 2023, 15, 109. https://doi.org/10.3390/w15010109
Siwek J, Mostowik K, Liova S, Rzonca B, Wacławczyk P. Baseflow Trends for Midsize Carpathian Catchments in Poland and Slovakia in 1970–2019. Water. 2023; 15(1):109. https://doi.org/10.3390/w15010109
Chicago/Turabian StyleSiwek, Janusz, Karolina Mostowik, Soňa Liova, Bartłomiej Rzonca, and Patryk Wacławczyk. 2023. "Baseflow Trends for Midsize Carpathian Catchments in Poland and Slovakia in 1970–2019" Water 15, no. 1: 109. https://doi.org/10.3390/w15010109
APA StyleSiwek, J., Mostowik, K., Liova, S., Rzonca, B., & Wacławczyk, P. (2023). Baseflow Trends for Midsize Carpathian Catchments in Poland and Slovakia in 1970–2019. Water, 15(1), 109. https://doi.org/10.3390/w15010109