Improving the Modified Universal Soil Loss Equation by Physical Interpretation of Its Factors
Abstract
:1. Introduction
2. Materials and Methods
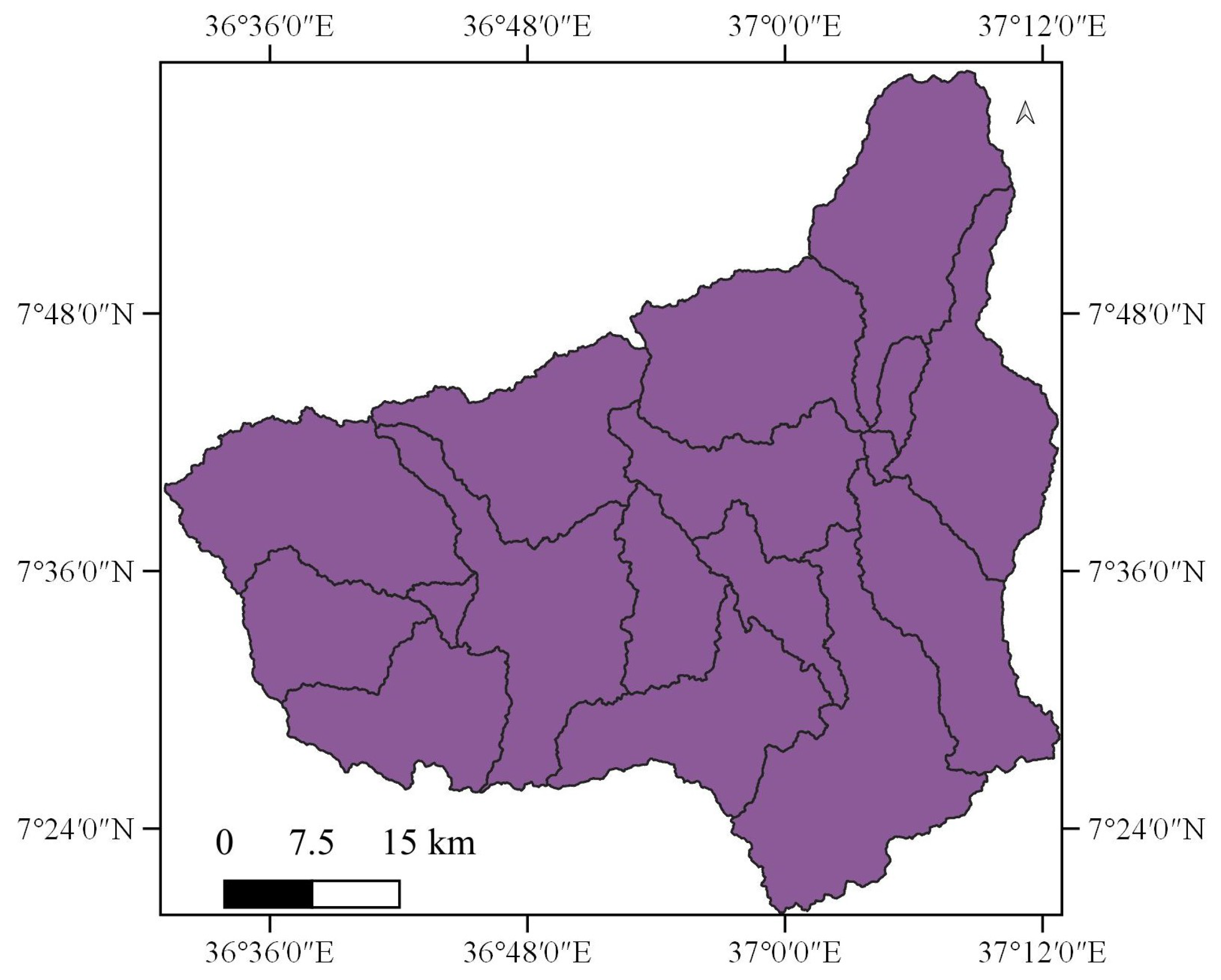
2.1. Description of Study Areas
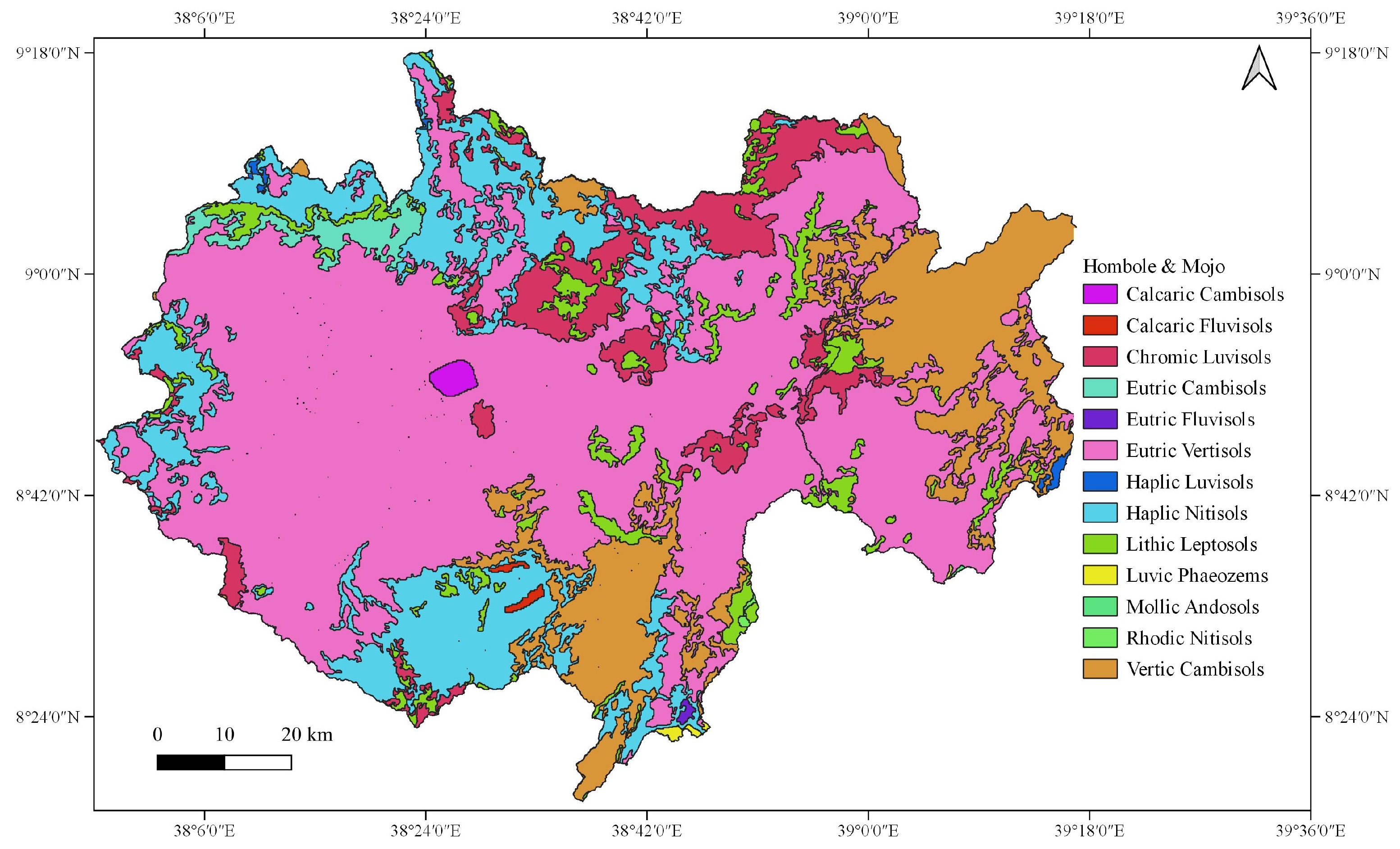
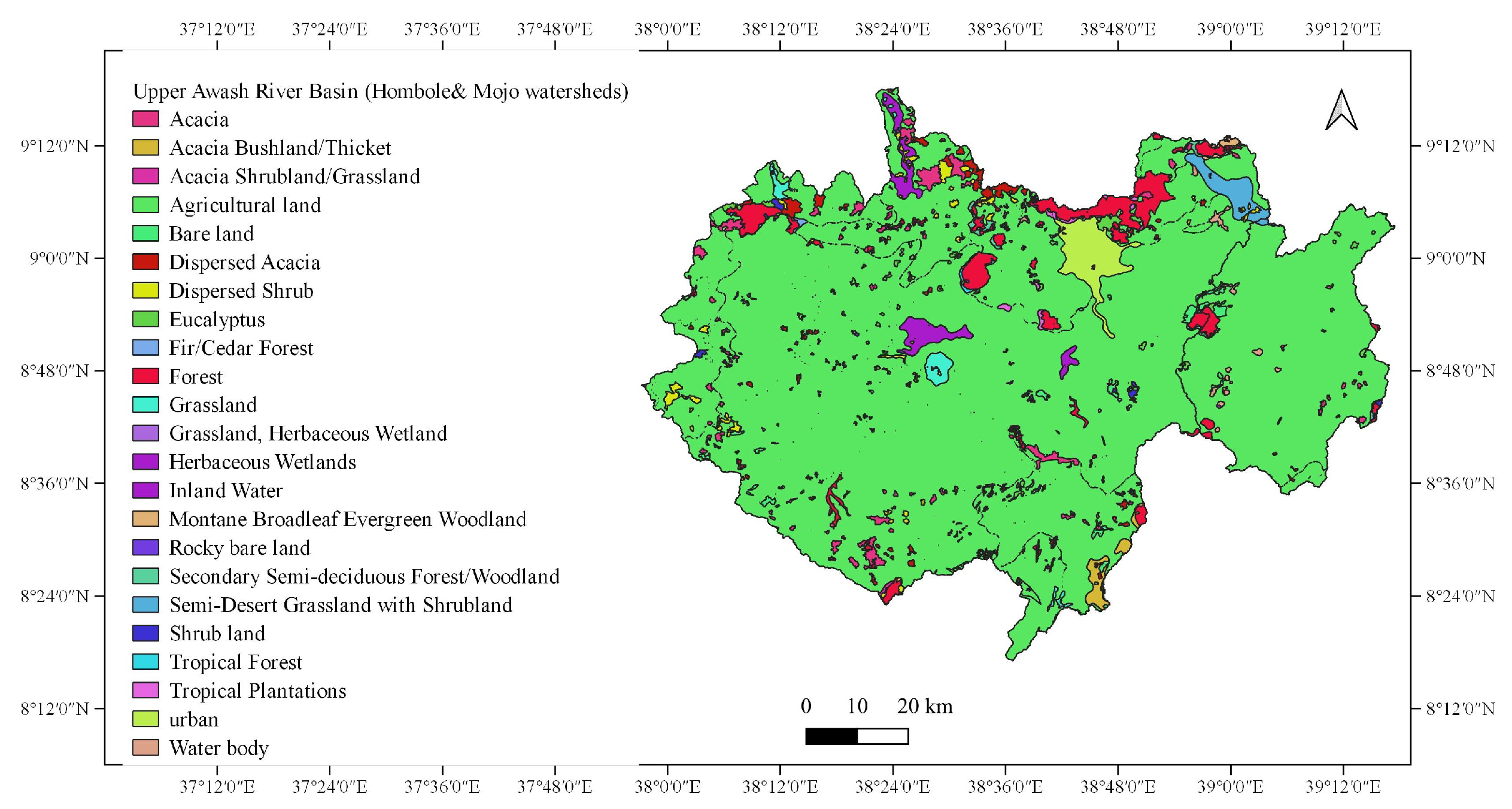
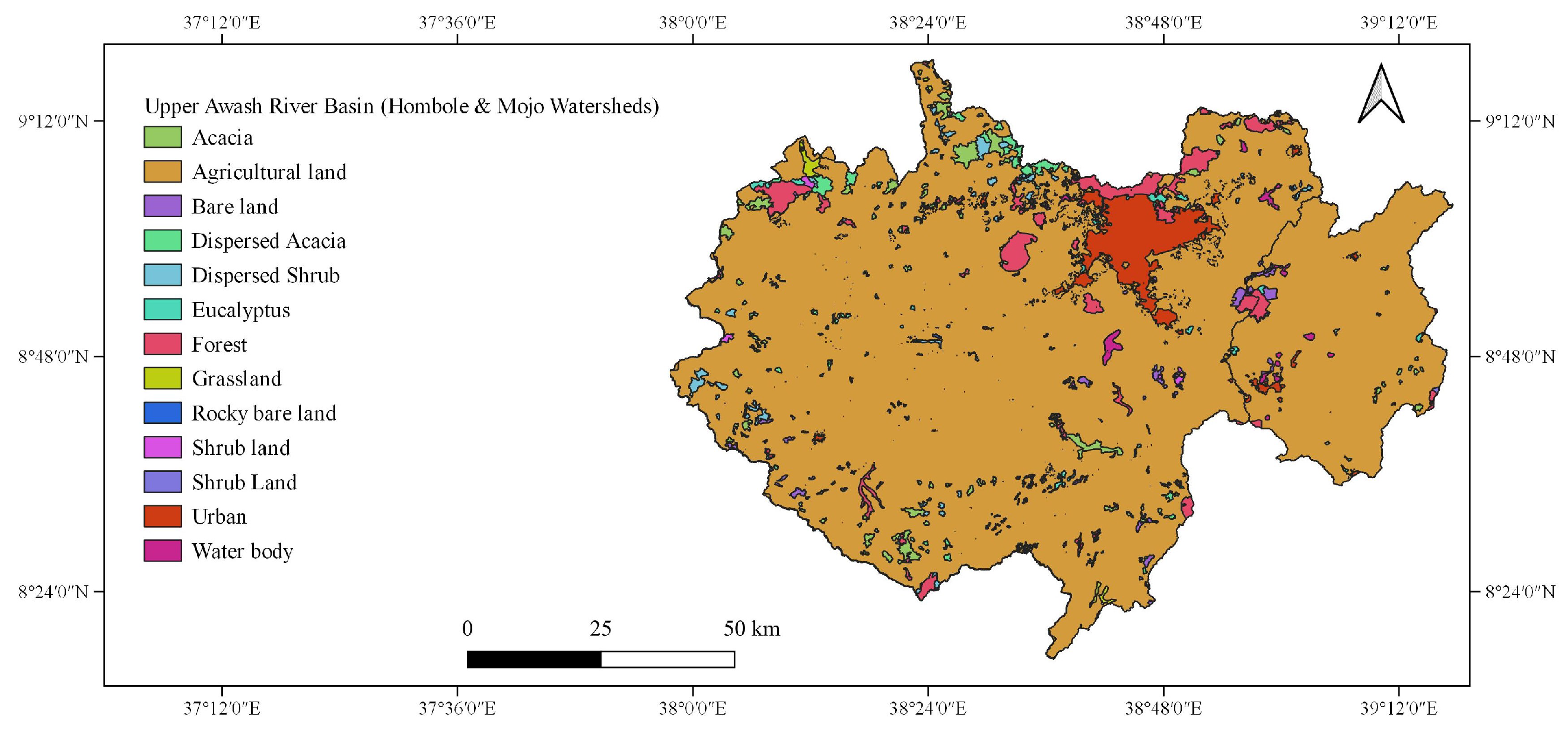
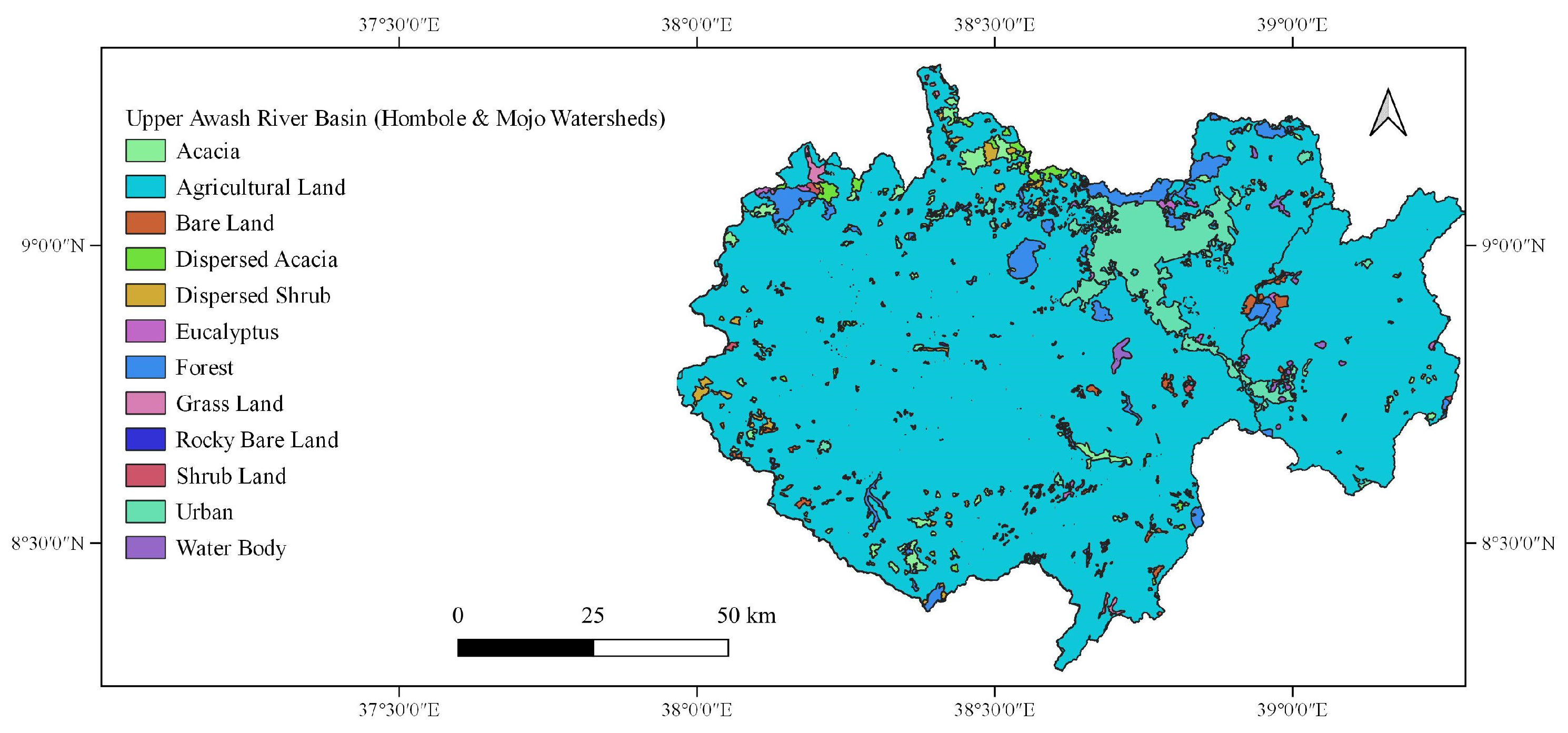
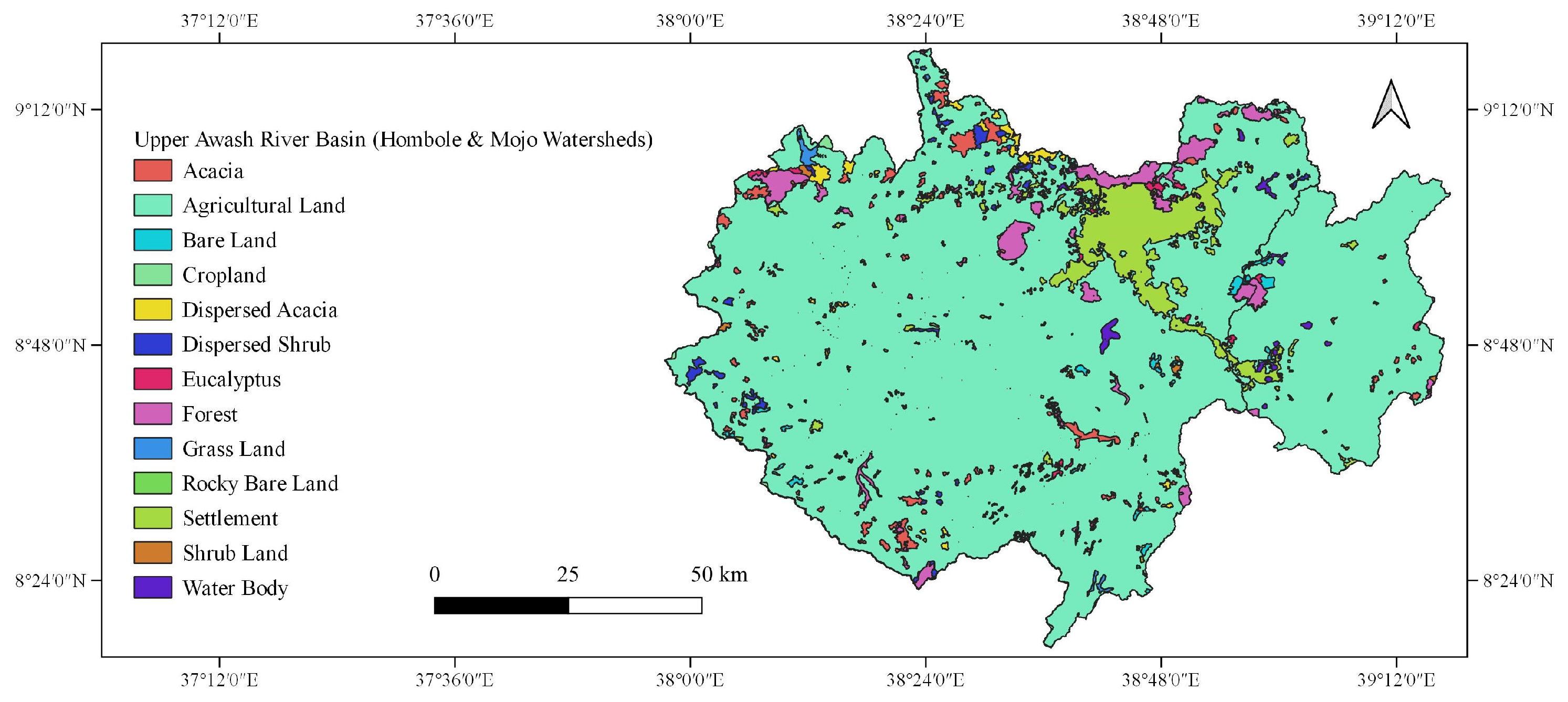
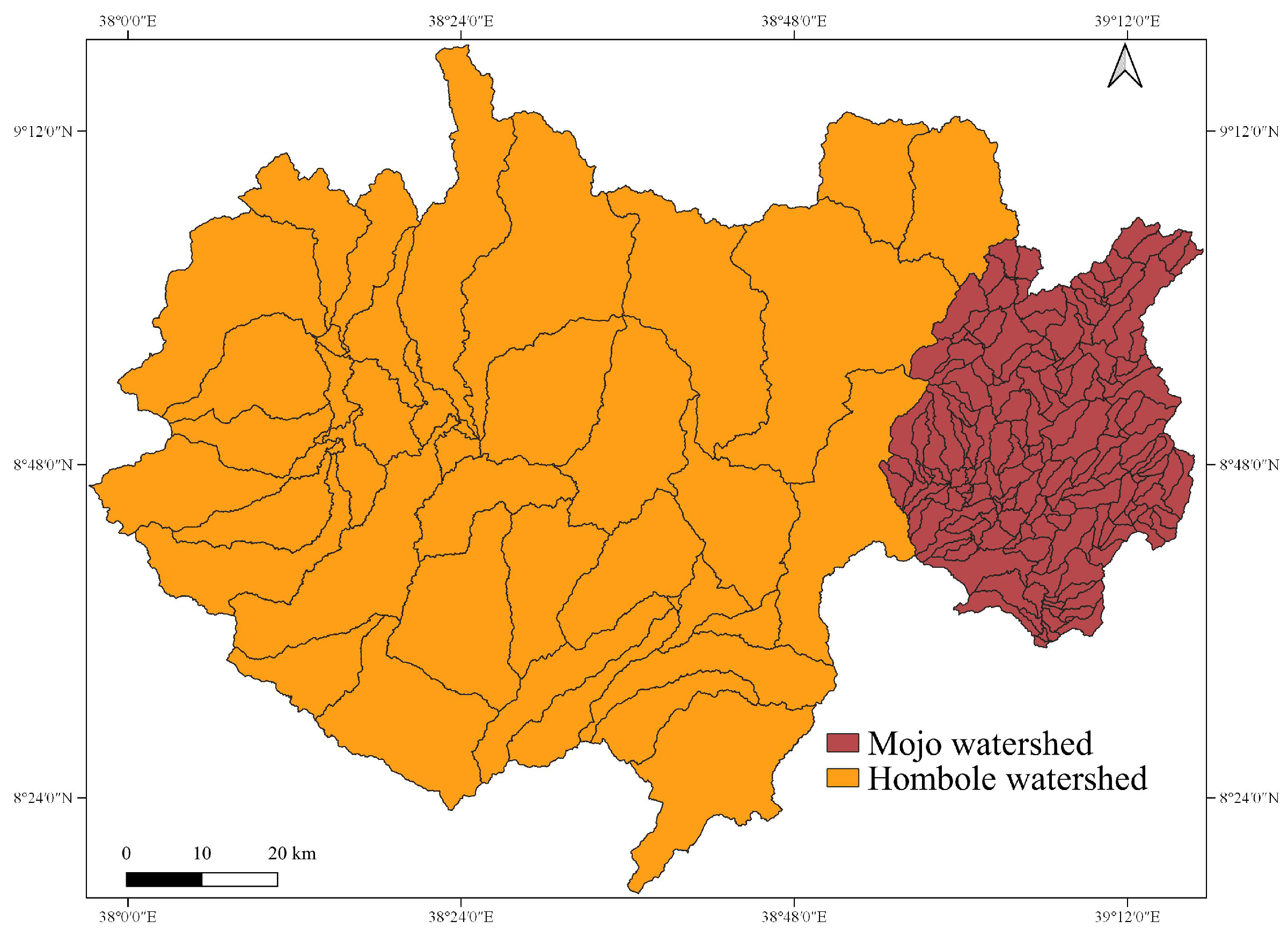
2.1.1. Upper Awash River Basin
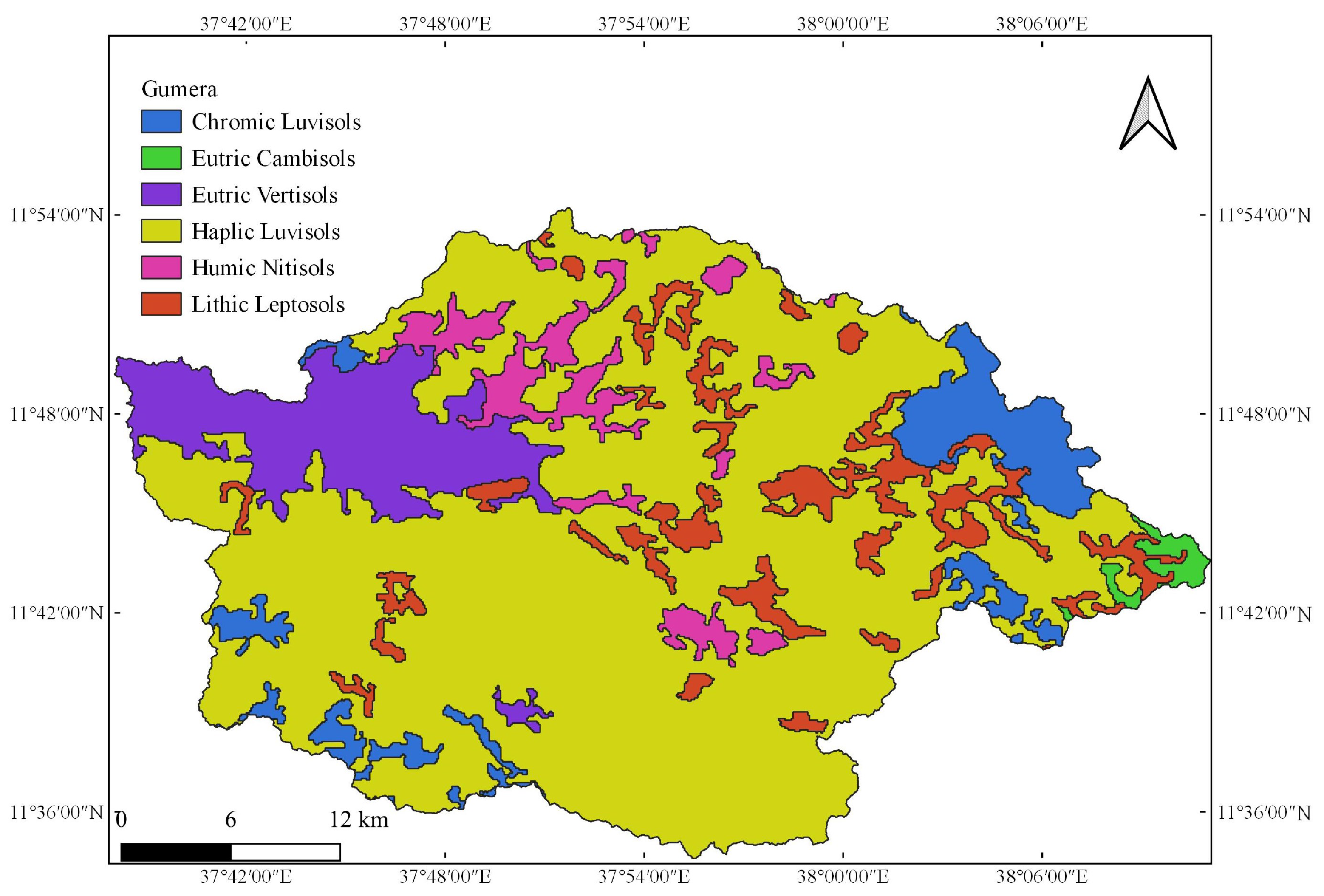
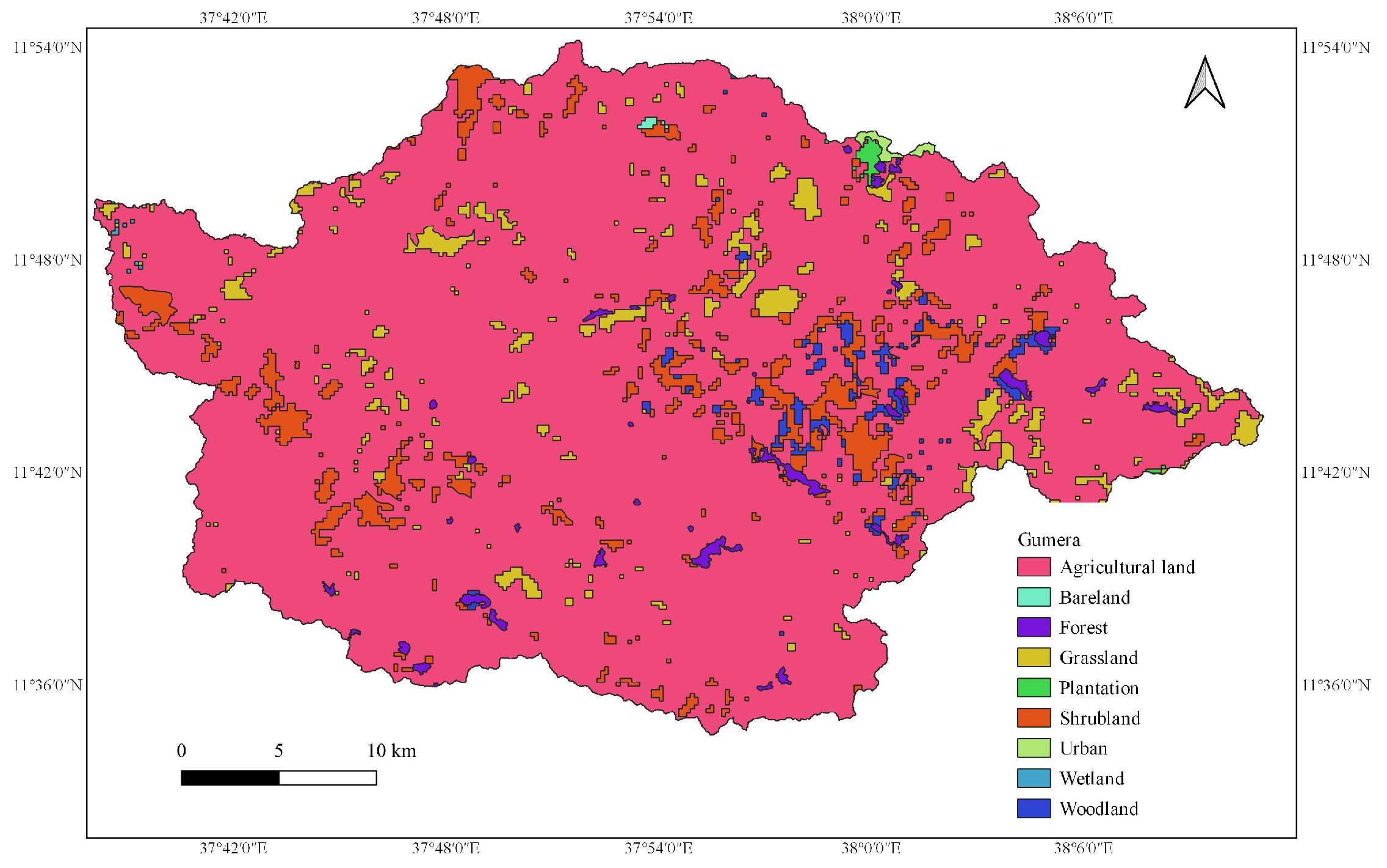
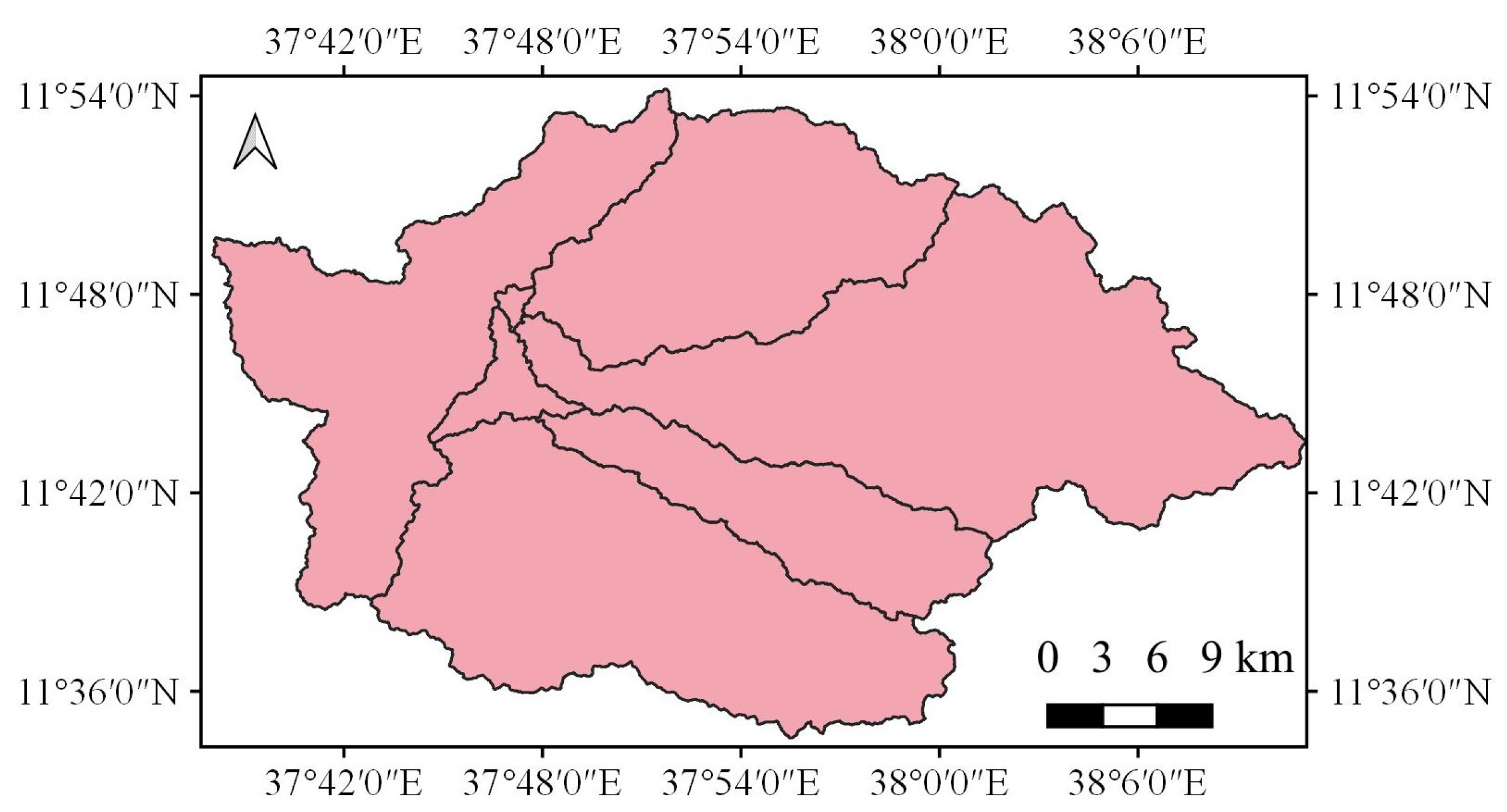
2.1.2. Gumera Watershed
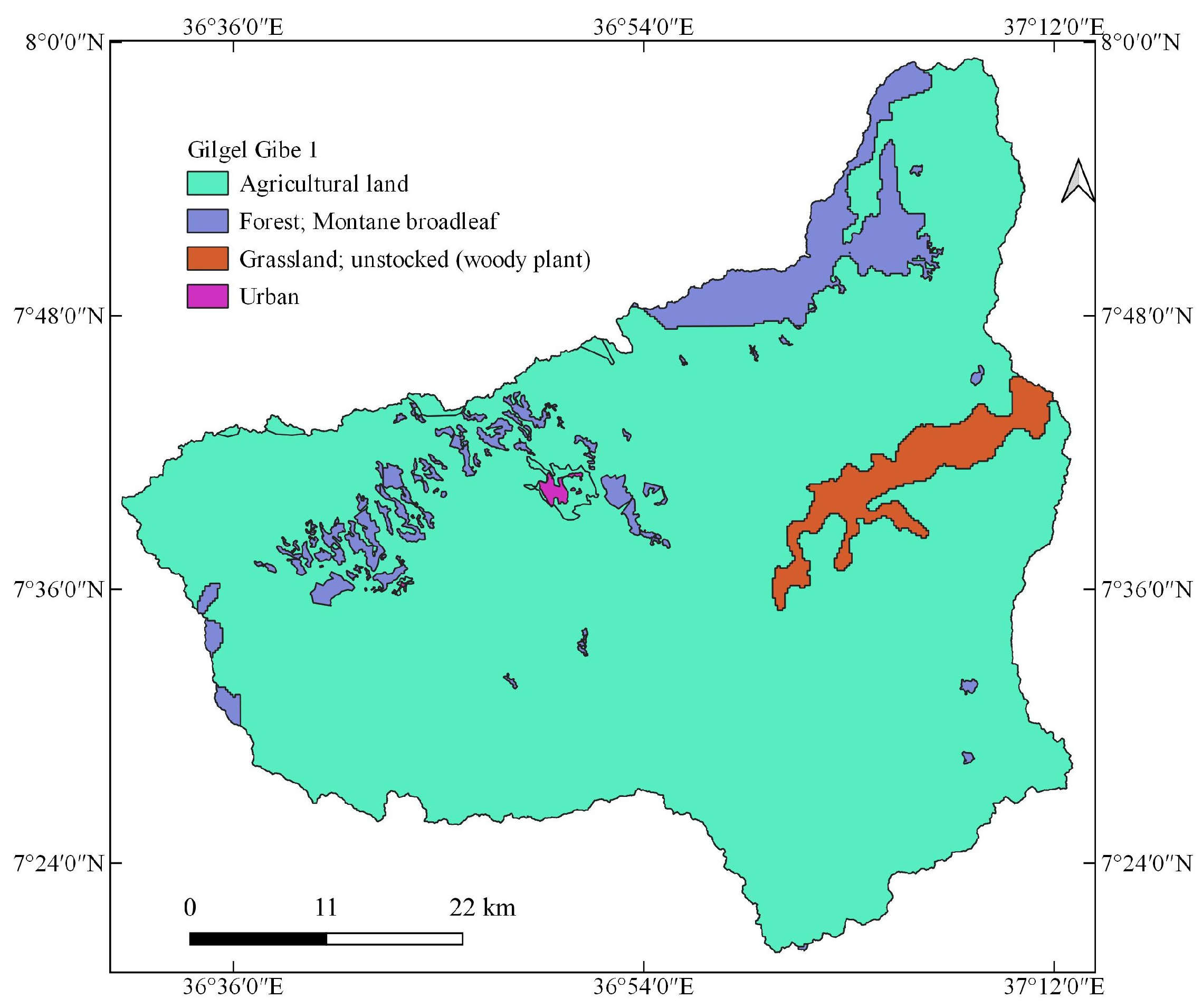
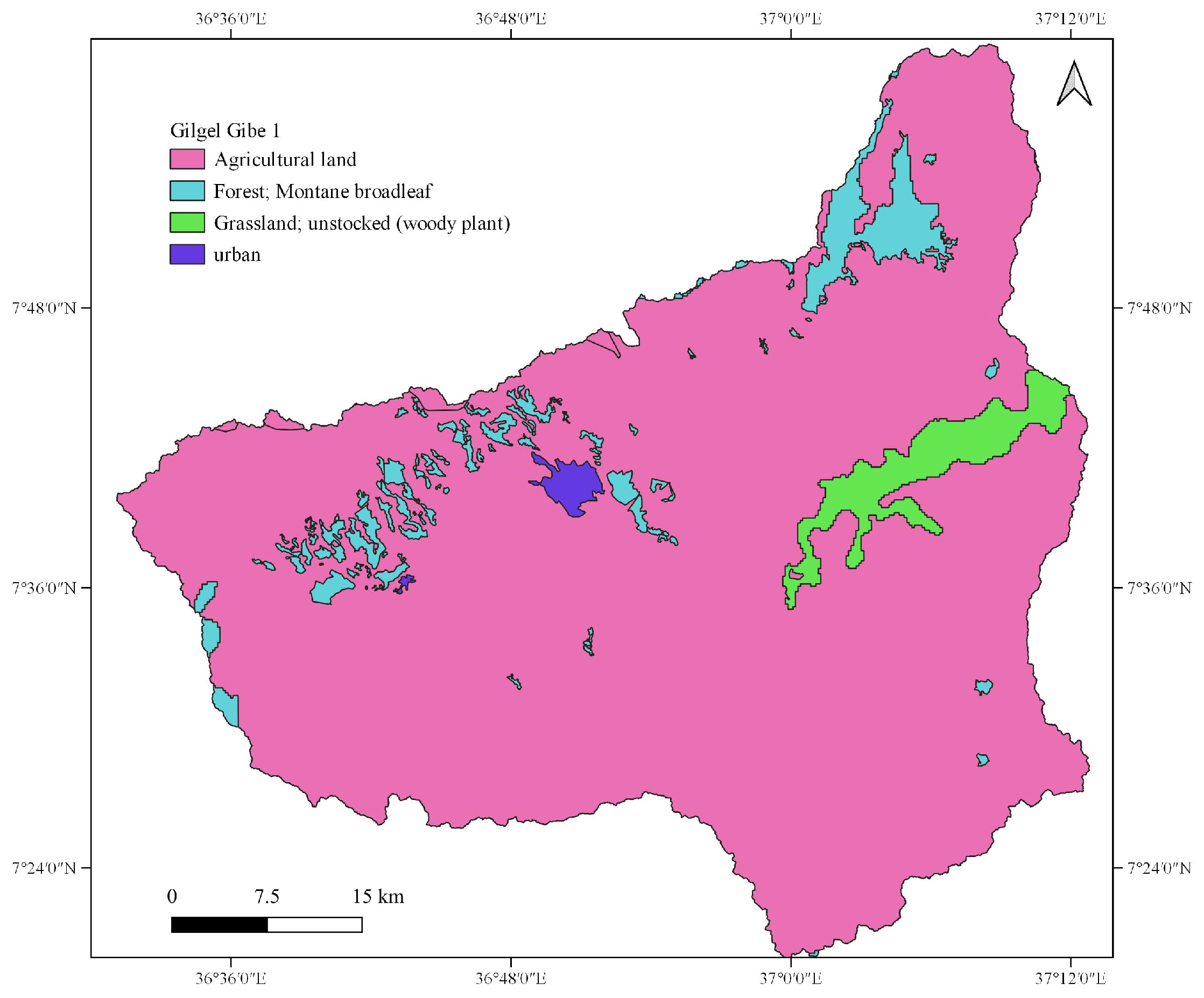
2.1.3. Gilgel Gibe 1 Watershed
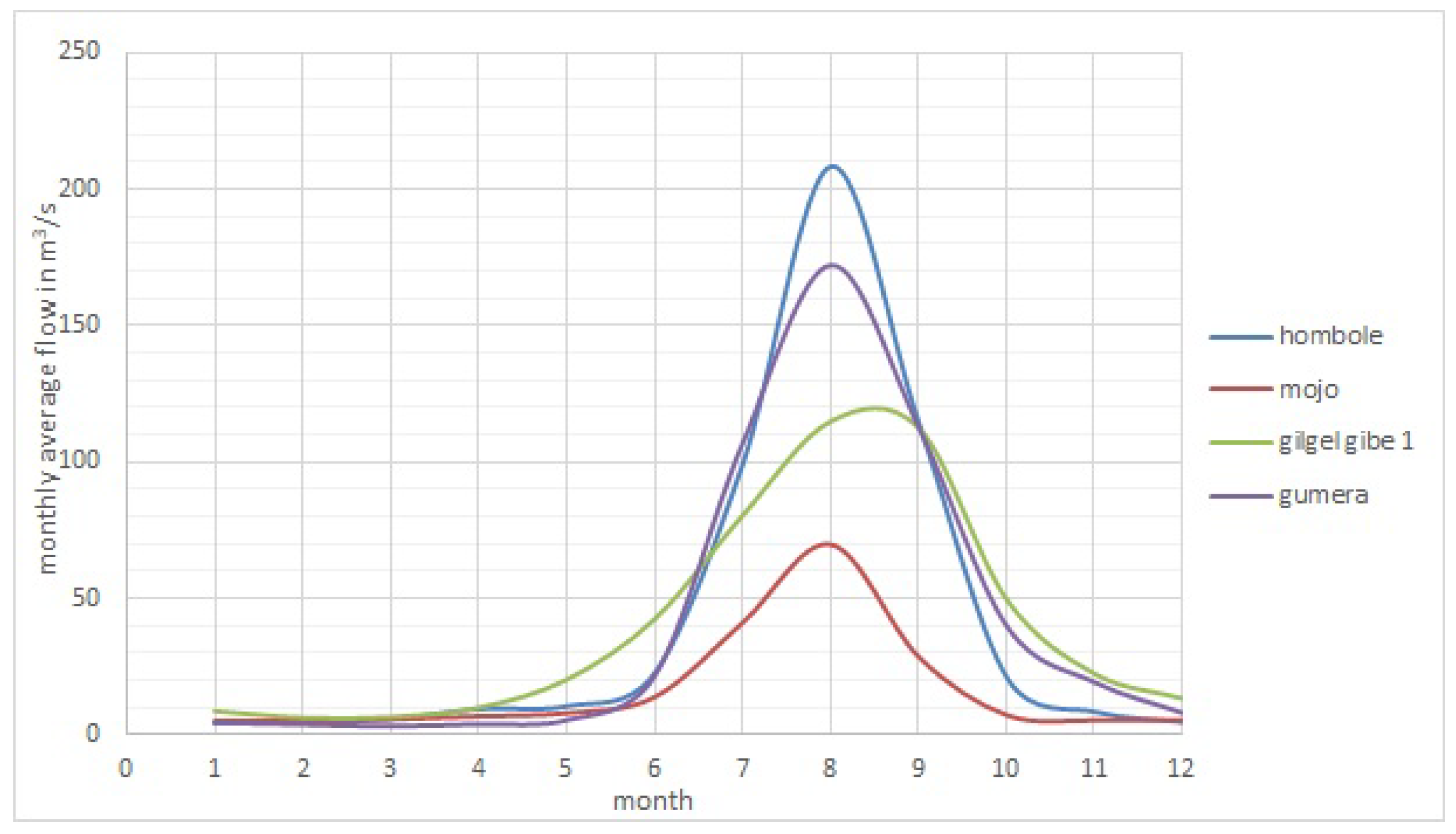
2.2. Sediment Rating Curves
3. Improving MUSLE
3.1. Estimating the Theoretical Exponent of the Improved MUSLE
3.2. Estimating the Factors of the Improved MUSLE
3.2.1. Estimation of Runoff Factor
3.2.2. Estimation of Soil Erodibility Factor (K-Factor)
- The K-factor that was originally developed in the soil conditions of the USA [8]:where K = soil erodibility in , , the particle size parameter, silt (%) = the percentage of silt, % very fine sand = the percentage of very fine sand (0.1–0.05 mm), clay (%) = the percentage of clay, the percentage of organic matter, the soil structure code used in soil classification, and the profile permeability class. For soils containing less than 70 percent silt and very fine sand, the nomograph [8] is used to solve the above equation.To comment on this equation, we did not have a percentage of very fine sand in our database to test the equation. Our source of data was the harmonized world soil data, which includes the texture, reference soil depth, drainage class, available water capacity, sand, silt and clay fractions, bulk density, gravel content, organic carbon content, pH, cation exchange capacity, base saturation, total exchangeable bases, calcium carbonate content, gypsum content, sodicity, and salinity content. As land tillage and mechanical compaction (due to rainfall impact) change the structure of the soil, the structure of the tilled, bare, or compacted soil varies at the temporal and spatial scales. As soil permeability depends on the soil texture and organic matter, their relationship should be explicitly shown. Unrealistic values were obtained for tropical soils from the equation’s erodibility nomograph (Mulengera and Payton, 1999; Ndomba, 2007), as cited in [6].
- The K-factor that was tested in the soil conditions of the Philippines [30]:where = the pH of the soil, = organic matter (%), S = the sand content (%), C = the clay ratio = % clay/(% sand + % silt), and = silt content = % silt/100.
- The K-factor that was originally developed in the volcanic soil of Hawaii, USA (El-Swaify and Dangler, 1976) as cited in [31]:where is the unstable aggregate size fraction (<0.250 mm) in percent, = modified silt (0.002–0.1 mm) (%) ∗ modified sand (0.1–2 mm) (%), = % base saturation, is the silt fraction (0.002–0.050 mm) (%), and is the modified sand fraction (0.1–2 mm) (%).We did not have an unstable aggregate size fraction or modified silt and sand data in our database to test the equation.
3.2.3. Estimation of the Slope Steepness and Slope Length Factors
- The topographic factor that was proposed for the topographic conditions in the USA [8]:where the slope length in feet, the angle of the slope, and m is dependent on the slope (0.5 if slope >5%, 0.4 if slope is between 3.5% and 4.5%, 0.3 if slope is between 1% and 3%, and 0.2 if slope is less than 1%).
- McCool et al. (1987) improved the LS factor from the classic USLE for use in terrain with steeper slopes, as cited in [25], for use in the RUSLE [39]:where is the slope length in meters, m is the dimensionless parameter, is the angle of the field slope in degrees (tan-1 (s/100)), and s is the field slope as a percentage.
- Foster et al. (1977) and McCool et al. (1987, 1989) proposed the following equations for the calculation of the LS factors, as cited in [31]:
- ;
- (Foster et al., 1977), as cited in [31];
- (McCool et al., 1989), as cited in [31];
- if the slope (s) is less than 9% (McCool et al., 1987), as cited in [31];
- if the slope is greater than or equal to 9% ( McCool et al., 1987), as cited in [31].
- if the slope length is shorter than 4.6 m (McCool et al., 1987), as cited in [31], for the condition where water drains freely from the slope end, and it is assumed that inter-rill erosion is insignificant on slopes shorter than 4.6 m [39]. Here, is the slope length (ft), is the angle of the slope, and m is dependent on the slope (0.5 if slope > 5%, 0.4 if the slope is between 3.5% and 4.5%, 0.3 if the slope is between 1% and 3%, and 0.2 if the slope is less than 1%). As a remark, when the conditions favor more inter-rill and less rill erosion, as in the cases of consolidated soils like those found in no-till agriculture, m should be decreased by halving the value, where a low rill to inter-rill erosion ratio is typical of the conditions in rangelands [39]. With thawing and cultivated soils dominated by surface flow, a constant value of 0.5 should be used (McCool et al., 1989, 1993), as cited in [39]. When freshly tilled soil was thawing, in a weakened state, and primarily subjected to surface flow, we used the following (McCool et al., 1993), as cited in [39]:
- The slope factor which is approximately equal to the LS factor in the topographic conditions of the Philippines [30]:where S is the slope factor, a = 0.1, b = 0.21, and is the slope in percent.
- The LS factor was developed in the topographic conditions of Britain [44]:where is the slope length (m) and s is the slope steepness (%).
- Apart from the LS factor of the USLE and RUSLE, the Chinese Soil Loss Equation [45] was developed while taking into consideration the Chinese soil environment and topographic conditions (including the modified equation that can calculate the LS factor in >10° conditions) [46]. In the Chinese soil loss equation, the LS factor is calculated by [46]where is the slope length (m), m is the variable slope length exponent, and is the slope angle (°).
3.2.4. Estimation of the Cover Factor (C Factor)
3.2.5. Estimation of Soil Conservation or Erosion Control Practice Factor (P-Factor)
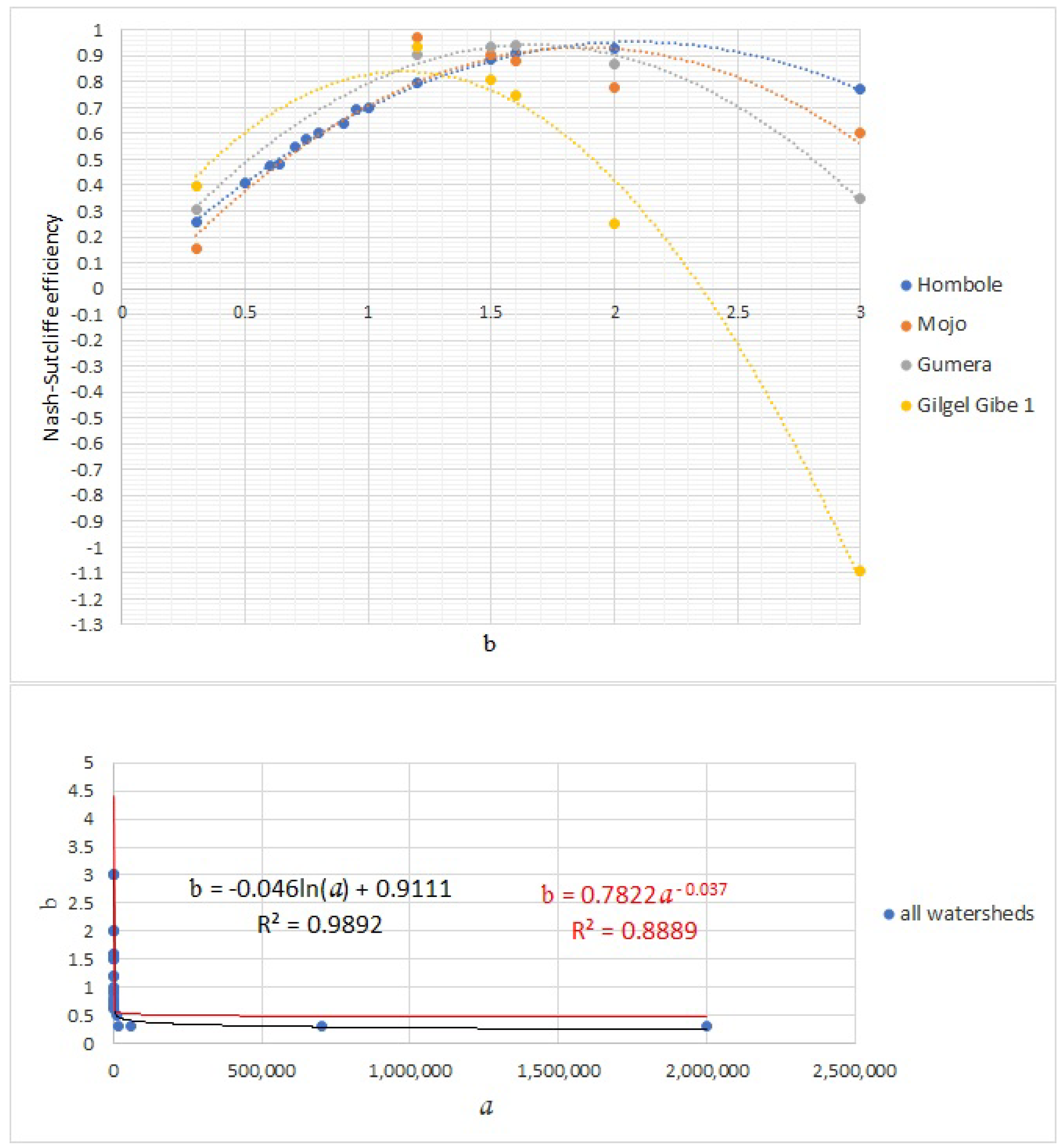
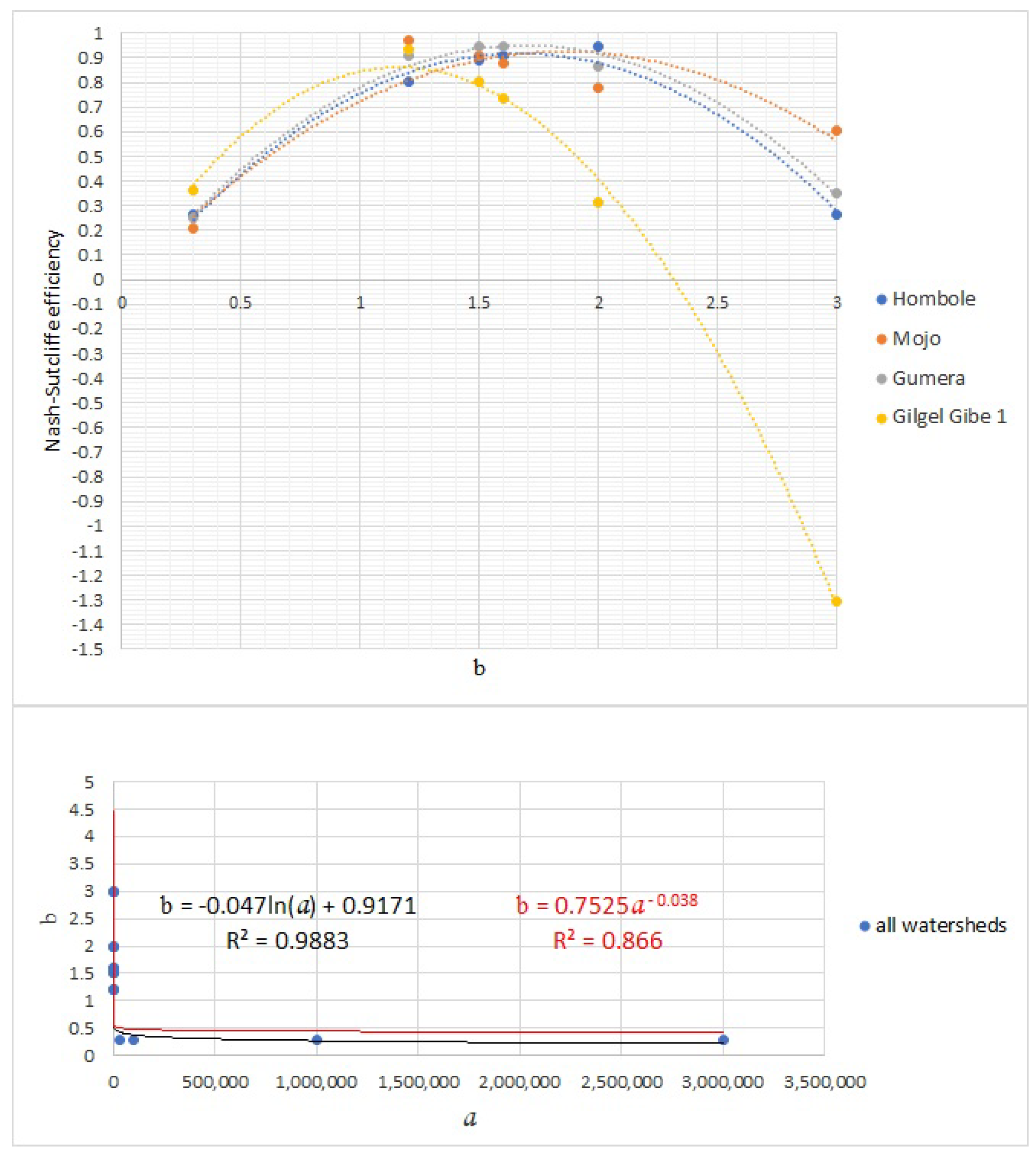
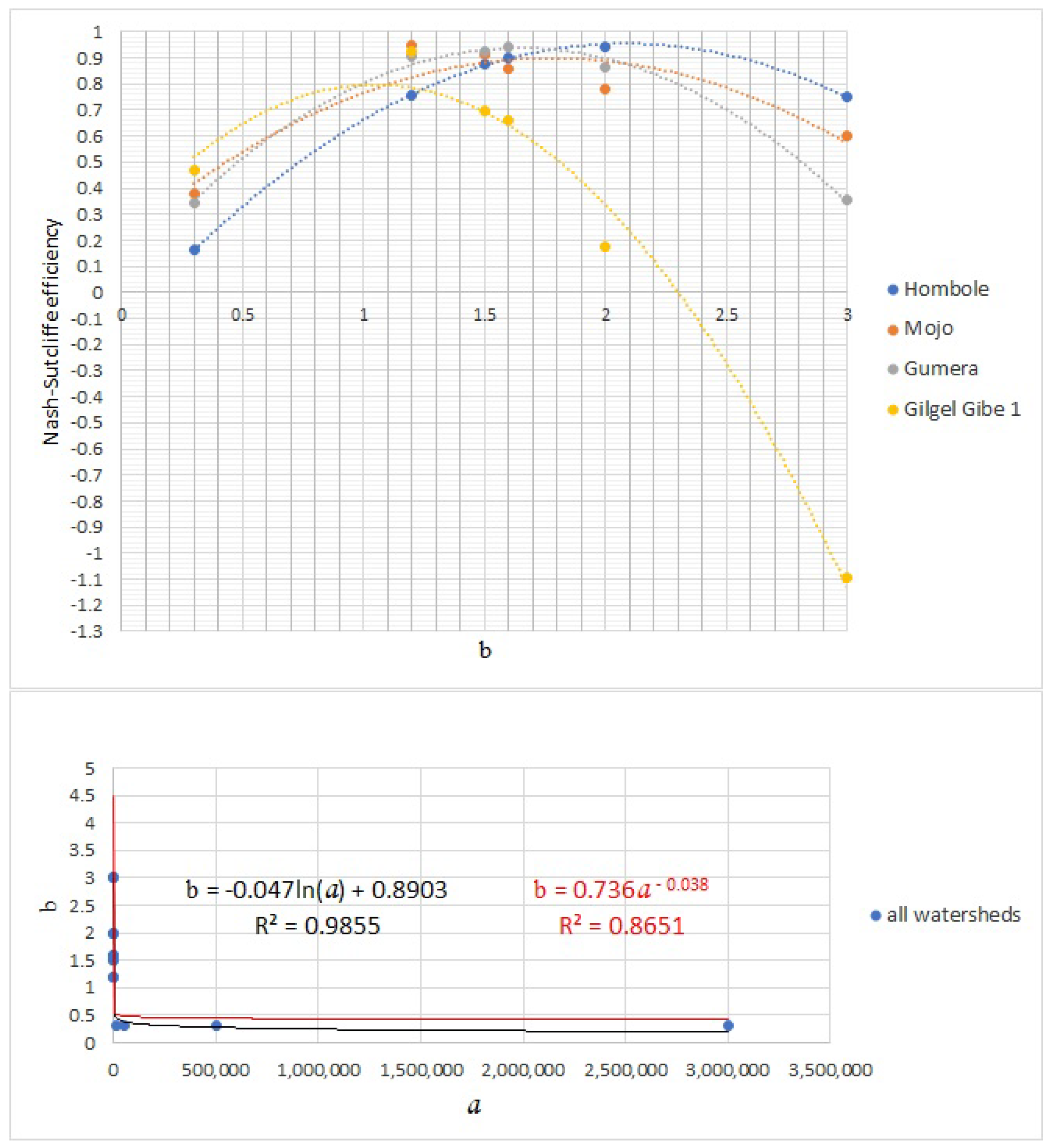
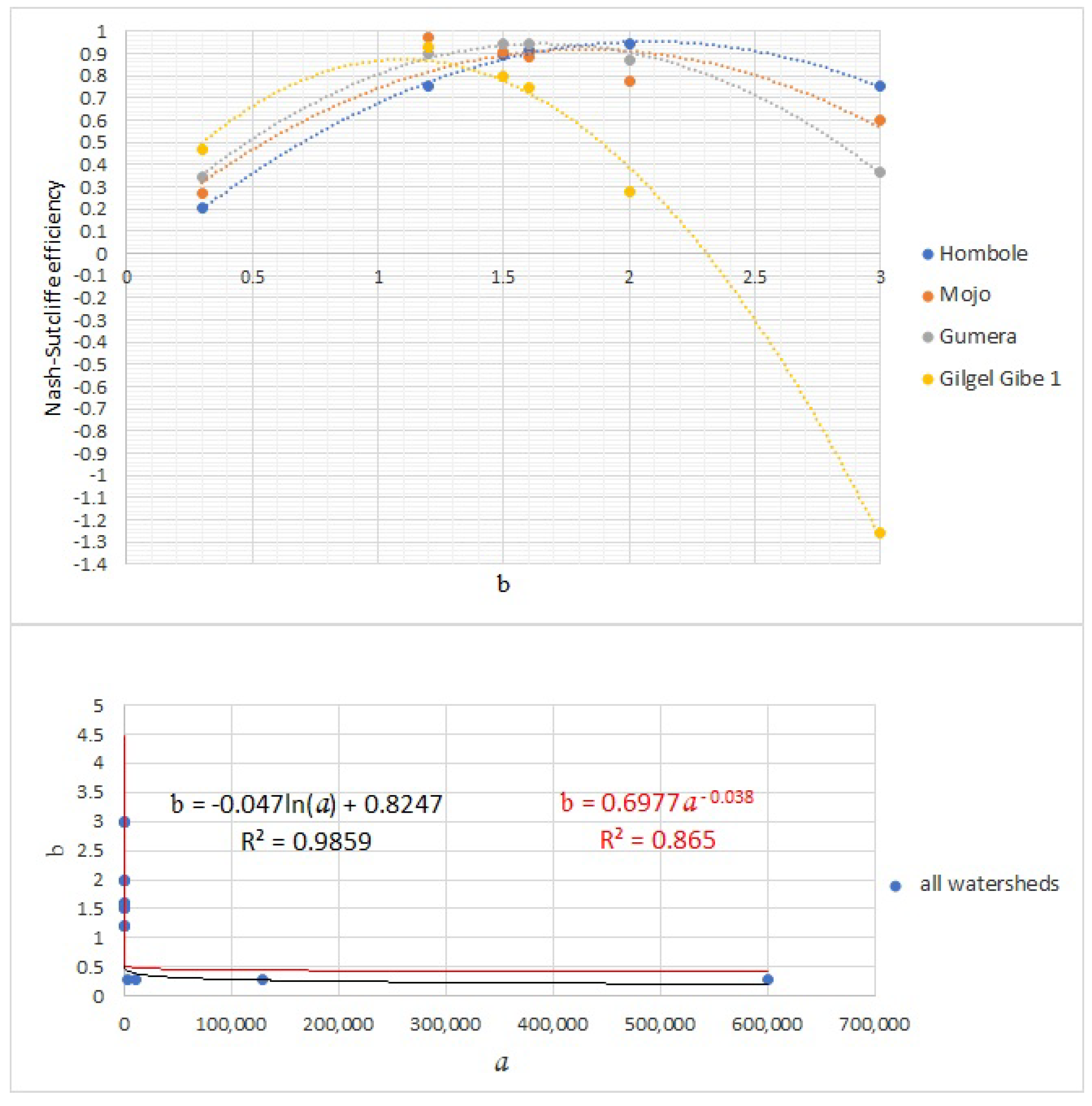
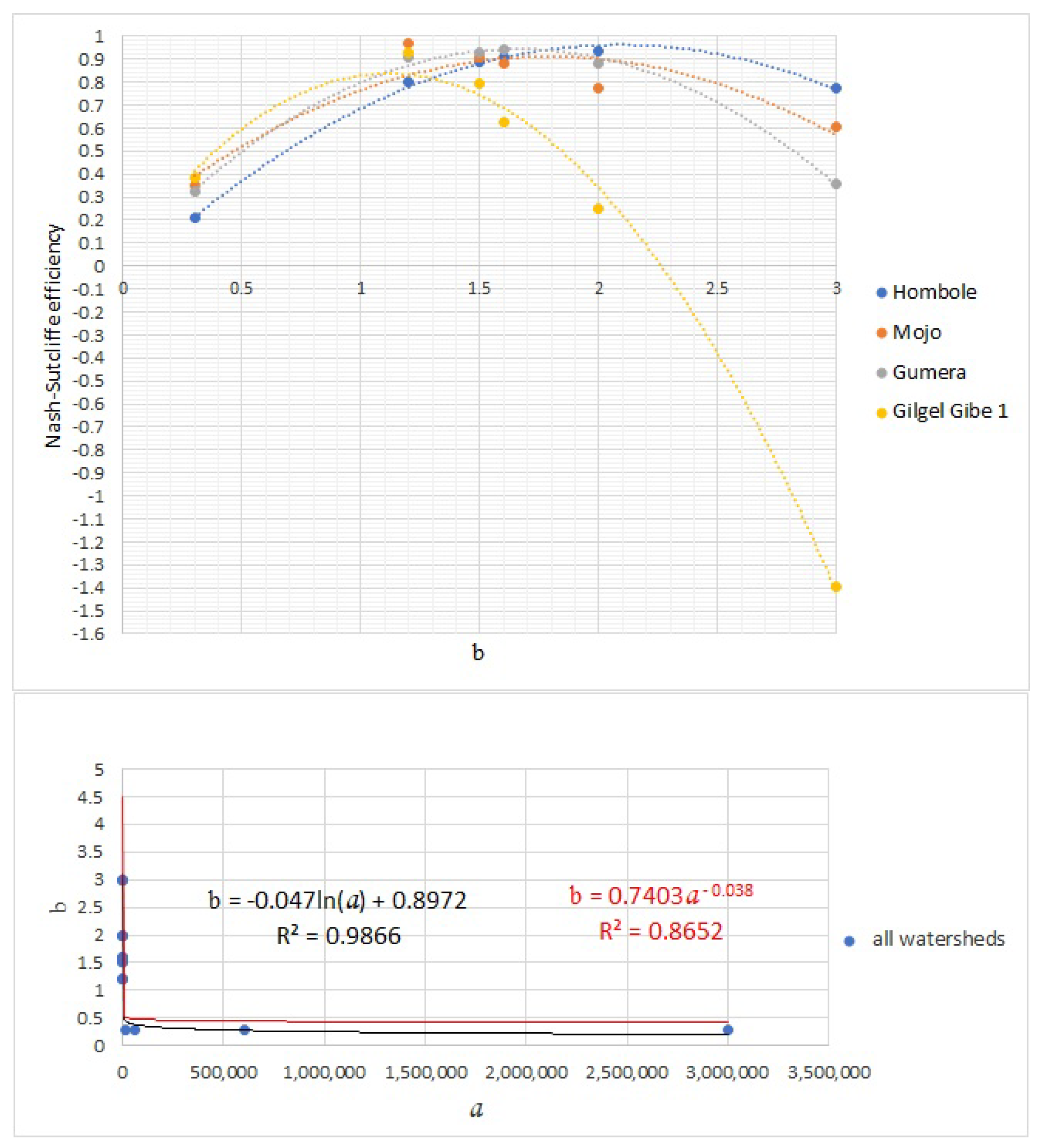
3.2.6. Estimation of Coefficient a and Exponent b through Calibration
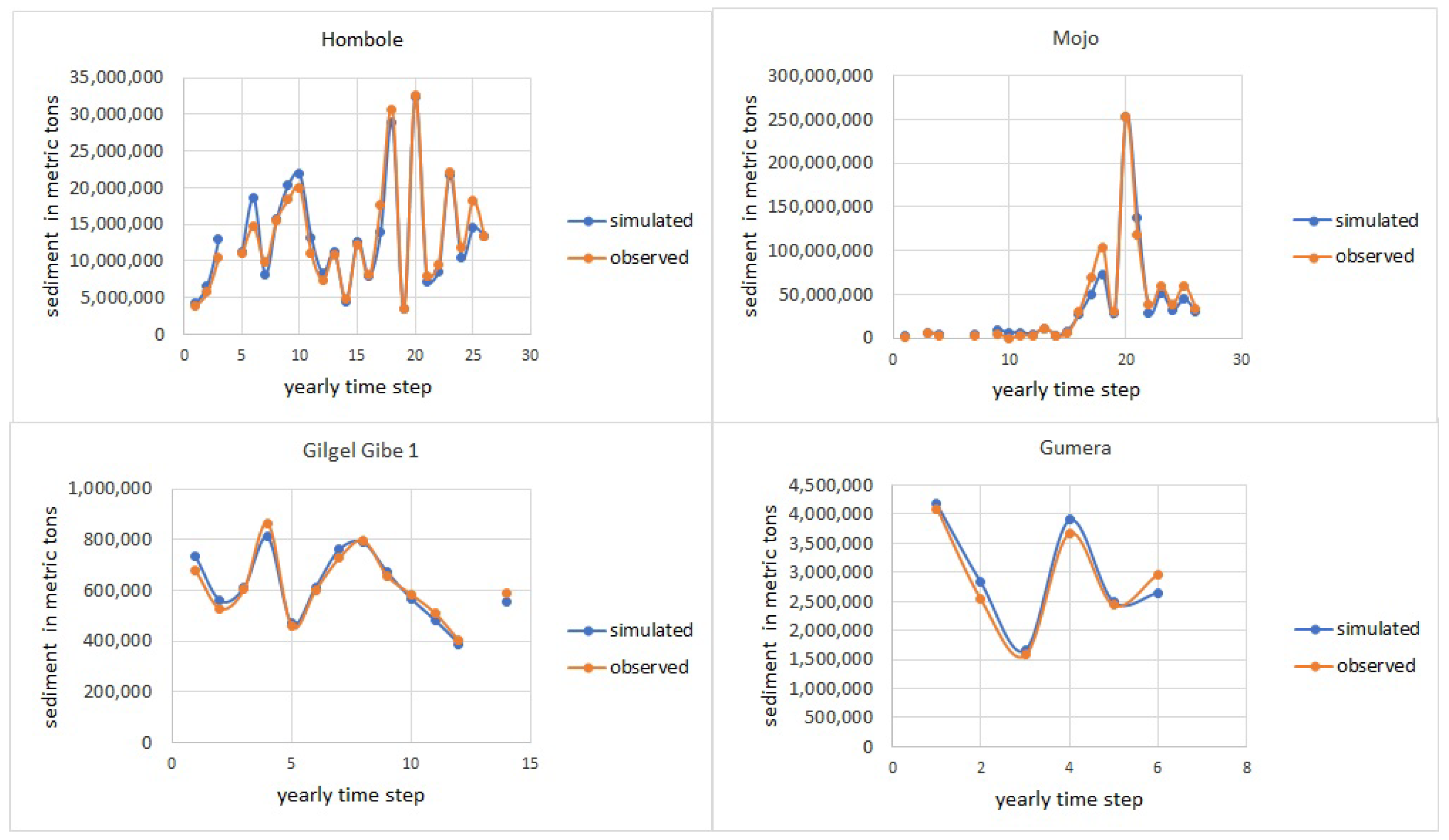
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

Appendix B

References
- Tsige, M.G.; Malcherek, A.; Seleshi, Y. Estimating the Best Exponent of the Modified Universal Soil Loss Equation and Regionalizing the Modified Universal Soil Loss Equation Under Hydro-climatic Condition of Ethiopia. Preprints 2022, 2022020163. [Google Scholar] [CrossRef]
- Williams, J.R. Sediment Routing for Agricultural Watersheds. Water Resour. Bull. 1975, 11, 965–974. [Google Scholar] [CrossRef]
- Williams, J.R.; Berndt, H.D. Sediment Yield Prediction Based on Watershed Hydrology. ASAE 1977, 20, 1100–1104. [Google Scholar] [CrossRef]
- Sadeghi, S.H.R.; Gholami, L.; Darvishan, A.K.; Saeidi, P. A review of the application of the MUSLE model worldwide. Hydrol. Sci. J. 2014, 59, 365–375. [Google Scholar] [CrossRef] [Green Version]
- Sadeghi, S.H.; Mizuyama, T.; Vangah, B.G. Conformity of MUSLE Estimates and Erosion Plot Data for Storm-Wise Sediment Yield Estimation. Terr. Atmos. Ocean. Sci. 2007, 18, 117–128. [Google Scholar] [CrossRef] [Green Version]
- Adegede, A.P.; Mbajiorgu, C.C. Event-Based Sediment Yield Modelling Using MUSLE in North-Central Nigeria. Agric. Eng. Int. Cigr J. 2019, 21, 7–17. Available online: https://cigrjournal.org/index.php/Ejounral/article/view/5231 (accessed on 23 January 2020).
- Muche, H.; Temesgen, M.; Yimer, F. Soil Loss Prediction Using USLE and MUSLE under Conservation Tillage Integrated with ‘Fanya Juus’ in Choke Mountain, Ethiopia. Int. J. Agric. Sci. 2013, 3, 46–52. Available online: https://internationalscholarsjournals.org/print.php?article=soil-loss-predictionusing (accessed on 10 November 2021).
- Wischmeier, W.H.; Smith, D. Predicting Rainfall Erosion Losses: A Guide to Conservation Planning; U.S. Department of Agriculture (USDA): Washington, DC, USA, 1978.
- Soil Conservation Service. Geologic Investigation for Watershed Planning; Technical Release No. 17 Geology; USDA: Washington, DC, USA, 1966. Available online: https://directives.sc.egov.usda.gov/OpenNonWebContent.aspx?content=18602.wba (accessed on 23 January 2020).
- Amare, S.; Langendoen, E.; Keesstra, S.; van der Ploeg, M.; Gelagay, H.; Lemma, H.; van der Zee, S.E.A.T.M. Susceptibility to Gully Erosion: Applying Random Forest (RF) and Frequency Ratio (FR) Approaches to a Small Catchment in Ethiopia. Water 2021, 13, 216. [Google Scholar] [CrossRef]
- Haregeweyn, N.; Tsunekawa, A.; Poesen, J.; Tsubo, M.; Meshesha, D.T.; Fenta, A.A.; Nyssen, J.; Adgo, E. Comprehensive assessment of soil erosion risk for better land use planning in river basins: Case study of the Upper Blue Nile River. Sci. Total Environ. 2017, 574, 95–108. [Google Scholar] [CrossRef] [Green Version]
- Kropače, K.J.; Schillaci, C.; Salvini, R.; Maerker, M. Assessment of Gully Erosion in the Upper Awash, Central Ethiopian Highlands Based on a Comparison of Archived Aerial Photographs and Very High Resolution Satellite Images. Geogr. Fis. Dinam. Quat. 2016, 39, 161–170. [Google Scholar]
- Frankl, A.; Deckers, J.; Moulaert, L.; Damme, A.V.; Haile, M.; Poesen, J.; Nyssen, J. Integrated Solutions for Combating Gully Erosion in Areas Prone to Soil Piping: Innovations from the Drylands of Northern Ethiopia. Land Degrad. Dev. 2014, 27, 1797–1804. [Google Scholar] [CrossRef]
- Haregeweyn, N.; Tsunekawa, A.; Nyssen, J.; Poesen, J.; Tsubo, M.; Meshesha, D.T.; Schutt, B.; Adgo, E.; Tegegne, F. Soil erosion and conservation in Ethiopia: A review. Prog. Phys. Geogr. 2015, 39, 750–774. [Google Scholar] [CrossRef] [Green Version]
- Horowitz, A.J. An evaluation of sediment rating curves for estimating suspended sediment concentrations for subsequent flux calculations. Hydrol. Process. 2003, 17, 3387–3409. [Google Scholar] [CrossRef]
- Heng, S.; Suetsugi, T. Comparison of regionalization approaches in parameterizing sediment rating curve in ungauged catchments for subsequent instantaneous sediment yield prediction. J. Hydrol. 2014, 512, 240–253. [Google Scholar] [CrossRef]
- Asselman, N.E.M. Fitting and interpretation of sediment rating curves. J. Hydrol. 2000, 234, 228–248. [Google Scholar] [CrossRef]
- Hapsari, D.; Onishi, T.; Imaizumi, F.; Noda, K.; Senge, M. The Use of Sediment Rating Curve under its Limitations to Estimate the Suspended Load. Rev. Agric. Sci. 2019, 7, 88–101. [Google Scholar] [CrossRef] [Green Version]
- Efthimiou, N. The role of sediment rating curve development methodology on river load modeling. Environ. Monit. Assess. 2019, 191, 108. [Google Scholar] [CrossRef]
- Talebia, A.; Bahrami, A.; Mardian, M.; Mahjoobi, J. Determination of optimized sediment rating equation and its relationship with physical characteristics of watershed in semiarid regions: A case study of Pol-Doab waters. Desert 2015, 20, 135–144. [Google Scholar] [CrossRef]
- Balamurugan, G. The Use of Suspended Sediment Rating Curves In Malaysia: Some Preliminary Considerations. Pertanika 1989, 12, 367–376. [Google Scholar]
- Doomen, A.M.C.; Wijma, E.; Zwolsman, J.J.K.; Middelkoop, H. Predicting suspended sediment concentrations in the Meuse River using a supply-based rating curve. Hydrol. Process. 2008, 22, 1846–1856. [Google Scholar] [CrossRef]
- Li, G.-L.; Zheng, T.-Z.; Fu, Y.; Li, B.-Q.; Zhang, T. Soil detachment and transport under the combined action of rainfall and runoff energy on shallow overland flow. J. Mt. Sci. 2017, 14, 1373–1383. [Google Scholar] [CrossRef]
- Desmet, P.J.J.; Govers, G. A GIS procedure for automatically calculating the USLE LS factor on topographically complex landscape units. J. Soil Water Conserv. 1996, 51, 427–433. [Google Scholar]
- Pongsai, S.; Vogt, D.S.; Shrestha, R.P.; Clemente, R.S.; Apisit, E. Calibration and validation of the Modified Universal Soil Loss Equation for estimating sediment yield on sloping plots: A case study in Khun Satan catchment of Northern Thailand. Can. J. Soil Sci. 2010, 90, 585–596. [Google Scholar] [CrossRef] [Green Version]
- Gwapedza, D.; Slaughter, A.; Hughes, D.; Mantel, S. Regionalising MUSLE factors for application to a data-scarce catchment. Water Resources Assessment ans Seasonal Prediction. In Proceedings of the International Association of Hydrological Sciences; Copernicus GmbH: Göttingen, Germany, 2018; Volume 377, pp. 19–24. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Qian, X.; Shi, Y. Critical Area Identification of Potential Soil Loss in a Typical Watershed of the Three Gorges Reservoir Region. Water Resour. Manag. 2011, 25, 3445–3463. [Google Scholar] [CrossRef]
- Cole, G.W.; Cooley, K.R.; Dyke, P.T.; Favis-Mortlock, D.T.; Foster, G.R.; Hanson, C.L.; Jones, C.A.; Jones, O.R.; Kiniry, J.R.; Laflen, J.M.; et al. EPIC—Erosion/Productivity Impact Calculator; Technical Bulletin Number 1768; United States Department of Agriculture, Agricultural Research Service: Washington, DC, USA, 1990.
- Kruk, E. Use of Chosen Methods for Determination of the USLE Soil Erodibility Factor on the Example of Loess Slope. J. Ecol. Eng. 2021, 22, 151–161. [Google Scholar] [CrossRef]
- David, W.P. Soil and Water Conservation Planning: Policy Issues and Recommendations. J. Philipp. Dev. 1988, XV, 47–84. [Google Scholar]
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; McCool, D.K.; Yoder, D.C. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation; Agriculture Handbook, No 703; USDA: Washington, DC, USA, 1997; p. 404.
- Wawer, R.; Nowocien, E.; Podolski, B. Real and Calculated KUSLE Erodibility Factor for Selected Polish Soils. Pol. J. Environ. Stud. 2005, 14, 655–658. [Google Scholar]
- Wischmeier, W.H.; Mannering, J.V. Relation of Soil Properties to its Erodibility. Soil Sci. Soc. Amer. Proc. 1969, 33, 131–137. [Google Scholar] [CrossRef]
- Wang, B.; Zheng, F.; Guan, Y. Improved USLE-K factor prediction: A case study on water erosion areas in China. Int. Soil Water Conserv. Res. 2016, 4, 168–176. [Google Scholar] [CrossRef] [Green Version]
- Panagos, P.; Meusburger, K.; Ballabio, C.; Borrelli, P.; Alewell, C. Soil erodibility in Europe: A high-resolution dataset based on LUCAS. Sci. Total Environ. 2014, 479–480, 189–200. [Google Scholar] [CrossRef]
- Liu, B.; Xie, Y.; Li, Z.; Liang, Y.; Zhang, W.; Fu, S.; Yin, S.; Wei, X.; Zhang, K.; Wang, Z.; et al. The assessment of soil loss by water erosion in China. Int. Soil Water Conserv. Res. 2020, 8, 430–439. [Google Scholar] [CrossRef]
- van der Knijff, J.M.; Jones, R.J.A.; Montanarella, L. Soil Erosion Risk Assessment in Europe; Publications Office of the European Union: Rue Mercier, Luxembourg, 2000; pp. 1–34. [Google Scholar]
- Ganasri, B.P.; Ramesh, H.H. Assessment of soil erosion by RUSLE model using remote sensing and GIS—A case study of Nethravathi Basin. Geosci. Front. 2016, 7, 953–961. [Google Scholar] [CrossRef] [Green Version]
- Renard, K.G.; Yoder, D.C.; Lightle, D.T.; Dabney, S.M. Handbook of Erosion Modelling: Universal Soil Loss Equation and Revised Universal Soil Loss Equation; Blackwell Publishing Ltd.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Moore, I.D.; Wilson, J.P. Length-slope factors for the Revised Universal Soil Loss Equation: Simplified method of estimation. J. Soil Water Conserv. 1992, 47, 423–428. [Google Scholar]
- Kinnell, P.I.A. Event soil loss, runoff and the Universal Soil Loss Equation family of models: A review. J. Hydrol. 2010, 385, 384–397. [Google Scholar] [CrossRef]
- Fagbohun, B.J.; Anifowose, A.Y.B.; Odeyemi, C.; Aladejana, O.O.; Aladeboyeje, A.I. GIS-based estimation of soil erosion rates and identification of critical areas in Anambra sub-basin, Nigeria. Model. Earth Syst. Environ. 2016, 2, 159. [Google Scholar] [CrossRef] [Green Version]
- Mitasova, H.; Hofierka, J.; Zlocha, M.; Iverson, L.R. Modelling topographic potential for erosion and deposition using GIS. Int. J. Geogr. Inf. Syst. 1996, 10, 629–641. [Google Scholar] [CrossRef]
- Morgan, R.P.C. Soil Erosion and Conservation; Blackwell Science Ltd.: Hoboken, NJ, USA, 2005; ISBN 1-4051-1781-8. [Google Scholar]
- Baoyuan, L.; Keli, Z.; Yun, X. An Empirical Soil Loss Equation. In Proceedings of the 12th International Soil Conservation Organization Conference, Beijing, China, 26–31 May 2002; pp. 21–25. Available online: https://www.tucson.ars.ag.gov/isco/isco12/VolumeII/AnEmpiricalSoilLossEquation.pdf (accessed on 10 September 2021).
- Zhang, H.; Wei, J.; Yang, Q.; Baartman, J.E.M.; Gai, L.; Yang, X.; Li, S.; Yu, J.; Ritsema, C.J.; Geissen, V. An improved method for calculating slope length and the LS parameters of the Revised Universal Soil Loss Equation for large watersheds. Geoderma 2017, 308, 36–45. [Google Scholar] [CrossRef]
- Schmidt, S.; Tresch, S.; Meusburger, K. Modification of the RUSLE slope length and steepness factor (LS-factor) based on rainfall experiments at steep alpine grasslands. MethodsX 2019, 6, 219–229. [Google Scholar] [CrossRef]
- Benavidez, R.; Jackson, B.; Maxwell, D.; Norton, K. A review of the (Revised) Universal Soil Loss Equation ((R)USLE): With a view to increasing its global applicability and improving soil loss estimates. Hydrol. Earth Syst. Sci. 2018, 22, 6059–6086. [Google Scholar] [CrossRef] [Green Version]
- Wang, L. Effects of land use changes on soil erosion in a fast developing area. Int. J. Environ. Sci. Technol. 2014, 11, 1549–1562. [Google Scholar] [CrossRef] [Green Version]
- Arekhi, S.; Shabani, A.; Rostamizad, G. Application of the modified universal soil loss equation (MUSLE) in prediction of sediment yield (Case study: Kengir Watershed, Iran. Arab J. Geosci. 2012, 5, 1259–1267. [Google Scholar] [CrossRef]
- Jang, C.; Shin, Y.; Kum, D.; Kim, R.; Yang, J.E.; Kim, S.C.; Hwang, S.I.; Lim, K.J.; Yoon, J.-K.; Park, Y.S.; et al. Assessment of soil loss in South Korea based on land-cover type. Stoch. Environ. Res. Risk Assess. 2015, 29, 2127–2141. [Google Scholar] [CrossRef]
- Luo, Y.; Yang, S.; Liu, X.; Liu, C.; Zhang, Y.; Zhou, Q.; Zhou, X.; Dong, G. Suitability of revision to MUSLE for estimating sediment yield in the Loess Plateau of China. Stoch. Environ. Res. Risk Assess. 2016, 30, 379–394. [Google Scholar] [CrossRef]




| Land Use Category | C Factor | P Factor |
|---|---|---|
| Acacia | 0.01 | 1 |
| Acacia Bushland, Thicket | 0.01 | 1 |
| Acacia Shrubland, Grassland | 0.01 | 1 |
| Agricultural Land | 0.525 | 0.52 |
| Bare Land | 1 | 1 |
| Dispersed Acacia | 0.01 | 1 |
| Dispersed Shrub | 0.01 | 1 |
| Eucalyptus | 0.001 | 1 |
| Fir or Cedar Forest | 0.001 | 1 |
| Forest | 0.001 | 1 |
| Forest, Montane Broadleaf | 0.001 | 1 |
| Grassland | 0.01 | 1 |
| Grassland, Herbaceous Wetland | 0.01 | 1 |
| Grassland, Unstocked (Woody Plant) | 0.01 | 1 |
| Herbaceous Wetlands | 0.01 | 1 |
| Montane Broadleaf Evergreen Woodland | 0.001 | 1 |
| Rocky Bare Land | 1 | 1 |
| Secondary Semi-Deciduous Forest or Woodland | 0.001 | 1 |
| Semi-Desert Grassland with Shrubland | 0.01 | 1 |
| Shrubland | 0.01 | 1 |
| Tropical Forest | 0.001 | 1 |
| Plantations | 0.001 | 1 |
| Tropical Plantations | 0.001 | 1 |
| Urban | 0 | 1 |
| Water Bodies | 0 | 0 |
| Wetland | 0.01 | 1 |
| Woodland | 0.01 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsige, M.G.; Malcherek, A.; Seleshi, Y. Improving the Modified Universal Soil Loss Equation by Physical Interpretation of Its Factors. Water 2022, 14, 1450. https://doi.org/10.3390/w14091450
Tsige MG, Malcherek A, Seleshi Y. Improving the Modified Universal Soil Loss Equation by Physical Interpretation of Its Factors. Water. 2022; 14(9):1450. https://doi.org/10.3390/w14091450
Chicago/Turabian StyleTsige, Manaye Getu, Andreas Malcherek, and Yilma Seleshi. 2022. "Improving the Modified Universal Soil Loss Equation by Physical Interpretation of Its Factors" Water 14, no. 9: 1450. https://doi.org/10.3390/w14091450
APA StyleTsige, M. G., Malcherek, A., & Seleshi, Y. (2022). Improving the Modified Universal Soil Loss Equation by Physical Interpretation of Its Factors. Water, 14(9), 1450. https://doi.org/10.3390/w14091450





