Parameter Estimation and Assessment of Infiltration Models for Madjez Ressoul Catchment, Algeria
Abstract
1. Introduction
2. Materials and Methods
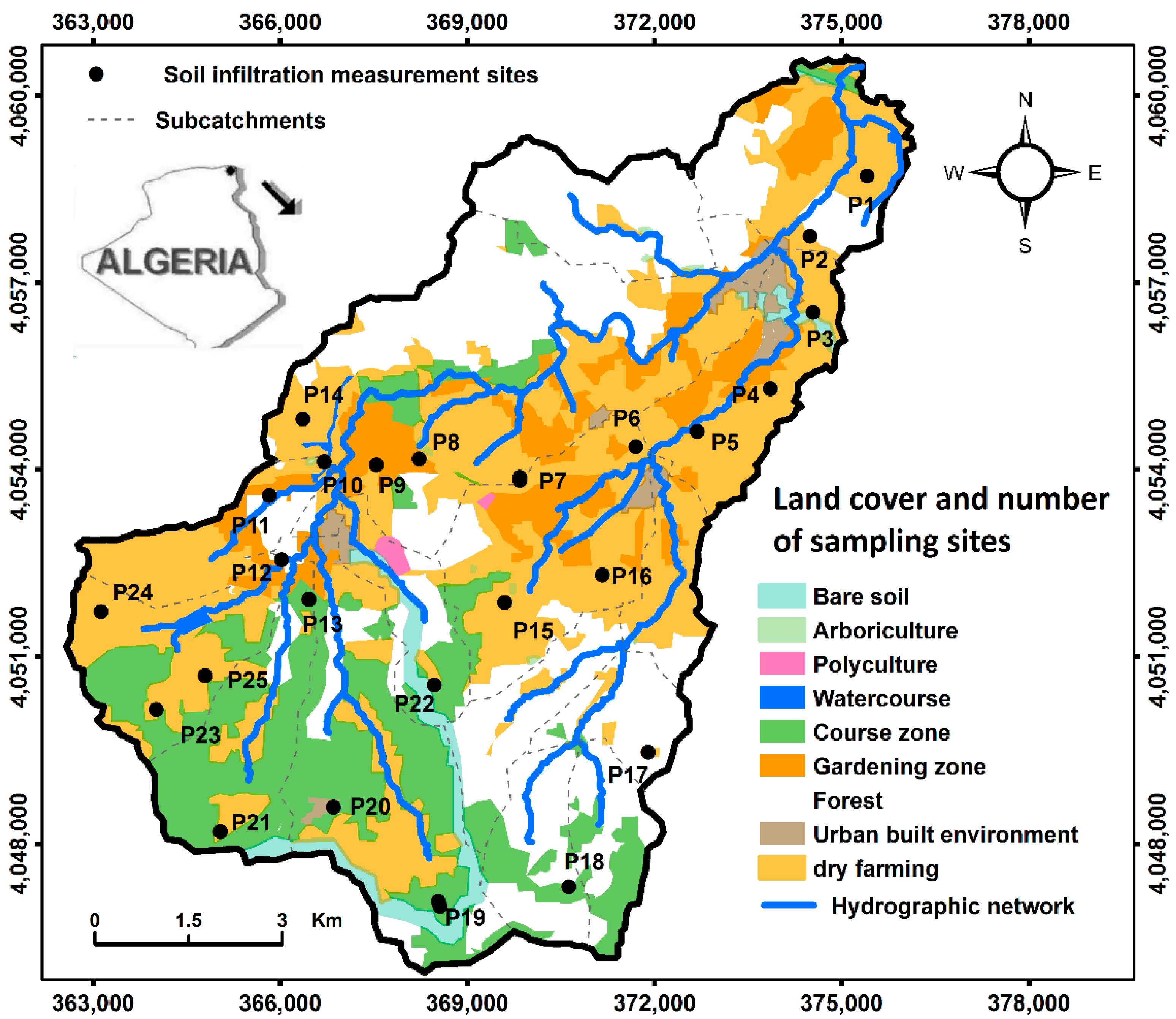
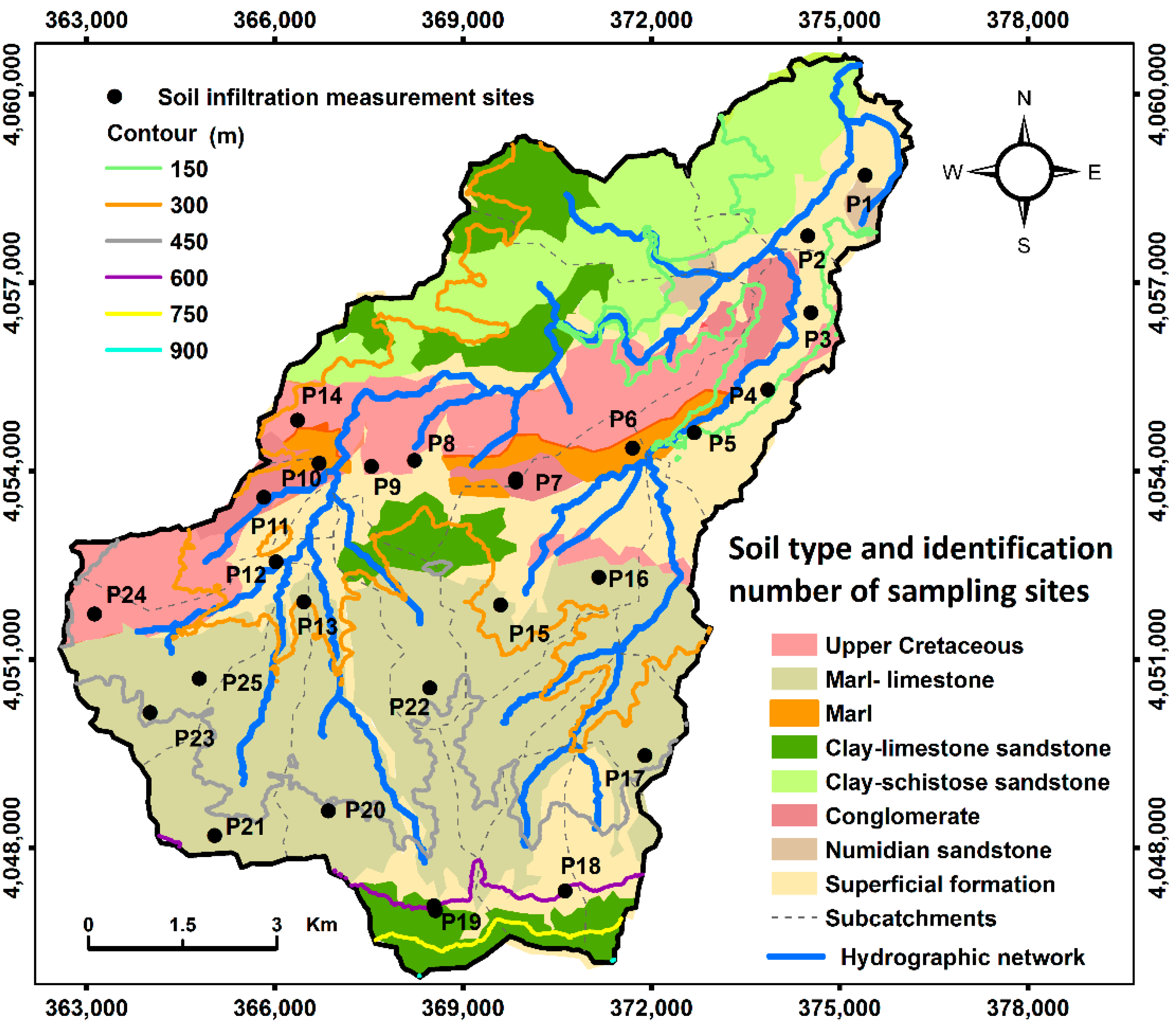
2.1. Study Area
2.2. Field Measurements and Measuring Methods
2.3. Parametrization of Infiltration Models for Madjez Ressoul Catchment
2.4. Model Calibration and Assessment of Model Parameters
3. Results
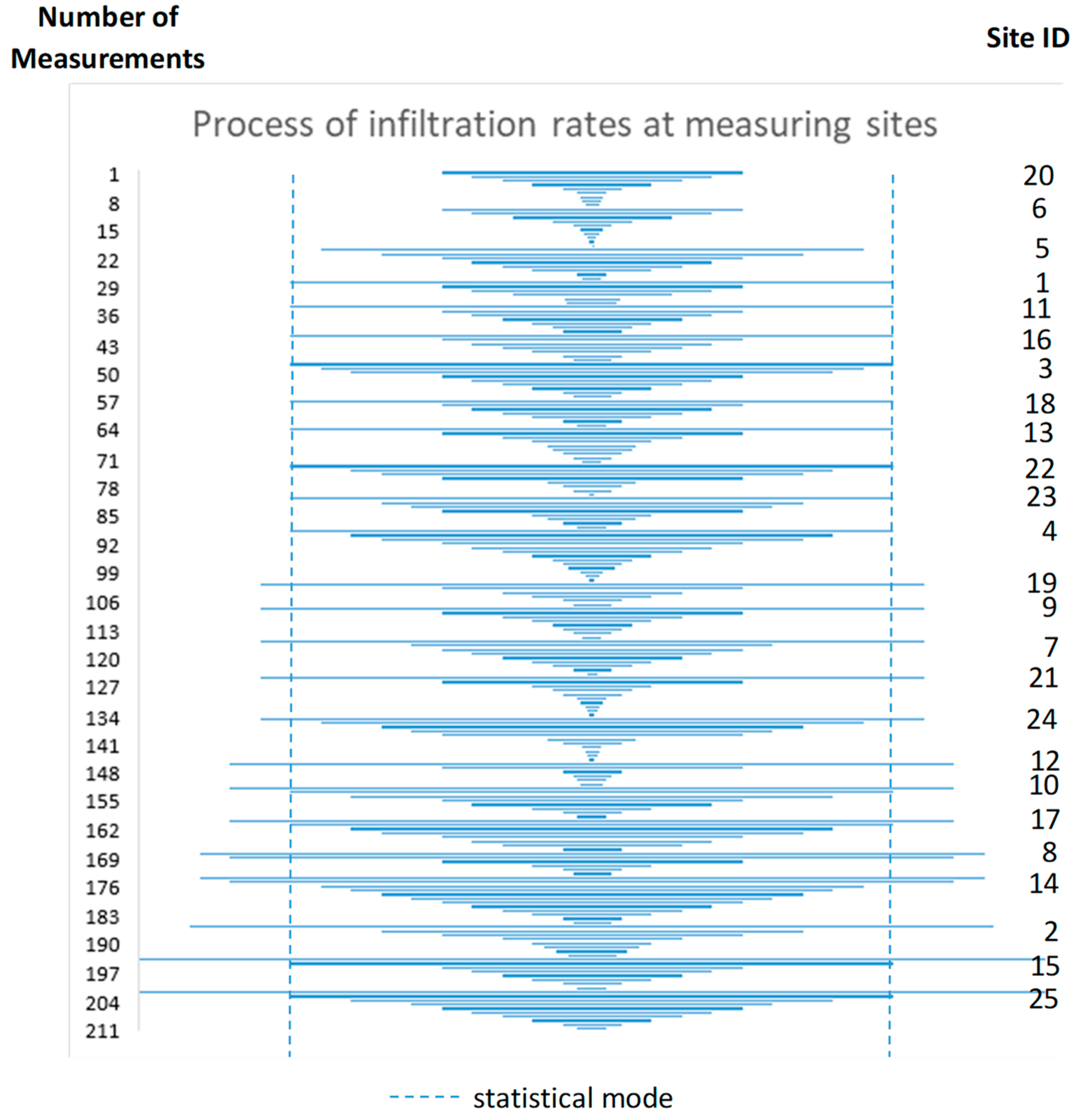
3.1. Effect of Soil Texture and Soil Moisture on Infiltration Rates
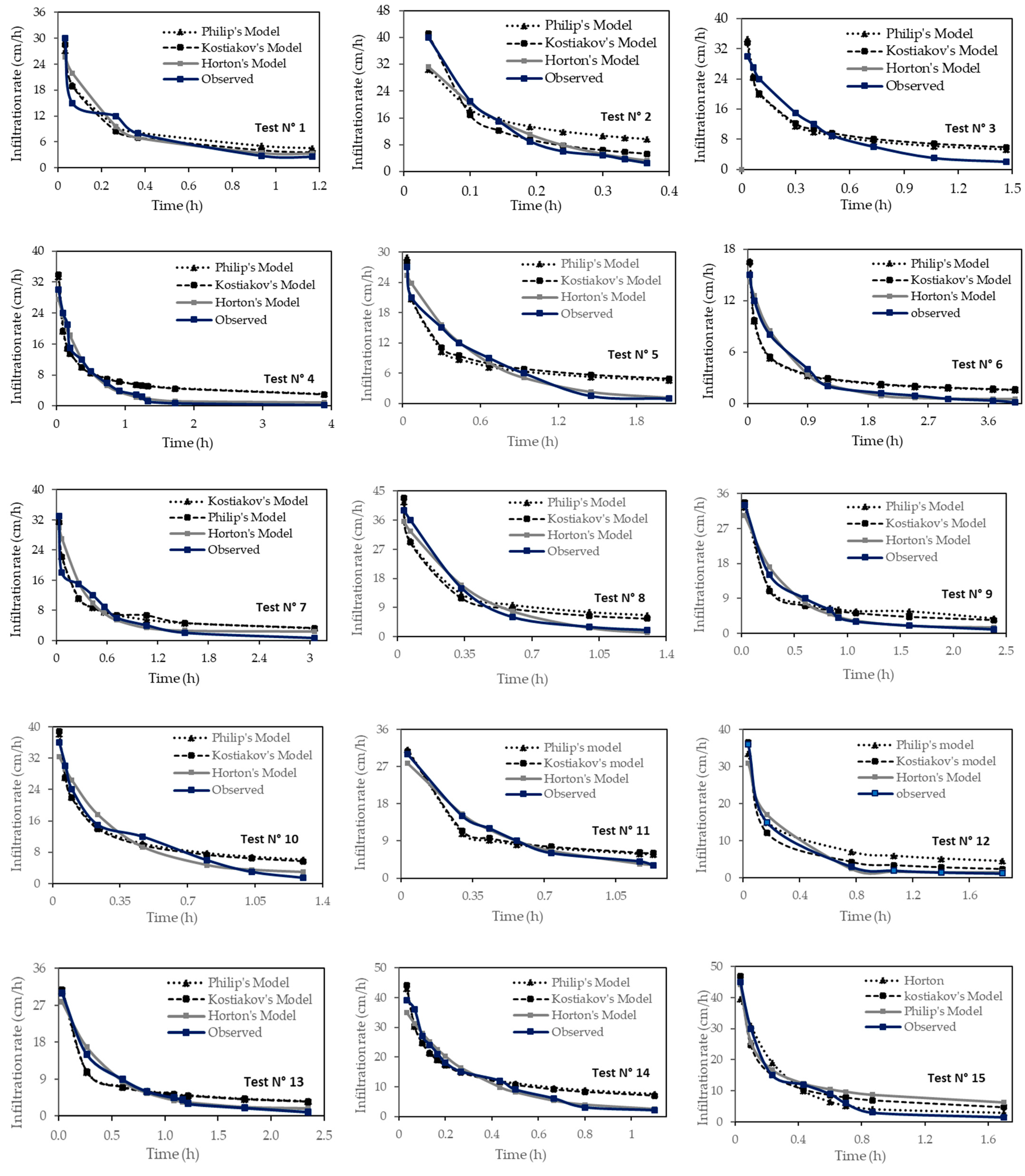
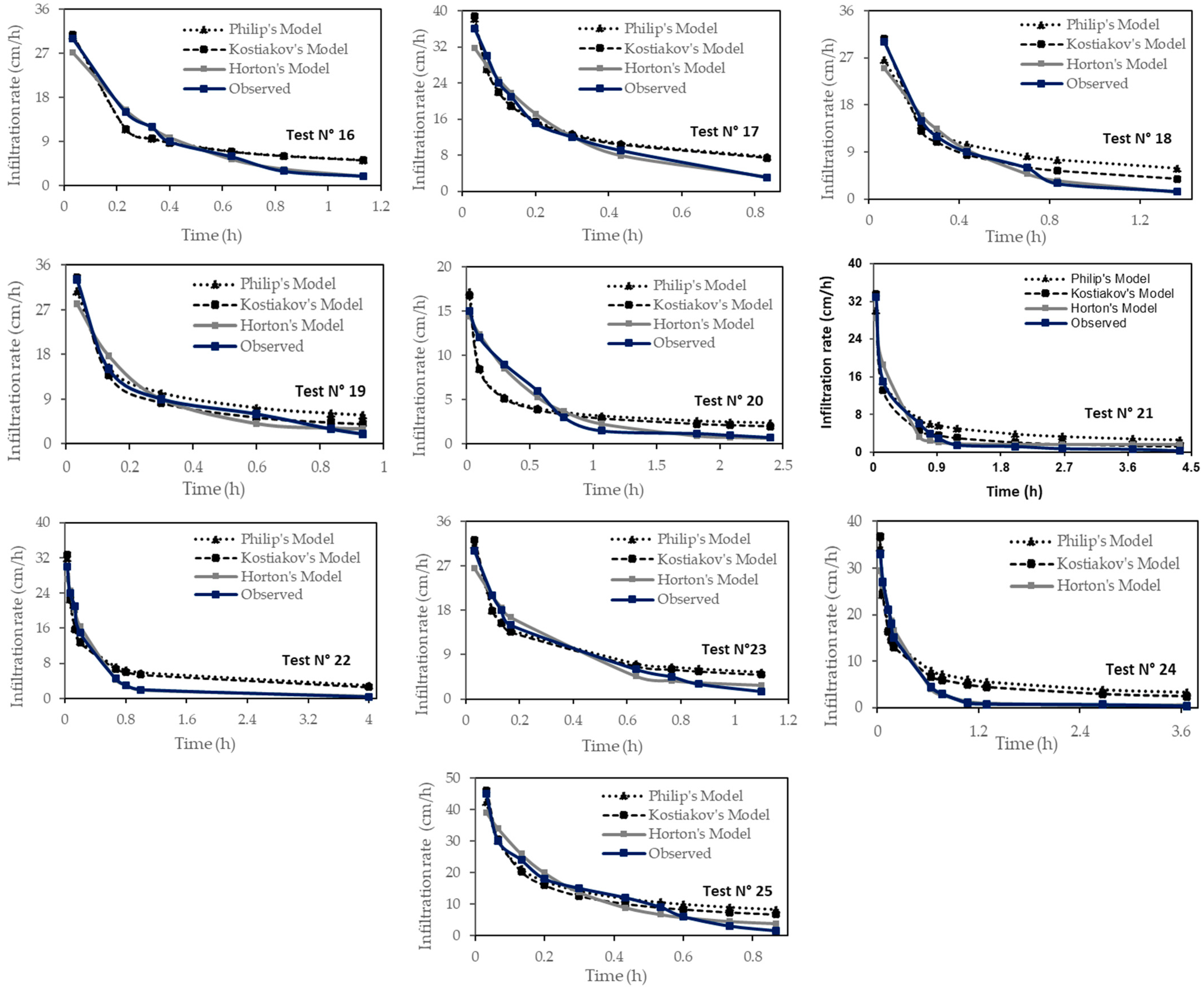
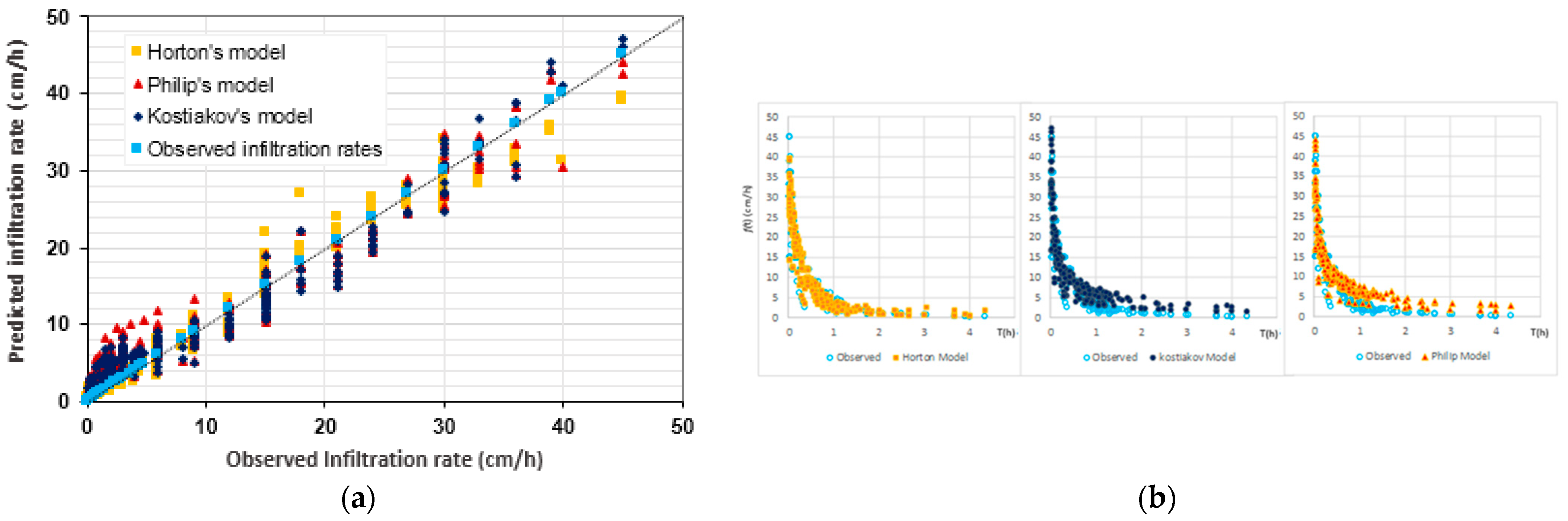
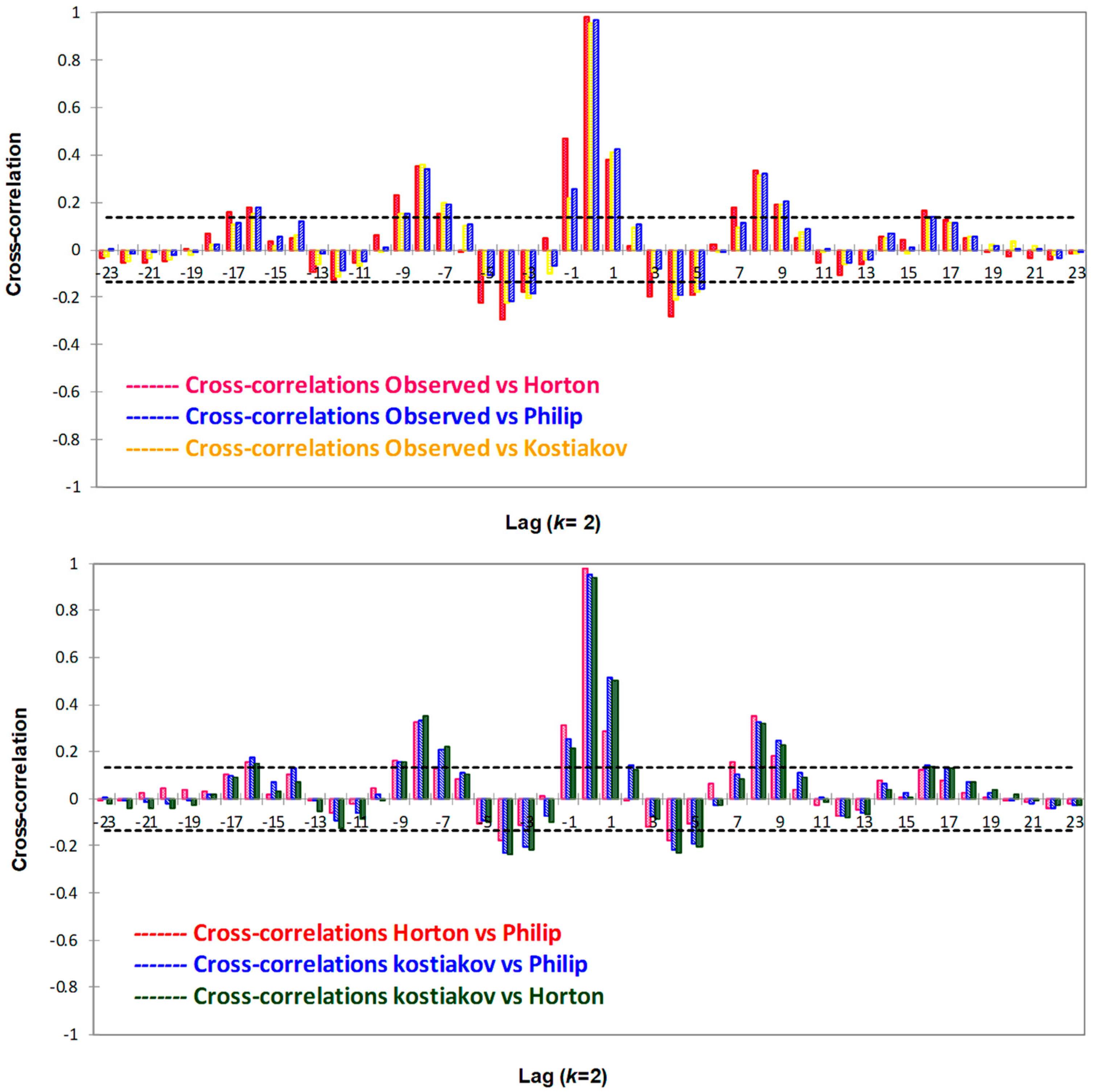
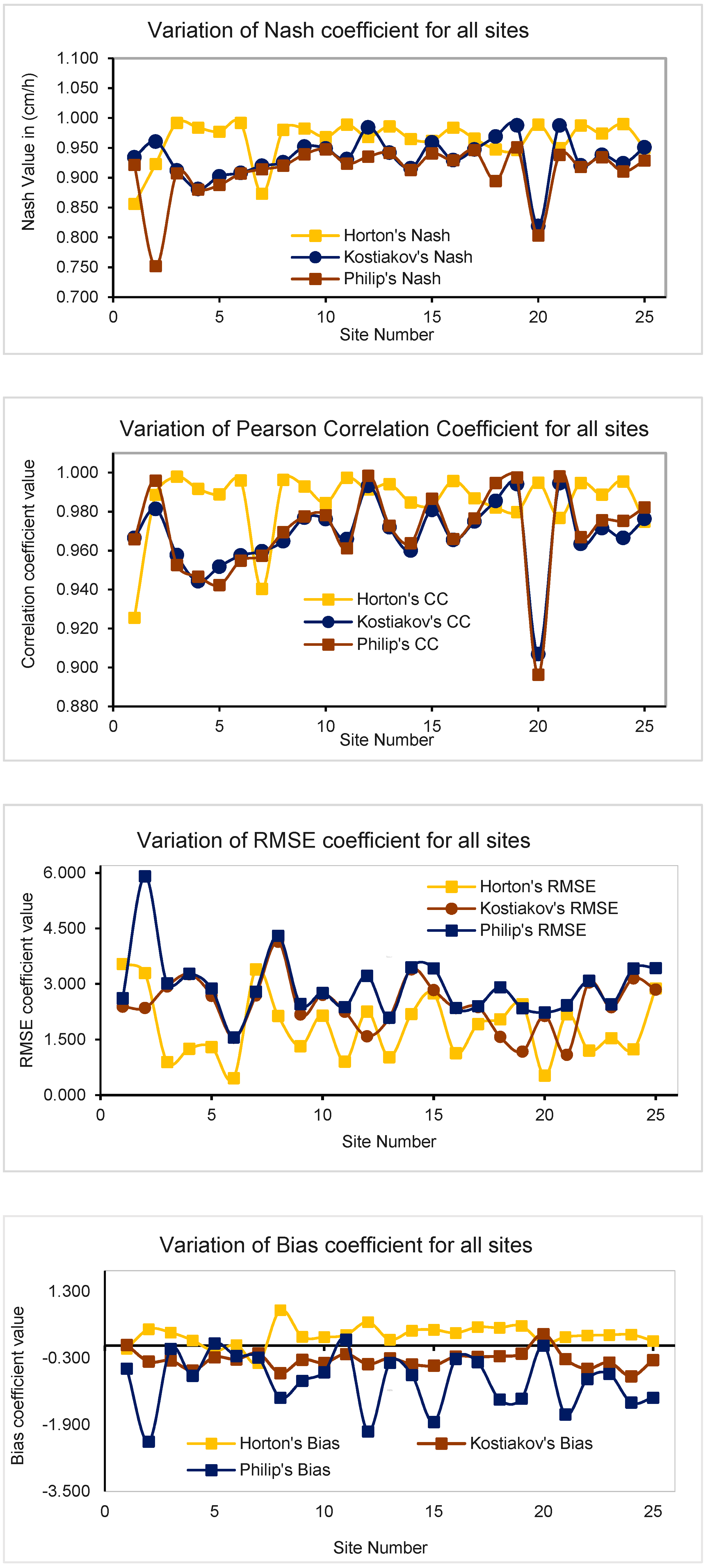
3.2. Performance Evaluation of Infiltration Models for Predicting Infiltration Rates
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Davidsen, S.; Löwe, R.; Ravn, N.H.; Jensen, L.N.; Arnbjerg-Nielsen, K. Initial Conditions of Urban Permeable Surfaces in Rainfall-Runoff Models Using Horton’s Infiltration. Water Sci. Technol. 2018, 77, 662–669. [Google Scholar] [CrossRef] [PubMed]
- Guellouz, L.; Askri, B.; Jaffré, J.; Bouhlila, R. Estimation of the soil hydraulic properties from field data by solving an inverse problem. Sci. Rep. 2020, 10, 9359. [Google Scholar] [CrossRef] [PubMed]
- Nartowska, E.; Kozłowski, T.; Gawdzik, J. Assessment of the influence of copper and zinc on the microstructural parameters and hydraulic conductivity of bentonites on the basis of SEM tests. Heliyon 2019, 5, e02142. [Google Scholar] [CrossRef] [PubMed]
- Sakellariou-Makrantonaki, M.; Angelaki, A.; Evangelides, C.; Bota, V.; Tsianou, E.; Floros, N. Experimental Determination of Hydraulic Conductivity at Unsaturated Soil Column. Procedia Eng. 2016, 162, 83–90. [Google Scholar] [CrossRef]
- Li, Y.; Shao, M. Effects of rainfall intensity on rainfall infiltration and redistribution in soil on Loess slope land. Ying Yong Sheng Tai Xue Bao 2006, 17, 2271–2276. [Google Scholar] [PubMed]
- Tsai, Y.J.; Yeh, H.-f. Effect of variations in rainfall intensity and different return period rainfall events on unsaturated slope stability. J. Taiwan Agric. Eng. 2019, 65, 34–50. [Google Scholar] [CrossRef]
- Lipiec, J.; Kuś, J.; Słowińska-Jurkiewicz, A.; Nosalewicz, A. Soil porosity and water infiltration as influenced by tillage methods. Soil Tillage Res. 2006, 89, 210–220. [Google Scholar] [CrossRef]
- Sajjadi, S.-A.-H.; Mirzaei, M.; Nasab, A.F.; Sarkardeh, H. Effect of Soil Physical Properties on Infiltration Rate. Geomech. Eng. 2016, 10, 727–736. [Google Scholar] [CrossRef]
- Barbosa, L.C.; de Souza, Z.M.; Franco, H.C.J.; Otto, R.; Rossi Neto, J.; Garside, A.L.; Carvalho, J.L.N. Soil texture affects root penetration in oxisols under sugarcane in Brazil. Geoderma Reg. 2018, 13, 15–25. [Google Scholar] [CrossRef]
- Biswas, A. Joint multifractal analysis for three variables: Characterizing the effect of topography and soil texture on soil water storage. Geoderma 2019, 334, 15–23. [Google Scholar] [CrossRef]
- Kalhoro, S.A.; Ding, K.; Zhang, B.; Chen, W.; Hua, R.; Hussain Shar, A.; Xu, X. Soil infiltration rate of forestland and grassland over different vegetation restoration periods at Loess Plateau in northern hilly areas of China. Landsc. Ecol. Eng. 2019, 15, 91–99. [Google Scholar] [CrossRef]
- Hino, M.; Odaka, Y.; Nadaoka, K.; Sato, A. Effect of initial soil moisture content on the vertical infiltration process—A guide to the problem of runoff-ratio and loss. J. Hydrol. 1988, 102, 267–284. [Google Scholar] [CrossRef]
- Schoener, G.; Stone, M.C. Impact of antecedent soil moisture on runoff from a semiarid catchment. J. Hydrol. 2019, 569, 627–636. [Google Scholar] [CrossRef]
- Avellaneda, E. Infiltration through Roadside Swales. Master’s Thesis, University of Central Florida, Orlando, FL, USA, 1985. [Google Scholar]
- Neris, J.; Tejedor, M.; Rodríguez, M.; Fuentes, J.; Jiménez, C. Effect of forest floor characteristics on water repellency, infiltration, runoff and soil loss in andisols of Tenerife (Canary Islands, Spain). CATENA 2013, 108, 50–57. [Google Scholar] [CrossRef]
- Pingping, H.; Xue, S.; Zhanbin, L. Effect of vegetation cover types on soil infiltration under simulating rainfall. Nat. Environ. Pollut. Technol. 2013, 12, 193–198. [Google Scholar]
- Zhao, C.; Jia, X.; Zhu, Y.; Shao, M.A. Long-term temporal variations of soil water content under different vegetation types in the Loess Plateau, China. CATENA 2017, 158, 55–62. [Google Scholar] [CrossRef]
- Rahman, M.A.; Moser, A.; Anderson, M.; Zhang, C.; Rötzer, T.; Pauleit, S. Comparing the infiltration potentials of soils beneath the canopies of two contrasting urban tree species. Urban For. Urban Green. 2019, 38, 22–32. [Google Scholar] [CrossRef]
- Vieux, B.E. Infiltration modeling. In Distributed Hydrologic Modeling Using GIS; Water Science and Technology Library; Springer: Dordrecht, The Netherlands, 2004; Volume 48, pp. 91–113. [Google Scholar] [CrossRef]
- Fox, D.M.; Bryan, R.B.; Price, A.G. The influence of slope angle on final infiltration rate for interrill conditions. Geoderma 1997, 80, 181–194. [Google Scholar] [CrossRef]
- Chatterjee, D.; Murali Krishna, A. Effect of slope angle on the stability of a slope under rainfall infiltration. Indian Geotech. J. 2019, 49, 708–717. [Google Scholar] [CrossRef]
- Patle, G.T.; Sikar, T.T.; Rawat, K.S.; Singh, S.K. Estimation of infiltration rate from soil properties using regression model for cultivated land. Geol. Ecol. Landsc. 2019, 3, 1–13. [Google Scholar] [CrossRef]
- Sihag, P.; Tiwari, N.K.; Ranjan, S. Support vector regression-based modeling of cumulative infiltration of sandy soil. ISH J. Hydraul. Eng. 2020, 26, 44–50. [Google Scholar] [CrossRef]
- Sihag, P.; Kumar, M.; Sammen, S.S. Predicting the infiltration characteristics for semi-arid regions using regression trees. Water Supply 2021, 21, 2583–2595. [Google Scholar] [CrossRef]
- Cortes-D, D.L.; Camacho-Tamayo, J.H.; Giraldo, R. Spatial prediction of soil infiltration using functional geostatistics. AUC Geogr. 2018, 53, 149–155. [Google Scholar] [CrossRef]
- Mishra, S.K.; Tyagi, J.V.; Singh, V.P. Comparison of Infiltration Models. Hydrol. Process. 2003, 24, 2629–2652. [Google Scholar] [CrossRef]
- Zakwan, M.; Muzzammil, M.; Alam, J. Application of spreadsheet to estimate infiltration parameters. Perspect. Sci. 2016, 8, 702–704. [Google Scholar] [CrossRef]
- Sihag, P.; Tiwari, N.K.; Ranjan, S. Estimation and intercomparison of infiltration models. Water Sci. Technol. 2017, 31, 34–43. [Google Scholar] [CrossRef]
- Singh, B.; Sihag, P.; Singh, K. Comparison of infiltration models in NIT. Kurukshetra Campus. Appl. Water Sci. 2018, 9, 63. [Google Scholar] [CrossRef]
- Vand, A.S.; Sihag, P.; Singh, B.; Zand, M. Comparative evaluation of infiltration models. KSCE J. Civ. Eng. 2018, 22, 4173–4184. [Google Scholar] [CrossRef]
- Farid, H.U.; Mahmood-Khan, Z.; Ahmad, I.; Shakoor, A.; Anjum, M.N.; Iqbal, M.M.; Mubeen, M.; Asghar, M. Estimation of infiltration models parameters and their comparison to simulate the onsite soil infiltration characteristics. Int. J. Agric. Biol. Eng. 2019, 2, 84–91. [Google Scholar]
- Ebrahimian, H.; Ghaffari, P.; Ghameshlou, A.N.; Tabatabaei, S.-H.; Alizadeh Dizaj, A.A. Extensive comparison of various infiltration estimation methods for furrow irrigation under different field conditions. Agric. Water Manag. 2020, 230, 105960. [Google Scholar] [CrossRef]
- Ramesh, V.B.; Bandhyopadhyay, K.K.; Sharma, K.L.; Bhattacharyya, T.; Wani, S.P. Land use and soil management effects on infiltration model parameters in semi-arid tropical alfisols. Ann. Arid. Zone 2010, 49, 1–8. [Google Scholar]
- Horton, R.E. Analysis of runoff-plat experiments with varying infiltration-capacity. Eos. Trans. Am. Geophys. Union 1939, 20, 693–711. [Google Scholar] [CrossRef]
- Holtan, H.N. A Concept of Infiltration Estimates in Watershed Engineering; ARS (Series) Agricultural Research Service 41–51; U.S. Department of Agriculture: Washington, DC, USA, 1961; pp. 1–32.
- Bauer, S.W. A modified Horton equation for infiltration during intermittent rainfall. Hydrol. Sci. Bull. 1974, 19, 219–225. [Google Scholar] [CrossRef]
- Gabellani, S.; Silvestro, F.; Rudari, R.; Boni, G. General calibration methodology for a combined Horton-SCS infiltration scheme in flash flood modeling. Nat. Hazards Earth Syst. Sci. 2008, 8, 1317–1327. [Google Scholar] [CrossRef]
- Verma, S.C. Modified Horton’s infiltration equation. J. Hydrol. 1982, 58, 383–388. [Google Scholar] [CrossRef]
- Akan, A.O. Horton Infiltration Equation revisited. J. Irrig. Drain. Eng. 1992, 118, 828–830. [Google Scholar] [CrossRef]
- Esen, I.I.; Almedeij, J. Generalized Horton Model for Low-Intensity rainfall. Soil Sci. 2013, 178, 174–179. [Google Scholar] [CrossRef]
- Green, I.R.A. An explicit solution of the modified Horton equation. J. Hydrol. 1986, 83, 23–27. [Google Scholar] [CrossRef]
- Aron, G. Adaptation of Horton and SCS infiltration equations to complex storms. J. Irrig. Drain. Eng. 1992, 118, 275–284. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M.; Bernhardt, G. A comprehensive surface-groundwater flow model. J. Hydrol. 1993, 142, 47–69. [Google Scholar] [CrossRef]
- Diskin, M.H.; Nazimov, N. Linear reservoir with feedback regulated inlet as a model for the infiltration process. J. Hydrol. 1995, 172, 313–330. [Google Scholar] [CrossRef]
- Ottoni Filho, T.B.O.; Ottoni, M.V.; Oliveira, M.B.; Macedo, J.R. Estimation of field capacity from ring infiltrometer-drainage data. Rev. Bras. Ciênc. Solo 2014, 38, 1765–1771. [Google Scholar] [CrossRef][Green Version]
- Razzaghi, S.; Khodaverdiloo, H.; Dashtaki, S.G. Effects of long-term wastewater irrigation on soil physical properties and performance of selected infiltration models in a semi-arid region. Hydrol. Sci. J. 2016, 61, 1778–1790. [Google Scholar] [CrossRef]
- Li, M.; Liu, T.; Duan, L.; Luo, Y.; Ma, L.; Zhang, J.; Zhou, Y.; Chen, Z. The scale effect of double-ring infiltration and soil infiltration zoning in a semi-arid steppe. Water 2019, 11, 1457. [Google Scholar] [CrossRef]
- Mbagwu, J.S.C. Analysis of Physical Properties Controlling Steady-State Infiltration Rates on Tropical Savannah Soils; IC—93/289; International Atomic Energy Agency: Vienna, Austria, 1993; Volume 25, pp. 1–11. [Google Scholar]
- Askari, M.; Tanaka, T.; Setiawan, B.I.; Saptomo, S.K. Infiltration characteristics of tropical soil based on water retention data. J. Jpn Soc. Hydrol. Water Resour. 2008, 21, 215–227. [Google Scholar] [CrossRef]
- Suryoputro, N.; Soetopo, W.; Suhartanto, E.S.; Limantara, L.M. Evaluation of infiltration models for mineral soils with different land uses in the tropics. J. Water Land Dev. 2018, 37, 153–160. [Google Scholar] [CrossRef]
- Bach, L.B.; Wierenga, P.J.; Ward, T.J. Estimation of the Philip Infiltration Parameters from Rainfall Simulation Data. Soil Sci. Soc. Am. J. 1986, 50, 1319–1323. [Google Scholar] [CrossRef]
- Mahapatra, S.; Jha, M.K.; Biswal, S.; Senapati, D. Assessing variability of infiltration characteristics and reliability of infiltration models in a tropical sub-humid region of India. Sci. Rep. 2020, 10, 1515. [Google Scholar] [CrossRef] [PubMed]
- Oku, E.; Aiyelari, A. Predictability of Philip and Kostiakov infiltration models under inceptisols in the humid forest zone, Nigeria. Kasetsart J. Nat. Sci. 2011, 45, 594–602. [Google Scholar]
- Utin, U.E.; Oguike, P.C. Evaluation of Philip’s and Kostiakov’s infiltration models on soils derived from three parent materials in Akwa Ibom state, Nigeria. J. Sci. Eng. Res. 2018, 5, 79–87. [Google Scholar]
- Zolfaghari, A.A.; Mirzaee, S.; Gorji, M. Comparison of different models for estimating cumulative infiltration. Int. J. Soil Sci. 2012, 7, 108–115. [Google Scholar] [CrossRef]
- Zakwan, M. Assessment of dimensionless form of Kostiakov model. Aquademia Water Environ. Technol. 2017, 1, 1. [Google Scholar] [CrossRef]
- Jagani, A.H.; Shrivastava, P.K.; Dwivedi, D.K. Evaluation of Kostiakov’s and Philip’s infiltration models on the soil of Dediapada, India. India J. Appl. Nat. Sci. 2018, 10, 1073–1077. [Google Scholar] [CrossRef]
- Igboekwe, M.U.; Adindu, R.U. Use of Kostiakov’s infiltration model on Michael Okpara University of Agriculture, Umudike soils, Southeastern, Nigeria. Water Resour. Prot. 2014, 6, 888–894. [Google Scholar] [CrossRef]
- Lei, G.; Fan, G.; Zeng, W.; Huang, J. Estimating parameters for the Kostiakov-Lewis infiltration model from soil physical properties. J. Soils Sediments 2020, 20, 166–180. [Google Scholar] [CrossRef]
- Thomas, A.; Ofosu, A.; Emmanuel, A.; De-Graft, A.; Ayine, A.; Asare, A.; Alexander, A. Comparison and Estimation of Four Infiltration Models. Open J. Soil Sci. 2020, 10, 45–57. [Google Scholar] [CrossRef]
- Ogbe, V.B.; Jayeoba, O.J.; Ode, S.O. Comparison of four soil infiltration models on a sandy soil in Lafia, Southern Guinea Savanna zone of Nigeria. Prod. Agric. Technol. 2011, 7, 116–126. [Google Scholar]
- Mohamoud, Y.M. Evaluating the green and αMPT infiltration parameter values for tilled and crusted soils. J. Hydrol. 1991, 123, 25–38. [Google Scholar] [CrossRef]
- Adindu, R.; Igbokwe, K.; Chigbu, T.; Ike-Amadi, C. Application of Kostiakov’s infiltration model on the soils of umudike, Abia state—Nigeria. Am. J. Environ. Eng. 2014, 4, 1–6. [Google Scholar]
- Rahmati, M.; Weihermüller, L.; Vanderborght, J.; Pachepsky, Y.A.; Mao, L.; Sadeghi, S.H.; Moosavi, N.; Kheirfam, H.; Montzka, C.; Van Looy, K.; et al. Development and analysis of the Soil water Infiltration Global database. PANGAEA 2018, 10, 1237–1263. [Google Scholar] [CrossRef]
- Zadjaoui, A. Numerical modelling of infiltration profiles in the silt Tlemcen (Algeria). E3S Web Conf. 2016, 9, 11015. [Google Scholar] [CrossRef]
- Smail, A.S.; Bouheraoua, A.; Abdesselam, M. Caractérisation hydrodynamique des sols de la haute vallée de l’oued Sébaou (Algérie): Étude expérimentale, numérique et analytique. Phys. Géo 2013, 7, 261–283. [Google Scholar] [CrossRef]
- Boers, T.M.; van Deurzen, F.J.M.P.; Eppink, L.A.A.J.; Ruytenberg, R.E. Comparison of infiltration rates measured with an infiltrometer, a rainulator and a permeameter for erosion research in SE Nigeria. Soil Technol. 1992, 5, 13–26. [Google Scholar] [CrossRef]
- Akinbile, C. Comparative analysis of infiltration measurements of two irrigated soils in Akure, Nigeria. Adv. Appl. Sci. Res. 2010, 1, 49–57. [Google Scholar]
- Mavimbela, S.S.W.; van Rensburg, L.D. Characterizing infiltration and internal drainage of South African dryland soils. Earth Surf. Process. Landf. 2017, 42, 414–425. [Google Scholar] [CrossRef]
- Lasisip, M.O.; Bof, P.; Awe, B.S. Assessment of infiltration capacity of agricultural soil in Ado-Ekiti southwestern Nigeria using selected empirical models. Int. J. Innov. Sci. Eng. Technol. 2017, 4, 111–117. [Google Scholar]
- Ehiomogue, P.; Ojedele, O.S.; Ikechuchu-Ede, C.E.; Okosa Iorji, F.N.; Ahaneku, I.E. Calibration of existing infiltration models on different amended soils. Am. J. Eng. Res. 2018, 7, 242–247. [Google Scholar]
- Robinson, A.R.; Rohwer, C. Measurement of canal seepage. Trans. ASCE 1957, 122, 347–363. [Google Scholar]
- Weiler, M.; Naef, F. An experimental tracer study of the role of macropores in infiltration in grassland soils. Hydrol. Process. 2003, 17, 477–493. [Google Scholar] [CrossRef]
- Horton, R.E. An approach toward a physical interpretation of infiltration-capacity. Soil Sci. Soc. Am. J. 1941, 5, 399–417. [Google Scholar] [CrossRef]
- Beven, K.; Robert, E. Horton’s perceptual model of infiltration processes. Hydrol. Process. 2004, 18, 3447–3460. [Google Scholar] [CrossRef]
- Kostiakov, A.N. The dynamics of the coefficients of water percolation in soils and the necessity for studying it from a dynamic point of view for purpose of amelioration. Soc. Soil Sci. 1932, 14, 17–21. [Google Scholar]
- Philip, J.R. The theory of infiltration: 1. The infiltration equation and its solutions. Soil Sci. 1957, 83, 345–358. [Google Scholar] [CrossRef]
- Monroe, J.S.; Wicander, R. The Changing Earth: Exploring Geology and Evolution, 5th ed.; Brooks Cole: Salt Lake City, UT, USA, 2008; p. 735. [Google Scholar]
- Ghosh, R.K. A note on Lewis-Kostiakov’s infiltration equation. Soil Sci. 1985, 139, 193–196. [Google Scholar] [CrossRef]
- Philip, J.R. Theory of Infiltration. Adv. Hydrosci. 1969, 5, 215–296. [Google Scholar] [CrossRef]
- Sir, M.; Kutilek, M.; Kuraz, V.; Krejca, M.; Kubik, F. Field estimation of the soil hydraulic characteristics. Soil Technol. 1988, 1, 63–75. [Google Scholar] [CrossRef]


| N° | X (m) | Y (m) | N° | X (m) | Y (m) |
|---|---|---|---|---|---|
| P1 | 375,425.62 | 4,058,710.17 | P14 | 366,337.18 | 4,054,866.19 |
| P2 | 374,496.25 | 4,057,723.53 | P15 | 369,589.50 | 4,051,912.45 |
| P3 | 374,533.68 | 4,056,506.43 | P16 | 371,186.40 | 4,052,366.52 |
| P4 | 373,893.76 | 4,055,315.90 | P17 | 371,897.50 | 4,049,519.69 |
| P5 | 372,720.30 | 4,054,656.09 | P18 | 370,680.00 | 4,047,361.72 |
| P6 | 371,720.73 | 4,054,348.72 | P19 | 368,502.03 | 4,047,109.89 |
| P7 | 369,870.38 | 4,053,866.53 | P20 | 366,831.31 | 4,048,601.47 |
| P8 | 368,255.99 | 4,054,208.03 | P21 | 365,040.89 | 4,048,188.93 |
| P9 | 367,492.01 | 4,054,096.72 | P22 | 368,495.87 | 4,050,579.35 |
| P10 | 366,726.87 | 4,054,144.07 | P23 | 363,989.19 | 4,050,114.83 |
| P11 | 365,854.40 | 4,053,583.85 | P24 | 363,162.02 | 4,051,752.15 |
| P12 | 366,080.29 | 4,052,571.78 | P25 | 364,839.14 | 4,050,714.70 |
| P13 | 366,465.12 | 4,051,965.49 |
| N° | Initial Infiltration Rate f0 at t = 2 min [cm/min] | Final Infiltration Rate fc min [cm/min] |
|---|---|---|
| P1 | 1 | 0.6 |
| P2 | 2.5 | 0.1 |
| P3 | 1 | 0.2 |
| P4 | 1 | 0.1 |
| P5 | 0.9 | 0.1 |
| P6 | 0.5 | 0.1 |
| P7 | 1.1 | 0.1 |
| P8 | 1.3 | 0.2 |
| P9 | 1.1 | 0.1 |
| P10 | 1.2 | 0.1 |
| P11 | 1 | 0.2 |
| P12 | 1.2 | 0.2 |
| P13 | 1 | 0.1 |
| P14 | 1.3 | 0.1 |
| P15 | 1.5 | 0.1 |
| P16 | 1 | 0.1 |
| P17 | 1.2 | 0.1 |
| P18 | 1 | 0.1 |
| P19 | 1.1 | 0.1 |
| P20 | 0.5 | 0.1 |
| P21 | 1.1 | 0.1 |
| P22 | 1 | 0.1 |
| P23 | 1 | 0.2 |
| P24 | 1.1 | 0.1 |
| P25 | 1.5 | 0.1 |
| N° | Day | Moisture Content (%) | N° | Day | Moisture Content (%) |
|---|---|---|---|---|---|
| P1 | 14 April 2019 | 21.21 | P14 | 28 April 2019 | 23.00 |
| P2 | 15 April 2019 | 40.06 | P15 | 6 May 2019 | 13.90 |
| P3 | 19 April 2019 | 26.58 | P16 | 6 May 2019 | 21.21 |
| P4 | 17 April 2019 | 29.03 | P17 | 7 May 2019 | 16.69 |
| P5 | 20 April 2019 | 25.79 | P18 | 7 May 2019 | 9.89 |
| P6 | 20 April 2019 | 14.81 | P19 | 9 May 2019 | 19.33 |
| P7 | 22 April 2019 | 8.58 | P20 | 9 May 2019 | 19.76 |
| P8 | 22 April 2019 | 12.11 | P21 | 11 May 2019 | 24.69 |
| P9 | 23 April 2019 | 13.77 | P22 | 11 May 2019 | 14.16 |
| P10 | 23 April 2019 | 16.82 | P23 | 12 May 2019 | 28.53 |
| P11 | 25 April 2019 | 14.81 | P24 | 12 May 2019 | 16.69 |
| P12 | 25 April 2019 | 12.11 | P25 | 13 May 2019 | 13.38 |
| P13 | 28 April 2019 | 20.77 |
| N° | Horton’s Model | Kostiakov’s Model | Philip’s Model | ||
|---|---|---|---|---|---|
| k (h−1) | A | B | S (cm/h0.5) | (cm/h) | |
| P1 | 5.403 | 3.875 | 0.586 | 9.893 | 0.012 |
| P2 | 6.744 | 2.174 | 0.890 | 11.688 | 0.014 |
| P3 | 2.18 | 6.975 | 0.462 | 12.647 | 0.0379 |
| P4 | 2.576 | 5.920 | 0.514 | 12.216 | 0.020 |
| P5 | 1.897 | 6.625 | 0.425 | 10.211 | 0.990 |
| P6 | 1.795 | 3.182 | 0.483 | 6.070 | 0.012 |
| P7 | 3.243 | 5.695 | 0.503 | 11.429 | 0.012 |
| P8 | 2.682 | 6.527 | 0.554 | 15.218 | 0.010 |
| P9 | 2.643 | 5.334 | 0.542 | 11.885 | 0.010 |
| P10 | 3.411 | 6.529 | 0.524 | 13.930 | 0.010 |
| P11 | 2.402 | 6.671 | 0.449 | 11.077 | 0.743 |
| P12 | 4.774 | 3.529 | 0.687 | 12.218 | 0.010 |
| P13 | 2.368 | 5.434 | 0.510 | 11.156 | 0.010 |
| P14 | 3.504 | 7.290 | 0.530 | 15.682 | 0.010 |
| P15 | 4.080 | 6.403 | 0.586 | 16.078 | 0.020 |
| P16 | 2.939 | 5.512 | 0.506 | 11.182 | 0/013 |
| P17 | 4.037 | 6.678 | 0.517 | 13.960 | 0.012 |
| P18 | 2.786 | 4.747 | 0.689 | 13.748 | 0.010 |
| P19 | 5.320 | 3.855 | 0.634 | 11.217 | 0.020 |
| P20 | 1.987 | 2.975 | 0.454 | 4.854 | 0.841 |
| P21 | 4.611 | 3.420 | 0.671 | 11.003 | 0.010 |
| P22 | 3.055 | 5.371 | 0.531 | 11.668 | 0.030 |
| P23 | 4.000 | 5.209 | 0.536 | 11.414 | 0.030 |
| P24 | 3.517 | 5.110 | 0.579 | 12.553 | 0.012 |
| P25 | 4.537 | 6.145 | 0.593 | 15.581 | 0.015 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dahak, A.; Boutaghane, H.; Merabtene, T. Parameter Estimation and Assessment of Infiltration Models for Madjez Ressoul Catchment, Algeria. Water 2022, 14, 1185. https://doi.org/10.3390/w14081185
Dahak A, Boutaghane H, Merabtene T. Parameter Estimation and Assessment of Infiltration Models for Madjez Ressoul Catchment, Algeria. Water. 2022; 14(8):1185. https://doi.org/10.3390/w14081185
Chicago/Turabian StyleDahak, Asma, Hamouda Boutaghane, and Tarek Merabtene. 2022. "Parameter Estimation and Assessment of Infiltration Models for Madjez Ressoul Catchment, Algeria" Water 14, no. 8: 1185. https://doi.org/10.3390/w14081185
APA StyleDahak, A., Boutaghane, H., & Merabtene, T. (2022). Parameter Estimation and Assessment of Infiltration Models for Madjez Ressoul Catchment, Algeria. Water, 14(8), 1185. https://doi.org/10.3390/w14081185







