Differences in Spatiotemporal Variability of Potential and Reference Crop Evapotranspirations
Abstract
:1. Introduction
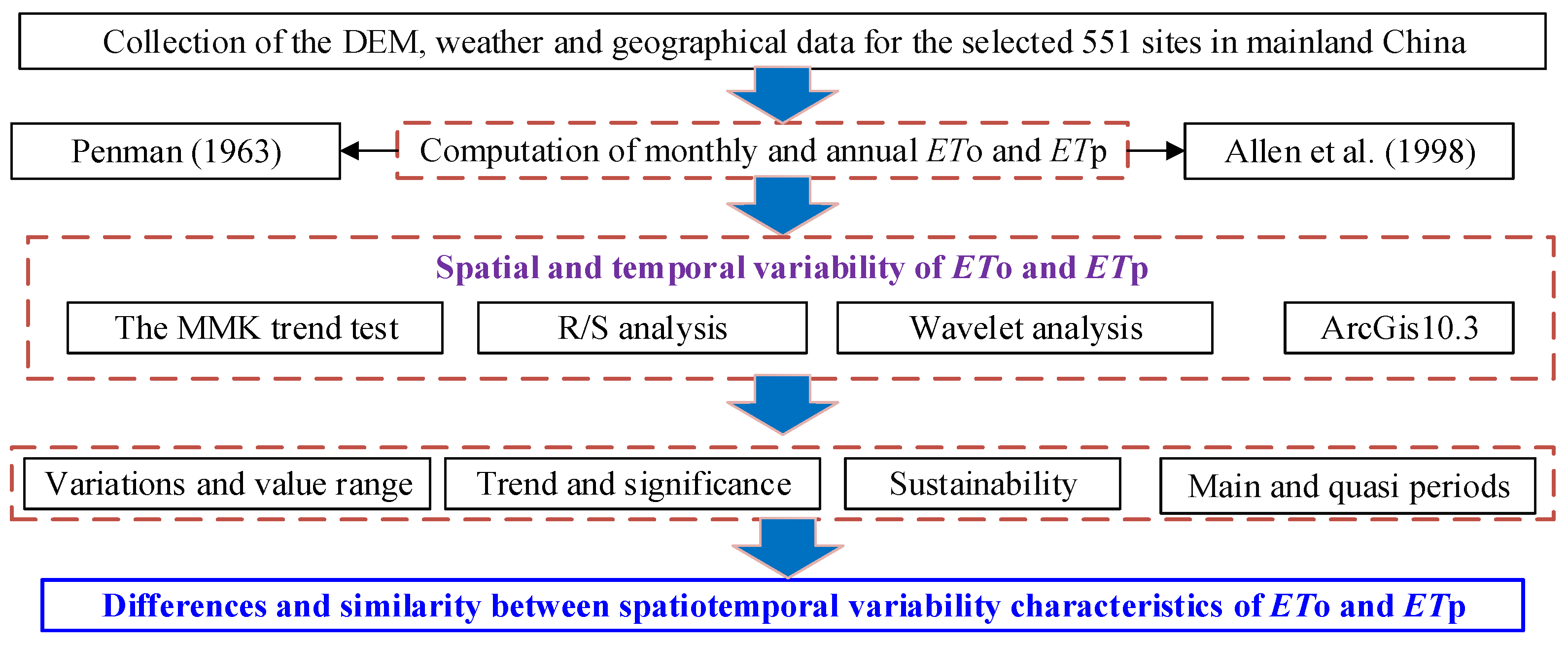
2. Data Collection and Methodology
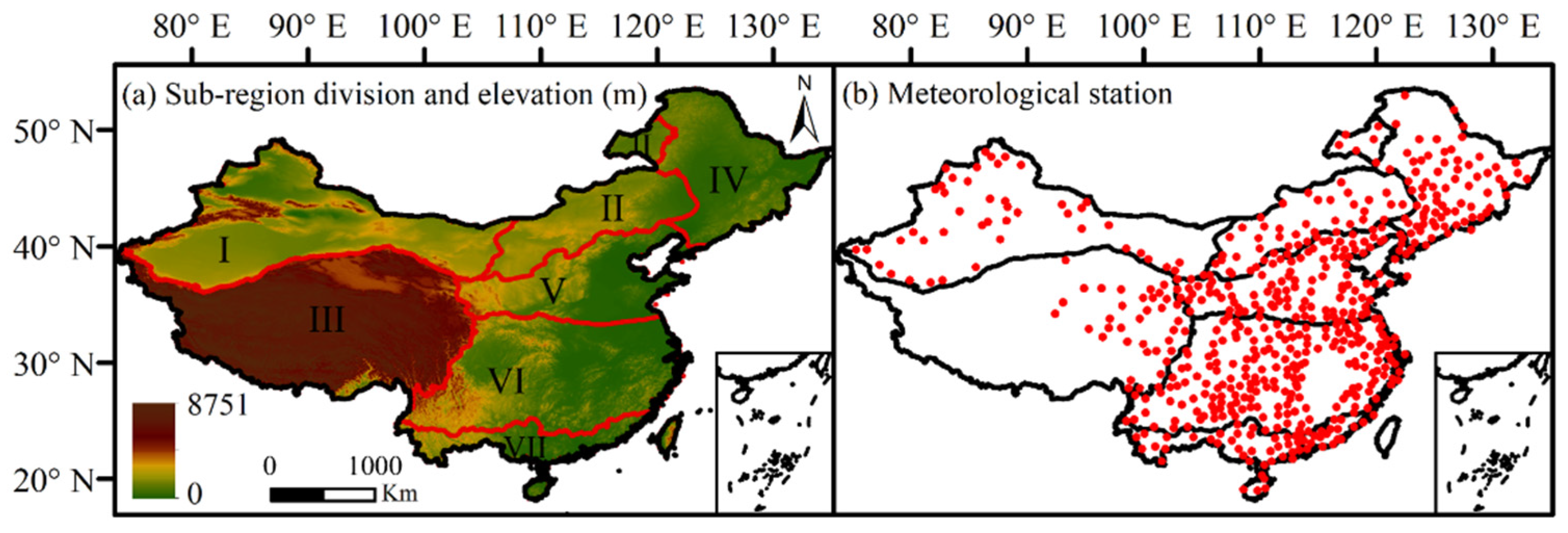
2.1. Study Area Description and Data Sources
2.2. Methodology
2.2.1. Equations for Estimating ETp and ETo
2.2.2. Trend and Abrupt-Change Year Analysis
2.2.3. The Rescaled (R/S) Analysis
2.2.4. The Wavelet Analysis
3. Results
3.1. The Differences between Monthly ETp and ETo
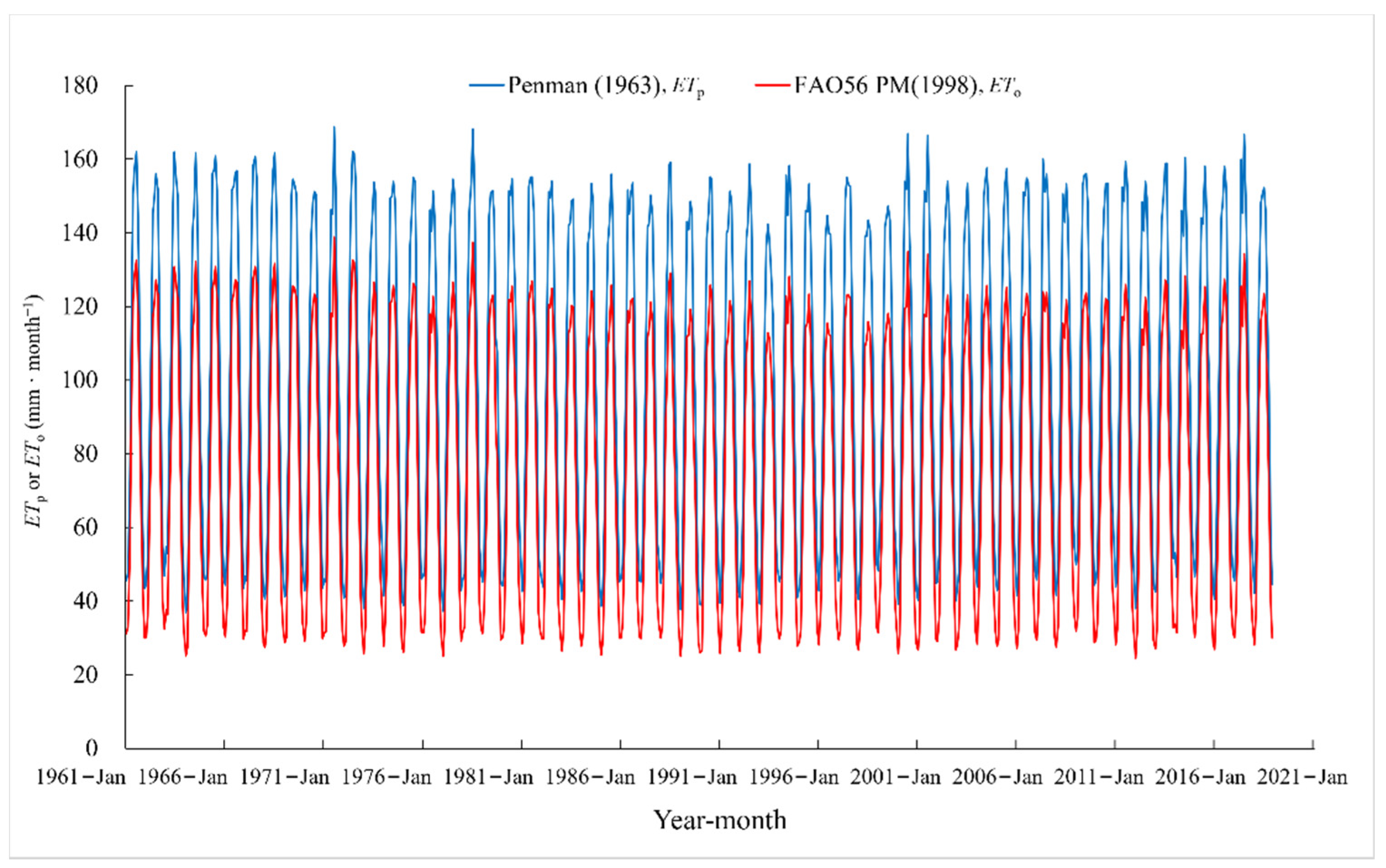
3.1.1. Temporal Differences
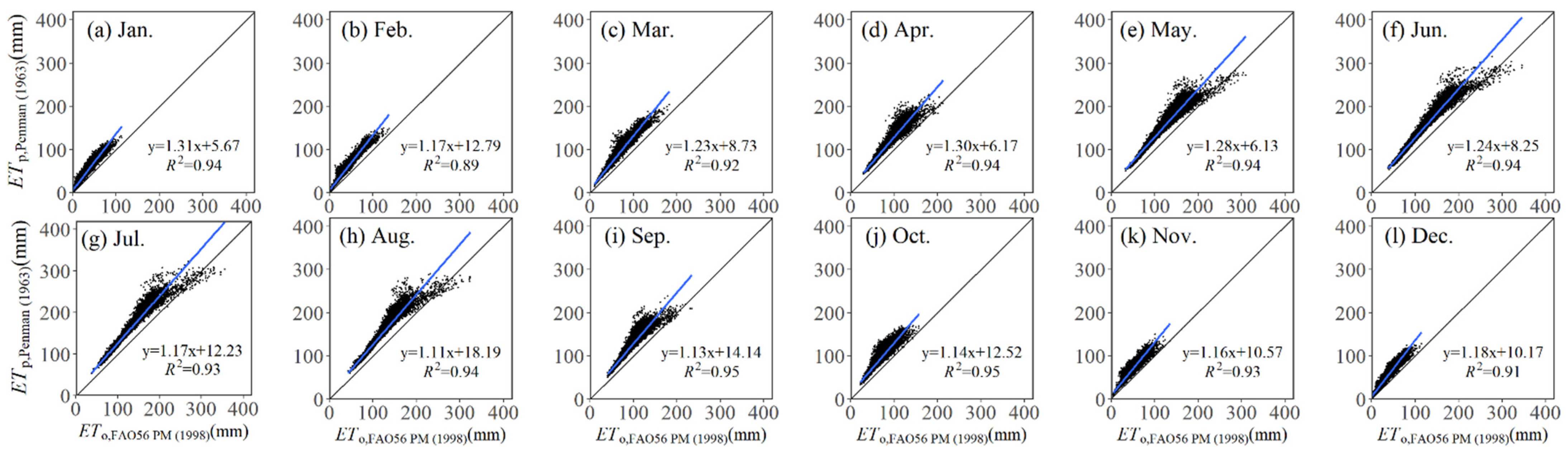
3.1.2. Spatial Differences
3.2. The Differences between Annual ETp and ETo
3.2.1. Temporal and Spatial Differences
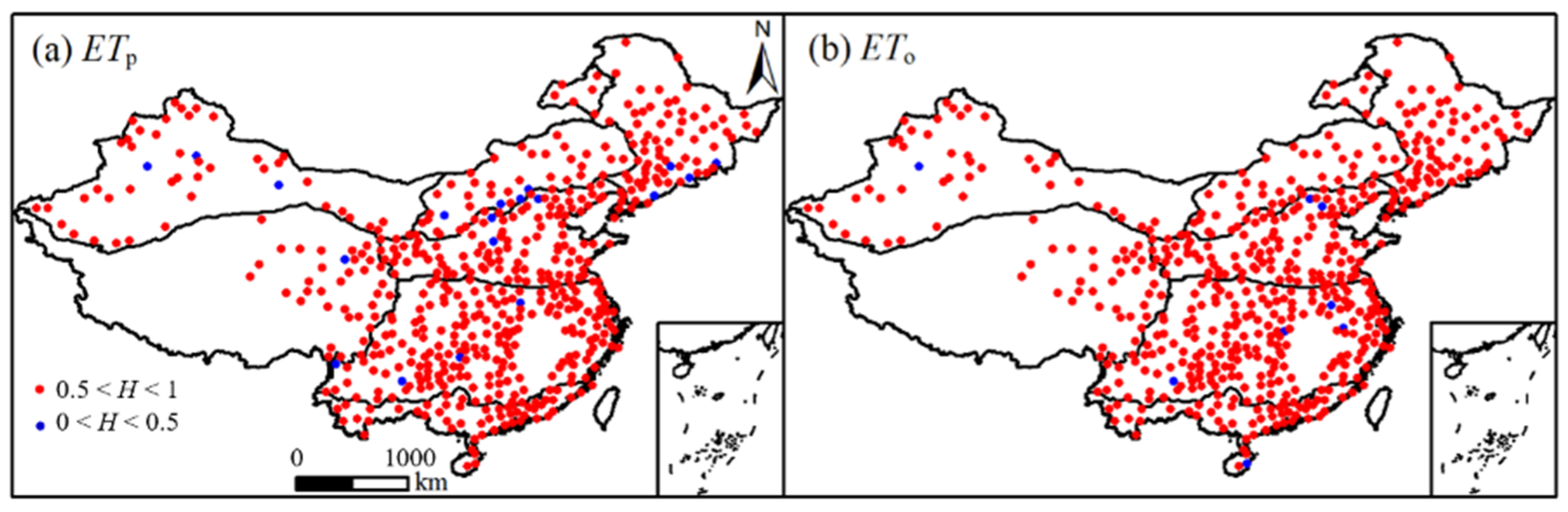
3.2.2. The Trends and Long—Term Dependence
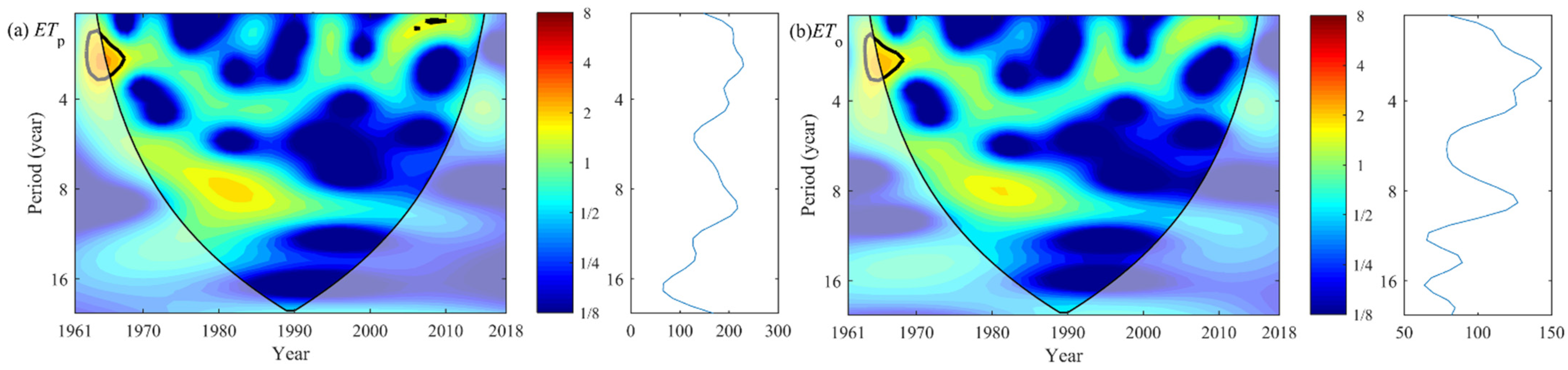
3.2.3. The Wavelet Periods
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
References
- Milly, P.C.D.; Dunne, K.A. Potential evapotranspiration and continental drying. Nat. Clim. Change 2016, 6, 946–949. [Google Scholar] [CrossRef]
- Peng, L.; Li, Y.; Feng, H. The best alternative for estimating reference crop evapotranspiration in different sub-regions of mainland China. Sci. Rep. 2017, 7, 5458. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vörösmarty, C.J.; Federer, C.A.; Schloss, A.L. Potential evaporation functions compared on US watersheds: Possible implications for global-scale water balance and terrestrial ecosystem modeling. J. Hydrol. 1998, 207, 147–169. [Google Scholar] [CrossRef]
- Yao, N.; Li, Y.; Dong, Q.G.; Li, L.; Peng, L.; Feng, H. Influence of the accuracy of reference crop evapotranspiration on drought monitoring using standardized precipitation evapotranspiration index in mainland China. Land. Degrad. Dev. 2020, 31, 266–282. [Google Scholar] [CrossRef]
- Zhang, Y. Estimation of Potential Evapotranspiration by Different Methods in Handan Eastern Plain, China. Water Sci. Eng. 2019, 4, 117. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration: Guidelines for computing crop water requirements. In Irrigation and Drainage Paper No 56; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 1998. [Google Scholar]
- Ohana-Levi, N.; Ben-Gal, A.; Munitz, S.; Netzer, Y. Grapevine crop evapotranspiration and crop coefficient forecasting using linear and non-linear multiple regression models. Agric. Water Manag. 2022, 262, 107317. [Google Scholar] [CrossRef]
- Hu, K.; Awange, J.; Kuhn, M.; Zerihun, A. Irrigated agriculture potential of Australia’s northern territory inferred from spatial assessment of groundwater availability and crop evapotranspiration. Agric. Water Manag. 2022, 264, 107466. [Google Scholar] [CrossRef]
- Gentilucci, M.; Barbieri, M.; Burt, P. (Eds.) Climate and territorial suitability for the Vineyards developed using GIS techniques. In Proceedings of the Conference of the Arabian Journal of Geosciences, Sousse, Tunisia, 2–5 November 2018. [Google Scholar]
- Saadi, S.; Todorovic, M.; Tanasijevic, L.; Pereira, L.S.; Pizzigalli, C.; Lionello, P. Climate change and Mediterranean agriculture: Impacts on winter wheat and tomato crop evapotranspiration, irrigation requirements and yield. Agric. Water Manag. 2015, 147, 103–115. [Google Scholar] [CrossRef]
- Fan, J.; Wu, L.; Zhang, F.; Xiang, Y.; Zheng, J. Climate change effects on reference crop evapotranspiration across different climatic zones of China during 1956–2015. J. Hydrol. 2016, 542, 923–937. [Google Scholar] [CrossRef]
- Saray, M.H.; Eslamian, S.S.; Klove, B.; Gohari, A. Regionalization of potential evapotranspiration using a modified region of influence. Theor. Appl. Climatol. 2019, 140, 115–127. [Google Scholar] [CrossRef] [Green Version]
- Silva, C.R.D.; Barbosa, L.A.; Finzi, R.R.; Riberio, B.T.; Dias, N.D.S. Accuracy of air temperature forecasts and its use for prediction of the reference evapotranspiration. Biosci. J. 2020, 36, 17–22. [Google Scholar] [CrossRef]
- Um, M.; Kim, Y.; Park, D.; Jung, K.; Wang, Z.; Kim, M.M.; Shin, H. Impacts of potential evapotranspiration on drought phenomena in different regions and climate zones. Sci. Total Environ. 2020, 703, 135590. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Roderick, M.L.; Zhang, S.; Mcvicar, T.R.; Donohue, R.J. Hydrologic implications of vegetation response to elevated CO2 in climate projections. Nat. Clim. Change 2019, 9, 44–48. [Google Scholar] [CrossRef]
- Li, J.; Wu, C.; Wang, X.; Peng, J.; Dong, D.; Lin, G.; Gonsamo, A. Satellite observed indicators of the maximum plant growth potential and their responses to drought over Tibetan Plateau (1982–2015). Ecol. Indic. 2020, 108, 105732. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, Z. Future trends of water resources and influences on agriculture in China. PLoS ONE 2020, 15, e0231671. [Google Scholar] [CrossRef]
- Shanmugam, M.; Mekonnen, M.; Ray, C. Grid-Based Model for Estimating Evapotranspiration Rates of Heterogeneous Land Surface. J. Irrig. Drain. Eng. 2020, 146, 04019030. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A.; Ghorbani, M.A.; Kashani, M.H.; Kisi, O.; Kim, S. The viability of co-active fuzzy inference system model for monthly reference evapotranspiration estimation: Case study of Uttarakhand State. Hydrol. Res. 2019, 50, 1623–1644. [Google Scholar] [CrossRef] [Green Version]
- You, G.; Arain, M.A.; Wang, S.; Lin, N.; Wu, D.; Mckenzie, S.; Zou, C.; Liu, B.; Zhang, X.; Gao, J. Trends of actual and potential evapotranspiration based on Bouchet’s complementary concept in a cold and arid steppe site of Northeastern Asia. Agr. For. Meteorol. 2019, 279, 107684. [Google Scholar] [CrossRef]
- Adhikari, A.; Mainali, K.P.; Rangwala, I.; Hansen, A.J. Various measures of potential evapotranspiration have species-specific impact on species distribution models. Ecol. Model. 2019, 414, 108836. [Google Scholar] [CrossRef]
- Guo, D.; Westra, S.; Maier, H.R. An R package for modelling actual, potential and reference evapotranspiration. Environ. Model. Softw. 2016, 78, 216–224. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An Approach toward a Rational Classification of Climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Penman, H.L. Evaporation: An introductory survey. Neth. J. Agri. Sci. 1956, 4, 9–29. [Google Scholar] [CrossRef]
- Penman, H.L. (Ed.) Vegetation and Hydrology, Tech. Commun. 53, Commonwealth Bureau of Soils; Soil Science: Harpenden, UK, 1963. [Google Scholar]
- Anon, J. Proceeding of the informal meeting on physics in agriculture. Neth. J. Agri. Sci. 1956, 4, 162–175. [Google Scholar]
- WMO. Sites for Wind-Power Installations; WMO No. 156, Technical Note No. 63; WMO: Geneva, Switzerland, 1963; Available online: https://library.wmo.int/index.php?lvl=notice_display&id=5475#.YjfmEHpBzDc (accessed on 8 February 2022).
- Jensen, M.E. Water Consumption by Agricultural Plants. In Plant Water Consumption & Response. Volume II. Water Deficits and Plant Growth; Kozlowski, T.T., Ed.; Academic Press: New York, NY, USA; London, UK, 1968; pp. 1–22. [Google Scholar]
- Granger, R.J. An examination of the concept of potential evaporation. J. Hydrol. 1989, 111, 9–19. [Google Scholar] [CrossRef]
- Doorenbos, J.; Pruitt, W. Guidelines for Predicting Crop Water Requirements, Irrigation and Drainage Paper No. 24; FAO: Rome, Italy, 1977. [Google Scholar]
- Ochoa-Sánchez, A.; Crespo, P.; Carrillo-Rojas, G.; Sucozhañay, A.; Célleri, R. Actual Evapotranspiration in the High Andean Grasslands: A Comparison of Measurement and Estimation Methods. Front. Earth Sci. 2019, 7, 55. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Liu, Y.; Axel, T. Climatic change on the Tibetan Plateau: Potential Evapotranspiration Trends from 1961–2000. Clim. Change 2006, 76, 291–319. [Google Scholar]
- Seiller, G.; Anctil, F. How do potential evapotranspiration formulas influence hydrological projections? Hydrolog. Sci. J. 2016, 61, 2249–2266. [Google Scholar] [CrossRef] [Green Version]
- Sun, C.; Zheng, Z.; Chen, W.; Wang, Y. Spatial and Temporal Variations of Potential Evapotranspiration in the Loess Plateau of China during 1960–2017. Sustainability 2020, 12, 354. [Google Scholar] [CrossRef] [Green Version]
- Sun, S.; Lei, S.; Jia, H.; Li, C.; Zhang, J.; Meng, P. Tree-Ring Analysis Reveals Density-Dependent Vulnerability to Drought in Planted Mongolian Pines. Forests 2020, 11, 98. [Google Scholar] [CrossRef] [Green Version]
- Gwate, O.; Mantel, S.K.; Palmer, A.R.; Gibson, L.; Munch, Z. Measuring and modelling evapotranspiration in a South African grassland: Comparison of two improved Penman-Monteith formulations. Water SA 2018, 44, 482–494. [Google Scholar] [CrossRef] [Green Version]
- Lewis, C.S.; Allen, L.N. Potential Crop Evapotranspiration and Surface Evaporation Estimates via a Gridded Weather Forcing Dataset. J. Hydrol. 2017, 546, 450–463. [Google Scholar] [CrossRef] [Green Version]
- Ding, H.; Xingming, H.; Ying, H.; Jingxiu, Q. Uncertainty assessment of potential evapotranspiration in arid areas, as estimated by the Penman-Monteith method. J. Arid. Land 2020, 12, 166–180. [Google Scholar]
- Oudin, L.; Hervieu, F.; Michel, C.; Perrin, C.; Andreassian, V.; Anctil, F.; Loumagne, C. Which potential evapotranspiration input for a lumped rainfall-runoff model? Part 2: Towards a simple and efficient potential evapotranspiration model for rainfall-runoff modelling. J. Hydrol. 2005, 303, 290–306. [Google Scholar] [CrossRef]
- Jensen, M.E.; Burman, R.D.; Allen, R.G. Evapotranspiration and Irrigation Water Requirements; Agriculture Society Civil Engineering: New York, NY, USA, 1990. [Google Scholar]
- Hargreaves, G.H.; Samani, Z.A. Estimating potential evapotranspiration. J. Irrig. Drain. Div. 1982, 108, 225–230. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Dinpashoh, Y.; Jhajharia, D.; Fakheri-Fard, A.; Singh, V.P.; Kahya, E. Trends in reference crop evapotranspiration over Iran. J. Hydrol. 2011, 399, 422–433. [Google Scholar] [CrossRef]
- Feng, Y.; Cui, N.; Zhao, L.; Hu, X.; Gong, D. Comparison of ELM, GANN, WNN and empirical models for estimating reference evapotranspiration in humid region of Southwest China. J. Hydrol. 2016, 536, 376–383. [Google Scholar] [CrossRef]
- Gong, L.; Xu, C.; Chen, D.; Halldin, S.; Chen, Y.D. Sensitivity of the Penman–Monteith reference evapotranspiration to key climatic variables in the Changjiang (Yangtze River) basin. J. Hydrol. 2006, 329, 620–629. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Allen, R.G. History and evaluation of Hargreaves evapotranspiration equation. J. Irrig. Drain. Eng. 2003, 129, 53–63. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, F.; Liu, W. Spatiotemporal characteristics of reference evapotranspiration during 1961–2009 and its projected changes during 2011–2099 on the Loess Plateau of China. Agr. For. Meteorol. 2012, 154, 147–155. [Google Scholar] [CrossRef]
- Mcvicar, T.R.; Van Niel, T.G.; Li, L.; Hutchinson, M.F.; Mu, X.; Liu, Z. Spatially distributing monthly reference evapotranspiration and pan evaporation considering topographic influences. J. Hydrol. 2007, 338, 196–220. [Google Scholar] [CrossRef]
- Tabari, H.; Marofi, S.; Aeini, A.; Talaee, P.H.; Mohammadi, K. Trend analysis of reference evapotranspiration in the western half of Iran. Agr. For. Meteorol. 2011, 151, 128–136. [Google Scholar] [CrossRef]
- Chattopadhyay, N.; Hulme, M. Evaporation and potential evapotranspiration in India under conditions of recent and future climate change. Agr. For. Meteorol. 1997, 87, 55–73. [Google Scholar] [CrossRef]
- Han, S.; Xu, D.; Wang, S. Decreasing potential evaporation trends in China from 1956 to 2005: Accelerated in regions with significant agricultural influence? Agr. For. Meteorol. 2012, 154, 44–56. [Google Scholar] [CrossRef]
- Wang, K.; Xu, Q.; Li, T. Does recent climate warming drive spatiotemporal shifts in functioning of high-elevation hydrological systems? Sci. Total Environ. 2020, 719, 137507. [Google Scholar] [CrossRef]
- Katerji, N.; Rana, G. Crop reference evapotranspiration: A discussion of the concept, analysis of the process and validation. Water Resour. Manag. 2011, 25, 1581–1600. [Google Scholar] [CrossRef]
- Xiang, K.; Li, Y.; Horton, R.; Feng, H. Similarity and difference of potential evapotranspiration and reference crop evapotranspiration -a review. Agric. Water Manag. 2020, 232, 106043. [Google Scholar] [CrossRef]
- Helsel, D.R.; Hirsch, R.M. Statistical Methods in Water Resources; Elsevier: Amsterdam, The Netherland, 1992. [Google Scholar]
- Ayantobo, O.O.; Li, Y.; Song, S.; Yao, N. Spatial comparability of drought characteristics and related return periods in mainland China over 1961–2013. J. Hydrol. 2017, 550, 549–567. [Google Scholar] [CrossRef]
- Yao, N.; Li, Y.; Lei, T.; Peng, L. Drought evolution, severity and trends in mainland China over 1961–2013. Sci. Total Environ. 2018, 616, 73–89. [Google Scholar] [CrossRef]
- Li, S.; Kang, S.; Zhang, L.; Zhang, J.; Du, T.; Tong, L.; Ding, R. Evaluation of six potential evapotranspiration models for estimating crop potential and actual evapotranspiration in arid regions. J. Hydrol. 2016, 543, 450–461. [Google Scholar] [CrossRef]
- Xu, K.; Yang, D.; Yang, H.; Li, Z.; Qin, Y.; Shen, Y. Spatio-temporal variation of drought in China during 1961–2012: A climatic perspective. J. Hydrol. 2015, 526, 253–264. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, R.; Song, Y.; Han, C.; Liu, J.; Liu, Z. Sensitivity of potential evapotranspiration to meteorological factors and their elevational gradients in the Qilian Mountains, northwestern China. J. Hydrol. 2019, 568, 147–159. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C.Y. Regional Streamflow Trend Detection with Consideration of Both Temporal and Spatial Correlation. Int. J. Climatol. 2002, 22, 933–946. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Auto Correlation Methods. Brit. J. Psychol. 1976, 25, 86–97. [Google Scholar]
- Li, Y.; Horton, R.; Ren, T.; Chen, C. Prediction of annual reference evapotranspiration using climatic data. Agric. Water Manag. 2010, 97, 300–308. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Wallis, J.R. Robustness of the rescaled range R/S in the measurement of noncyclic long run statistical dependence. Water Resour. Res. 1969, 5, 967–988. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-term storage capacity of reservoirs. Trans. Am. Soc. Civil. Eng. 1951, 116, 770–808. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.; Li, L.; Chen, C. Spatiotemporal Variability of Monthly and Annual Snow Depths in Xinjiang, China over 1961–2015 and the Potential Effects. Water 2019, 11, 1666. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Yao, N.; Li, Y.; Liu, D.L.; Wang, B.; Ayantobo, O.O. Future projections of extreme temperature events in different sub-regions of China. Atmos. Res. 2019, 217, 150–164. [Google Scholar] [CrossRef]
- Djaman, K.; Balde, A.B.; Sow, A.; Muller, B.; Irmak, S.; N’Diaye, M.K.; Manneh, B.; Moukoumbi, Y.D.; Futakuchi, K.; Saito, K. Evaluation of sixteen reference evapotranspiration methods under sahelian conditions in the Senegal River Valley. J. Hydrol. 2015, 3, 139–159. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Xu, C.; Zhong, X.; Li, Y.; Yuan, X.; Cao, J. Comparison of 16 models for reference crop evapotranspiration against weighing lysimeter measurement. Agric. Water Manag. 2017, 184, 145–155. [Google Scholar] [CrossRef]
- Sentelhas, P.C.; Gillespie, T.J.; Santos, E.A. Evaluation of FAO Penman–Monteith and alternative methods for estimating reference evapotranspiration with missing data in Southern Ontario, Canada. Agric. Water Manag. 2010, 97, 635–644. [Google Scholar] [CrossRef]
- Valipour, M.; Sefidkouhi, M.A.G.; Raeini, M. Selecting the best model to estimate potential evapotranspiration with respect to climate change and magnitudes of extreme events. Agric. Water Manag. 2017, 180, 50–60. [Google Scholar] [CrossRef]
- Dakhlaoui, H.; Seibert, J.; Hakala, K. Sensitivity of discharge projections to potential evapotranspiration estimation in Northern Tunisia. Reg. Environ. Change 2020, 20, 34. [Google Scholar] [CrossRef] [Green Version]
- Burke, E.J.; Brown, S.I.J.; Christidis, N. Modeling the Recent Evolution of Global Drought and Projections for the Twenty-First Century with the Hadley Centre Climate Model. J. Hydrometeorol. 2006, 7, 1113–1125. [Google Scholar] [CrossRef]
- Li, Y.; Sun, C. Impacts of the superimposed climate trends on droughts over 1961–2013 in Xinjiang, China. Theor. Appl. Climatol. 2017, 129, 977–994. [Google Scholar] [CrossRef]
- Yao, N.; Li, L.; Feng, P.; Feng, H.; Liu, D.L.; Liu, Y.; Jiang, K.; Hu, X.; Li, Y. Projections of drought characteristics in China based on a standardized precipitation and evapotranspiration index and multiple GCMs. Sci. Total Environ. 2020, 704, 135245. [Google Scholar] [CrossRef]
- Anselin, L. Local indicators of spatial association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]

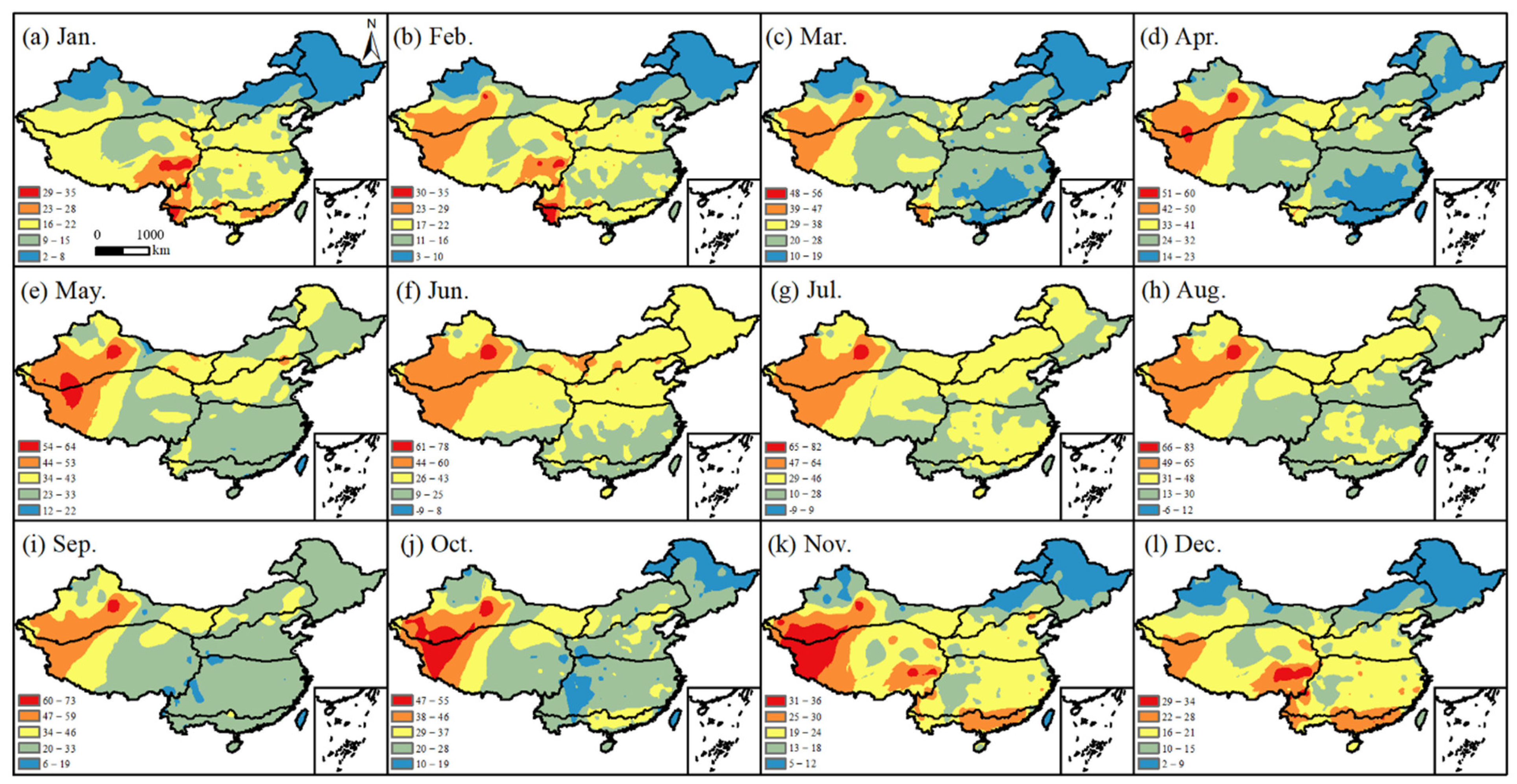
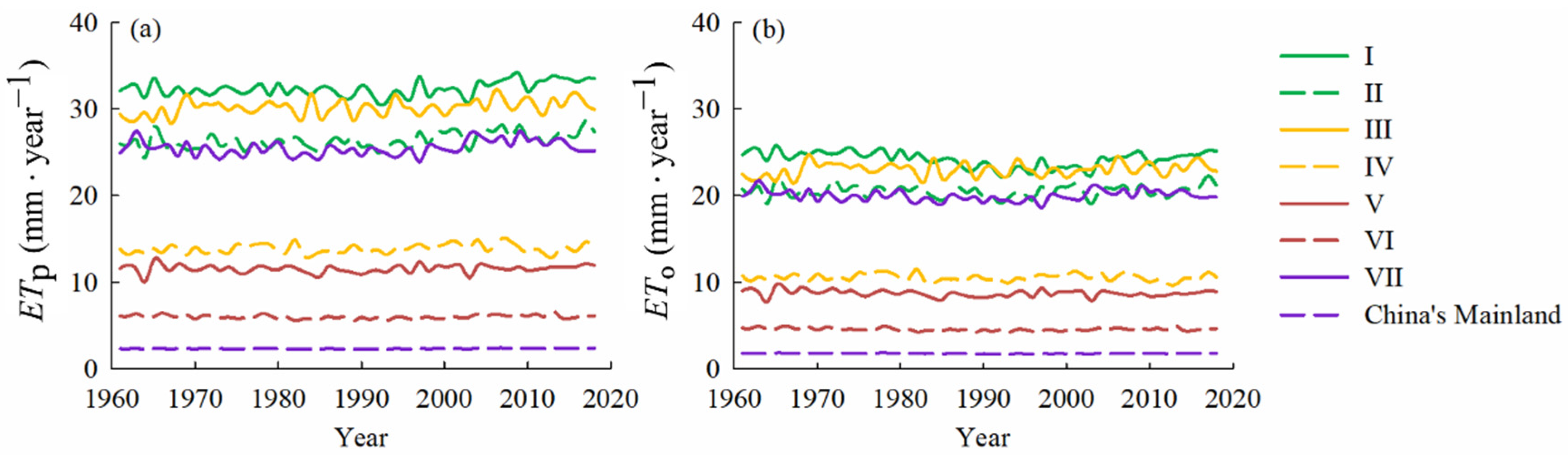
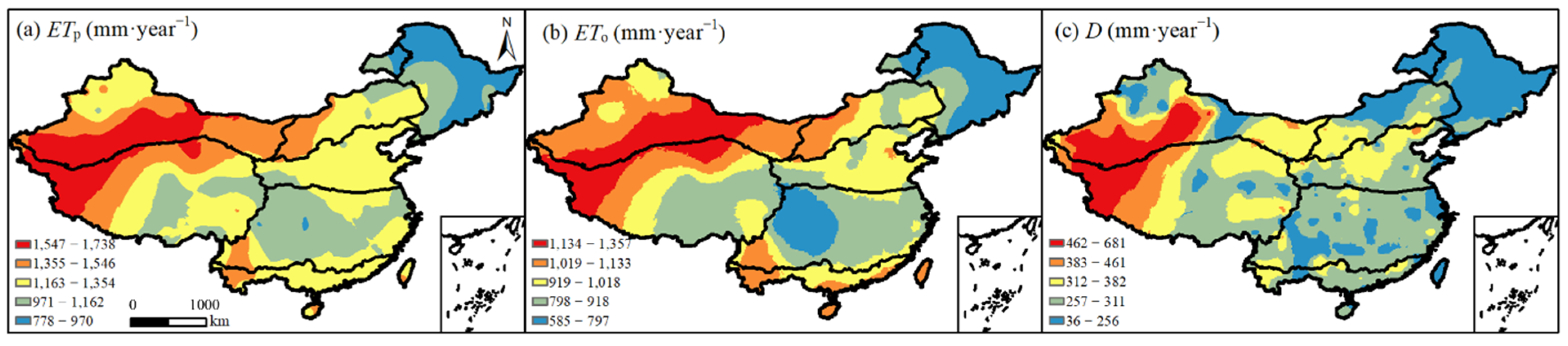
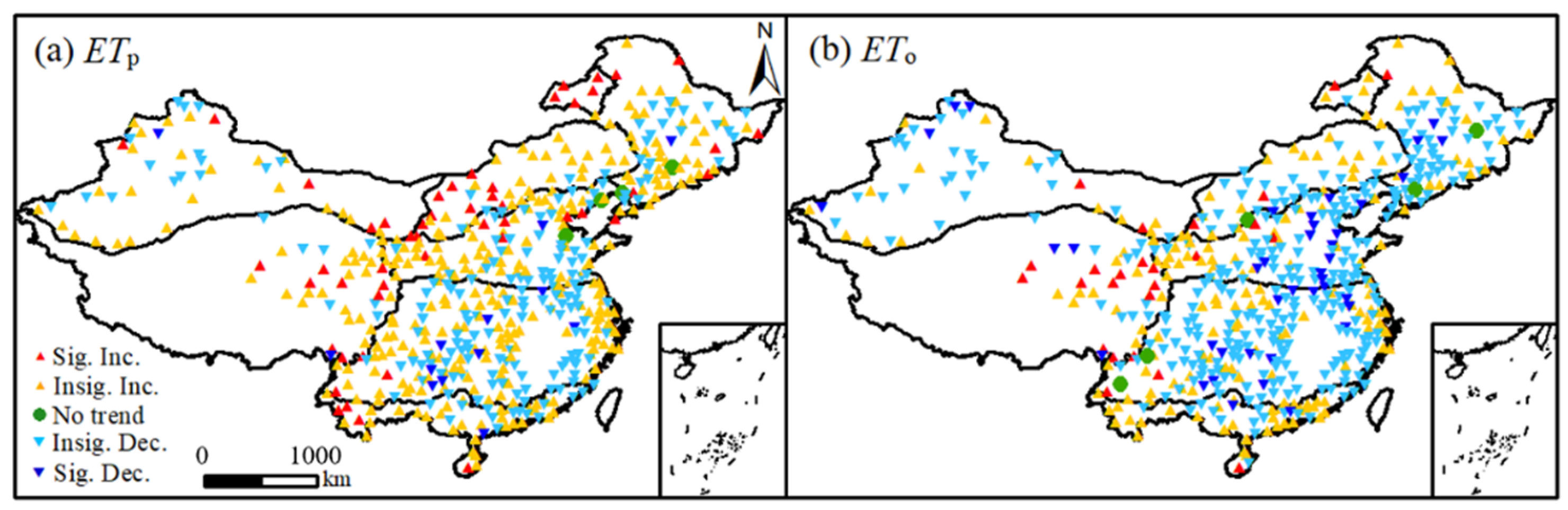

| Month | Sub-Region | ||||||
|---|---|---|---|---|---|---|---|
| I | II | III | IV | V | VI | VII | |
| January | 15 | 11 | 9 | 20 | 6 | 16 | 16 |
| February | 15 | 15 | 12 | 20 | 8 | 17 | 16 |
| March | 22 | 26 | 21 | 27 | 17 | 25 | 21 |
| April | 27 | 34 | 28 | 30 | 24 | 30 | 24 |
| May | 31 | 39 | 34 | 32 | 31 | 35 | 27 |
| June | 30 | 40 | 36 | 29 | 31 | 35 | 25 |
| July | 30 | 42 | 35 | 29 | 27 | 30 | 28 |
| August | 29 | 42 | 33 | 28 | 26 | 29 | 28 |
| September | 27 | 38 | 30 | 24 | 26 | 28 | 24 |
| October | 24 | 31 | 24 | 24 | 20 | 26 | 23 |
| November | 18 | 19 | 14 | 22 | 11 | 19 | 19 |
| December | 16 | 12 | 10 | 21 | 7 | 16 | 18 |
| Term | Trend | Sub-Region | Subtotal | ||||||
|---|---|---|---|---|---|---|---|---|---|
| I | II | III | IV | V | VI | VII | |||
| ETP | Significant increase Insignificant increase | 3 | 5 | 2 | 2 | 8 | 25 | 5 | 50 |
| 23 | 24 | 19 | 36 | 55 | 117 | 29 | 303 | ||
| No trend | 0 | 0 | 0 | 0 | 0 | 4 | 0 | 4 | |
| Insignificant decrease | 20 | 15 | 16 | 28 | 41 | 43 | 18 | 181 | |
| Significant decrease | 0 | 3 | 2 | 3 | 4 | 1 | 0 | 13 | |
| ET0 | Significant increase | 0 | 1 | 0 | 2 | 5 | 14 | 3 | 25 |
| Insignificant increase | 17 | 16 | 9 | 24 | 34 | 60 | 16 | 176 | |
| No trend | 0 | 0 | 0 | 0 | 1 | 4 | 0 | 5 | |
| Insignificant decrease | 27 | 27 | 25 | 36 | 60 | 100 | 30 | 305 | |
| Significant decrease | 2 | 3 | 5 | 7 | 8 | 12 | 3 | 40 | |
| Sub-Region | I | II | III | IV | V | VI | VII | Subtotal | |
|---|---|---|---|---|---|---|---|---|---|
| ETP | 0.5 < H < 1 | 43 | 43 | 38 | 65 | 105 | 186 | 52 | 532 |
| 0 < H < 0.5 | 3 | 4 | 1 | 4 | 3 | 4 | 0 | 19 | |
| ET0 | 0.5 < H < 1 | 45 | 47 | 39 | 69 | 106 | 186 | 51 | 543 |
| 0 < H < 0.5 | 1 | 0 | 0 | 0 | 2 | 4 | 1 | 8 | |
| Timesclae | Monthly | Yearly | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Moran’s I | January | February | March | April | May | June | July | Auguest | September | October | November | December | ||
| NS | 338 | 370 | 342 | 337 | 328 | 285 | 406 | 435 | 407 | 391 | 367 | 341 | 383 | |
| HH | 97 | 78 | 96 | 95 | 88 | 102 | 63 | 48 | 61 | 67 | 76 | 89 | 79 | |
| HL | 0 | 1 | 3 | 4 | 4 | 3 | 3 | 3 | 2 | 3 | 1 | 1 | 3 | |
| LH | 2 | 4 | 7 | 8 | 7 | 6 | 6 | 5 | 6 | 5 | 5 | 3 | 7 | |
| LL | 114 | 98 | 103 | 107 | 124 | 155 | 73 | 60 | 75 | 85 | 102 | 117 | 79 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, K.; Zhang, X.; Peng, X.; Yao, N.; Biswas, A.; Liu, D.; Zou, Y.; Pulatov, B.; Li, Y.; Liu, F. Differences in Spatiotemporal Variability of Potential and Reference Crop Evapotranspirations. Water 2022, 14, 988. https://doi.org/10.3390/w14060988
Xiang K, Zhang X, Peng X, Yao N, Biswas A, Liu D, Zou Y, Pulatov B, Li Y, Liu F. Differences in Spatiotemporal Variability of Potential and Reference Crop Evapotranspirations. Water. 2022; 14(6):988. https://doi.org/10.3390/w14060988
Chicago/Turabian StyleXiang, Keyu, Xuan Zhang, Xiaofeng Peng, Ning Yao, Asim Biswas, Deli Liu, Yufeng Zou, Bakhtiyor Pulatov, Yi Li, and Fenggui Liu. 2022. "Differences in Spatiotemporal Variability of Potential and Reference Crop Evapotranspirations" Water 14, no. 6: 988. https://doi.org/10.3390/w14060988







