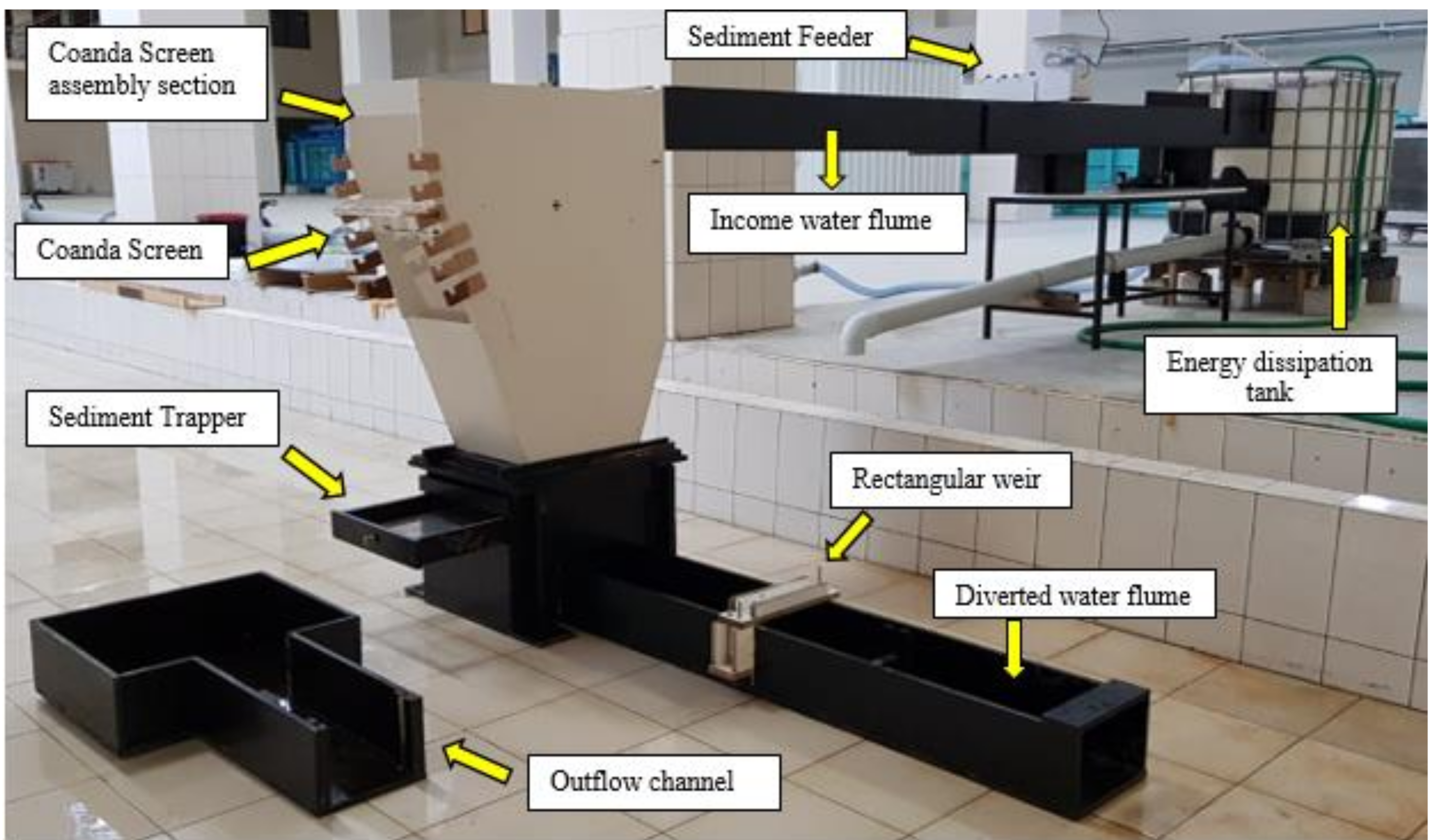
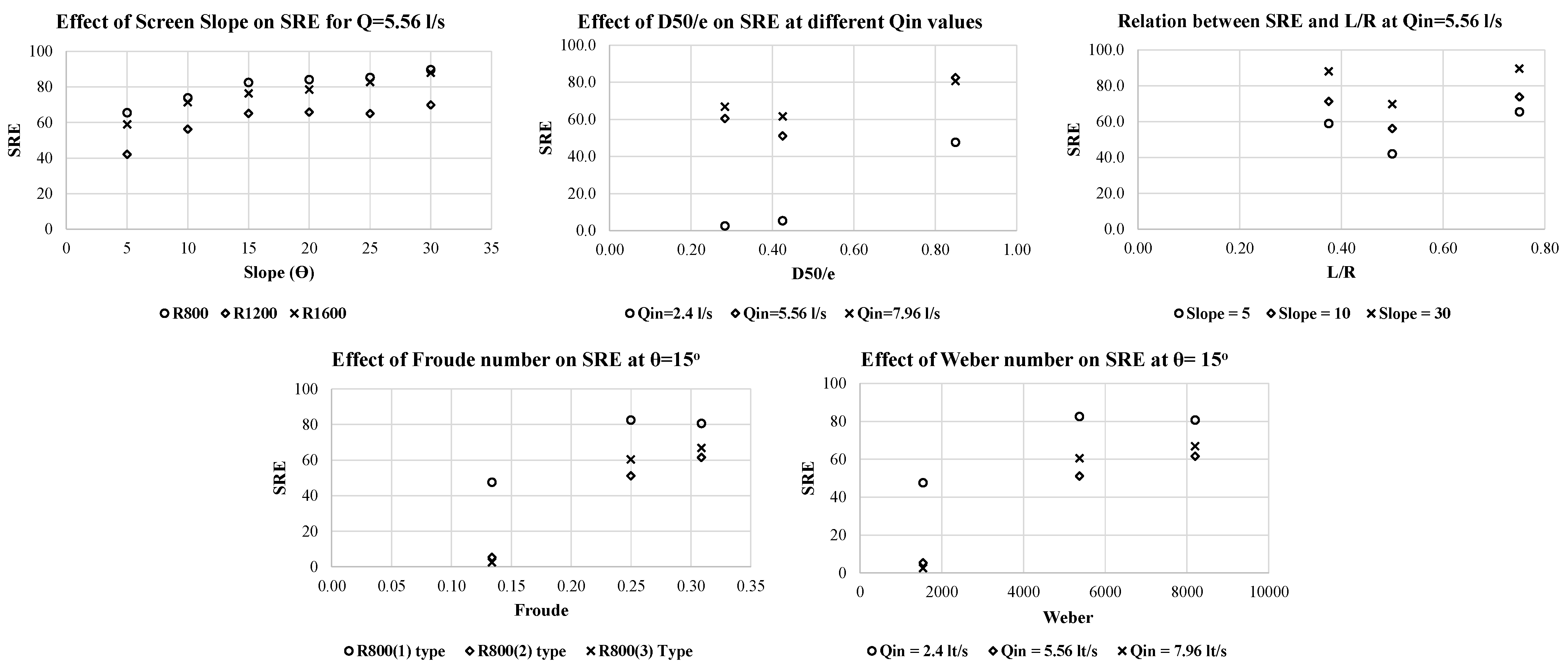
1. Introduction
Intake structures are used to divert water from channels and river systems for various purposes, such as energy production, irrigation, and domestic use [
1,
2,
3]. Tyrolean and Coanda types of water intake structures are the most widely used bottom intake structures in the world. No matter the type of intake, the expected purpose from any intake structure is to supply required water while filtering most of sediments and other unwanted particles as much as possible [
4,
5]. This is because energy production stages are carried out with different types of high-value machinery developed for working under clear water conditions. They are sensitive to sediment particles within water. In addition, sediment particles can become a shelter for various types of bacteria and protozoa and reduce sanitation efficiency, especially for ultraviolet disinfection operations [
6]. In addition, heavy metals can become attached to particles, contaminating water in time. Therefore, water that is not purified well from sediment and other particles can cause important health problems.
Withdrawal water and filtered sediment amounts depend on both structural design parameters such as bar spacing of an intake, screen length, screen slope inclination, etc. and incoming flow conditions such as discharge rate and sediment concentration of incoming flow. Therefore, estimation and determination of withdrawal water and excluded sediment amounts are highly important to obtain maximum efficiency from an intake structure.
Some researchers have tried to find an optimum design to overcome the clogging problem by performing experimental studies. A series of experiments were performed by Orth, et al. [
7] using Tyrolean type water intakes. They have proposed that a bar profile with a rounded top has high sediment retention and clogging. Rounded shape bars were found to be more susceptible to clogging by Krochin and Sviatoslav [
8], who have recommended that screen bars should be made of iron and their shapes should be rectangular or trapezoidal, bar spacing should range between 2 and 6 cm, and screen inclination should be 20. Bouvard [
9] worked with Tyrolean type intakes and expressed that screen slope should be between 10 and 60% to avoid clogging. In the case of screening for hydroelectric power plant operations, bar spacing was expressed by Raudkiwi [
10] as at least 5 mm and the screen slope as 20% to overcome any possible clogging problem.
There is a structural difference between Tyrolean and Coanda intakes. Tyrolean-type water intakes have straight screen bars which are oriented parallel to flow direction. On the other hand, Coanda-type water intakes have concave screen geometry where screen bars are placed perpendicular to the flow direction. An increment on screen slope reduces water column height on the intake screen, reducing both the orifice effect and withdrawn water discharge. Effect of screen inclination on withdrawn water for Tyrolean-type water intakes was studied by Castillo, et al. [
11]. According to their clear water experiments, the best water capturing performance was obtained at 0% screen inclination and the worst results were obtained at 30%. On the other hand, in the case of sediment-laden flow, maximum water capture performance was obtained at 30% screen inclination and the worst result was obtained at 0% [
11]. The difference is caused by screen clogging due to sediment particles. On the other hand, when Coanda intake is used instead of a Tyrolean intake, even in steeper screen inclinations, the shear mechanism becomes more dominant, keeping withdrawal water discharge relatively high. The self-cleaning ability and high-water withdrawal capacity make Coanda-type water intakes more preferable than Tyrolean ones. In addition, the study of Nøvik, et al. [
12] indicates that Coanda screens mostly show satisfactory performance under cold climate conditions. Furthermore, Coanda type water intakes are environmentally friendly structures since they can allow fish and invertebrates to pass through downstream of a river [
13]. Hence, this study has focused on Coanda-type water intakes.
An important study on Coanda intake structures was done by Wahl [
14], who has proposed empirical equations for offset height of screen bar and orifice effect. He mentions that wire tilt angle, which is directly related to offset height, affects the screen capacity. It increases the shear effect and withdrawal of water quantity. However, it can cause some disadvantages to the screen performance such as sediment retention and clogging of the screen. He also concludes that changing sloth width or wire size directly affects the screen porosity and the screen flow capacity. In another study, Wahl [
15] investigated the effect of changes in screen parameters, such as wire tilt angle, screen curvature (arc) radius, and screen length on the withdrawal water discharge. The studies of Wahl [
14,
15] are important for investigating the effect of various screen parameters on the unit withdrawal discharge under clear water conditions. A numerical model for clear water conditions to predict water discharge through the intake in case of different screen design parameters and variations was developed by Dzafo and Dzaferovic [
16]. Another numeric model to analyze flow in a diversion channel in order to indicate how the numerical (Delft3D-FLOW) and physical models can be used to observe flow patterns nearby a diversion channel, with Coanda intake to estimate design parameters, was developed by Hosseini and Coonrod [
17].
In real-life applications, Coanda type intake structures face sediment-laden flow conditions as the other intake structures. Some studies have considered sediment-laden flow for Coanda type intakes. For example, a series of experimental studies were performed by Howarth [
18] to investigate Coanda screens. Three Coanda screens that have different sloth widths (bar opening) were used by Huber [
19] who has indicated that the sediment exclusion efficiency is increasing with decreasing sloth width. On the other hand, a smaller sloth width increases the risk of clogging. Some experiments were performed by May [
20] by considering both clear water and sediment-laden flow using three different Coanda screens which had different screen openings. May [
20] summarizes that screens having smaller wire openings show good performance for sediment exclusion but are more susceptible to clogging. Both studies [
19,
20] have investigated the effect of different discharge rates and sloth widths. However, constant screen slope and curvature radius were used in their studies. On the other hand, a series of experiments at Izmir Institute of Technology (IZTECH) Hydraulic Laboratory was performed by Hazar and Elci [
21] by using sediment-laden flows using Coanda intakes. Parameters of Water Capturing Performance (WCP) and Sediment Release Efficiency (SRE) were defined to explain the screen performances under different conditions. The multi-linear equations for both WCP and SRE of Coanda screens were developed using the linear regression as a statistical analysis method. However, these equations were not validated since all the data were employed in their construction.
The relations between WCP and related parameters of water flow, sediment, and intake characteristics are not linear but rather highly nonlinear, which is also true for SRE. This implies that nonlinear empirical equations can represent the actual physical processes. The advantage of developing such empirical equations can be beneficial for designing optimal intakes and for predicting diverted water amount and corresponding sediment concentration in the diverted water. Hence, there is a need for developing nonlinear empirical equations to predict WCP and SRE as a function of Coanda intake structural characteristics, water, fluid, and sediment parameters. This study would be the first one, to the knowledge of the authors, in the literature to develop such empirical equations. To develop the equations, the dimensionless parameters are first to be subjected to the multicollinearity analysis. Empirical nonlinear equations, whose coefficients and exponents would be determined by applying the method of Genetic Algorithm (GA), would be proposed. The construction of the empirical equations would be carried out by using 70% of the data for the calibration and 30% for the validation.
4. Discussion
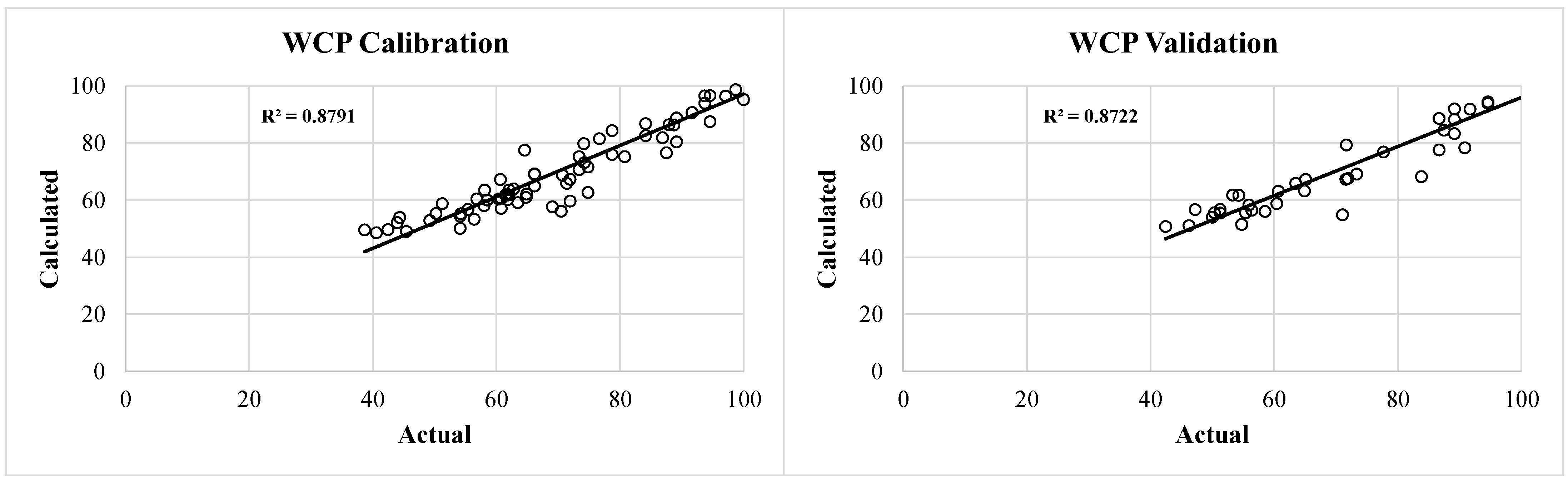
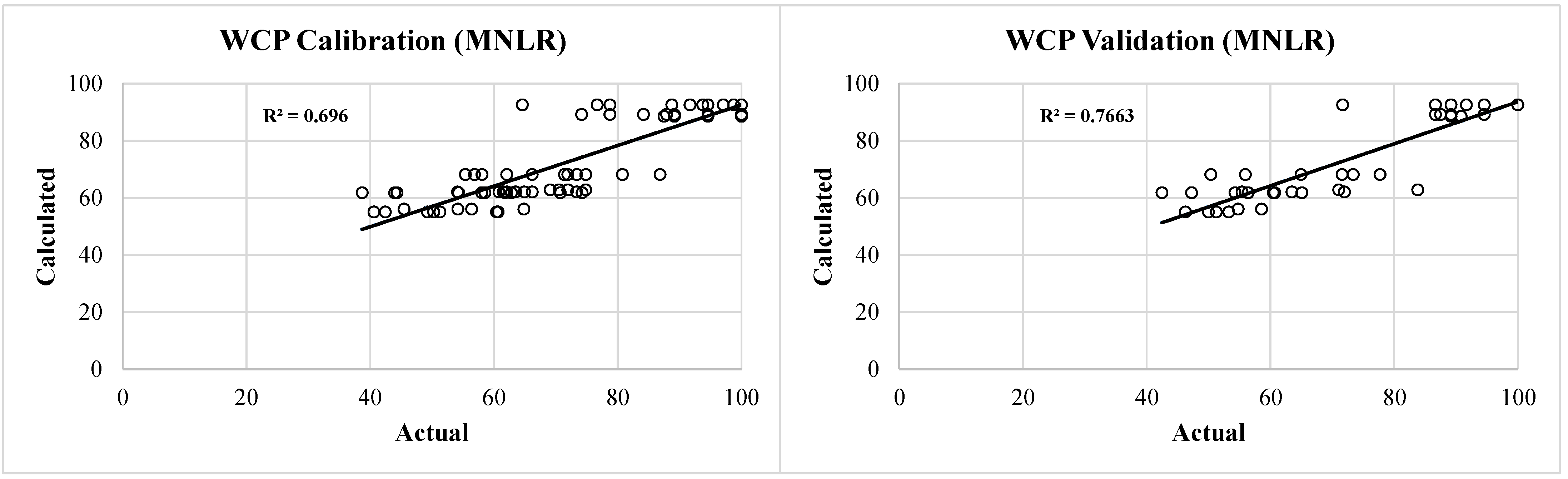
The calibration and validation of Equation (8), the GA-based empirical equation predicting WCP as a function of the intake geometric and flow characteristics variables, was successfully accomplished with low errors (MAE = 4.32, RMSE = 5.72 for the calibration stage, and MAE = 4.71, RMSE = 6.15 for the validation stage) and high R
2 values of 0.88 (calibration) and 0.87 (validation). When its success is compared against that of the MNLR equation (Equation (12)), it is clearly seen that the empirical equation outperformed the MNLR one, which produces relatively low R
2 = 0.70 and high errors of MAE = 6.95, RMSE = 9.12, at the calibration stage and MAE = 6.28, RMSE = 8.48, R
2 = 0.77 at the validation stage (see
Table 14). The GA-based empirical model produced comparable results against those of the ANN, which is a very powerful soft computing method for nonlinear problems. Although ANN produced less errors and high R
2 values, as seen in
Table 14, they do not yield any mathematical equation, as opposed to the empirical one.
The calibration and validation of Equation (9), the GA-based empirical equation predicting SRE as a function of the intake geometric, fluid, sediment, and flow characteristics variables, was successfully accomplished with low errors (MAE = 10.32, RMSE = 13.18 for calibration, and MAE = 10.77, RMSE = 12.99 for validation) and high R
2 values of 0.75 (calibration) and 0.80 (validation). When its success was compared against that of the MNLR equation (Equation (13)), it was seen that the empirical equation outperformed the MNLR one, which had produced high errors and very low R
2 values of 0.22 (calibration) and 0.17 (validation) (see
Table 15). It may be stated that the MNLR method had produced a worse performance for SRE than for WCP. The GA-based empirical model produced comparable results against those of the ANN, as seen in
Table 15. However, as it is pointed out above, ANNs do not accomplish any mathematical relations between the dependent and independent variables. They are, as it is pointed out in the literature, very powerful interpolators but poor extrapolators and they are black box models [
25]. The empirical models, on the other hand, can be easily employed for both the interpolation and extrapolation purposes.
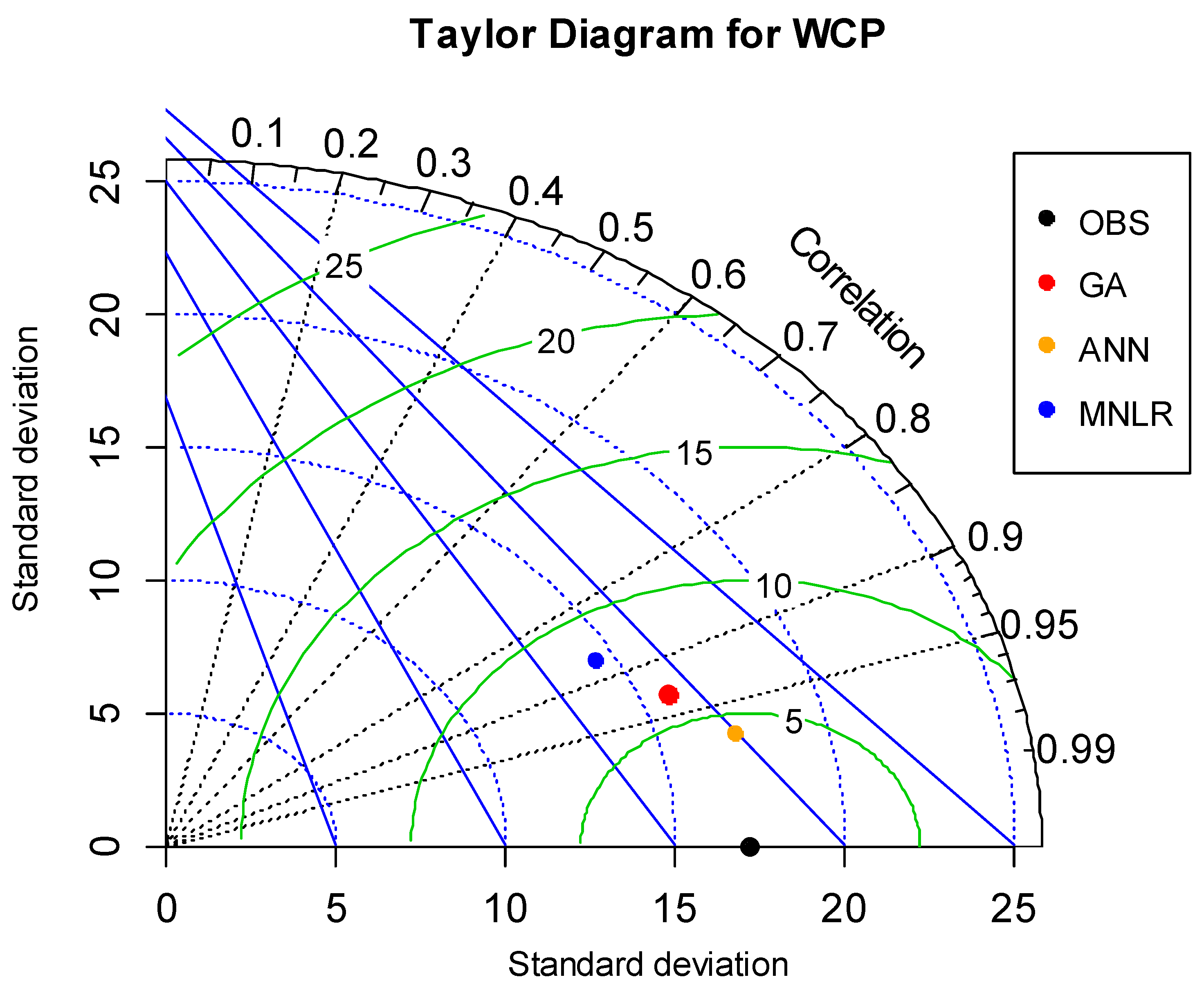
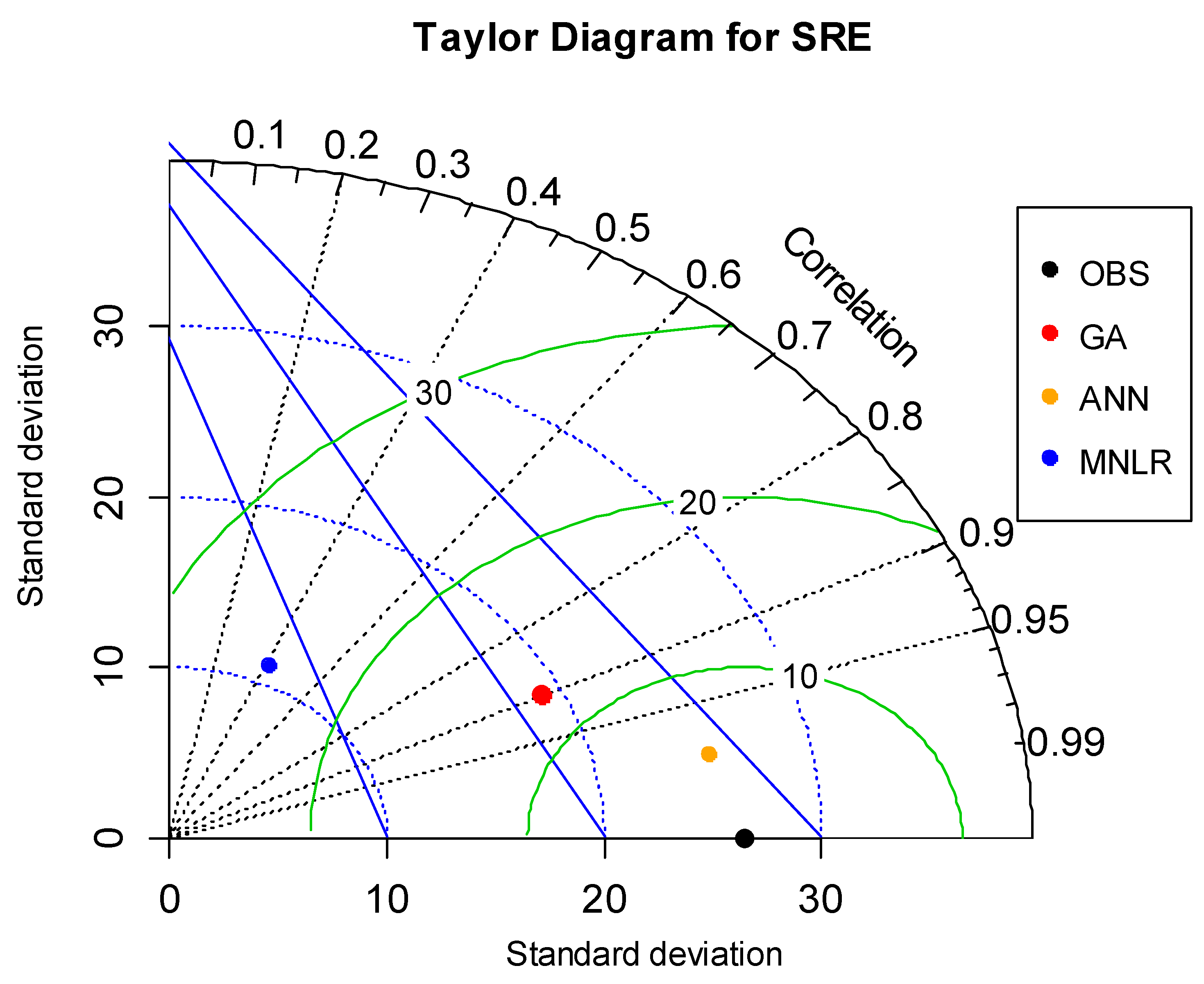
The above model validation performance results were also summarized by using the Taylor Diagram, which quantifies the degree of correspondence between predicted and measured data [
26]. For this purpose, it employs three different statistics called (1) the Pearson correlation coefficient, (2) the centered RMSE, and (3) the Standard deviation.
Figure 14 and
Figure 15 present these statistics for WCP and SRE performance results for the validation stages, respectively. In these figures, the correlation coefficient is related to the azimuthal angle and shown by black contours; the centered RMSE is represented by green arc contours and blue-dashed contours show the standard deviation. As seen in
Figure 14 and
Figure 15, the corresponding three statistics for each case are compatible with the performance measures presented in
Table 14 and
Table 15.
It is worth noting that this study is the first one developing empirical equations for the SRE and the WCP as functions of water, sediment, fluid, and flow parameters and Coanda intake physical characteristics. Based on the results of the experiments, an optimum design based on curvature radius was developed to prevent clogging during the intake operations. As pointed out in the Introduction section, there is a limited number of studies on Coanda intakes, especially subjected to the sediment-laden flows. These studies have involved mostly experimental works that lack any equation development. Therefore, discussing the developed empirical equations within the framework of existing literature becomes quite limited. Hazar and Elci [
21] have only attempted to propose multilinear regression (MLR) equations for the variables of SRE and WCP. Apart from the fact that the process is nonlinear rather than linear, they have employed all the data for the calibration stage and they have not verified their equations. In this study, however, the nonlinear empirical equations were calibrated with about 70% of the data and validated using the rest (about 30%). These equations were compared against those of the MNLR ones. The results have shown the superiority of the empirical equations.
Note that when Equation (8) was developed, about 76 sets of data were used in its calibration. The so-developed equation was then employed to make the predictions of the other 32 WCP values, which were not presented to the model at all during its calibration stage. As discussed above, the equation made good predictions of the measured 32 WCP values and outperformed the MNLR model (see
Table 14 and
Figure 14). This success points to the right form of the equation. In a similar fashion, in the development of Equation (9), 76 sets of data were used in its construction and the rest (32 sets) were employed to test its performance. As discussed above, the equation made successful predictions of SRE values and outperformed the MNLR model (see
Table 15 and
Figure 15). This also conforms to the right form of the constructed equation.
5. Summary and Conclusions
The main aim of this study is to develop nonlinear empirical equations for WCP and SRE, as functions of fluid, sediment, flow, and intake structure parameters for Coanda type intakes. To develop comprehensive but at the same time practical and user-friendly equations, the number of parameters and variables was first reduced from 14 to 10 by creating the dimensionless parameters. Then, the multicollinearity analysis was performed to remove any possible collinearity problem. As a result, only five dimensionless parameters for the WCP and five for the SRE were considered in the development of the equations. Next, the forms of the equations were decided upon by investigating direct or inverse variation between each parameter and the respected output variable of SRE and WCP. The optimal values of the exponents and coefficients of the proposed equations were obtained using the GA. The proposed equations were successfully calibrated with 70% of the data and validated with the rest. The developed equations were then compared against the MNLR and ANN. Results have shown that the GA-based empirical equations have reliable predictive capability and outperform the MNLR ones.
The performance of the GA_based empirical equations is comparable to that of the ANNs that produce less error and high R2 values. Yet, the ANN cannot accomplish neither any mathematical relations nor can they be used for the extrapolation purpose, unlike the empirical equations. The sensitivity analysis results carried out by the ANNs reveal that the geometric characteristics parameters of Coanda intakes are comparably more sensitive than the flow ones for the WCP. Similarly, both the geometric and sediment parameters are more sensitive than the flow characteristics in the case of the SRE.
Note that each nonlinear empirical equation (Equations (8) and (9)) was developed using 76 sets of data and verified by being applied to another 32 validation data sets that were not presented to the model at all during the respected calibration stage. The successful predictions of the validation data conform to the right form of each proposed equation. Therefore, this study concludes that the developed empirical equations can be employed to predict WCP and SRE for Coanda type intakes. It needs to be pointed out, however, that the equations developed in this study have used laboratory data. Thus, it would be suggested to test these equations in field conditions.
With the advantage of reducing the number of variables that describe a system, the empirical equations derived from non-dimensional numbers reduce the number of experiments enabling correlations of physical phenomena to scalable systems. It is noted that all the experiments were conducted using constant angled T-shape bars and a screen length of 60 cm. In a future study, at higher discharge rates and varying angled T-shape bars, different screen lengths can be investigated, and accordingly, the proposed empirical equations can be revised.