Characterizing the Groundwater Flow Regime in a Landslide Recharge Area Using Stable Isotopes: A Case Study of the Urbas Landslide Area in NW Slovenia
Abstract
:1. Introduction
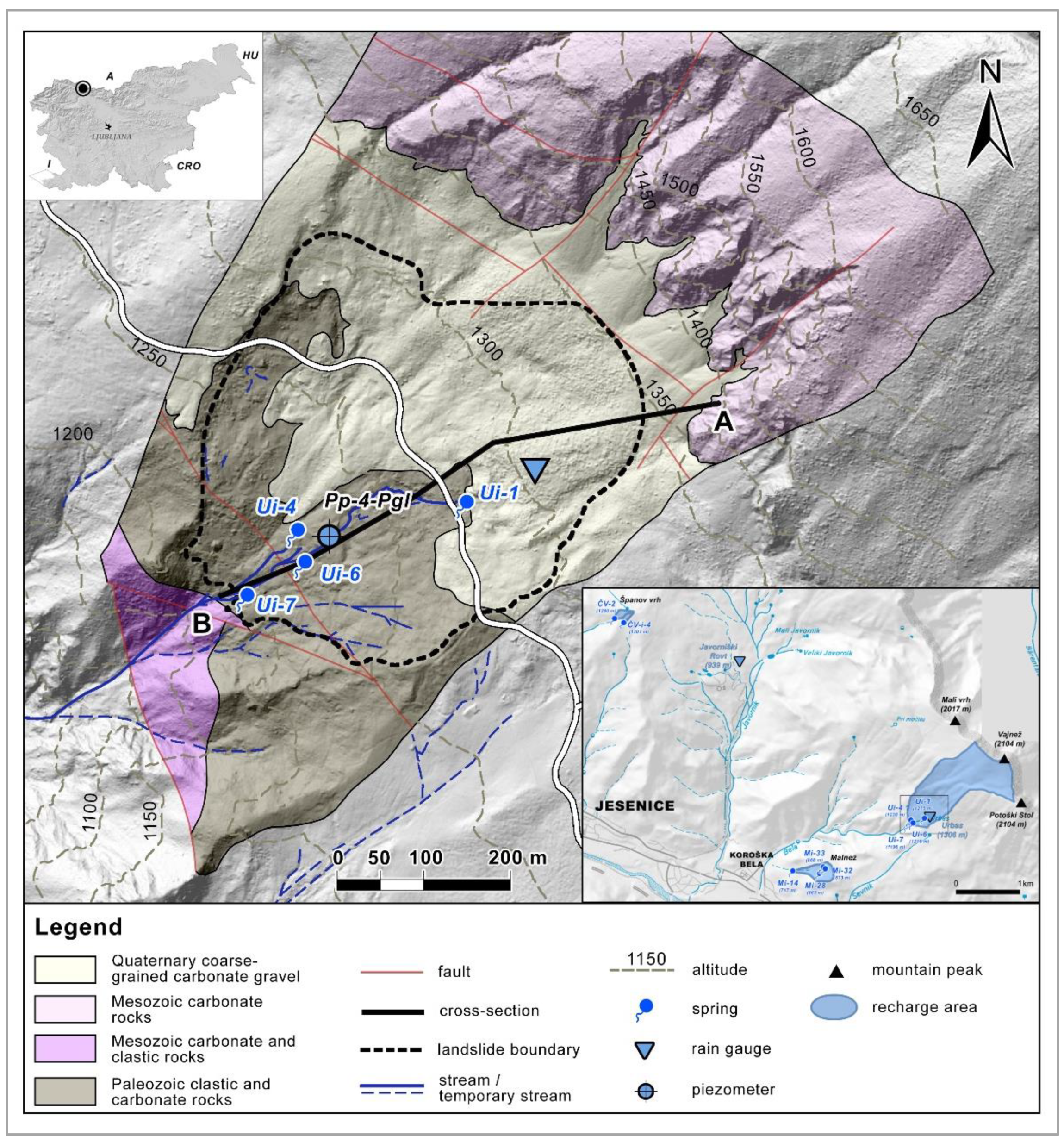
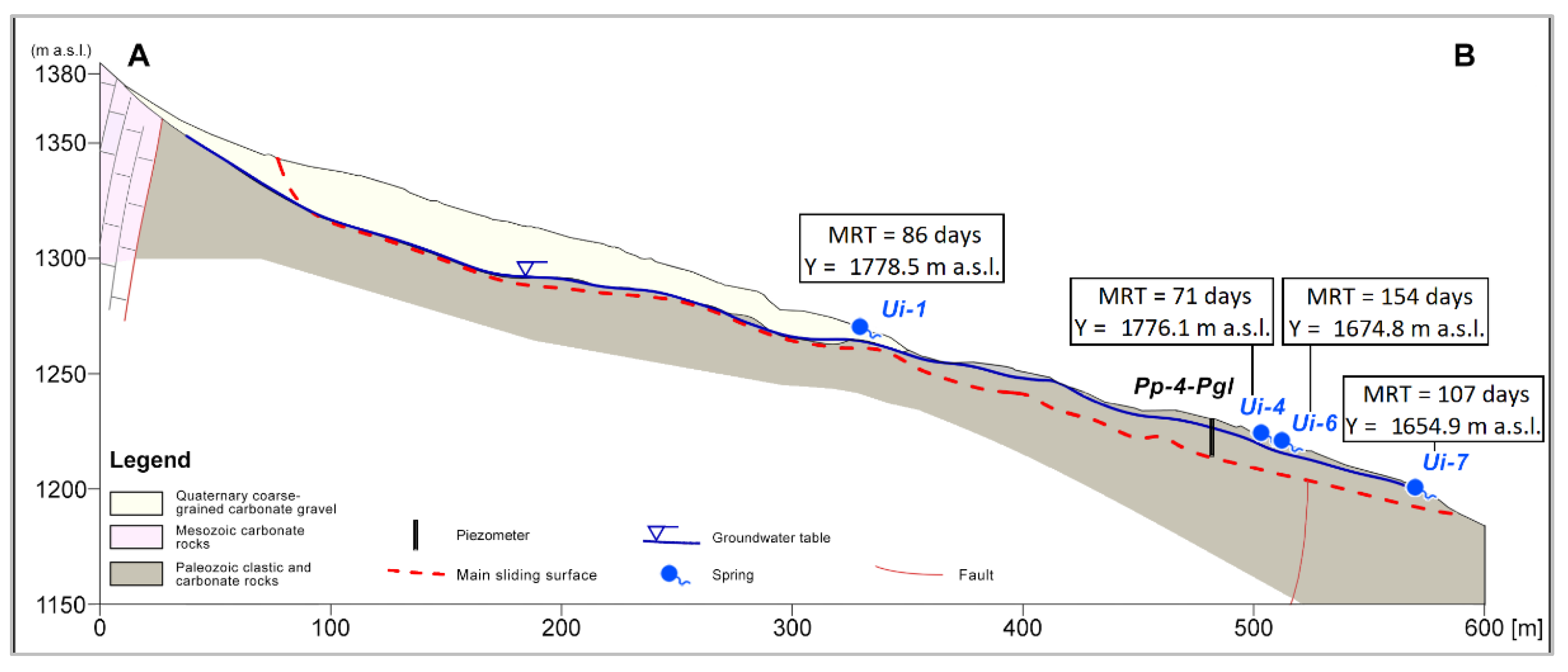
The Study Area
2. Materials and Methods
2.1. Water Sampling and Field Measurements
2.2. Chemical and Isotopic Analysis
2.2.1. Analysis of Major Cations and Anions
2.2.2. Oxygen-18 and Deuterium analyses
2.3. Statistical Data Analysis
2.4. Determination of Water Type
2.5. Estimation of the Local Meteoric Water Line (LMWL)
2.6. Average Recharge Altitude Calculation
2.7. Seasonal Trends in δ18O Values
2.8. Estimation of Groundwater Residence Time
3. Results and Discussion
3.1. Hydro-Chemical Facies of Water in the Recharge Area
3.2. Data Statistical Analysis
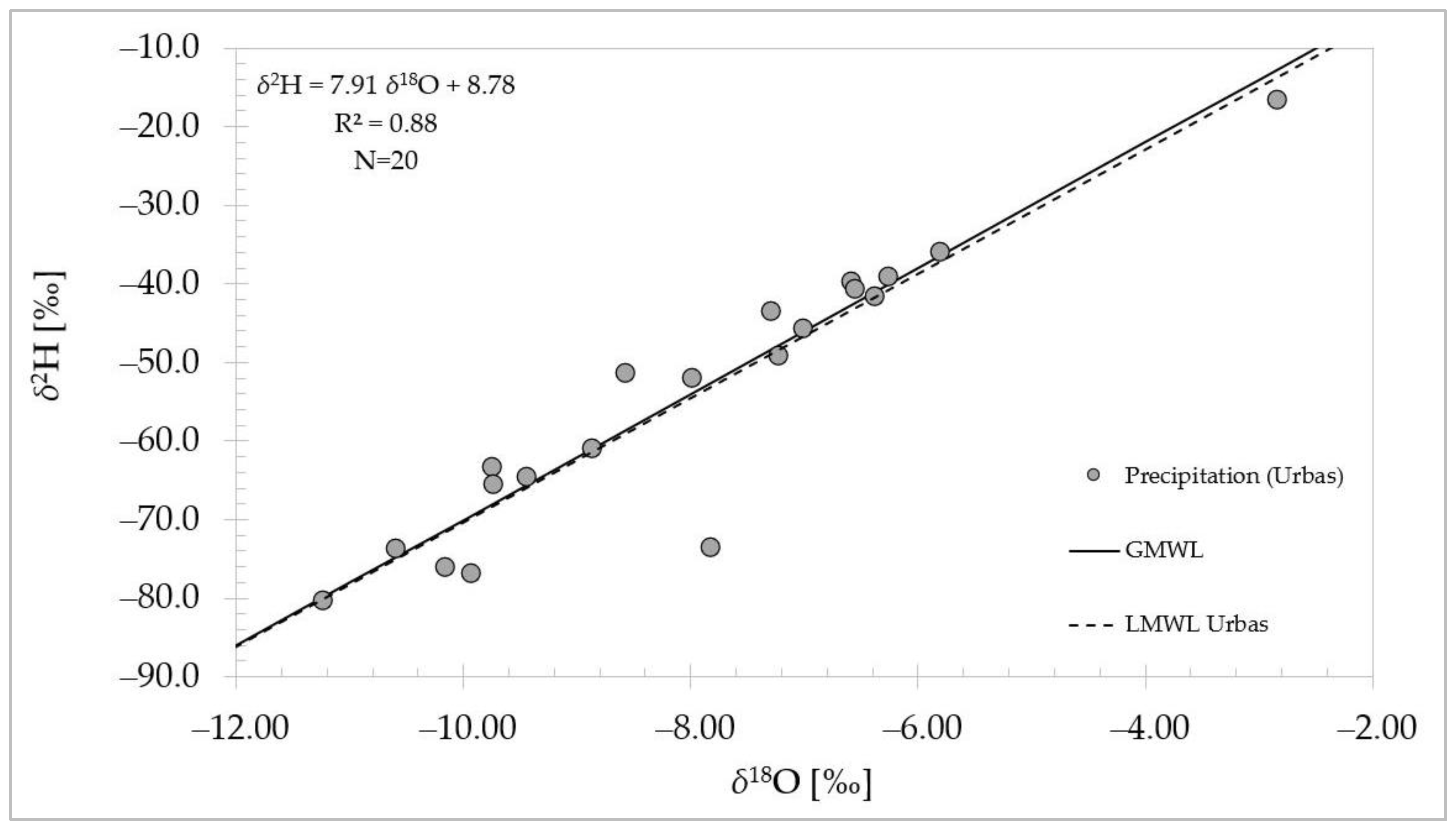
3.3. Stable Isotope Composition of Local Precipitation
3.4. Stable Isotope Composition of the Groundwater Samples
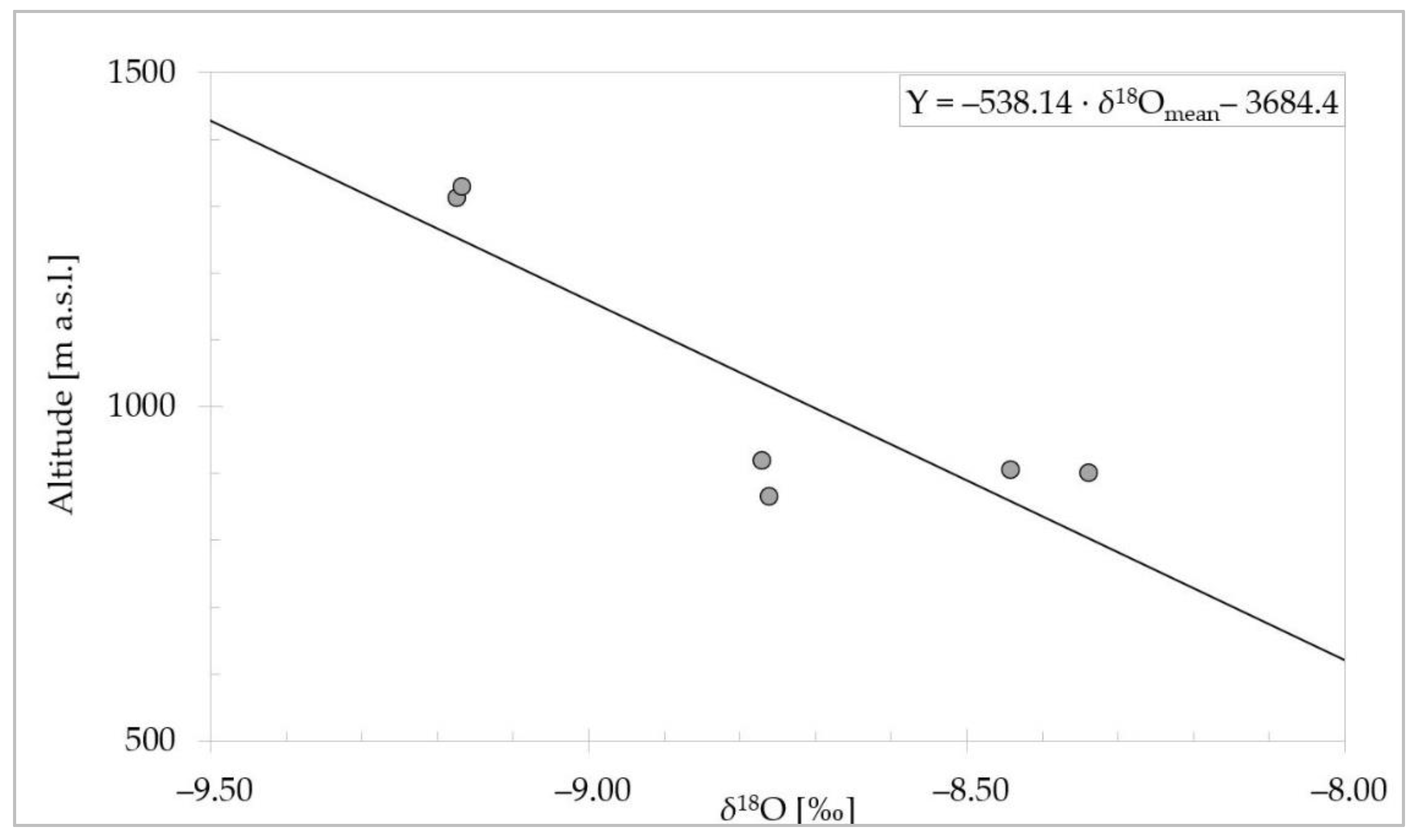
3.5. Average Recharge Altitude of Springs
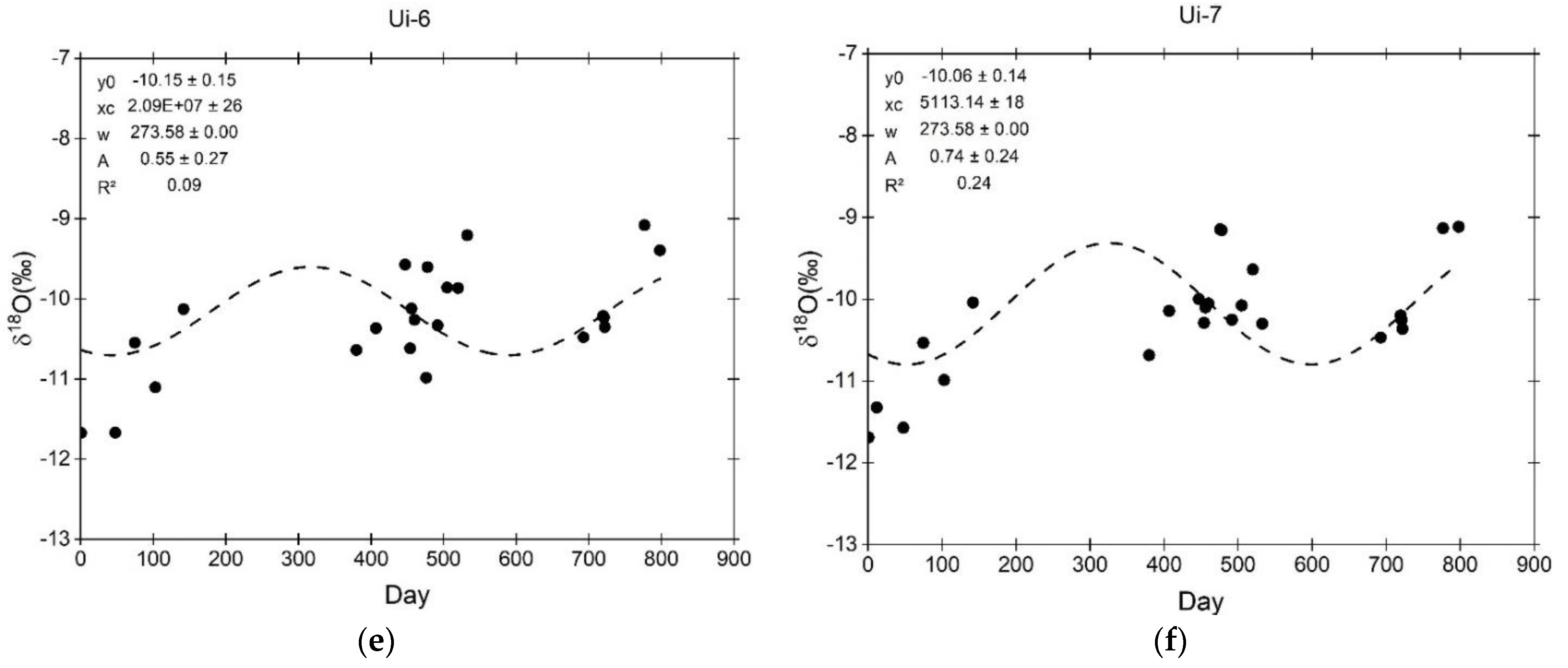
3.6. Estimated Mean Residence Time of Springs
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Auflič, M.J.; Šinigoj, J.; Krivic, M.; Podboj, M.; Peternel, T.; Komac, M. Landslide prediction system for rainfall induced landslides in Slovenia (Masprem). Geologija 2016, 59, 259–271. [Google Scholar] [CrossRef]
- Jordanova, G.; Gariano, S.L.; Melillo, M.; Peruccacci, S.; Brunetti, M.T.; Jemec Auflič, M. Determination of Empirical Rainfall Thresholds for Shallow Landslides in Slovenia Using an Automatic Tool. Water 2020, 12, 1449. [Google Scholar] [CrossRef]
- Sidle, R.; Greco, R.; Bogaard, T. Overview of Landslide Hydrology. Water 2019, 11, 148. [Google Scholar] [CrossRef] [Green Version]
- Peng, T.-R.; Wang, C.-H.; Hsu, S.-M.; Chen, N.-C.; Su, T.-W.; Lee, J.-F. Use of stable water isotopes to assess sources and influences of slope groundwater on slope failure. Hydrol. Processes 2012, 26, 345–355. [Google Scholar] [CrossRef]
- Mebrahtu, T.K.; Banning, A.; Girmay, E.H.; Wohnlich, S. The effect of hydrogeological and hydrochemical dynamics on landslide triggering in the central highlands of Ethiopia. Hydrogeol. J. 2021, 29, 1239–1260. [Google Scholar] [CrossRef]
- Malet, J.P.; van Asch, T.W.J.; van Beek, R.; Maquaire, O. Forecasting the behaviour of complex landslides with a spatially distributed hydrological model. Nat. Hazards Earth Syst. Sci. 2005, 5, 71–85. [Google Scholar] [CrossRef] [Green Version]
- Matsuura, S.; Asano, S.; Okamoto, T. Relationship between rain and/or meltwater, pore-water pressure and displacement of a reactivated landslide. Eng. Geol. 2008, 101, 49–59. [Google Scholar] [CrossRef]
- François, B.; Tacher, L.; Bonnard, C.; Laloui, L.; Triguero, V. Corrigendum: Numerical modelling of the hydrogeological and geomechanical behaviour of a large slope movement: The Triesenberg landslide (Liechtenstein). Can. Geotech. J. 2009, 46, 1009. [Google Scholar] [CrossRef] [Green Version]
- Padilla, C.; Onda, Y.; Iida, T.; Takahashi, S.; Uchida, T. Characterization of the groundwater response to rainfall on a hillslope with fractured bedrock by creep deformation and its implication for the generation of deep-seated landslides on Mt. Wanitsuka, Kyushu Island. Geomorphology 2014, 204, 444–458. [Google Scholar] [CrossRef]
- Ponziani, F.; Pandolfo, C.; Stelluti, M.; Berni, N.; Brocca, L.; Moramarco, T. Assessment of rainfall thresholds and soil moisture modeling for operational hydrogeological risk prevention in the Umbria region (central Italy). Landslides 2011, 9, 229–237. [Google Scholar] [CrossRef]
- Deiana, M.; Cervi, F.; Pennisi, M.; Mussi, M.; Bertrand, C.; Tazioli, A.; Corsini, A.; Ronchetti, F. Chemical and isotopic investigations (δ18O, δ2H, 3H, 87Sr/86Sr) to define groundwater processes occurring in a deep-seated landslide in flysch. Hydrogeol. J. 2018, 26, 2669–2691. [Google Scholar] [CrossRef]
- Sajinkumar, K.S.; Unnikrishnan Warrier, C.; Muraleedharan, C.; Shahul Hameed, A.; Rani, V.R.; Pradeepkumar, A.P.; Sundarajan, P. A study on landslides and subsurface piping, facilitated by dykes, using vertical electrical sounding and δO18 and δH2 stable isotopes. Bull. Eng. Geol. Environ. 2017, 76, 1297–1306. [Google Scholar] [CrossRef]
- Marc, V.; Bertrand, C.; Malet, J.-P.; Carry, N.; Simler, R.; Cervi, F. Groundwater-Surface waters interactions at slope and catchment scales: Implications for landsliding in clay-rich slopes. Hydrol. Processes 2017, 31, 364–381. [Google Scholar] [CrossRef]
- Peng, T.-R.; Wang, C.-H.; Lai, T.-C.; Ho, F.S.-K. Using hydrogen, oxygen, and tritium isotopes to identify the hydrological factors contributing to landslides in a mountainous area, central Taiwan. Environ. Geol. 2007, 52, 1617–1629. [Google Scholar] [CrossRef]
- Niinikoski, P.I.; Hendriksson, N.M.; Karhu, J.A. Using stable isotopes to resolve transit times and travel routes of river water: A case study from southern Finland. Isot. Environ. Health Stud. 2016, 52, 380–392. [Google Scholar] [CrossRef] [PubMed]
- Fritz, P. River waters. In Stable Isotope Hydrology: Deuterium and Oxygen-18 in the Water Cycle; Gat, J.R., Gonfiantini, R., Eds.; IAEA: Vienna, Austria, 1981; pp. 111–130. [Google Scholar]
- McCarthy, K.A.; McFarland, W.D.; Wilkinson, J.M.; White, L.D. The dynamic relationship between ground water and the Columbia River: Using deuterium and oxygen-18 as tracers. J. Hydrol. 1992, 135, 1–12. [Google Scholar] [CrossRef]
- Lipfert, G.; Reeve, A. Characterization of Three Water Types in a Fractured Schist, High Arsenic, Watershed in Maine; University of Maine: Orono, ME, USA, 2004; pp. 638–646. [Google Scholar]
- Chebotarev, I.I. Metamorphism of natural waters in the crust of weathering-1. Geochim. et Cosmochim. Acta 1955, 8, 22–48. [Google Scholar] [CrossRef]
- Driscoll, F.G. Groundwater and Wells; U.S. Filter/Johnson Screens: St. Paul, MN, USA, 1995. [Google Scholar]
- Gibbs, J.R. Mechanisms controling world water chemisty. Science 1970, 80, 1088–1090. [Google Scholar] [CrossRef] [PubMed]
- Marandi, A.; Shand, P. Groundwater chemistry and the Gibbs Diagram. Appl. Geochem. 2018, 97, 209–212. [Google Scholar] [CrossRef]
- Janža, M.; Serianz, L.; Šram, D.; Klasinc, M. Hydrogeological investigation of landslides Urbas and Čikla above the settlement of Koroška Bela (NW Slovenia). Geologija 2018, 61, 191–203. [Google Scholar] [CrossRef]
- Peternel, T.; Jež, J.; Milanič, B.; Markelj, A.; Jemec Auflič, M. Engineering-geological conditions of landslides above the settlement of Koroška Bela (NW Slovenia). Geologija 2018, 61, 177–189. [Google Scholar] [CrossRef]
- Bezak, N.; Sodnik, J.; Maček, M.; Jurček, T.; Jež, J.; Peternel, T.; Mikoš, M. Investigation of potential debris flows above the Koroška Bela settlement, NW Slovenia, from hydro-technical and conceptual design perspectives. Landslides 2021, 18, 3891–3906. [Google Scholar] [CrossRef]
- Šegina, E.; Peternel, T.; Urbančič, T.; Realini, E.; Zupan, M.; Jež, J.; Caldera, S.; Gatti, A.; Tagliaferro, G.; Consoli, A.; et al. Monitoring Surface Displacement of a Deep-Seated Landslide by a Low-Cost and near Real-Time GNSS System. Remote Sens. 2020, 12, 3375. [Google Scholar] [CrossRef]
- Peternel, T.; Šegina, E.; Zupan, M.; Jemec Auflič, M.; Jež, J. Preliminary Result of Real-Time Landslide Monitoring in the Case of the Hinterland of Koroška Bela, NW Slovenia. In Understanding and Reducing Landslide Disaster Risk; Springer International Publishing: Berlin/Heidelberg, Germany, 2021; pp. 459–464. [Google Scholar]
- Jemec Auflič, M.; Mikoš, M.; Verbovšek, T. Advances in Ladslide Research. In Proceedings of the 3rd Regional Symposium on Landslides in the Adriatic Balcan Region, Ljubljana, Slovenia, 11–13 October 2017. [Google Scholar]
- Jež, J.; Mikoš, M.; Trajanova, M.; Kumelj, Š.; Budkovič, T.; Bavec, M. Koroška Bela alluvial fan—The result of the catastrophic slope events; Karavanke Mountains, NW Slovenia). Geologija 2008, 51, 219–227. [Google Scholar] [CrossRef]
- SEA. Annual Data (1981–2019) at Javorniški Rovt. Available online: http://meteo.arso.gov.si/met/sl/app/webmet/#webmet==8Sdwx2bhR2cv0WZ0V2bvEGcw9ydlJWblR3LwVnaz9SYtVmYh9iclFGbt9SaulGdugXbsx3cs9mdl5WahxXYyNGapZXZ8tHZv1WYp5mOnMHbvZXZulWYnwCchJXYtVGdlJnOn0UQQdSf (accessed on 20 November 2021).
- Črepinšek, Z.; Kunšič, A.; Kralj, T.; Kajfež-Bogataj, L. Precipitation analysis of the wider area of the Triglav national park for the period 1961–2009. Acta Agric. Slov. 2011, 97, 295–304. [Google Scholar]
- Kunšič, A. Precipitation Analysis of the Wider Area of the Triglav National Park. Graduation Thesis, University of Ljubljana, Ljubljana, Slovenia, 2011. [Google Scholar]
- SEA. Environmental Atlas of Slovenia. Available online: http://gis.arso.gov.si/atlasokolja/profile.aspx?id=Atlas_Okolja_AXL@ARSO&culture=en-US (accessed on 10 January 2022).
- Vreča, P.; Brenčič, M.; Sinjur, I.; Vertačnik, G.; Volk, M.; Ortar, J.; Torkar, A.; Stibilj, V.; Pavšek, M. Izotopska sestava padavin in snega na območju Julijskih Alp in Karavank. In Proceedings of the Raziskave iz Področja Geodezije in Geofizike—18. Strokovno Srečanje Slovenskega Združenja za Geodezijo in Geofiziko, Ljubljana, Slovenia, 29 January 2013. [Google Scholar]
- Aggarwal, P.K.; Araguas, L.; Garner, W.A.; Groening, M.; Kulkarni, K.M. Sampling Procedures for Isotope Hydrology. 2009, p. 8. Available online: http://www-naweb.iaea.org/napc/ih/documents/other/Sampling%20booklet%20web.pdf (accessed on 23 January 2022).
- Kendall, C.; McDonnell, J.J. Isotope Tracers in Catchment Hydrology; Elsevier Science: Amsterdam, The Netherlands, 1998. [Google Scholar]
- WTW. Manual WTW ph.Cond 340i; ba52312e; WTW: Weilheim, Germany, 2004. [Google Scholar]
- WTW. Manual WTW FDO 925; ba75898defs01; WTW: Weilheim, Germany, 2010. [Google Scholar]
- WTW. Manual WTW SenTiX ORP. Pt. Au. Ag.; ba75741defs01; WTW: Weilheim, Germany, 2008. [Google Scholar]
- Picarro. Operation, Maintenance and Troubleshooting L2140-i, L2130-i or L2120-i Analyzer and Peripherals—User’s Manual; Picarro: Santa Clara, CA, USA, 2015; p. 2. [Google Scholar]
- Picarro. Picarro L2130-i Isotopic Water Analyzer. Available online: http://www.ebd.csic.es/lie/PDF/Picarro_L2130-i_Isotopic_Water_Analyzer.pdf (accessed on 20 November 2021).
- IAEA. WICO 2020 δ¹⁸O /δ²H Intercomparison Test Laboratory Report; IAEA: Vienna, Austria, 2020; p. 8. [Google Scholar]
- USGS. Report of Stable Isotopic Composition Reference Material USGS46 Ice Core Water (Hydrogen and Oxygen Isotopes in Water); United State Geological Survey-Reston Stable Isotope Laboratory: Reston, VA, USA, 2019; p. 3. [Google Scholar]
- USGS. Report of Stable Isotopic Composition Reference Material USGS47 Lake Louise Drinking Water (Hydrogen and Oxygen Isotopes in Water); United States Geological Survey-Reston Stable Isotope Laboratory: Reston, VA, USA, 2019. [Google Scholar]
- USGS. Report of Stable Isotopic Composition Reference Material USGS48 Puerto Rico Precipitation (Hydrogen and Oxygen Isotopes in Water); United States Geological Survey-Reston Stable Isotope Laboratory: Reston, VA, USA, 2020. [Google Scholar]
- Vreča, P.; Krajcar Bronić, I.; Leis, A.; Brenčič, M. Isotopic composition of precipitation in Ljubljana (Slovenia). Geologija 2008, 51, 169–180. [Google Scholar] [CrossRef]
- Drezner, Z.; Turel, O.; Zerom, D. A Modified Kolmogorov–Smirnov Test for Normality. Commun. Stat. Simul. Comput. 2010, 39, 693–704. [Google Scholar] [CrossRef] [Green Version]
- Bliss, C. Statistics in Biology; McGraw-Hill Book Co.: New York, UY, USA, 1970; Volume 2. [Google Scholar]
- Rodgers, P.; Soulsby, C.; Waldron, S.; Tetzlaff, D. Using stable isotope tracers to assess hydrological flow paths, residence times and landscape influences in a nested mesoscale catchment. Hydrol. Earth Syst. Sc. 2005, 9, 139–155. [Google Scholar] [CrossRef] [Green Version]
- Lentech. Water Analysis Accuracy Tester. Available online: https://www.lenntech.com/calculators/accuracy/accuracy-water-analysis.htm (accessed on 23 January 2022).
- Ahmed, M.F.; Waqas, U.; Khan, M.S.; Rashid, H.M.A.; Saqib, S. Evaluation and classification of water quality of glacier-fed channels using supervised learning and water quality index. Water Environ. J. 2021, 35, 1174–1191. [Google Scholar] [CrossRef]
- Domenico, P.A.; Schwartz, F.W. Physical and Chemical Hydrogeology; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Sajil Kumar, P.J. Interpretation of groundwater chemistry using piper and hadha`s diagrams: A comparative study from perambalur taluk. Elixir Geosci. 2013, 54, 12208–12211. [Google Scholar]
- Ravikumar, P.; Somashekar, R.K.; Prakash, K.L. A comparative study on usage of Durov and Piper diagrams to interpret hydrochemical processes in groundwater from SRLIS river basin, Karnataka, India. Elixir Earth Sci. 2015, 80, 31073–31077. [Google Scholar]
- Waterloo. AquaChem 2014.2. A Professional Application for Water Quality Data Analysis. Plotting. Reporting. And Modelling. Demonstration Guide; Waterloo Hydrogeologic: Waterloo, ON, Canada, 2014; p. 67. [Google Scholar]
- Craig, H. Isotopic Variations in Meteoric Waters. Science 1961, 133, 1702–1703. [Google Scholar] [CrossRef] [PubMed]
- Durowoju, O.S.; Odiyo, J.O.; Ekosse, G.-I.E. Determination of isotopic composition of rainwater to generate local meteoric water line in Thohoyandou, Limpopo Province, South Africa. Water SA 2019, 45, 183–189. [Google Scholar] [CrossRef] [Green Version]
- Yurtsever, Y.; Araguas, L.A. Environmental isotope applications in hydrology: An overview of the IAEA’s activities, experiences, and prospects. In Proceedings of the Tracers in Hydrology (Proceedings of the Yokohama Symposium), Yokohama, Japan, 21–23 July 1993. [Google Scholar]
- Benjamin, L.; Knobel, L.L.; Hall, F.L.; Cecil, L.D.; Green, J.R. Development of a Local Meteoric Water Line for Southeastern Idaho, Western Wyoming, and South-Central Montana; USGS: New York, NY, USA, 2004; 23p. [Google Scholar]
- Helsel, D.R.; Hirsch, R.M. Statistical Methods in Water Resources; USGS: New York, NY, USA, 1992; 522p. [Google Scholar]
- Dansgaard, W. Stable isotopes in precipitation. Tellus XVI 1964, 4, 33. [Google Scholar]
- Jefferson, A.; Grant, G.; Rose, T. Influence of volcanic history on groundwater patterns on the west slope of the Oregon High Cascades. Water Resour. Res. 2006, 42, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Roses, T.P.; Davisson, M.L.; Criss, R.E. Isotope hydrology of voluminous cold springs in fractured rock from an active volcanic region, northeastern California. J. Hydrol. 1996, 179, 207–236. [Google Scholar] [CrossRef]
- Torkar, A. Analysis of Groundwater Outflow through Springs in Fluvioglacial Intergranular Aquifers. Ph.D. Thesis, University of Ljubljana, Ljubljana, Slovenia, 2016. [Google Scholar]
- Torkar, A.; Brenčič, M.; Vreča, P. Chemical and isotopic characteristics of groundwater-dominated Radovna River (NW Slovenia). Environ. Earth Sci. 2016, 75, 1296. [Google Scholar] [CrossRef]
- OriginLab. OriginPro; OriginLab Corporation: Northampton, MA, USA, 2019. [Google Scholar]
- Burgman, J.O.; Calles, B.; Weatman, F. Conclusions from a ten year study of oxygen-18 in precipitation and runoff in Sweden. In Isotope Techniques in Water Resources Development; International Atomic Energy Agency: Vienna, Austria, 1987; pp. 579–590. [Google Scholar]
- Aggarwal, P.; Gourcy, L.; Birks, J.; Edwards, T.; Gibson, J. GNIP Maps and Animations. Available online: http://www-naweb.iaea.org/napc/ih/documents/userupdate/Waterloo/ (accessed on 23 January 2022).
- IJS. SLONIP-Slovenian Network of Isotopes in Precipitation. Available online: https://slonip.ijs.si/accounts/login/?next=/data/6 (accessed on 6 December 2021).
- Vreča, P.; Kanduč, T.; Kocman, D.; Lojen, S.; Robinson, J.; Štrok, M. Slovenska mreza opazovanj izotopske sestave padavin (SLONIP). In Proceedings of the Drugi Slovenski Kongres o Vodah, Podčetrtek, Slovenia, 19–20 April 2017. [Google Scholar]
- Serianz, L.; Cerar, S.; Vreča, P. Using stable isotopes and major ions to identify recharge characteristics of the Alpine groundwater-flow dominated Triglavska Bistrica River. Geologija 2021, 64, 205–220. [Google Scholar] [CrossRef]
- Davis, J.C. Statistics and Data Analysis in Geology; Wiley: New York, NY, USA, 2002. [Google Scholar]
- McLeod, S.A. Introduction to the Normal Distribution (Bell Curve). Simply Psychology. Available online: https://www.simplypsychology.org/normal-distribution.html (accessed on 22 November 2021).
- Kastelec, D. Use of Universal Kriging for Objective Spatial Interpolation of Average Yearly Precipitation in Slovenia; Zbornik Biotehniške fakultete Univerze v Ljubljani: Kmetijstvo, Ljubljana, 1999; pp. 301–314. [Google Scholar]
- Serianz, L.; Rman, N.; Brenčič, M. Hydrogeochemical Characterization of a Warm Spring System in a Carbonate Mountain Range of the Eastern Julian Alps, Slovenia. Water 2020, 12, 1427. [Google Scholar] [CrossRef]
- Mezga, K. Natural Hydrochemical Background and Dynamics of Groundwater in Slovenia. Ph.D. Thesis, University of Nova Gorica, Nova Gorica, Slovenia, 2014. [Google Scholar]
- Serianz, L. Hydrogeological Analysis of Thermal Water Outflow from a Carbonate Aquifer in the Eastern Part of the Julian Alps. Ph.D. Thesis, University of Ljubljana, Ljubljana, Slovenia, 2022. [Google Scholar]



| Sampling Point | Ui-1 (1275.4 m a.s.l.) | Pp-4-Pgl (1229.7 m a.s.l.) | Ui-4 (1237.45 m a.s.l.) | Ui-6 (1218.5 m a.s.l.) | Ui-7 (1195.8 m a.s.l.) |
|---|---|---|---|---|---|
| Object type | spring | piezometer | spring | spring | spring |
| T (°C) | 3.9 | 6.4 | 5.2 | 5.1 | 6.6 |
| EC (µS/cm) | 175 | 322 | 217 | 211 | 235 |
| pH (/) | 8.3 | 8.1 | 7.9 | 7.9 | 8.0 |
| DO (mg/L) | 11.9 | 10.0 | 11.0 | 11.3 | 10.7 |
| O2 (%) | 105.3 | 94 | 100 | 102.4 | 100.4 |
| Eh (mV) | 347 | 365 | 469 | 440 | 442 |
| Na+ (mg/L) | 1.0 | 1.4 | 1.4 | 1.1 | 1.5 |
| K+ (mg/L) | <0.25 * | 0.32 | 0.31 | <0.25 * | 0.35 |
| Ca2+ (mg/L) | 32 | 38 | 40 | 39 | 44 |
| Mg2+ (mg/L) | 4.5 | 5.6 | 5.5 | 5.5 | 5.7 |
| HCO3− (mg/L) | 123 | 143 | 150 | 143 | 157 |
| SO42− (mg/L) | <1.50 * | 3.30 | 3.45 | 1.89 | 3.84 |
| Cl− (mg/L) | <0.75 * | <0.75 * | <0.75 * | <0.75 * | <0.75 * |
| NO3− (mg/L) | <2.2 * | <2.2 * | <2.2 * | <2.2 * | <2.2 * |
| ICBE (%) | 1.14 | 0.31 | 0.82 | 0.78 | 1.05 |
| Hydro-chemical facies | Ca–HCO3 | Ca–HCO3 | Ca–HCO3 | Ca–HCO3 | Ca–HCO3 |
| Number of Samples | Mean | Median | Minimum | Maximum | SD | |
|---|---|---|---|---|---|---|
| Ui-1 | ||||||
| δ18O (‰) | 24 | −10.64 | −10.39 | −11.90 | −9.61 | 0.69 |
| δ2H (‰) | 24 | −72.9 | −73.0 | −80.9 | −64.0 | 4.82 |
| Ui-4 | ||||||
| δ18O (‰) | 24 | −10.68 | −10.39 | −12.27 | −9.74 | 0.80 |
| δ2H (‰) | 24 | −73.0 | −72.4 | −84.9 | −65.0 | 5.71 |
| Ui-6 | ||||||
| δ18O (‰) | 23 | −10.28 | −10.26 | −11.68 | −9.08 | 0.68 |
| δ2H (‰) | 23 | −70.4 | −69.7 | −80.1 | −59.7 | 4.64 |
| Ui-7 | ||||||
| δ18O (‰) | 24 | −10.23 | −10.22 | −11.69 | −9.11 | 0.70 |
| δ2H (‰) | 24 | −70.3 | −70.6 | −79.7 | −59.7 | 4.80 |
| Sampling Point | Number of Samples | Location | Altitude (m a.s.l.) | Estimated Y (m a.s.l.) | δ18Omean (‰) | δ2Hmean (‰) |
|---|---|---|---|---|---|---|
| ČV-2 | 2 | Španov vrh | 1280.0 | 1311.9 | −9.17 | −59.4 |
| ČVi-4 | 2 | Španov vrh | 1307.0 | 1328.5 | −9.17 | −59.8 |
| Mi-14 | 2 | Malnež | 717.1 | 865.1 | −8.76 | −57.8 |
| Mi-28 | 2 | Malnež | 862.7 | 918.5 | −8.77 | −58.2 |
| Mi-32 | 2 | Malnež | 873.0 | 905.0 | −8.44 | −55.7 |
| Mi-33 | 2 | Malnež | 867.5 | 899.7 | −8.34 | −54.9 |
| Spring | Number of Samples | Altitude (m a.s.l.) | δ18Omean (‰) | (Y) (m a.s.l.) |
|---|---|---|---|---|
| Ui-1 | 6 | 1275.40 | −10.15 | 1778.5 |
| Ui-4 | 6 | 1237.45 | −10.15 | 1776.1 |
| Ui-6 | 6 | 1218.50 | −9.96 | 1674.8 |
| Ui-7 | 6 | 1195.80 | −9.92 | 1654.9 |
| Sampling Point | Object Type | Amplitude | R2 | MRT (Years) Based on Urbas | MRT (Years) Based on Zgornja Radovna |
|---|---|---|---|---|---|
| Urbas | Rain gauge | 2.66 | 0.21 | - | p |
| Zgornja Radovna | Rain gauge | 2.07 | 0.42 | ||
| Ui-1 | Spring | 0.88 | 0.35 | 0.23 | 0.32 |
| Ui-4 | Spring | 1.00 | 0.38 | 0.19 | 0.27 |
| Ui-6 | Spring | 0.55 | 0.09 | 0.42 | 0.56 |
| Ui-7 | Spring | 0.74 | 0.24 | 0.29 | 0.40 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koren, K.; Serianz, L.; Janža, M. Characterizing the Groundwater Flow Regime in a Landslide Recharge Area Using Stable Isotopes: A Case Study of the Urbas Landslide Area in NW Slovenia. Water 2022, 14, 912. https://doi.org/10.3390/w14060912
Koren K, Serianz L, Janža M. Characterizing the Groundwater Flow Regime in a Landslide Recharge Area Using Stable Isotopes: A Case Study of the Urbas Landslide Area in NW Slovenia. Water. 2022; 14(6):912. https://doi.org/10.3390/w14060912
Chicago/Turabian StyleKoren, Katja, Luka Serianz, and Mitja Janža. 2022. "Characterizing the Groundwater Flow Regime in a Landslide Recharge Area Using Stable Isotopes: A Case Study of the Urbas Landslide Area in NW Slovenia" Water 14, no. 6: 912. https://doi.org/10.3390/w14060912






