A New Method of Estimating Groundwater Evapotranspiration at Sub-Daily Scale Using Water Table Fluctuations
Abstract
:1. Introduction
2. Site Descriptions and Data Collection
3. Methods
3.1. Water Balance in the Riparian Zone
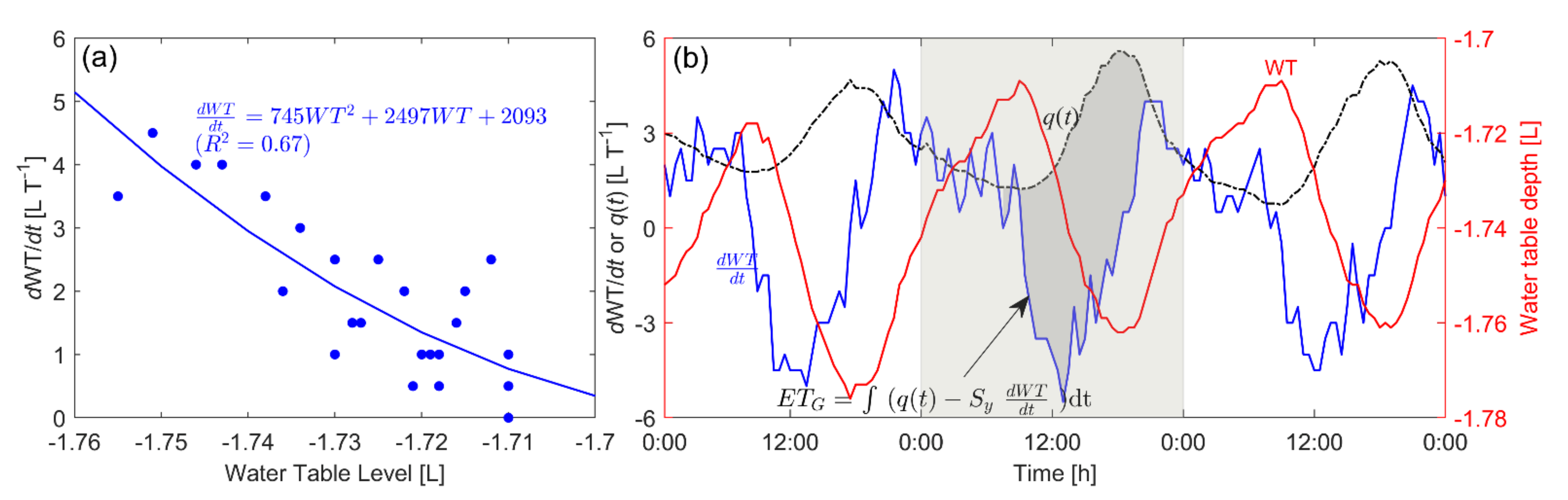
3.2. Hydraulic Theory-Based ETG Estimation Method
3.3. Determination of Specific Yield
- Step 1:
- Calculating daily ETS from the soil moisture observations using Equation (2);
- Step 2:
- Selecting a random value of β from a prior interval of specific yield for silt loam soil (i.e., from 0 to 0.2), and calculating ETG using Equation (7) combined with selected β and diurnal water table records;
- Step 3:
- Calculating RSS using Equation (8);
- Step 4:
- Repeating the Steps 2 and 3 for 10,000 times, and selecting the value of β with minimum RSS as the optimal estimate of Sy. The best 500 values of β with minimum RSSs were also used to calculate the standard deviation of Sy.
3.4. Evaluating the Hydraulic Theory-Based ETG Estimation Method
4. Results
4.1. Environmental Variables
4.2. Determination of Specific Yield
4.3. Evaluating the Performances of the ETG Estimation Method
4.4. Water Use Pattern
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reynolds, J.F.; Smith, D.M.; Lambin, E.F.; Turner, B.L.; Mortimore, M.; Batterbury, S.P.; Downing, T.E.; Dowlatabadi, H.; Fernandez, R.J.; Herrick, J.E.; et al. Global desertification: Building a science for dryland development. Science 2007, 316, 847–851. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rohde, M.M.; Stella, J.C.; Roberts, D.A.; Singer, M.B. Groundwater dependence of riparian woodlands and the disrupting effect of anthropogenically altered streamflow. Proc. Natl. Acad. Sci. USA 2021, 118, e2026453118. [Google Scholar] [CrossRef] [PubMed]
- Eamus, D.; Zolfaghar, S.; Villalobos-Vega, R.; Cleverly, J.; Huete, A. Groundwater-dependent ecosystems: Recent insights from satellite and field-based studies. Hydrol. Earth Syst. Sci. 2015, 19, 4229–4256. [Google Scholar] [CrossRef] [Green Version]
- Orellana, F.; Verma, P.; Loheide, S.P.; Daly, E. Monitoring and modeling water-vegetation interactions in groundwater dependent ecosystems. Rev. Geophys. 2012, 50, RG3003. [Google Scholar] [CrossRef]
- White, W.N. A Method of Estimating Ground-Water Supplies Based on Discharge by Plants and Evaporation from Soil: Results of Investigations in Escalante Valley, Utah; Geological Survey Water Supply Paper 659-A; US Government Printing Office: Washington, DC, USA, 1932; p. 105. [Google Scholar]
- Hays, K.B. Water Use by Saltcedar (Tamarix sp.) and Associated Vegetation on the Canadian, Colorado and Pecos Rivers in Texas. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2003. [Google Scholar]
- Loheide, I.I.S.P. A method for estimating subdaily evapotranspiration of shallow groundwater using diurnal water table fluctuations. Ecohydrology 2008, 1, 59–66. [Google Scholar] [CrossRef]
- Gribovszki, Z.; Kalicz, P.; Szilagyi, J.; Kucsara, M. Riparian zone evapotranspiration estimation from diurnal groundwater level fluctuations. J. Hydrol. 2008, 349, 6–17. [Google Scholar] [CrossRef]
- Soylu, M.E.; Lenters, J.D.; Istanbulluoglu, E.; Loheide, I.; Steven, P. On evapotranspiration and shallow groundwater fluctuations: A fourier-based improvement to the white method. Water Resour. Res. 2012, 48, W06506. [Google Scholar] [CrossRef] [Green Version]
- Fahle, M.; Dietrich, O. Estimation of evapotranspiration using diurnal groundwater level fluctuations: Comparison of different approaches with groundwater lysimeter data. Water Resour. Res. 2014, 50, 273–286. [Google Scholar] [CrossRef]
- Vincke, C.; Thiry, Y. Water table is a relevant source for water uptake by a Scots pine (Pinus sylvestris L.) stand: Evidences from continuous evapotranspiration and water table monitoring. Agric. For. Meteorol. 2008, 148, 1419–1432. [Google Scholar] [CrossRef]
- Miller, G.R.; Chen, X.; Rubin, Y.; Ma, S.; Baldocchi, D.D. Groundwater uptake by woody vegetation in a semiarid oak savanna. Water Resour. Res. 2010, 46, W10503. [Google Scholar] [CrossRef] [Green Version]
- Fan, J.; Oestergaard, K.T.; Guyot, A.; Lockington, D.A. Estimating groundwater recharge and evapotranspiration from water table fluctuations under three vegetation covers in a coastal sandy aquifer of subtropical Australia. J. Hydrol. 2016, 519, 1120–1129. [Google Scholar] [CrossRef] [Green Version]
- Yue, W.F.; Wang, T.J.; Franz, T.E.; Chen, X.H. Spatiotemporal patterns of water table fluctuations and evapotranspiration induced by riparian vegetation in a semiarid area. Water Resour. Res. 2016, 52, 1948–1960. [Google Scholar] [CrossRef] [Green Version]
- Zhang, P.; Yuan, G.; Shao, M.-A.; Yi, X.; Du, T. Performance of the White method for estimating groundwater evapotranspiration under conditions of deep and fluctuating. Hydrol. Process. 2016, 30, 106–118. [Google Scholar] [CrossRef]
- Troxell, H.C. The diurnal fluctuation in the ground-water and flow of the Santa Ana river and its meaning. Eos Trans. Am. Geophys. Union 1936, 17, 496–504. [Google Scholar] [CrossRef]
- Kool, J.; Parker, J. Development and evaluation of closed form expressions for hysteretic soil hydraulic properties. Water Resour. Res. 1987, 23, 105–114. [Google Scholar] [CrossRef]
- Healy, R.; Cook, P. Using underground levels to estimate recharge. Hydrogeol. J. 2002, 10, 91–109. [Google Scholar] [CrossRef]
- Nachabe, M. Analytical expressions for transient specific yield and shallow water table drainage. Water Resour. Res. 2002, 38, 1193–1199. [Google Scholar] [CrossRef] [Green Version]
- Crosbie, R.; Binning, P.; Kalma, J. A time series approach to inferring groundwater recharge using the water table fluctuation method. Water Resour. Res. 2005, 41, 1–9. [Google Scholar] [CrossRef]
- Loheide, I.I.S.P.; Butler, J.J., Jr.; Gorelick, S.M. Estimation of groundwater consumption by phreatophytes using diurnal water table fluctuations: A saturated-unsaturated flow assessment. Water Resour. Res. 2005, 41, W07030. [Google Scholar] [CrossRef]
- Ehleringer, J.R.; Dawson, T.E. Water uptake by plants: Perspectives from stable isotope composition. Plant Cell Environ. 1992, 15, 1073–1082. [Google Scholar] [CrossRef]
- Lanning, M.; Wang, L.X.; Benson, M.; Zhang, Q.; Novick, Q.K. Canopy isotopic investigation reveals different water uptake dynamics of maples and oaks. Phytochemistry 2020, 175, 112389. [Google Scholar] [CrossRef] [PubMed]
- Dawson, T.E.; Pate, J.S. Seasonal water uptake and movement in root systems of Australian phraeatophytic plants of dimorphic root morphology: A stable isotope investigation. Oecologia 1996, 107, 13–20. [Google Scholar] [CrossRef] [PubMed]
- Zencich, S.J.; Froend, R.H.; Turner, J.V.; Gailitis, V. Influence of groundwater depth on the seasonal sources of water accessed by Banksia tree species on a shallow, sandy coastal aquifer. Oecologia 2002, 131, 8–19. [Google Scholar] [CrossRef] [PubMed]
- Barbeta, A.; Mejia-Chang, M.; Ogaya, R.; Voltas, J.; Dawson, T.E.; Penuelas, J. The combined effects of a long-term experimental drought and an extreme drought on the use of plant-water sources in a Mediterranean forest. Glob. Chang. Biol. 2015, 21, 1213–1225. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Voltas, J.; Lucabaugh, D.; Chambel, M.R.; Ferrio, J.P. Intraspecific variation in the use of water sources by the circum Mediterranean conifer Pinus halepensis. New Phytol. 2015, 208, 1031–1041. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fahey, T.J.; Yanai, R.D.; Gonzales, K.E.; Lombardi, J.A. Sampling and processing roots from rocky forest soils. Ecosphere 2017, 8, e01863. [Google Scholar] [CrossRef] [Green Version]
- Si, J.; Feng, Q.; Wen, X.; Xi, H.; Yu, T.; Li, W.; Zhao, C. Modeling soil water content in extreme arid area using an adaptive neuro-fuzzy inference system. J. Hydrol. 2015, 527, 679–687. [Google Scholar] [CrossRef]
- Yu, T.F.; Feng, Q.; Si, J.H.; Xi, H.Y.; Li, W. Patterns, magnitude, and controlling factors of hydraulic redistribution of soil water by Tamarix ramosissima roots. J. Arid Land 2013, 5, 396–407. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Cheng, G.D.; Liu, S.M.; Xiao, Q.; Ma, M.G.; Jin, R.; Che, T.; Liu, Q.H.; Wang, W.Z.; Qi, Y.; et al. Heihe watershed allied telemetry experimental research (HiWATER): Scientific objectives and experimental design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Liu, S.M.; Xu, Z.W.; Song, L.S.; Zhao, Q.Y.; Ge, Y.; Xu, T.R.; Ma, Y.F.; Zhu, Z.L.; Jia, Z.Z.; Zhang, F. Upscaling evapotranspiration measurements from multi-site to the satellite pixel scale over heterogeneous land surfaces. Agric. For. Meteorol. 2016, 230, 97–113. [Google Scholar] [CrossRef]
- Xu, Z.W.; Ma, Y.F.; Liu, S.M.; Shi, W.J.; Wang, J.M. Assessment of the energy balance closure under advective conditions and its impact using remote sensing data. J. Appl. Meteorol. Clim. 2017, 56, 127–140. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, S.; Zhu, Z.; Zhou, J.; Shi, W.; Xu, T.; Yang, F.; Zhang, Y.; He, X. Exploring evapotranspiration changes in a typical endorheic basin through the integrated observatory network. Agric. For. Meteorol. 2020, 290, 108010. [Google Scholar] [CrossRef]
- Dolan, T.J.; Hermann, A.J.; Bayley, S.E.; Zoltek, J. Evapotranspiration of a Florida, USA, fresh-water wetland. J. Hydrol. 1984, 74, 355–371. [Google Scholar] [CrossRef]
- Harr, M.E. Groundwater and Seepage; McGraw-Hill: New York, NY, USA, 1962; p. 315. [Google Scholar]
- Zhu, G.F.; Li, X.; Zhang, K.; Ding, Z.Y.; Han, T.; Ma, J.Z.; Huang, C.L.; He, J.H.; Ma, T. Multi-model ensemble prediction of terrestrial evapotranspiration across north China using Bayesian model averaging. Hydrol. Process. 2016, 30, 2861–2879. [Google Scholar] [CrossRef]
- Lautz, L.K. Estimating groundwater evapotranspiration rates using diurnal water-table fluctuations in a semi-arid riparian zone. Hydrogeol. J. 2008, 16, 483–497. [Google Scholar] [CrossRef]
- Johnson, A. Specific Yield-Compilation of Specific Yields for Various Materials; Geological Survey Water Supply Paper 1662 (D); US Government Printing Office: Washington, DC, USA, 1967. [Google Scholar]
- Singhal, B.B.S.; Gupta, R.P. Applied Hydrogeology of Fractured Rocks; Kluwer Academic Publisher: Dordrecht, The Netherlands, 1999. [Google Scholar]
- Fayer, M.; Hillel, D. Air encapsulation: I. Measurement in a field soil. Soil Sci. Soc. Am. J. 1986, 50, 568–571. [Google Scholar] [CrossRef]
- Xu, H.; Li, Y. Water-use strategy of three central Asian desert shrubs and their responses to rain pulse events. Plant Soil 2006, 285, 5–17. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, H.; Zheng, X.-J.; Li, Y.; Tang, L.-S. Seasonal changes in the water use strategies of three co-occurring desert shrubs. Hydrol. Process. 2014, 28, 6265–6275. [Google Scholar] [CrossRef]
- Tiemuerbieke, B.; Min, X.-J.; Zang, Y.-X.; Xing, P.; Ma, J.-Y.; Sun, W. Water use patterns of co-occurring C3 and C4 shrubs in the Gurbantonggut desert in northwestern China. Sci. Total Environ. 2018, 634, 341–354. [Google Scholar] [CrossRef]
- Zhao, L.; Xie, C.; Liu, X.; Wang, N.; Yu, Z.; Dong, X.; Wang, L. Water sources of major plant species along a strong climatic gradient in the inland Heihe River Basin. Plant Soil 2020, 455, 439–466. [Google Scholar] [CrossRef]
- Fan, J.; Ostergaard, K.T.; Guyot, A.; Fujiwara, S.; Lockington, D.A. Estimating groundwater evapotranspiration by a subtropical pine plantation using diurnal water table fluctuations: Implications from night-time water use. J. Hydrol. 2014, 542, 679–685. [Google Scholar] [CrossRef] [Green Version]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Y.; Feng, Q.; Zhu, G.; Wang, Y.; Zhang, Q. A New Method of Estimating Groundwater Evapotranspiration at Sub-Daily Scale Using Water Table Fluctuations. Water 2022, 14, 876. https://doi.org/10.3390/w14060876
Su Y, Feng Q, Zhu G, Wang Y, Zhang Q. A New Method of Estimating Groundwater Evapotranspiration at Sub-Daily Scale Using Water Table Fluctuations. Water. 2022; 14(6):876. https://doi.org/10.3390/w14060876
Chicago/Turabian StyleSu, Yonghong, Qi Feng, Gaofeng Zhu, Yunquan Wang, and Qi Zhang. 2022. "A New Method of Estimating Groundwater Evapotranspiration at Sub-Daily Scale Using Water Table Fluctuations" Water 14, no. 6: 876. https://doi.org/10.3390/w14060876





