Joint Effects of the DEM Resolution and the Computational Cell Size on the Routing Methods in Hydrological Modelling
Abstract
1. Introduction
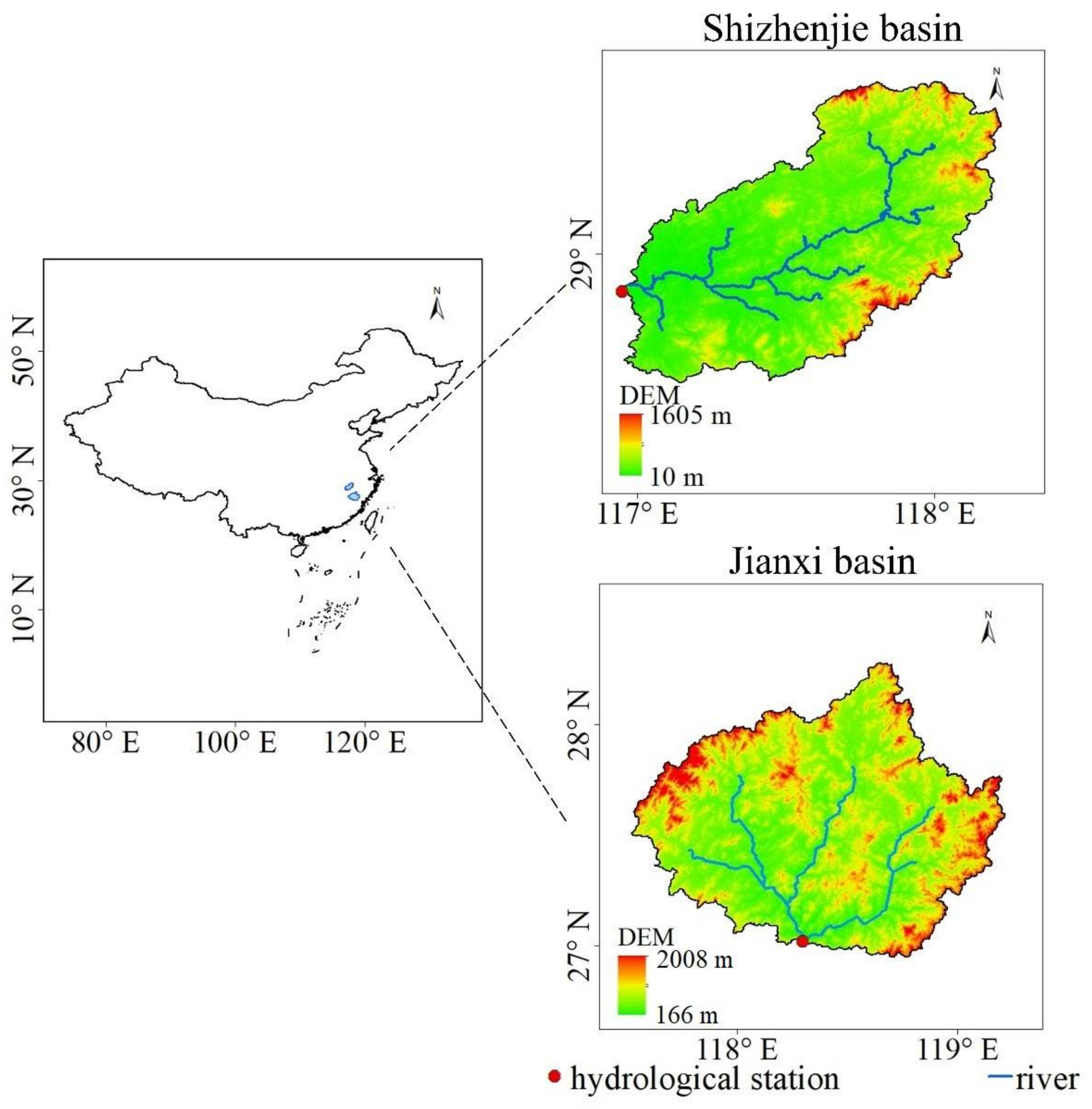
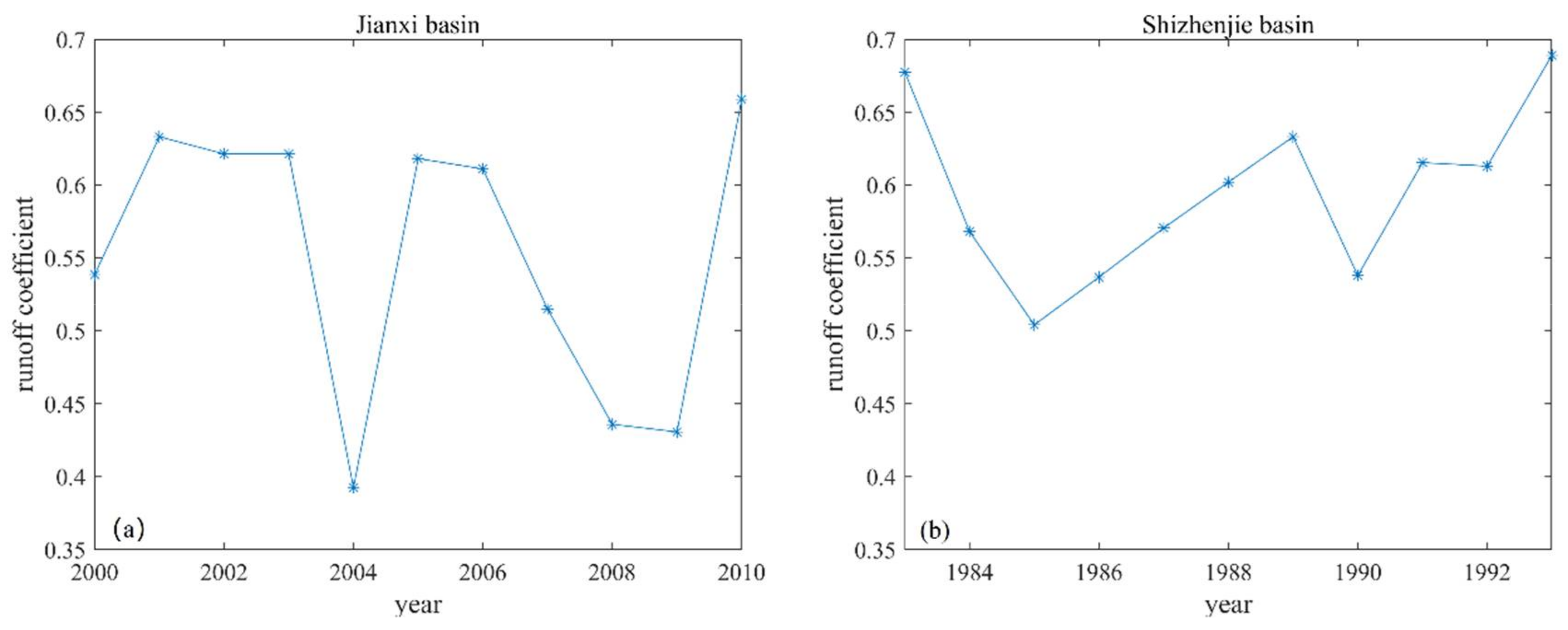
2. Study Area and Data
3. Methods
3.1. Routing Methods
3.1.1. The Improved Aggregated Network-Response Function Routing Method
3.1.2. Linear Reservoir Routing Method
3.2. Runoff Generation Models
3.2.1. SIMHYD
3.2.2. Water and Snow Balance Modelling System (WASMOD)
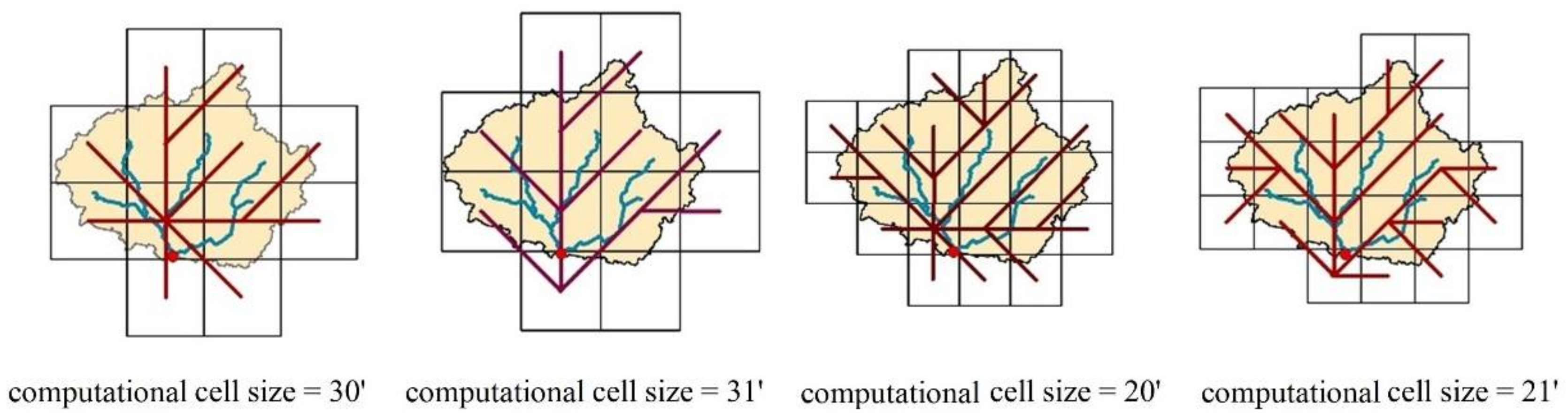
3.3. Different Computational Cell Sizes and Interpolation Method
3.4. Calibration Algorithms
3.5. Experimental Design
3.5.1. Optimal Routing Parameters
Calibration of I-NRF Routing Parameters
- Several initial routing parameter sets are drafted. For the I-NRF routing method, there are two parameters to be calibrated. Table 2 defines 49 initial routing parameter set values. The number of the initial values is m (m = 1~49).
- The optimal simulation performance for each initial routing parameter for a given DEM resolution and a given computational cell size is calculated using Monte Carlo calibration algorithm. The optimal model performance for each parameter set is denoted as , where i corresponds to the DEM resolution and j corresponds to the computational cell size. Then 48 values using the four different DEM dataset resolutions (i = 1–4) and the 12 computational cell sizes (5 arc-min to 60 arc-min with an interval of 5 arc-min) (j = 1–12) are obtained. In the calibration process, 300 runoff generation parameter arrays are produced as the model input by Latin-Hypercube sampling [70] according to the initial parameter range (Table 4). The applied marginal distribution is the uniform distribution.
- The comprehensive simulation performance for each initial routing parameter set of each DEM resolution () is calculated, where .
- The optimal routing parameter set is selected from the initial routing parameter sets. For each DEM resolution, the optimal routing parameter set for a given basin is selected using as a criterion and listed in Table 5.
Calibration of LRR Routing Parameters
- Several initial routing parameters are drafted. For the LRR routing method, there is only one parameter to be calibrated. Table 2 defines 6 initial values. The number of the initial values is n (n = 1–6).
- The optimal simulation performance for each routing parameter for a given DEM resolution and a given computational cell size is calculated using CMA-ES algorithm, denoted as . With 4 DEM resolutions (i = 1–4) and 12 computational cell sizes (5 arc-min to 60 arc-min with an interval of 5 arc-min) (j = 1–12), 48 values are obtained. In the calibration process, the initial range of runoff generation parameters is given in Table 4.
- The comprehensive simulation performance () for each parameter of each DEM resolution is calculated. Here, .
- The optimal routing parameter is selected from the initial routing parameters. For each DEM resolution, the optimal routing parameter set for the basin is selected using as a criterion and the results are listed in Table 5.
3.5.2. Optimal Runoff Generation Parameters
4. Results
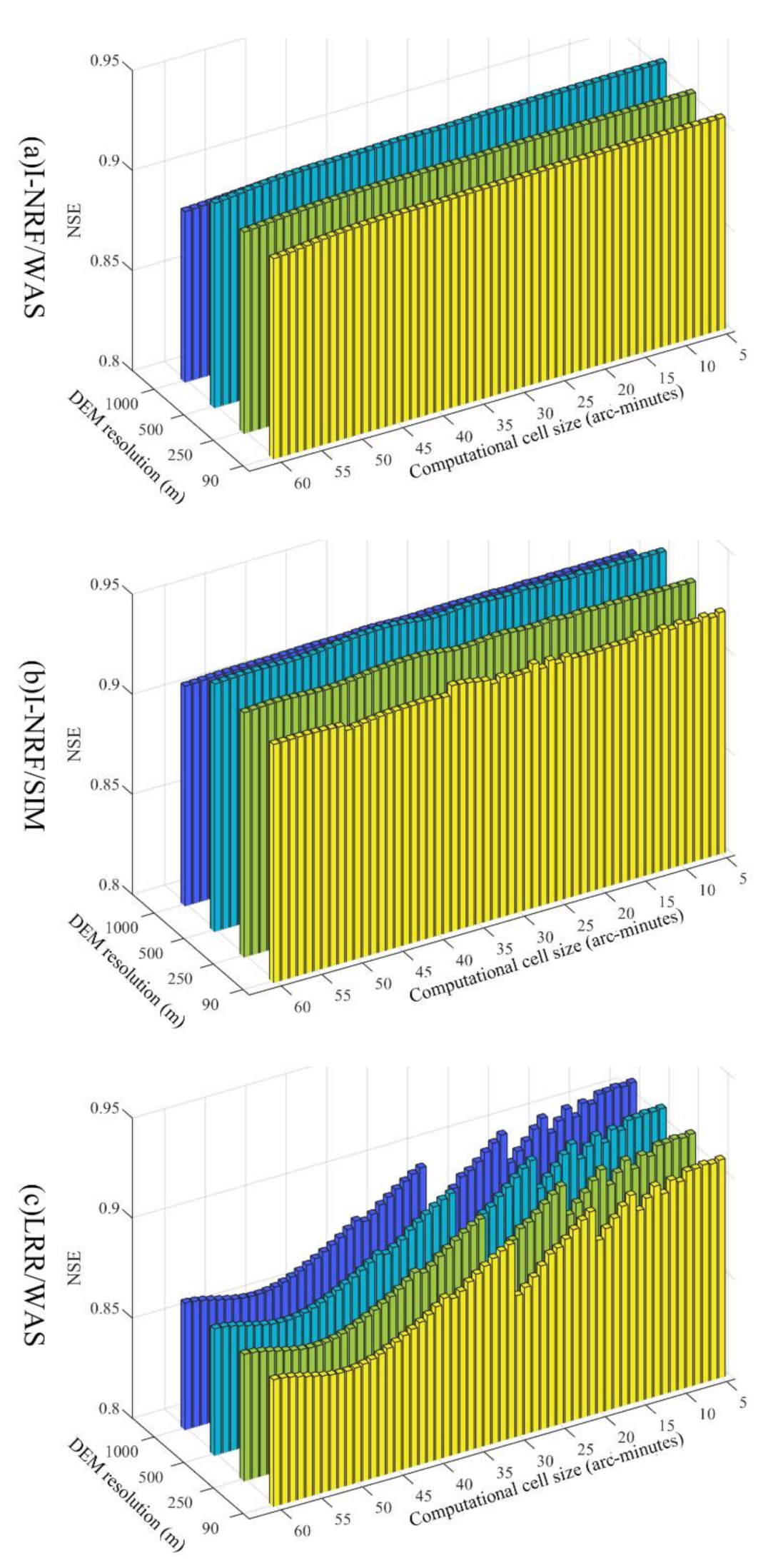
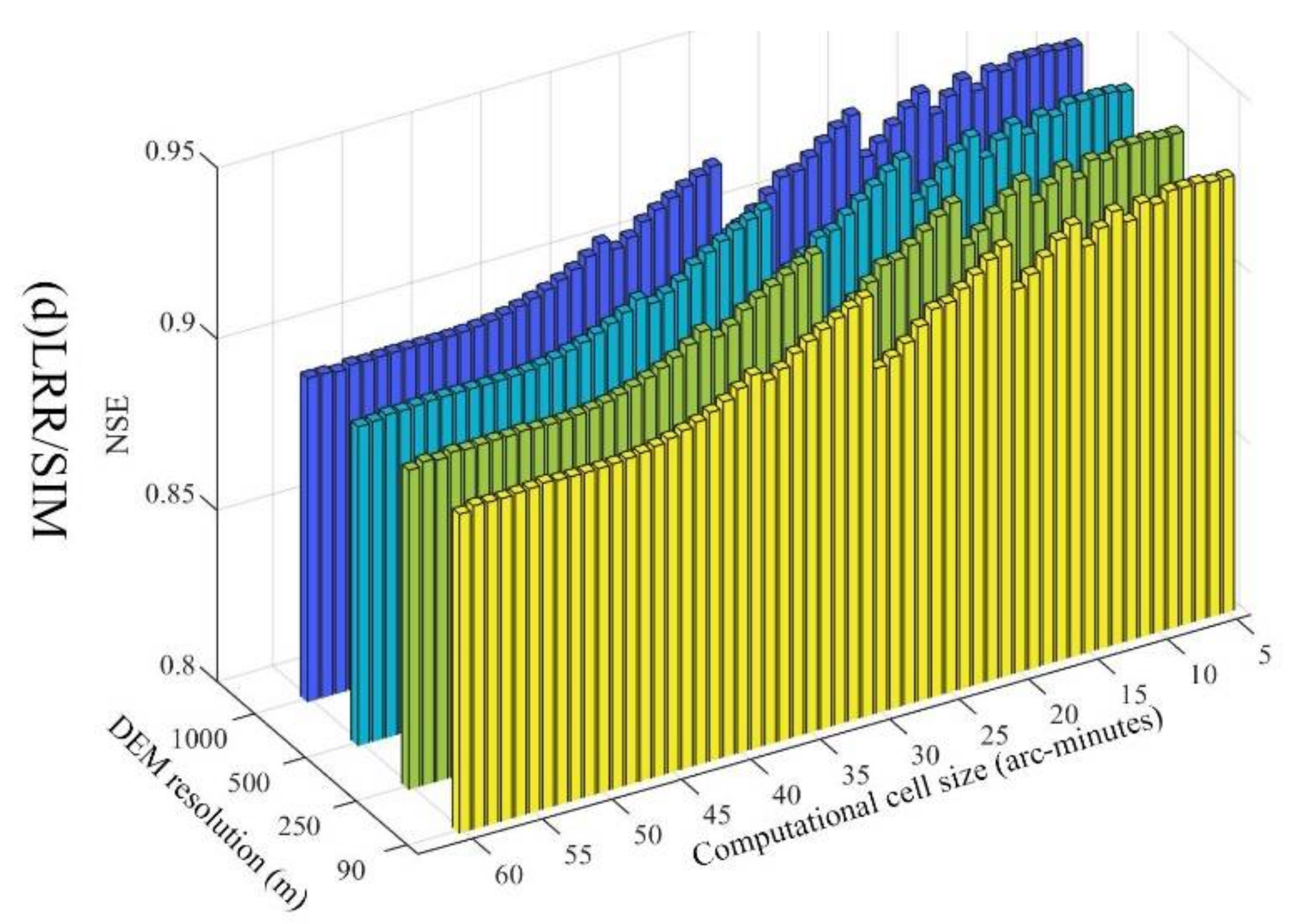
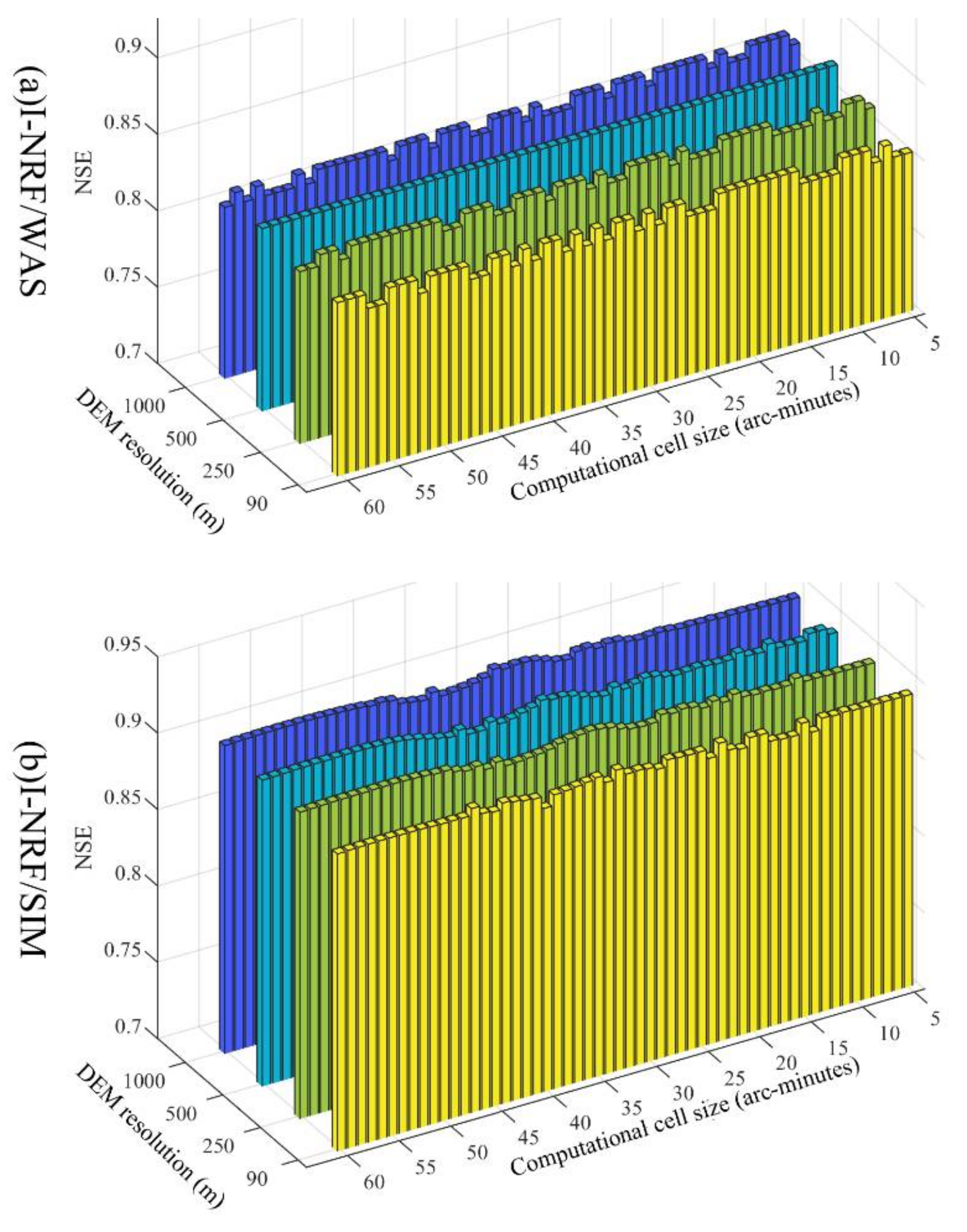
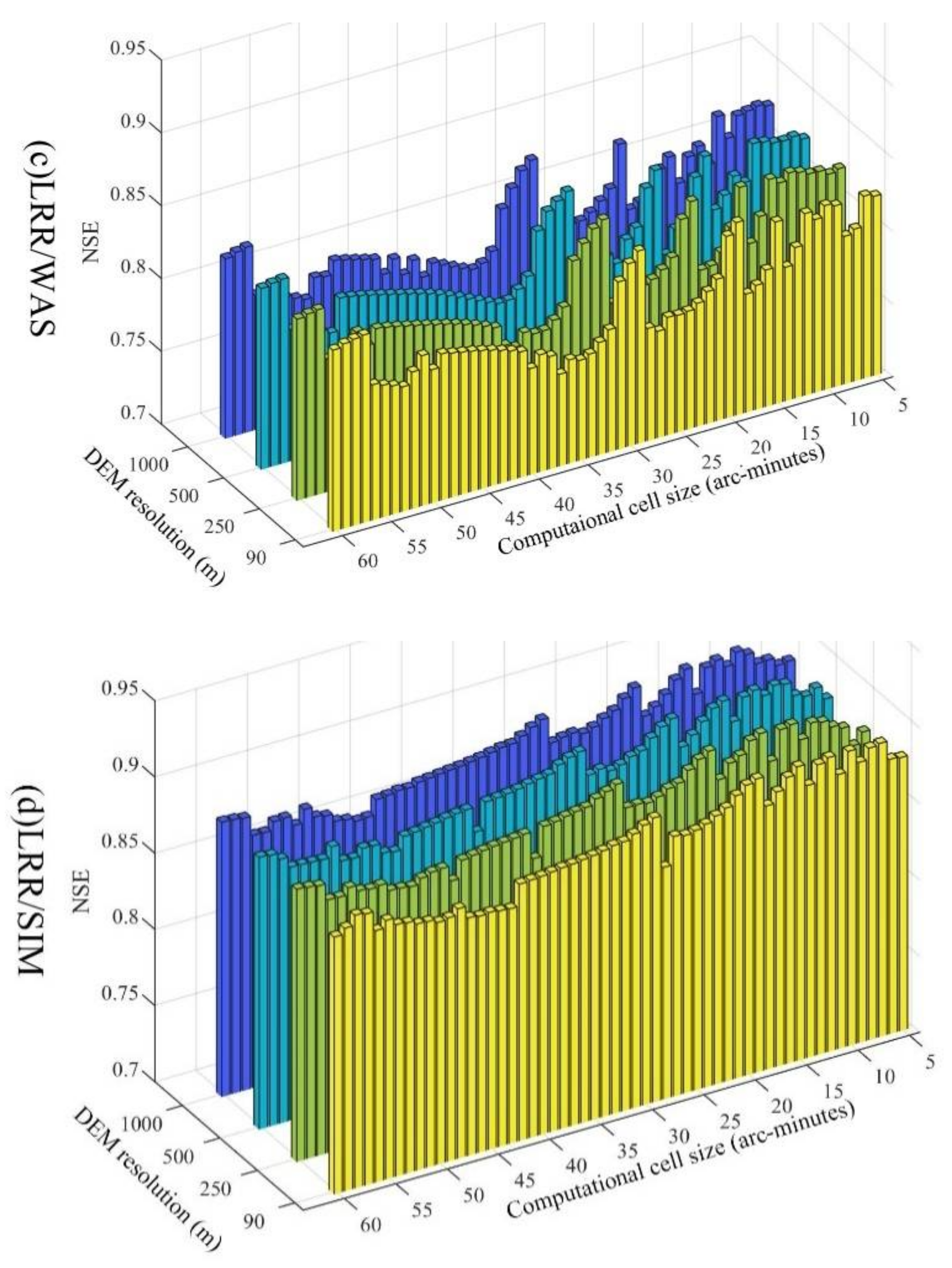
4.1. The Effect of Computational Cell Size on the Discharge Simulation Performance
4.2. The Effect of the DEM Resolution on the Discharge Simulation Performance
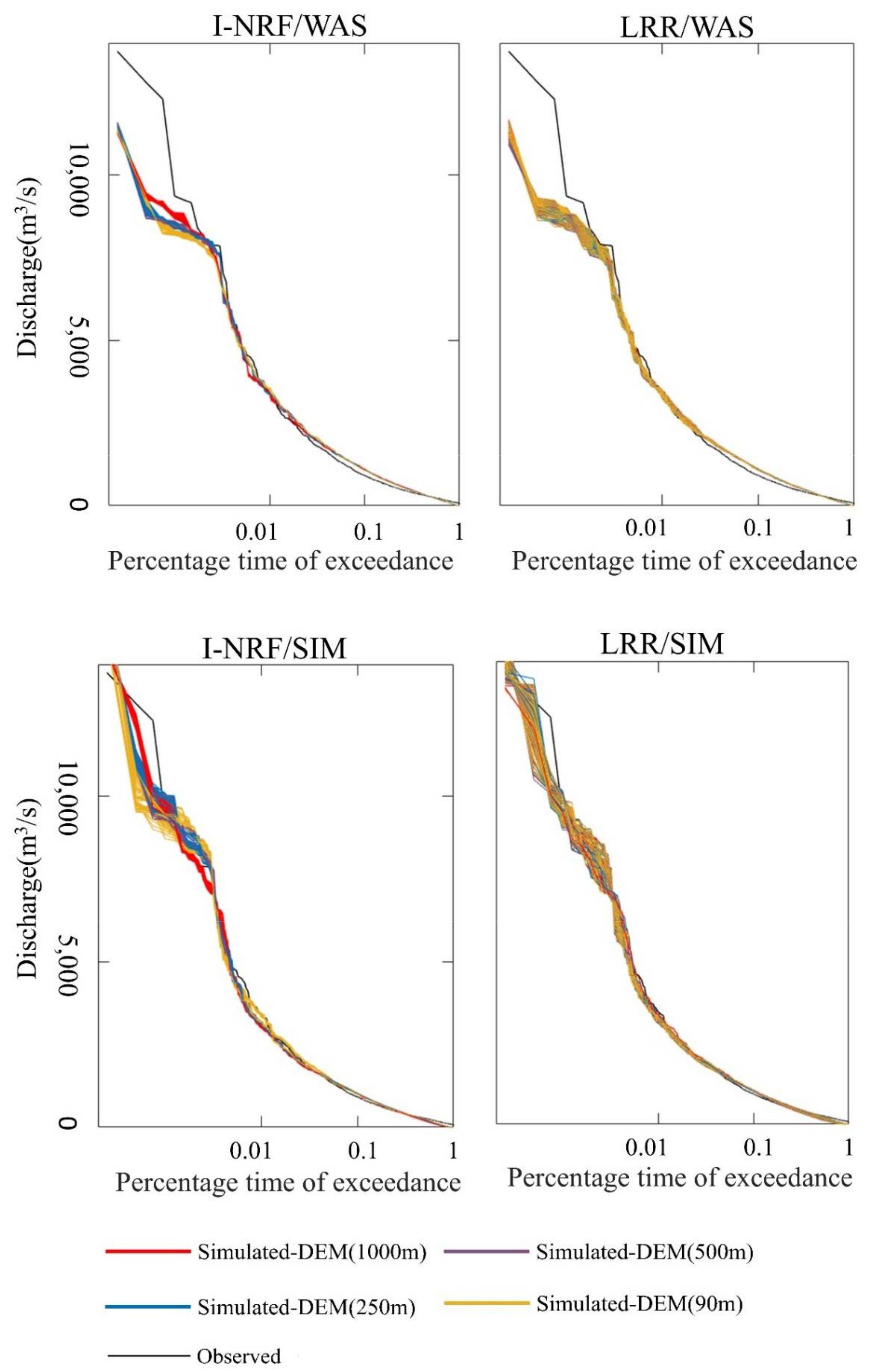
4.3. Analysis of Discharge Duration Curves
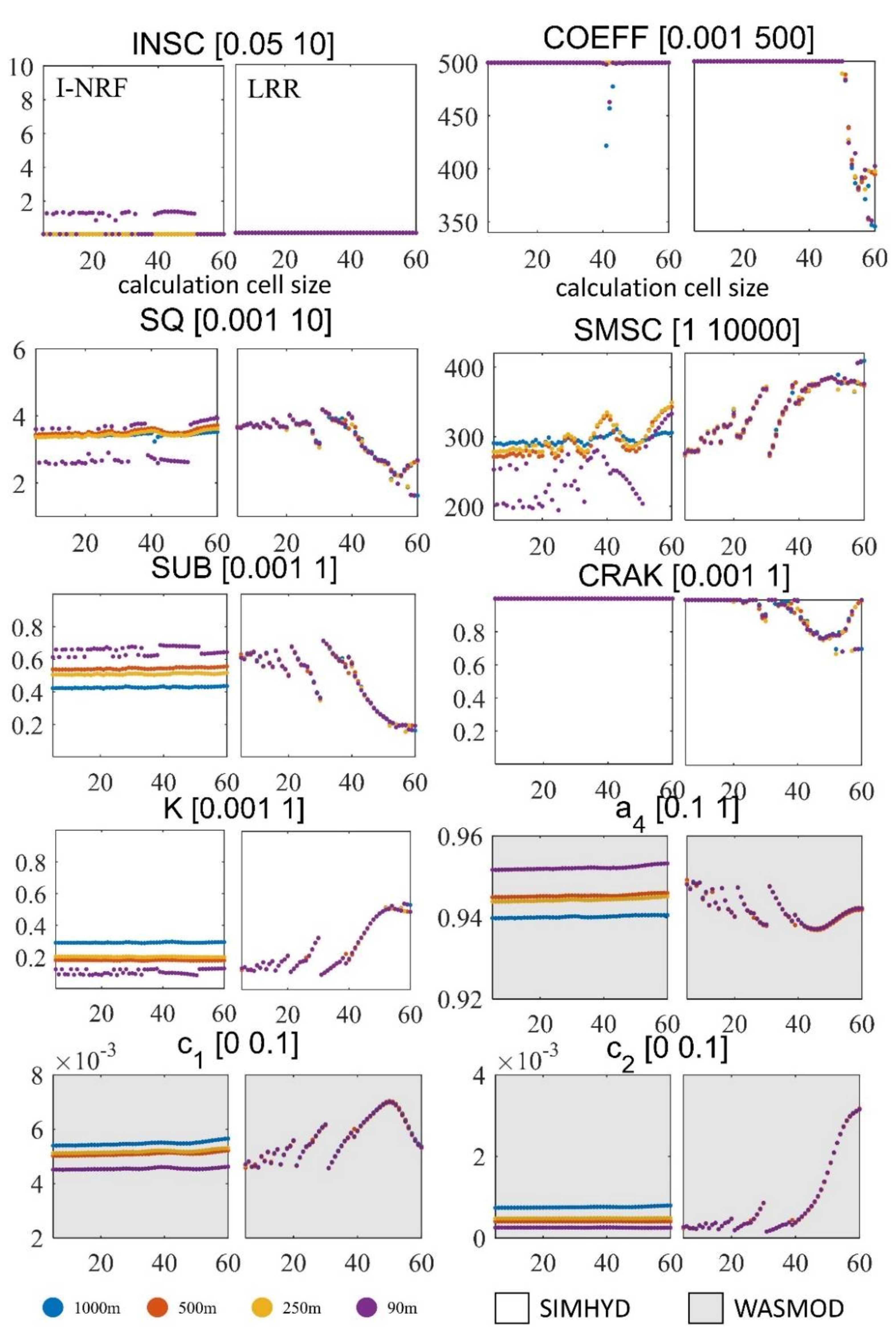
4.4. Analysis of Runoff Generation Parameters
5. Conclusions
- 1.
- The DEM resolution has a larger impact on the I-NRF discharge simulation performance than it does for the LRR method. However, the overall I-NRF discharge simulation performance is not consistently correlated with DEM resolution. As the computational cell size increases, the I-NRF discharge simulation performance is relatively stable because the I-NRF method is largely independent of the computational cell size. The DEM resolution and the computational cell size exert no joint influence on the I-NRF discharge simulation performance.
- 2.
- The DEM resolution has little effect on the LRR discharge simulation performance. The LRR discharge simulation performance changes drastically with the computational cell size for both runoff generation models. In general, finer computational cell size leads to better results, while the LRR discharge simulation performance oscillates heavily as the computational cell size increases. The joint effect of DEM resolution and the computational cell size on the performance of the LRR routing method can be ignored in hydrological modelling.
- 3.
- The effects of the computational cell size and the DEM resolution on the simulated discharge accuracy are mainly reflected in the high-flow range. In this study, the performance of SIMHYD is better than that of WASMOD in the high-flow range, when they are combined with both routing methods.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gao, L.; Tao, B.; Miao, Y.; Zhang, L.; Xu, X. A global dataset for economic losses of extreme hydrological events during 1960–2014. Water Resour. Res. 2019, 55, 5165–5175. [Google Scholar] [CrossRef]
- Funk, C.; Shukla, S.; Thiaw, W.M.; Rowland, J.; Hoell, A.; McNally, A.; Husak, G.; Novella, N.; Budde, M.; Peters-Lidard, C. Recognizing the Famine Early Warning Systems Network: Over 30 Years of Drought Early Warning Science Advances and Partnerships Promoting Global Food Security. Bull. Am. Meteorol. Soc. 2019, 100, 1011–1027. [Google Scholar] [CrossRef]
- Abnakorn, S.; Ruangpan, L.; Tangdamrongsub, N.; Suryadi, F.X.; Fraiture, C.D. Improving flood and drought management in agricultural river basins: An application to the Mun River Basin in Thailand. Water Policy 2021, 23, 1153–1169. [Google Scholar] [CrossRef]
- Lu, E.; Luo, Y.; Zhang, R.; Wu, Q.; Liu, L. Regional atmospheric anomalies responsible for the 2009–2010 severe drought in China. J. Geophys. Res. Atmos. 2011, 116, D21114. [Google Scholar] [CrossRef]
- Nyandiko, N.O. Devolution and Disaster Risk Reduction in Kenya: Progress, challenges and opportunities. Int. J. Disast. Risk Reduct. 2020, 51, 101832. [Google Scholar] [CrossRef]
- Bruno, M.; Florian, E.; Michael, K.; Bernhard, M.; Schröter, K.; Steffi, U.-E. The extreme flood in June 2013 in Germany. La Houille Blanche 2014, 1, 5–10. [Google Scholar]
- Ulbrich, U.; Brücher, T.; Fink, A.H.; Leckebusch, G.C.; Krüger, A.; Pinto, J.G. The central European floods of August 2002: Part 1—Rainfall periods and flood development. Weather 2003, 58, 371–377. [Google Scholar] [CrossRef]
- Lal, P.; Prakash, A.; Kumar, A.; Srivastava, P.K.; Khan, M.L. Evaluating the 2018 extreme flood hazard events in Kerala, India. Remote Sens. Lett. 2020, 11, 436–445. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Y.; Lei, C.; Li, G.; Han, L.; Song, S.; Yang, L.; Deng, X. Spatio-temporal characteristics of precipitation and dryness/wetness in Yangtze River Delta, eastern China, during 1960–2012. Atmos. Res. 2016, 172–173, 196–205. [Google Scholar] [CrossRef]
- Denić, N.; Petković, D.; Spasic, B. Global Economy Increasing by Enterprise Resource Planning. In Reference Module in Materials Science and Materials Engineering; Elsevier Inc.: London, UK, 2020; pp. 331–337. [Google Scholar]
- Denić, N.; Petković, D.; Siljkovi, B.; Ivkovi, R. Opportunities for Digital Marketing in the Viticulture of Kosovo and Metohija. In Reference Module in Materials Science and Materials Engineering; Elsevier Inc.: London, UK, 2020. [Google Scholar]
- Petkovic, D.; Petković, B.; Kuzman, B. Appraisal of information system for evaluation of kinetic parameters of biomass oxidation. Biomass-Convers. Biorefinery 2020, 10, 1–9. [Google Scholar] [CrossRef]
- Lakovic, N.; Khan, A.; Petković, B.; Petkovic, D.; Kuzman, B.; Resic, S.; Jermsittiparsert, K.; Azam, S. Management of higher heating value sensitivity of biomass by hybrid learning technique. Biomass Convers. Biorefinery 2021, 1–8. [Google Scholar] [CrossRef]
- Mili, M.; Petkovi, B.; Selmi, A.; Petkovi, D.; Kuzman, B. Computational evaluation of microalgae biomass conversion to biodiesel. Biomass Convers. Biorefin. 2021, 11, 1–8. [Google Scholar] [CrossRef]
- Milićević, V.; Denić, N.; Milićević, Z.; Arsić, L.; Spasić-Stojković, M.; Petković, D.; Stojanović, J.; Krkic, M.; Milovančević, N.S.; Jovanović, A. E-learning perspectives in higher education institutions. Technol. Forecast. Soc. Chang. 2021, 166, 120618. [Google Scholar] [CrossRef]
- Spasi, B.; Siljkovi, B.; Deni, N.; Petkovi, D.; Vujovi, V. Natural Lignite Resources in Kosovo and Metohija and Their Influence on the Environment. Min. Metall. Eng. Bor 2020, 1, 561–566. [Google Scholar]
- Kuzman, B.; Petkovi, B.; Denić, N.; Petkovi, D.; Momir, M. Estimation of optimal fertilizers for optimal crop yield by adaptive neuro fuzzy logic. Rhizosphere 2021, 18, 100358. [Google Scholar] [CrossRef]
- Gong, L.; Widen-Nilsson, E.; Halldin, S.; Xu, C.-Y. Large-scale runoff routing with an aggregated network-response function. J. Hydrol. 2009, 368, 237–250. [Google Scholar] [CrossRef]
- Papaioannou, G.; Loukas, A.; Vasiliades, L.; Aronica, G.T. Sensitivity analysis of a probabilistic flood inundation mapping framework for ungauged catchments. Water 2017, 60, 9–16. [Google Scholar]
- Bellos, V.; Kourtis, I.M.; Moreno-Rodenas, A.; Tsihrintzis, V.A. Quantifying Roughness Coefficient Uncertainty in Urban Flooding Simulations through a Simplified Methodology. Water 2017, 9, 944. [Google Scholar] [CrossRef]
- Hui, J.; Wu, Y.; Zhao, F.; Lei, X.; Li, J. Parameter Optimization for Uncertainty Reduction and Simulation Improvement of Hydrological Modeling. Remote Sens. 2020, 12, 4069. [Google Scholar] [CrossRef]
- Pappenberger, F.; Matgen, P.; Beven, K.J.; Henry, J.B.; Pfister, L.; De, P.F. Influence of uncertain boundary conditions and model structure on flood inundation predictions. Adv. Water Resour. 2006, 29, 1430–1449. [Google Scholar] [CrossRef]
- Samela, C.; Manfreda, S.; Paola, F.D.; Giugni, M.; Fiorentino, M. DEM-Based Approaches for the Delineation of Flood-Prone Areas in an Ungauged Basin in Africa. J. Hydrol. Eng. 2016, 21, 06015010. [Google Scholar] [CrossRef]
- Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.; Dutta, D.; Kim, S. Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environ. Modell. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Rozos, E.; Dimitriadis, P.; Bellos, V. Machine Learning in Assessing the Performance of Hydrological Models. Hydrology 2022, 9, 5. [Google Scholar] [CrossRef]
- Wang, M.; Hjelmfelt, A.T. DEM Based Overland Flow Routing Model. J. Hydrol. Eng. 1998, 3, 1–8. [Google Scholar] [CrossRef]
- Bates, P.D.; Roo, A. A simple raster-based model for flood inundation simulation. J. Hydrol. 2000, 236, 54–77. [Google Scholar] [CrossRef]
- Bellos, V.; Tsakiris, G. A hybrid method for flood simulation in small catchments combining hydrodynamic and hydrological techniques. J. Hydrol. 2016, 540, 331–339. [Google Scholar] [CrossRef]
- Li, H.; Beldring, S.; Xu, C.-Y. Implementation and testing of routing algorithms in the distributed Hydrologiska Byråns Vattenbalansavdelning model for mountainous catchments. Hydrol. Res. 2014, 45, 322–333. [Google Scholar] [CrossRef]
- Olivera, F.; Famiglietti, J.; Asante, K. Global-scale flow routing using a source-to-sink algorithm. Water Resour. Res. 2000, 36, 2197–2207. [Google Scholar] [CrossRef]
- Arora, V.K.; Boer, G.J. A variable velocity flow routing algorithm for GCMs. J. Geophys. Res.-Atmos. 1999, 104, 30965–30979. [Google Scholar] [CrossRef]
- Huang, P.C.; Lee, K.T. Efficient DEM-based overland flow routing using integrated recursive algorithms. Hydrol. Process. 2017, 31, 1007–1017. [Google Scholar] [CrossRef]
- Sausen, R.; Schubert, S.; Dümenil, L. A model of river runoff for use in coupled atmosphere-ocean models. J. Hydrol. 1994, 155, 337–352. [Google Scholar] [CrossRef]
- Miller, J.R.; Russell, G.L.; Caliri, G. Continental-scale river flow in climate models. J. Clim. 1994, 7, 914–928. [Google Scholar] [CrossRef]
- Gong, L.; Halldin, S.; Xu, C.-Y. Global-scale river routing—An efficient time-delay algorithm based on HydroSHEDS high-resolution hydrography. Hydrol. Process. 2011, 25, 1114–1128. [Google Scholar] [CrossRef]
- Lu, G.; Liu, J.; Wu, Z.; Hai, H.; Xu, H.; Lin, Q. Development of a Large-Scale Routing Model with Scale Independent by Considering the Damping Effect of Sub-Basins. Water Resour. Manag. 2015, 29, 5237–5253. [Google Scholar] [CrossRef]
- Ducharne, A.; Golaz, C.; Leblois, E.; Laval, K.; Polcher, J.; Ledoux, E.; de Marsily, G. Development of a high resolution runoff routing model, calibration and application to assess runoff from the LMD GCM. J. Hydrol. 2003, 280, 207–228. [Google Scholar] [CrossRef]
- Harrigan, S.; Zsoter, E.; Alfieri, L.; Prudhomme, C.; Pappenberger, F. GloFAS-ERA5 operational global river discharge reanalysis 1979-present. Earth Syst. Sci. Data 2020, 12, 2043–2060. [Google Scholar] [CrossRef]
- Van Der Knijff, J.M.; Younis, J.; De Roo, A.P.J. LISFLOOD: A GIS-based distributed model for river basin scale water balance and flood simulation. Int. J. Geogr. Inf. Sci. 2010, 24, 189–212. [Google Scholar] [CrossRef]
- Hersbach, H.; Rosnay, P.; Bell, B.; Schepers, D. Operational Global Reanalysis: Progress, Future Directions and Synergies with NWP; European Centre for Medium Range Weather Forecasts: Reading, UK, 2018. [Google Scholar]
- Xie, Z.; Yuan, F.; Duan, Q.; Zheng, J.; Liang, M.; Chen, F. Regional parameter estimation of the VIC land surface model: Methodology and application to river basins in China. J. Hydrometeorol. 2007, 8, 447–468. [Google Scholar] [CrossRef]
- Niu, J.; Chen, J.; Wang, K.; Sivakumar, B. Multi-scale streamflow variability responses to precipitation over the headwater catchments in southern China. J. Hydrol. 2017, 551, 14–28. [Google Scholar] [CrossRef]
- Avand, M.; Kuriqi, A.; Khazaei, M.; Ghorbanzadeh, O. DEM resolution effects on machine learning performance for flood probability mapping. J. Hydro-Environ. Res. 2022, 40, 1–16. [Google Scholar] [CrossRef]
- Du, J.; Xie, H.; Hu, Y.; Xu, Y.; Xu, C.-Y. Development and testing of a new storm runoff routing approach based on time variant spatially distributed travel time method. J. Hydrol. 2009, 369, 44–54. [Google Scholar] [CrossRef]
- Arora, V.; Seglenieks, F.; Kouwen, N.; Soulis, E. Scaling aspects of river flow routing. Hydrol. Process 2001, 15, 461–477. [Google Scholar] [CrossRef]
- Song, X.; Qi, Z.; Du, L.P.; Kou, C.L. The Influence of DEM Resolution on Hydrological Simulation in the Huangshui River Basin. Int. J. Geogr. Inf. Sci. 2012, 518, 4299–4302. [Google Scholar] [CrossRef]
- Jeon, J.H.; Ham, J.H.; Yoon, C.G.; Kim, S.J. Effects of DEM Resolution on Hydrological Simulation in, BASINS-BSPF Modeling. Mag. Korean Soc. Agric. Eng. 2002, 44, 25–35. [Google Scholar]
- Chaubey, I.; Cotter, A.S.; Costello, T.A.; Soerens, T.S. Effect of DEM data resolution on SWAT output uncertainty. Hydrol. Process. 2005, 19, 621–628. [Google Scholar] [CrossRef]
- Li, J.; Zhao, H.; Zhang, J.; Chen, H.; Xu, C.; Li, L.; Chen, J.; Guo, S. An improved routing algorithm for a large scale distributed hydrological model with consideration of underlying surface impact. Hydrol. Res. 2020, 51, 834–852. [Google Scholar] [CrossRef]
- USGS HYDRO1k Elevation Derivative Database. Available online: https://www.usgs.gov/centers/eros/science/usgs-eros-archive-digital-elevation-hydro1k?qt-science_center_objects=0#qt-science_center_objects (accessed on 14 January 2022).
- Dimitriadis, P.; Koutsoyiannis, D.; Iliopoulou, T.; Papanicolaou, P. A Global-Scale Investigation of Stochastic Similarities in Marginal Distribution and Dependence Structure of Key Hydrological-Cycle Processes. Hydrology 2021, 8, 59. [Google Scholar] [CrossRef]
- Courant, R.; Friedrichs, K.; Lewy, H. On the partial difference equations of mathematical physics. IBM J. Res. Dev. 1967, 11, 215–234. [Google Scholar] [CrossRef]
- Chiew, F.H.S.; Peel, M.C.; Western, A.W.; Singh, V.P.; Frevert, D. Application and testing of the simple rainfall-runoff model SIMHYD. In Mathematical Models of Small Watershed Hydrology and Applications; Water Resources Publication: Highlands Ranch, CO, USA, 2002. [Google Scholar]
- Wang, J.; Wang, G.; Elmahdi, A.; Bao, Z.; Song, M. Comparison of hydrological model ensemble forecasting based on multiple members and ensemble methods. Open Geosci. 2021, 13, 401–415. [Google Scholar] [CrossRef]
- Chiew, F.H.S.; Teng, J.; Vaze, J.; Post, D.A.; Perraud, J.M.; Kirono, D.G.; Viney, N.R. Estimating climate change impact on runoff across southeast Australia: Method, results, and implications of the modeling method. Water Resour. Res. 2009, 45, 82–90. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Y. Regionalising rainfall-runoff modelling for predicting daily runoff: Comparing gridded spatial proximity and gridded integrated similarity approaches against their lumped counterparts. J. Hydrol. 2017, 550, 279–293. [Google Scholar] [CrossRef]
- Liang, K.; Liu, C.; Liu, X.; Song, X. Impacts of climate variability and human activity on streamflow decrease in a sediment concentrated region in the Middle Yellow River. Stoch. Env. Res. A 2013, 27, 1741–1749. [Google Scholar] [CrossRef]
- Xu, C.Y. WASMOD—The water and snow balance modeling system. In Mathematical Models of Small Watershed Hydrology Applications; Singh, V.P., Frevert, D., Eds.; Water Resources Publication: Highlands Ranch, CO, USA, 2002; Volume 17, pp. 555–590. [Google Scholar]
- Li, Z.; Xu, Z.; Li, Z. Performance of WASMOD and SWAT on hydrological simulation in Yingluoxia watershed in northwest of China. Hydrol. Process. 2011, 25, 2001–2008. [Google Scholar] [CrossRef]
- Kizza, M.; Rodhe, A.; Xu, C.Y.; Ntale, H.K. Modelling catchment inflows into Lake Victoria: Uncertainties in rainfall–runoff modelling for the Nzoia River. Int. Assoc. Sci. Hydrol. 2011, 56, 1210–1226. [Google Scholar] [CrossRef]
- Li, Z.; Shao, Q.; Xu, Z.; Xu, C.Y. Uncertainty issues of a conceptual water balance model for a semi-arid watershed in north-west of China. Hydrol. Process. 2013, 27, 304–312. [Google Scholar] [CrossRef]
- Widén-Nilsson, E.; Halldin, S.; Xu, C.-Y. Global water-balance modelling with WASMOD-M: Parameter estimation and regionalisation. J. Hydrol. 2007, 340, 105–118. [Google Scholar] [CrossRef]
- Fekete, B.M.; Vörösmarty, C.J.; Lammers, R.B. Scaling gridded river networks for macroscale hydrology: Development, analysis, and control of error. Water Resour. Res. 2001, 37, 1955–1967. [Google Scholar] [CrossRef]
- Shepard, D. A Two-Dimensional Interpolation Function for Irregularly-Spaced Data. In Proceedings of the 23rd ACM National Conference, Las Vegas, NV, USA, 27–29 August 1968; ACM Press: New York, NY, USA, 27–29 August 1968; pp. 517–524. [Google Scholar]
- Barraquand, J.; Latombe, J.C. A Monte-Carlo algorithm for Path Planning with Many Degrees of Freedom. In Proceedings of the IEEE International Conference on Robotics & Automation, Cincinnati, OH, USA, 13–18 May 1990. [Google Scholar]
- Hansen, N.; Ros, R. Benchmarking a weighted negative covariance matrix update on the BBOB-2010 noisy testbed. In Proceedings of the Conference Companion on Genetic & Evolutionary Computation, Portland, OR, USA, 7–11 July 2010. [Google Scholar]
- Klemeš, V. Operational testing of hydrological simulation models. Hydrol. Sci. J. 1986, 31, 13–24. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of Automatic Calibration for Hydrologic Models: Comparison With Multilevel Expert Calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Mckay, M.D.; Beckkman, R.J.; Conover, W.J. A Comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 2000, 42, 55–61. [Google Scholar] [CrossRef]
- Horritt, M.S.; Bates, P.D. Effects of spatial resolution on a raster based model of flood flow. J. Hydrol. 2001, 253, 239–249. [Google Scholar] [CrossRef]
- Cook, A.; Merwade, V. Effect of topographic data, geometric configuration and modeling approach on flood inundation mapping. J. Hydrol. 2009, 377, 131–142. [Google Scholar] [CrossRef]
- Beven, K.; Freer, J. Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology. J. Hydrol. 2001, 249, 11–29. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. GLUE: 20 years on. Hydrol. Process. 2014, 28, 5897–5918. [Google Scholar] [CrossRef]
- Merwade, V.; Olivera, F.; Arabi, M.; Edleman, S. Uncertainty in Flood Inundation Mapping: Current Issues and Future Directions. J. Hydrol. Eng. 2008, 13, 608–620. [Google Scholar] [CrossRef]
- Neal, J.; Villanueva, I.; Wright, N.; Willis, T.; Fewtrell, T.; Bates, P. How much physical complexity is needed to model flood inundation? Hydrol. Process 2012, 26, 2264–2282. [Google Scholar] [CrossRef]





| Mean | Standard Deviation | Skewness Coefficient | Kurtosis Coefficient | ||
|---|---|---|---|---|---|
| Jianxi basin | discharge | 463 m3/s | 753.07 | 7.88 | 95.83 |
| precipitation | 1741 mm/year | 10.55 | 4.05 | 25.20 | |
| air temperature | 18 °C | 7.66 | −0.30 | 1.94 | |
| relative humidity | 78 | 9.78 | −0.22 | 2.84 | |
| Shizhenjie basin | discharge | 297 m3/s | 515.53 | 5.40 | 43.77 |
| precipitation | 1868 mm/year | 11.50 | 3.91 | 23.62 | |
| air temperature | 17 °C | 8.81 | −0.13 | 1.79 | |
| relative humidity | 79 | 10.06 | −0.31 | 2.91 |
| Routing Method | Parameters | Explanation | Prior Range for Calibration | |
|---|---|---|---|---|
| I-NRF | (m/s) | the wave velocity of a grid whose slope is 45° | 4, 5, 6, 7, 8, 9, 10 | The combination of all values generate 49 routing parameter-value sets |
| b (-) | power exponent reflecting how sensitive is the v to slope | 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5 | ||
| LRR | (m/s) | The wave velocity | Jianxi: 0.6, 0.8, 1.0, 1.2, 1.4, 1.6 Shizhenjie: 0.2, 0.4, 0.6, 0.8, 1.0, 1.2 | There are 6 routing parameter values |
| Parameters | Description | Prior Range for Calibration |
|---|---|---|
| INSC (mm) | Interception store capacity | [0.05 10] |
| COEFF (mm) | Maximum infiltration loss | [0 500] |
| SQ (-) | Infiltration loss exponent | [0 10] |
| SMSC (mm) | Soil moisture store capacity | [0 1000] |
| SUB (-) | Constant of proportionality in interflow equation | [0 1] |
| CRAK (-) | Constant of proportionality in groundwater recharge equation | [0 1] |
| K(-) | Base-flow linear recession parameter | [0 1] |
| Parameters | About | Prior Range for Calibration |
|---|---|---|
| a4 (-) | Actual evaporation | [0.1 0.999] |
| c1 (1/mm) | Fast runoff | [0 0.1] |
| c2 (1/mm) | Slow runoff | [0 0.1] |
| c4 (-) | Potential evaporation | [0.1 0.999] |
| c5 (-) | Precipitation | [0.5 1.5] |
| DEM Resolution (m × m) | Jianxi Basin | Shizhenjie Basin | ||||
|---|---|---|---|---|---|---|
| v45 (I-NRF) | b (I-NRF) | v (LRR) | v45 (I-NRF) | b (I-NRF) | v (LRR) | |
| 90 × 90 | 10 | 0.35 | 1.2 | 4 | 0.25 | 0.6 |
| 250 × 250 | 5 | 0.2 | 1.2 | 6 | 0.3 | 0.6 |
| 500 × 500 | 9 | 0.3 | 1.2 | 8 | 0.35 | 0.6 |
| 1000 × 1000 | 7 | 0.2 | 1.2 | 9 | 0.35 | 0.6 |
| I-NRF | LRR | ||
|---|---|---|---|
| Jianxi Bain (1000 m) | 5 arc-min | 1768 s | 2450 s |
| 60 arc-min | 165 s | 225 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Chen, H.; Xu, C.-Y.; Li, L.; Zhao, H.; Huo, R.; Chen, J. Joint Effects of the DEM Resolution and the Computational Cell Size on the Routing Methods in Hydrological Modelling. Water 2022, 14, 797. https://doi.org/10.3390/w14050797
Li J, Chen H, Xu C-Y, Li L, Zhao H, Huo R, Chen J. Joint Effects of the DEM Resolution and the Computational Cell Size on the Routing Methods in Hydrological Modelling. Water. 2022; 14(5):797. https://doi.org/10.3390/w14050797
Chicago/Turabian StyleLi, Jingjing, Hua Chen, Chong-Yu Xu, Lu Li, Haoyuan Zhao, Ran Huo, and Jie Chen. 2022. "Joint Effects of the DEM Resolution and the Computational Cell Size on the Routing Methods in Hydrological Modelling" Water 14, no. 5: 797. https://doi.org/10.3390/w14050797
APA StyleLi, J., Chen, H., Xu, C.-Y., Li, L., Zhao, H., Huo, R., & Chen, J. (2022). Joint Effects of the DEM Resolution and the Computational Cell Size on the Routing Methods in Hydrological Modelling. Water, 14(5), 797. https://doi.org/10.3390/w14050797









