Methodological Contribution to the Assessment of Generation and Sediment Transport in Tropical Hydrographic Systems
Abstract
:1. Introduction
2. Materials and Methods
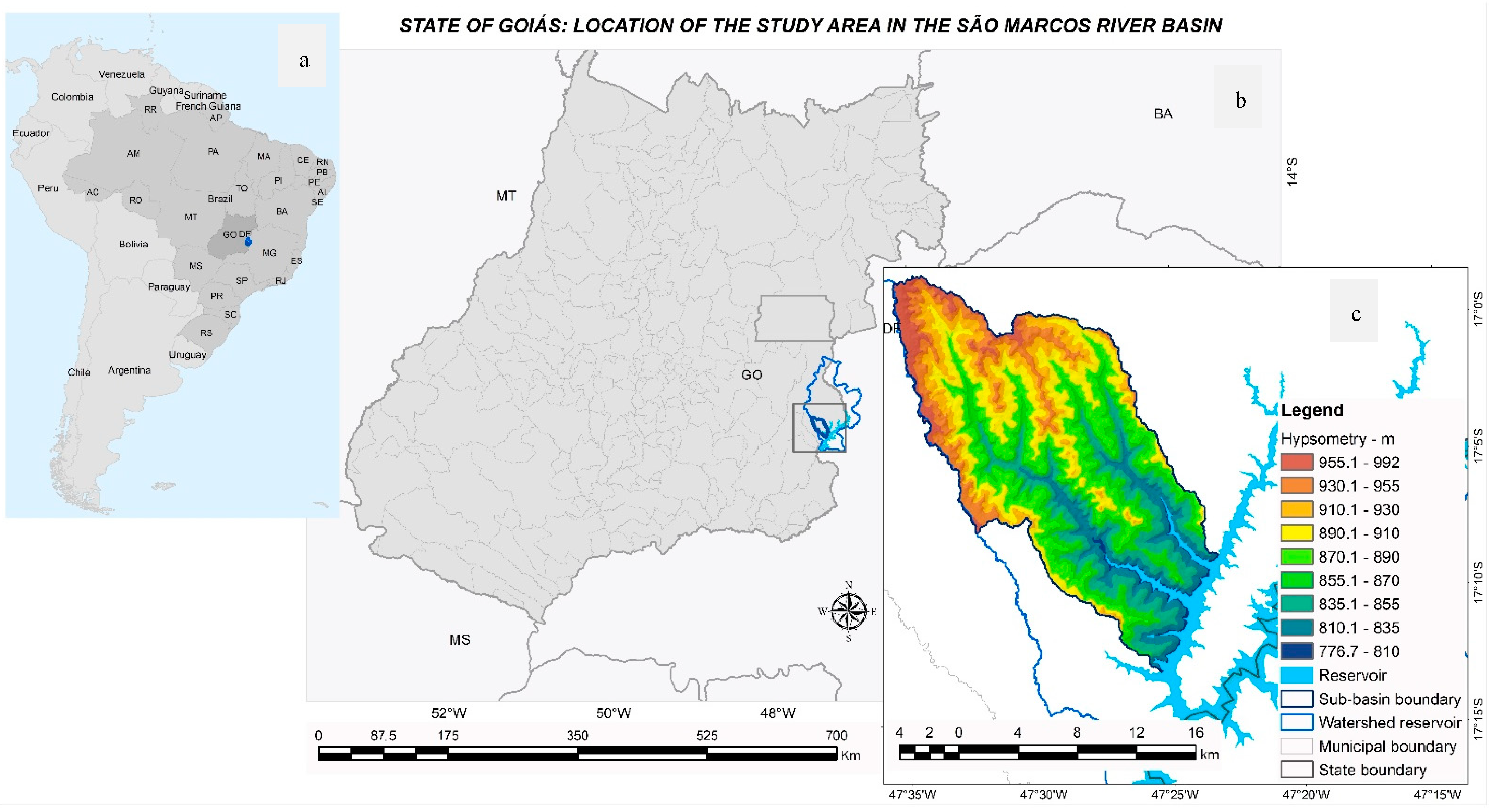
2.1. Location and Characterization of the Study Area
2.2. Methodology
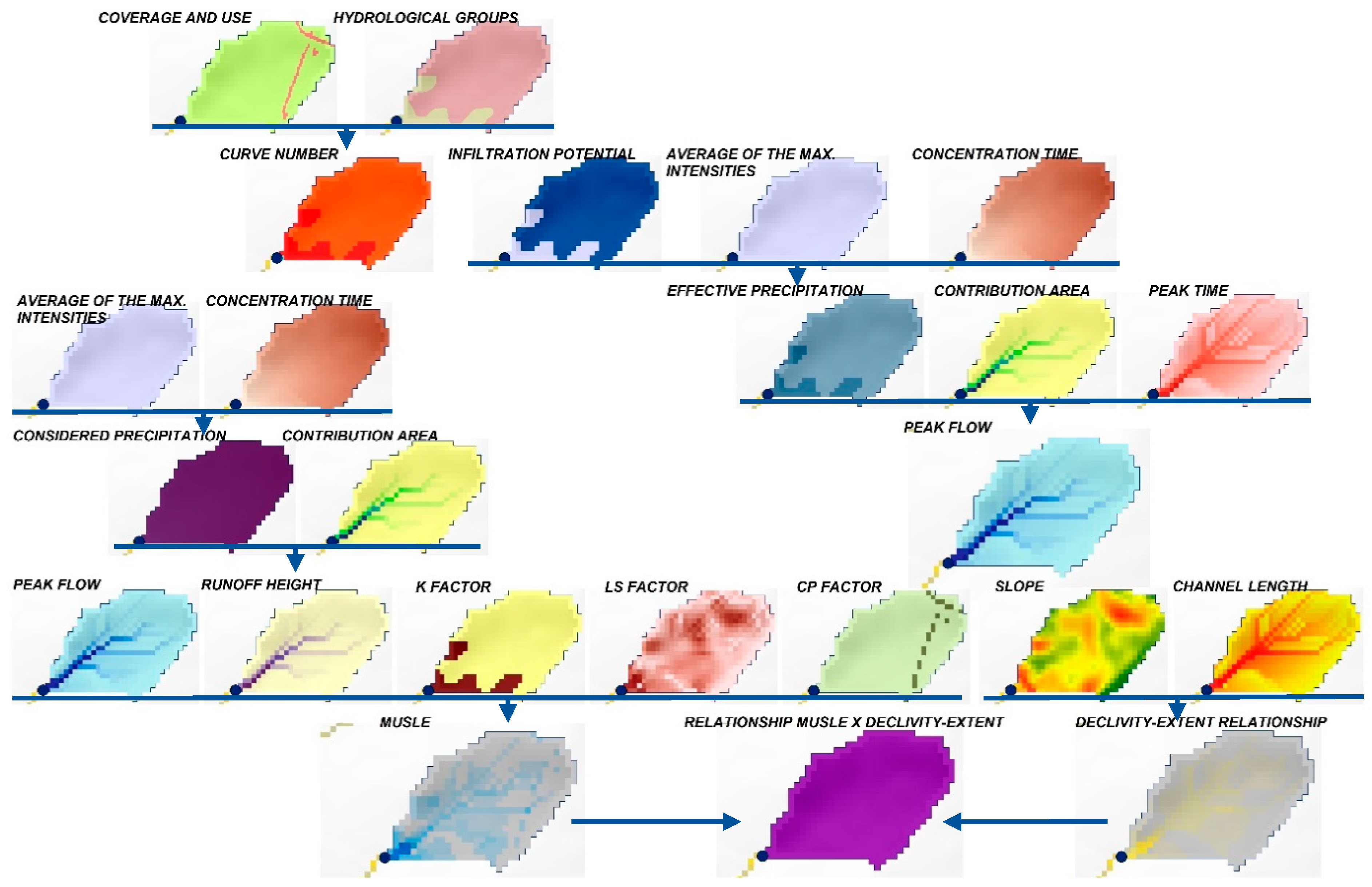
2.2.1. Sediment Generation Estimate
2.2.2. Sediment Transport Capacity Estimates
3. Results and Discussion
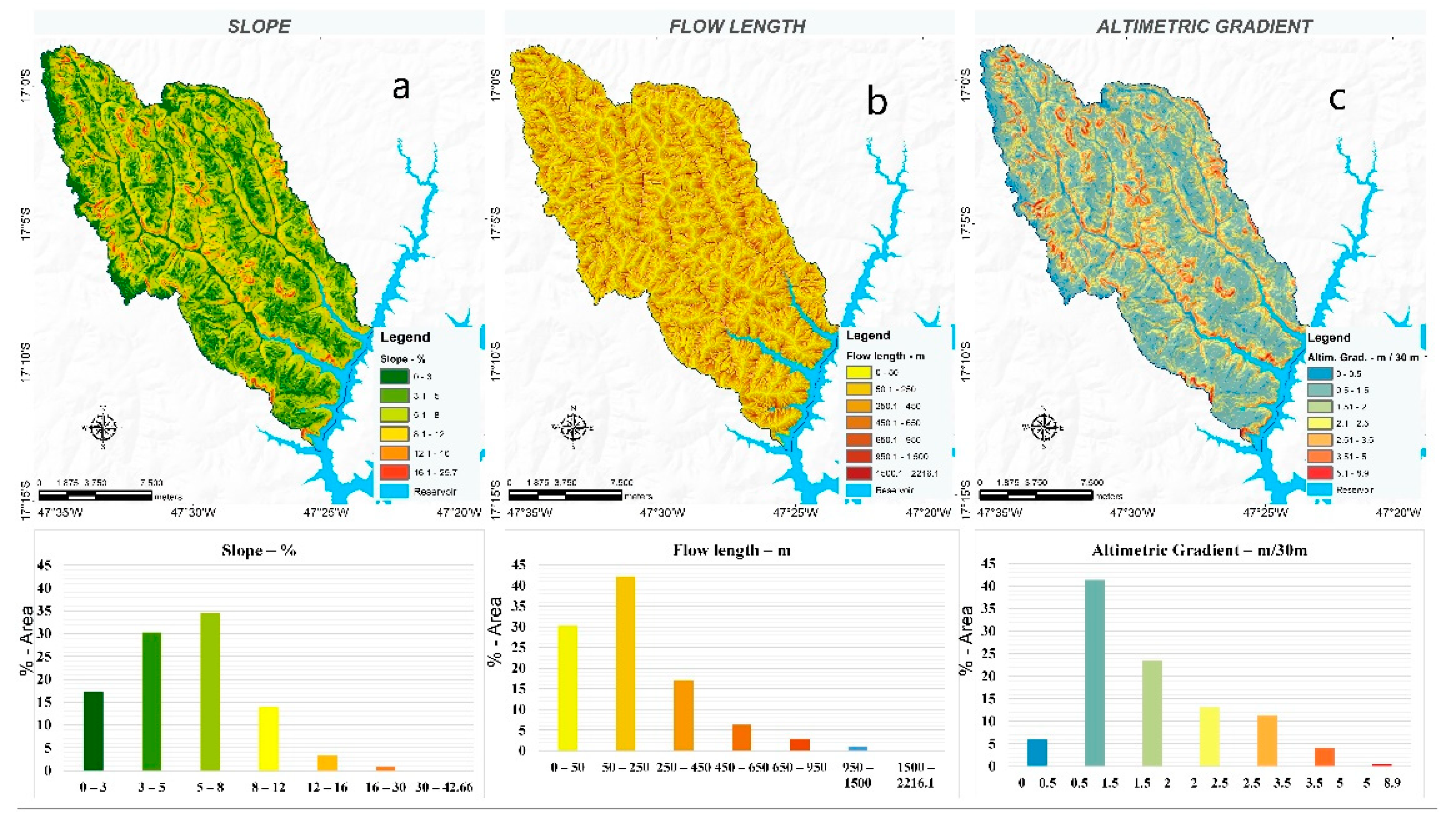
3.1. Morphometric and Morphographic Configuration of the Basins
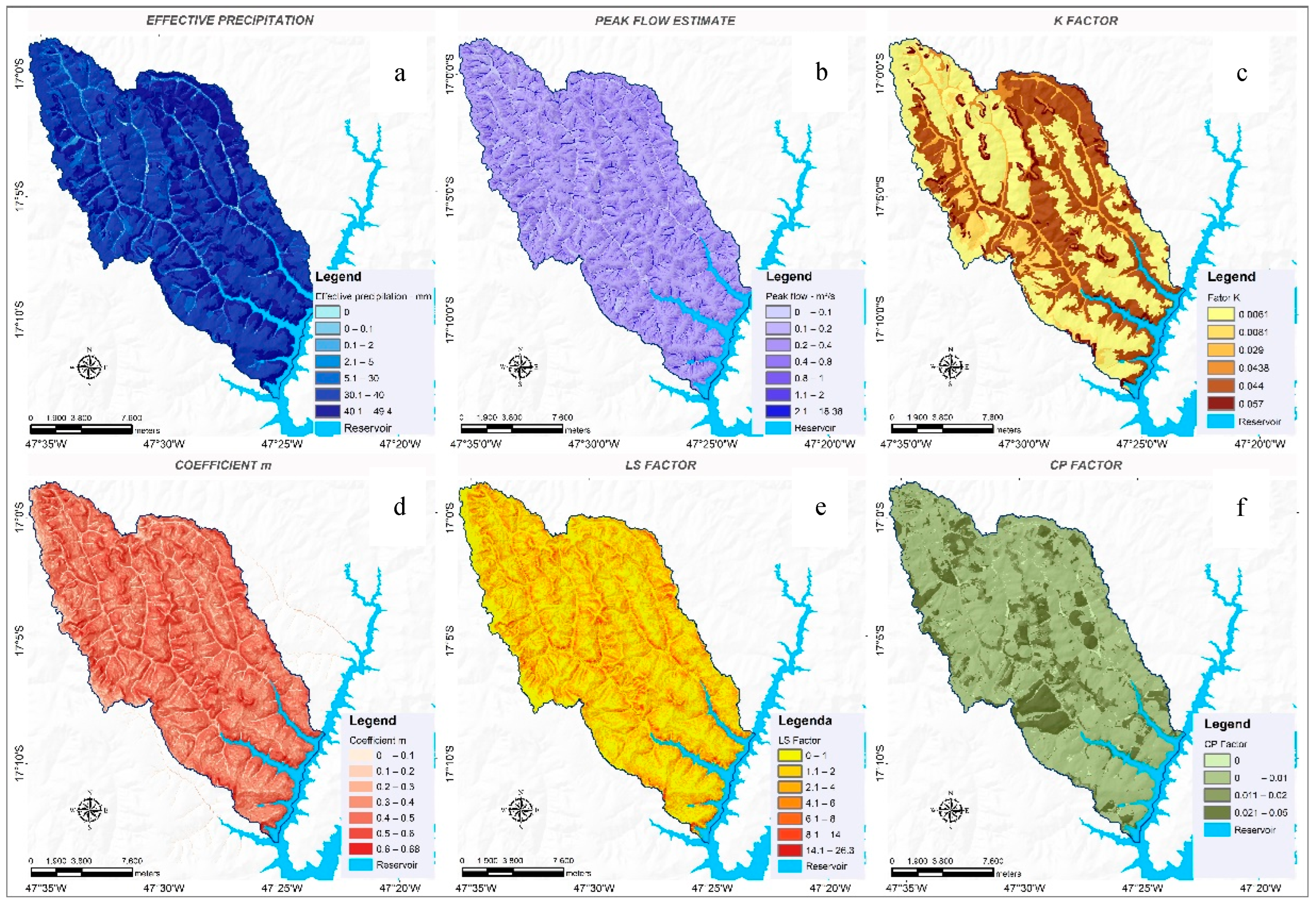
3.2. Rainfall–Runoff Relationship, Soil Erodibility, Topographic Factor, Land Use Cover and Conservation Practices in Sediment Generation Estimates
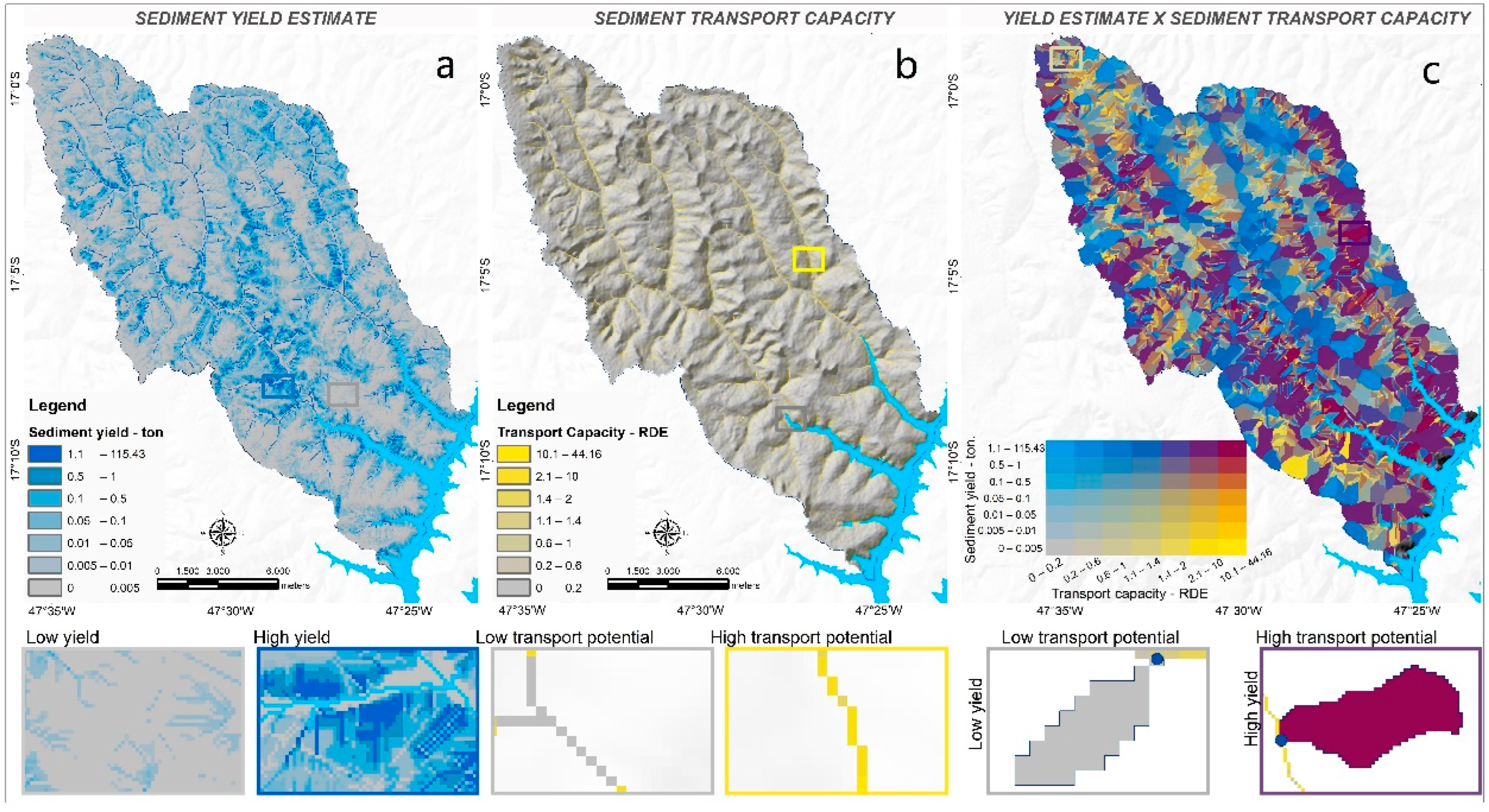
3.3. Bivariate Relationship between Estimates of Sediment Generation and Transport Capacity
4. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, C.; Walling, D.E.; He, Y. Review: The International Sediment Initiative case studies of sediment problems in river basins and their management. Int. J. Sediment Res. 2018, 33, 216–219. [Google Scholar] [CrossRef]
- Ayele, G.T.; Kuriqi, A.; Jemberrie, M.A.; Saia, S.M.; Seka, A.M.; Teshale, E.Z.; Daba, M.H.; Ahmad Bhat, S.; Demissie, S.S.; Jeong, J.; et al. Sediment Yield and Reservoir Sedimentation in Highly Dynamic Watersheds: The Case of Koga Reservoir, Ethiopia. Water 2021, 13, 3374. [Google Scholar] [CrossRef]
- Phuong, T.T.; Shrestha, R.P.; Chuong, H.V. Simulation of Soil Erosion Risk in the Upstream Area of Bo River Watershed. In Re-Defining Diversity and Dynamism of Natural Resource Management in Asia; Thang, T.N., Dung, N.T., Hulse, D., Sharma, S., Shivakoti, G.P., Eds.; Elsevier: Amsterdam, The Netherlands, 2017; Volume 3, pp. 87–99. [Google Scholar] [CrossRef]
- Wang, H.W.; Kondolf, M.; Tullos, D.; Kuo, W.C. Sediment Management in Taiwan’s Reservoirs and Barriers to Implementation. Water 2018, 10, 1034. [Google Scholar] [CrossRef] [Green Version]
- Fox, G.A.; Sheshukov, A.; Cruse, R.; Kolar, R.L.; Guertault, L.; Gesh, K.R.; Dutnell, R.C. Reservoir Sedimentation and Upstream Sediment Sources: Perspectives and Future Research Needs on Streambank and Gully Erosion. Environ. Manag. 2016, 57, 945–955. [Google Scholar] [CrossRef] [Green Version]
- Iradukunda, P.; Bwambale, E. Reservoir sedimentation and its effect on storage capacity–A case study of Murera reservoir, Kenya. Cogent Eng. 2021, 8, 1. [Google Scholar] [CrossRef]
- Obialor, C.A.; Okeke, O.C.; Onunkwo, A.A.; Fagorite, V.I.; Ehujuo, N.N. Reservoir Sedimentation: Causes, Effects and Mitigation. Int. J. Adv. Acad. Res.–Sci. Technol. Eng. 2019, 5, 92–109. [Google Scholar]
- Benavidez, B.; Jackson, B.; Maxwell, D.; Norton, K. A review of the (Revised) Universal Soil Loss Equation ((R)USLE): With a view to increasing its global applicability and improving soil loss estimates. Hydrol. Earth Syst. Sci. 2018, 22, 6059–6086. [Google Scholar] [CrossRef] [Green Version]
- Ezzaouini, M.A.; Mahé, G.; Kacimi, I.; Zerouali, A. Comparison of the MUSLE Model and Two Years of Solid Transport Measurement, in the Bouregreg Basin, and Impact on the Sedimentation in the Sidi Mohamed Ben Abdellah Reservoir, Morocco. Water 2020, 12, 1882. [Google Scholar] [CrossRef]
- Arekhi, S.; Shabani, A.; Rostamizad, G. Application of the modified universal soil loss equation (MUSLE) in prediction of sediment yield (Case study: Kengir Watershed, Iran). Arab. J. Geosci. 2012, 5, 1259–1267. [Google Scholar] [CrossRef]
- Kumar, P.S.; Praveen, T.V.; Prasad, M.A. Simulation of Sediment Yield over Un-gauged Stations Using MUSLE and Fuzzy Model. Aquat. Procedia 2015, 4, 1291–1298. [Google Scholar] [CrossRef]
- Colman, C.B.; Garcia, K.M.P.; Pereira, R.B.; Shinma, E.A.; Lima, F.E.; Gomes, A.O.; Oliveira, P.T.S. Different approaches to estimate the sediment yield in a tropical watershed. Braz. J. Water Resour. 2018, 23, e47. [Google Scholar] [CrossRef] [Green Version]
- Morris, G.L. Classification of Management Alternatives to Combat Reservoir Sedimentation. Water 2020, 12, 861. [Google Scholar] [CrossRef] [Green Version]
- Thomas, K.; Chen, W.; Lin, B.-S.; Seeboonruang, U. Evaluation of the SEdiment Delivery Distributed (SEDD) Model in the Shihmen Reservoir Watershed. J. Sustain. 2020, 12, 6221. [Google Scholar] [CrossRef]
- Miranda, L.E. Reservoir Fish Habitat Management; Lightning Press: Totowa, NJ, USA, 2017. [Google Scholar]
- De Rosa, P.; Fredduzzi, A.; Cencetti, C. Stream Power Determination in GIS: An Index to Evaluate the Most ‘Sensitive’ Points of a River. Water 2019, 11, 1145. [Google Scholar] [CrossRef] [Green Version]
- Yuan, X.P.; Braun, J.; Guerit, L.; Rouby, D.; Cordonnier, G. A New Efficient Method to Solve the Stream Power Law Model Taking Into Account Sediment Deposition. J. Geophys. Res. Earth Surf. 2019, 124, 1346–1365. [Google Scholar] [CrossRef] [Green Version]
- Song, S.; Schmalz, B.; Fohrer, N. Simulation and comparison of stream power in-channel and on the floodplain in a German lowland area. J. Hydrol. Hydromech. 2014, 62, 133–144. [Google Scholar] [CrossRef] [Green Version]
- Whipple, K.X.; Tucker, G.E. Dynamics of the stream-power river incision model: Implications for height limits of mountain ranges, landscape response timescales, and research needs. J. Geophys. Res. Solid Earth 1999, 104, 17661–17674. [Google Scholar] [CrossRef]
- Albo-Salih, H.; Mays, L.W.; Che, D. Application of an Optimization/Simulation Model for the Real-Time Flood Operation of River-Reservoir Systems with One-and Two-Dimensional Unsteady Flow Modeling. Water 2022, 14, 87. [Google Scholar] [CrossRef]
- Vente, J.; Poesen, J.; Arabkhedri, M.; Verstraeten, G. The sediment delivery problem revisited. Prog. Phys. Geogr. Earth Environ. 2007, 31, 155–178. [Google Scholar] [CrossRef] [Green Version]
- Mishra, K.; Sinha, R.; Jain, V.; Nepal, S.; Uddin, K. Towards the assessment of sediment connectivity in a large Himalayan River basin. Sci. Total Environ. 2019, 661, 251–265. [Google Scholar] [CrossRef]
- Hack, J.T. Stream-profile analysis and stream-gradient index. J. Res. U.S. Geol. Surv. 1973, 1, 421–429. [Google Scholar]
- Mitasova, H.; Barton, M.; Ullah, I.; Hofierka, J.; Harmon, R.S. GIS-Based Soil Erosion Modeling. In Treatise on Geomorphology; Shroder, J.F., Ed.; Academic Press: San Diego, CA, USA, 2013; Volume 3, pp. 228–258. [Google Scholar] [CrossRef]
- Pereira Júnior, L.C.; Ferreira, N.C.; Miziara, F. A Expansão da Irrigação Por Pivôs Centrais no Estado de Goiás (1984–2015). Bol. Goiano Geogr. 2017, 37, 323–341. [Google Scholar] [CrossRef] [Green Version]
- Nunes, E.D.; Romão, P.A.; Sales, M.M.; Luz, M.P. Geoprocessing Applied in the Estimate of Infiltration and Surface Runoff in HPP’s Contribution Watershed. J. Geogr. Inf. Syst. 2021, 13, 643–659. [Google Scholar] [CrossRef]
- Faria, A. Geologia do Domo de Cristalina, Goiás. Rev. Bras. Geociências 1985, 15, 231–240. [Google Scholar] [CrossRef]
- Resende, M.J.G. Classes de Solos dos Municípios Goianos–2016; EMATER: Goiânia, Brazil, 2016. [Google Scholar]
- Rosa, L.E.; Santos, N.B.F.; Bayer, M.; Castro, S.S.; Nunes, E.D.; Cherem, L.F.S. Atributos Para Mapeamento Digital de Solos: O Estudo de Caso na Bacia do Ribeirão Arrojado, Município de Cristalina–Goiás. In Elementos da Natureza e Propriedades dos Solos; Oliveira, A.C., Ed.; Atena Editora: Ponta Grossa, Brazil, 2018; pp. 68–82. [Google Scholar] [CrossRef]
- Monteiro, C.A.F. Notas para o estudo do clima do Centro-Oeste Brasileiro. Rev. Bras. Geogr. 1951, 13, 3–46. [Google Scholar]
- Novais, G.T. Climate Classification Applied to the State of Goiás and the Federal District, Brazil. Bol. Goiano Geogr. 2020, 40, 1–29. [Google Scholar]
- Williams, J.R. Sediment-Yield Prediction with Universal Equation Using Runoff Energy Factor. In Present and Prospective Technology for Predicting Sediment Yield and Sources; USDA–Agriculture Research Service: Washington, DC, USA, 1975; pp. 244–252. [Google Scholar]
- Williams, J.R. Testing the modified Universal Soil Loss Equation. In Proceedings of the Workshop on Estimating Erosion and Sediment Yield on Rangelands; USDA–Agriculture Research Service: Tucson, AZ, USA, 1981; pp. 157–165. [Google Scholar]
- Smith, S.J.; Williams, J.R.; Menzel, R.G.; Coleman, G.A. Prediction of sediment yield from Southern Plains Grasslands with the Modified Universal Soil Loss Equation. Rangel. Ecol. Manag. J. 1984, 37, 295–297. [Google Scholar] [CrossRef]
- NRCS—Natural Resources Conservation Service. National Engineering Handbook, Part 630 Hydrology, Chapter 10 Estimation of Direct Runoff from Storm Rainfall; USDA: Washington, DC, USA, 2004; pp. 1–79. [Google Scholar]
- Sun, Y.; Wendi, D.; Kim, D.E.; Liong, S.-Y. Deriving intensity–duration–frequency (IDF) curves using downscaled in situ rainfall assimilated with remote sensing data. Geosci. Lett. 2019, 6, 17. [Google Scholar] [CrossRef] [Green Version]
- Balmaceda, E.G.; López-Ramos, A.; Martínez-Acosta, L.; Medrano-Barboza, J.P.; López, J.F.R.; Seingier, G.; Daesslé, L.W.; López-Lambraño, A.A. Rainfall Intensity-Duration-Frequency Relationship. Case Study: Depth-Duration Ratio in a Semi-Arid Zone in Mexico. Hydrology 2020, 7, 78. [Google Scholar] [CrossRef]
- Villela, S.M.; Mattos, A. Hidrologia Aplicada; McGrawHill do Brasil: São Paulo, Brazil, 1975; p. 245. [Google Scholar]
- Oliveira, L.F.C.; Cortês, F.C.; Wehr, T.R.; Borges, L.B.; Sarmento, P.H.L.; Griebeler, N.P. Intensidade-Duração-Frequência de Chuvas Intensas Para Localidades no Estado de Goiás e Distrito Federal. Pesqui. Agropecuária Trop. 2005, 35, 13–18. [Google Scholar]
- Watt, W.E.; Chow, K.C.A. A General Expression for Basin Lag Time. Can. J. Civ. Eng. 1985, 12, 294–300. [Google Scholar] [CrossRef]
- Tucci, C.E.M. Águas urbanas. Estud. Avançados 2008, 22, 97–112. [Google Scholar] [CrossRef]
- Tucci, C.E.M.; Marques, D.M.L.M. Avaliação e Controle da Drenagem Urbana; UFRGS: Porto Alegre, Brazil, 2000; 558p. [Google Scholar]
- Mannigel, A.R.; Carvalho, M.P.; Moreti, D.; Medeiros. Fator erodibilidade e tolerância de perda dos solos do Estado de São Paulo. Acta Sci. Agron. 2002, 24, 1335–1340. [Google Scholar] [CrossRef]
- Stein, D.P.; Donzelli, P.L.; Gimenez, F.A.; Ponçano, E.L.; Lombardi Neto, F. Potencial de Erosão Laminar, Natural e Antrópica na Bacia do Peixe-Paranapanema. In Simpósio Nacional de Controle de Erosão; ABGE: Marília, Brazil, 1987; pp. 105–135. [Google Scholar]
- Oliveira, J.S. Avaliação de Modelos de Elevação na Estimativa de Perda de Solos em Ambiente SIG. Master’s Thesis, Escola Superior de Agricultura Luiz de Queiroz—Universidade de São Paulo, Piracicaba, Brazil, 2012. [Google Scholar]
- Schwab, G.O.; Fangmeier, D.D.; Elliot, W.J.; Frevert, R.K. Soil and Water Conservation Engineering, 4th ed.; John Wiley & Sons: Chichester, UK, 1993; p. 528. [Google Scholar]
- NASA JPL. NASADEM Merged DEM Global 1 arc Second V001 [Data Set] 2020. Distributed by NASA EOSDIS Land Processes DAAC. Available online: https://lpdaac.usgs.gov/products/nasadem_hgtv001/ (accessed on 2 April 2021). [CrossRef]
- McCool, D.K.; Brown, L.C.; Foster, G.R.; Mutchler, C.K.; Meyer, L.D. Revised slope steepness factor for the Universal Soil Loss Equation. Trans. Am. Soc. Agric. Biol. Eng. 1987, 30, 1387–1396. [Google Scholar] [CrossRef]
- Kand, M.; Yoo, C. Application of the SCS–CN Method to the Hancheon Basin on the Volcanic Jeju Island, Korea. Water 2020, 12, 3350. [Google Scholar] [CrossRef]
- Caletka, M.; Michalková, M.S.; Karásek, P.; Fucík, P. Improvement of SCS-CN Initial Abstraction Coefficient in the Czech Republic: A Study of Five Catchments. Water 2020, 12, 1964. [Google Scholar] [CrossRef]
- Krajewski, A.; Sikorska-Senoner, A.; Hejduk, A.; Hejduk, L. Variability of the Initial Abstraction Ratio in an Urban and an Agroforested Catchment. Water 2020, 12, 415. [Google Scholar] [CrossRef] [Green Version]
- Shi, W.; Wang, N. An Improved SCS-CN Method Incorporating Slope, Soil Moisture, and Storm Duration Factors for Runoff Prediction. Water 2020, 12, 1335. [Google Scholar] [CrossRef]
- Psomiadis, E.; Soulis, K.X.; Efthimiou, N. Using SCS-CN and Earth Observation for the Comparative Assessment of the Hydrological Effect of Gradual and Abrupt Spatiotemporal Land Cover Changes. Water 2020, 12, 1386. [Google Scholar] [CrossRef]
- Mlynski, D.; Walega, A.; Ksiazek, L.; Florek, J.; Petroslli, A. Possibility of Using Selected Rainfall-Runoff Models for Determining the Design Hydrograph in Mountainous Catchments: A Case Study in Poland. Water 2020, 12, 1450. [Google Scholar] [CrossRef]
- Ajmal, M.; Waseem, M.; Kim, D.; Kim, T.-W. A Pragmatic Slope-Adjusted Curve Number Model to Reduce Uncertainty in Predicting Flood Runoff from Steep Watersheds. Water 2020, 12, 1469. [Google Scholar] [CrossRef]
- Soulis, K.X. Soil Conservation Service Curve Number (SCS-CN) Method: Current Applications, Remaining Challenges, and Future Perspectives. Water 2021, 13, 192. [Google Scholar] [CrossRef]
- Ling, L.; Yusop, Z.; Yap, W.-S.; Tan, W.L.; Chow, M.F.; Ling, J.L. A Calibrated, Watershed-Specific SCS-CN Method: Application to Wangjiaqiao Watershed in the Three Gorges Area, China. Water 2020, 12, 60. [Google Scholar] [CrossRef] [Green Version]
- Cui, M.; Sun, Y.; Huang, C.; Li, M. Water Turbidity Retrieval Based on UAV Hyperspectral Remote Sensing. Water 2022, 14, 128. [Google Scholar] [CrossRef]
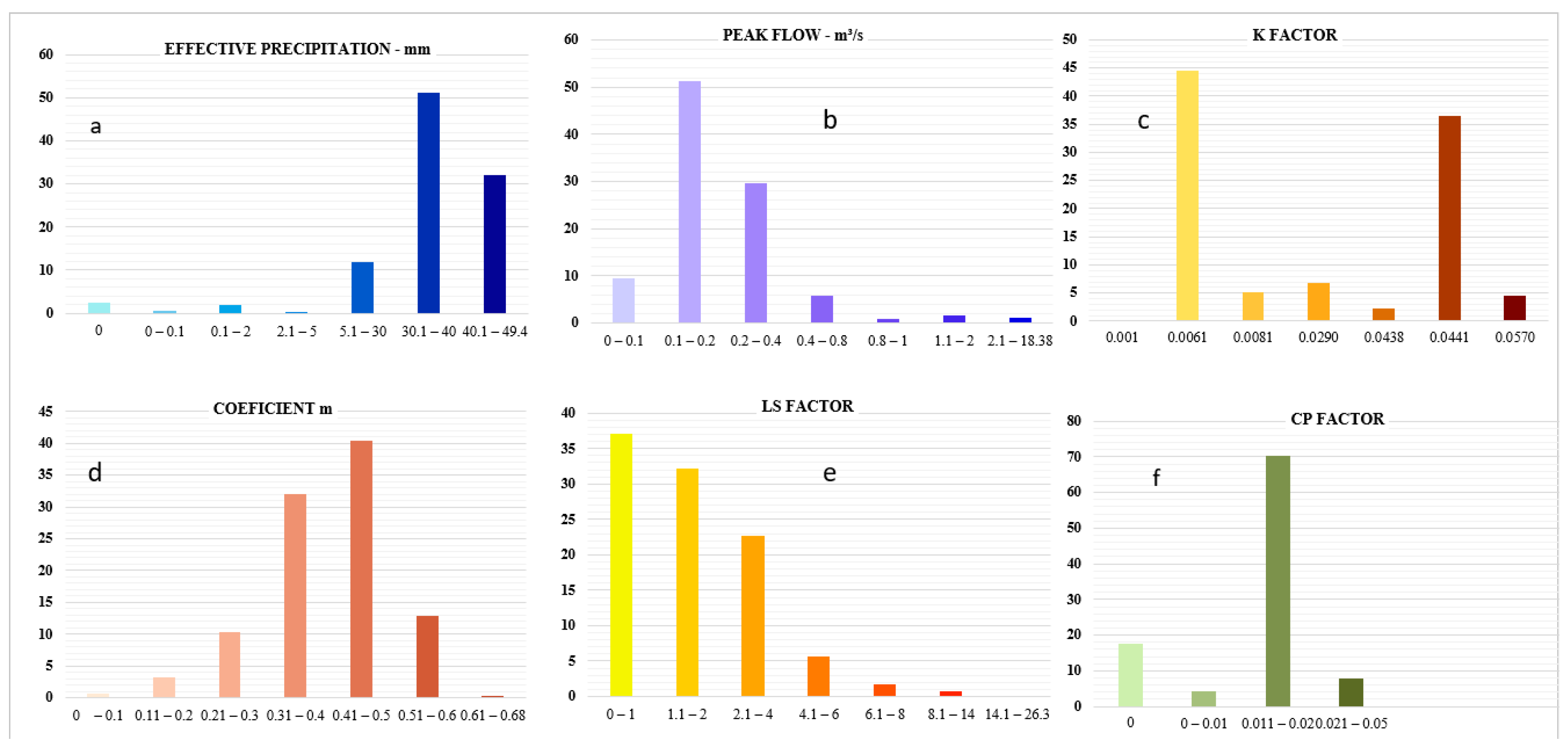
| Soil Class | Texture | Hydrological Group | K Factor |
|---|---|---|---|
| Cambisol (Dystrophic Haplic) | Clayey to Mean | C | 0.0441 |
| Ferralsol (Dystrophic Red) | Clayey to Very Clayey | B | 0.0061 |
| Ferralsol (Dystrophic Yellow-Red) | Clayey | B | 0.0081 |
| Fluvisol (Dystrophic) | Mean to Sandy | A | 0.0290 |
| Plintossol (Concretionary Petric) | Clayey to Gravel | C | 0.0438 |
| Leptsol (Dystrophic) | Sandy to Gravel | D | 0.0570 |
| Coverage and Use Classes | Hydrological Group | CP Factor | |||
|---|---|---|---|---|---|
| A | B | C | D | ||
| Curve Number | |||||
| Agriculture—level terracing | 60 | 71 | 79 | 82 | 0.005775 |
| Bare ground—with conservation | 62 | 71 | 78 | 81 | 0.051365 |
| Pasture—medium and low transpiration | 47 | 67 | 81 | 88 | 0.005 |
| Reforestation—medium transpiration | 36 | 60 | 70 | 76 | 0.01635 |
| Forests—dense and high transpiration | 26 | 52 | 62 | 69 | 0.00004 |
| Savannas—medium transpiration | 36 | 60 | 73 | 79 | 0.0007 |
| Permanent grasslands—dense coverage and high transpiration | 25 | 55 | 70 | 77 | 0.01 |
| Permanent grasslands—dense coverage and mean transpiration | 36 | 60 | 73 | 79 | 0.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nunes, E.D.; Romão, P.d.A.; Sales, M.M.; Souza, N.M.d.; Luz, M.P.d. Methodological Contribution to the Assessment of Generation and Sediment Transport in Tropical Hydrographic Systems. Water 2022, 14, 4091. https://doi.org/10.3390/w14244091
Nunes ED, Romão PdA, Sales MM, Souza NMd, Luz MPd. Methodological Contribution to the Assessment of Generation and Sediment Transport in Tropical Hydrographic Systems. Water. 2022; 14(24):4091. https://doi.org/10.3390/w14244091
Chicago/Turabian StyleNunes, Elizon D., Patrícia de A. Romão, Maurício M. Sales, Newton M. de Souza, and Marta P. da Luz. 2022. "Methodological Contribution to the Assessment of Generation and Sediment Transport in Tropical Hydrographic Systems" Water 14, no. 24: 4091. https://doi.org/10.3390/w14244091





