Numerical Modelling of an Innovative Conical Pile Head Breakwater
Abstract
:1. Introduction
2. Modelling of CPHB Structure
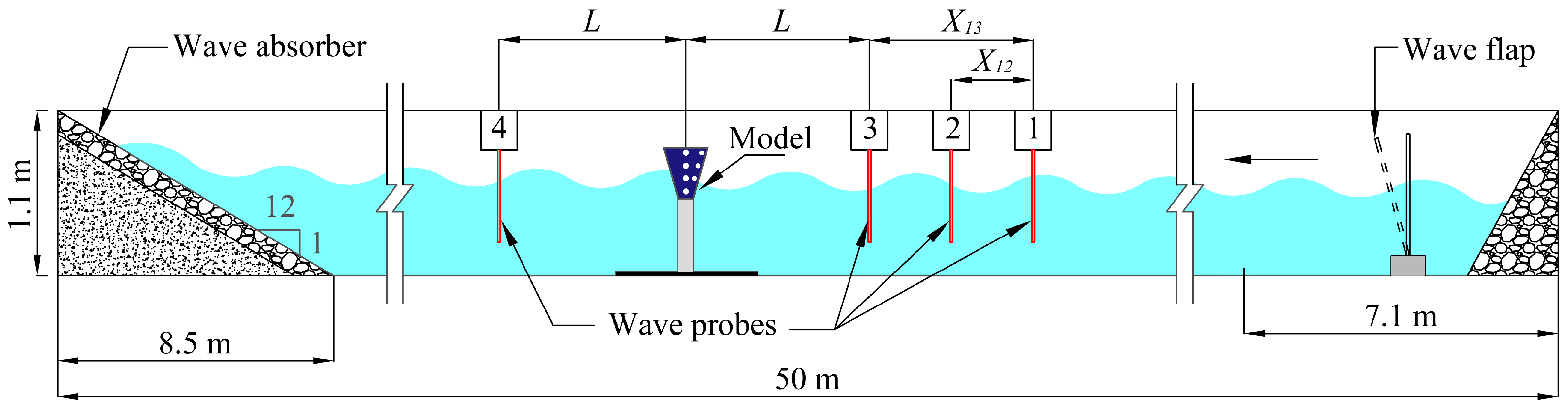
2.1. Details of Physical Modelling
2.2. Numerical Modelling
2.2.1. REEF3D
2.2.2. Numerical Model Setup
3. Results and Discussion
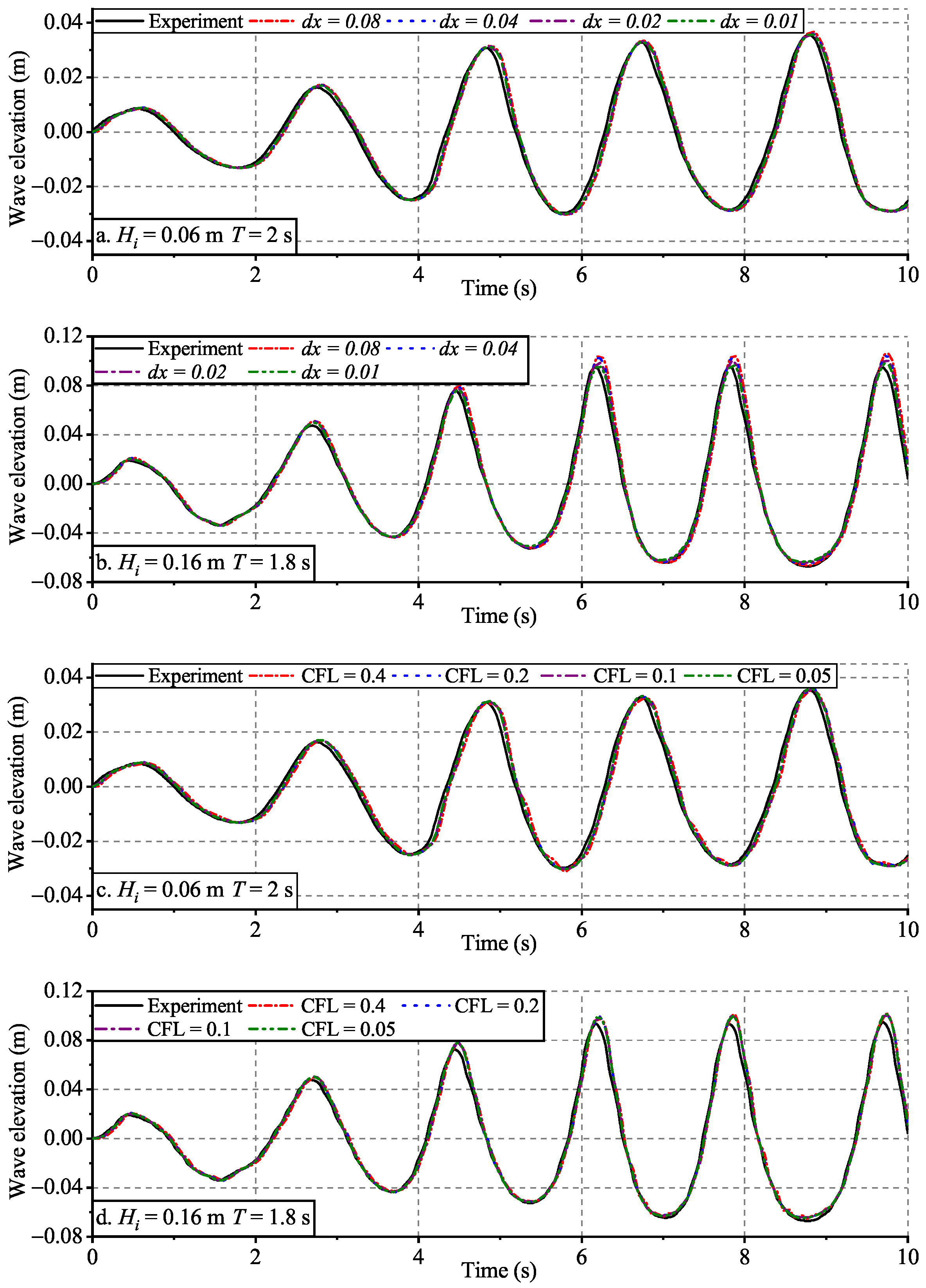
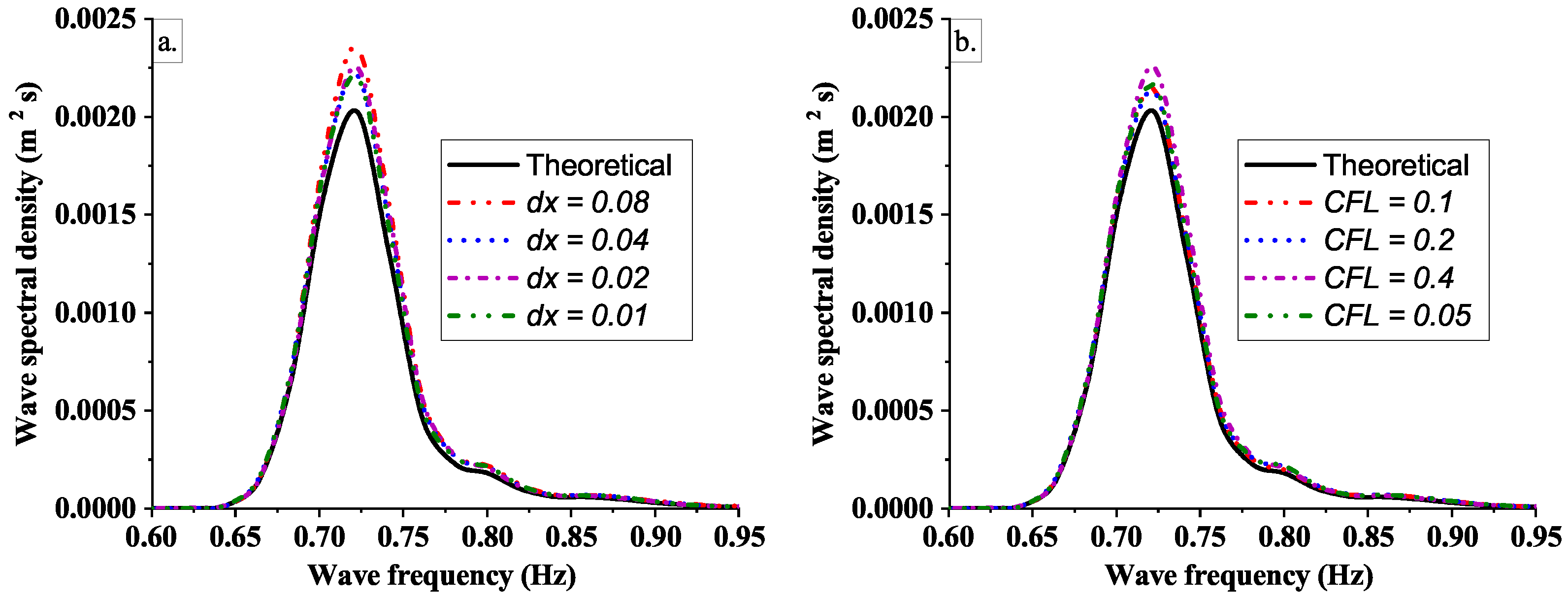
3.1. Validation of Wave Generation
3.1.1. Monochromatic Waves
3.1.2. Irregular Waves
3.2. Performance of CPHB with Monochromatic Waves
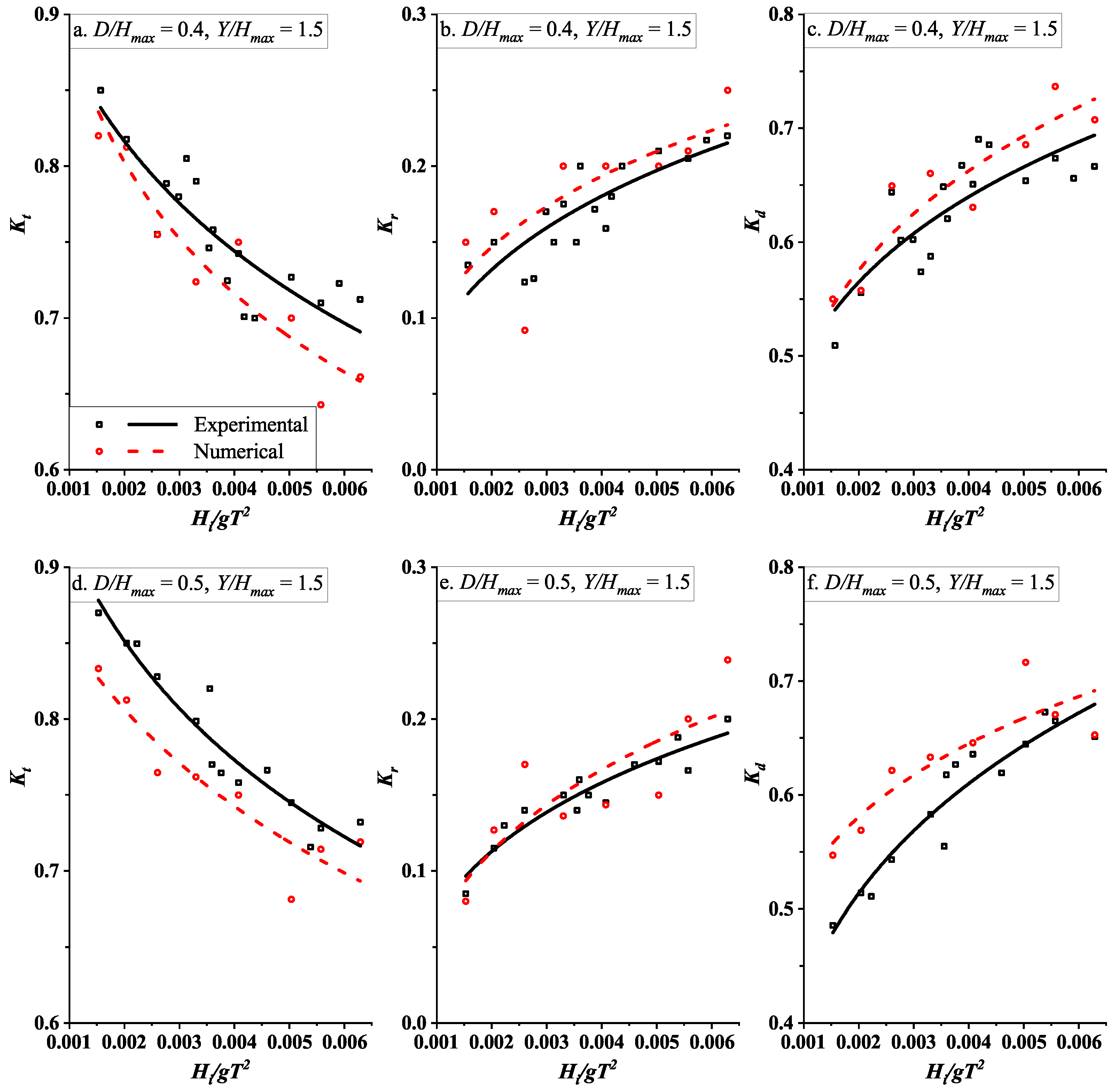
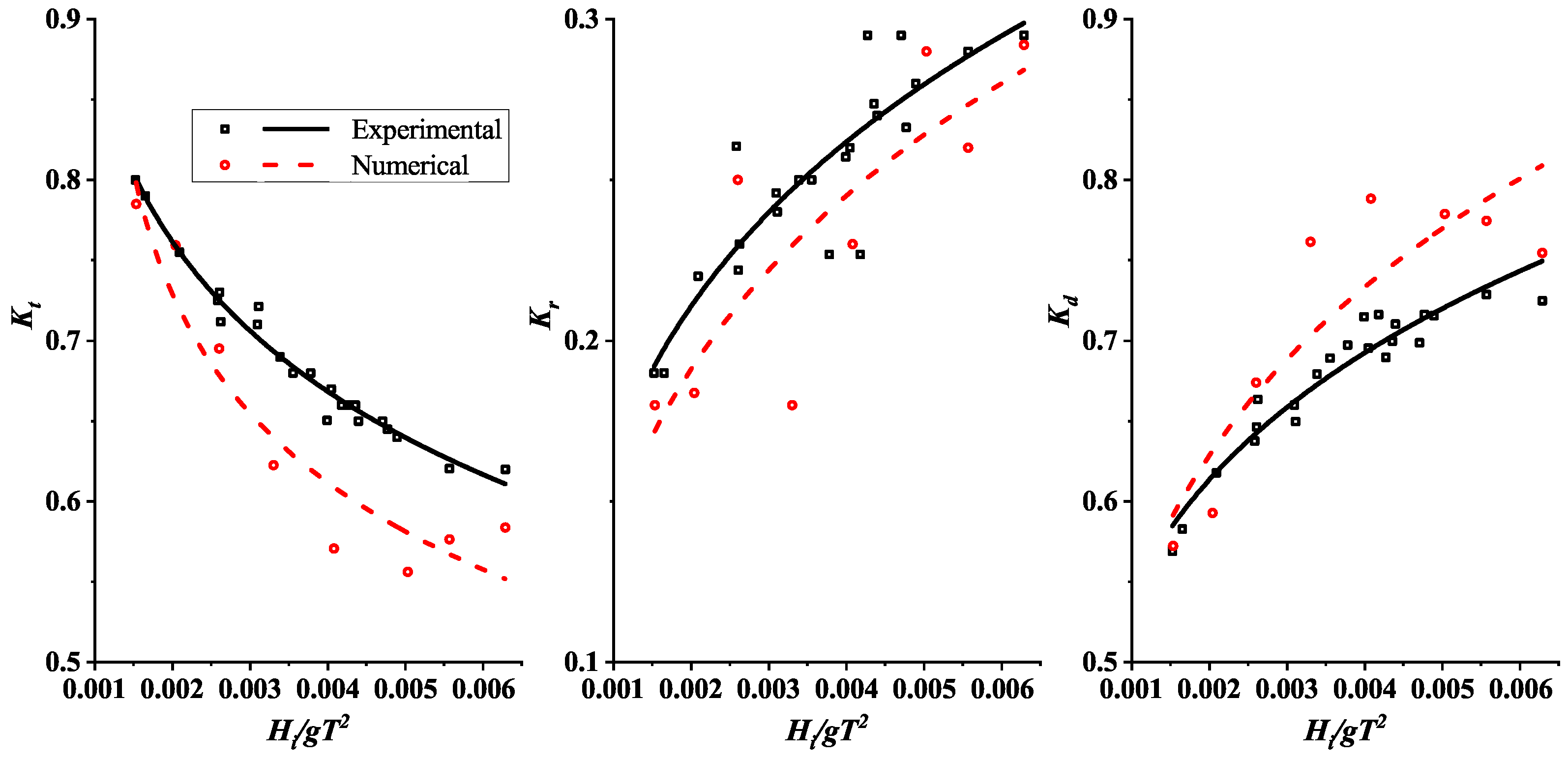
3.2.1. Validation of Numerical Results with Experimental Data
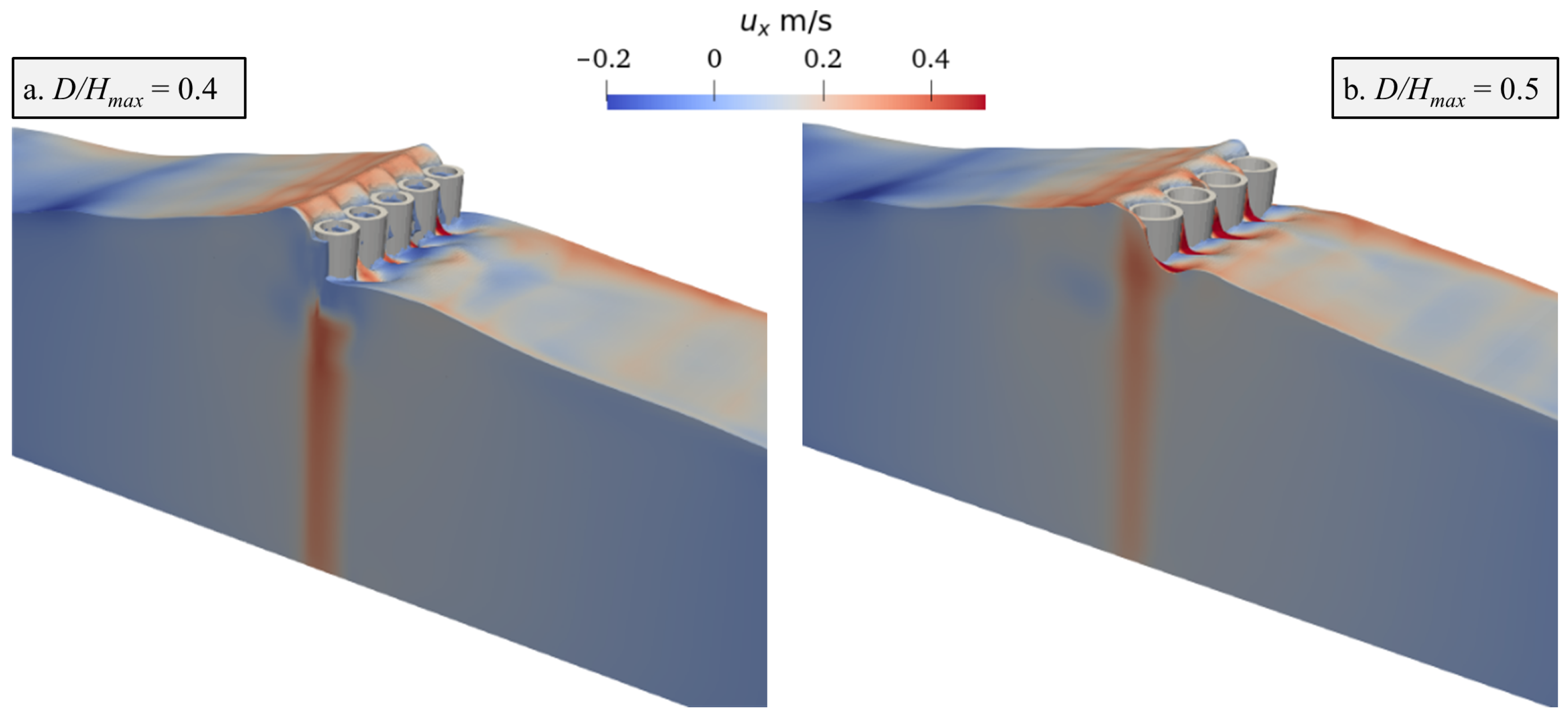
3.2.2. Effect of Relative Pile Head Diameter
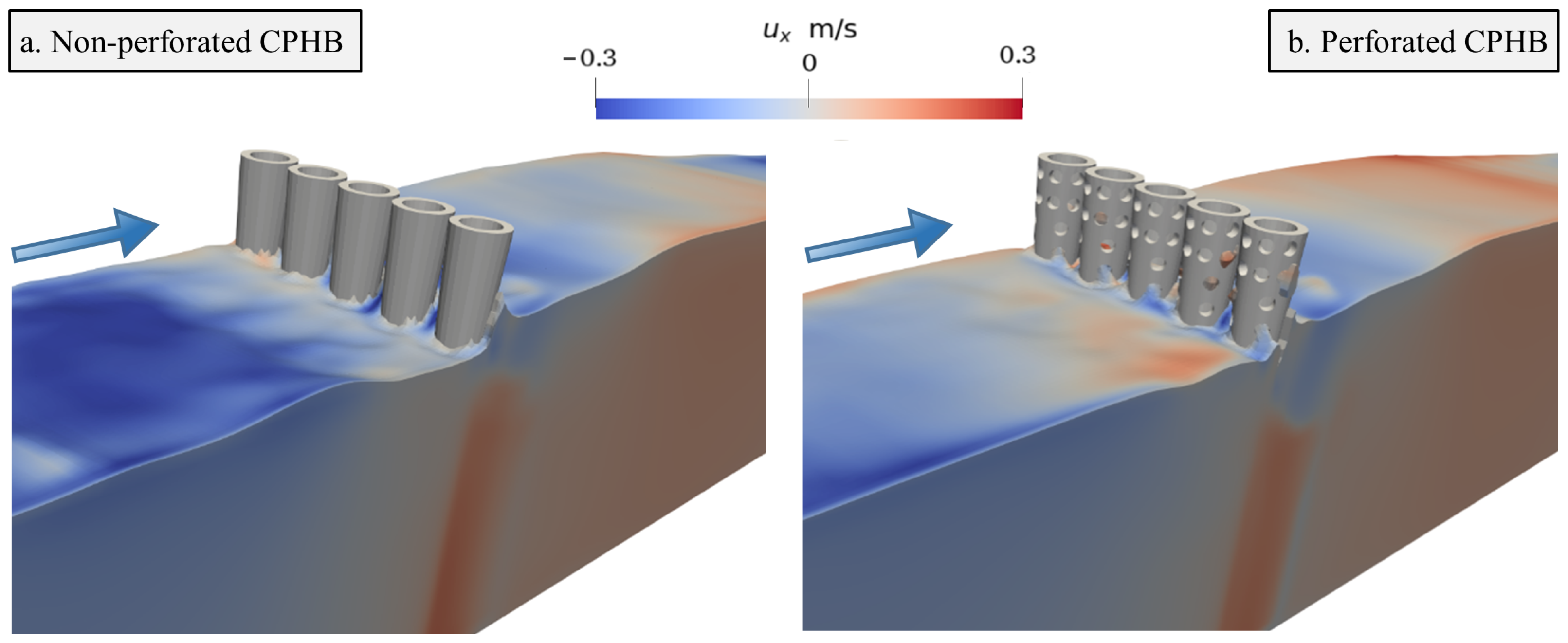
3.2.3. Effect of Perforations
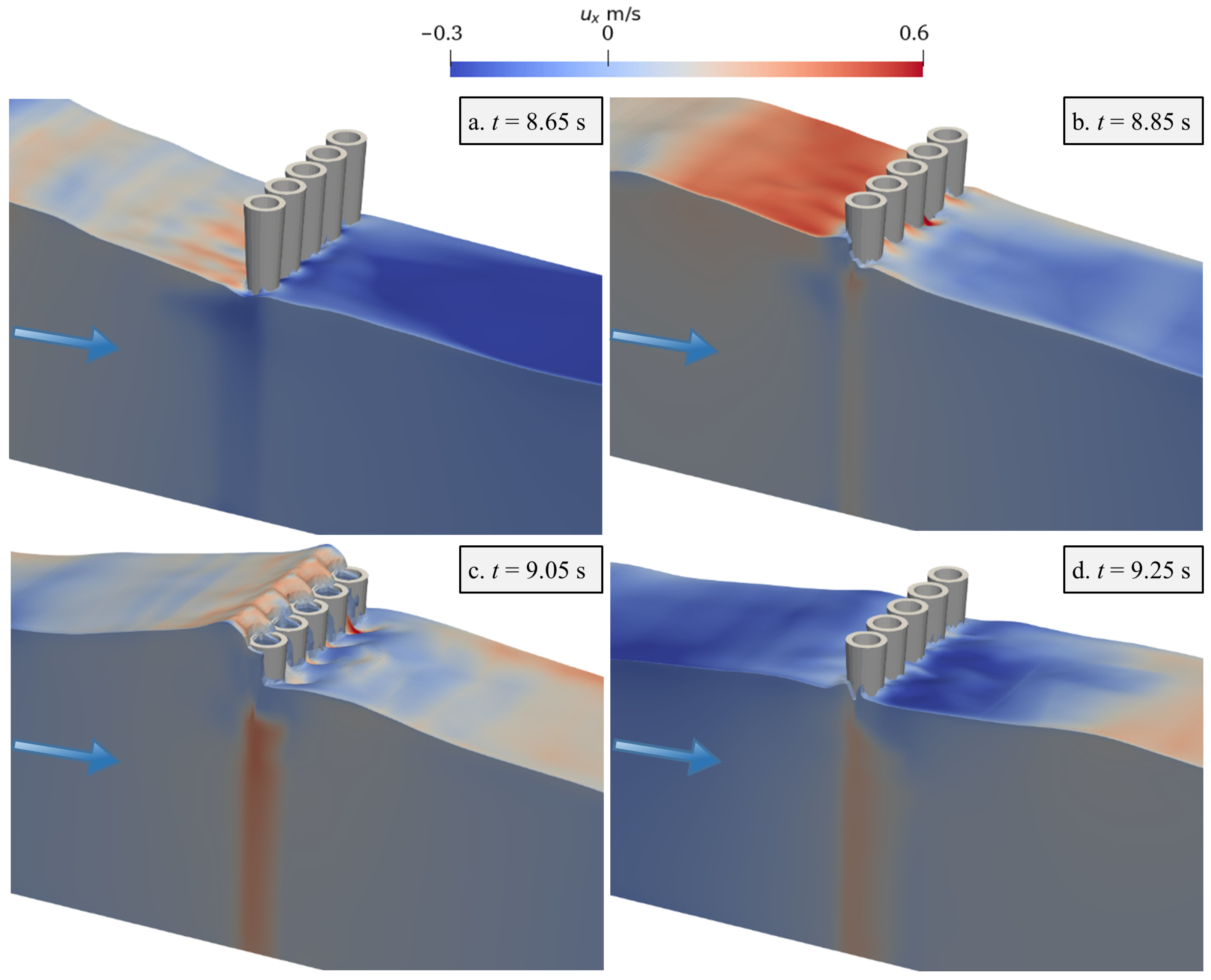
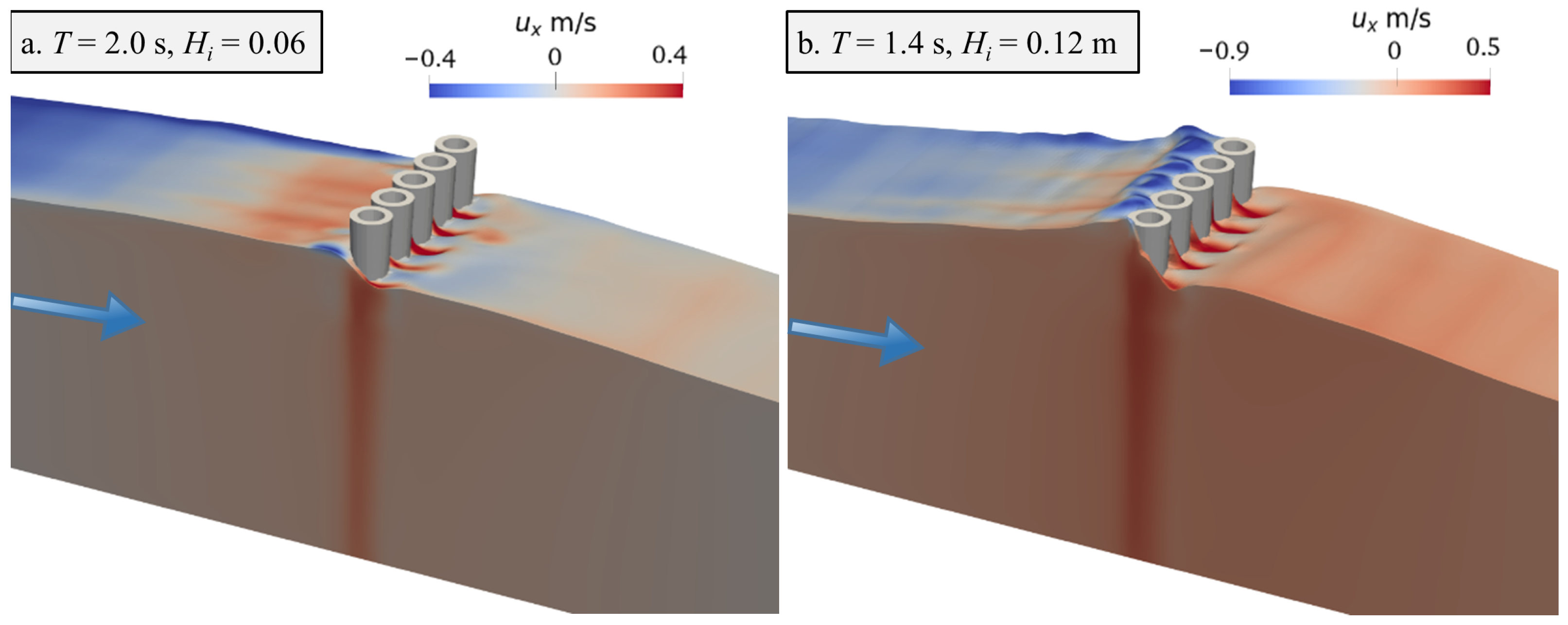
3.2.4. Effect of Wave Steepness
3.2.5. Performance Comparison with Other Pile Breakwater Structures
3.3. Comparison of CPHB Performance with Monochromatic and Irregular Waves
4. Conclusions
- (1)
- In general, Kt is found to be indirectly proportional to the wave steepness, whereas Kr and Kd exhibit the opposite pattern.
- (2)
- Validation of the numerical results with the experimental data shows that REEF3D produces reliable results with acceptable RMSE values.
- (3)
- The hydraulic performance of the CPHB structure is found to be more conservative with monochromatic waves than with irregular waves.
- (4)
- In the case of irregular waves, Kt ranges from 0.72 to 0.36 for the non-perforated CPHB with an optimum configuration of D/ = 0.4, = 1.5 and = 0.1. For the same configuration, Kt ranges between 0.83 and 0.64 with monochromatic waves.
- (5)
- Introducing perforations with the optimum configuration ( = 50%, = 0.25 and P = 19.2%) on the CPHs enhanced the transmission capability of the CPHB by about 5% to 16.5% with monochromatic waves and 5% to 10% with irregular waves.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhu, D.T.; Xie, Y.F. Hydrodynamic characteristics of offshore and pile breakwaters. Ocean Eng. 2015, 104, 257–265. [Google Scholar] [CrossRef]
- Gao, J.; He, Z.; Huang, X.; Liu, Q.; Zang, J.; Wang, G. Effects of free heave motion on wave resonance inside a narrow gap between two boxes under wave actions. Ocean Eng. 2021, 224, 108753. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Dong, G.; Chen, H.; Liu, Q.; Zang, J. Investigation on the effects of Bragg reflection on harbor oscillations. Coast. Eng. 2021, 170, 103977. [Google Scholar] [CrossRef]
- Herbich, J.B.; Douglas, B. Wave transmission through a double-row pile breakwater. In Proceedings of the 21st Coastal Engineering Conference, Costa del Sol-Malaga, Spain, 20–25 June 1988; pp. 2229–2241. [Google Scholar]
- Hutchinson, P.; Raudkivi, A. Case history of a spaced pile breakwater at Half Moon Bay Marina Auckland, New Zealand. In Proceedings of the 19th International Conference on Coastal Engineering, Houston, TX, USA, 3–7 September 1984; Volume 84, pp. 2530–2533. [Google Scholar]
- Koraim, A.; Salem, T. The hydrodynamic characteristics of a single suspended row of half pipes under regular waves. Ocean Eng. 1984 2012, 50, 1–9. [Google Scholar] [CrossRef]
- Jeya, T.J.; Sriram, V.; Sundar, V. Hydrodynamic characteristics of vertical and quadrant face pile supported breakwater under oblique waves. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2022, 236, 62–73. [Google Scholar] [CrossRef]
- Yin, M.; Zhao, X.; Luo, M.; Sun, H. Flow pattern and hydrodynamic parameters of pile breakwater under solitary wave using OpenFOAM. Ocean Eng. 2021, 235, 109381. [Google Scholar] [CrossRef]
- Elsharnouby, B.; Soliman, A.; Elnaggar, M.; Elshahat, M. Study of environment friendly porous suspended breakwater for the Egyptian Northwestern Coast. Ocean Eng. 2012, 48, 47–58. [Google Scholar] [CrossRef]
- Liu, H.; Ghidaoui, M.S.; Huang, Z.; Yuan, Z.; Wang, J. Numerical investigation of the interactions between solitary waves and pile breakwaters using BGK-based methods. Comput. Math. Appl. 2011, 61, 3668–3677. [Google Scholar] [CrossRef] [Green Version]
- Park, W.S.; Kim, B.H.; Suh, K.D.; Lee, K.S. Scattering of irregular waves by vertical cylinders. Coast. Eng. J. 2000, 42, 253–271. [Google Scholar] [CrossRef] [Green Version]
- Suh, K.D.; Shin, S.; Cox, D.T. Hydrodynamic characteristics of pile-supported vertical wall breakwaters. J. Waterw. Port Coast. Ocean Eng. 2006, 132, 83–96. [Google Scholar] [CrossRef]
- Zhu, D. Hydrodynamic characteristics of a single-row pile breakwater. Coast. Eng. 2011, 58, 446–451. [Google Scholar] [CrossRef]
- Zhu, D.T. Full wave solution for hydrodynamic behaviors of pile breakwater. China Ocean Eng. 2013, 27, 323–334. [Google Scholar] [CrossRef]
- Van Weele, B.J.; Herbich, J.B. Wave reflection and transmission for pile arrays. In Proceedings of the 13th Conference on Coastal Engineering, Vancouver, BC, Canada, 10–14 July 1972; pp. 1935–1953. [Google Scholar]
- Ahmed, H.; Schlenkhoff, A. Numerical investigation of wave interaction with double vertical slotted walls. World Acad. Sci. Eng. Technol. Int. J. Environ. Ecol. Geol. Min. Eng. 2014, 8, 536–543. [Google Scholar]
- Koraim, A.; Iskander, M.; Elsayed, W. Hydrodynamic performance of double rows of piles suspending horizontal c shaped bars. Coast. Eng. 2014, 84, 81–96. [Google Scholar] [CrossRef]
- Ramnarayan, S.K.; Sannasiraj, S.; Sundar, V. Hydrodynamic characteristics of curved and vertical front face pile-supported breakwaters in regular waves. Ocean Eng. 2020, 216, 108105. [Google Scholar] [CrossRef]
- Suvarna, P.S.; Sathyanarayana, A.H.; Umesh, P.; Shirlal, K.G. Laboratory investigation on hydraulic performance of enlarged pile head breakwater. Ocean Eng. 2020, 217, 107989. [Google Scholar] [CrossRef]
- Ramnarayan, S.K.; Sundar, V.; Sannasiraj, S. Hydrodynamic performance of concave front pile-supported breakwaters integrated with a louver wave screen. Ocean Eng. 2022, 254, 111394. [Google Scholar] [CrossRef]
- Huang, Z.; Li, Y.; Liu, Y. Hydraulic performance and wave loadings of perforated/slotted coastal structures: A review. Ocean Eng. 2011, 38, 1031–1053. [Google Scholar] [CrossRef]
- Kondo, H.; Toma, S. Reflection and transmission for a porous structure. In Proceedings of the 13th Conference on Coastal Engineering, Vancouver, BC, Canada, 10–14 July 1972; pp. 1847–1866. [Google Scholar]
- Rao, S.; Rao, N. Laboratory investigation on wave reflection characteristics of suspended perforated pipe breakwater. ISH J. Hydraul. Eng. 1999, 5, 22–32. [Google Scholar] [CrossRef]
- Rao, S.; Rao, N.B.S.; Sathyanarayana, V.S. Laboratory investigation on wave transmission through two rows of perforated hollow piles. Ocean Eng. 1999, 26, 675–699. [Google Scholar] [CrossRef]
- Rao, S.; Rao, N. Laboratory investigation on wave transmission through suspended perforated pipes. ISH J. Hydraul. Eng. 2001, 7, 23–32. [Google Scholar] [CrossRef]
- Rao, S.; Shirlal, K.G.; Rao, N. Wave transmission and reflection for two rows of perforated hollow piles. Indian J. Mar. Sci. 2002, 31, 283–289. [Google Scholar]
- Sathyanarayana, A.H.; Suvarna, P.S.; Umesh, P.; Shirlal, K.G. Performance characteristics of a conical pile head breakwater: An experimental study. Ocean Eng. 2021, 235, 109395. [Google Scholar] [CrossRef]
- Sathyanarayana, A.H.; Suvarna, P.S.; Umesh, P.; Shirlal, K.G. Investigation on innovative pile head breakwater for coastal protection. J. Eng. Marit. Environ. 2022, submitted.
- Teh, H.M.; Venugopal, V.; Bruce, T. Hydrodynamic characteristics of a free-surface semicircular breakwater exposed to irregular waves. J. Waterw. Port Coast. Ocean Eng. 2012, 138, 149–163. [Google Scholar] [CrossRef]
- Sarpkaya, T. Vortex Shedding and Resistance in Harmonic Flow about Smooth and Rough Circular Cylinders at High Reynolds Numbers; Technical Report; Naval Postgraduate School: Monterey, CA, USA, 1976. [Google Scholar]
- Hughes, S.A. Physical Models and Laboratory Techniques in Coastal Engineering; World Scientific: Singapore, 1993; Volume 7. [Google Scholar]
- Isaacson, M. Measurement of regular wave reflection. J. Waterw. Port Coast. Ocean Eng. 1991, 117, 553–569. [Google Scholar] [CrossRef]
- KREC Study Team. Study on Coastal Erosion (Dakshina Kannada District), Input to Environmental Master Plan Study; Karnataka Regional Engineering College: Surathkal, India, 1994; pp. 80–125. [Google Scholar]
- Bihs, H.; Kamath, A.; Chella, M.A.; Aggarwal, A.; Arntsen, Ø.A. A new level set numerical wave tank with improved density interpolation for complex wave hydrodynamics. Comput. Fluids 2016, 140, 191–208. [Google Scholar] [CrossRef]
- Aggarwal, A.; Bihs, H.; Shirinov, S.; Myrhaug, D. Estimation of breaking wave properties and their interaction with a jacket structure. J. Fluids Struct. 2019, 91, 102722. [Google Scholar] [CrossRef]
- Kamath, A.; Roy, T.; Seiffert, B.R.; Bihs, H. Experimental and numerical study of waves breaking over a submerged three-dimensional bar. J. Waterw. Port Coast. Ocean. Eng. 2022, 148, 04021052. [Google Scholar] [CrossRef]
- Bihs, H.; Chella, M.A.; Kamath, A.; Arntsen, Ø.A. Numerical investigation of focused waves and their interaction with a vertical cylinder using REEF3D. J. Offshore Mech. Arct. Eng. 2017, 139. [Google Scholar] [CrossRef]
- Kamath, A.; Bihs, H.; Alagan Chella, M.; Arntsen, Ø.A. Upstream-cylinder and downstream-cylinder influence on the hydrodynamics of a four-cylinder group. J. Waterw. Port, Coast. Ocean. Eng. 2016, 142, 04016002. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, N.; Bihs, H.; Myrhaug, D.; Kamath, A.; Arntsen, Ø.A. Numerical modeling of breaking wave induced seawall scour. Coast. Eng. 2019, 150, 108–120. [Google Scholar] [CrossRef]
- Sasikumar, A.; Kamath, A.; Bihs, H. Modeling porous coastal structures using a level set method based VRANS-solver on staggered grids. Coast. Eng. J. 2020, 62, 198–216. [Google Scholar] [CrossRef]
- Srineash, V.; Kamath, A.; Murali, K.; Bihs, H. Numerical simulation of wave Interaction with submerged porous structures and application for coastal resilience. J. Coast. Res. 2020, 36, 752–770. [Google Scholar] [CrossRef]
- Martin, T.; Kamath, A.; Bihs, H. A Lagrangian approach for the coupled simulation of fixed net structures in a Eulerian fluid model. J. Fluids Struct. 2020, 94, 102962. [Google Scholar] [CrossRef]
- Chorin, A.J. Numerical solution of the Navier-Stokes equations. Math. Comput. 1968, 22, 745–762. [Google Scholar] [CrossRef]
- Van der Vorst, H.A. Bi-CGSTAB: A fast and smoothly converging variant of Bi-CG for the solution of nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 1992, 13, 631–644. [Google Scholar] [CrossRef]
- Jiang, G.S.; Shu, C.W. Efficient implementation of weighted ENO schemes. J. Comput. Phys. 1996, 126, 202–228. [Google Scholar] [CrossRef] [Green Version]
- Shu, C.W.; Osher, S. Efficient implementation of essentially non-oscillatory shock-capturing schemes. J. Comput. Phys. 1988, 77, 439–471. [Google Scholar] [CrossRef] [Green Version]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Wilcox, D. Turbulence Modelling for CFD; DCW Industries: La Canada, CA, USA, 1994. [Google Scholar]
- Shu, C.W.; Osher, S. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar]
- Aggarwal, A.; Pákozdi, C.; Bihs, H.; Myrhaug, D.; Chella, M. Free Surface Reconstruction for Phase Accurate Irregular Wave Generation. J. Mar. Sci. Eng. 2018, 6, 105. [Google Scholar] [CrossRef] [Green Version]
- Mansard, E.; Funke, E. The measurement of incident and reflected spectra using a least squares method. In Proceedings of the 17th Coastal Engineering Conference, Sydney, Australia, 23–28 March 1980; Volume 1, pp. 154–172. [Google Scholar]
- Miquel, A.; Kamath, A.; Chella, M.A.; Archetti, R.; Bihs, H. Analysis of different methods for wave generation and absorption in a CFD-based numerical wave tank. J. Mar. Sci. Eng. 2018, 6, 73. [Google Scholar] [CrossRef] [Green Version]
- Dattatri, J.; Raman, H.; Shankar, N.J. Performance characteristics of submerged breakwaters. Coast. Eng. Proc. 1978, 16, 130. [Google Scholar] [CrossRef]
- Kumar, V.; Kumar, K.; Anand, N. Characteristics of Waves off Goa, West Coast of India. J. Coast. Res. 2000, 16, 782–789. [Google Scholar]
- Kumar, V.; Anand, N.; Ashok Kumar, K.; Mandal, S. Multipeakedness and groupiness of shallow water waves along Indian coast. J. Coast. Res. 2003, 19, 1052–1065. [Google Scholar]
- Narasimhan, S.; Deo, M. Spectral Analysis of Ocean Waves—A Study. Proc. Conf. Civ. Eng. Ocean. 1979, 1, 877–892. [Google Scholar]
- Wiegel, R. Design wave. In Lecture Notes of Short Term Course on Small Harbour Engineering; Indian Institute of Technology: Bombay, Mumbai, 1980; Volume 1, pp. 4.1–4.55. [Google Scholar]
- Huang, Z. Wave interaction with one or two rows of closely spaced rectangular cylinders. Ocean Eng. 2007, 34, 1584–1591. [Google Scholar] [CrossRef]
- Mani, J. Experimental and numerical investigations on zigzag porous screen breakwater. Nat. Hazards 2009, 49, 401–409. [Google Scholar] [CrossRef]
- Neelamani, S.; Vedagiri, M. Wave interaction with partially immersed twin vertical barriers. Ocean Eng. 2002, 29, 215–238. [Google Scholar] [CrossRef]
- Neelamani, S.; Rajendran, R. Wave interaction with T-type breakwaters. Ocean Eng. 2002, 29, 151–175. [Google Scholar] [CrossRef]
- Neelamani, S.; Rajendran, R. Wave interaction with ‘⊥’-type breakwaters. Ocean Eng. 2002, 29, 561–589. [Google Scholar] [CrossRef]








| Governing Parameters | Expression | Test Range |
|---|---|---|
| Maximum wave height (m) | Hmax | 0.16 |
| Top diameter of conical pile head (m) | D | 0.064, 0.080 |
| Diameter of supporting pile (m) | d | 0.04 |
| Height of conical pile head (m) | Y | 0.24 |
| Draft or submergence of pile head (m) | y | 0.12 |
| Size of perforation (m) | S | 0.016 |
| Water depth (m) | h | 0.40 |
| Wave period (s) | T | 1.4, 1.6, 1.8, 2.0 |
| Incident wave height (m) | Hi | 0.06, 0.08, 0.10, 0.12, 0.14, 0.16 |
| Angle of wave attack (degrees) | 90 | |
| Non-Dimensional Parameters | ||
| Relative pile head diameter | D/Hmax | 0.4, 0.5 |
| Relative pile head height | Y/Hmax | 1.5 |
| Clear spacing between pile heads | b/D | 0.1 |
| Clear spacing between the supporting piles | b0/d | 0.76 |
| Distribution of perforations (%) | Pa | 50 |
| Percentage of perforation (%) | P | 19.2 |
| Relative size of perforations | S/D | 0.25 |
| Incident wave steepness | Hi/gT2 | 0.00152 to 0.0062 |
| T (s) | H (m) | Grid Study (with CFL = 0.1) | CFL Study (with dx = 0.02 m) | ||
|---|---|---|---|---|---|
| dx (m) | RMSE | CFL No. | RMSE | ||
| 2.0 | 0.06 | 0.08 | 0.0033 | 0.40 | 0.0025 |
| 0.04 | 0.0021 | 0.20 | 0.0025 | ||
| 0.02 | 0.0020 | 0.10 | 0.0023 | ||
| 0.01 | 0.0018 | 0.05 | 0.0023 | ||
| 1.8 | 0.16 | 0.08 | 0.0085 | 0.40 | 0.0068 |
| 0.04 | 0.0053 | 0.20 | 0.0063 | ||
| 0.02 | 0.0053 | 0.10 | 0.0055 | ||
| 0.01 | 0.0036 | 0.05 | 0.0045 | ||
| Cases | T (s) | Hi (m) | L (m) | Hi/gT2 | Wave Theory |
|---|---|---|---|---|---|
| M1 | 1.4 | 0.12 | 2.39 | 0.00624 | Stokes 3rd order |
| M2 | 1.6 | 0.14 | 2.84 | 0.00557 | Stokes 3rd order |
| M3 | 1.8 | 0.16 | 3.27 | 0.00503 | Cnoidal |
| M4 | 1.8 | 0.10 | 3.27 | 0.00315 | Stokes 3rd order |
| M5 | 2.0 | 0.16 | 3.70 | 0.00408 | Cnoidal |
| M6 | 2.0 | 0.10 | 3.70 | 0.00255 | Stokes 3rd order |
| M7 | 2.0 | 0.08 | 3.70 | 0.00204 | Stokes 2nd order |
| M8 | 2.0 | 0.06 | 3.70 | 0.00153 | Stokes 2nd order |
| CPHB | D/Hmax | RMSE | ||
|---|---|---|---|---|
| Kt | Kr | Kd | ||
| Non-perforated | 0.4 | 0.0313 | 0.0142 | 0.0242 |
| 0.5 | 0.0355 | 0.0090 | 0.0476 | |
| Perforated | 0.4 | 0.048 | 0.017 | 0.0422 |
| Type of Breakwater | Structural Details | No. of | Kt | Kr | Kd | ||
|---|---|---|---|---|---|---|---|
| d (m) | b0/d | P (%) | Pile Units | ||||
| (per m) | |||||||
| Non-perforated hollow piles [24,26] | 0.034 | 0.15 | NA | 25.96 | 0.71 to 0.78 | 0.28 to 0.29 | 0.56 to 0.64 |
| Perforated hollow piles [24,26] | 0.034 | 0.15 | 25 | 25.96 | 0.66 to 0.73 | 0.22 to 0.30 | 0.64 to 0.69 |
| Non-perforated suspended pipes [23,25] | 0.034 | 0.15 | NA | 25.96 | 0.73 to 0.82 | 0.19 to 0.25 | 0.55 to 0.64 |
| Perforated suspended pipes [23,25] | 0.034 | 0.15 | 25 | 25.96 | 0.67 to 0.79 | 0.16 to 0.22 | 0.59 to 0.71 |
| Rectangular piles [58] | 0.006 | 1.77 | 21 | 56.41 | 0.73 to 0.88 | 0.09 to 0.28 | 0.49 to 0.64 |
| Zigzag porous screens [59] | 0.040 | 0.22 | 40 | 20.49 | 0.67 to 0.83 | 0.16 to 0.18 | 0.57 to 0.73 |
| Non-perforated CPHB | 0.040 | 0.76 | NA | 14.20 | 0.66 to 0.83 | 0.13 to 0.23 | 0.55 to 0.73 |
| Perforated CPHB | 0.040 | 0.76 | 19.2 | 14.20 | 0.54 to 0.80 | 0.17 to 0.28 | 0.59 to 0.80 |
| Cases | T (s) | Hi (m) | Hi/gT2 |
|---|---|---|---|
| M1 | 1.4 | 0.12 | 0.00624 |
| M2 | 1.8 | 0.10 | 0.00315 |
| M3 | 1.8 | 0.16 | 0.00503 |
| M4 | 2.0 | 0.06 | 0.00153 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sathyanarayana, A.H.; Suvarna, P.S.; Umesh, P.; Shirlal, K.G.; Bihs, H.; Kamath, A. Numerical Modelling of an Innovative Conical Pile Head Breakwater. Water 2022, 14, 4087. https://doi.org/10.3390/w14244087
Sathyanarayana AH, Suvarna PS, Umesh P, Shirlal KG, Bihs H, Kamath A. Numerical Modelling of an Innovative Conical Pile Head Breakwater. Water. 2022; 14(24):4087. https://doi.org/10.3390/w14244087
Chicago/Turabian StyleSathyanarayana, Arunakumar Hunasanahally, Praveen S. Suvarna, Pruthviraj Umesh, Kiran G. Shirlal, Hans Bihs, and Arun Kamath. 2022. "Numerical Modelling of an Innovative Conical Pile Head Breakwater" Water 14, no. 24: 4087. https://doi.org/10.3390/w14244087
APA StyleSathyanarayana, A. H., Suvarna, P. S., Umesh, P., Shirlal, K. G., Bihs, H., & Kamath, A. (2022). Numerical Modelling of an Innovative Conical Pile Head Breakwater. Water, 14(24), 4087. https://doi.org/10.3390/w14244087










