A Machine Learning Method for Engineering Risk Identification of Goaf
Abstract
:1. Introduction
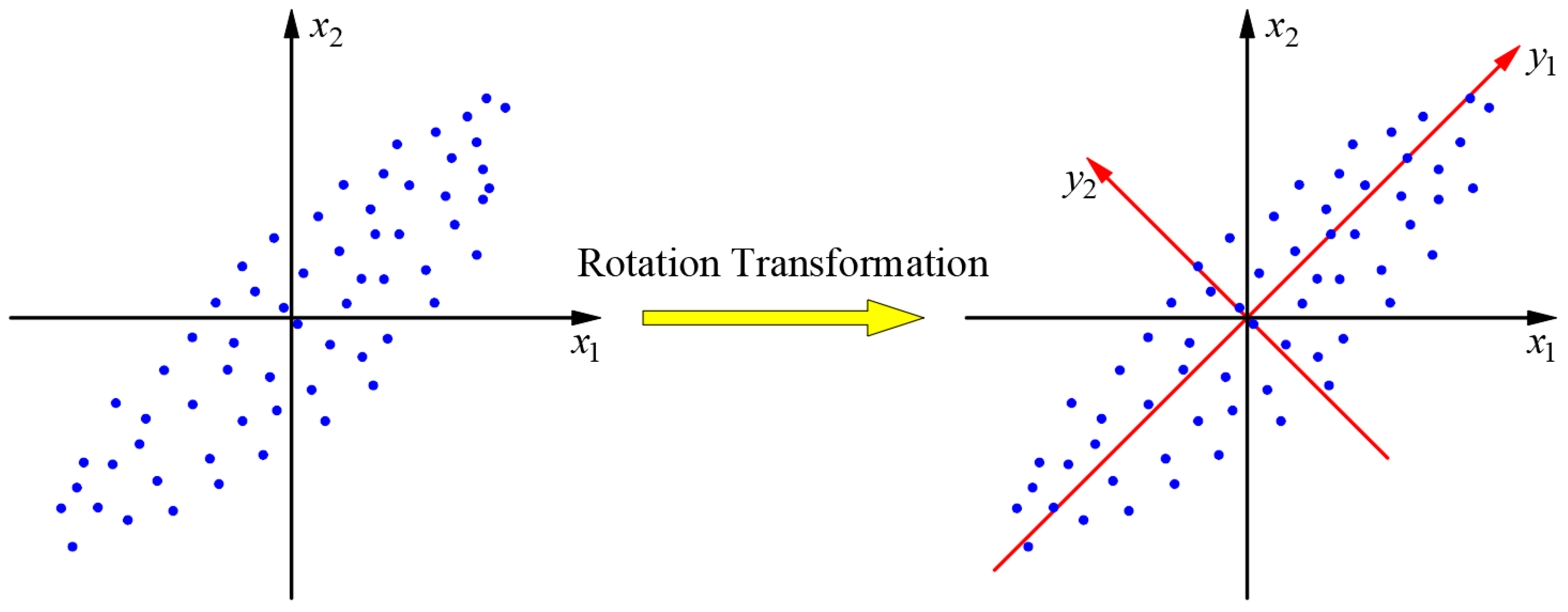
2. Principal Component Analysis
2.1. Basic Principles
2.2. Mathematical Model
- (1)
- (1) ;
- (2)
- cov(yi, yj) = 0(i ≠ j; i, j = 1, 2,…, m), namely, the components of principal analysis are independent and there is no overlapping information;
- (3)
- var(y1) ≥ var(y2) ≥ … ≥ var(ym), namely, the principal components are sorted according to the standard deviation, where: y1, y2,…, ym, obtained through the above process, can be determined as the principal components of 1, 2,…, m of the original variables.
2.3. Geometric Interpretation
3. Multi-Classification Support Vector Machine (SVM)
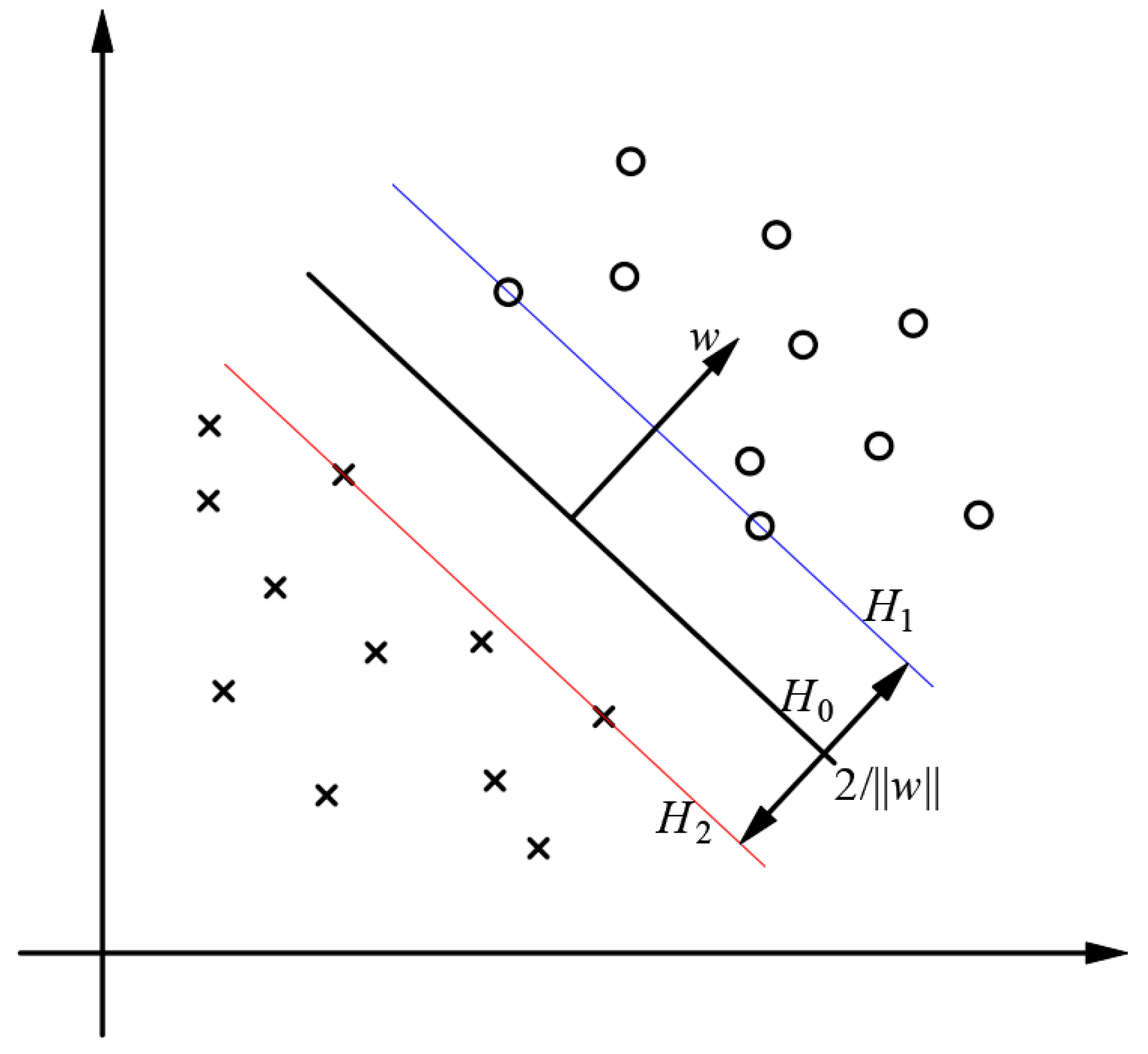
3.1. Basic Principles of SVM
3.2. Constructing a Multi-Classification Support Vector Machine
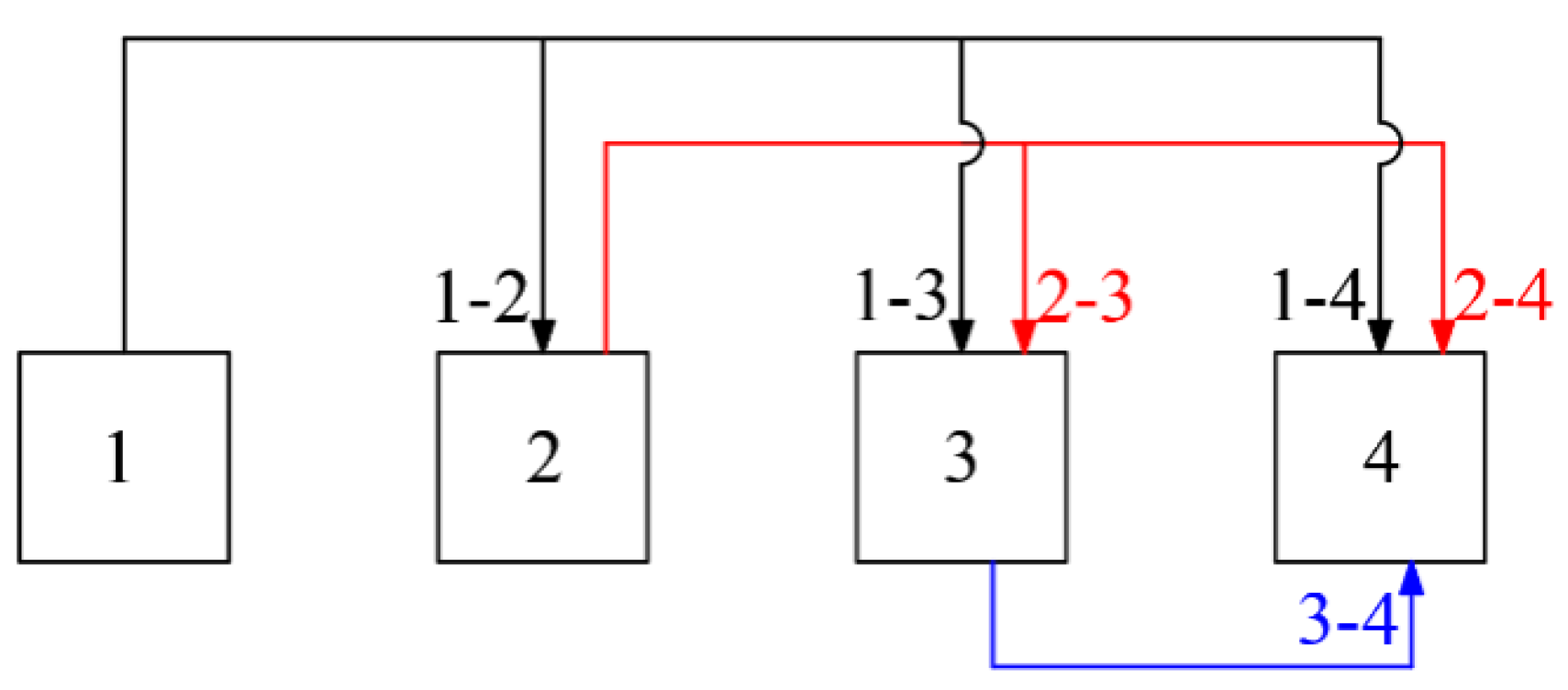
3.3. Cross-Validation
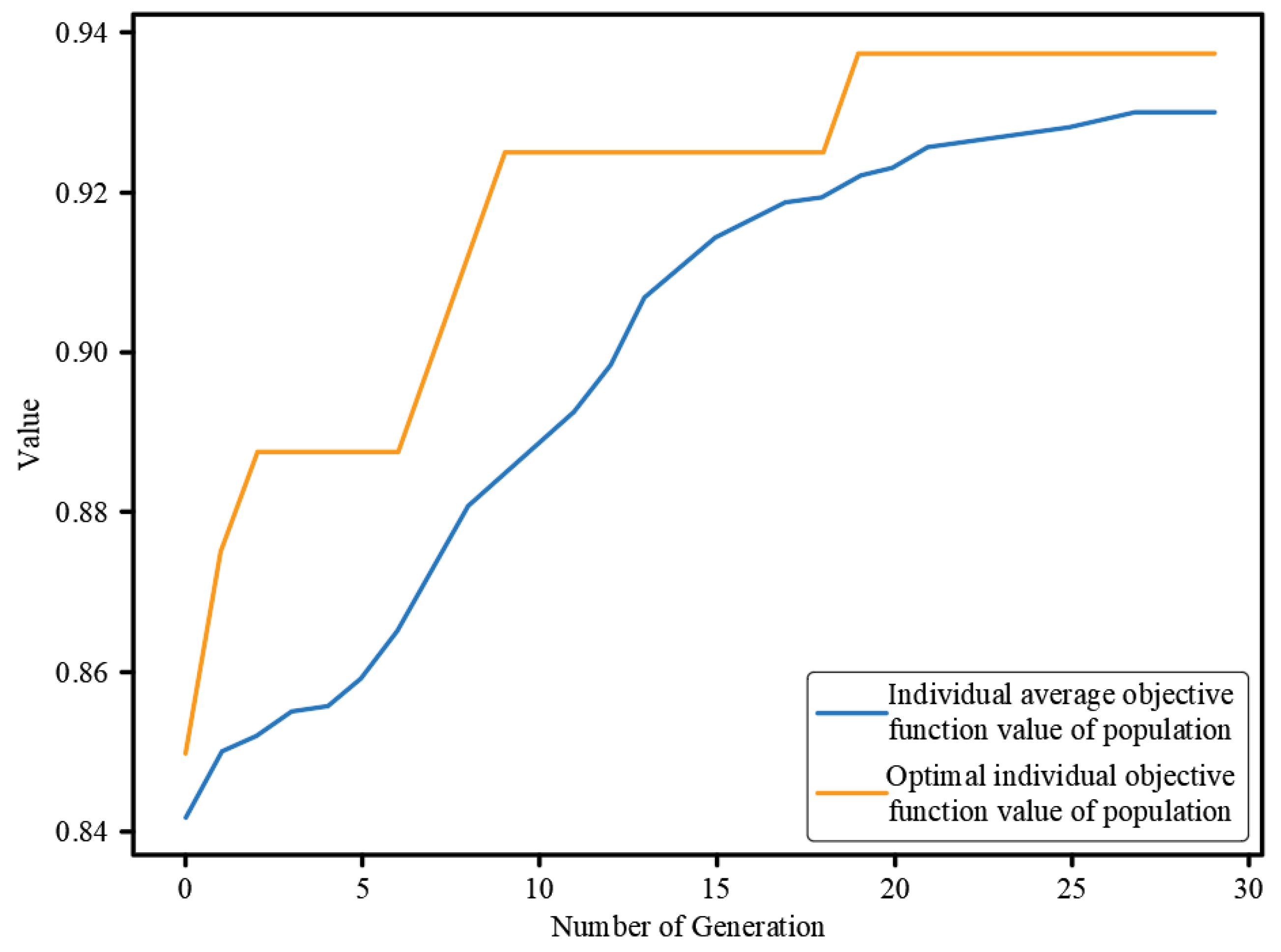
3.4. Parameter Optimization of the Differential Evolution Algorithm
4. Engineering Examples
Y2 = −0.751X1 + 0.519X2 + 0.766X3 − 0.158X4 + 0.638X5 − 0.019X6 + 0.583X7 − 0.001X8 − 0.123X9;
Y3 = −0.031X1 + 0.219X2 + 0.211X3 + 0.110X4 − 0.454X5 − 0.065X6 + 0.191X7 + 0.405X8 + 0.846X9;
Y4 = 0.296X1 − 0.363X2 + 0.451X3 − 0.173X4 + 0.367X5 + 0.103X6 − 0.246X7 − 0.288X8 + 0.413X9;
Y5 = 0.117X1 − 0.251X2 − 0.182X3 − 0.043X4 − 0.067X5 + 0.060X6 + 0.697X7 − 0.343X8 + 0.096X9.
5. Conclusions
- (1)
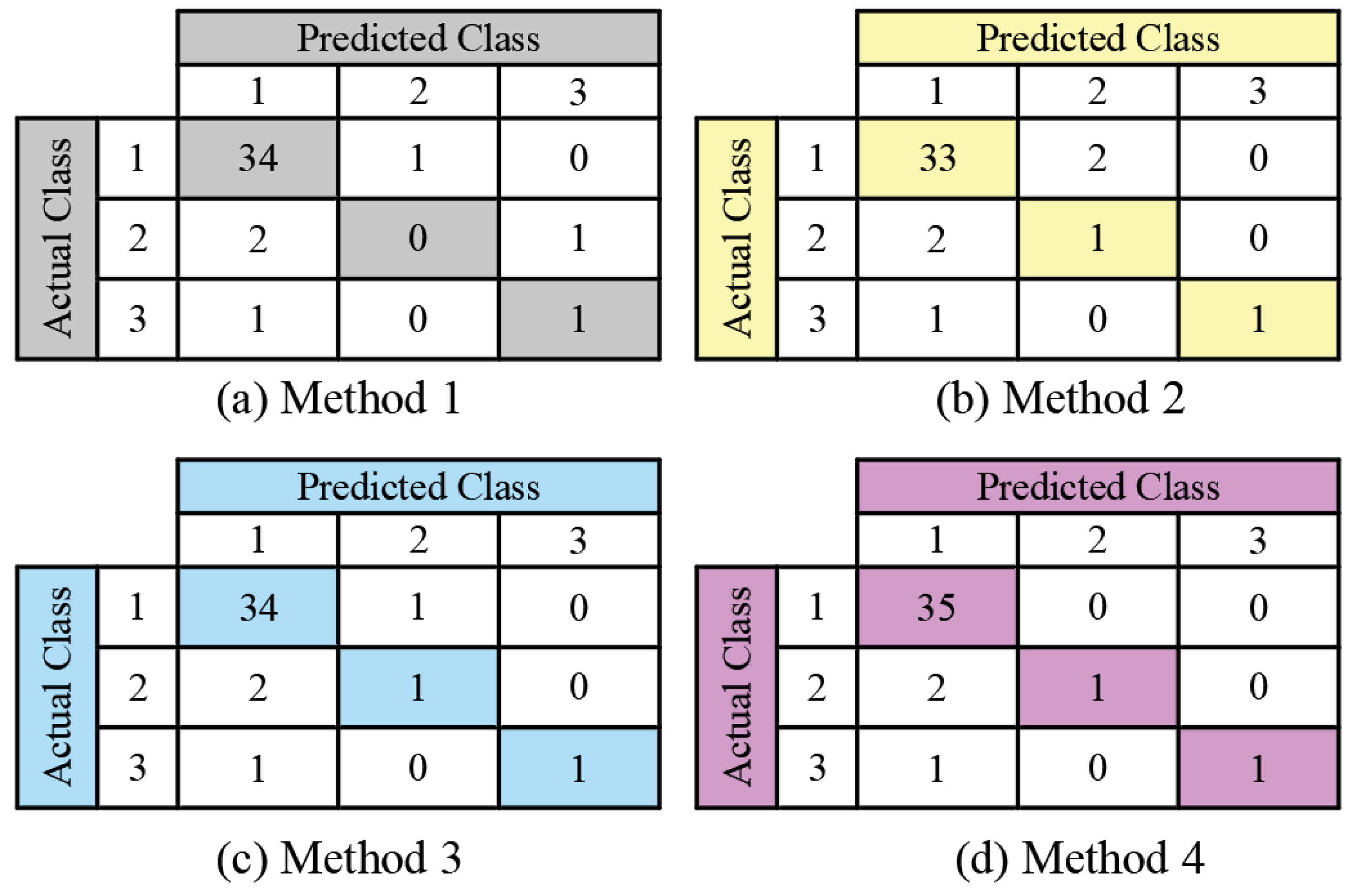
- The ‘one-against-one’ method is used to construct a multi-classification SVM. In order to prevent the overfitting of the model, the K-fold cross-validation method will be employed to select it. Above all, the research results reveal that the SVM has the desirable ability of generalization. Compared with the neural network, the apparent advantages lie in solving the problems of overfitting and it is easy to fall into the local minimum that can be detected in the SVM under the conditions of small samples.
- (2)
- PCA is used to preprocess the original data of multi-source impact indicators for goaf risk identification, which can realize the dimensionality reduction and data denoising, and can simultaneously improve the prediction accuracy and classification efficiency while retaining the most information.
- (3)
- Using the strategy of DE and a global optimization search mechanism, the optimal solution of the problems to be optimized will be automatically obtained, namely, the kernel function parameter of SVM, ‘γ’, and the penalty factor, ‘C’. Moreover, the engineering calculation example further verifies that the DE has the characteristics of clear logic, strong convergence, and good robustness.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yi, H.; Zhang, X.; Yang, H.; Li, M.; Gao, Q.; Jinke. Goaf collapse vibration analysis and disposal based on a experiment of heavy ball touchdown. Explos. Shock Waves 2019, 39, 91–103. [Google Scholar]
- Zhao, Y.; Tang, J.; Chen, Y.; Zhang, L.; Wang, W.; Wan, W.; Liao, J. Hydromechanical coupling tests for mechanical and permeability characteristics of fractured limestone in complete stress-strain process. Environ. Earth Sci. 2017, 76, 24. [Google Scholar] [CrossRef]
- Zhao, Y.; Luo, S.; Wang, Y.; Wang, W.; Zhang, L.; Wan, W. Numerical Analysis of Karst Water Inrush and a Criterion for Establishing the Width of Water-resistant Rock Pillars. Mine Water Environ. 2017, 36, 508–519. [Google Scholar] [CrossRef]
- Liao, Y.; Yu, G.; Liao, Y.; Jiang, L.; Liu, X. Environmental Conflict Risk Assessment Based on AHP-FCE: A Case of Jiuhua Waste Incineration Power Plant Project. Sustainability 2018, 10, 4095. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Jia, Q.; Wang, W.; Zhang, N.; Zhao, Y. Experimental Test on Nonuniform Deformation in the Tilted Strata of a Deep Coal Mine. Sustainability 2022, 13, 13280. [Google Scholar] [CrossRef]
- Du, K.; Li, X.; Liu, K.; Zhao, X.; Zhou, Z.; Dong, L. Comprehensive evaluation of underground goaf risk and engineering application. J. Cent. South Univ. 2011, 42, 2802–2811. [Google Scholar]
- Yuan, Z.; Zhai, J.; Li, S.; Jiang, Z.; Huang, F. A Unified Solution for Surrounding Rock of Roadway Considering Seepage, Dilatancy, Strain-Softening and Intermediate Principal Stress. Sustainability 2022, 14, 8099. [Google Scholar] [CrossRef]
- Liu, Y.; Hao, Y.; Lu, Y. Improved Design of Risk Assessment Model for PPP Project under the Development of Marine Architecture. J. Coast. Res. 2021, 9, 74–80. [Google Scholar] [CrossRef]
- Liu, S.; Nie, Y.; Hu, W.; Ashiru, M.; Li, Z.; Zou, J. The Influence of Mixing Degree between Coarse and Fine Particles on the Strength of Offshore and Coast Foundations. Sustainability 2022, 14, 9177. [Google Scholar] [CrossRef]
- Chen, W.; Wan, W.; Zhao, Y.; Peng, W. Experimental Study of the Crack Predominance of Rock-Like Material Containing Parallel Double Fissures under Uniaxial Compression. Sustainability 2020, 12, 5188. [Google Scholar] [CrossRef]
- Zhang, Y.; Chang, X.; Liang, J. Comparison of different algorithms for calculating the shading effects of topography on solar irradiance in a mountainous area. Environ. Earth Sci. 2017, 76, 295. [Google Scholar] [CrossRef]
- Feng, T.; Chen, H.; Wang, K.; Nie, Y.; Zhang, X.; Mo, H. Assessment of underground soil loss via the tapering grikes on limestone hillslopes. Agric. Ecosyst. Environ. 2020, 5, 297. [Google Scholar] [CrossRef]
- Chen, J.; Liu, L.; Zhou, Z.; Yong, X. Optimization of mining methods based on combination of principal component analysis and neural networks. J. Cent. South Univ. 2010, 41, 1967–1972. [Google Scholar]
- Wang, X.; Duan, Y.; Peng, X. Fuzzy Synthetic Assessment of the Danger Degree of Mined-out Area Disaster. Min. Res. Dev. 2005, 25, 83–85. [Google Scholar]
- Zhou, J.; Shi, X. Evaluation of the alternatives for mined out area disposal based on the identical degree of set pair analysis. Met. Mine 2009, 396, 10–13. [Google Scholar]
- Wang, X.; Ding, D.; Duan, Y. Applications of the grey relation analysis in the evaluation of the risk degree of the underground mined-out stopes. J. Saf. Sci. Technol. 2006, 2, 35–39. [Google Scholar]
- Gong, F.; Li, X.; Dong, L.; Liu, X. Underground goaf risk evaluation based on uncertainty measurement theory. Chin. J. Rock Mech. Eng. 2008, 27, 323–330. [Google Scholar]
- Hu, Y.; Li, X. Bayes discriminant analysis method to identify risky of complicated goaf in mines and its application. Trans. Nonferrous Met. Soc. China 2012, 22, 425–431. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, X.; Cheng, A.; Zhang, Q.; Zhao, J. Method optimization of underground goaf risk evaluation. J. Cent. South Univ. 2013, 44, 2881–2888. [Google Scholar]
- Wang, Z.; Guo, J.; Wang, L. Recognition of goaf risk based on support vector machines method. J. Chongqing Univ. 2015, 38, 85–90. [Google Scholar]
- Wang, H.; Li, X.; Dong, L.; Liu, K.; Tong, H. Classification of goaf stability based on support vector machine. J. Saf. Sci. Technol. 2014, 10, 154–159. [Google Scholar]
- Fang, X.; Ding, Z.; Shu, X. Hydrogen yield prediction model of hydrogen production from low rank coal based on support vector machine optimized by genetic algorithm. J. China Coal Soc. 2010, 35, 205–209. [Google Scholar]
- Hsu, C.-W.; Lin, C.-J. A comparison of methods for multi-class support vector machines. IEEE Trans. Neural Netw. 2002, 13, 415–425. [Google Scholar] [PubMed]
- Kebel, U. Pairwise Classification and Support Vector Machines. In Advances in Kernel Methods-Support Vector Learning; MIT Press: Cambridge, MA, USA, 1999; pp. 255–258. [Google Scholar]
- Platt, J.C.; Cristianini, N.; Shawe-Taylor, J. Large Margin DAGs for Multi-class Classification. Adv. Neural Inf. Process. Syst. 2000, 12, 547–553. [Google Scholar]
- Bennett, K.P.; Blue, J.A. A support vector machine approach to decision tree. Rensselaer Polytech. Inst. 1997, 3, 2396–2401. [Google Scholar]
- Zhou, Z. Machine Learning; Tsinghua University Press: Beijing, China, 2017; pp. 121–139. [Google Scholar]
- Liang, N.; Tuo, Y.; Deng, Y.; Jia, Y. Classification model of ice transport and accumulation in front of channel flat sluice based on PCA-SVM. Chin. J. Theor. Appl. Mech. 2021, 53, 703–713. [Google Scholar]
- Chen, X.; Yang, G.; Huang, M. Real-coded Quantum Differential Evolution Algorithm. J. Chin. Comput. Syst. 2013, 34, 1141–1146. [Google Scholar]
- Xu, Z.; Zhou, D.; Luo, Y. Fuzzy Neural Network Based on Principal Component. Comput. Eng. Appl. 2006, 42, 34–36. [Google Scholar]



| Sample Serial Number | Exploitation Depth X1/m | Mining Methods X2 | Goaf Mining Height X3/m | Maximum Exposure Area X4/m2 | Maximum Exposure Height X5/m | Maximum Exposed Span X6/m | Pillar Situation X7 | Measured Volume X8 /m3 | Governance Rate X9 | Risk Rank |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 130 | 1 | 35 | 3589 | 35 | 39 | 0 | 57,481.1 | 0.0 | 2 |
| 2 | 130 | 1 | 20 | 1208 | 0.99 | 24 | 1 | 12,141.3 | 94.4 | 1 |
| 3 | 130 | 1 | 35 | 1735 | 5.97 | 28 | 0 | 31,595.7 | 96.3 | 1 |
| 4 | 130 | 1 | 35 | 1644 | 35 | 32 | 2 | 17,144.4 | 100.0 | 1 |
| 5 | 130 | 1 | 25 | 2489.5 | 25 | 39 | 2 | 19,377.7 | 100.0 | 1 |
| …… | ||||||||||
| 119 | 220 | 1 | 15 | 349 | 15 | 17 | 0 | 3200 | 0.0 | 1 |
| 120 | 220 | 1 | 15 | 259 | 15 | 10 | 0 | 2867 | 0.0 | 1 |
| Index | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 |
|---|---|---|---|---|---|---|---|---|---|
| X1 | 1.000 | ||||||||
| X2 | −0.366 | 1.000 | |||||||
| X3 | −0.389 | 0.273 | 1.000 | ||||||
| X4 | 0.001 | −0.432 | −0.084 | 1.000 | |||||
| X5 | −0.325 | −0.045 | 0.512 | 0.089 | 1.000 | ||||
| X6 | −0.050 | −0.465 | 0.097 | 0.695 | 0.227 | 1.000 | |||
| X7 | −0.342 | 0.163 | 0.296 | 0.086 | 0.236 | 0.103 | 1.000 | ||
| X8 | −0.046 | −0.150 | 0.098 | 0.594 | 0.019 | 0.370 | 0.110 | 1.000 | |
| X9 | 0.104 | 0.010 | 0.153 | −0.039 | −0.309 | −0.093 | −0.005 | 0.061 | 1.000 |
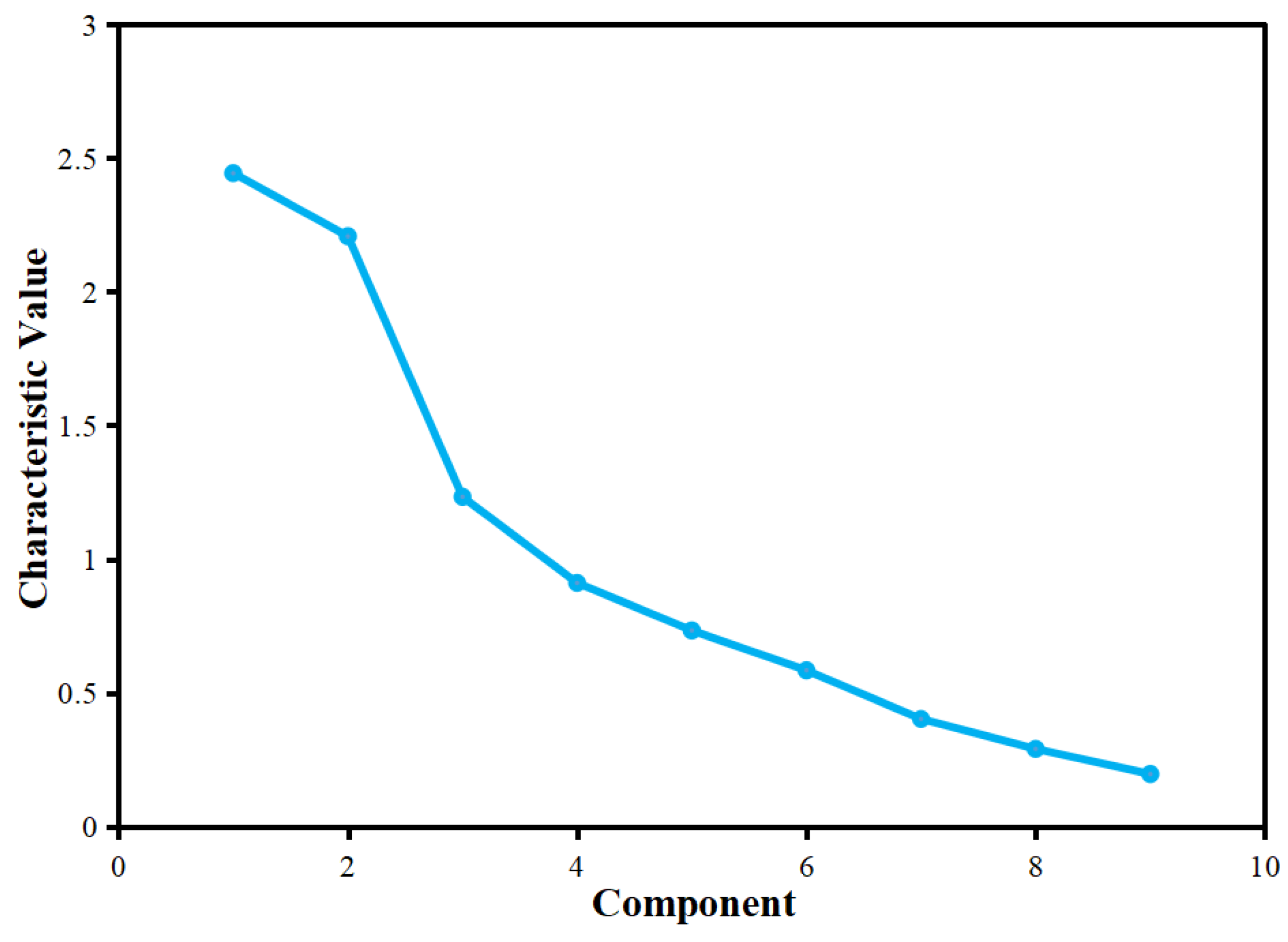
| Component | Initial Characteristic Value | Sum of Squares of Extracted Loads | ||||
|---|---|---|---|---|---|---|
| Total | Percentage Variance | Accumulation/% | Total | Percentage Variance | Accumulation/% | |
| 1 | 2.444 | 27.150 | 27.150 | 2.444 | 27.150 | 27.150 |
| 2 | 2.208 | 24.528 | 51.678 | 2.208 | 24.528 | 51.678 |
| 3 | 1.233 | 13.698 | 65.377 | 1.233 | 13.698 | 65.377 |
| 4 | 0.911 | 10.127 | 75.504 | 0.911 | 10.127 | 75.504 |
| 5 | 0.733 | 8.139 | 83.643 | 0.733 | 8.139 | 83.643 |
| 6 | 0.584 | 6.493 | 90.136 | |||
| 7 | 0.402 | 4.470 | 94.607 | |||
| 8 | 0.290 | 3.217 | 97.824 | |||
| 9 | 0.196 | 2.176 | 100.000 | |||
| Index | Principal Component | ||||
|---|---|---|---|---|---|
| Y1 | Y2 | Y3 | Y4 | Y5 | |
| X1 | −0.059 | −0.751 | −0.031 | 0.296 | 0.117 |
| X2 | −0.565 | 0.519 | 0.219 | −0.363 | −0.251 |
| X3 | 0.100 | 0.766 | 0.211 | 0.451 | −0.182 |
| X4 | 0.884 | −0.158 | 0.110 | −0.173 | −0.043 |
| X5 | 0.321 | 0.638 | −0.454 | 0.367 | −0.067 |
| X6 | 0.858 | −0.019 | −0.065 | 0.103 | 0.060 |
| X7 | 0.188 | 0.583 | 0.191 | −0.246 | 0.697 |
| X8 | 0.664 | −0.001 | 0.405 | −0.288 | −0.343 |
| X9 | −0.118 | −0.123 | 0.846 | 0.413 | 0.096 |
| Sample Serial Number | Y1 | Y2 | Y3 | Y4 | Y5 | Risk Rank |
|---|---|---|---|---|---|---|
| 1 | 0.9692 | 1.8113 | 0.1422 | 0.3396 | −0.6124 | 2 |
| 2 | −0.1286 | 1.0236 | 1.2293 | 0.1273 | 0.0872 | 1 |
| 3 | 0.0849 | 1.2046 | 1.2507 | 0.5023 | −0.4067 | 1 |
| 4 | 0.5255 | 2.3128 | 1.0500 | 0.6140 | 0.2771 | 1 |
| 5 | 0.6189 | 1.8470 | 1.1160 | 0.3447 | 0.3573 | 1 |
| …… | ||||||
| 119 | −0.2744 | 0.6973 | 0.0772 | 0.0678 | −0.2842 | 1 |
| 120 | −0.4014 | 0.7017 | 0.0838 | 0.0565 | −0.2910 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, H.; Cao, Z.; Xiong, L.; Li, H.; Wang, Y. A Machine Learning Method for Engineering Risk Identification of Goaf. Water 2022, 14, 4075. https://doi.org/10.3390/w14244075
Yuan H, Cao Z, Xiong L, Li H, Wang Y. A Machine Learning Method for Engineering Risk Identification of Goaf. Water. 2022; 14(24):4075. https://doi.org/10.3390/w14244075
Chicago/Turabian StyleYuan, Haiping, Zhanhua Cao, Lijun Xiong, Hengzhe Li, and Yixian Wang. 2022. "A Machine Learning Method for Engineering Risk Identification of Goaf" Water 14, no. 24: 4075. https://doi.org/10.3390/w14244075
APA StyleYuan, H., Cao, Z., Xiong, L., Li, H., & Wang, Y. (2022). A Machine Learning Method for Engineering Risk Identification of Goaf. Water, 14(24), 4075. https://doi.org/10.3390/w14244075







