Abstract
Predicting the condition of sewer pipes plays a vital role in the formulation of predictive maintenance strategies to ensure the efficient renewal of sewer pipes. This study explores the potential application of ten machine learning (ML) algorithms to predict sewer pipe conditions in Ålesund, Norway. Ten physical factors (age, diameter, depth, slope, length, pipe type, material, network type, pipe form, and connection type) and ten environmental factors (rainfall, geology, landslide area, population, land use, building area, groundwater, traffic volume, distance to road, and soil type) were used to develop the ML models. The filter, wrapper, and embedded methods were used to assess the significance of the input factors. A dataset consisting of 1159 inspected sewer pipes was used to construct the sewer condition models, and 290 remaining inspections were used to verify the models. The results showed that sewer material and age are the most significant factors, otherwise the network type is the least contributor affecting the sewer conditions in the study area. Among the considered ML models, the Extra Trees Regression (R2 = 0.90, MAE = 11.37, and RMSE = 40.75) outperformed the other ML models and it is recommended for predicting sewer conditions for the study area. The results of this study can support utilities and relevant agencies in planning predictive maintenance strategies for their sewer networks.
1. Introduction
A sewer network is one of the most important components of the urban water infrastructure [1]. This network plays a vital role in the collection and transport of wastewater and stormwater from the urban landscape to reduce the incidence of flooding, mitigate environmental pollution and protect public health [2,3]. However, sewer networks in operation are subjected to different intrinsic and extrinsic factors that contribute to their deterioration and failures [4], thereby preventing the network from realizing its intended objectives. Failures in the sewer system often result in debilitating impacts on infrastructure, the environment, and public health with a significant economic burden on society [5]. Therefore, investments in maintenance programs that reduce the incidence of sewer pipe failure are a priority in many countries [6,7].
Maintenance management approaches can be generally categorized into Reactive Maintenance (RaM), Preventive Maintenance (PvM), and Predictive Maintenance (PdM) [8]. The RaM, or run-to-failure, is the simplest approach that is only implemented when break(s) in sewer pipes occur. This reactive maintenance approach is also the least effective one. The PvM, or proactive maintenance, is implemented based on predetermined intervals (usually time or event-based triggers). This approach is more effective than the RaM method because many failures can be prevented. However, several unnecessary corrective actions are usually implemented [8]. The PdM approach mainly focuses on assessing sewer pipes based on condition assessment. In this way historical data are combined with analytic and prediction tools to predict the condition of sewer pipes, and maintenance strategies are scheduled.
A predictive maintenance strategy cannot be implemented effectively without a deep understanding of the system, and an efficient water management strategy requires a proper condition assessment framework [9]. Many condition assessment models have been developed in literature and they can be divided into three main groups: physical, statistical, and machine learning models [10]. The physical models assess the deterioration process based on the influence of the physical properties and the mechanical processes in the sewer pipes [11,12]. However, these types of models are suitable for the construction period and initial operation, and data for the simulation of the deterioration mechanism are not always available [13]. The statistical models (e.g., linear regression, cohort survival model, or Markov chains) can produce good accuracy but they are limited in revealing the physical relationship between limited physical factors and the target [14]. In recent times, machine learning (ML) algorithms have been widely used to model sewer pipe deterioration because they are capable of handling the complex non-linear interlinked processes involved in the deterioration of sewer pipes [15]. However, a large number of input factors and observations are needed to improve the accuracy of these models [6].
The output of a mathematical model in general, and an ML model in particular, significantly depends on the quality of input data. Factors considered for building condition assessment models can be divided into three groups: physical, operational, and environmental factors [16]. In general, physical data on most sewer networks are readily available. The same can be said about data on environmental factors. However, when it comes to operational data, it is most often scarce [9]. Therefore, considering the quality of input data plays a vital role in improving the ML models’ predictive performance. The importance of the input data should be assessed to prioritize inputs while collecting and preparing data before building condition assessment models. Therefore, defining significant factors for building condition assessment models is a key task to improve the efficiency of the predictive models. This task is accomplished via feature selection methods that can be grouped into filter, wrapper, and embedded methods [17]. The filter methods assess the importance of input variables, mainly based on their statistical properties and relationship with the output variable. The wrapper methods select a sensitive subset of features by adding and removing subsets based on the performance of the model. In the embedded methods, the effectiveness of input variables is assessed by tuning predictive models [17]. The important degree of different feature selection methods may be incompatible due to randomness in selecting and combining subsets [18]. In this study, all three types of feature selection are investigated, and the insignificant features are eliminated based on a consensus of the three methods used.
Closed-circuit television (CCTV) is the most widely used method for assessing the condition of the sewer network because it can directly provide sewer pipes statements with very high accuracy [19]. To inspect the sewer pipes’ status, a camera is put inside pipelines or drains without needing to conduct more invasive methods like digging, removing walls, or flooring to gain access to plumbing. Based on the recovered CCTV videos, the trained inspectors can monitor the status of sewers in real-time (while controlling the camera inside pipes) or offline (after finishing the inspection). Depending on the status (e.g., roots, sediments, cracks, deformations), the local and global damaged score can be assigned for the particular sewer pipe and rehabilitation schedules and be prioritized [20]. However, this method is time-consuming and expensive because workers need to inspect sewer pipes individually. As a result, only a small fraction of all sewer pipes, depending on their role and importance, are inspected during a specific period [21]. This data can be used to construct sewer condition models using ML algorithms, and derived ML models can be used to predict the sewer’s status for the entire network.
Although ML models used for regression problems have been successfully applied in many fields [22,23], their application in sewer status prediction is still limited. Moreover, no ML model is the best in all cases for modeling sewer deterioration and a comprehensive comparison of prediction performance between these models needs to be investigated. In the literature the influence of factors on sewer condition is still controversial, and the determination of the significance of these factors is valuable for local water utilities to prioritize their maintenance and rehabilitation activities. This work is an attempt to partly fill these gaps by developing ML models for sewer condition status prediction and assessing the importance of factors affecting sewer condition. In this study, ten state-of-the-art ML algorithms are explored to predict the damage score of the sewer network in Ålesund city, Norway. Ten physical factors (i.e., age, diameter, depth, slope, length, pipe type, material, network type, pipe form, and connection type) and ten environmental factors (i.e., rainfall, geology, landslide area, population, land use, building area, groundwater level, traffic volume, distance to road, and soil type) were used for training ML models. The best model is selected to predict the sewer’s damage score and it can help water engineers/workers predict sewer status on the large scale in a short time. Consequently, the model effectively supports water network management and maintenance. The final condition assessment model can help local water utilities/managers to have an overview of the status of the sewer network and support maintenance strategies in the future.
The rest of the paper is organized as follows: Section 2 describes the study area and data used. The overview of the feature selection techniques, the basic theory of used algorithms, the criteria for evaluating the developed models, and the framework for modeling the condition of sewer pipes are also discussed in this section. Section 3 presents and discusses the results. Finally, Section 4 presents the conclusions of the work.
2. Materials and Methods
2.1. Sewer Network
The sewer network of Ålesund, which is a coastal city in the eastern part of Norway, was used as a case study (Figure 1). The city is located between longitudes of 62°25′07″ E and 62°30′37″ E and between latitudes of 6°05′08″ N and 6°40′56″ N, with an area of 607.3 km2 and a population of 66,600 in 2021 [24]. With the characteristics of an ocean climate, the average annual rainfall in Ålesund city is 2100 mm with an average temperature of 8.1 °C [25].

Figure 1.
Location of the study area and sewer network ((a) Location of Ålesund in Norway, (b) entire sewer network in Ålesund city, and (c) sewer network in a selected area of Ålesund).
The sewer network is located in the central area of the city where the elevation fluctuates from 0 to 100 m. The western and eastern parts of the city are hilly and mountainous areas with altitudes of 300 m and 500 m, respectively. As a coastal city, Ålesund has been affected by consequences of the climate change such as extreme weather events and sea level rise [26,27]. Figure 1a shows an overview of the study area in Norway, while Figure 1b shows the entire sewer network in Ålesund city, and Figure 1c captures the sewer network in a specific area.
2.2. Proposed Framework for Sewer Condition Assessment
The framework for the sewer condition assessment is shown in Figure 2. The main steps for constructing the models include: (1) collecting and processing physical and environmental data; (2) digitalizing data using Geographic Information System (GIS) tools; (3) splitting the data into training and testing datasets; (4) determining feature importance and removing redundant features; (5) constructing the ML models; and (6) validating and selecting ML model for sewer condition assessment.

Figure 2.
The flowchart for sewer condition assessment modeling.
2.3. Data Used
2.3.1. Physical Factors
In this study, ten physical factors comprising age, diameter, depth, slope, length, pipe type, material, network type, pipe form, and connection type of sewer network were used. Seven of these factors including diameter, length, pipe type, material, network type, pipe form, and connection type were obtained from the database of Ålesund Municipality.
The remaining factors (i.e., age, depth, and slope) were obtained by doing additional computations. Specifically, the age of sewer pipes was calculated as the difference between the installation and the inspection years [28]. The depth of pipes was computed as the distance from the ground surface to the centroid of the pipe. The elevation of the ground surface was obtained from a Digital Elevation Model (DEM) with pixels of received from the Norwegian Mapping Authority (NMA) (https://www.kartverket.no/ (accessed on 20 March 2020)). The slope of sewer pipes was computed from the elevation of the start point and the endpoint of each pipe. All the above computations were implemented using the open-source QGIS software.
The processed data in the entire city consisted of 31,293 pipes with a total length of 703.0 km (Figure 1). In this dataset, the length and the number of wastewater, stormwater, and combined pipes were 339.0 km, 276.6 km, 87.4 km and 15,409, 12,722, 3163, respectively. After comparing the pipe index in this dataset with the corresponding pipes index in the inspected dataset, a total of 1449 sewer pipes were used to train and validate the condition assessment models. The detail of the physical factors is summarized in Table 1.

Table 1.
Summary of physical factors in this study.
2.3.2. Environmental Factors
The environmental factors used in this study are presented in Table 2. The selection of these environmental factors was based on the study of Hawari, Alkadour, Elmasry and Zayed [10].

Table 2.
Environmental factors in this analysis.
The rainfall map was interpolated from the annual average rainfall provided by nine weather stations (Table A1) inside and outside of the study area using the Inverse Distance Weighting (IDW) method [29]. Data on annual average rainfall at the weather stations were obtained from the Norwegian Climate Service Center (NCSC) (https://klimaservicesenter.no/ (accessed on 14 February 2020)).
The land use map was obtained from the Sentinel-2 images Level 1C downloaded from the website of Copernicus Open Access Hub (https://scihub.copernicus.eu/ (accessed on 17 January 2020)). A Google background satellite image was superimposed on the Sentinel-2 image to get the land use classifications (e.g., forest areas, roads, residential areas, etc.). The samples of different land uses were taken and assigned specific values, and different bands of the Sentinel-2 image overlapped. Finally, object-based classification was applied to cluster areas in the image into different objects based on given land uses [30].
The groundwater map for the study area was interpolated from 31 drills received from the Norwegian Geological Survey (NGS) (https://www.ngu.no/ (accessed on 24 April 2020)) using the IDW method. The map of traffic volume was received from the Norwegian Public Roads Administration (NPRA) (https://www.vegvesen.no/en/ (accessed on 13 February 2020)). Finally, the environmental factors maps were resampled to a spatial resolution of and transformed into a grid database using the QGIS before developing ML models. Maps of the environmental factors are shown in Figure A1.
Categorical factors such as pipe type, material, network type, pipe form, connection type, land use, road class, geology, building area, landslide area, and soil type were coded by integer values before constructing ML algorithms and feature selection. Furthermore, concrete, other, polypropylene, and polyvinyl chloride (PVC) pipes were coded by values 0, 1, 2, 3, and 4, respectively, for analysis in this study.
2.3.3. Sewer Damage Score
The damaged scores are obtained from CCTV datasets, and for this study damage scores based on the CCTV dataset of 1449 pipes (55.8 km) provided by the Ålesund Municipality were used for the condition assessment model. All damage score data were processed and integrated into a GIS database.
2.4. Description of Feature Selection Methods
2.4.1. Pearson Correlation Method
Pearson correlation is a filter feature selection method that defines the linear relationship between independent variables and the output target (e.g., a higher correlation value reflects a stronger relationship between input and output) [31]. Pearson’s correlation coefficient (PR) falls between −1 and +1 to indicate the extent to which two variables are linearly related. A value closer to 0 implies a weaker correlation, and a value closer to +1 (or −1) implies a stronger positive (or negative) correlation. In other words, the variables that have PR closer to +1 (or −1) are more important than the variables closer to 0 [32].
The Pearson correlation is computed as follows [17]:
where is the variable, is the output, and are the covariance and variance, respectively.
2.4.2. Boruta Method
Boruta works as a wrapper algorithm around Random Forest [33]. This method is a suitable candidate for reducing the dimensionality of the data [34]. The Boruta algorithm uses the Out-of-Bag (OOB) error to define the important score of the input features [33]. Steps for implementing the Boruta algorithm are shown in Figure 3.
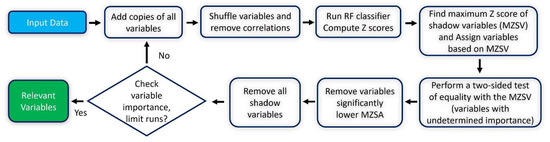
Figure 3.
Overview of the Boruta feature selection method.
The Z-Score in the Boruta algorithm is computed by the following equation [33]:
where is the number of decision trees, is the indicator function, and are predicted values before and after permuting, is the prediction error of each of the training samples based on bootstrap aggregation, and is the standard deviation of accuracy losses.
2.4.3. Random Forest Method
Random Forest is one of the most popular embedded feature selection methods [35]. For regression problems, the final value of the importance of variable () can be computed as follows [36]:
where is the average importance of variable () for each tree , is an average overall tree, is the standard deviation of the , and and are mean squared error before and after permuting and root mean squared error (RMSE).
Feature selection methods are implemented using the related packages in R software, and the ML library Scikit-Learn is used to construct ML models. GIS is used to collect, preprocess, and aggregate data before constructing condition assessment models. In this paper, the libraries “corrplot”, “Boruta”, and “randomforest” in R were used to implement the Pearson correlation, Boruta, and Random Forest feature selection methods, respectively.
2.5. Regression-Based Machine Learning Algorithms
2.5.1. Gaussian Process Regression
A Gaussian Process Regression (GPR) is a subset of Gaussian Processes used for dealing with regression problems [37]. The GPR is an effective tool for interpolating data points in high-dimensional input space and can be defined as follows [38]:
where is the total number of inspected sewer pipes, is the damage score, is the observation error, and are the mean and covariance functions, respectively.
In Gaussian Process, the covariance function is determined using a single or a combination of kernel functions (i.e., Radial-basis function, Dot-Product, Matérn, Rational Quadratic, Exp-Sine-Squared, and White kernels) and their hyperparameters (i.e., noise level, length-scale, scale mixture, or periodicity) [39]. This method has been applied for assessing sewer deterioration in previous studies but only for specific purposes such as sediment-related blockage or corrosion [40,41].
2.5.2. K-Nearest Neighbor
A K-Nearest Neighbor (KNN) regression introduced by Lall and Sharma [42] is a non-parametric method that approximates the association between factors (e.g., physical and environmental factors) and the sewer damage score by averaging the observations in the same neighborhood. The KNN model predicts the status of new sewer pipes based on using the similarity of K neighbor pipes in the training dataset. Therefore, the main advantages of KNN are the quick computational time, easy interpretability, versatility, and no need for any assumptions [43]. However, this algorithm is sensitive to irrelevant features which can be addressed by feature selection. Moreover, because it stores the distances from the new test point to all the training data points during implementation, this algorithm can be costly in the case of large datasets.
The basic steps for KNN implementation are as follows [44]:
- Step 1: Loading sewer inspection (training) dataset for constructing the KNN model;
- Step 2: Choose the value of K neighbors to define the nearest data points;
- Step 3: For each new sewer data point: (1) calculated distance between a new sewer data point to the training data points; (2) sort calculated distances in ascending order; (3) select the top K features from the sorted array; and (4) assign the sewer damage score to the new data point using weights calculated from distances neighbors’ data points;
- Step 4: Repeat steps 2 and 3 until all new sewer data points have been assigned new values.
2.5.3. Classification and Regression Trees
A Decision Tree (DT) regression creates regression models in the form of a tree structure in which the sewer training dataset is split into smaller and smaller subsets while at the same time an associated decision tree is developed. The decision tree consists of four basic components: root, internal nodes, leaf nodes, and branches. The root node contains all the factors, an internal node can contain two or more branches that are associated with a decision function, and the leaf node indicates the sewer damage score. A decision tree can be constructed via several steps [45]: (1) assigning all observations in the root node; (2) splitting the root node into branches based on the predicted sewer damage score using the decision function; (3) distributing observations on the higher node to the lower nodes; and (4) repeating the process until all sewer pipes have been processed.
A Classification and Regression Trees (CART) algorithm was used in this study. The decision trees created by CART have two branches for each decision node. Difference from the decision tree for classification, which uses Gini Impurity or Entropy values as criteria for splitting root/decision nodes, the “goodness” criterion is applied in the CART algorithm to split root/decision nodes and is computed as follows [46]:
where is the number of sewer inspections, is a measure of “goodness of fit”, and are the left and right children of a candidate split at node , respectively, and are the proportions of records at and , respectively, and are the proportions of class at and , respectively.
2.5.4. Random Forest
Random Forest (RF) regression is an ensemble learning method that uses multiple decision trees as base learning models for regression problems. The bagging (or bootstrap aggregation) algorithm is generally used to create the RF model. In this way, each decision tree in the RF is created from different samples at each node and produces an individual prediction. This model generates hundreds or thousands of regression decision trees and the average sewer status predicted from the individual trees is calculated for the final result [47]. As a result, the RF regression model generally has higher performance compared to the DT because it can avoid the correlation of different trees and the final results are obtained from the diversity of the trees [48].
2.5.5. Support Vector Regression
A Support Vector Regression (SVR) is one type of Support Vector Machine used for regression problems. This algorithm creates and finds the best-fit hyperplane in n-dimensional space that is close to as many of the data points as possible [49]. For regression problems, the linear form of the hyperplane can be computed as follows [50]:
where is the predicted value, is the input vector of the data point, and are the slope and intercept.
The goal function of the SVR model can be defined as follows [51]:
where is the predicted value, is the number of sewer inspections, is the input vector of the data point, and are the slope and intercept, respectively, are Lagrange multipliers, the constant is the trade-off between the flatness of the and the amount up to which deviations larger than the insensitive loss function, is kernel function (e.g., linear function, polynomial function, radial basis function, or sigmoid function).
2.5.6. Multi-Layer Perceptron Neural Network
A Multi-layer Perceptron Neural Network (MLP) is a fully connected class of feedforward artificial neural networks. This architecture normally consists of three or more layers (i.e., an input layer, an output layer, and one or more hidden layers) and each layer contains different neurons. In general, the number of neurons in the input layer is equal to the number of input factors, the number of neurons in the output layer is equal to one for the regression problem, and the number of hidden layers and hidden neurons fluctuates depending on the complexity of the MLP architecture. Determining the number of hidden layers and hidden neurons is generally implemented using a trial-and-error approach [52].
Each neuron in the hidden layer computes its input signals and produces its output based on the following equation:
where is the number of sewer inspections in the training dataset; is an activation function; and are connection weight and bias, respectively.
In this study, a single-layer MLP architecture was used. The number of hidden neurons, various activation functions in the hidden layer, and several optimization solvers were tuned using the Scikit-learn ML library. The early-stopping technique was used to avoid overfitting while training the model.
2.5.7. Extra Trees Regression
An Extra Trees Regression (ETR) is a tree-based structure ensemble learning algorithm used for regression problems. This algorithm uses an entire learning sample (instead of a bootstrap replica) to split nodes by choosing cut points entirely randomly. In the regression problem, the result is obtained by averaging predictions from decision trees. The relative variance reduction is used as the score measure in the regression problems for the ETR algorithm [53]:
where is the variance of the output in the sample , and are two subsets of cases from the sample corresponding to the two outcomes of a split , respectively.
2.5.8. AdaBoost
An AdaBoost regression (AdaBoost) is an ensemble learning method that uses an adaptive resampling approach to improve predictive performance from the mistakes of the base algorithm [54]. The basic idea of the AdaBoost algorithm is to build models via iterations in which models in the next iterations are built to rectify the errors present in the previous model. This process is ended when it reaches a terminated condition, and the final model is obtained from a weighted sum of all the base models.
Although AdaBoost can be used to combine various weak base learners, a combination of AdaBoost with the decision tree is often referred to as the best out-of-the-box classifier [55] and is used in this study.
2.5.9. Gradient Boosting
A Gradient Boosting Regression (GBR) improves predictive performance by combining weaker learners with strong learners via the iteration approach [56]. The decision tree is one of the most popular weak learners in the GBR [39]. The gradient boosting algorithm suffers from over-fitting if the iteration process is not regularized properly [57].
The decision tree solves the problems by transforming the data into a tree representation. Each internal node of the tree denotes an attribute, and each leaf node denotes a prediction. In the gradient boosting approach, decision trees have been added repeatedly and the next decision tree will correct the previous decision tree error [58].
2.5.10. Histogram-Based Gradient Boosting
A Histogram-based Gradient Boosting regression (HGB) is a modified version of the GBR to significantly increase the speed of decision tree split. During the training period of the HGB, factors were divided into bins and a histogram of factors was constructed [59]. The number of histogram bins is significantly less than the number of sewer inspections in the training set. The sewer damage score was predicted using the best split points based on the feature histograms [60].
2.6. Model Implementation
An ML regression model tries to fit the data by drawing rule(s) that minimize the difference between the actual value and the predicted value. The smaller the differences are, the better the model behaved for the point. Different ML models effectively fit with different hyperparameters to produce the optimal prediction. Therefore, the ML models need to be tuned to find the sensitive hyperparameters for the specific dataset. In this analysis, the Grid-Search (GS) method with a 5-fold cross-validation approach, which is integrated into the Scikit-learn ML library, was used to tune parameters for developed ML models.
The obtained GIS database was split into training and validation datasets to construct and validate ML models. In general, there is no consensus on the ratio of training and testing datasets when building an ML model. Choosing training and testing ratios mainly depends on the particular study and the subjective opinion of researchers. For example, a ratio of 80/20 was selected to build structural condition models in some studies [61]. In contrast, a ratio of 70/30 was used to predict the sewer’s status [28]. In this study, the ratio of 80/20 was used to split the dataset. Accordingly, a total of 1159 sewer pipes were used to construct the ML models and 290 sewer pipes were used for model validation.
Feature selection methods were used to assess the significance of each factor. After that, the least significant factors influencing the sewer damage score were eliminated from the training data. The final data were used in the sewer condition models.
The constructed ML models were compared to select the best model for the sewer condition prediction. In this study, the predictive performance of the ten ML regression models was assessed using the coefficient of determination (), mean absolute error (), and root mean square error () expressed as follows:
where is the total number of measurements; is the mean value of the actual measurements; and are the actual and predicted measurements.
The Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) was applied to rank the ML models [62]. This method is a common approach for ranking ML algorithms, using multiple criteria on a single dataset by choosing the alternatives that have the shortest distance to the positive-ideal solution and the longest distance to the negative-ideal solution [63]. These distances relate to the alternative weights that are used to compute the overall performance score [64]. Interested readers can find more detailed information on the TOPSIS in Behzadian, Khanmohammadi Otaghsara, Yazdani and Ignatius [63]. In this study, the package “TOPSIS” in R was used to implement the TOPSIS method [65].
3. Results and Discussions
3.1. Feature Selection
Results of feature selection using the filter, wrapper, and embedded methods are shown in Figure A2. The results revealed slight differences in determining the most significant factors by each feature selection method. For instance, while the RF feature selection method identifies slope as the most significant factor, followed by length, both the Pearson correlation and the Boruta methods identify age (PR = 0.30) and material (PR = −0.25) as the most significant factors. The Boruta method also identifies age (Z-score = 12) and material (Z-score = 10) as the most significant factors for sewer damage. In Figure A2a, the negative values represent the inverse relationships between physical/environmental variables and a sewer’s damaged scores, and vice versa. A positive correlation between a continuous input variable and the output shows that when the values of the input increase, the value of the output increase as well [66]. For example, the sewer’s age has a positive correlation (PR = 0.30) with the sewer’s damaged score, showing that when the age of the sewer pipe increases (old pipes) the damaged score of the sewer pipe will rises (worse condition). Material has a negative correlation (PR = −0.25) with the damaged score indicating that sewer pipes in concrete material are more durable than sewer pipes in polypropylene and PVC materials.
In contrast, there is a less significant difference between the feature selection methods in terms of the least important determinations of sewer condition. For example, the Pearson correlation coefficients revealed network type and groundwater do not affect the sewer pipe condition (PRs = 0.00). Two factors associated with distance to road (PR = 0.01), land use and depth (PRs = −0.03), and diameter (PRs = 0.03) are the six lowest significant factors (Figure A2a). For the Boruta method, landslide area, building area, pipe form, network type, depth, and diameter were assessed as insignificant factors (Figure A2b). Network type, pipe form, landslide area, geology, pipe type, and connection were identified as the least significant factors in the RF feature selection method (Figure A2c).
Table 3 summarizes the importance of the factors from each feature selection method, where the number represents the important degree (1: the highest importance, 20: the lowest importance). The same important factors, which have similar PR values, are denoted by the slash. For example, the rainfall factor and connection factor have the same importance. In conclusion, all feature selection methods show that network type is the least significant factor. Therefore, this factor was eliminated from the dataset before building the condition assessment models.

Table 3.
Summary of feature selection.
3.2. Model Comparison
The optimal hyperparameters used for tuning the ML models are shown in Table A2. The performance of ten ML models was compared based on the training and validation phases as presented in Table 4.

Table 4.
Performance of the machine learning models in this analysis.
The results in Table 4 show that the GPR, DT, and ETR models fit very well with the training dataset (the values of R2 and errors are equal to 1.0 and 0.0, respectively). In contrast, the KNN model performed poorly in predicting the sewers’ damage scores (R2 is almost equal to zero) indicating the worst ML model. The predictive capability of the ML models on the testing dataset is presented in Figure A3.
In general, predictive models have been assessed as effective tools if they can effectively predict unseen data that are not used for model construction. Therefore, the validation data are used to assess the constructed ML models. In the validation phase, the ETR has the best performance (R2 = 0.90, MAE = 11.37, RMSE = 40.75), followed by the GPR (R2 = 0.86, MAE = 14.36, RMSE = 46.95) and the RF model (R2 = 0.81, MAE = 30.59, RMSE = 58.19). The KNN (R2 = 0.07, MAE = 76.07, RMSE = 122.96) and MLP (R2 = 0.10, MAE = 73.93, RMSE = 126.07) performed poorly in predicting the condition status of the sewer pipes.
Even though all ensembles ETR, RF, HGB, AdaBoost, and GB use the DT as the base learner, their predictive performance is significantly different. For instance, the ETR and RF remarkably improve the predictive performance of the original DT algorithm (R2 = 0.76, MAE = 15.19, RMSE = 69.96). In contrast, the HGB (R2 = 0.17, MAE = 64.18, RMSE = 117.10), AdaBoost (R2 = 0.20, MAE = 58.86, RMSE = 113.15), and GB (R2 = 0.20, MAE = 63.20, and RMSE = 113.45) significantly reduce the predictive capability of the DT algorithm. These results show that the adaptive boosting and gradient boosting techniques are unsuitable approaches for the dataset in the study area; in contrast, the randomly generated threshold method (in the ETR algorithm) or the bootstrap aggregation method (in the RF algorithm) is a more suitable option.
The prediction performance of the KNN model mainly depends on the number of neighbors that were obtained based on similar characteristics [44]; limited data in the study area may not provide enough information for the KNN algorithm to effectively distinguish clusters resulting in the low prediction performance. The GPR model with high interpolating ability can deal with high-dimensional input for the complex process of sewer deterioration in the study area [38].
In this study, the MLP algorithm has a low prediction capability in modeling sewer pipes’ damage scores. This agrees with a previous study in which the neural network-based models have lower performance in regression problems [67]. Similarly, the prediction capabilities of KNN, SVM, AdaBoost, GB, and HGB models were low in both training and validation datasets. The reason is that there are several sewer pipes that have excessive damage score values (over 1000); meanwhile, the majority of sewer pipes (approximately 90%) have damage score values below 1000. To test the prediction ability of ML algorithms in distinguishing these values, we prioritized using the original dataset. The results showed that the overmentioned models did not effectively distinguish the excessive values of sewer pipes, indicating they are unsuitable for the study area. In conclusion, among the constructed models, the ETR is the most suitable ML algorithm for modeling the sewer conditions in the study area.
The constructed ML algorithms have been ranked using the TOPSIS method and the results are shown in Table 5. According to these results, the ETR is the most suitable ML algorithm and the KNN is the worst ML algorithm for modeling the sewer’s condition in Ålesund city.

Table 5.
The rank of the machine learning algorithm.
Although sewer damage scores can be used to predict sewer status using regression-based ML models they present varied levels of accuracy (Table 4). This can be attributed to the skewness of damage score data, which affects the predictive performance of the models due to the large variability [68,69]. To address this problem, sewer damage scores are aggregated into classes and the regression problem is converted into a classification problem. It is therefore recommended that future studies consider the classification-based approach to ML models for sewer condition assessment.
4. Conclusions
This paper investigated the potential application of ten state-of-the-art regression-based machine learning algorithms to model sewer conditions in the city of Ålesund, Norway. A dataset consisting of 1449 CCTV inspections and 20 physical and environmental factors was considered to construct and verify the sewer condition assessment models. Three feature-selection methods were applied to assess the importance of variables. The study revealed that:
- Age and material are the most sensitive factors affecting the sewer condition, while network type is the least contributor. Water utilities can refer to the age and material of sewer pipes as the priority factors when building predictive maintenance strategies;
- The performance of the ML models used was affected by the skewness and variability of the damage score data. Damage scores should be clustered into fewer condition classes to make the predictive results more convergent and improve prediction performance;
- The ETR model outperformed other ML models and this algorithm should be considered for modeling the sewer pipe condition in the study area;
- The results from this study can be critical for local water managers or engineers in assessing the condition of the entire sewer network. Based on the framework developed in this work, future sewer conditions can be predicted if the input factors are quantified. For instance, if rainfall/groundwater or population factors in the future are computed based on climate projection or annual population increase, respectively, the condition status of the sewer pipes in the corresponding time can be obtained. This is very important because local water organizations not only assess the current status of sewer pipes, but they also monitor the changes in the entire sewer network over time. It is a very useful tool supporting rehabilitation and maintenance strategies;
- Another advantage of our work is that all software and packages used in this work are open and free. Water engineers can easily add available observations and factors, reimplement, and reproduce the results under different scenarios;
- A limitation of this study is the lack of operational factors which were not available when undertaking the work. In the future, this limitation could be addressed by using operational factors and more sewer pipe inspections.
Author Contributions
Conceptualization, L.V.N. and R.S.; methodology, L.V.N. and R.S.; software, L.V.N.; validation, L.V.N.; investigation, L.V.N.; writing—original draft preparation, L.V.N.; writing—review and editing, L.V.N. and R.S.; supervision, R.S.; project administration, R.S.; funding acquisition, R.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Smart Water Project, the grant number is 90392200 financed by Ålesund Municipality and Norwegian University of Science and Technology (NTNU), Norway.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the Norwegian Mapping Authority, the Norwegian Climate Service Center, the Norwegian Water Resources and Energy Directorate, the Weather Atlas, the Mapping Authority, and the Norwegian Geological Survey for providing data for this research.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
| Abbreviation | Meaning |
| RaM | Reactive Maintenance |
| PvM | Preventive Maintenance |
| PdM | Predictive Maintenance |
| CCTV | Closed-Circuit Television |
| ML | Machine Learning |
| GIS | Geographic Information System |
| DEM | Digital Elevation Model |
| NMA | the Norwegian Mapping Authority |
| NCSC | the Norwegian Climate Service Center |
| NGS | the Norwegian Geological Survey |
| NPRA | the Norwegian Public Roads Administration |
| IDW | Inverse Distance Weighting |
| PVC | Polyvinyl Chloride |
| PR | Pearson’s Correlation Coefficient |
| OOB | Out-of-Bag |
| RMSE | Root Mean Squared Error |
| GPR | Gaussian Process Regression |
| KNN | K-Nearest Neighbor |
| DT | Decision Tree |
| CART | Classification and Regression Trees |
| RF | Random Forest |
| SVR | Support Vector Regression |
| MLP | Multi-layer Perceptron Neural Network |
| ETR | Extra Trees Regression |
| GB | Gradient Boosting |
| HGB | Histogram-based Gradient Boosting |
| R2 | coefficient of determination |
| MAE | Mean Absolute Error |
| TOPSIS | Technique for Order Preference by Similarity to Ideal Solution |
| length-scale | |
| smoothness function | |
| the number of neighbors | |
| ball_tree | ball tree nearest neighbors search algorithm |
| squared_error | mean squared error |
| the number of features to choose the best subset | |
| the number of trees | |
| rbf | Radial basis function |
| C | regularization parameter |
| kernel width | |
| relu | Rectified Linear Unit |
| lbfgs | Limited-memory Broyden–Fletcher–Goldfarb–Shanno algorithm |
| the number of neurons in the hidden layer | |
| the maximum number of iterations of the boosting process | |
| the maximum depth of each tree | |
| the number of boosting iterations |
Appendix A

Table A1.
The weather stations used in this analysis.
Table A1.
The weather stations used in this analysis.
| Weather Station | Latitude | Longitude | Average Rainfall (mm) | Period |
|---|---|---|---|---|
| Brusdalsvann | 62°27′59.8″ | 6°27′45.4″ | 157.0 | 01.1907–12.1972 |
| Brusdalsvann II | 62°27′55.4″ | 6°24′04.7″ | 152.1 | 01.1973–12.2014 |
| Skodje | 62°30′00.0″ | 6°42′01.4″ | 139.8 | 01.1961–12.1979 |
| Ålesund | 62°28′31.1″ | 6°09′04.0″ | 105.8 | 01.1895–12.1930 |
| Ålesund II | 62°28′25.3″ | 6°10′22.4″ | 95.5 | 01.1908–12.1954 |
| Ålesund III | 62°28′31.4″ | 6°12′06.1″ | 125.9 | 01.1955–12.2004 |
| Ørskog | 62°28′39.0″ | 6°49′00.1″ | 130.7 | 01.1896–12.2019 |
| Hildre | 62°36′05.8″ | 6°19′07.0″ | 125.5 | 01.1970–12.2018 |
| Vigra | 62°33′40.7″ | 6°06′40.7″ | 113.7 | 01.1959–12.2019 |

Table A2.
Tuned hyperparameters for machine learning models.
Table A2.
Tuned hyperparameters for machine learning models.
| Model | Range of Hyperparameters | Tuned Hyperparameters |
|---|---|---|
| GPR |
|
|
| KNN |
|
|
| DTR |
|
|
| RFR |
|
|
| SVR |
|
|
| ETR |
|
|
| MLP |
|
|
| AdaBoost |
|
|
| GBR |
|
|
| HGBR |
|
|

Figure A1.
Maps of environmental factors: (a) Rainfall, (b) Groundwater, (c) Geology, (d) Landslide and building area, (e) Population, (f) Land use, (g) Distance to road, (h) Traffic volume, and (i) Soil type.
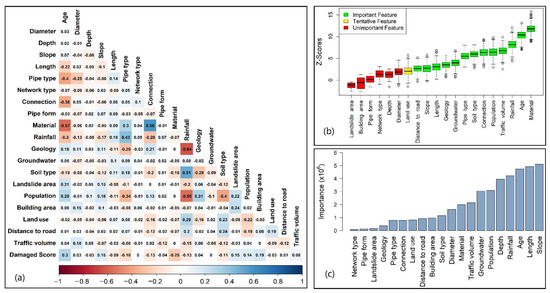
Figure A2.
The features’ importance: (a) Pearson’s correlation, (b) Boruta, and (c) Random Forest.

Figure A3.
R2 of the constructed machine learning models using the test dataset: (a) Gaussian Process Regression, (b) K-Nearest Neighbor, (c) Classification and Regression Trees, (d) Random Forest, (e) Support Vector Regression, (f) Multi-layer Perceptron Neural Network, (g) Extra Trees Regression, (h) AdaBoost, (i) Gradient Boosting, and (j) Histogram-Based Gradient Boosting.
References
- Ana, E.V.; Bauwens, W. Modeling the structural deterioration of urban drainage pipes: The state-of-the-art in statistical methods. Urban Water J. 2010, 7, 47–59. [Google Scholar] [CrossRef]
- Farkas, K.; Hillary, L.S.; Malham, S.K.; McDonald, J.E.; Jones, D.L. Wastewater and public health: The potential of wastewater surveillance for monitoring COVID-19. Curr. Opin. Environ. Sci. Health 2020, 17, 14–20. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.A.; Djordjević, S.; Khu, S.-T. A general framework for flood risk-based storm sewer network design. Urban Water J. 2011, 8, 13–27. [Google Scholar] [CrossRef]
- Ana, E.; Bauwens, W.; Pessemier, M.; Thoeye, C.; Smolders, S.; Boonen, I.; De Gueldre, G. An investigation of the factors influencing sewer structural deterioration. Urban Water J. 2009, 6, 303–312. [Google Scholar] [CrossRef]
- Anand, U.; Li, X.; Sunita, K.; Lokhandwala, S.; Gautam, P.; Suresh, S.; Sarma, H.; Vellingiri, B.; Dey, A.; Bontempi, E.; et al. SARS-CoV-2 and other pathogens in municipal wastewater, landfill leachate, and solid waste: A review about virus surveillance, infectivity, and inactivation. Environ. Res. 2022, 203, 111839. [Google Scholar] [CrossRef]
- Yin, X.; Chen, Y.; Bouferguene, A.; Al-Hussein, M. Data-driven bi-level sewer pipe deterioration model: Design and analysis. Autom. Constr. 2020, 116, 103181. [Google Scholar] [CrossRef]
- Beheshti, M.; Sægrov, S.; Ugarelli, R. Infiltration/inflow assessment and detection in urban sewer system. Vannforeningen 2015, 1, 24–34. [Google Scholar]
- Susto, G.A.; Schirru, A.; Pampuri, S.; McLoone, S.; Beghi, A. Machine Learning for Predictive Maintenance: A Multiple Classifier Approach. IEEE Trans. Ind. Inform. 2015, 11, 812–820. [Google Scholar] [CrossRef]
- Chughtai, F.; Zayed, T. Sewer pipeline operational condition prediction using multiple regression. In Pipelines 2007: Advances and Experiences with Trenchless Pipeline Projects; ASCE: Fairfax County, VA, USA, 2007; pp. 1–11. [Google Scholar]
- Hawari, A.; Alkadour, F.; Elmasry, M.; Zayed, T. A state of the art review on condition assessment models developed for sewer pipelines. Eng. Appl. Artif. Intell. 2020, 93, 103721. [Google Scholar] [CrossRef]
- Heydarzadeh, R.; Tabesh, M.; Scholz, M. Dissolved oxygen determination in sewers using flow hydraulic parameters as part of a physical-biological simulation model. J. Hydroinforma. 2021, 24, 1–15. [Google Scholar] [CrossRef]
- Hadzilacos, T.; Kalles, D.; Preston, N.; Melbourne, P.; Camarinopoulos, L.; Eimermacher, M.; Kallidromitis, V.; Frondistou-Yannas, S.; Saegrov, S. UtilNets: A water mains rehabilitation decision-support system. Comput. Environ. Urban Syst. 2000, 24, 215–232. [Google Scholar] [CrossRef]
- Tscheikner-Gratl, F.; Caradot, N.; Cherqui, F.; Leitão, J.P.; Ahmadi, M.; Langeveld, J.G.; Le Gat, Y.; Scholten, L.; Roghani, B.; Rodríguez, J.P.; et al. Sewer asset management—State of the art and research needs. Urban Water J. 2019, 16, 662–675. [Google Scholar] [CrossRef]
- Fan, X.; Wang, X.; Zhang, X.; Asce Xiong Yu, P.E.F. Machine learning based water pipe failure prediction: The effects of engineering, geology, climate and socio-economic factors. Reliab. Eng. Syst. Saf. 2022, 219, 108185. [Google Scholar] [CrossRef]
- Uddin, S.; Khan, A.; Hossain, M.E.; Moni, M.A. Comparing different supervised machine learning algorithms for disease prediction. BMC Med. Inform. Decis. Mak. 2019, 19, 281. [Google Scholar] [CrossRef]
- Hawari, A.; Firas, A.; Elmasry, M.; Zayed, T. Simulation-Based Condition Assessment Model for Sewer Pipelines. J. Perform. Constr. Facil. 2016, 31, 04016066. [Google Scholar] [CrossRef]
- Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. An Introduction to Feature Selection. In Applied Predictive Modeling; Springer: New York, NY, USA, 2013; pp. 487–519. [Google Scholar] [CrossRef]
- Caradot, N.; Riechel, M.; Rouault, P.; Caradot, A.; Lengemann, N.; Eckert, E.; Ringe, A.; Clemens, F.; Cherqui, F. The influence of condition assessment uncertainties on sewer deterioration modelling. Struct. Infrastruct. Eng. 2020, 16, 287–296. [Google Scholar] [CrossRef]
- Bairaktaris, D.; Delis, V.; Emmanouilidis, C.; Frondistou-Yannas, S.; Gratsias, K.; Kallidromitis, V.; Rerras, N. Decision-Support System for the Rehabilitation of Deteriorating Sewers. J. Perform. Constr. Facil. 2007, 21, 240–248. [Google Scholar] [CrossRef]
- Hansen, B.D.; Jensen, D.G.; Rasmussen, S.H.; Tamouk, J.; Uggerby, M.; Moeslund, T.B. General Sewer Deterioration Model Using Random Forest. In Proceedings of the 2019 IEEE Symposium Series on Computational Intelligence (SSCI), Xiamen, China, 6–9 December 2019; pp. 834–841. [Google Scholar]
- Nusinovici, S.; Tham, Y.C.; Chak Yan, M.Y.; Wei Ting, D.S.; Li, J.; Sabanayagam, C.; Wong, T.Y.; Cheng, C.-Y. Logistic regression was as good as machine learning for predicting major chronic diseases. J. Clin. Epidemiol. 2020, 122, 56–69. [Google Scholar] [CrossRef]
- Song, X.; Liu, X.; Liu, F.; Wang, C. Comparison of machine learning and logistic regression models in predicting acute kidney injury: A systematic review and meta-analysis. Int. J. Med. Inform. 2021, 151, 104484. [Google Scholar] [CrossRef]
- Population, C. Municipality in Møre og Romsdal (Norway). Available online: https://www.citypopulation.de/en/norway/admin/m%C3%B8re_og_romsdal/1507__%C3%A5lesund/ (accessed on 10 February 2022).
- Climate, D. Ålesund Climate: Average Temperature, Weather by Month, Ålesund Water Temperature—Climate-Data.org. Available online: https://en.climate-data.org/europe/norway/m%C3%B8re-og-romsdal/alesund-9937/ (accessed on 20 April 2022).
- Kvitsjøen, J.; Paus, K.; Bjerkholt, J.T.; Fergus, T.; Lindholm, O. Intensifying rehabilitation of combined sewer systems using trenchless technology in combination with low impact development and green infrastructure. Water Sci. Technol. 2021, 83, 2947–2962. [Google Scholar] [CrossRef] [PubMed]
- Hanssen-Bauer, I.; Drange, H.; Førland, E.; Roald, L.; Børsheim, K.; Hisdal, H.; Lawrence, D.; Nesje, A.; Sandven, S.; Sorteberg, A. Climate in Norway 2100—A Knowledge Base for Climate Adaptation. In Background information to NOU Climate Adaptation (In Norwegian: Klima i Norge 2100. Bakgrunnsmateriale til NOU Klimatilplassing); Norsk Klimasenter: Oslo, Norway, 2017. [Google Scholar]
- Laakso, T.; Kokkonen, T.; Mellin, I.; Vahala, R. Sewer Condition Prediction and Analysis of Explanatory Factors. Water 2018, 10, 1239. [Google Scholar] [CrossRef]
- Belief, E. GIS based spatial modeling to mapping and estimation relative risk of different diseases using inverse distance weighting (IDW) interpolation algorithm and evidential belief function (EBF) (Case study: Minor Part of Kirkuk City, Iraq). Int. J. Eng. Technol. 2018, 7, 185–191. [Google Scholar]
- Sánchez-Espinosa, A.; Schröder, C. Land use and land cover mapping in wetlands one step closer to the ground: Sentinel-2 versus landsat 8. J. Environ. Manag. 2019, 247, 484–498. [Google Scholar] [CrossRef]
- Schober, P.; Boer, C.; Schwarte, L.A. Correlation coefficients: Appropriate use and interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef]
- Adler, J.; Parmryd, I. Quantifying colocalization by correlation: The Pearson correlation coefficient is superior to the Mander’s overlap coefficient. Cytom. Part A 2010, 77A, 733–742. [Google Scholar] [CrossRef]
- Masrur Ahmed, A.A.; Deo, R.C.; Feng, Q.; Ghahramani, A.; Raj, N.; Yin, Z.; Yang, L. Deep learning hybrid model with Boruta-Random forest optimiser algorithm for streamflow forecasting with climate mode indices, rainfall, and periodicity. J. Hydrol. 2021, 599, 126350. [Google Scholar] [CrossRef]
- Nanda, M.A.; Seminar, K.B.; Maddu, A.; Nandika, D. Identifying relevant features of termite signals applied in termite detection system. Ecol. Inform. 2021, 64, 101391. [Google Scholar] [CrossRef]
- Liu, H.; Zhou, M.; Liu, Q. An embedded feature selection method for imbalanced data classification. IEEE/CAA J. Autom. Sin. 2019, 6, 703–715. [Google Scholar] [CrossRef]
- Dewi, C.; Chen, R.-C. Random forest and support vector machine on features selection for regression analysis. Int. J. Innov. Comput. Inf. Control 2019, 15, 2027–2037. [Google Scholar]
- Gibson, N.P.; Aigrain, S.; Roberts, S.; Evans, T.M.; Osborne, M.; Pont, F. A Gaussian process framework for modelling instrumental systematics: Application to transmission spectroscopy. Mon. Not. R. Astron. Soc. 2012, 419, 2683–2694. [Google Scholar] [CrossRef]
- Meng, L.; Zhang, J. Process Design of Laser Powder Bed Fusion of Stainless Steel Using a Gaussian Process-Based Machine Learning Model. JOM 2020, 72, 420–428. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Pulido, E.S.; Arboleda, C.V.; Rodríguez Sánchez, J.P. Study of the spatiotemporal correlation between sediment-related blockage events in the sewer system in Bogotá (Colombia). Water Sci. Technol. 2019, 79, 1727–1738. [Google Scholar] [CrossRef]
- Zhang, J.; Li, B.; Fan, X.; Wang, Y.; Chen, F. Sewer Corrosion Prediction for Sewer Network Sustainability. In Humanity Driven AI: Productivity, Well-being, Sustainability and Partnership; Chen, F., Zhou, J., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 181–194. [Google Scholar] [CrossRef]
- Lall, U.; Sharma, A. A Nearest Neighbor Bootstrap For Resampling Hydrologic Time Series. Water Resour. Res. 1996, 32, 679–693. [Google Scholar] [CrossRef]
- Yao, Z.; Ruzzo, W.L. A Regression-based K nearest neighbor algorithm for gene function prediction from heterogeneous data. BMC Bioinform. 2006, 7, S11. [Google Scholar] [CrossRef]
- Kohli, S.; Godwin, G.T.; Urolagin, S. Sales Prediction Using Linear and KNN Regression; Springer Nature Singapore Pte Ltd.: Singapore, 2020; pp. 321–329. [Google Scholar]
- Syachrani, S.; Jeong, H.S.D.; Chung, C.S. S. Decision Tree–Based Deterioration Model for Buried Wastewater Pipelines. J. Perform. Constr. Facil. 2013, 27, 633–645. [Google Scholar] [CrossRef]
- Larose, D.T.; Larose, C.D. Discovering Knowledge in Data: An Introduction to Data Mining; John Wiley & Sons: New York, NY, USA, 2014; Volume 4. [Google Scholar]
- Kumar, S.S.; Shaikh, T. Empirical Evaluation of the Performance of Feature Selection Approaches on Random Forest. In Proceedings of the 2017 International Conference on Computer and Applications (ICCA), Doha, Qatar, 6–7 September 2017; pp. 227–231. [Google Scholar]
- Li, Y.; Zou, C.; Berecibar, M.; Nanini-Maury, E.; Chan, J.C.W.; van den Bossche, P.; Van Mierlo, J.; Omar, N. Random forest regression for online capacity estimation of lithium-ion batteries. Appl. Energy 2018, 232, 197–210. [Google Scholar] [CrossRef]
- Trafalis, T.B.; Ince, H. Support vector machine for regression and applications to financial forecasting. In Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks. IJCNN 2000. Neural Computing: New Challenges and Perspectives for the New Millennium, Como, Italy, 27 July 2000; Volume 346, pp. 348–353. [Google Scholar]
- Wauters, M.; Vanhoucke, M. Support Vector Machine Regression for project control forecasting. Autom. Constr. 2014, 47, 92–106. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Orhan, U.; Hekim, M.; Ozer, M. EEG signals classification using the K-means clustering and a multilayer perceptron neural network model. Expert Syst. Appl. 2011, 38, 13475–13481. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Hong, H.; Liu, J.; Bui, D.T.; Pradhan, B.; Acharya, T.D.; Pham, B.T.; Zhu, A.X.; Chen, W.; Ahmad, B.B. Landslide susceptibility mapping using J48 Decision Tree with AdaBoost, Bagging and Rotation Forest ensembles in the Guangchang area (China). CATENA 2018, 163, 399–413. [Google Scholar] [CrossRef]
- Kégl, B. The return of AdaBoost. MH: Multi-class Hamming trees. arXiv 2013, arXiv:1312.6086. [Google Scholar]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A comparative analysis of gradient boosting algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Ayyadevara, V.K. Gradient Boosting Machine. In Pro Machine Learning Algorithms: A Hands-On Approach to Implementing Algorithms in Python and R; Apress: Berkeley, CA, USA, 2018; pp. 117–134. [Google Scholar] [CrossRef]
- Aljamaan, H.; Alazba, A. Software defect prediction using tree-based ensembles. In Proceedings of the 16th ACM international conference on predictive models and data analytics in software engineering, Virtual, 8–9 November 2020; pp. 1–10. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 9. [Google Scholar]
- Kabir, G.; Balek, N.B.C.; Tesfamariam, S. Sewer Structural Condition Prediction Integrating Bayesian Model Averaging with Logistic Regression. J. Perform. Constr. Facil. 2018, 32, 04018019. [Google Scholar] [CrossRef]
- Vazquezl, M.Y.L.; Peñafiel, L.A.B.; Muñoz, S.X.S.; Martinez, M.A.Q. A Framework for Selecting Machine Learning Models Using TOPSIS; Springer Nature Switzerland AG: Cham, Switzerland, 2020; pp. 119–126. [Google Scholar]
- Behzadian, M.; Khanmohammadi Otaghsara, S.; Yazdani, M.; Ignatius, J. A state-of the-art survey of TOPSIS applications. Expert Syst. Appl. 2012, 39, 13051–13069. [Google Scholar] [CrossRef]
- Chakraborty, S. TOPSIS and Modified TOPSIS: A comparative analysis. Decis. Anal. J. 2022, 2, 100021. [Google Scholar] [CrossRef]
- Ihaka, R.; Gentleman, R. R: A Language for Data Analysis and Graphics. J. Comput. Graph. Stat. 1996, 5, 299–314. [Google Scholar] [CrossRef]
- Taylor, R. Interpretation of the correlation coefficient: A basic review. J. Diagn. Med. Sonogr. 1990, 6, 35–39. [Google Scholar] [CrossRef]
- Bui, K.-T.T.; Torres, J.F.; Gutiérrez-Avilés, D.; Nhu, V.-H.; Bui, D.T.; Martínez-Álvarez, F. Deformation forecasting of a hydropower dam by hybridizing a long short-term memory deep learning network with the coronavirus optimization algorithm. Comput.—Aided Civ. Infrastruct. Eng. 2022, 37, 1368–1386. [Google Scholar] [CrossRef]
- Bellon-Maurel, V.; Fernandez-Ahumada, E.; Palagos, B.; Roger, J.-M.; McBratney, A. Critical review of chemometric indicators commonly used for assessing the quality of the prediction of soil attributes by NIR spectroscopy. TrAC Trends Anal. Chem. 2010, 29, 1073–1081. [Google Scholar] [CrossRef]
- Krawczyk, B. Learning from imbalanced data: Open challenges and future directions. Prog. Artif. Intell. 2016, 5, 221–232. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).