A Hydrograph-Based Approach to Improve Satellite-Derived Snow Water Equivalent at the Watershed Scale
Abstract
:1. Introduction
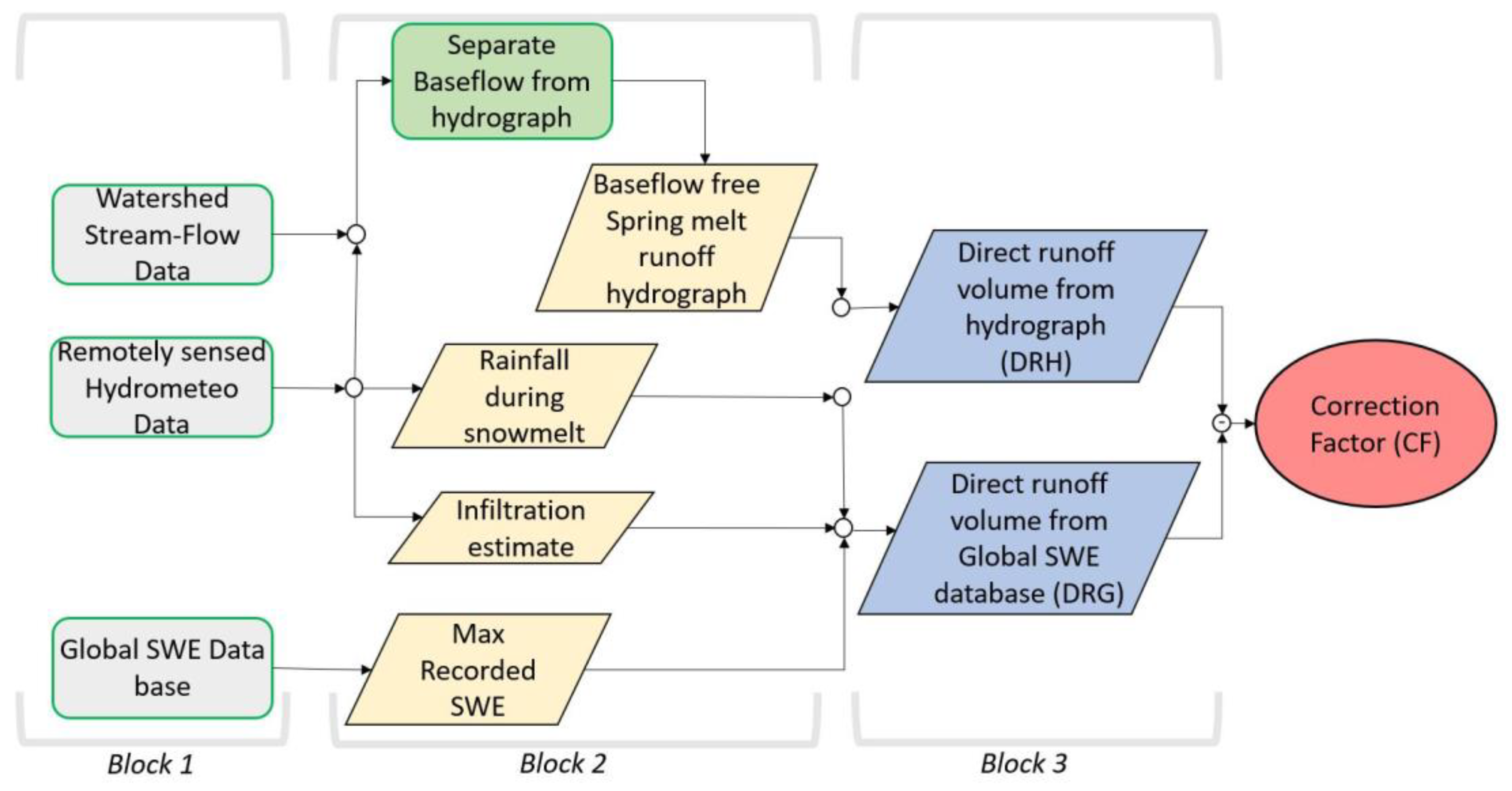
2. Materials and Methods
2.1. WSC Overview
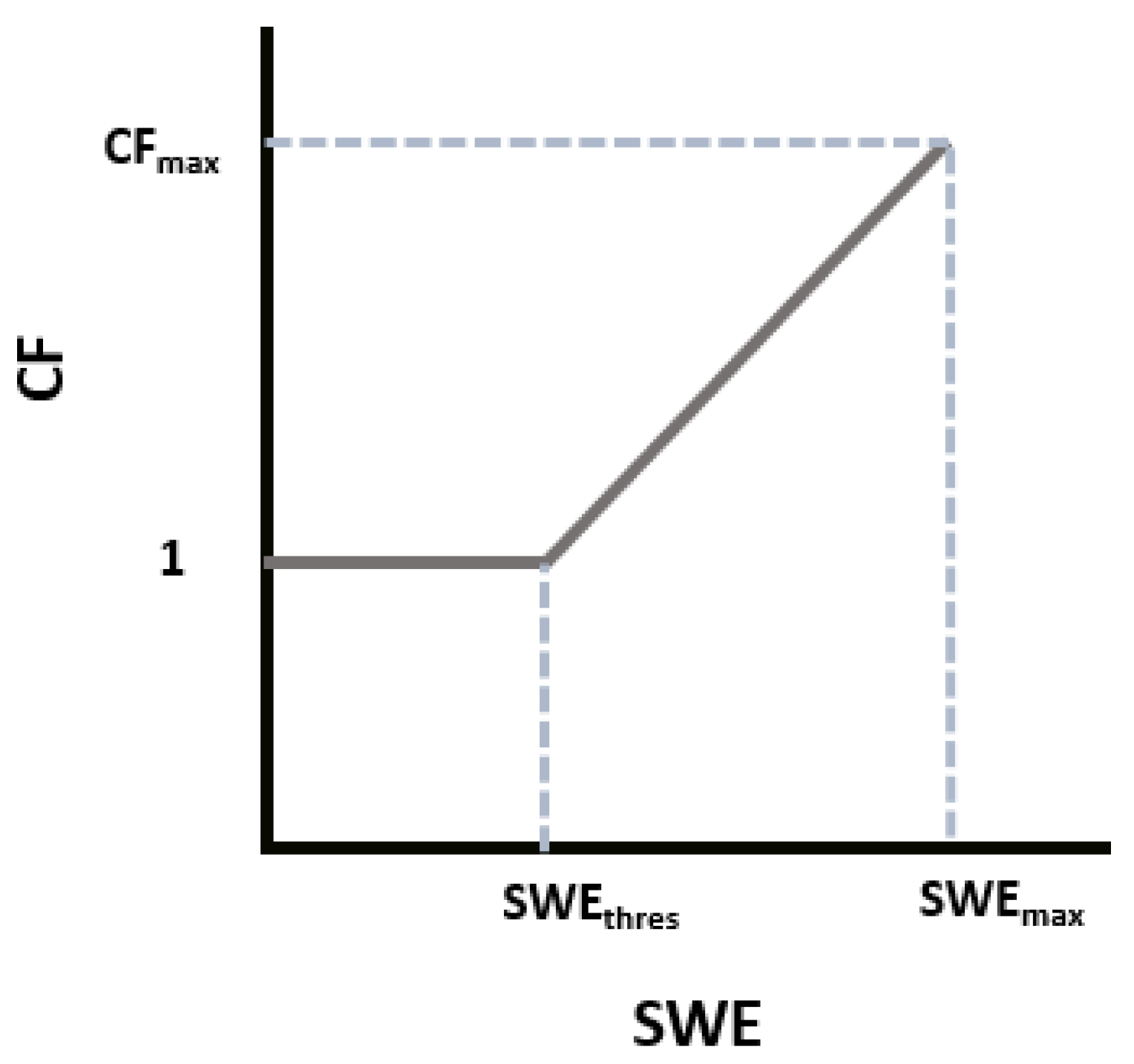
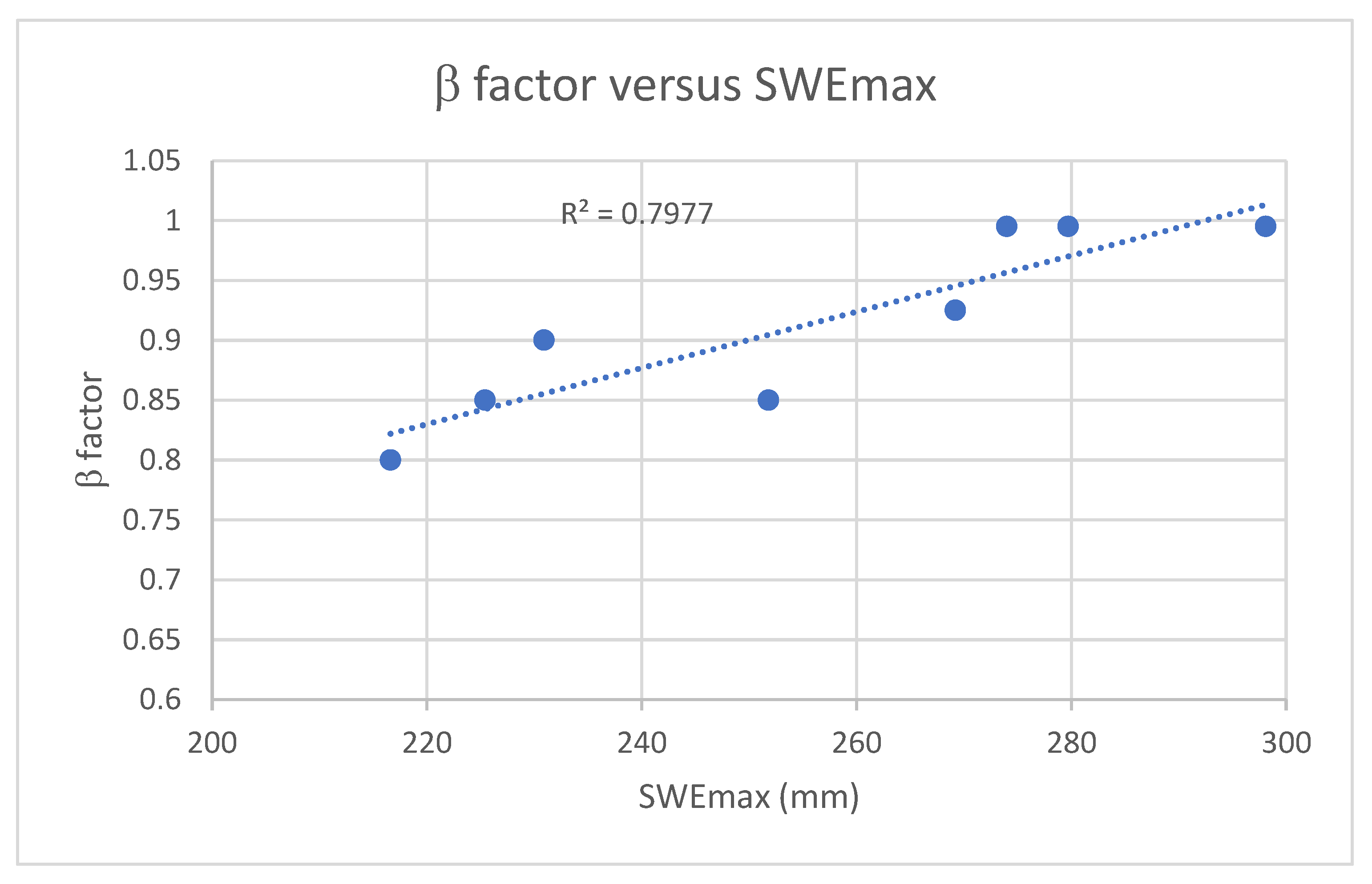
- is derived using the HUT model. GlobSnow V1 and V2 [12] assume that the snowpack is made of a single homogeneous layer, while V3 [11] represents the snowpack as a stacked system of snow layers. Despite this improvement over the original HUT model, uncertainties in SWEmax estimation remain, especially when the snowpack undergoes multiple freeze-thaw and rain-on snow events, which will be reflected by changing CF values.
- Because of the limited penetration depth of the PM signal, it is expected that the CF will be larger when deeper snowpack conditions are encountered.
- Flow measurements also have errors related to the rating curve used to convert stream water level into streamflow.
- Finally, other sources of uncertainty related to precipitation, baseflow, and infiltration estimates will also affect CF.
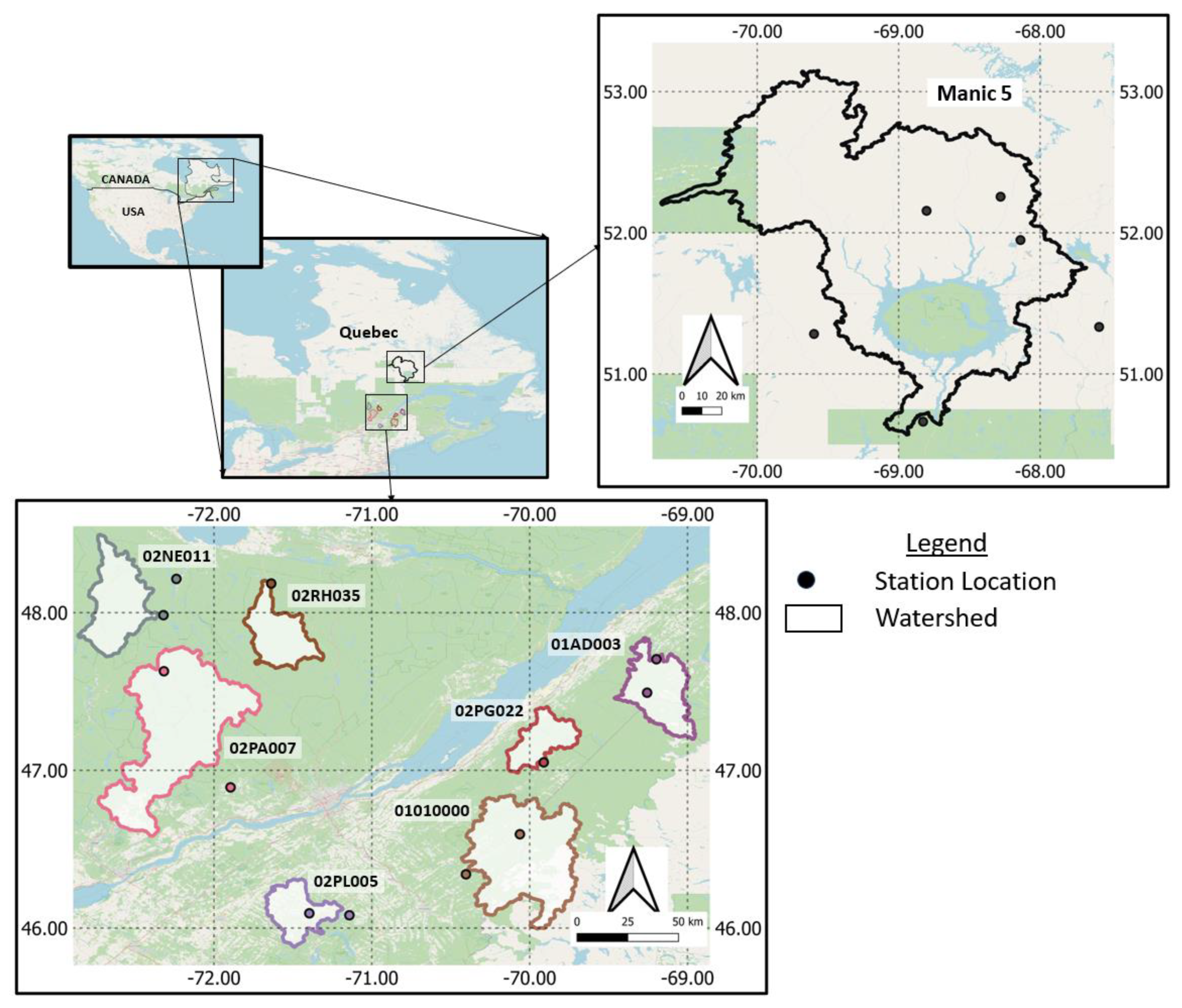
2.2. Study Area
2.3. Data
2.3.1. GlobSnow
2.3.2. ERA5
2.3.3. Streamflow Data
2.3.4. In Situ Data
3. Results
4. Discussion
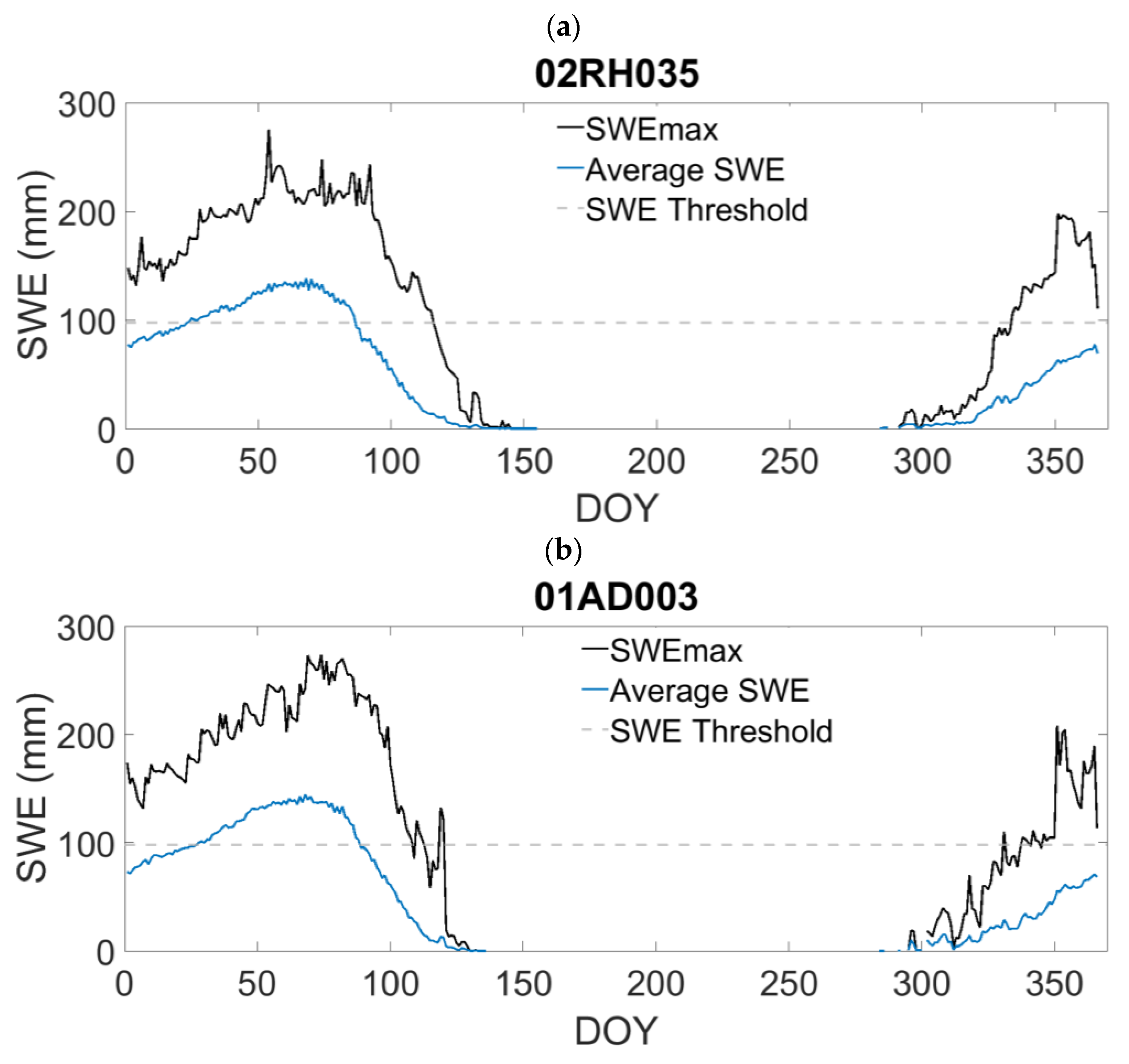
4.1. Baseflow Separation as a Source of Uncertainty
4.2. Other Sources of Uncertainty
4.3. The SWC Approach as Part of an Ensemble Flow Forecast System
4.4. Validation of the WSC Approach: An Issue of Scale Mismatch
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Buttle, J.M.; Allen, D.M.; Caissie, D.; Davison, B.; Peters, D.L.; Pomeroy, J.W.; Simonovic, S.; St-Hilaire, A.; Whitfield, P.H. Flood Processes in Canada: Regional and Special Aspects. Can. Water Resour. J. 2016, 41, 7–30. [Google Scholar] [CrossRef]
- Foulon, É.; Rousseau, A.N.; Gagnon, P. Development of a Methodology to Assess Future Trends in Low Flows at the Watershed Scale Using Solely Climate Data. J. Hydrol. 2018, 557, 774–790. [Google Scholar] [CrossRef] [Green Version]
- Neumann, N.N.; Derkens, C.; Smith, C.; Goodison, B. Characterizing Local Scale Snow Cover Using Point Measurements during the Winter Season. Atmosphere-Ocean 2006, 44, 257–269. [Google Scholar] [CrossRef]
- De Gregorio, L.; Günther, D.; Callegari, M.; Strasser, U.; Zebisch, M.; Bruzzone, L.; Notarnicola, C. Improving SWE Estimation by Fusion of Snow Models with Topographic and Remotely Sensed Data. Remote Sens. 2019, 11, 2033. [Google Scholar] [CrossRef] [Green Version]
- Vuyovich, C.; Jacobs, J.M. Remote Sensing of Environment Snowpack and Runoff Generation Using AMSR-E Passive Microwave Observations in the Upper Helmand Watershed, Afghanistan. Remote Sens. Environ. 2011, 115, 3313–3321. [Google Scholar] [CrossRef]
- Tiuri, M.E.; Sihvola, A.H.; Nyfors, E.G.; Hallikaiken, M.T. The Complex Dielectric Constant of Snow at Microwave Frequencies. IEEE J. Ocean. Eng. 1984, 9, 377–382. [Google Scholar] [CrossRef]
- Larue, F.; Royer, A.; De Sève, D.; Langlois, A.; Roy, A.; Brucker, L. Validation of GlobSnow-2 Snow Water Equivalent over Eastern Canada. Remote Sens. Environ. 2017, 194, 264–277. [Google Scholar] [CrossRef] [Green Version]
- Derksen, C.; Walker, A.E.; Goodison, B.E.; Strapp, J.W. Integrating In Situ and Multiscale Passive Microwave Data for Estimation of Subgrid Scale Snow Water Equivalent Distribution and Variability. IEEE Trans. Geosci. Remote Sens. 2005, 43, 960–972. [Google Scholar] [CrossRef]
- Koenig, L.S.; Forster, R.R. Evaluation of Passive Microwave Snow Water Equivalent Algorithms in the Depth Hoar-Dominated Snowpack of the Kuparuk River Watershed, Alaska, USA. Remote Sens. Environ. 2004, 93, 511–527. [Google Scholar] [CrossRef]
- Pulliainen, J. Mapping of Snow Water Equivalent and Snow Depth in Boreal and Sub-Arctic Zones by Assimilating Space-Borne Microwave Radiometer Data and Ground-Based Observations. Remote Sens. Environ. 2006, 101, 257–269. [Google Scholar] [CrossRef]
- Luojus, K.; Pulliainen, J.; Takala, M.; Lemmetyinen, J.; Mortimer, C.; Derksen, C.; Mudryk, L.; Moisander, M.; Hiltunen, M.; Smolander, T.; et al. GlobSnow v3.0 Northern Hemisphere Snow Water Equivalent Dataset. Sci. Data 2021, 8, 163. [Google Scholar] [CrossRef]
- Takala, M.; Luojus, K.; Pulliainen, J.; Derksen, C.; Lemmetyinen, J.; Kärnä, J.; Koskinen, J.; Bojkov, B. Remote Sensing of Environment Estimating Northern Hemisphere Snow Water Equivalent for Climate Research through Assimilation of Space-Borne Radiometer Data and Ground-Based Measurements. Remote Sens. Environ. 2011, 115, 3517–3529. [Google Scholar] [CrossRef]
- Pulliainen, J.; Hallikainen, M. Retrieval of Regional Snow Water Equivalent from Space-Borne Passive Microwave Observations. Remote Sens. Environ. 2001, 75, 76–85. [Google Scholar] [CrossRef]
- Larue, F.; Royer, A.; De Sève, D.; Roy, A.; Picard, G.; Vionnet, V.; Cosme, E. Simulation and Assimilation of Passive Microwave Data Using a Snowpack Model Coupled to a Calibrated Radiative Transfer Model Over Northeastern Canada. Water Resour. Res. 2018, 54, 4823–4848. [Google Scholar] [CrossRef]
- Tang, W.; Carey, S.K. HydRun: A MATLAB Toolbox for Rainfall—Runoff Analysis. Hydrol. Process. 2017, 31, 2670–2682. [Google Scholar] [CrossRef]
- Nathan, R.J.; McMahon, T.A. Evaluation of Automated Techniques for Base Flow and Recession Analyses. Water Resour. Res. 1990, 26, 1465–1473. [Google Scholar] [CrossRef]
- Gan, R.; Zuo, Q. Assessing the Digital Filter Method for Base Flow Estimation in Glacier Melt Dominated Basins. Hydrol. Process. 2016, 30, 1367–1375. [Google Scholar] [CrossRef]
- Mau, D.P.; Winter, T.C. Estimating Ground-Water Recharge from Streamflow Records. Ground Water 1997, 35, 291–304. [Google Scholar] [CrossRef]
- Hammond, J.C.; Kampf, S.K. Subannual Streamflow Responses to Rainfall and Snowmelt Inputs in Snow-Dominated Watersheds of the Western United States. Water Resour. Res. 2020, 56, e2019WR026132. [Google Scholar] [CrossRef]
- Voutchkova, D.D.; Miller, S.N.; Gerow, K.G. Parameter Sensitivity of Automated Baseflow Separation for Snowmelt-Dominated Watersheds and New Filtering Procedure for Determining End of Snowmelt Period. Hydrol. Process. 2018, 33, 876–888. [Google Scholar] [CrossRef]
- Fan, Y.; Chen, Y.; Liu, Y.; Li, W. Variation of Baseflows in the Headstreams of the Tarim River Basin during 1960–2007. J. Hydrol. 2013, 487, 98–108. [Google Scholar] [CrossRef]
- Gray, D.M.; Toth, B.; Zhao, L.; Pomeroy, J.W.; Granger, R.J. Estimating Areal Snowmelt Infiltration into Frozen Soils. Hydrol. Process. 2001, 15, 3095–3111. [Google Scholar] [CrossRef]
- Nicholaichuk, W.; Gray, D.M. Snow Trapping and Moisture Infiltration Enhancement. In Proceedings of the 5th Annual Western Provinces Conference Rationalization of Soil and Water Research and Management, Calgary, AB, Canada, 18–20 November 1986. [Google Scholar]
- Zhao, L.; Gray, D.M. Estimating Snowmelt Infiltration into Frozen Soils. Hydrol. Process. 1999, 1842, 1827–1842. [Google Scholar] [CrossRef]
- De Sève, D.; Évora, N.D.; Tapsoba, D. Comparison of Three Algorithms for Estimating Snow Water Equivalent (SWE) over the La Grande River Watershed Using SSM/I Data in the Context of Hydro-Qúbec’s Hydraulic Power Management. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–27 July 2007; pp. 4257–4260. [Google Scholar] [CrossRef]
- Langlois, A.; Royer, A.; Derksen, C.; Montpetit, B.; Dupont, F.; Gota, K. Coupling the Snow Thermodynamic Model SNOWPACK with the Microwave Emission Model of Layered Snowpacks for Subarctic and Arctic Snow Water Equivalent Retrievals. Water Resour. Res. 2012, 48, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Luojus, K.A.R.I.L.; Ulliainen, J.O.P.; Akala, M.A.T.; Emmetyinen, J.U.H.A.L.; Angwa, M.W.K.; Molander, T.U.S. Algorithm Theoretical Basis Document—SWE-Algorithm. 2013. Available online: https://www.globsnow.info/docs/GS2_SWE_ATBD.pdf (accessed on 6 October 2022).
- Chen, J.; Brissette, F.P.; Chaumont, D.; Braun, M. Performance and Uncertainty Evaluation of Empirical Downscaling Methods in Quantifying the Climate Change Impacts on Hydrology over Two North American River Basins. J. Hydrol. 2013, 479, 200–214. [Google Scholar] [CrossRef]
- Badreddine, S.F.; Goïta, K.; Vachon, F.; De Sherbrooke, U. Comparison of Quebec Snow Grid Data and GlobSnow Products over the La Grande and Manicouagan Watersheds in Canda from 2006 to 2010. In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 5216–5219. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Leconte, R. Uncertainty of Downscaling Method in Quantifying the Impact of Climate Change on Hydrology. J. Hydrol. 2011, 401, 190–202. [Google Scholar] [CrossRef]
- Arsenault, R.; Brissette, F.; Martel, J.; Troin, M.; Lévesque, G.; Davidson-chaput, J.; Gonzalez, M.C.; Ameli, A.; Poulin, A. A Comprehensive, Multisource Database for Hydrometeorological Modeling of 14, 425 North American Watersheds. Sci. Data 2020, 7, 243. [Google Scholar] [CrossRef] [PubMed]
- Takala, M.; Ikonen, J.; Luojus, K.; Lemmetyinen, J.; Metsamaki, S.; Cohen, J.; Arslan, A.N.; Pulliainen, J. New Snow Water Equivalent Processing System with Improved Resolution over Europe and Its Applications in Hydrology. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 10, 428–436. [Google Scholar] [CrossRef]
- Luojus, K.; Lemmetyinen, J.; Pulliainen, J.; Takala, M.; Moisander, M.; Cohen, J.; Ikonen, J. Copernicus Global Land Operations “Cryosphere and Water” Algorithm Theoretical Basis Document. 2017. Available online: https://land.copernicus.eu/global/sites/cgls.vito.be/files/products/CGLOPS2_ATBD_SWE-NH-5km-V1_I1.01.pdf (accessed on 6 October 2022).
- Tang, W.; Qin, J.; Yang, K.; Zhu, F.; Zhou, X. Does ERA5 Outperform Satellite Products in Estimating Atmospheric Downward Longwave Radiation at the Surface? Atmos. Res. 2021, 252, 105453. [Google Scholar] [CrossRef]
- Muñoz-sabater, J.; Dutra, E.; Agustí-panareda, A.; Albergel, C.; Hersbach, H.; Martens, B.; Miralles, D.G.; Piles, M.; Rodríguez-fernández, N.J. ERA5-Land: A State-of-the-Art Global Reanalysis Dataset for Land Applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Nicolas, J.; Peubey, C.; Radu, R.; Bonavita, M.; Dee, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Kang, D.; Lee, K.; Kim, E.J. Improving Cold-Region Streamflow Estimation by Winter Precipitation Adjustment Using Passive Microwave Snow Remote Sensing Datasets. Environ. Res. Lett. 2021, 16, 044055. [Google Scholar] [CrossRef]
- Allan, C.J.; Roulet, N.T. Runoff Generation in Zero-order Precambrian Shield Catchments: The Stormflow Response of a Heterogeneous Landscape. Hydrol. Process. 1994, 8, 369–388. [Google Scholar] [CrossRef]
- Peters, D.L.; Buttle, J.M.; Taylor, C.H.; LaZerte, B.D. Runoff Production in a Forested, Shallow Soil, Canadian Shield Basin. Water Resour. Res. 1995, 31, 1291–1304. [Google Scholar] [CrossRef]
- Xiong, W.; Tang, G.; Wang, T.; Ma, Z.; Wan, W. Partitioning on the Global Scale. Water 2022, 14, 1122. [Google Scholar] [CrossRef]
- Crossett, C.C.; Betts, A.K.; Dupigny-Giroux, L.A.L.; Bomblies, A. Evaluation of Daily Precipitation from the Era5 Global Reanalysis against Ghcn Observations in the Northeastern United States. Climate 2020, 8, 148. [Google Scholar] [CrossRef]
- Hartemink, A.E.; Krasilnikov, P.; Bockheim, J.G. Soil Map of the World. Nature 1957, 179, 1168. [Google Scholar] [CrossRef]
- Domeneghetti, A.; Castellarin, A.; Brath, A. Assessing Rating-Curve Uncertainty and Its Effects on Hydraulic Model Calibration. Hydrol. Earth Syst. Sci. 2012, 16, 1191–1202. [Google Scholar] [CrossRef]
- Wu, H.; Li, Z.L. Scale Issues in Remote Sensing: A Review on Analysis, Processing and Modeling. Sensors 2009, 9, 1768–1793. [Google Scholar] [CrossRef]
- Barrett, A.P. National Operational Hydrologic Remote Sensing Center Snow Data Assimilation System (SNODAS) Products at NSIDC; National Snow and Ice Data Center: Boulder, CO, USA, 2003. [Google Scholar]
- Vionnet, V.; Mortimer, C.; Brady, M.; Arnal, L.; Brown, R. Canadian Historical Snow Water Equivalent Dataset (CanSWE, 1928–2020). Earth Syst. Sci. Data 2021, 13, 4603–4619. [Google Scholar] [CrossRef]



| Long Term Averaged Measured Values | |||||
|---|---|---|---|---|---|
| Watershed ID | Station Name | Data Period | Area (km2) | SWEmax (mm) | Peak Flow (m3/s) |
| 02RH035 | aux Écorces River at highway-bridge 169 | 1985–2013 | 1110 | 298 | 166 |
| 01AD003 | St. Francis River at outlet of Glasier lake | 1985–2016 | 1359 | 231 | 200 |
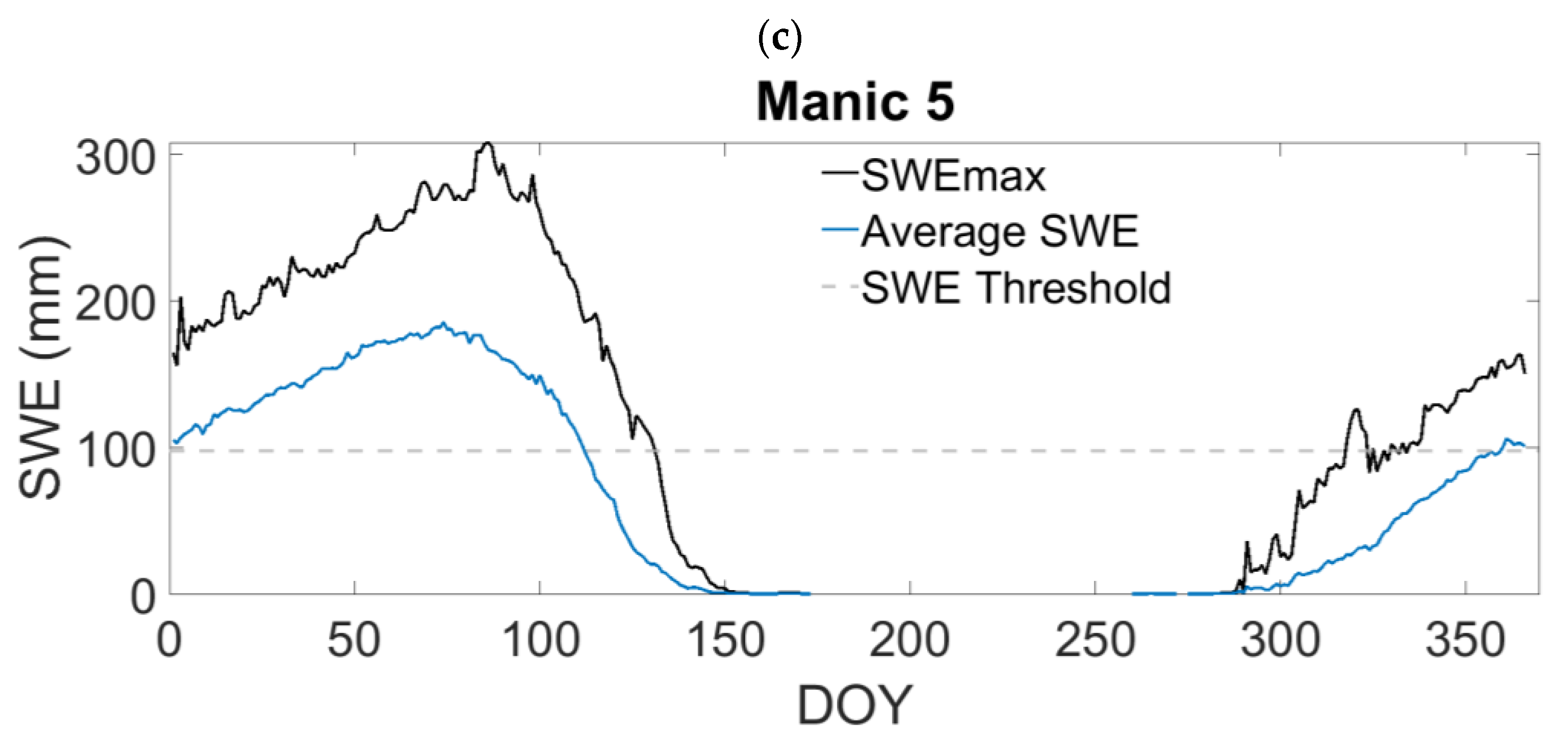
| Manic5 | Manicouagan 5 | 2006–2016 | 24,698 | 269 | 2018 |
| 01010000 | St. John River at Ninemile Bridge | 1985–2016 | 3473 | 225 | 690 |
| 02NE011 | Croche River downstream of Changy Brook | 1985–2013 | 1570 | 274 | 190 |
| 02PA007 | Batiscan River downstream of des Envies River | 1985–2013 | 4480 | 280 | 551 |
| 02PL005 | Bécancour River upstream Palmer River | 1985–2013 | 919 | 217 | 214 |
| 02PG022 | Ouelle River near St. Gabriel de Kamouraska | 1986–2013 | 795 | 252 | 207 |
| Watershed ID | Data Period | Average SWEmax | |
|---|---|---|---|
| GlobSnow Product | In Situ Measurements | ||
| 02RH035 | 1985–2013 | 171 | 298 |
| 01AD003 | 1985–2016 | 178 | 231 |
| Manic5 | 2006–2016 | 185 | 269 |
| 01010000 | 1985–2016 | 162 | 225 |
| 02NE011 | 1997–2013 | 158 | 274 |
| 02PA007 | 1985–2013 | 162 | 279 |
| 02PL005 | 1985–2013 | 151 | 216 |
| 02PG022 | 1985–2013 | 181 | 252 |
| Watershed ID | Area | GlobSnow Average SWEmax (mm) | CF | |||
|---|---|---|---|---|---|---|
| Average | Std Dev | Min | Max | |||
| 02RH035 | 1110 | 171 | 1.37 | 0.43 | 1.01 | 2.57 |
| 01AD003 | 1359 | 178 | 1.43 | 0.37 | 1.01 | 2.52 |
| Manic5 | 24,698 | 185 | 1.43 | 0.41 | 1.01 | 2.51 |
| 01010000 | 3473 | 162 | 1.78 | 0.53 | 1.10 | 3.47 |
| 02NE011 | 1570 | 158 | 1.29 | 0.29 | 1.02 | 2.27 |
| 02PA007 | 4480 | 162 | 1.36 | 0.33 | 1.01 | 2.66 |
| 02PL005 | 919 | 151 | 1.91 | 0.52 | 1.20 | 4.08 |
| 02PG022 | 795 | 181 | 1.74 | 0.40 | 1.15 | 2.77 |
| Watershed | Average SWEmax (mm) | Range (mm) | Bias (%) | Correlation Coefficient | RMSE (mm) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Glob | C-Glob | Glob | C-Glob | Glob | C-Glob | Glob | C-Glob | Glob | C-Glob | |
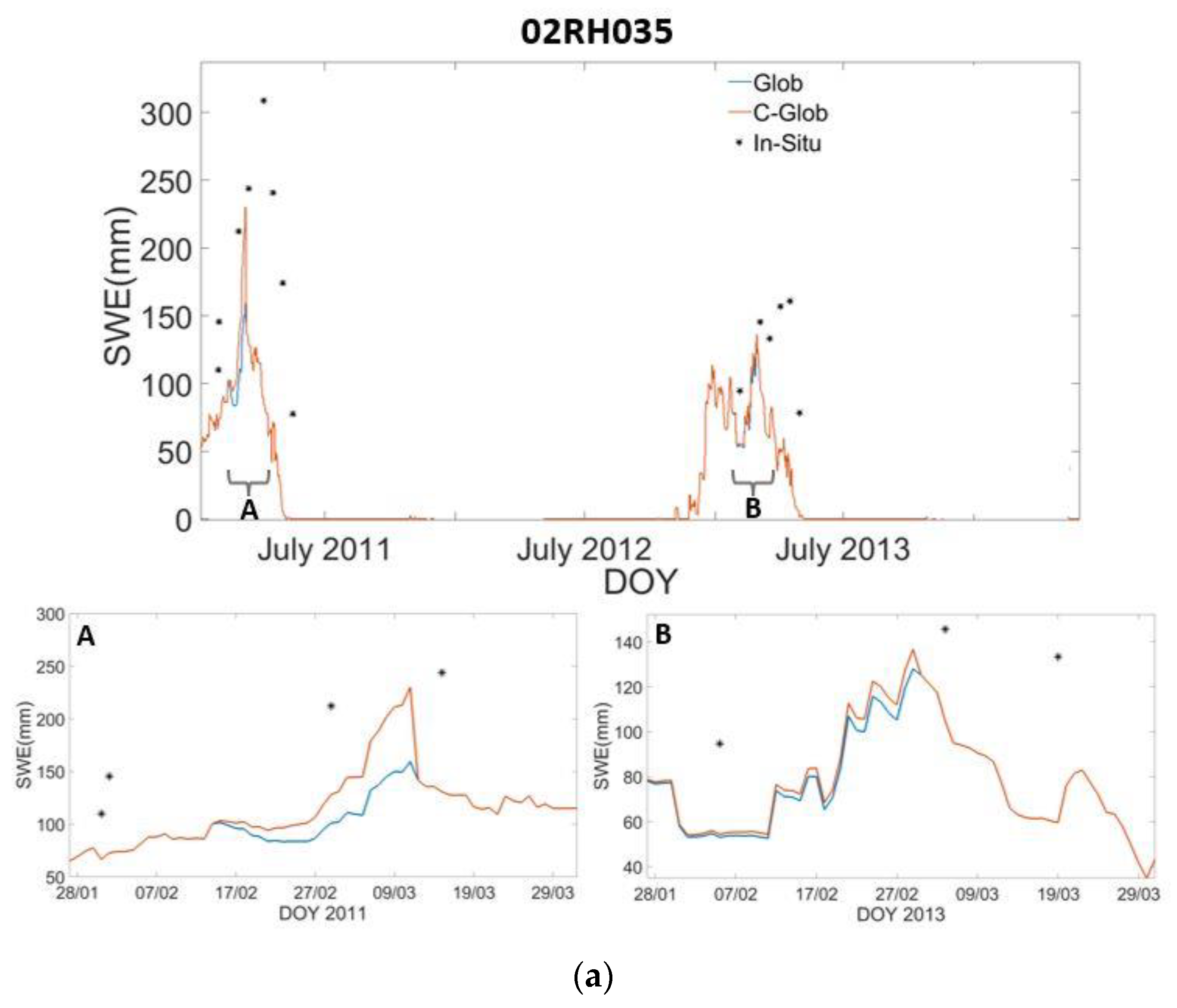
| 02RH035 | 171 | 228 | 119–276 | 137–357 | −42.4 | −23.5 | 0.525 | 0.636 | 136.8 | 85 |
| 01AD003 | 178 | 241 | 108–273 | 137–410 | −23.2 | 4.54 | 0.646 | 0.671 | 66.4 | 50.5 |
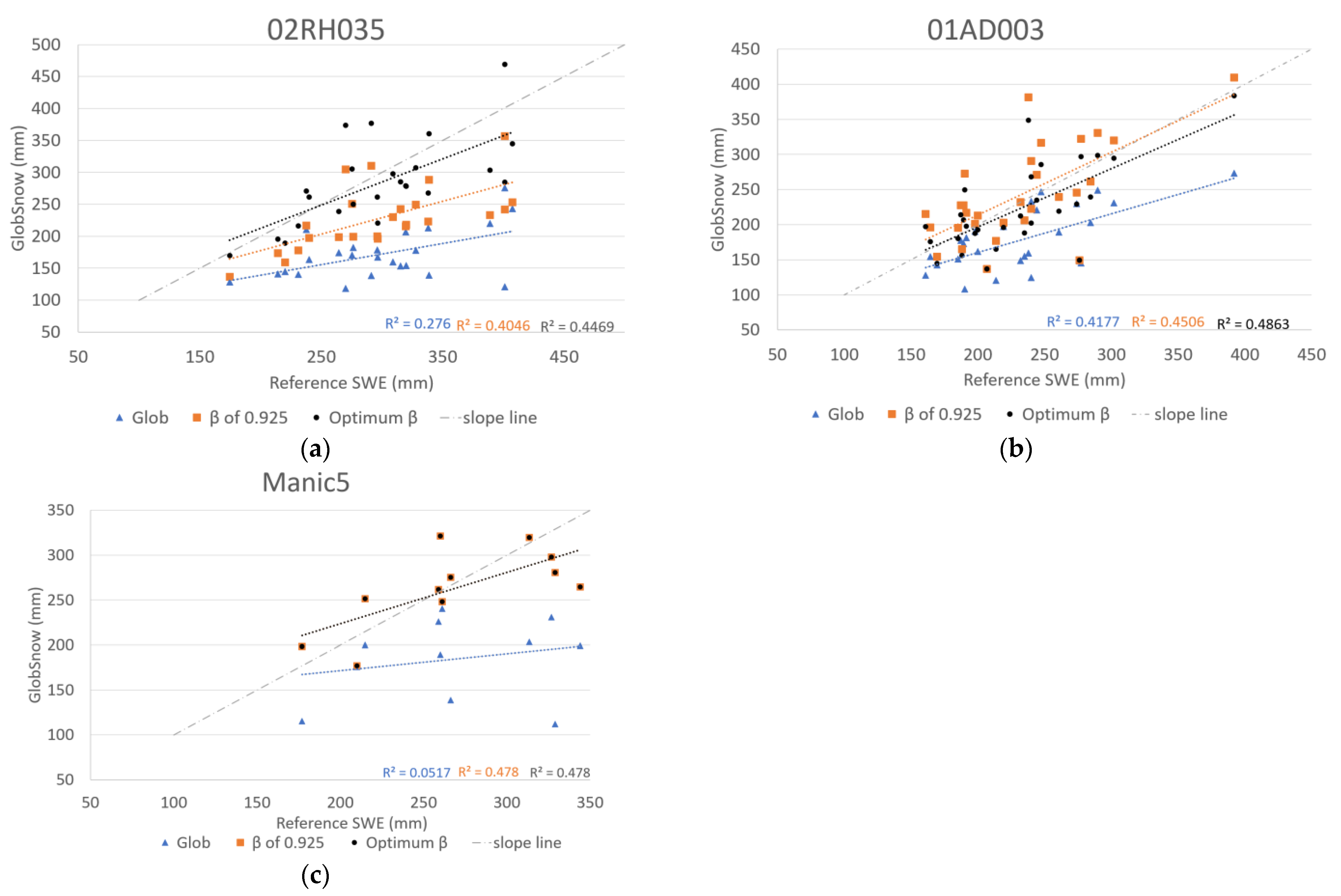
| Manic5 | 185 | 263 | 112–240 | 177–321 | −31.4 | −2.2 | 0.227 | 0.691 | 103.3 | 38.6 |
| 01010000 | 162 | 264 | 104–277 | 114–417 | −28.2 | 17.1 | 0.461 | 0.475 | 86.3 | 78.1 |
| 02NE011 | 158 | 196 | 93–277 | 93–314 | −42.2 | −28.3 | 0.756 | 0.639 | 123.5 | 93.1 |
| 02PA007 | 162 | 208 | 111–265 | 121–319 | −42.1 | −25.8 | 0.791 | 0.691 | 124.9 | 85.6 |
| 02PL005 | 151 | 275 | 103–232 | 142–558 | −30.2 | 27.1 | 0.711 | 0.442 | 74.4 | 89.1 |
| 02PG022 | 181 | 292 | 127–281 | 132–441 | −28.1 | 15.9 | 0.583 | 0.306 | 83.9 | 85.8 |
| Watershed | In Situ SWE Max | % Difference from In Situ SWEmax Measurements | |||||||
|---|---|---|---|---|---|---|---|---|---|
| GlobSnow | Baseflow Separation Factor β | ||||||||
| 0.800 | 0.825 | 0.850 | 0.900 | 0.925 | 0.975 | 0.995 | |||
| 02RH035 | 298.1 | −42.4 | −42.4 | −38.0 | −35.6 | −29.2 | −23.5 | −8.1 | −1.9 |
| 01AD003 | 230.9 | −23.2 | −19.1 | −17.1 | −14.3 | −3.7 | 4.5 | 27.1 | 40 |
| Manic5 | 269.2 | −31.4 | −24.3 | −22.1 | −16.8 | −6.5 | −2.2 | 13.4 | 21.6 |
| 02PA007 | 279.7 | −42.1 | −41.4 | −40.4 | −38.7 | −31.7 | −25.8 | −8.4 | −0.7 |
| 02PG022 | 251.8 | −28.1 | −9.2 | −6.1 | −2.0 | 8.8 | 15.9 | 34.0 | 42.4 |
| 02PL005 | 216.6 | −30.2 | −0.1 | 3.9 | 8.42 | 19.8 | 27.1 | 46.0 | 60.7 |
| 02NE011 | 274.0 | −42.2 | −42.2 | −40.4 | −39.3 | −33.7 | −28.3 | −14.1 | −5.4 |
| 1010000 | 225.4 | −28.2 | −10.1 | −6.3 | −1.8 | 9.5 | 17.1 | 35.8 | 46.1 |
| Watershed | Average SWEmax (mm) | Range (mm) | Bias (%) | Correlation Coefficient | RMSE (mm) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| β = 0.925 | βopt | β = 0.925 | βopt | β = 0.925 | βopt | β = 0.925 | βopt | β = 0.925 | βopt | |
| 02RH035 | 228.1 | 292.5 | 137–357 | 173–484 | −23.5 | −1.9 | 0.636 | 0.653 | 85 | 55.2 |
| 01AD003 | 241.4 | 222.5 | 137–410 | 137–384 | 4.5 | −3.7 | 0.671 | 0.697 | 50.5 | 44.2 |
| Manic5 | 263.2 | 263.2 | 177–321 | 177–321 | −2.2 | −2.2 | 0.691 | 0.691 | 38.6 | 38.6 |
| 02PA007 | 207.5 | 281.5 | 121–319 | 121–443 | −25.8 | 0.7 | 0.691 | 0.570 | 85.6 | 62.1 |
| 02PG022 | 291.9 | 246 | 132–441 | 130–365 | 15.9 | −2.0 | 0.306 | 0.286 | 85.8 | 65.7 |
| 02PL005 | 275.2 | 216.5 | 143–558 | 139–443 | 27.1 | 0.1 | 0.442 | 0.360 | 89.1 | 58.0 |
| 02NE011 | 196.6 | 259 | 93–315 | 93–406 | −28.3 | −5.3 | 0.639 | 0.560 | 93.1 | 68.8 |
| 01010000 | 263 | 221 | 114–417 | 114–345 | 17.1 | −1.8 | 0.475 | 0.485 | 78.1 | 59.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Whittaker, C.; Leconte, R. A Hydrograph-Based Approach to Improve Satellite-Derived Snow Water Equivalent at the Watershed Scale. Water 2022, 14, 3575. https://doi.org/10.3390/w14213575
Whittaker C, Leconte R. A Hydrograph-Based Approach to Improve Satellite-Derived Snow Water Equivalent at the Watershed Scale. Water. 2022; 14(21):3575. https://doi.org/10.3390/w14213575
Chicago/Turabian StyleWhittaker, Charles, and Robert Leconte. 2022. "A Hydrograph-Based Approach to Improve Satellite-Derived Snow Water Equivalent at the Watershed Scale" Water 14, no. 21: 3575. https://doi.org/10.3390/w14213575





