Hybridized Adaptive Neuro-Fuzzy Inference System with Metaheuristic Algorithms for Modeling Monthly Pan Evaporation
Abstract
:1. Introduction
2. Case Study
3. Methods
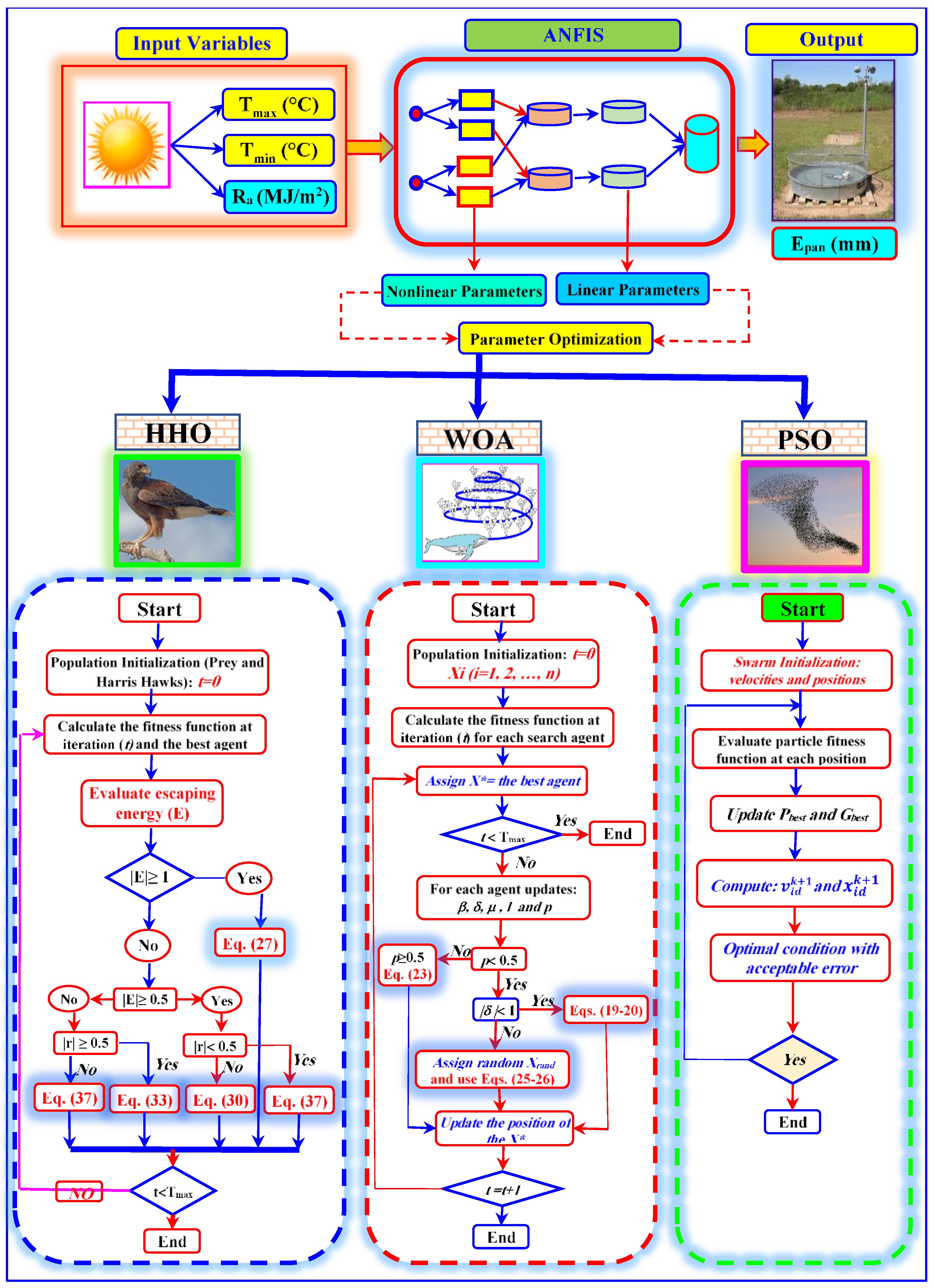
3.1. Adaptive Neuro-Fuzzy Inference System (ANFIS)
3.2. Particle Swarm Optimization (PSO)
3.3. Whale Optimization Algorithm (WOA)
3.4. Harris Hawk Optimization (HHO)
3.5. ANFIS Optimization Using PSO, WOA, and HHO
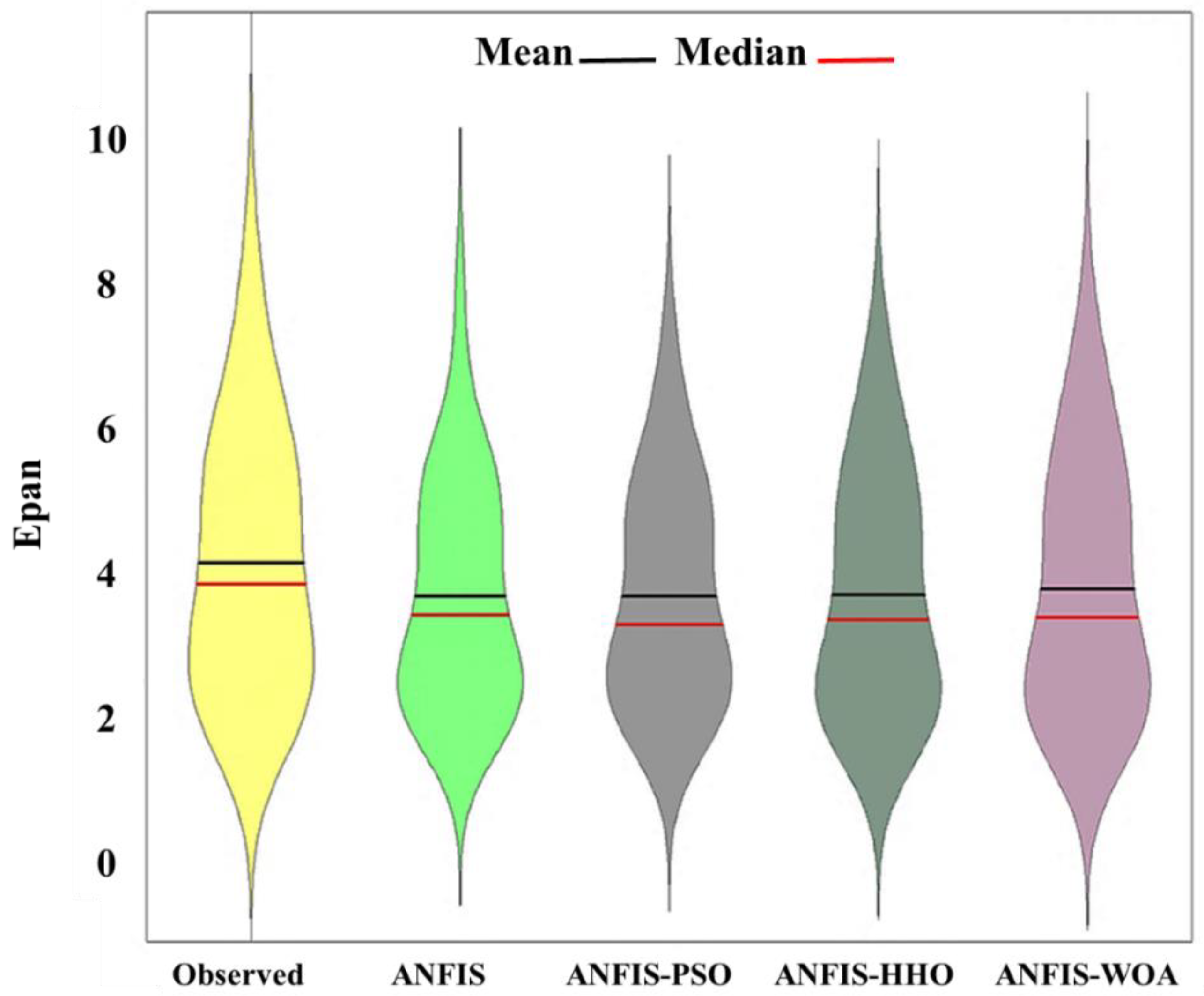
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zounemat-Kermani, M.; Keshtegar, B.; Kisi, O.; Scholz, M. Towards a comprehensive assessment of statistical versus soft computing models in hydrology: Application to monthly pan evaporation prediction. Water 2021, 13, 2451. [Google Scholar] [CrossRef]
- Jasmine, M.; Mohammadian, A.; Bonakdari, H. On the Prediction of Evaporation in Arid Climate Using Machine Learning Model. Math. Comput. Appl. 2022, 27, 32. [Google Scholar] [CrossRef]
- Piri, J.; Amin, S.; Moghaddamnia, A.; Keshavarz, A.; Han, D.; Remesan, R. Daily pan evaporation modeling in a hot and dry climate. J. Hydrol. Eng. 2009, 14, 803–811. [Google Scholar] [CrossRef]
- Schwalm, C.R.; Huntinzger, D.N.; Michalak, A.M.; Fisher, J.B.; Kimball, J.S.; Mueller, B.; Zhang, K.; Zhang, Y. Sensitivity of inferred climate model skill to evaluation decisions: A case study using CMIP5 evapotranspiration. Environ. Res. Lett. 2013, 8, 024028. [Google Scholar] [CrossRef]
- Quan, Q.; Liang, W.; Yan, D.; Lei, J. Influences of joint action of natural and social factors on atmospheric process of hydrological cycle in Inner Mongolia, China. Urban Clim. 2022, 41, 101043. [Google Scholar] [CrossRef]
- Adnan, R.M.; Malik, A.; Kumar, A.; Parmar, K.S.; Kisi, O. Pan evaporation modeling by three different neuro-fuzzy intelligent systems using climatic inputs. Arab. J. Geosci. 2019, 12, 1–14. [Google Scholar] [CrossRef]
- Kisi, O.; Genc, O.; Dinc, S.; Zounemat-Kermani, M. Daily pan evaporation modeling using chi-squared automatic interaction detector, neural networks, classification and regression tree. Comput. Electron. Agric. 2016, 122, 112–117. [Google Scholar] [CrossRef]
- Sudheer, K.; Gosain, A.; Mohana Rangan, D.; Saheb, S. Modelling evaporation using an artificial neural network algorithm. Hydrol. Process. 2002, 16, 3189–3202. [Google Scholar] [CrossRef]
- Wang, L.; Kisi, O.; Zounemat-Kermani, M.; Li, H. Pan evaporation modeling using six different heuristic computing methods in different climates of China. J. Hydrol. 2017, 544, 407–427. [Google Scholar] [CrossRef]
- Keskin, M.E.; Terzi, Ö. Artificial neural network models of daily pan evaporation. J. Hydrol. Eng. 2006, 11, 65–70. [Google Scholar] [CrossRef]
- Al Sudani, Z.A.; Salem, G.S.A. Evaporation Rate Prediction Using Advanced Machine Learning Models: A Comparative Study. Adv. Meteorol. 2022, 2022, 1433835. [Google Scholar] [CrossRef]
- Chen, J.-L.; Yang, H.; Lv, M.-Q.; Xiao, Z.-L.; Wu, S.J. Estimation of monthly pan evaporation using support vector machine in Three Gorges Reservoir Area, China. Theor. Appl. Climatol. 2019, 138, 1095–1107. [Google Scholar] [CrossRef]
- Guven, A.; Kişi, Ö. Daily pan evaporation modeling using linear genetic programming technique. Irrig. Sci. 2011, 29, 135–145. [Google Scholar] [CrossRef]
- Goyal, M.K.; Bharti, B.; Quilty, J.; Adamowski, J.; Pandey, A. Modeling of daily pan evaporation in sub tropical climates using ANN, LS-SVR, Fuzzy Logic, and ANFIS. Expert Syst. Appl. 2014, 41, 5267–5276. [Google Scholar] [CrossRef]
- Allawi, M.F.; Ahmed, M.L.; Aidan, I.A.; Deo, R.C.; El-Shafie, A. Developing reservoir evaporation predictive model for successful dam management. Stoch. Environ. Res. Risk Assess. 2021, 35, 499–514. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A.; Kisi, O. Daily pan evaporation estimation using heuristic methods with gamma test. J. Irrig. Drain Eng 2018, 144, 4018023. [Google Scholar] [CrossRef]
- Wu, L.; Huang, G.; Fan, J.; Ma, X.; Zhou, H.; Zeng, W. Hybrid extreme learning machine with meta-heuristic algorithms for monthly pan evaporation prediction. Comput. Electron. Agric. 2020, 168, 105115. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Al-Juboori, A.M.; Beyaztas, U.; Al-Ansari, N.; Chau, K.-W.; Qi, C.; Ali, M.; Salih, S.Q.; Shahid, S. Prediction of evaporation in arid and semi-arid regions: A comparative study using different machine learning models. Eng. Appl. Comput. Fluid Mech. 2020, 14, 70–89. [Google Scholar] [CrossRef] [Green Version]
- Emadi, A.; Zamanzad-Ghavidel, S.; Fazeli, S.; Zarei, S.; Rashid-Niaghi, A. Multivariate modeling of pan evaporation in monthly temporal resolution using a hybrid evolutionary data-driven method (case study: Urmia Lake and Gavkhouni basins). Environ. Monit. Assess. 2021, 193, 1–32. [Google Scholar] [CrossRef]
- Dehghanipour, M.H.; Karami, H.; Ghazvinian, H.; Kalantari, Z.; Dehghanipour, A.H. Two comprehensive and practical methods for simulating pan evaporation under different climatic conditions in iran. Water 2021, 13, 2814. [Google Scholar] [CrossRef]
- Shiri, J.; Dierickx, W.; Pour-Ali Baba, A.; Neamati, S.; Ghorbani, M. Estimating daily pan evaporation from climatic data of the State of Illinois, USA using adaptive neuro-fuzzy inference system (ANFIS) and artificial neural network (ANN). Hydrol. Res. 2011, 42, 491–502. [Google Scholar] [CrossRef]
- Kişi, Ö. Evolutionary neural networks for monthly pan evaporation modeling. J. Hydrol. 2013, 498, 36–45. [Google Scholar] [CrossRef]
- Ikram, R.M.A.; Goliatt, L.; Kisi, O.; Trajkovic, S.; Shahid, S. Covariance Matrix Adaptation Evolution Strategy for Improving Machine Learning Approaches in Streamflow Prediction. Mathematics 2022, 10, 2971. [Google Scholar] [CrossRef]
- Ikram, R.M.A.; Dai, H.L.; Ewees, A.A.; Shiri, J.; Kisi, O.; Zounemat-Kermani, M. Application of improved version of multi verse optimizer algorithm for modeling solar radiation. Energy Reports 2022, 8, 12063–12080. [Google Scholar] [CrossRef]
- Zhao, Y.; Foong, L.K. Predicting Electrical Power Output of Combined Cycle Power Plants Using a Novel Artificial Neural Network Optimized by Electrostatic Discharge Algorithm. Measurement 2022, 198, 111405. [Google Scholar] [CrossRef]
- Foong, L.K.; Zhao, Y.; Bai, C.; Xu, C. Efficient metaheuristic-retrofitted techniques for concrete slump simulation. Smart Struct. Syst. Int. J. 2021, 27, 745–759. [Google Scholar]
- Zhao, Y.; Zhong, X.; Foong, L.K. Predicting the splitting tensile strength of concrete using an equilibrium optimization model. Steel Compos. Struct. Int. J. 2021, 39, 81–93. [Google Scholar]
- Adnan, R.M.; Mostafa, R.R.; Islam, A.R.M.T.; Kisi, O.; Kuriqi, A.; Heddam, S. Estimating reference evapotranspiration using hybrid adaptive fuzzy inferencing coupled with heuristic algorithms. Comput. Electron. Agric. 2021, 191, 106541. [Google Scholar] [CrossRef]
- Adnan, R.M.; Mostafa, R.R.; Elbeltagi, A.; Yaseen, Z.M.; Shahid, S.; Kisi, O. Development of new machine learning model for streamflow prediction: Case studies in Pakistan. Stoch. Environ. Res. Risk Assess. 2022, 36, 999–1033. [Google Scholar] [CrossRef]
- Zhao, Y.; Yan, Q.; Yang, Z.; Yu, X.; Jia, B. A novel artificial bee colony algorithm for structural damage detection. Adv. Civ. Eng. 2020, 2020, 3743089. [Google Scholar] [CrossRef] [Green Version]
- Devaraj, R.; Mahalingam, S.K.; Esakki, B.; Astarita, A.; Mirjalili, S. A hybrid GA-ANFIS and F-Race tuned harmony search algorithm for Multi-Response optimization of Non-Traditional Machining process. Expert Syst. Appl. 2022, 199, 116965. [Google Scholar] [CrossRef]
- Bazrafshan, O.; Ehteram, M.; Latif, S.D.; Huang, Y.F.; Teo, F.Y.; Ahmed, A.N.; El-Shafie, A. Predicting crop yields using a new robust Bayesian averaging model based on multiple hybrid ANFIS and MLP models. Ain Shams Eng. J. 2022, 13, 101724. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A.; Kisi, O. Monthly pan-evaporation estimation in Indian central Himalayas using different heuristic approaches and climate based models. Comput. Electron. Agric. 2017, 143, 302–313. [Google Scholar] [CrossRef]
- Arya Azar, N.; Ghordoyee Milan, S.; Kayhomayoon, Z. Predicting monthly evaporation from dam reservoirs using LS-SVR and ANFIS optimized by Harris hawks optimization algorithm. Environ. Monit. Assess. 2021, 193, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Seifi, A.; Ehteram, M.; Soroush, F.; Haghighi, A.T. Multi-model ensemble prediction of pan evaporation based on the Copula Bayesian Model Averaging approach. Eng. Appl. Artif. Intell. 2022, 114, 105124. [Google Scholar] [CrossRef]
- Khalaf, M.M. Algorithms and optimal choice for power plants based on M-polar fuzzy soft set decision making criterions. Acta Electron Malays. 2020, 4, 11–23. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November 1995; pp. 1942–1948. [Google Scholar]
- Purba, S.; Amarilies, H.; Rachmawati, N.; Redi, A. Implementation of particle swarm optimization algorithm in cross-docking distribution problem. Acta Inform. Malays 2021, 5, 16–20. [Google Scholar] [CrossRef]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Jiang, R.; Yang, M.; Wang, S.; Chao, T. An improved whale optimization algorithm with armed force program and strategic adjustment. Appl. Math. Model. 2020, 81, 603–623. [Google Scholar] [CrossRef]
- Zhao, Y.; Moayedi, H.; Bahiraei, M.; Foong, L.K. Employing TLBO and SCE for optimal prediction of the compressive strength of concrete. Smart Struct. Syst. 2020, 26, 753–763. [Google Scholar]
- Yin, L.; Wang, L.; Huang, W.; Liu, S.; Yang, B.; Zheng, W. Spatiotemporal analysis of haze in Beijing based on the multi-convolution model. Atmosphere 2021, 12, 1408. [Google Scholar] [CrossRef]
- Aljarah, I.; Faris, H.; Mirjalili, S. Optimizing connection weights in neural networks using the whale optimization algorithm. Soft Comput. 2018, 22, 1–15. [Google Scholar] [CrossRef]
- Gharehchopogh, F.S.; Gholizadeh, H. A comprehensive survey: Whale Optimization Algorithm and its applications. Swarm and Evol. Comput. 2019, 48, 1–24. [Google Scholar] [CrossRef]


| Study | Developed Model(s) | Performance Comparison |
|---|---|---|
| Jasmin et al. [2] | ANFIS and hybridized ANFIS with FFA, GA, and PSO | The ANFIS-PSO model with R2 = 0.99 and RMSE = 9.73 performed the best. |
| Wang et al. [9] | Multi-layer perceptron (MLP), generalized regression neural network (GRNN), fuzzy genetic (FG), LSSVM, MARS, ANFIS with grid partition (ANFIS-GP) | The ANFIS-GP model did not perform better than MLP and GRNN. It provided less accurate results than SVM. Therefore, the use of metaheuristic algorithms was recommended for improving ANFIS. |
| Malik et al. [33] | MLP, co-active ANFIS (CANFIS), radial basis neural network (RBNN), and self-organizing map neural network (SOMNN) | The hybridized CANFIS model with RMSE = 0.627 was ranked among the most accurate models. |
| Arya Azar et al. [34] | Least-squares support vector regression (LS-SVR), ANFIS, and ANFIS-HHO | The hybridized ANFIS-HHO (RMSE = 2.35 and NSE = 0.95) model successfully outperformed the other models. |
| Seifi et al. [35] | Copula-based Bayesian Model Averaging (CBMA) and hybridized ANFIS with seagull optimization algorithm (SOA), crow search algorithm (CA), FA, and PSO | The hybridized models improved prediction accuracy by 20.35–64.36%. Thus, solidifying ANFIS with metaheuristic algorithms was recommended. |
| Jingzhou Station | Nanxian Station | Yueyang Station | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Whole Data | Training | Testing | Whole Data | Training | Testing | Whole Data | Training | Testing | |
| Tmin | |||||||||
| Mean | 13.336 | 13.016 | 13.639 | 13.562 | 13.444 | 13.918 | 14.384 | 14.193 | 14.960 |
| Min. | −2.360 | −2.360 | 0.742 | −1.303 | −1.303 | 0.761 | −0.935 | −0.935 | 1.426 |
| Max. | 26.039 | 26.039 | 25.165 | 27.148 | 26.706 | 27.148 | 28.165 | 27.952 | 28.165 |
| Skewness | −0.102 | −0.850 | −0.071 | −0.051 | −0.050 | −0.047 | −0.051 | −0.046 | −0.056 |
| Std. dev. | 7.928 | 8.743 | 7.671 | 8.325 | 8.373 | 8.170 | 8.375 | 8.444 | 8.138 |
| Tmax | |||||||||
| Mean | 21.397 | 21.301 | 21.685 | 20.774 | 20.681 | 21.053 | 20.769 | 20.716 | 20.929 |
| Min. | 4.448 | 4.448 | 6.448 | 3.162 | 3.162 | 5.706 | 2.852 | 2.852 | 5.677 |
| Max. | 36.284 | 36.284 | 34.726 | 35.084 | 35.084 | 34.445 | 35.174 | 35.174 | 34.116 |
| Skewness | −0.138 | −0.125 | −0.176 | −0.139 | −0.130 | −0.162 | −0.122 | −0.111 | −0.154 |
| Std. dev. | 8.446 | 8.514 | 8.232 | 8.534 | 8.614 | 8.283 | 8.511 | 8.600 | 8.236 |
| Extraterrestrial radiation | |||||||||
| Mean | 31.398 | 31.398 | 31.397 | 31.696 | 31.696 | 31.695 | 31.888 | 31.888 | 31.887 |
| Min. | 19.753 | 19.753 | 19.753 | 20.382 | 20.382 | 20.382 | 20.797 | 20.797 | 20.797 |
| Max. | 41.133 | 41.133 | 41.133 | 41.016 | 41.016 | 41.016 | 40.934 | 40.934 | 40.934 |
| Skewness | −0.185 | −0.185 | −0.187 | −0.199 | −0.200 | −0.201 | −0.210 | −0.210 | −0.212 |
| Std. dev. | 7.639 | 7.639 | 7.640 | 7.377 | 7.377 | 7.378 | 7.202 | 7.202 | 7.203 |
| Evaporation | |||||||||
| Mean | 3.630 | 3.653 | 3.562 | 3.385 | 3.256 | 3.773 | 3.956 | 3.872 | 4.207 |
| Min. | 0.884 | 0.961 | 0.884 | 0.803 | 0.803 | 0.997 | 0.911 | 0.911 | 1.116 |
| Max. | 10.619 | 10.619 | 7.861 | 9.087 | 9.087 | 9.045 | 11.119 | 11.119 | 11.029 |
| Skewness | 0.605 | 0.666 | 0.332 | 0.706 | 0.753 | 0.543 | 0.846 | 0.894 | 0.729 |
| Std. dev. | 1.816 | 1.857 | 1.683 | 1.810 | 1.751 | 1.926 | 2.185 | 2.177 | 2.189 |
| Method/Algorithm | Parameter | Value |
|---|---|---|
| ANFIS | Error goal | 0 |
| Increase rate | 1.1 | |
| Initial step | 0.01 | |
| ANFIS-DEcrease rate | 0.9 | |
| Maximum epochs | 100 | |
| PSO | Cognitive component () | 2 |
| Social component () | 2 | |
| inertia weight | 0.2–0.9 | |
| HHO | 1.5 | |
| WOA | ||
| All algorithms | Population | 30 |
| Number of iterations | 150 | |
| Number of runs for each algorithm | 10 |
| Model Inputs | Training | Test | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | NSE | RMSE | MAE | R2 | NSE | |
| ANFIS | ||||||||
| Tmin | 0.8500 | 0.6285 | 0.7907 | 0.7884 | 0.8846 | 0.6902 | 0.7464 | 0.7436 |
| Tmax | 0.6340 | 0.4837 | 0.8836 | 0.8817 | 0.6508 | 0.5210 | 0.8956 | 0.8922 |
| Ra | 1.0604 | 0.7956 | 0.6740 | 0.6712 | 0.8408 | 0.6658 | 0.7545 | 0.7521 |
| Tmin, Tmax | 0.5162 | 0.3991 | 0.9246 | 0.9193 | 0.5135 | 0.4124 | 0.9185 | 0.9163 |
| Tmin, Ra | 0.7856 | 0.5680 | 0.8211 | 0.8184 | 0.9212 | 0.7285 | 0.7845 | 0.7816 |
| Tmax, Ra | 0.5744 | 0.4378 | 0.9044 | 0.9017 | 0.6186 | 0.4853 | 0.9109 | 0.9070 |
| Tmin, Tmax, Ra | 0.4593 | 0.3562 | 0.9388 | 0.9362 | 0.4412 | 0.3510 | 0.9455 | 0.9426 |
| Opt inputs, α | 0.4698 | 0.3587 | 0.9360 | 0.9321 | 0.4582 | 0.3534 | 0.9417 | 0.9378 |
| Mean | 0.6687 | 0.5035 | 0.8592 | 0.8561 | 0.6661 | 0.5260 | 0.8622 | 0.8592 |
| ANFIS-PSO | ||||||||
| Tmin | 0.8111 | 0.6063 | 0.8093 | 0.8074 | 0.7851 | 0.6249 | 0.7798 | 0.7752 |
| Tmax | 0.6182 | 0.4753 | 0.8892 | 0.8876 | 0.5628 | 0.4577 | 0.9020 | 0.8996 |
| Ra | 1.0502 | 0.7867 | 0.6802 | 0.6775 | 0.8327 | 0.6560 | 0.7597 | 0.7564 |
| Tmin, Tmax | 0.5121 | 0.3917 | 0.9269 | 0.9237 | 0.5180 | 0.4244 | 0.9236 | 0.9215 |
| Tmin, Ra | 0.7493 | 0.5501 | 0.8312 | 0.8284 | 0.7706 | 0.5989 | 0.8105 | 0.7905 |
| Tmax, Ra | 0.5305 | 0.4110 | 0.9184 | 0.9167 | 0.5326 | 0.4419 | 0.9183 | 0.9158 |
| Tmin, Tmax, Ra | 0.4590 | 0.3529 | 0.9389 | 0.9358 | 0.4365 | 0.3218 | 0.9561 | 0.9542 |
| Opt inputs, α | 0.4627 | 0.3565 | 0.9382 | 0.9362 | 0.4476 | 0.3327 | 0.9521 | 0.9493 |
| Mean | 0.6491 | 0.4913 | 0.8665 | 0.8642 | 0.6107 | 0.4823 | 0.8753 | 0.8703 |
| ANFIS-HHO | ||||||||
| Tmin | 0.8029 | 0.5987 | 0.8131 | 0.8115 | 0.7368 | 0.5781 | 0.8168 | 0.8143 |
| Tmax | 0.6163 | 0.4658 | 0.8899 | 0.8862 | 0.5268 | 0.4247 | 0.9094 | 0.9067 |
| Ra | 0.8419 | 0.6159 | 0.7794 | 0.7754 | 0.7185 | 0.5647 | 0.8263 | 0.8242 |
| Tmin, Tmax | 0.5051 | 0.3865 | 0.9290 | 0.9268 | 0.3749 | 0.2993 | 0.9609 | 0.9573 |
| Tmin, Ra | 0.7498 | 0.5445 | 0.8370 | 0.8341 | 0.6813 | 0.5383 | 0.8439 | 0.8422 |
| Tmax, Ra | 0.5132 | 0.3903 | 0.9236 | 0.9205 | 0.4892 | 0.3815 | 0.9261 | 0.9236 |
| Tmin, Tmax, Ra | 0.4569 | 0.3528 | 0.9395 | 0.9372 | 0.3646 | 0.2958 | 0.9623 | 0.9604 |
| Opt inputs, α | 0.4439 | 0.3405 | 0.9429 | 0.9404 | 0.3322 | 0.2746 | 0.9691 | 0.9675 |
| Mean | 0.6163 | 0.4619 | 0.8818 | 0.8790 | 0.5280 | 0.4196 | 0.9019 | 0.8995 |
| ANFIS-WOA | ||||||||
| Tmin | 0.6970 | 0.4977 | 0.8590 | 0.8563 | 0.7155 | 0.5646 | 0.8274 | 0.8243 |
| Tmax | 0.5722 | 0.4326 | 0.9051 | 0.9026 | 0.5148 | 0.4160 | 0.9125 | 0.9103 |
| Ra | 0.8342 | 0.6083 | 0.7945 | 0.7918 | 0.7119 | 0.5585 | 0.8294 | 0.8261 |
| Tmin, Tmax | 0.4385 | 0.3181 | 0.9443 | 0.9421 | 0.3643 | 0.2961 | 0.9618 | 0.9595 |
| Tmin, Ra | 0.6943 | 0.4914 | 0.8602 | 0.8579 | 0.6706 | 0.5291 | 0.8480 | 0.8452 |
| Tmax, Ra | 0.4947 | 0.3565 | 0.9291 | 0.9274 | 0.4147 | 0.3435 | 0.9447 | 0.9417 |
| Tmin, Tmax, Ra | 0.4203 | 0.3122 | 0.9488 | 0.9457 | 0.3214 | 0.2604 | 0.9691 | 0.9658 |
| Opt inputs, α | 0.4098 | 0.3050 | 0.9513 | 0.9492 | 0.3127 | 0.2561 | 0.9726 | 0.9704 |
| Mean | 0.5701 | 0.4152 | 0.8990 | 0.8966 | 0.5032 | 0.4030 | 0.9082 | 0.9054 |
| Model Inputs | Training | Test | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | NSE | RMSE | MAE | R2 | NSE | |
| ANFIS | ||||||||
| Tmin | 0.6732 | 0.5114 | 0.8523 | 0.8503 | 1.0000 | 0.7716 | 0.8126 | 0.8103 |
| Tmax | 0.5479 | 0.4118 | 0.9023 | 0.9014 | 0.8130 | 0.6330 | 0.9092 | 0.9067 |
| Ra | 1.0960 | 0.8547 | 0.6082 | 0.6058 | 1.2974 | 0.9336 | 0.6258 | 0.6225 |
| Tmin, Tmax | 0.4819 | 0.3566 | 0.9243 | 0.9221 | 0.7961 | 0.5879 | 0.9087 | 0.9064 |
| Tmin, Ra | 0.6509 | 0.4962 | 0.8602 | 0.8583 | 0.9712 | 0.7511 | 0.8053 | 0.8032 |
| Tmax, Ra | 0.5272 | 0.3971 | 0.9094 | 0.9067 | 0.7928 | 0.6259 | 0.9053 | 0.9027 |
| Tmin, Tmax, Ra | 0.4395 | 0.3318 | 0.9370 | 0.9342 | 0.7738 | 0.5837 | 0.9114 | 0.9093 |
| Opt inputs, α | 0.4548 | 0.3340 | 0.9328 | 0.9301 | 0.7792 | 0.5877 | 0.9091 | 0.9075 |
| 0.6089 | 0.4617 | 0.8658 | 0.8636 | 0.9029 | 0.6843 | 0.8484 | 0.8461 | |
| ANFIS-PSO | ||||||||
| Tmin | 0.6548 | 0.4979 | 0.8602 | 0.8583 | 0.9631 | 0.7320 | 0.8312 | 0.8283 |
| Tmax | 0.5338 | 0.4048 | 0.9061 | 0.9042 | 0.7775 | 0.5987 | 0.9183 | 0.9156 |
| Ra | 1.0342 | 0.7981 | 0.6512 | 0.6503 | 1.2263 | 0.8799 | 0.6744 | 0.6717 |
| Tmin, Tmax | 0.4781 | 0.3500 | 0.9255 | 0.9228 | 0.7829 | 0.5947 | 0.9384 | 0.9352 |
| Tmin, Ra | 0.6389 | 0.4878 | 0.8627 | 0.8601 | 0.9518 | 0.7155 | 0.8202 | 0.8179 |
| Tmax, Ra | 0.5236 | 0.3903 | 0.9106 | 0.9084 | 0.7841 | 0.6032 | 0.9185 | 0.9156 |
| Tmin, Tmax, Ra | 0.4333 | 0.3174 | 0.9388 | 0.9356 | 0.7635 | 0.5672 | 0.9321 | 0.9305 |
| Opt inputs, α | 0.4395 | 0.3318 | 0.9370 | 0.9342 | 0.7692 | 0.5742 | 0.9286 | 0.9253 |
| 0.5920 | 0.4473 | 0.8740 | 0.8717 | 0.8773 | 0.6582 | 0.8702 | 0.8675 | |
| ANFIS-HHO | ||||||||
| Tmin | 0.6382 | 0.4943 | 0.8672 | 0.8647 | 0.8859 | 0.6745 | 0.8565 | 0.8537 |
| Tmax | 0.5318 | 0.4014 | 0.9078 | 0.9053 | 0.7757 | 0.5975 | 0.9226 | 0.9205 |
| Ra | 0.6944 | 0.5117 | 0.8428 | 0.8402 | 0.9909 | 0.7659 | 0.8126 | 0.8103 |
| Tmin, Tmax | 0.4557 | 0.3478 | 0.9323 | 0.9304 | 0.7624 | 0.5782 | 0.9418 | 0.9402 |
| Tmin, Ra | 0.6390 | 0.4950 | 0.8669 | 0.8652 | 0.8689 | 0.6570 | 0.8583 | 0.8563 |
| Tmax, Ra | 0.5130 | 0.3831 | 0.9142 | 0.9127 | 0.7660 | 0.5912 | 0.9251 | 0.9227 |
| Tmin, Tmax, Ra | 0.4273 | 0.3159 | 0.9405 | 0.9387 | 0.7484 | 0.5689 | 0.9413 | 0.9394 |
| Opt inputs, α | 0.4197 | 0.3094 | 0.9426 | 0.9403 | 0.7243 | 0.5637 | 0.9432 | 0.9408 |
| 0.5399 | 0.4073 | 0.9018 | 0.8997 | 0.8153 | 0.6246 | 0.9002 | 0.8980 | |
| ANFIS-WOA | ||||||||
| Tmin | 0.5540 | 0.4073 | 0.8999 | 0.8973 | 0.8437 | 0.6499 | 0.8715 | 0.8702 |
| Tmax | 0.5241 | 0.3850 | 0.9104 | 0.9082 | 0.7726 | 0.5955 | 0.9233 | 0.9214 |
| Ra | 0.6925 | 0.5103 | 0.8436 | 0.8407 | 0.9853 | 0.7563 | 0.8153 | 0.8127 |
| Tmin, Tmax | 0.3991 | 0.2846 | 0.9481 | 0.9456 | 0.7367 | 0.5131 | 0.9516 | 0.9493 |
| Tmin, Ra | 0.5474 | 0.3982 | 0.9023 | 0.9007 | 0.8201 | 0.6345 | 0.8748 | 0.8721 |
| Tmax, Ra | 0.4485 | 0.3396 | 0.9344 | 0.9324 | 0.7581 | 0.5842 | 0.9266 | 0.9234 |
| Tmin, Tmax, Ra | 0.3687 | 0.2709 | 0.9557 | 0.9531 | 0.6643 | 0.5177 | 0.9472 | 0.9456 |
| Opt inputs, α | 0.3643 | 0.2690 | 0.9567 | 0.9548 | 0.5886 | 0.4629 | 0.9526 | 0.9507 |
| 0.4873 | 0.3581 | 0.9189 | 0.9166 | 0.7712 | 0.5893 | 0.9079 | 0.9057 | |
| Model Inputs | Training | Test | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | NSE | RMSE | MAE | R2 | NSE | |
| ANFIS | ||||||||
| Tmin | 0.7807 | 0.5907 | 0.8716 | 0.8694 | 0.9335 | 0.7200 | 0.8545 | 0.8524 |
| Tmax | 0.7081 | 0.5217 | 0.8944 | 0.8917 | 0.8843 | 0.6562 | 0.8663 | 0.8638 |
| Ra | 1.3904 | 1.0628 | 0.5920 | 0.5906 | 1.3849 | 1.0313 | 0.6239 | 0.6207 |
| Tmin, Tmax | 0.5888 | 0.4411 | 0.9269 | 0.9243 | 0.8178 | 0.6095 | 0.8911 | 0.8893 |
| Tmin, Ra | 0.7277 | 0.5562 | 0.8883 | 0.8856 | 0.8831 | 0.6875 | 0.8548 | 0.8524 |
| Tmax, Ra | 0.6508 | 0.4872 | 0.9107 | 0.9082 | 0.8210 | 0.6139 | 0.8816 | 0.8793 |
| Tmin, Tmax, Ra | 0.5479 | 0.4225 | 0.9369 | 0.9337 | 0.8178 | 0.6095 | 0.8911 | 0.8902 |
| Opt inputs, α | 0.5227 | 0.4163 | 0.9423 | 0.9221 | 0.8013 | 0.6010 | 0.8960 | 0.8936 |
| 0.7396 | 0.5623 | 0.8704 | 0.8657 | 0.9180 | 0.6911 | 0.8449 | 0.8427 | |
| ANFIS-PSO | ||||||||
| Tmin | 0.7203 | 0.5499 | 0.8905 | 0.8884 | 0.8510 | 0.6482 | 0.8576 | 0.8543 |
| Tmax | 0.6882 | 0.5097 | 0.9000 | 0.8986 | 0.8087 | 0.6412 | 0.8918 | 0.8893 |
| Ra | 1.3282 | 1.0065 | 0.6277 | 0.6253 | 1.3177 | 0.9778 | 0.6616 | 0.6594 |
| Tmin, Tmax | 0.5453 | 0.4245 | 0.9373 | 0.9352 | 0.7234 | 0.5715 | 0.9247 | 0.9225 |
| Tmin, Ra | 0.7122 | 0.5466 | 0.8930 | 0.8907 | 0.8565 | 0.6624 | 0.8756 | 0.9726 |
| Tmax, Ra | 0.6314 | 0.4759 | 0.9159 | 0.9124 | 0.7655 | 0.5968 | 0.9094 | 0.9071 |
| Tmin, Tmax, Ra | 0.5328 | 0.4207 | 0.9401 | 0.9383 | 0.7244 | 0.5533 | 0.9275 | 0.9253 |
| Opt inputs, α | 0.5146 | 0.4011 | 0.9441 | 0.9425 | 0.7135 | 0.5360 | 0.9300 | 0.9287 |
| 0.7091 | 0.5419 | 0.8811 | 0.8789 | 0.8451 | 0.6484 | 0.8723 | 0.8824 | |
| ANFIS-HHO | ||||||||
| Tmin | 0.7133 | 0.5482 | 0.8926 | 0.8901 | 0.8181 | 0.6167 | 0.8671 | 0.8643 |
| Tmax | 0.6774 | 0.5040 | 0.9010 | 0.8993 | 0.8003 | 0.6042 | 0.8993 | 0.8972 |
| Ra | 0.8873 | 0.6461 | 0.8338 | 0.8316 | 1.0387 | 0.7964 | 0.7984 | 0.7958 |
| Tmin, Tmax | 0.5365 | 0.4244 | 0.9393 | 0.9374 | 0.7202 | 0.5452 | 0.9257 | 0.9235 |
| Tmin, Ra | 0.7022 | 0.5383 | 0.8959 | 0.8932 | 0.7728 | 0.6045 | 0.8826 | 0.8804 |
| Tmax, Ra | 0.6286 | 0.4746 | 0.9166 | 0.9145 | 0.7363 | 0.5749 | 0.9188 | 0.9157 |
| Tmin, Tmax, Ra | 0.5108 | 0.3992 | 0.9467 | 0.9451 | 0.7093 | 0.5331 | 0.9333 | 0.9306 |
| Opt inputs, α | 0.5041 | 0.3990 | 0.9464 | 0.9448 | 0.6649 | 0.5244 | 0.9396 | 0.9372 |
| 0.6450 | 0.4917 | 0.9090 | 0.9070 | 0.7826 | 0.5999 | 0.8956 | 0.8931 | |
| ANFIS-WOA | ||||||||
| Tmin | 0.6565 | 0.4804 | 0.9090 | 0.9072 | 0.8028 | 0.6025 | 0.8749 | 0.8723 |
| Tmax | 0.6135 | 0.4371 | 0.9206 | 0.9183 | 0.7896 | 0.5957 | 0.9049 | 0.9027 |
| Ra | 0.8862 | 0.6455 | 0.8342 | 0.8316 | 1.0365 | 0.7954 | 0.7991 | 0.7973 |
| Tmin, Tmax | 0.4658 | 0.3378 | 0.9542 | 0.9524 | 0.7161 | 0.5378 | 0.9278 | 0.9252 |
| Tmin, Ra | 0.6135 | 0.4524 | 0.9206 | 0.9182 | 0.7533 | 0.5795 | 0.8888 | 0.8856 |
| Tmax, Ra | 0.5076 | 0.3780 | 0.9456 | 0.9427 | 0.7278 | 0.5647 | 0.9211 | 0.9202 |
| Tmin, Tmax, Ra | 0.4658 | 0.3378 | 0.9542 | 0.9523 | 0.6508 | 0.5034 | 0.9433 | 0.9413 |
| Opt inputs, α | 0.4636 | 0.3330 | 0.9546 | 0.9531 | 0.6370 | 0.5052 | 0.9422 | 0.9404 |
| 0.5841 | 0.4253 | 0.9241 | 0.9220 | 0.7642 | 0.5855 | 0.9003 | 0.8981 | |
| Model Inputs | Training | Test | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | NSE | RMSE | MAE | R2 | NSE | |
| ANFIS | ||||||||
| Tmin | 0.6863 | 0.5122 | 0.8467 | 0.8436 | 1.0422 | 0.9208 | 0.6846 | 0.6814 |
| Tmax | 0.5509 | 0.4148 | 0.9012 | 0.8994 | 0.8229 | 0.6129 | 0.8752 | 0.8723 |
| Ra | 1.0948 | 0.8537 | 0.6091 | 0.6072 | 1.2963 | 0.9326 | 0.6266 | 0.6237 |
| Tmin, Tmax | 0.5229 | 0.3871 | 0.9109 | 0.9083 | 0.8157 | 0.6326 | 0.8326 | 0.8302 |
| Tmin, Ra | 0.6536 | 0.4943 | 0.8608 | 0.8574 | 0.9752 | 0.8636 | 0.7236 | 0.7208 |
| Tmax, Ra | 0.5340 | 0.4054 | 0.9070 | 0.9046 | 0.8122 | 0.6354 | 0.8708 | 0.8682 |
| Tmin, Tmax, Ra | 0.5252 | 0.3871 | 0.9107 | 0.9081 | 0.8077 | 0.6133 | 0.8548 | 0.8517 |
| Opt inputs, α | 0.5042 | 0.3775 | 0.9171 | 0.9153 | 0.8051 | 0.5966 | 0.8842 | 0.8823 |
| ANFIS-PSO | ||||||||
| Tmin | 0.6432 | 0.4883 | 0.8651 | 0.8623 | 0.9629 | 0.6984 | 0.8099 | 0.8073 |
| Tmax | 0.5435 | 0.4107 | 0.9037 | 0.9014 | 0.8130 | 0.5933 | 0.8760 | 0.8732 |
| Ra | 1.0193 | 0.7841 | 0.6612 | 0.6592 | 1.2116 | 0.8695 | 0.6841 | 0.6814 |
| Tmin, Tmax | 0.5174 | 0.3839 | 0.9127 | 0.9103 | 0.8048 | 0.5793 | 0.8876 | 0.8852 |
| Tmin, Ra | 0.6384 | 0.4889 | 0.8671 | 0.8652 | 0.9496 | 0.8353 | 0.8165 | 0.8137 |
| Tmax, Ra | 0.5172 | 0.3938 | 0.9128 | 0.9101 | 0.8078 | 0.6172 | 0.8846 | 0.8824 |
| Tmin, Tmax, Ra | 0.5032 | 0.3806 | 0.9172 | 0.9154 | 0.7661 | 0.5931 | 0.8936 | 0.8917 |
| Opt inputs, α | 0.5004 | 0.3779 | 0.9183 | 0.9166 | 0.7561 | 0.5569 | 0.9049 | 0.9025 |
| ANFIS-HHO | ||||||||
| Tmin | 0.6377 | 0.4882 | 0.8674 | 0.8652 | 0.9155 | 0.6904 | 0.8456 | 0.8423 |
| Tmax | 0.5427 | 0.4101 | 0.9040 | 0.9027 | 0.7970 | 0.5808 | 0.8956 | 0.8934 |
| Ra | 0.6943 | 0.5118 | 0.8428 | 0.8403 | 0.9909 | 0.7659 | 0.8126 | 0.8102 |
| Tmin, Tmax | 0.5077 | 0.3787 | 0.9159 | 0.9127 | 0.7733 | 0.5683 | 0.9124 | 0.9096 |
| Tmin, Ra | 0.6318 | 0.4823 | 0.8698 | 0.8674 | 0.9181 | 0.7057 | 0.8474 | 0.8455 |
| Tmax, Ra | 0.5124 | 0.3915 | 0.9144 | 0.9126 | 0.7761 | 0.5696 | 0.9102 | 0.9081 |
| Tmin, Tmax, Ra | 0.4963 | 0.3692 | 0.9197 | 0.9173 | 0.7447 | 0.5520 | 0.9163 | 0.9145 |
| Opt inputs, α | 0.4850 | 0.3634 | 0.9233 | 0.9204 | 0.7197 | 0.5290 | 0.9257 | 0.9223 |
| ANFIS-WOA | ||||||||
| Tmin | 0.5445 | 0.3947 | 0.9033 | 0.9014 | 0.9125 | 0.6886 | 0.8474 | 0.8453 |
| Tmax | 0.5137 | 0.3791 | 0.9140 | 0.9126 | 0.7233 | 0.5627 | 0.9054 | 0.9024 |
| Ra | 0.6925 | 0.5103 | 0.8436 | 0.8415 | 0.9854 | 0.7566 | 0.8152 | 0.8126 |
| Tmin, Tmax | 0.4256 | 0.3038 | 0.9409 | 0.9382 | 0.7655 | 0.5545 | 0.9183 | 0.9157 |
| Tmin, Ra | 0.5155 | 0.3794 | 0.9133 | 0.9104 | 0.9056 | 0.6803 | 0.8518 | 0.8485 |
| Tmax, Ra | 0.4676 | 0.3478 | 0.9287 | 0.9257 | 0.7672 | 0.5526 | 0.9173 | 0.9152 |
| Tmin, Tmax, Ra | 0.4265 | 0.3141 | 0.9407 | 0.9383 | 0.7434 | 0.5505 | 0.9216 | 0.9184 |
| Opt inputs, α | 0.4157 | 0.3029 | 0.9436 | 0.9405 | 0.7085 | 0.5086 | 0.9281 | 0.9252 |
| Model Inputs | Training | Test | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | NSE | RMSE | MAE | R2 | NSE | |
| ANFIS | ||||||||
| Tmin | 0.6251 | 0.4813 | 0.8727 | 0.8702 | 0.9422 | 0.7294 | 0.8598 | 0.8573 |
| Tmax | 0.5666 | 0.4249 | 0.8954 | 0.8923 | 0.8696 | 0.6485 | 0.8893 | 0.8871 |
| Ra | 1.0969 | 0.8553 | 0.6076 | 0.6054 | 1.2981 | 0.9344 | 0.6253 | 0.6228 |
| Tmin, Tmax | 0.5031 | 0.3775 | 0.9175 | 0.9156 | 0.8303 | 0.6020 | 0.9061 | 0.9043 |
| Tmin, Ra | 0.5992 | 0.4639 | 0.8829 | 0.8801 | 0.9159 | 0.7081 | 0.8435 | 0.8407 |
| Tmax, Ra | 0.5478 | 0.4116 | 0.9022 | 0.9004 | 0.8343 | 0.6328 | 0.8928 | 0.8902 |
| Tmin, Tmax, Ra | 0.4574 | 0.3545 | 0.9318 | 0.9295 | 0.7993 | 0.6249 | 0.9231 | 0.9224 |
| Opt inputs, α | 0.4845 | 0.3649 | 0.9236 | 0.9208 | 0.8245 | 0.6295 | 0.9094 | 0.9075 |
| ANFIS-PSO | ||||||||
| Tmin | 0.5909 | 0.4588 | 0.8861 | 0.8843 | 0.8513 | 0.6550 | 0.8617 | 0.8593 |
| Tmax | 0.5560 | 0.4171 | 0.8992 | 0.8971 | 0.8379 | 0.6317 | 0.8986 | 0.8962 |
| Ra | 1.0370 | 0.7993 | 0.6493 | 0.6472 | 1.2267 | 0.8791 | 0.6744 | 0.6721 |
| Tmin, Tmax | 0.4762 | 0.3648 | 0.9261 | 0.9245 | 0.8131 | 0.6309 | 0.9104 | 0.9075 |
| Tmin, Ra | 0.5914 | 0.4592 | 0.8859 | 0.8827 | 0.8887 | 0.6897 | 0.8540 | 0.8523 |
| Tmax, Ra | 0.5301 | 0.3976 | 0.9084 | 0.9060 | 0.8163 | 0.6384 | 0.9052 | 0.9027 |
| Tmin, Tmax, Ra | 0.4545 | 0.3437 | 0.9326 | 0.9304 | 0.7676 | 0.6138 | 0.9253 | 0.9228 |
| Opt inputs, α | 0.4663 | 0.3575 | 0.9291 | 0.9275 | 0.8065 | 0.6248 | 0.9115 | 0.9095 |
| ANFIS-HHO | ||||||||
| Tmin | 0.5879 | 0.4567 | 0.8873 | 0.8852 | 0.8328 | 0.6272 | 0.8757 | 0.8724 |
| Tmax | 0.5580 | 0.4201 | 0.8985 | 0.8956 | 0.8058 | 0.6170 | 0.9045 | 0.9023 |
| Ra | 0.6944 | 0.5117 | 0.8427 | 0.8403 | 0.9909 | 0.7659 | 0.8126 | 0.8105 |
| Tmin, Tmax | 0.4617 | 0.3594 | 0.9305 | 0.9283 | 0.7903 | 0.5989 | 0.9165 | 0.9146 |
| Tmin, Ra | 0.5737 | 0.4471 | 0.8927 | 0.8904 | 0.8067 | 0.6245 | 0.8755 | 0.8721 |
| Tmax, Ra | 0.5250 | 0.3953 | 0.9101 | 0.9085 | 0.7979 | 0.6116 | 0.9153 | 0.9127 |
| Tmin, Tmax, Ra | 0.4399 | 0.3336 | 0.9369 | 0.9337 | 0.7665 | 0.6065 | 0.9272 | 0.9258 |
| Opt inputs, α | 0.4549 | 0.3483 | 0.9328 | 0.9302 | 0.7825 | 0.6058 | 0.9167 | 0.9149 |
| ANFIS-WOA | ||||||||
| Tmin | 0.5377 | 0.4062 | 0.9057 | 0.9028 | 0.8079 | 0.6223 | 0.8769 | 0.8742 |
| Tmax | 0.5048 | 0.3599 | 0.9169 | 0.9137 | 0.7963 | 0.6159 | 0.9097 | 0.9074 |
| Ra | 0.6925 | 0.5103 | 0.8436 | 0.8405 | 0.9852 | 0.7561 | 0.8153 | 0.8125 |
| Tmin, Tmax | 0.4260 | 0.3142 | 0.9408 | 0.9382 | 0.7806 | 0.5840 | 0.9225 | 0.9203 |
| Tmin, Ra | 0.5009 | 0.3771 | 0.9182 | 0.9157 | 0.7995 | 0.6216 | 0.8941 | 0.8917 |
| Tmax, Ra | 0.4516 | 0.3390 | 0.9335 | 0.9305 | 0.7923 | 0.6023 | 0.9199 | 0.9174 |
| Tmin, Tmax, Ra | 0.4186 | 0.3113 | 0.9422 | 0.9401 | 0.7442 | 0.5771 | 0.9299 | 0.9268 |
| Opt inputs, α | 0.4182 | 0.3082 | 0.9430 | 0.9416 | 0.7344 | 0.5768 | 0.9330 | 0.9283 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adnan Ikram, R.M.; Jaafari, A.; Milan, S.G.; Kisi, O.; Heddam, S.; Zounemat-Kermani, M. Hybridized Adaptive Neuro-Fuzzy Inference System with Metaheuristic Algorithms for Modeling Monthly Pan Evaporation. Water 2022, 14, 3549. https://doi.org/10.3390/w14213549
Adnan Ikram RM, Jaafari A, Milan SG, Kisi O, Heddam S, Zounemat-Kermani M. Hybridized Adaptive Neuro-Fuzzy Inference System with Metaheuristic Algorithms for Modeling Monthly Pan Evaporation. Water. 2022; 14(21):3549. https://doi.org/10.3390/w14213549
Chicago/Turabian StyleAdnan Ikram, Rana Muhammad, Abolfazl Jaafari, Sami Ghordoyee Milan, Ozgur Kisi, Salim Heddam, and Mohammad Zounemat-Kermani. 2022. "Hybridized Adaptive Neuro-Fuzzy Inference System with Metaheuristic Algorithms for Modeling Monthly Pan Evaporation" Water 14, no. 21: 3549. https://doi.org/10.3390/w14213549
APA StyleAdnan Ikram, R. M., Jaafari, A., Milan, S. G., Kisi, O., Heddam, S., & Zounemat-Kermani, M. (2022). Hybridized Adaptive Neuro-Fuzzy Inference System with Metaheuristic Algorithms for Modeling Monthly Pan Evaporation. Water, 14(21), 3549. https://doi.org/10.3390/w14213549










