Estimation of Latent Heat Flux Using a Non-Parametric Method
Abstract
:1. Introduction
2. Experiments
2.1. Grassland
2.2. Peat Bog
2.3. Forest
3. Methodology
3.1. Penman–Monteith Equation
3.2. Priestley–Taylor Equation
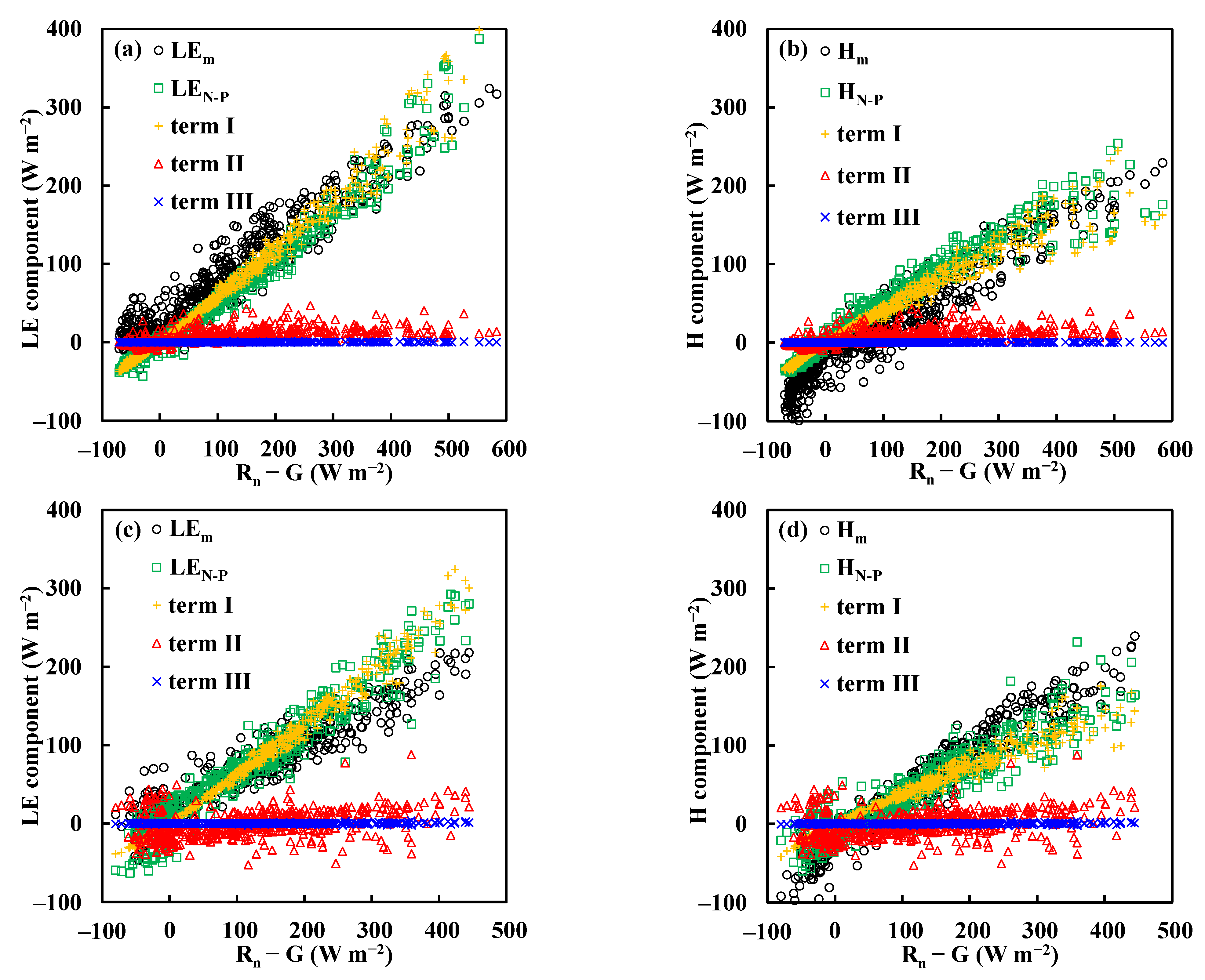
3.3. Non-Parametric Method
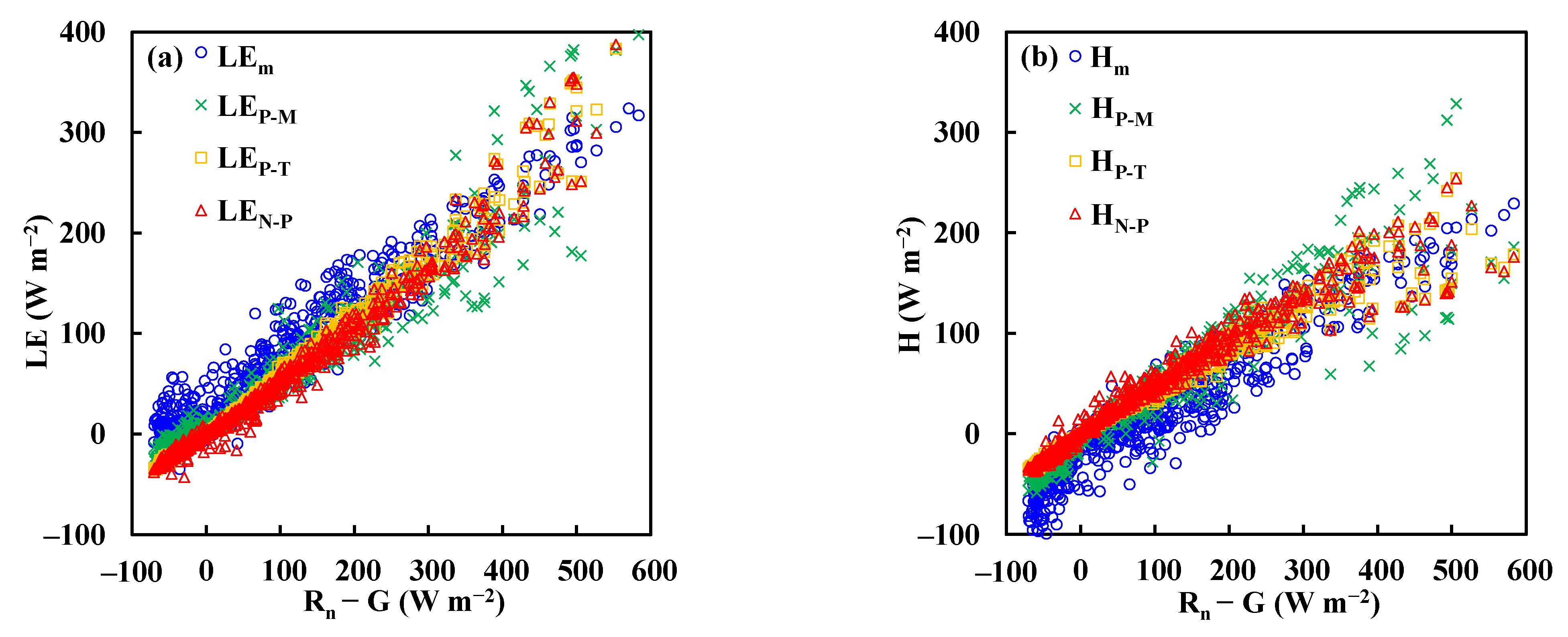
4. Results and Discussion
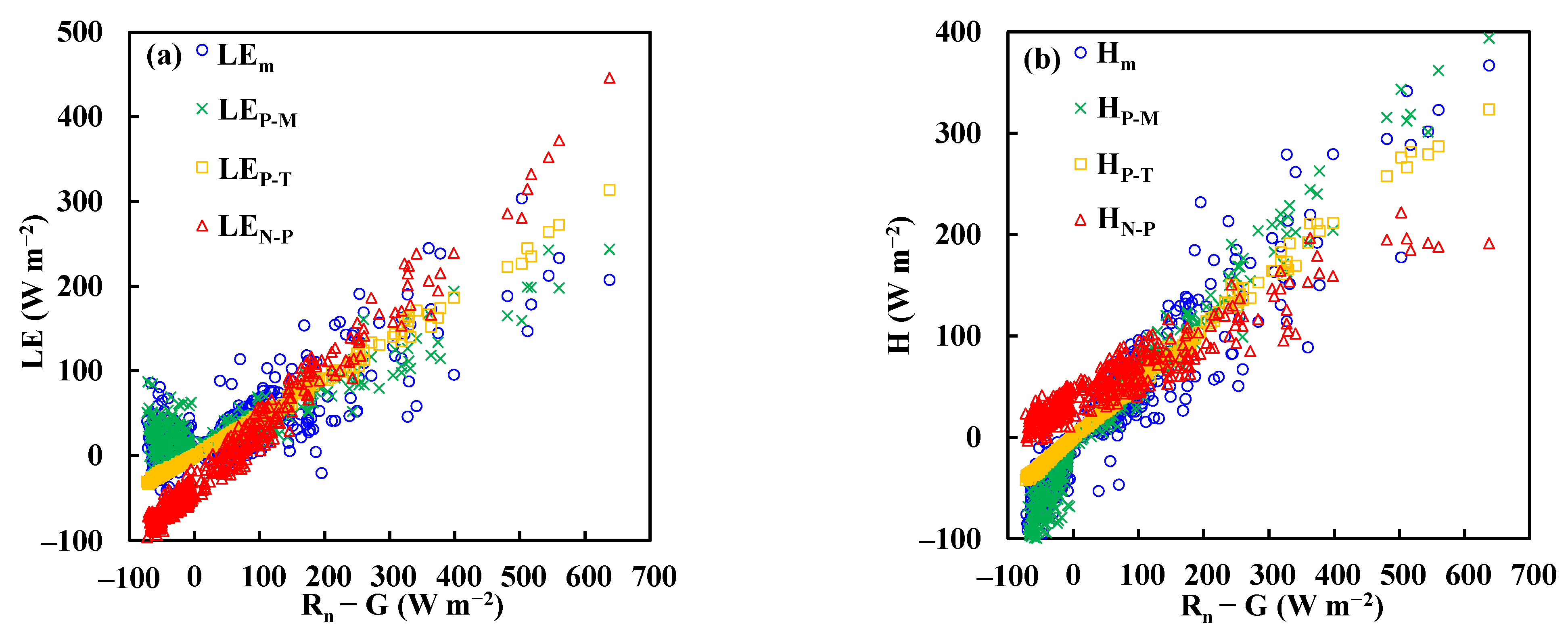
4.1. Performances of P–M, P–T, and N-P Methods
4.1.1. Grassland
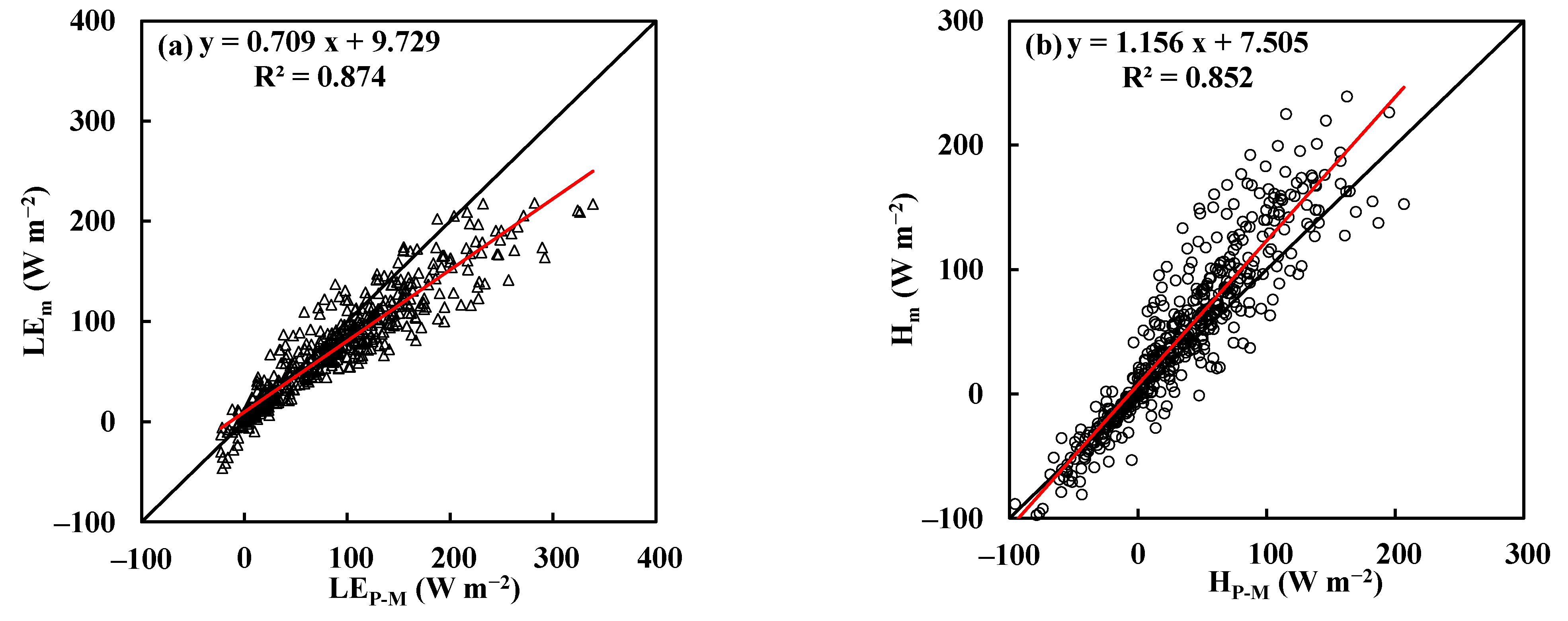
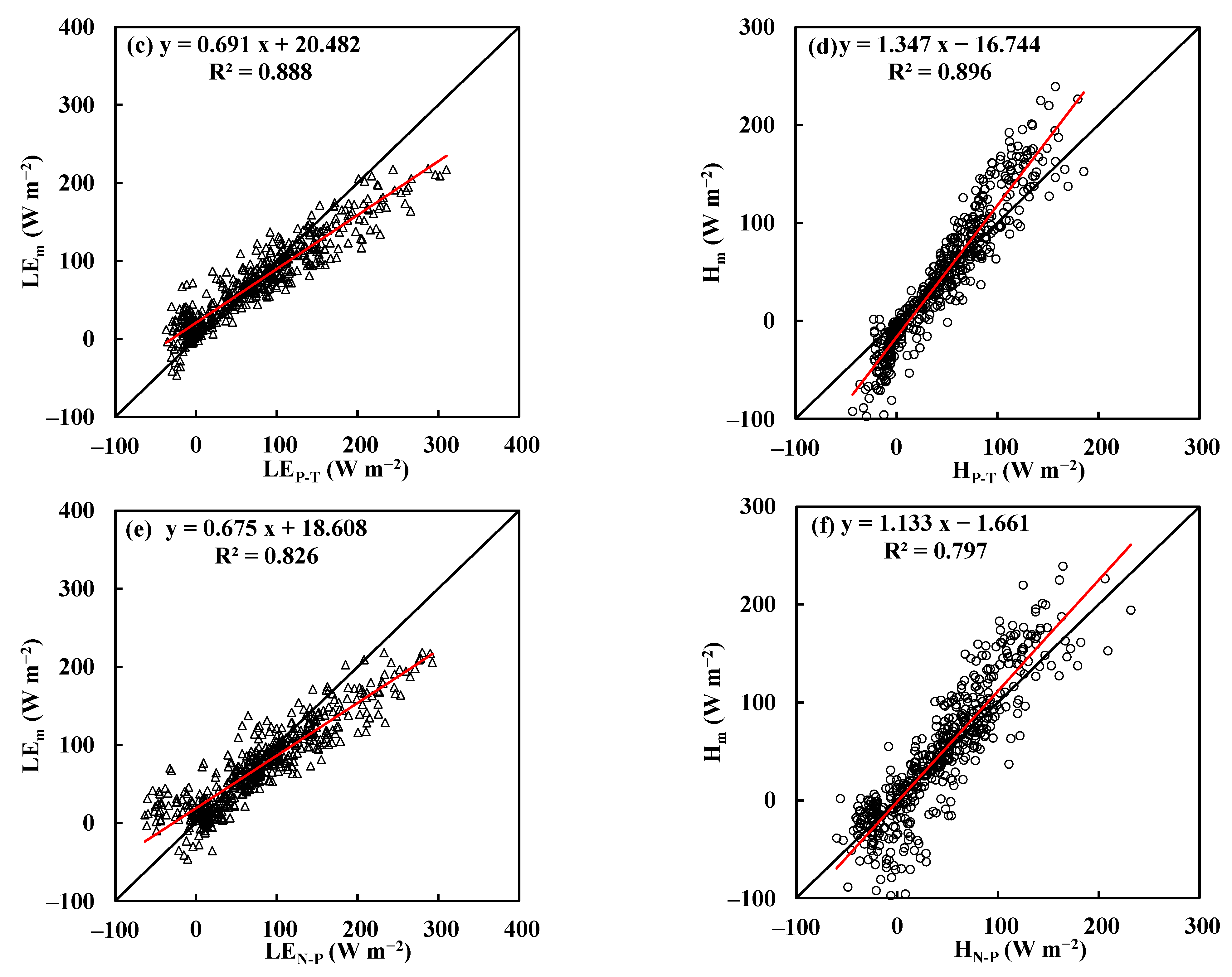
4.1.2. Peat Bog
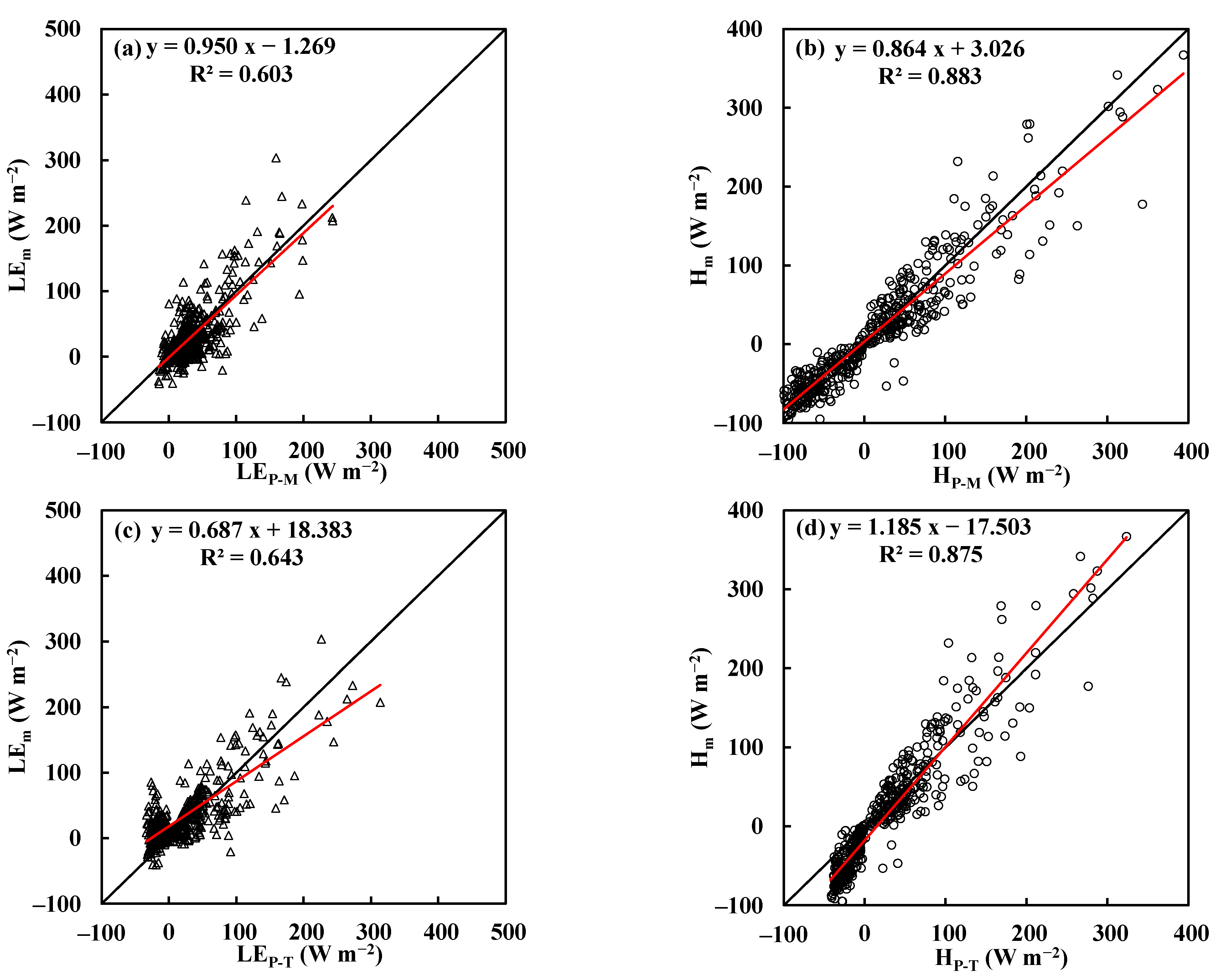
4.1.3. Forest
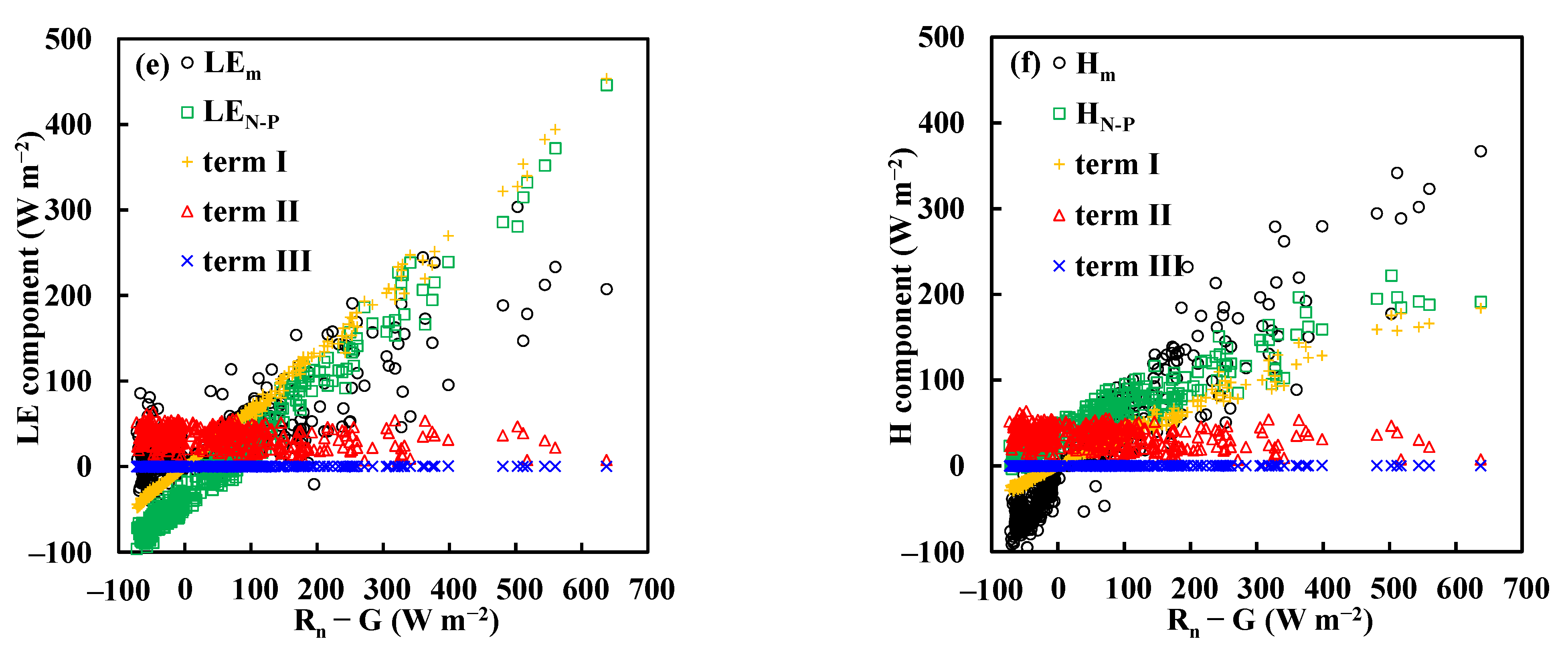
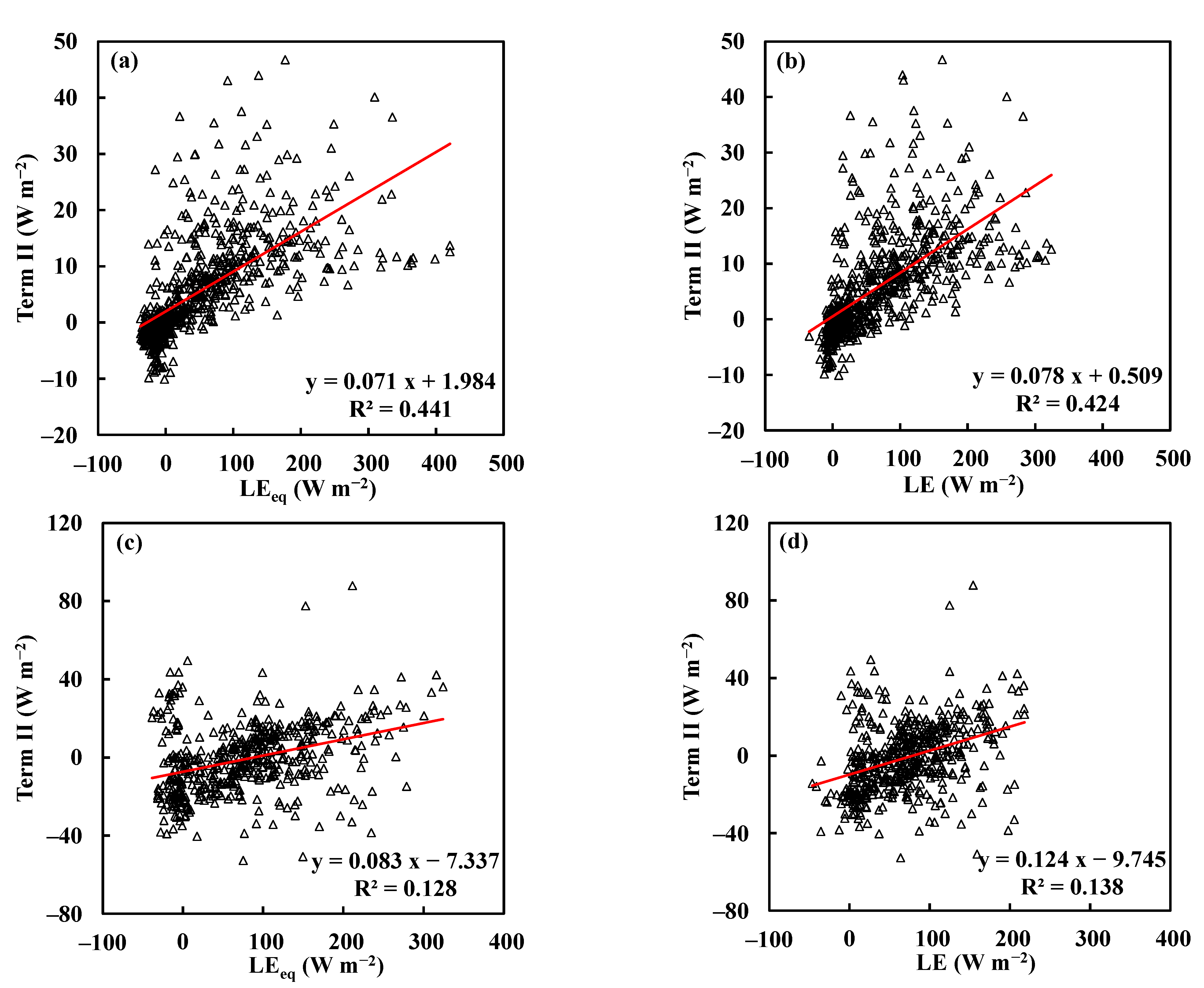
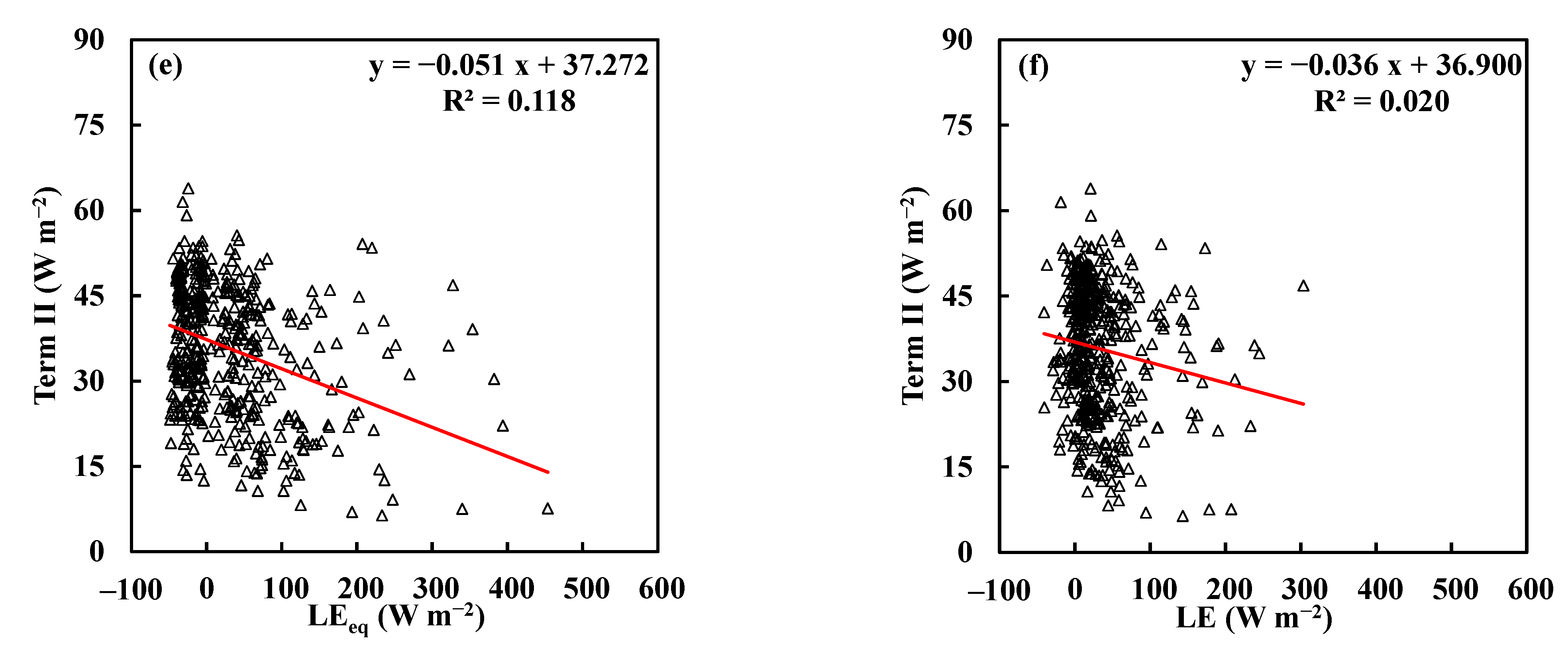
4.2. Limitation of the Non-Parametric Method
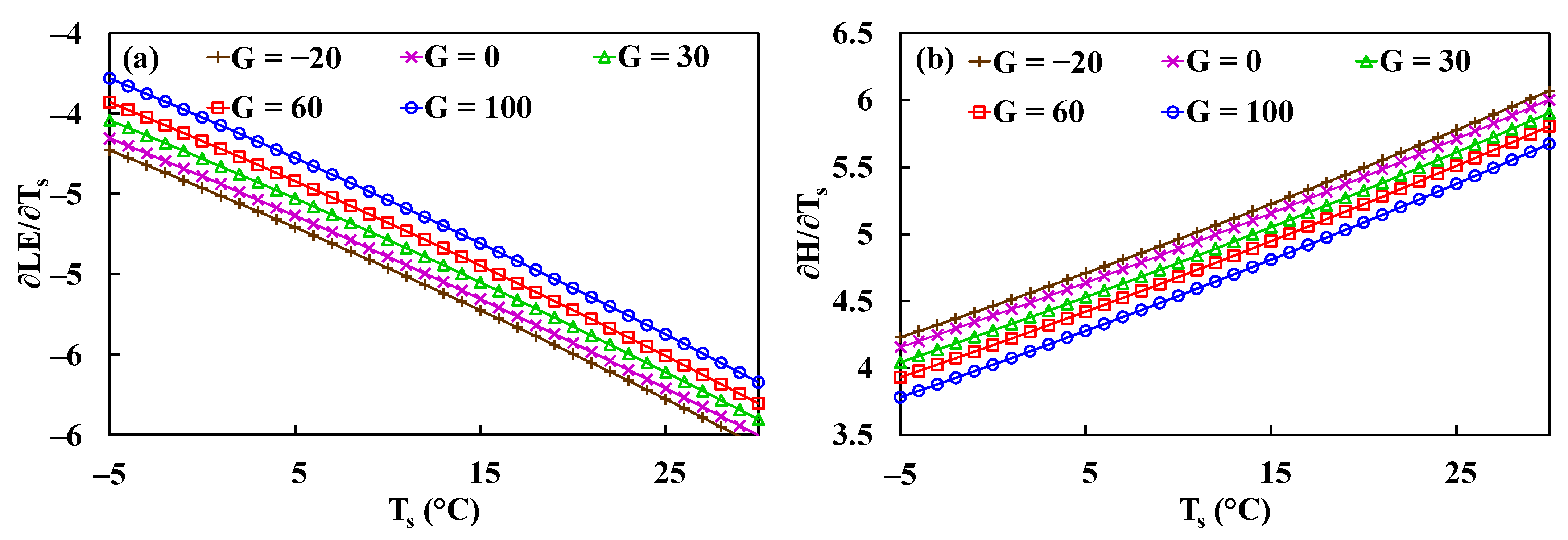
4.3. Sensitivity of the N-P Method on Surface Temperature
5. Conclusions
- (1)
- The evapotranspiration rates above the grassland and peat bog were close to the equilibrium evaporation (P–T constant ≈ 0.96). The forest’s evapotranspiration rate was 69% of the equilibrium evaporation, and about 60% of the net radiation energy was distributed to sensible heat flux.
- (2)
- Both the P–M and P–T equations performed well at estimating water vapor and sensible heat fluxes for all of the three sites. However, the canopy resistance in the P–M equation and the Priestley–Taylor constant in the P–T equation must be known a priori.
- (3)
- The water vapor flux predictions by the N-P method were in agreement with the measurements above the grassland and peat bog. However, this was not the case for the forest site.
- (4)
- Our analysis shows that with one degree of change in Ts, the predicted LE is only changed by 4 to 6 (W m−2). Hence, the LE predictions by the N-P method are not sensitive to the uncertainty of Ts measurements.
- (5)
- Field measurements from the three sites reveal that the second term of the N-P method is about ±10% (from −0.05 to 0.08) of the equilibrium evapotranspiration. For applying the N-P method to estimate LE, the actual evapotranspiration of the site should be around 0.89–1.05 times the equilibrium evapotranspiration.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Symbol | Description |
| Cp | specific heat of air (J kg−1 K−1) |
| D | vapor pressure deficit (kPa) |
| G | ground heat flux (W m−2) |
| H | sensible heat flux (W m−2) |
| k | von Karman constant (= 0.4) |
| LE | latent heat flux (W m−2) |
| Lv | latent heat of evaporation (J kg−1) |
| P | atmospheric pressure (kPa) |
| Rn | net radiation (W m−2) |
| rc | canopy resistance (s m−1) |
| rav | aerodynamic resistance (s m−1) |
| Ta | air temperature (°C) |
| Ts | surface temperature (°C) |
| U | wind speed (m s−1) |
| z | measurement height (m) |
| zo | surface roughness for momentum (m) |
| zov | surface roughness for water vapor (m) |
| α | Priestly–Taylor constant |
| γ | psychrometric constant (kPa K−1) |
| Δ | slope of the saturated vapor pressure (kPa K−1) |
| ε | land surface emissivity |
| σ | Stefan–Boltzmann constant (= 5.67 × 10−8) (W m−2 K−4) |
References
- Liu, Y.; Hiyama, T.; Yasunari, T.; Tanaka, H. A nonparametric approach to estimating terrestrial evaporation: Validation in eddy covariance sites. Agric. For. Meteorol. 2012, 157, 49–59. [Google Scholar] [CrossRef]
- Shuttleworth, W.J. Putting the “vap” into evaporation. Hydrol. Earth Syst. Sci. 2007, 11, 210–244. [Google Scholar] [CrossRef] [Green Version]
- Monteith, J.L. Evaporation and surface temperature. Q. J. R. Meteor. Soc. 1981, 107, 1–27. [Google Scholar] [CrossRef]
- Raupach, M.R. Influences of local feedbacks on land–air exchanges of energy and carbon. Glob. Change Biol. 1998, 4, 477–494. [Google Scholar] [CrossRef]
- Irmak, S.; Mutiibwa, D. On the dynamics of canopy resistance: Generalized linear estimation and relationships with primary micrometeorological variables. Water Resour. Res. 2010, 46, 8. [Google Scholar] [CrossRef] [Green Version]
- Lin, B.S.; Lei, H.; Hu, M.C.; Visessri, S.; Hsieh, C.I. Canopy resistance and estimation of evapotranspiration above a humid cypress forest. Adv. Meteorol. 2020, 2020, 4232138. [Google Scholar] [CrossRef] [Green Version]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Pereira, A.R. The Priestley–Taylor parameter and the decoupling factor for estimating reference evapotranspiration. Agric. For. Meteorol. 2004, 125, 305–313. [Google Scholar] [CrossRef]
- Bottazzi, M.; Bancheri, M.; Mobilia, M.; Bertoldi, G.; Longobardi, A.; Rigon, R. Comparing evapotranspiration estimates from the geoframe-prospero model with Penman–Monteith and Priestley-Taylor approaches under different climate conditions. Water 2021, 13, 1221. [Google Scholar] [CrossRef]
- Qiu, R.J.; Liu, C.W.; Cui, N.B.; Wu, Y.J.; Wang, Z.C.; Li, G. Evapotranspiration estimation using a modified Priestley-Taylor model in a rice-wheat rotation system. Agric. Water Manag. 2019, 224, 105755. [Google Scholar] [CrossRef]
- Magyari, E.; Keller, B. Hamiltonian description of the heat conduction. Heat Mass Transf. 1999, 34, 453–459. [Google Scholar] [CrossRef]
- Pan, X.; Liu, Y.; Fan, X. Satellite retrieval of surface evapotranspiration with nonparametric approach: Accuracy assessment over a semiarid region. Adv. Meteorol. 2016, 2016, 1584316. [Google Scholar] [CrossRef] [Green Version]
- Pan, X.; Liu, Y.; Gan, G.; Fan, X.; Yang, Y. Estimation of evapotranspiration using a nonparametric approach under all sky: Accuracy evaluation and error analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2528–2539. [Google Scholar] [CrossRef]
- Pan, X.; You, C.; Liu, Y.; Shi, C.; Han, S.; Yang, Y.; Hu, J. Evaluation of satellite-retrieved evapotranspiration based on a nonparametric approach over an arid region. Int. J. Remote Sens. 2020, 41, 7605–7623. [Google Scholar] [CrossRef]
- Wu, B.; Zhu, W.; Yan, N.; Xing, Q.; Xu, J.; Ma, Z.; Wang, L. Regional actual evapotranspiration estimation with land and meteorological variables derived from multi-source satellite data. Remote Sens. 2020, 12, 332. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Su, H.; Qi, J. A critical evaluation of the nonparametric approach to estimate terrestrial evaporation. Adv. Meteorol. 2016, 2016, 5343718. [Google Scholar] [CrossRef] [Green Version]
- Jaksic, V.; Kiely, G.; Albertson, J.; Oren, R.; Katul, G.; Leahy, P.; Byrne, K.A. Net ecosystem exchange of grassland in contrasting wet and dry years. Agric. Forest. Meteorol. 2006, 139, 323–334. [Google Scholar] [CrossRef]
- Lawton, D.; Leahy, P.; Kiely, G.; Byrne, K.A.; Calanca, P. Modeling of net ecosystem exchange and its components for a humid grassland ecosystem. J. Geophys. Res. Biogeosciences 2006, 111, G04013. [Google Scholar] [CrossRef] [Green Version]
- Byrne, K.A.; Kiely, G.; Leahy, P. CO2 fluxes in adjacent new and permanent temperate grasslands. Agric. For. Meteorol. 2005, 135, 82–92. [Google Scholar] [CrossRef]
- Peichl, M.; Leahy, P.; Kiely, G. Six-year stable annual uptake of carbon dioxide in intensively managed humid temperate grassland. Ecosystems 2011, 14, 112–126. [Google Scholar] [CrossRef]
- Lewis, C.; Albertson, J.; Xu, X.; Kiely, G. Spatial variability of hydraulic conductivity and bulk density along a blanket peatland hillslope. Hydrol. Process. 2012, 26, 1527–1537. [Google Scholar] [CrossRef]
- Laine, A.; Sottocornola, M.; Kiely, G.; Byrne, K.A.; Wilson, D.; Tuittila, E.S. Estimating net ecosystem exchange in a patterned ecosystem: Example from blanket bog. Agric. For. Meteorol. 2006, 138, 231–243. [Google Scholar] [CrossRef]
- Sottocornola, M.; Laine, A.; Kiely, G.; Byrne, K.A.; Tuittila, E.S. Vegetation and environmental variation in an Atlantic blanket bog in South-western Ireland. Plant Ecol. 2009, 203, 69–81. [Google Scholar] [CrossRef]
- Sottocornola, M.; Kiely, G. Hydro-meteorological controls on the CO2 exchange variation in an Irish blanket bog. Agric. For. Meteorol. 2010, 150, 287–297. [Google Scholar] [CrossRef]
- McVeigh, P.; Sottocornola, M.; Foley, N.; Leahy, P.; Kiely, G. Meteorological and functional response partitioning to explain interannual variability of CO2 exchange at an Irish Atlantic blanket bog. Agric. For. Meteorol. 2014, 194, 8–19. [Google Scholar] [CrossRef]
- Gong, X.; Qiu, R.; Ge, J.; Bo, G.; Ping, Y.; Xin, Q.; Wang, S. Evapotranspiration partitioning of greenhouse grown tomato using a modified Priestley–Taylor model. Agric. Water Manag. 2021, 247, 106709. [Google Scholar] [CrossRef]
- Eichinger, W.E.; Parlange, M.B.; Stricker, H. On the concept of equilibrium evaporation and the value of the Priestley-Taylor coefficient. Water Resour. Res. 1996, 32, 161–164. [Google Scholar] [CrossRef] [Green Version]
- Shuttleworth, W.J.; Calder, I.R. Has the Priestley-Taylor Equation Any Relevance to Forest Evaporation? J. Appl. Meteorol. 1979, 18, 639–646. [Google Scholar] [CrossRef]
- Wang, J.; Bras, R.L.; Lerdau, M.; Salvucci, G.D. A maximum hypothesis of transpiration. J. Geophys. Res. Biogeosciences 2007, 112, W03010. [Google Scholar] [CrossRef]
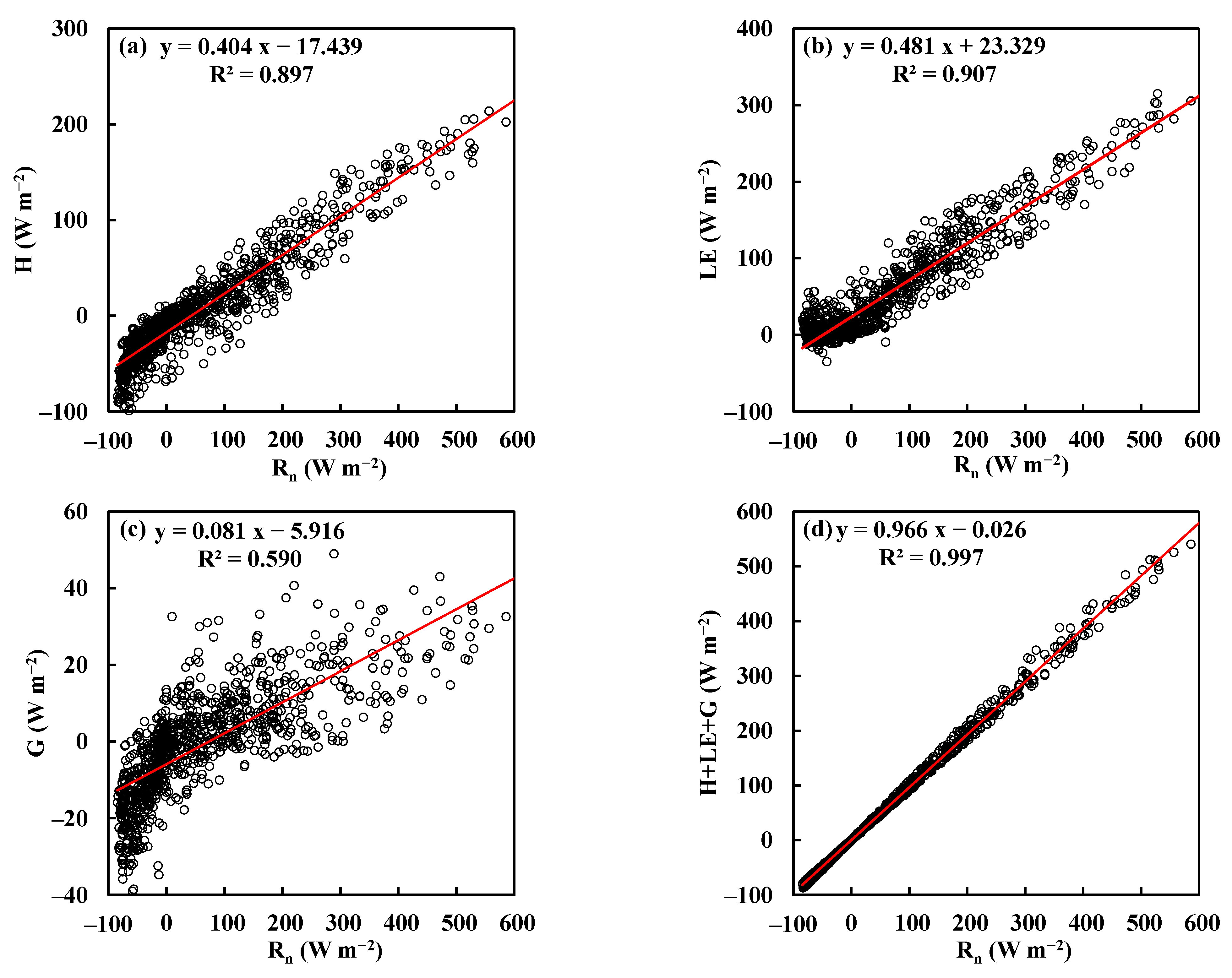
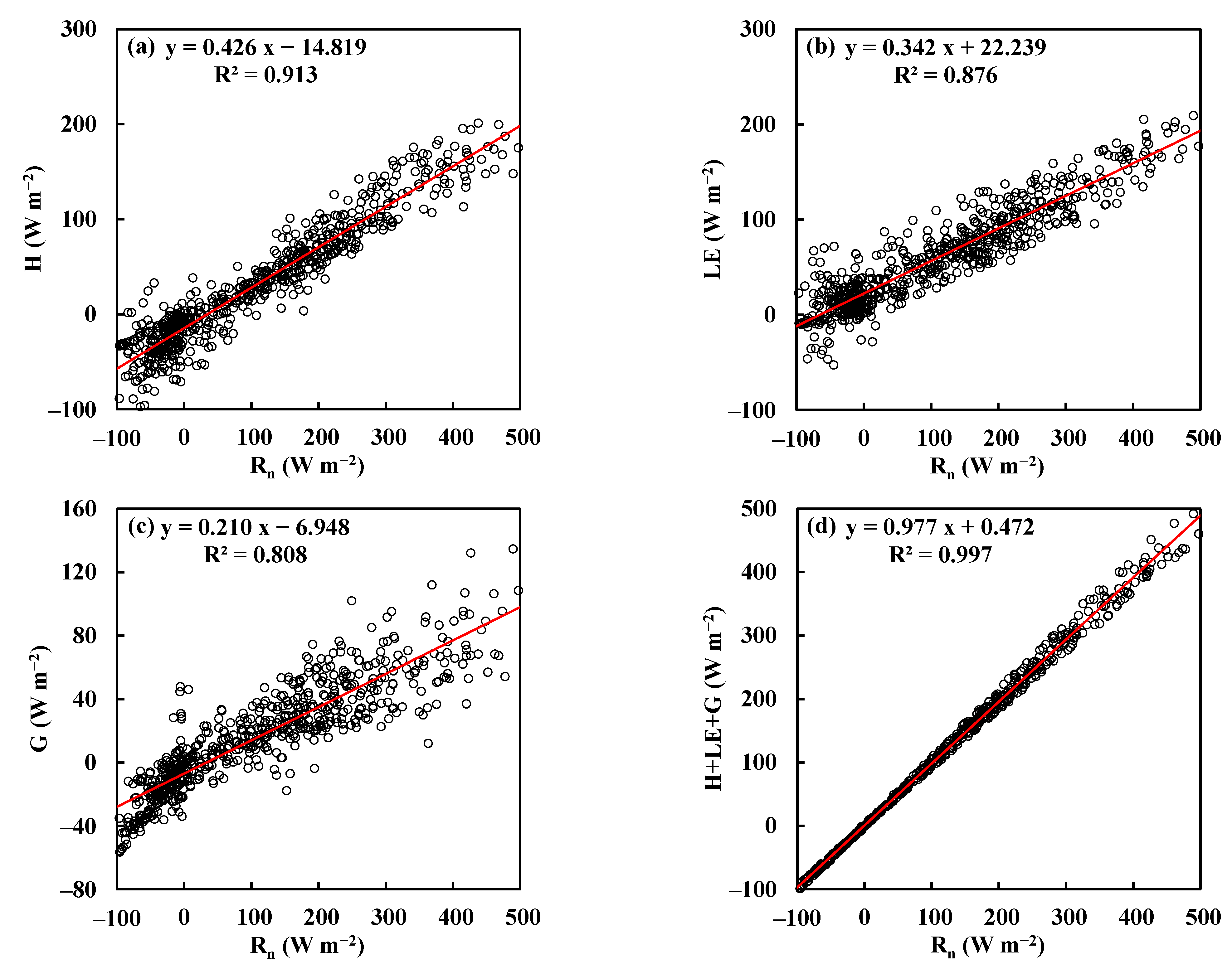
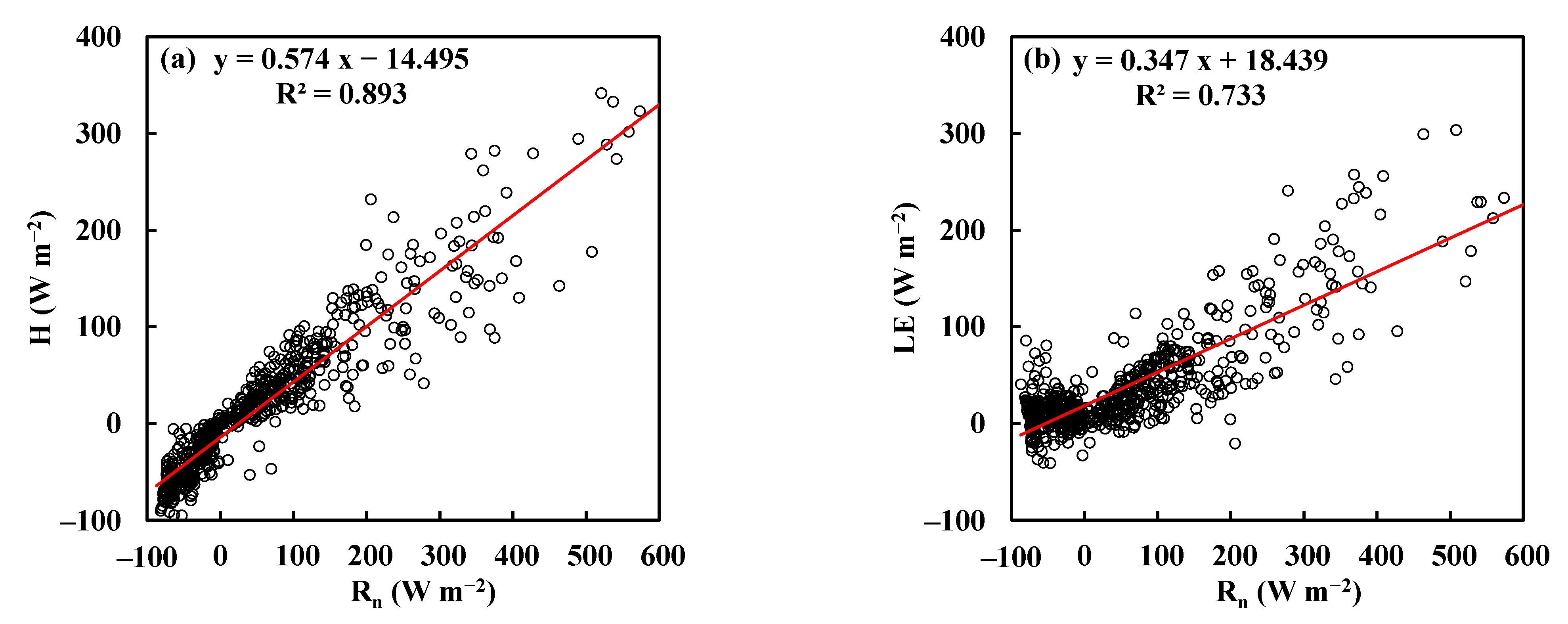
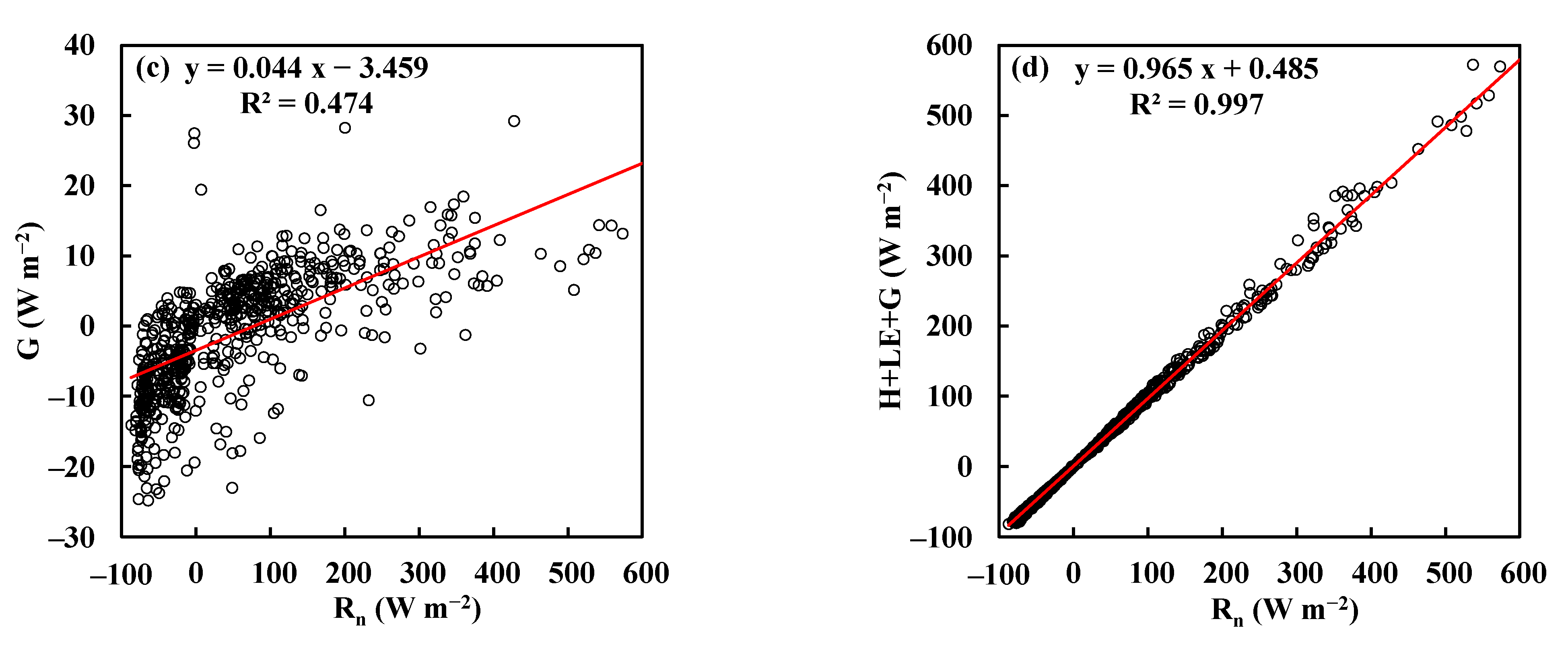



| Site | Grassland | Peat Bog | Forest |
|---|---|---|---|
| Data period | 1 January 2013–31 December 2013 | 1 January 2013–31 December 2013 | 22 May 2009–31 July 2010 |
| Altitude (m) | 195 | 150 | 1252 |
| Location | 59°59′ N, 8°45′ W | 51°55′ N, 9°55′ W | 23°39′51.09″ N, 120°47′44.57″ E |
| Climate type | Temperate | Temperate | Sub-tropical |
| Annual rainfall (mm) | 1161 | 1834 | 2635 |
| Mean temperature (°C) | 9 | 10.1 | 16.6 |
| Mean humidity (%) | 92 | 82 | 89 |
| Canopy height (m) | 0.3 | 0.1 | 26 |
| Surface emissivity | 0.95 | 0.99 | 0.98 |
| Canopy resistance (s m−1) | 60 | 63 | 134 |
| Priestley–Taylor constant | 0.962 | 0.956 | 0.692 |
| Measurement height (m) | |||
| Eddy covariance system | 5 | 3 | 28 |
| Air temperature & humidity sensor | 5 | 3 | 28 |
| Net radiometer | 4 | 2 | 27.5 |
| Soil heat flux plate | −0.1 | −0.1 | −0.05 |
| Soil thermometer | −0.015, −0.025, −0.075 | −0.1 | −0.05, −0.1 |
| Soil moisture meter | −0.05 | −0.1 | −0.05, −0.1 |
| Grassland | Peat Bog | Forest | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Flux | a | b | R2 | a | b | R2 | a | b | R2 |
| H | 0.404 | −17.439 | 0.897 | 0.426 | −14.819 | 0.913 | 0.574 | −14.495 | 0.893 |
| LE | 0.481 | 23.329 | 0.907 | 0.342 | 22.239 | 0.876 | 0.347 | 18.439 | 0.733 |
| G | 0.081 | −5.916 | 0.590 | 0.210 | −6.948 | 0.808 | 0.044 | −3.459 | 0.474 |
| H+LE+G | 0.966 | −0.026 | 0.997 | 0.977 | 0.472 | 0.997 | 0.965 | 0.485 | 0.997 |
| Latent Heat Flux | Sensible Heat Flux | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Site | Model | a | b | R2 | RMSE | a | b | R2 | RMSE |
| Grassland | P–M | 0.930 | 18.221 | 0.895 | 28.338 | 0.874 | −13.689 | 0.869 | 29.310 |
| P–T | 0.884 | 21.336 | 0.922 | 27.362 | 1.039 | −19.791 | 0.894 | 27.251 | |
| N-P | 0.906 | 23.484 | 0.913 | 29.866 | 0.974 | −21.189 | 0.882 | 30.447 | |
| Peat Bog | P–M | 0.709 | 9.729 | 0.874 | 32.507 | 1.156 | 7.505 | 0.852 | 29.781 |
| P–T | 0.691 | 20.482 | 0.888 | 29.047 | 1.347 | −16.744 | 0.896 | 26.967 | |
| N-P | 0.675 | 18.608 | 0.826 | 33.161 | 1.133 | −1.661 | 0.797 | 31.063 | |
| Forest | P–M | 0.950 | −1.269 | 0.603 | 28.799 | 0.864 | 3.026 | 0.883 | 29.575 |
| P–T | 0.687 | 18.383 | 0.643 | 33.945 | 1.185 | −17.503 | 0.875 | 33.004 | |
| N-P | 0.433 | 35.156 | 0.601 | 66.553 | 1.823 | −81.167 | 0.734 | 64.657 | |
| Site | Grassland | Peat Bog | Forest |
|---|---|---|---|
| α from Equation (7) | 0.929 | 0.917 | 1.051 |
| α from Equation (8) | 0.928 | 0.890 | 1.037 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsieh, C.-I.; Chiu, C.-J.; Huang, I.-H.; Kiely, G. Estimation of Latent Heat Flux Using a Non-Parametric Method. Water 2022, 14, 3474. https://doi.org/10.3390/w14213474
Hsieh C-I, Chiu C-J, Huang I-H, Kiely G. Estimation of Latent Heat Flux Using a Non-Parametric Method. Water. 2022; 14(21):3474. https://doi.org/10.3390/w14213474
Chicago/Turabian StyleHsieh, Cheng-I, Cheng-Jiun Chiu, I-Hang Huang, and Gerard Kiely. 2022. "Estimation of Latent Heat Flux Using a Non-Parametric Method" Water 14, no. 21: 3474. https://doi.org/10.3390/w14213474






